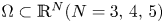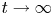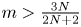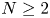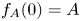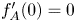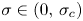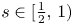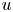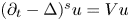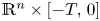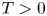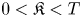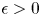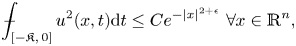263 results in 35Kxx
The evolution problem for the 1D nonlocal Fisher-KPP equation with a top hat kernel. Part 1. The Cauchy problem on the real line
- Part of
-
- Journal:
- European Journal of Applied Mathematics , First View
- Published online by Cambridge University Press:
- 25 October 2024, pp. 1-36
-
- Article
-
- You have access
- Open access
- HTML
- Export citation
WELL-POSEDNESS RESULTS FOR GENERAL REACTION–DIFFUSION TRANSPORT OF OXYGEN IN ENCAPSULATED CELLS
- Part of
-
- Journal:
- Bulletin of the Australian Mathematical Society , First View
- Published online by Cambridge University Press:
- 18 October 2024, pp. 1-10
-
- Article
-
- You have access
- HTML
- Export citation
Travelling wavefronts for the Belousov–Zhabotinsky system with non-local delayed interaction
- Part of
-
- Journal:
- European Journal of Applied Mathematics , First View
- Published online by Cambridge University Press:
- 10 October 2024, pp. 1-37
-
- Article
-
- You have access
- Open access
- HTML
- Export citation
Boundary crossing problems and functional transformations for Ornstein–Uhlenbeck processes
- Part of
-
- Journal:
- Journal of Applied Probability , First View
- Published online by Cambridge University Press:
- 07 October 2024, pp. 1-27
-
- Article
-
- You have access
- HTML
- Export citation
Stabilization in a chemotaxis system modelling T-cell dynamics with simultaneous production and consumption of signals
- Part of
-
- Journal:
- European Journal of Applied Mathematics , First View
- Published online by Cambridge University Press:
- 18 September 2024, pp. 1-14
-
- Article
-
- You have access
- Open access
- HTML
- Export citation
The roles of nonlinear diffusion, haptotaxis and ECM remodelling in determining the global solvability of a cancer invasion model
- Part of
-
- Journal:
- Proceedings of the Royal Society of Edinburgh. Section A: Mathematics , First View
- Published online by Cambridge University Press:
- 13 September 2024, pp. 1-32
-
- Article
-
- You have access
- HTML
- Export citation
Asymptotic profiles of a nonlocal dispersal SIS epidemic model with saturated incidence
- Part of
-
- Journal:
- Proceedings of the Royal Society of Edinburgh. Section A: Mathematics , First View
- Published online by Cambridge University Press:
- 14 May 2024, pp. 1-33
-
- Article
-
- You have access
- HTML
- Export citation
Unified framework for the separation property in binary phase-segregation processes with singular entropy densities
- Part of
-
- Journal:
- European Journal of Applied Mathematics , First View
- Published online by Cambridge University Press:
- 09 May 2024, pp. 1-28
-
- Article
-
- You have access
- Open access
- HTML
- Export citation
Threshold dynamics scenario of a plants-pollinators cooperative system with impulsive effect on a periodically evolving domain
- Part of
-
- Journal:
- European Journal of Applied Mathematics , First View
- Published online by Cambridge University Press:
- 02 May 2024, pp. 1-26
-
- Article
-
- You have access
- Open access
- HTML
- Export citation
Global boundedness and large time behaviour in a higher-dimensional quasilinear chemotaxis system with consumption of chemoattractant
- Part of
-
- Journal:
- Proceedings of the Royal Society of Edinburgh. Section A: Mathematics , First View
- Published online by Cambridge University Press:
- 30 April 2024, pp. 1-26
-
- Article
-
- You have access
- HTML
- Export citation
Eternal solutions to a porous medium equation with strong non-homogeneous absorption. Part I: radially non-increasing profiles
- Part of
-
- Journal:
- Proceedings of the Royal Society of Edinburgh. Section A: Mathematics , First View
- Published online by Cambridge University Press:
- 14 March 2024, pp. 1-22
-
- Article
-
- You have access
- HTML
- Export citation
Decay at infinity for solutions to some fractional parabolic equations
- Part of
-
- Journal:
- Proceedings of the Royal Society of Edinburgh. Section A: Mathematics , First View
- Published online by Cambridge University Press:
- 14 March 2024, pp. 1-37
-
- Article
-
- You have access
- HTML
- Export citation
Unbounded Sturm attractors for quasilinear parabolic equations
- Part of
-
- Journal:
- Proceedings of the Edinburgh Mathematical Society / Volume 67 / Issue 2 / May 2024
- Published online by Cambridge University Press:
- 08 March 2024, pp. 542-565
-
- Article
-
- You have access
- HTML
- Export citation
Bifurcations and pattern formation in a host–parasitoid model with nonlocal effect
- Part of
-
- Journal:
- Proceedings of the Royal Society of Edinburgh. Section A: Mathematics , First View
- Published online by Cambridge University Press:
- 04 March 2024, pp. 1-40
-
- Article
-
- You have access
- HTML
- Export citation
On determining and breaking the gauge class in inverse problems for reaction-diffusion equations
- Part of
-
- Journal:
- Forum of Mathematics, Sigma / Volume 12 / 2024
- Published online by Cambridge University Press:
- 26 February 2024, e25
-
- Article
-
- You have access
- Open access
- HTML
- Export citation
Global dynamics and spatiotemporal heterogeneity of a preytaxis model with prey-induced acceleration
- Part of
-
- Journal:
- European Journal of Applied Mathematics / Volume 35 / Issue 5 / October 2024
- Published online by Cambridge University Press:
- 26 January 2024, pp. 601-633
-
- Article
-
- You have access
- Open access
- HTML
- Export citation
On degenerate reaction-diffusion epidemic models with mass action or standard incidence mechanism
- Part of
-
- Journal:
- European Journal of Applied Mathematics / Volume 35 / Issue 5 / October 2024
- Published online by Cambridge University Press:
- 22 January 2024, pp. 634-661
-
- Article
-
- You have access
- Open access
- HTML
- Export citation
The fully parabolic multi-species chemotaxis system in
 $\mathbb{R}^{2}$
$\mathbb{R}^{2}$
- Part of
-
- Journal:
- European Journal of Applied Mathematics / Volume 35 / Issue 5 / October 2024
- Published online by Cambridge University Press:
- 19 January 2024, pp. 675-706
-
- Article
-
- You have access
- Open access
- HTML
- Export citation
Adhesion and volume filling in one-dimensional population dynamics under Dirichlet boundary condition
- Part of
-
- Journal:
- Proceedings of the Royal Society of Edinburgh. Section A: Mathematics , First View
- Published online by Cambridge University Press:
- 08 January 2024, pp. 1-49
-
- Article
-
- You have access
- HTML
- Export citation
Solvability of Hessian quotient equations in exterior domains
- Part of
-
- Journal:
- Canadian Journal of Mathematics , First View
- Published online by Cambridge University Press:
- 14 December 2023, pp. 1-31
-
- Article
-
- You have access
- HTML
- Export citation