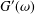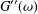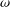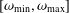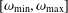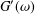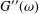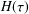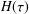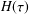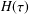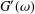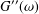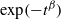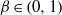25 results in 65Rxx
A MESHLESS LOCAL GALERKIN INTEGRAL EQUATION METHOD FOR SOLVING A TYPE OF DARBOUX PROBLEMS BASED ON RADIAL BASIS FUNCTIONS
- Part of
-
- Journal:
- The ANZIAM Journal / Volume 63 / Issue 4 / October 2021
- Published online by Cambridge University Press:
- 09 November 2021, pp. 469-492
-
- Article
- Export citation
MODELLING HUMAN CARRYING CAPACITY AS A FUNCTION OF FOOD AVAILABILITY
- Part of
-
- Journal:
- The ANZIAM Journal / Volume 62 / Issue 3 / July 2020
- Published online by Cambridge University Press:
- 18 December 2020, pp. 318-333
-
- Article
- Export citation
Semi-analytical solution of a McKean–Vlasov equation with feedback through hitting a boundary
- Part of
-
- Journal:
- European Journal of Applied Mathematics / Volume 32 / Issue 6 / December 2021
- Published online by Cambridge University Press:
- 16 December 2019, pp. 1035-1068
-
- Article
- Export citation
Non-convex Optimization via Strongly Convex Majorization-minimization
- Part of
-
- Journal:
- Canadian Mathematical Bulletin / Volume 63 / Issue 4 / December 2020
- Published online by Cambridge University Press:
- 10 December 2019, pp. 726-737
- Print publication:
- December 2020
-
- Article
- Export citation
Estimation of a Regularisation Parameter for a Robin Inverse Problem
- Part of
-
- Journal:
- East Asian Journal on Applied Mathematics / Volume 7 / Issue 2 / May 2017
- Published online by Cambridge University Press:
- 02 May 2017, pp. 325-342
- Print publication:
- May 2017
-
- Article
- Export citation
BREAKING THE COHERENCE BARRIER: A NEW THEORY FOR COMPRESSED SENSING
- Part of
-
- Journal:
- Forum of Mathematics, Sigma / Volume 5 / 2017
- Published online by Cambridge University Press:
- 15 February 2017, e4
-
- Article
-
- You have access
- Open access
- Export citation
A High-Accuracy Mechanical Quadrature Method for Solving the Axisymmetric Poisson's Equation
- Part of
-
- Journal:
- Advances in Applied Mathematics and Mechanics / Volume 9 / Issue 2 / April 2017
- Published online by Cambridge University Press:
- 09 January 2017, pp. 393-406
- Print publication:
- April 2017
-
- Article
- Export citation
Artificial Boundary Conditions for Nonlocal Heat Equations on Unbounded Domain
- Part of
-
- Journal:
- Communications in Computational Physics / Volume 21 / Issue 1 / January 2017
- Published online by Cambridge University Press:
- 05 December 2016, pp. 16-39
- Print publication:
- January 2017
-
- Article
- Export citation
A Discrete-Ordinate Discontinuous-Streamline Diffusion Method for the Radiative Transfer Equation
- Part of
-
- Journal:
- Communications in Computational Physics / Volume 20 / Issue 5 / November 2016
- Published online by Cambridge University Press:
- 02 November 2016, pp. 1443-1465
- Print publication:
- November 2016
-
- Article
- Export citation
Numerical Solution of Euler-Lagrange Equation with Caputo Derivatives
- Part of
-
- Journal:
- Advances in Applied Mathematics and Mechanics / Volume 9 / Issue 1 / February 2017
- Published online by Cambridge University Press:
- 11 October 2016, pp. 173-185
- Print publication:
- February 2017
-
- Article
- Export citation
Moving Finite Element Methods for a System of Semi-Linear Fractional Diffusion Equations
- Part of
-
- Journal:
- Advances in Applied Mathematics and Mechanics / Volume 8 / Issue 6 / December 2016
- Published online by Cambridge University Press:
- 19 September 2016, pp. 911-931
- Print publication:
- December 2016
-
- Article
- Export citation
A Simple Method for Computing Singular or Nearly Singular Integrals on Closed Surfaces
- Part of
-
- Journal:
- Communications in Computational Physics / Volume 20 / Issue 3 / September 2016
- Published online by Cambridge University Press:
- 31 August 2016, pp. 733-753
- Print publication:
- September 2016
-
- Article
- Export citation
Forward Scattering and Volterra Renormalization for Acoustic Wavefield Propagation in Vertically Varying Media
- Part of
-
- Journal:
- Communications in Computational Physics / Volume 20 / Issue 2 / August 2016
- Published online by Cambridge University Press:
- 21 July 2016, pp. 353-373
- Print publication:
- August 2016
-
- Article
- Export citation
SIMPLE JOINT INVERSION LOCALIZED FORMULAE FOR RELAXATION SPECTRUM RECOVERY
- Part of
-
- Journal:
- The ANZIAM Journal / Volume 58 / Issue 1 / July 2016
- Published online by Cambridge University Press:
- 05 July 2016, pp. 1-9
-
- Article
-
- You have access
- Export citation
Spectral-Collocation Method for Volterra Delay Integro-Differential Equations with Weakly Singular Kernels
- Part of
-
- Journal:
- Advances in Applied Mathematics and Mechanics / Volume 8 / Issue 4 / August 2016
- Published online by Cambridge University Press:
- 27 May 2016, pp. 648-669
- Print publication:
- August 2016
-
- Article
- Export citation
A Numerical Scheme for Generalized Peierls-Nabarro Model of Dislocations Based on the Fast Multipole Method and Iterative Grid Redistribution
- Part of
-
- Journal:
- Communications in Computational Physics / Volume 18 / Issue 5 / November 2015
- Published online by Cambridge University Press:
- 23 November 2015, pp. 1282-1312
- Print publication:
- November 2015
-
- Article
- Export citation
Numerical Path Integral Approach to Quantum Dynamics and Stationary Quantum States
- Part of
-
- Journal:
- Communications in Computational Physics / Volume 18 / Issue 1 / July 2015
- Published online by Cambridge University Press:
- 03 July 2015, pp. 91-103
- Print publication:
- July 2015
-
- Article
- Export citation
Joint Densities of First Hitting Times of a Diffusion Process Through Two Time-Dependent Boundaries
- Part of
-
- Journal:
- Advances in Applied Probability / Volume 46 / Issue 1 / March 2014
- Published online by Cambridge University Press:
- 22 February 2016, pp. 186-202
- Print publication:
- March 2014
-
- Article
-
- You have access
- Export citation
Wicksell's Problem in Local Stereology
- Part of
-
- Journal:
- Advances in Applied Probability / Volume 45 / Issue 4 / December 2013
- Published online by Cambridge University Press:
- 04 January 2016, pp. 925-944
- Print publication:
- December 2013
-
- Article
-
- You have access
- Export citation
APPROXIMATING THE KOHLRAUSCH FUNCTION BY SUMS OF EXPONENTIALS
- Part of
-
- Journal:
- The ANZIAM Journal / Volume 54 / Issue 4 / April 2013
- Published online by Cambridge University Press:
- 04 September 2013, pp. 306-323
-
- Article
-
- You have access
- Export citation



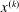
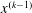
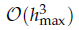 and low computing complexities. Moreover, the multivariate asymptotic error expansion of MQM accompanied with
and low computing complexities. Moreover, the multivariate asymptotic error expansion of MQM accompanied with 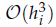 for all mesh widths
for all mesh widths 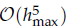 by the splitting extrapolation algorithm (SEA). Meanwhile, a posteriori asymptotic error estimate is derived, which can be used to construct self-adaptive algorithms. The numerical examples support our theoretical analysis.
by the splitting extrapolation algorithm (SEA). Meanwhile, a posteriori asymptotic error estimate is derived, which can be used to construct self-adaptive algorithms. The numerical examples support our theoretical analysis.