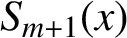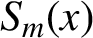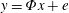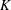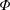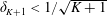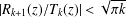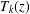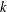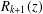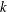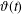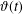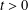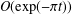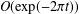73 results in 65Dxx
MONTE CARLO VARIANCE REDUCTION METHODS WITH APPLICATIONS IN STRUCTURAL RELIABILITY ANALYSIS
- Part of
-
- Journal:
- Bulletin of the Australian Mathematical Society / Volume 108 / Issue 3 / December 2023
- Published online by Cambridge University Press:
- 31 August 2023, pp. 518-521
- Print publication:
- December 2023
-
- Article
-
- You have access
- HTML
- Export citation
RATIONAL AND GENERALISED RATIONAL CHEBYSHEV APPROXIMATION PROBLEMS AND THEIR APPLICATIONS
- Part of
-
- Journal:
- Bulletin of the Australian Mathematical Society / Volume 107 / Issue 2 / April 2023
- Published online by Cambridge University Press:
- 13 January 2023, pp. 349-350
- Print publication:
- April 2023
-
- Article
-
- You have access
- HTML
- Export citation
Reconstruction problems of convex bodies from surface area measures and lightness functions
- Part of
-
- Journal:
- Canadian Journal of Mathematics / Volume 75 / Issue 5 / October 2023
- Published online by Cambridge University Press:
- 03 October 2022, pp. 1685-1710
- Print publication:
- October 2023
-
- Article
- Export citation
Computing harmonic maps between Riemannian manifolds
- Part of
-
- Journal:
- Canadian Journal of Mathematics / Volume 75 / Issue 2 / April 2023
- Published online by Cambridge University Press:
- 18 February 2022, pp. 531-580
- Print publication:
- April 2023
-
- Article
- Export citation
CONFIDENCE INTERVALS IN GENERAL REGRESSION MODELS THAT UTILISE UNCERTAIN PRIOR INFORMATION
- Part of
-
- Journal:
- Bulletin of the Australian Mathematical Society / Volume 105 / Issue 3 / June 2022
- Published online by Cambridge University Press:
- 08 February 2022, pp. 516-517
- Print publication:
- June 2022
-
- Article
-
- You have access
- HTML
- Export citation
ALGORITHM TO CONSTRUCT INTEGRO SPLINES
- Part of
-
- Journal:
- The ANZIAM Journal / Volume 63 / Issue 3 / July 2021
- Published online by Cambridge University Press:
- 13 September 2021, pp. 359-375
-
- Article
- Export citation
Asymptotic variance of Newton–Cotes quadratures based on randomized sampling points
- Part of
-
- Journal:
- Advances in Applied Probability / Volume 52 / Issue 4 / December 2020
- Published online by Cambridge University Press:
- 03 December 2020, pp. 1284-1307
- Print publication:
- December 2020
-
- Article
- Export citation
IMPLEMENTATION OF HIGH-ORDER, DISCONTINUOUS GALERKIN TIME STEPPING FOR FRACTIONAL DIFFUSION PROBLEMS
- Part of
-
- Journal:
- The ANZIAM Journal / Volume 62 / Issue 2 / April 2020
- Published online by Cambridge University Press:
- 06 November 2020, pp. 121-147
-
- Article
- Export citation
A New Method for High-Degree Spline Interpolation: Proof of Continuity for Piecewise Polynomials
- Part of
-
- Journal:
- Canadian Mathematical Bulletin / Volume 63 / Issue 3 / September 2020
- Published online by Cambridge University Press:
- 09 December 2019, pp. 655-669
- Print publication:
- September 2020
-
- Article
- Export citation
Perturbation Analysis of Orthogonal Least Squares
- Part of
-
- Journal:
- Canadian Mathematical Bulletin / Volume 62 / Issue 4 / December 2019
- Published online by Cambridge University Press:
- 22 March 2019, pp. 780-797
- Print publication:
- December 2019
-
- Article
- Export citation
Multidimensional regular C-fraction with independent variables corresponding to formal multiple power series
- Part of
-
- Journal:
- Proceedings of the Royal Society of Edinburgh. Section A: Mathematics / Volume 150 / Issue 4 / August 2020
- Published online by Cambridge University Press:
- 12 March 2019, pp. 1853-1870
- Print publication:
- August 2020
-
- Article
- Export citation
JOINT MODELS FOR NONLINEAR LONGITUDINAL AND TIME-TO-EVENT DATA USING PENALISED SPLINES
- Part of
-
- Journal:
- Bulletin of the Australian Mathematical Society / Volume 99 / Issue 2 / April 2019
- Published online by Cambridge University Press:
- 07 January 2019, pp. 349-352
- Print publication:
- April 2019
-
- Article
-
- You have access
- Export citation
ON THE ACCURACY OF ASYMPTOTIC APPROXIMATIONS TO THE LOG-GAMMA AND RIEMANN–SIEGEL THETA FUNCTIONS
- Part of
-
- Journal:
- Journal of the Australian Mathematical Society / Volume 107 / Issue 3 / December 2019
- Published online by Cambridge University Press:
- 21 December 2018, pp. 319-337
- Print publication:
- December 2019
-
- Article
- Export citation
A NEW MINIMIZATION PRINCIPLE FOR THE POISSON EQUATION LEADING TO A FLEXIBLE FINITE ELEMENT APPROACH
- Part of
-
- Journal:
- The ANZIAM Journal / Volume 59 / Issue 2 / October 2017
- Published online by Cambridge University Press:
- 03 October 2017, pp. 232-239
-
- Article
-
- You have access
- Export citation
Sparse Recovery via ℓq-Minimization for Polynomial Chaos Expansions
- Part of
-
- Journal:
- Numerical Mathematics: Theory, Methods and Applications / Volume 10 / Issue 4 / November 2017
- Published online by Cambridge University Press:
- 12 September 2017, pp. 775-797
- Print publication:
- November 2017
-
- Article
- Export citation
Application of High Dimensional B-Spline Interpolation in Solving the Gyro-Kinetic Vlasov Equation Based on Semi-Lagrangian Method
- Part of
-
- Journal:
- Communications in Computational Physics / Volume 22 / Issue 3 / September 2017
- Published online by Cambridge University Press:
- 06 July 2017, pp. 789-802
- Print publication:
- September 2017
-
- Article
- Export citation
Error Splitting Preservation for High Order Finite Difference Schemes in the Combination Technique
- Part of
-
- Journal:
- Numerical Mathematics: Theory, Methods and Applications / Volume 10 / Issue 3 / August 2017
- Published online by Cambridge University Press:
- 20 June 2017, pp. 689-710
- Print publication:
- August 2017
-
- Article
- Export citation
Multidimensional Iterative Filtering Method for the Decomposition of High–Dimensional Non–Stationary Signals
- Part of
-
- Journal:
- Numerical Mathematics: Theory, Methods and Applications / Volume 10 / Issue 2 / May 2017
- Published online by Cambridge University Press:
- 09 May 2017, pp. 278-298
- Print publication:
- May 2017
-
- Article
- Export citation
High Order Mass-Lumping Finite Elements on Simplexes
- Part of
-
- Journal:
- Numerical Mathematics: Theory, Methods and Applications / Volume 10 / Issue 2 / May 2017
- Published online by Cambridge University Press:
- 09 May 2017, pp. 331-350
- Print publication:
- May 2017
-
- Article
- Export citation
Delaunay Graph Based Inverse Distance Weighting for Fast Dynamic Meshing
- Part of
-
- Journal:
- Communications in Computational Physics / Volume 21 / Issue 5 / May 2017
- Published online by Cambridge University Press:
- 27 March 2017, pp. 1282-1309
- Print publication:
- May 2017
-
- Article
- Export citation