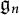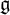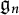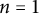235 results in 17Bxx
DT INVARIANTS FROM VERTEX ALGEBRAS
- Part of
-
- Journal:
- Journal of the Institute of Mathematics of Jussieu , First View
- Published online by Cambridge University Press:
- 20 September 2024, pp. 1-49
-
- Article
-
- You have access
- HTML
- Export citation
Laurent family of simple modules over quiver Hecke algebras
- Part of
-
- Journal:
- Compositio Mathematica / Volume 160 / Issue 8 / August 2024
- Published online by Cambridge University Press:
- 11 September 2024, pp. 1916-1940
- Print publication:
- August 2024
-
- Article
-
- You have access
- HTML
- Export citation
EXCEPTIONAL SIMPLE REAL LIE ALGEBRAS
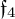 $\mathfrak {f}_4$ AND
$\mathfrak {f}_4$ AND 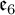 $\mathfrak {e}_6$ VIA CONTACTIFICATIONS
$\mathfrak {e}_6$ VIA CONTACTIFICATIONS
- Part of
-
- Journal:
- Journal of the Institute of Mathematics of Jussieu , First View
- Published online by Cambridge University Press:
- 03 July 2024, pp. 1-45
-
- Article
-
- You have access
- HTML
- Export citation
A classification of automorphic Lie algebras on complex tori
- Part of
-
- Journal:
- Proceedings of the Edinburgh Mathematical Society , First View
- Published online by Cambridge University Press:
- 28 May 2024, pp. 1-43
-
- Article
-
- You have access
- Open access
- HTML
- Export citation
Twisted Whittaker category on affine flags and the category of representations of the mixed quantum group
- Part of
-
- Journal:
- Compositio Mathematica / Volume 160 / Issue 6 / June 2024
- Published online by Cambridge University Press:
- 13 May 2024, pp. 1349-1417
- Print publication:
- June 2024
-
- Article
-
- You have access
- HTML
- Export citation
On Donkin's tilting module conjecture II: counterexamples
- Part of
-
- Journal:
- Compositio Mathematica / Volume 160 / Issue 6 / June 2024
- Published online by Cambridge University Press:
- 02 May 2024, pp. 1167-1193
- Print publication:
- June 2024
-
- Article
-
- You have access
- HTML
- Export citation
SPHERICAL REPRESENTATIONS FOR
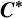 $\boldsymbol C^{\boldsymbol {*}}$-FLOWS III: WEIGHT-EXTENDED BRANCHING GRAPHS
$\boldsymbol C^{\boldsymbol {*}}$-FLOWS III: WEIGHT-EXTENDED BRANCHING GRAPHS
- Part of
-
- Journal:
- Journal of the Australian Mathematical Society / Volume 117 / Issue 2 / October 2024
- Published online by Cambridge University Press:
- 15 April 2024, pp. 239-272
- Print publication:
- October 2024
-
- Article
-
- You have access
- HTML
- Export citation
Whittaker categories of quasi-reductive lie superalgebras and quantum symmetric pairs
- Part of
-
- Journal:
- Forum of Mathematics, Sigma / Volume 12 / 2024
- Published online by Cambridge University Press:
- 02 April 2024, e37
-
- Article
-
- You have access
- Open access
- HTML
- Export citation
Skew group categories, algebras associated to Cartan matrices and folding of root lattices
- Part of
-
- Journal:
- Proceedings of the Royal Society of Edinburgh. Section A: Mathematics , First View
- Published online by Cambridge University Press:
- 01 April 2024, pp. 1-45
-
- Article
-
- You have access
- HTML
- Export citation
The restricted quantum double of the Yangian
- Part of
-
- Journal:
- Canadian Journal of Mathematics , First View
- Published online by Cambridge University Press:
- 16 February 2024, pp. 1-72
-
- Article
-
- You have access
- Open access
- HTML
- Export citation
Shi arrangements and low elements in affine Coxeter groups
- Part of
-
- Journal:
- Canadian Journal of Mathematics , First View
- Published online by Cambridge University Press:
- 12 February 2024, pp. 1-31
-
- Article
-
- You have access
- Open access
- HTML
- Export citation
Classification of simple smooth modules over the Heisenberg–Virasoro algebra
- Part of
-
- Journal:
- Proceedings of the Royal Society of Edinburgh. Section A: Mathematics , First View
- Published online by Cambridge University Press:
- 17 January 2024, pp. 1-45
-
- Article
-
- You have access
- HTML
- Export citation
Virasoro Constraints for Toric Bundles
- Part of
-
- Journal:
- Forum of Mathematics, Pi / Volume 12 / 2024
- Published online by Cambridge University Press:
- 01 January 2024, e4
-
- Article
-
- You have access
- Open access
- HTML
- Export citation
COEFFICIENT QUIVERS,
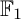 ${\mathbb {F}}_1$-REPRESENTATIONS, AND EULER CHARACTERISTICS OF QUIVER GRASSMANNIANS
${\mathbb {F}}_1$-REPRESENTATIONS, AND EULER CHARACTERISTICS OF QUIVER GRASSMANNIANS
- Part of
-
- Journal:
- Nagoya Mathematical Journal / Volume 255 / September 2024
- Published online by Cambridge University Press:
- 13 December 2023, pp. 561-617
- Print publication:
- September 2024
-
- Article
-
- You have access
- HTML
- Export citation
Irreducible modules of modular Lie superalgebras and super version of the first Kac–Weisfeiler conjecture
- Part of
-
- Journal:
- Canadian Mathematical Bulletin / Volume 67 / Issue 3 / September 2024
- Published online by Cambridge University Press:
- 11 December 2023, pp. 554-573
- Print publication:
- September 2024
-
- Article
-
- You have access
- HTML
- Export citation
On the representability of actions of Leibniz algebras and Poisson algebras
- Part of
-
- Journal:
- Proceedings of the Edinburgh Mathematical Society / Volume 66 / Issue 4 / November 2023
- Published online by Cambridge University Press:
- 22 November 2023, pp. 998-1021
-
- Article
-
- You have access
- HTML
- Export citation
Webs of type P
- Part of
-
- Journal:
- Canadian Journal of Mathematics , First View
- Published online by Cambridge University Press:
- 27 October 2023, pp. 1-50
-
- Article
-
- You have access
- Open access
- HTML
- Export citation
Prime representations in the Hernandez–Leclerc category: classical decompositions
- Part of
-
- Journal:
- Canadian Journal of Mathematics , First View
- Published online by Cambridge University Press:
- 27 October 2023, pp. 1-32
-
- Article
-
- You have access
- HTML
- Export citation
The Frobenius semiradical, generic stabilizers, and Poisson center for nilradicals
- Part of
-
- Journal:
- Canadian Journal of Mathematics , First View
- Published online by Cambridge University Press:
- 27 October 2023, pp. 1-30
-
- Article
-
- You have access
- HTML
- Export citation
Category
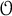 $\mathcal {O}$ for truncated current Lie algebras
$\mathcal {O}$ for truncated current Lie algebras
- Part of
-
- Journal:
- Canadian Journal of Mathematics , First View
- Published online by Cambridge University Press:
- 19 October 2023, pp. 1-27
-
- Article
-
- You have access
- Open access
- HTML
- Export citation





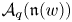
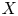
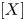
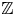
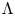
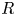
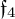
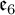















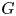
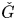
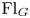
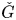
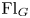
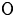
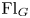
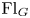
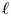
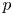
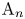
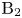
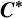
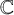
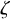
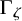

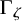
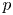
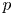
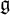
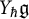
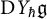
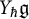
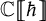
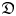
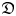
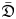
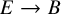
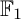
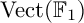
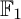
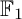
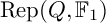
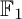
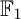
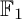
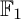
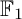
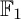
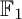





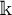
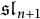
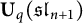
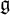
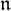
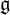

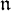
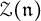 of the symmetric algebra
of the symmetric algebra 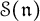 ,
, 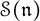 as
as 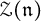 -module, and
-module, and