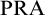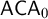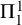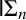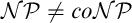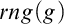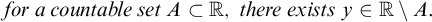116 results in 03FXX
ARROW’S THEOREM, ULTRAFILTERS, AND REVERSE MATHEMATICS
- Part of
-
- Journal:
- The Review of Symbolic Logic , First View
- Published online by Cambridge University Press:
- 29 February 2024, pp. 1-24
-
- Article
-
- You have access
- Open access
- HTML
- Export citation
Functorial Fast-Growing Hierarchies
- Part of
-
- Journal:
- Forum of Mathematics, Sigma / Volume 12 / 2024
- Published online by Cambridge University Press:
- 26 January 2024, e15
-
- Article
-
- You have access
- Open access
- HTML
- Export citation
A WALK WITH GOODSTEIN
- Part of
-
- Journal:
- Bulletin of Symbolic Logic / Volume 30 / Issue 1 / March 2024
- Published online by Cambridge University Press:
- 17 January 2024, pp. 1-19
- Print publication:
- March 2024
-
- Article
- Export citation
ON THE EXISTENCE OF STRONG PROOF COMPLEXITY GENERATORS
- Part of
-
- Journal:
- Bulletin of Symbolic Logic / Volume 30 / Issue 1 / March 2024
- Published online by Cambridge University Press:
- 22 November 2023, pp. 20-40
- Print publication:
- March 2024
-
- Article
-
- You have access
- Open access
- HTML
- Export citation
ONTOLOGICAL PURITY FOR FORMAL PROOFS
- Part of
-
- Journal:
- The Review of Symbolic Logic / Volume 17 / Issue 2 / June 2024
- Published online by Cambridge University Press:
- 13 November 2023, pp. 395-434
- Print publication:
- June 2024
-
- Article
-
- You have access
- Open access
- HTML
- Export citation
BIG IN REVERSE MATHEMATICS: MEASURE AND CATEGORY
- Part of
-
- Journal:
- The Journal of Symbolic Logic , First View
- Published online by Cambridge University Press:
- 17 October 2023, pp. 1-46
-
- Article
- Export citation
DECIDABLE FRAGMENTS OF THE QUANTIFIED ARGUMENT CALCULUS
- Part of
-
- Journal:
- The Review of Symbolic Logic , First View
- Published online by Cambridge University Press:
- 29 September 2023, pp. 1-26
-
- Article
-
- You have access
- Open access
- HTML
- Export citation
WEAK WELL ORDERS AND FRAÏSSÉ’S CONJECTURE
- Part of
-
- Journal:
- The Journal of Symbolic Logic , First View
- Published online by Cambridge University Press:
- 27 September 2023, pp. 1-16
-
- Article
-
- You have access
- Open access
- HTML
- Export citation
A PROOF COMPLEXITY CONJECTURE AND THE INCOMPLETENESS THEOREM
- Part of
-
- Journal:
- The Journal of Symbolic Logic , First View
- Published online by Cambridge University Press:
- 19 September 2023, pp. 1-5
-
- Article
-
- You have access
- Open access
- HTML
- Export citation
EXTENDED FRAMES AND SEPARATIONS OF LOGICAL PRINCIPLES
- Part of
-
- Journal:
- Bulletin of Symbolic Logic / Volume 29 / Issue 3 / September 2023
- Published online by Cambridge University Press:
- 26 July 2023, pp. 311-353
- Print publication:
- September 2023
-
- Article
- Export citation
‘A REMARKABLE ARTIFICE’: LAPLACE, POISSON AND MATHEMATICAL PURITY
- Part of
-
- Journal:
- The Review of Symbolic Logic , First View
- Published online by Cambridge University Press:
- 24 July 2023, pp. 1-37
-
- Article
- Export citation
A SIMPLIFIED PROOF OF THE EPSILON THEOREMS
- Part of
-
- Journal:
- The Review of Symbolic Logic , First View
- Published online by Cambridge University Press:
- 10 July 2023, pp. 1-16
-
- Article
- Export citation
CLASSICAL DETERMINATE TRUTH I
- Part of
-
- Journal:
- The Journal of Symbolic Logic / Volume 89 / Issue 1 / March 2024
- Published online by Cambridge University Press:
- 05 July 2023, pp. 218-261
- Print publication:
- March 2024
-
- Article
-
- You have access
- Open access
- HTML
- Export citation
BIG IN REVERSE MATHEMATICS: THE UNCOUNTABILITY OF THE REALS
- Part of
-
- Journal:
- The Journal of Symbolic Logic , First View
- Published online by Cambridge University Press:
- 29 June 2023, pp. 1-34
-
- Article
-
- You have access
- Open access
- HTML
- Export citation
THE STRENGTH OF AN AXIOM OF FINITE CHOICE FOR BRANCHES IN TREES
- Part of
-
- Journal:
- The Journal of Symbolic Logic / Volume 88 / Issue 4 / December 2023
- Published online by Cambridge University Press:
- 14 June 2023, pp. 1367-1386
- Print publication:
- December 2023
-
- Article
-
- You have access
- Open access
- HTML
- Export citation
NON-CONTRACTIVE LOGICS, PARADOXES, AND MULTIPLICATIVE QUANTIFIERS
- Part of
-
- Journal:
- The Review of Symbolic Logic , First View
- Published online by Cambridge University Press:
- 05 June 2023, pp. 1-22
-
- Article
-
- You have access
- Open access
- HTML
- Export citation
UNDER LOCK AND KEY: A PROOF SYSTEM FOR A MULTIMODAL LOGIC
- Part of
-
- Journal:
- Bulletin of Symbolic Logic / Volume 29 / Issue 2 / June 2023
- Published online by Cambridge University Press:
- 20 April 2023, pp. 264-293
- Print publication:
- June 2023
-
- Article
-
- You have access
- Open access
- HTML
- Export citation
A CLASSICAL MODAL THEORY OF LAWLESS SEQUENCES
- Part of
-
- Journal:
- Bulletin of Symbolic Logic / Volume 29 / Issue 3 / September 2023
- Published online by Cambridge University Press:
- 09 March 2023, pp. 406-452
- Print publication:
- September 2023
-
- Article
- Export citation
COMPLETENESS OF THE GÖDEL–LÖB PROVABILITY LOGIC FOR THE FILTER SEQUENCE OF NORMAL MEASURES
- Part of
-
- Journal:
- The Journal of Symbolic Logic / Volume 89 / Issue 1 / March 2024
- Published online by Cambridge University Press:
- 23 February 2023, pp. 163-174
- Print publication:
- March 2024
-
- Article
- Export citation
TREE THEORY: INTERPRETABILITY BETWEEN WEAK FIRST-ORDER THEORIES OF TREES
- Part of
-
- Journal:
- Bulletin of Symbolic Logic / Volume 29 / Issue 4 / December 2023
- Published online by Cambridge University Press:
- 10 February 2023, pp. 465-502
- Print publication:
- December 2023
-
- Article
-
- You have access
- Open access
- HTML
- Export citation