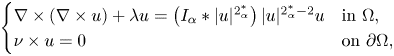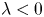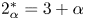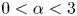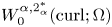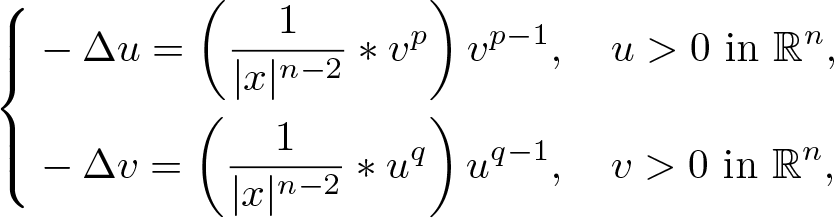12 results in 45Gxx
On a critical time-harmonic Maxwell equation in nonlocal media
- Part of
-
- Journal:
- Proceedings of the Royal Society of Edinburgh. Section A: Mathematics , First View
- Published online by Cambridge University Press:
- 29 February 2024, pp. 1-45
-
- Article
- Export citation
On Liouville theorems of a Hartree–Poisson system
- Part of
-
- Journal:
- Proceedings of the Edinburgh Mathematical Society / Volume 66 / Issue 4 / November 2023
- Published online by Cambridge University Press:
- 26 October 2023, pp. 1154-1178
-
- Article
- Export citation
OPTIMAL STOPPING PROBLEMS WITH A RANDOM TIME HORIZON
- Part of
-
- Journal:
- Bulletin of the Australian Mathematical Society / Volume 108 / Issue 2 / October 2023
- Published online by Cambridge University Press:
- 29 June 2023, pp. 345-346
- Print publication:
- October 2023
-
- Article
-
- You have access
- HTML
- Export citation
Propagation of minima for nonlocal operators
- Part of
-
- Journal:
- Proceedings of the Royal Society of Edinburgh. Section A: Mathematics , First View
- Published online by Cambridge University Press:
- 23 May 2023, pp. 1-14
-
- Article
-
- You have access
- Open access
- HTML
- Export citation
Hardy–Littlewood–Sobolev inequality and existence of the extremal functions with extended kernel
- Part of
-
- Journal:
- Proceedings of the Royal Society of Edinburgh. Section A: Mathematics / Volume 153 / Issue 5 / October 2023
- Published online by Cambridge University Press:
- 31 October 2022, pp. 1683-1705
- Print publication:
- October 2023
-
- Article
- Export citation
Steady-state solutions of one-dimensional competition models in an unstirred chemostat via the fixed point index theory
- Part of
-
- Journal:
- Proceedings of the Royal Society of Edinburgh. Section A: Mathematics / Volume 151 / Issue 1 / February 2021
- Published online by Cambridge University Press:
- 11 March 2020, pp. 240-264
- Print publication:
- February 2021
-
- Article
- Export citation
A NOTE ON RADIAL SYMMETRY FOR AN INTEGRAL EQUATION OF WOLFF TYPE
- Part of
-
- Journal:
- Bulletin of the Australian Mathematical Society / Volume 100 / Issue 2 / October 2019
- Published online by Cambridge University Press:
- 20 February 2019, pp. 323-327
- Print publication:
- October 2019
-
- Article
- Export citation
Mass-conserving solutions to the Smoluchowski coagulation equation with singular kernel
- Part of
-
- Journal:
- Proceedings of the Royal Society of Edinburgh. Section A: Mathematics / Volume 150 / Issue 4 / August 2020
- Published online by Cambridge University Press:
- 19 February 2019, pp. 1805-1825
- Print publication:
- August 2020
-
- Article
- Export citation
Non-Zero Radial Solutions for Elliptic Systems with Coupled Functional BCs in Exterior Domains
- Part of
-
- Journal:
- Proceedings of the Edinburgh Mathematical Society / Volume 62 / Issue 3 / August 2019
- Published online by Cambridge University Press:
- 30 January 2019, pp. 747-769
-
- Article
- Export citation
SPATIAL HAMILTONIAN IDENTITIES FOR NONLOCALLY COUPLED SYSTEMS
- Part of
-
- Journal:
- Forum of Mathematics, Sigma / Volume 6 / 2018
- Published online by Cambridge University Press:
- 14 November 2018, e22
-
- Article
-
- You have access
- Open access
- Export citation
Forward Scattering and Volterra Renormalization for Acoustic Wavefield Propagation in Vertically Varying Media
- Part of
-
- Journal:
- Communications in Computational Physics / Volume 20 / Issue 2 / August 2016
- Published online by Cambridge University Press:
- 21 July 2016, pp. 353-373
- Print publication:
- August 2016
-
- Article
- Export citation
A biharmonic equation with singular nonlinearity
- Part of
-
- Journal:
- Proceedings of the Edinburgh Mathematical Society / Volume 55 / Issue 1 / February 2012
- Published online by Cambridge University Press:
- 14 June 2011, pp. 155-166
-
- Article
-
- You have access
- Export citation