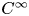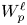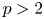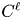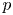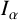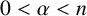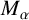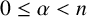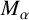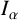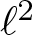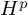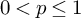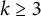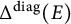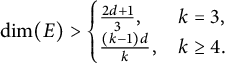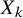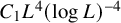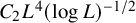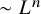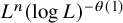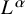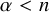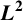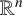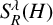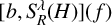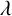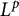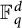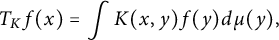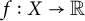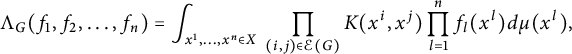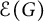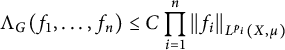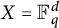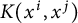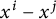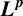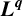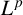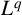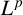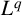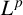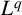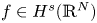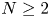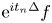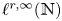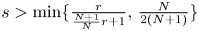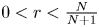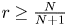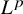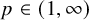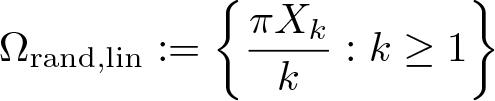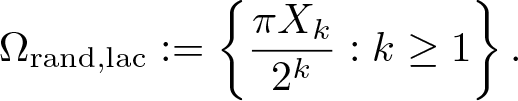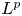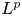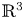239 results in 42Bxx
On a localization-in-frequency approach for a class of elliptic problems with singular boundary data
- Part of
-
- Journal:
- Proceedings of the Royal Society of Edinburgh. Section A: Mathematics , First View
- Published online by Cambridge University Press:
- 21 May 2024, pp. 1-35
-
- Article
- Export citation
On some convexity questions of Handelman
- Part of
-
- Journal:
- Canadian Mathematical Bulletin , First View
- Published online by Cambridge University Press:
- 16 May 2024, pp. 1-4
-
- Article
- Export citation
Unconditional convergence of eigenfunction expansions for abstract and elliptic operators
- Part of
-
- Journal:
- Proceedings of the Royal Society of Edinburgh. Section A: Mathematics , First View
- Published online by Cambridge University Press:
- 05 April 2024, pp. 1-19
-
- Article
- Export citation
CHOQUET INTEGRALS, HAUSDORFF CONTENT AND FRACTIONAL OPERATORS
- Part of
-
- Journal:
- Bulletin of the Australian Mathematical Society , First View
- Published online by Cambridge University Press:
- 19 March 2024, pp. 1-12
-
- Article
- Export citation
L2 to Lp bounds for spectral projectors on the Euclidean two-dimensional torus
- Part of
-
- Journal:
- Proceedings of the Edinburgh Mathematical Society / Volume 67 / Issue 2 / May 2024
- Published online by Cambridge University Press:
- 15 March 2024, pp. 431-459
-
- Article
- Export citation
Dispersive and Strichartz estimates for 3D wave equation with a Laguerre potential
- Part of
-
- Journal:
- Canadian Journal of Mathematics , First View
- Published online by Cambridge University Press:
- 07 March 2024, pp. 1-28
-
- Article
- Export citation
TRILINEAR FOURIER MULTIPLIERS ON HARDY SPACES
- Part of
-
- Journal:
- Journal of the Institute of Mathematics of Jussieu , First View
- Published online by Cambridge University Press:
- 15 February 2024, pp. 1-62
-
- Article
- Export citation
On restricted Falconer distance sets
- Part of
-
- Journal:
- Canadian Journal of Mathematics , First View
- Published online by Cambridge University Press:
- 05 February 2024, pp. 1-18
-
- Article
-
- You have access
- Open access
- HTML
- Export citation
Degrees of maps and multiscale geometry
- Part of
-
- Journal:
- Forum of Mathematics, Pi / Volume 12 / 2024
- Published online by Cambridge University Press:
- 18 January 2024, e2
-
- Article
-
- You have access
- Open access
- HTML
- Export citation
A WEIGHTED
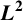 $\boldsymbol {L}^{\boldsymbol {2}}$ ESTIMATE OF COMMUTATORS OF BOCHNER–RIESZ OPERATORS FOR HERMITE OPERATOR
$\boldsymbol {L}^{\boldsymbol {2}}$ ESTIMATE OF COMMUTATORS OF BOCHNER–RIESZ OPERATORS FOR HERMITE OPERATOR
- Part of
-
- Journal:
- Journal of the Australian Mathematical Society / Volume 116 / Issue 3 / June 2024
- Published online by Cambridge University Press:
- 15 January 2024, pp. 308-330
- Print publication:
- June 2024
-
- Article
- Export citation
Trigonometric convexity of the multidimensional indicator
- Part of
-
- Journal:
- Canadian Journal of Mathematics , First View
- Published online by Cambridge University Press:
- 05 January 2024, pp. 1-16
-
- Article
- Export citation
Multi-linear forms, graphs, and
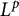 $L^p$-improving measures in
$L^p$-improving measures in 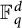 ${\Bbb F}_q^d$
${\Bbb F}_q^d$
- Part of
-
- Journal:
- Canadian Journal of Mathematics , First View
- Published online by Cambridge University Press:
- 27 December 2023, pp. 1-44
-
- Article
- Export citation
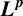 $\boldsymbol {L}^{\boldsymbol {p}}$–
$\boldsymbol {L}^{\boldsymbol {p}}$–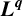 $\boldsymbol {L}^{\boldsymbol {q}}$ MULTIPLIERS ON COMMUTATIVE HYPERGROUPS
$\boldsymbol {L}^{\boldsymbol {q}}$ MULTIPLIERS ON COMMUTATIVE HYPERGROUPS
- Part of
-
- Journal:
- Journal of the Australian Mathematical Society / Volume 115 / Issue 3 / December 2023
- Published online by Cambridge University Press:
- 18 October 2023, pp. 375-395
- Print publication:
- December 2023
-
- Article
- Export citation
Sharp convergence for sequences of Schrödinger means and related generalizations
- Part of
-
- Journal:
- Proceedings of the Royal Society of Edinburgh. Section A: Mathematics , First View
- Published online by Cambridge University Press:
- 25 September 2023, pp. 1-17
-
- Article
- Export citation
On a multi-parameter variant of the Bellow–Furstenberg problem
- Part of
-
- Journal:
- Forum of Mathematics, Pi / Volume 11 / 2023
- Published online by Cambridge University Press:
- 19 September 2023, e23
-
- Article
-
- You have access
- Open access
- HTML
- Export citation
Discrete restriction estimates for forms in many variables
- Part of
-
- Journal:
- Proceedings of the Edinburgh Mathematical Society / Volume 66 / Issue 4 / November 2023
- Published online by Cambridge University Press:
- 18 September 2023, pp. 923-939
-
- Article
-
- You have access
- Open access
- HTML
- Export citation
Estimates for evolutionary partial differential equations in classical function spaces
- Part of
-
- Journal:
- Forum of Mathematics, Sigma / Volume 11 / 2023
- Published online by Cambridge University Press:
- 01 September 2023, e76
-
- Article
-
- You have access
- Open access
- HTML
- Export citation
Perron’s capacity of random sets
- Part of
-
- Journal:
- Proceedings of the Edinburgh Mathematical Society / Volume 66 / Issue 4 / November 2023
- Published online by Cambridge University Press:
- 01 September 2023, pp. 960-970
-
- Article
- Export citation
Sharp Sobolev regularity of restricted X-ray transforms
- Part of
-
- Journal:
- Proceedings of the Royal Society of Edinburgh. Section A: Mathematics , First View
- Published online by Cambridge University Press:
- 30 August 2023, pp. 1-21
-
- Article
- Export citation
Remarks on countable subadditivity
- Part of
-
- Journal:
- Proceedings of the Royal Society of Edinburgh. Section A: Mathematics , First View
- Published online by Cambridge University Press:
- 23 August 2023, pp. 1-14
-
- Article
- Export citation