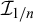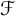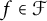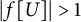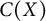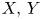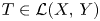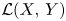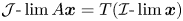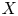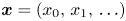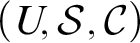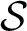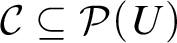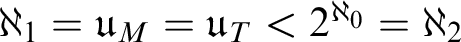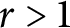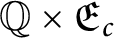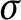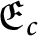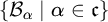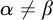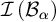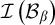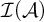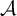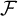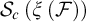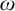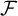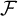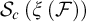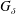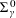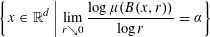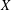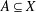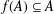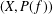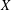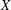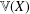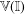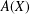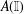39 results in 54Axx
A UNIFIED APPROACH TO HINDMAN, RAMSEY, AND VAN DER WAERDEN SPACES
- Part of
-
- Journal:
- The Journal of Symbolic Logic , First View
- Published online by Cambridge University Press:
- 12 February 2024, pp. 1-53
-
- Article
- Export citation
Nowhere constant families of maps and resolvability
- Part of
-
- Journal:
- Canadian Mathematical Bulletin , First View
- Published online by Cambridge University Press:
- 06 February 2024, pp. 1-5
-
- Article
-
- You have access
- Open access
- HTML
- Export citation
Regular matrices of unbounded linear operators
- Part of
-
- Journal:
- Proceedings of the Royal Society of Edinburgh. Section A: Mathematics , First View
- Published online by Cambridge University Press:
- 31 January 2024, pp. 1-29
-
- Article
-
- You have access
- Open access
- HTML
- Export citation
Invariant ideals and their applications to the turnpike theory
- Part of
-
- Journal:
- Canadian Mathematical Bulletin / Volume 66 / Issue 3 / September 2023
- Published online by Cambridge University Press:
- 12 January 2023, pp. 959-975
- Print publication:
- September 2023
-
- Article
- Export citation
TAMING THE ‘ELSEWHERE’: ON EXPRESSIVITY OF TOPOLOGICAL LANGUAGES
- Part of
-
- Journal:
- The Review of Symbolic Logic / Volume 17 / Issue 1 / March 2024
- Published online by Cambridge University Press:
- 28 March 2022, pp. 144-153
- Print publication:
- March 2024
-
- Article
- Export citation
SET THEORY AND A MODEL OF THE MIND IN PSYCHOLOGY
- Part of
-
- Journal:
- The Review of Symbolic Logic / Volume 16 / Issue 4 / December 2023
- Published online by Cambridge University Press:
- 14 March 2022, pp. 1233-1259
- Print publication:
- December 2023
-
- Article
- Export citation
On a topological Ramsey theorem
- Part of
-
- Journal:
- Canadian Mathematical Bulletin / Volume 66 / Issue 1 / March 2023
- Published online by Cambridge University Press:
- 07 March 2022, pp. 156-165
- Print publication:
- March 2023
-
- Article
-
- You have access
- Open access
- HTML
- Export citation
A characterization of the product of the rational numbers and complete Erdős space
- Part of
-
- Journal:
- Canadian Mathematical Bulletin / Volume 66 / Issue 1 / March 2023
- Published online by Cambridge University Press:
- 27 January 2022, pp. 87-102
- Print publication:
- March 2023
-
- Article
- Export citation
MORE ON FRÉCHET–URYSOHN IDEALS
- Part of
-
- Journal:
- The Journal of Symbolic Logic / Volume 87 / Issue 2 / June 2022
- Published online by Cambridge University Press:
- 10 June 2021, pp. 829-851
- Print publication:
- June 2022
-
- Article
- Export citation
A Common Extension of Arhangel’skĭ’s Theorem and the Hajnal–Juhász Inequality
- Part of
-
- Journal:
- Canadian Mathematical Bulletin / Volume 63 / Issue 1 / March 2020
- Published online by Cambridge University Press:
- 06 January 2020, pp. 197-203
- Print publication:
- March 2020
-
- Article
- Export citation
ON GENERALISED METRISABILITY AND CARDINAL INVARIANTS IN QUASITOPOLOGICAL GROUPS
- Part of
-
- Journal:
- Bulletin of the Australian Mathematical Society / Volume 99 / Issue 2 / April 2019
- Published online by Cambridge University Press:
- 17 October 2018, pp. 302-310
- Print publication:
- April 2019
-
- Article
-
- You have access
- Export citation
CONTINUITY ON GENERALISED TOPOLOGICAL SPACES VIA HEREDITARY CLASSES
- Part of
-
- Journal:
- Bulletin of the Australian Mathematical Society / Volume 97 / Issue 2 / April 2018
- Published online by Cambridge University Press:
- 21 February 2018, pp. 320-330
- Print publication:
- April 2018
-
- Article
-
- You have access
- Export citation
ON THE
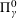 $\unicode[STIX]{x1D6F1}_{\unicode[STIX]{x1D6FE}}^{0}$-COMPLETENESS AND
$\unicode[STIX]{x1D6F1}_{\unicode[STIX]{x1D6FE}}^{0}$-COMPLETENESS AND 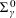 $\unicode[STIX]{x1D6F4}_{\unicode[STIX]{x1D6FE}}^{0}$-COMPLETENESS OF MULTIFRACTAL DECOMPOSITION SETS
$\unicode[STIX]{x1D6F4}_{\unicode[STIX]{x1D6FE}}^{0}$-COMPLETENESS OF MULTIFRACTAL DECOMPOSITION SETS
- Part of
-
- Journal:
- Mathematika / Volume 64 / Issue 1 / 2018
- Published online by Cambridge University Press:
- 06 February 2018, pp. 77-114
- Print publication:
- 2018
-
- Article
- Export citation
HOMOGENEOUS FUNCTIONALLY ALEXANDROFF SPACES
- Part of
-
- Journal:
- Bulletin of the Australian Mathematical Society / Volume 97 / Issue 2 / April 2018
- Published online by Cambridge University Press:
- 08 November 2017, pp. 331-339
- Print publication:
- April 2018
-
- Article
-
- You have access
- Export citation
SUBSPACES OF THE FREE TOPOLOGICAL VECTOR SPACE ON THE UNIT INTERVAL
- Part of
-
- Journal:
- Bulletin of the Australian Mathematical Society / Volume 97 / Issue 1 / February 2018
- Published online by Cambridge University Press:
- 07 August 2017, pp. 110-118
- Print publication:
- February 2018
-
- Article
-
- You have access
- Export citation
The Inner Corona Algebra of a C 0(X)-Algebra
- Part of
-
- Journal:
- Proceedings of the Edinburgh Mathematical Society / Volume 60 / Issue 2 / May 2017
- Published online by Cambridge University Press:
- 19 September 2016, pp. 299-318
-
- Article
- Export citation
G/G/∞ queues with renewal alternating interruptions
- Part of
-
- Journal:
- Advances in Applied Probability / Volume 48 / Issue 3 / September 2016
- Published online by Cambridge University Press:
- 19 September 2016, pp. 812-831
- Print publication:
- September 2016
-
- Article
- Export citation
A TOPOLOGICAL VARIATION OF THE RECONSTRUCTION CONJECTURE
- Part of
-
- Journal:
- Glasgow Mathematical Journal / Volume 59 / Issue 1 / January 2017
- Published online by Cambridge University Press:
- 10 June 2016, pp. 221-235
- Print publication:
- January 2017
-
- Article
-
- You have access
- Export citation
RESOLVABILITY OF MEASURABLE SPACES
- Part of
-
- Journal:
- Bulletin of the Australian Mathematical Society / Volume 94 / Issue 1 / August 2016
- Published online by Cambridge University Press:
- 11 January 2016, pp. 70-79
- Print publication:
- August 2016
-
- Article
-
- You have access
- Export citation
RESOLVABILITY PROPERTIES OF SIMILAR TOPOLOGIES
- Part of
-
- Journal:
- Bulletin of the Australian Mathematical Society / Volume 92 / Issue 3 / December 2015
- Published online by Cambridge University Press:
- 03 September 2015, pp. 470-477
- Print publication:
- December 2015
-
- Article
-
- You have access
- Export citation