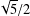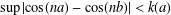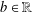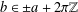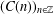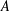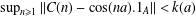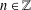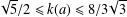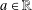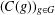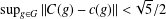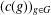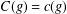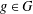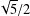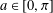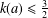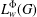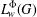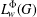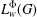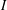55 results in 46Jxx
A CALCULATION OF THE PERFECTOIDIZATION OF SEMIPERFECTOID RINGS
- Part of
-
- Journal:
- Nagoya Mathematical Journal / Volume 255 / September 2024
- Published online by Cambridge University Press:
- 23 February 2024, pp. 742-759
- Print publication:
- September 2024
-
- Article
-
- You have access
- Open access
- HTML
- Export citation
On the Extension of Bounded Holomorphic Maps from Gleason Parts of the Maximal Ideal Space of
 $H^\infty $
$H^\infty $
- Part of
-
- Journal:
- Canadian Mathematical Bulletin / Volume 67 / Issue 3 / September 2024
- Published online by Cambridge University Press:
- 08 January 2024, pp. 624-632
- Print publication:
- September 2024
-
- Article
-
- You have access
- HTML
- Export citation
Projective freeness and stable rank of algebras of complex-valued BV functions
- Part of
-
- Journal:
- Canadian Mathematical Bulletin / Volume 66 / Issue 3 / September 2023
- Published online by Cambridge University Press:
- 16 January 2023, pp. 844-853
- Print publication:
- September 2023
-
- Article
-
- You have access
- Open access
- HTML
- Export citation
ON THE ALGEBRAS
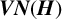 $\boldsymbol {VN(H)}$ AND
$\boldsymbol {VN(H)}$ AND 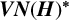 $\boldsymbol {VN(H)^{*}} $ OF AN ULTRASPHERICAL HYPERGROUP
$\boldsymbol {VN(H)^{*}} $ OF AN ULTRASPHERICAL HYPERGROUP 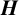 $\boldsymbol {H}$
$\boldsymbol {H}$
- Part of
-
- Journal:
- Journal of the Australian Mathematical Society / Volume 115 / Issue 3 / December 2023
- Published online by Cambridge University Press:
- 12 December 2022, pp. 337-353
- Print publication:
- December 2023
-
- Article
- Export citation
Point Degree Spectra of Represented Spaces
- Part of
-
- Journal:
- Forum of Mathematics, Sigma / Volume 10 / 2022
- Published online by Cambridge University Press:
- 27 May 2022, e31
-
- Article
-
- You have access
- Open access
- HTML
- Export citation
THE BOCHNER–SCHOENBERG-EBERLEIN PROPERTY OF EXTENSIONS OF BANACH ALGEBRAS AND BANACH MODULES
- Part of
-
- Journal:
- Bulletin of the Australian Mathematical Society / Volume 105 / Issue 1 / February 2022
- Published online by Cambridge University Press:
- 09 July 2021, pp. 134-145
- Print publication:
- February 2022
-
- Article
- Export citation
Characterizations of Hankel operators in the essential commutant of quasicontinuous Toeplitz operators
- Part of
-
- Journal:
- Canadian Mathematical Bulletin / Volume 65 / Issue 1 / March 2022
- Published online by Cambridge University Press:
- 09 February 2021, pp. 44-51
- Print publication:
- March 2022
-
- Article
- Export citation
A SPHERICAL VERSION OF THE KOWALSKI–SŁODKOWSKI THEOREM AND ITS APPLICATIONS
- Part of
-
- Journal:
- Journal of the Australian Mathematical Society / Volume 111 / Issue 3 / December 2021
- Published online by Cambridge University Press:
- 03 December 2020, pp. 386-411
- Print publication:
- December 2021
-
- Article
- Export citation
AMENABILITY AND ORLICZ FIGÀ-TALAMANCA HERZ ALGEBRAS
- Part of
-
- Journal:
- Journal of the Australian Mathematical Society / Volume 112 / Issue 2 / April 2022
- Published online by Cambridge University Press:
- 05 October 2020, pp. 218-229
- Print publication:
- April 2022
-
- Article
-
- You have access
- Open access
- Export citation
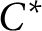 $C^*$
-algebra structure on certain Banach algebra products
$C^*$
-algebra structure on certain Banach algebra products
- Part of
-
- Journal:
- Canadian Mathematical Bulletin / Volume 64 / Issue 3 / September 2021
- Published online by Cambridge University Press:
- 07 September 2020, pp. 678-686
- Print publication:
- September 2021
-
- Article
- Export citation
MULTIPLICATIVE SPECTRAL FUNCTIONALS ON
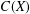 $C(X)$
$C(X)$
- Part of
-
- Journal:
- Bulletin of the Australian Mathematical Society / Volume 102 / Issue 2 / October 2020
- Published online by Cambridge University Press:
- 08 January 2020, pp. 303-307
- Print publication:
- October 2020
-
- Article
- Export citation
Topology of Gleason Parts in Maximal Ideal Spaces with no Analytic Discs
- Part of
-
- Journal:
- Canadian Journal of Mathematics / Volume 73 / Issue 1 / February 2021
- Published online by Cambridge University Press:
- 15 November 2019, pp. 177-194
- Print publication:
- February 2021
-
- Article
- Export citation
SOME CONVERGENCE THEOREMS IN FOURIER ALGEBRAS
- Part of
-
- Journal:
- Bulletin of the Australian Mathematical Society / Volume 96 / Issue 3 / December 2017
- Published online by Cambridge University Press:
- 03 July 2017, pp. 487-495
- Print publication:
- December 2017
-
- Article
-
- You have access
- Export citation
The algebra of symmetric analytic functions on L∞
- Part of
-
- Journal:
- Proceedings of the Royal Society of Edinburgh. Section A: Mathematics / Volume 147 / Issue 4 / August 2017
- Published online by Cambridge University Press:
- 31 May 2017, pp. 743-761
- Print publication:
- August 2017
-
- Article
- Export citation
A ZERO-
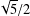 $\!\sqrt{5}/2$
LAW FOR COSINE FAMILIES
$\!\sqrt{5}/2$
LAW FOR COSINE FAMILIES
- Part of
-
- Journal:
- Journal of the Australian Mathematical Society / Volume 104 / Issue 2 / April 2018
- Published online by Cambridge University Press:
- 17 April 2017, pp. 195-217
- Print publication:
- April 2018
-
- Article
-
- You have access
- Export citation
DITKIN CONDITIONS
- Part of
-
- Journal:
- Glasgow Mathematical Journal / Volume 60 / Issue 1 / January 2018
- Published online by Cambridge University Press:
- 27 February 2017, pp. 153-163
- Print publication:
- January 2018
-
- Article
-
- You have access
- Export citation
The Inner Corona Algebra of a C 0(X)-Algebra
- Part of
-
- Journal:
- Proceedings of the Edinburgh Mathematical Society / Volume 60 / Issue 2 / May 2017
- Published online by Cambridge University Press:
- 19 September 2016, pp. 299-318
-
- Article
- Export citation
Orthogonally Additive Polynomials and Orthosymmetric Maps in Banach Algebras with Properties 𝔸 and 𝔹
- Part of
-
- Journal:
- Proceedings of the Edinburgh Mathematical Society / Volume 59 / Issue 3 / August 2016
- Published online by Cambridge University Press:
- 15 December 2015, pp. 559-568
-
- Article
- Export citation
WEIGHTED ORLICZ ALGEBRAS ON LOCALLY COMPACT GROUPS
- Part of
-
- Journal:
- Journal of the Australian Mathematical Society / Volume 99 / Issue 3 / December 2015
- Published online by Cambridge University Press:
- 02 September 2015, pp. 399-414
- Print publication:
- December 2015
-
- Article
-
- You have access
- Export citation
UNIFORMLY BOUNDED COMPOSITION OPERATORS
- Part of
-
- Journal:
- Bulletin of the Australian Mathematical Society / Volume 92 / Issue 3 / December 2015
- Published online by Cambridge University Press:
- 30 July 2015, pp. 463-469
- Print publication:
- December 2015
-
- Article
-
- You have access
- Export citation










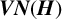
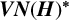
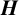
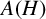
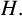
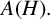
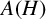
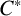
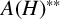
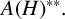
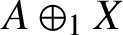
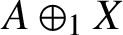
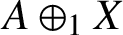
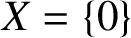

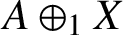
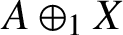
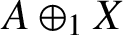
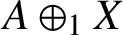
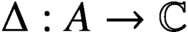
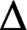
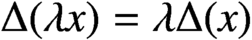
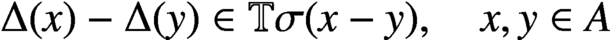
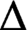
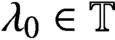
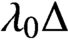
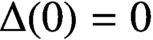
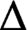
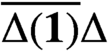
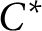
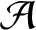
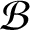
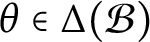
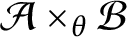
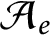
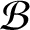
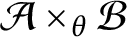
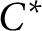
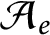
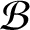
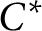
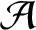
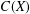
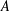
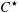
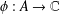
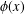

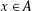
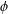
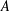
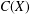

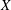
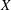
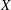
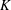
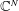
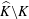
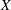
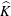
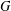
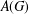
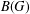
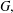

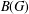
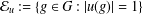
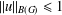
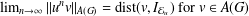
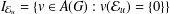
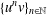
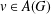
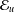
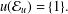
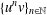
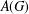
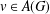
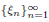 such that
such that 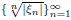 is bounded and turns to be separable. All this follows from our main result that the subalgebra of
is bounded and turns to be separable. All this follows from our main result that the subalgebra of