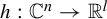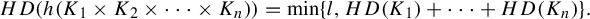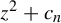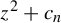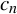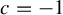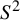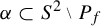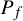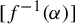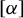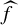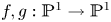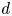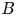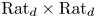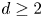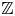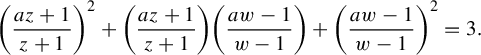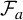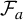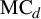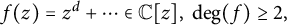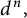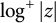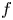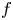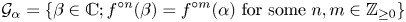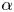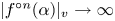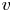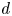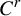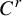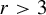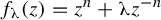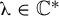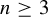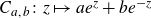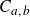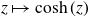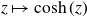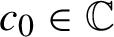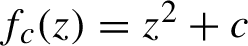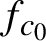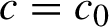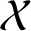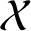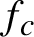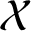110 results in 37Fxx
Scale recurrence lemma and dimension formula for Cantor sets in the complex plane
- Part of
-
- Journal:
- Ergodic Theory and Dynamical Systems , First View
- Published online by Cambridge University Press:
- 25 March 2024, pp. 1-42
-
- Article
- Export citation
On the stochastic bifurcations regarding random iterations of polynomials of the form
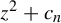 $z^{2} + c_{n}$
$z^{2} + c_{n}$
- Part of
-
- Journal:
- Ergodic Theory and Dynamical Systems , First View
- Published online by Cambridge University Press:
- 26 February 2024, pp. 1-27
-
- Article
-
- You have access
- Open access
- HTML
- Export citation
ON THE ITERATIONS AND THE ARGUMENT DISTRIBUTION OF MEROMORPHIC FUNCTIONS
- Part of
-
- Journal:
- Journal of the Australian Mathematical Society / Volume 116 / Issue 2 / April 2024
- Published online by Cambridge University Press:
- 15 February 2024, pp. 145-170
- Print publication:
- April 2024
-
- Article
- Export citation
Eliminating Thurston obstructions and controlling dynamics on curves
- Part of
-
- Journal:
- Ergodic Theory and Dynamical Systems , First View
- Published online by Cambridge University Press:
- 17 January 2024, pp. 1-79
-
- Article
-
- You have access
- Open access
- HTML
- Export citation
Dynamics on ℙ1: preperiodic points and pairwise stability
- Part of
-
- Journal:
- Compositio Mathematica / Volume 160 / Issue 2 / February 2024
- Published online by Cambridge University Press:
- 05 January 2024, pp. 356-387
- Print publication:
- February 2024
-
- Article
- Export citation
Levy and Thurston obstructions of finite subdivision rules
- Part of
-
- Journal:
- Ergodic Theory and Dynamical Systems , First View
- Published online by Cambridge University Press:
- 15 December 2023, pp. 1-51
-
- Article
-
- You have access
- Open access
- HTML
- Export citation
Zeros, chaotic ratios and the computational complexity of approximating the independence polynomial
- Part of
-
- Journal:
- Mathematical Proceedings of the Cambridge Philosophical Society / Volume 176 / Issue 2 / March 2024
- Published online by Cambridge University Press:
- 24 November 2023, pp. 459-494
- Print publication:
- March 2024
-
- Article
- Export citation
Equidistribution for matings of quadratic maps with the modular group
- Part of
-
- Journal:
- Ergodic Theory and Dynamical Systems / Volume 44 / Issue 3 / March 2024
- Published online by Cambridge University Press:
- 12 May 2023, pp. 859-887
- Print publication:
- March 2024
-
- Article
-
- You have access
- Open access
- HTML
- Export citation
Multiply connected wandering domains of meromorphic functions: the pursuit of uniform internal dynamics
- Part of
-
- Journal:
- Ergodic Theory and Dynamical Systems / Volume 44 / Issue 3 / March 2024
- Published online by Cambridge University Press:
- 11 April 2023, pp. 727-748
- Print publication:
- March 2024
-
- Article
-
- You have access
- Open access
- HTML
- Export citation
A fixed-point curve theorem for finite-orbits local diffeomorphisms
- Part of
-
- Journal:
- Ergodic Theory and Dynamical Systems / Volume 43 / Issue 12 / December 2023
- Published online by Cambridge University Press:
- 16 February 2023, pp. 4138-4165
- Print publication:
- December 2023
-
- Article
- Export citation
The moduli space of polynomial maps and their fixed-point multipliers: II. Improvement to the algorithm and monic centered polynomials
- Part of
-
- Journal:
- Ergodic Theory and Dynamical Systems / Volume 43 / Issue 11 / November 2023
- Published online by Cambridge University Press:
- 03 February 2023, pp. 3777-3795
- Print publication:
- November 2023
-
- Article
- Export citation
Mahler measure of polynomial iterates
- Part of
-
- Journal:
- Canadian Mathematical Bulletin / Volume 66 / Issue 3 / September 2023
- Published online by Cambridge University Press:
- 12 January 2023, pp. 881-885
- Print publication:
- September 2023
-
- Article
-
- You have access
- Open access
- HTML
- Export citation
Polynomial dynamics and local analysis of small and grand orbits
- Part of
-
- Journal:
- Compositio Mathematica / Volume 159 / Issue 1 / January 2023
- Published online by Cambridge University Press:
- 12 January 2023, pp. 53-86
- Print publication:
- January 2023
-
- Article
-
- You have access
- Open access
- HTML
- Export citation
STRUCTURAL STABILITY OF MEANDERING-HYPERBOLIC GROUP ACTIONS
- Part of
-
- Journal:
- Journal of the Institute of Mathematics of Jussieu / Volume 23 / Issue 2 / March 2024
- Published online by Cambridge University Press:
- 27 December 2022, pp. 753-810
- Print publication:
- March 2024
-
- Article
- Export citation
Asymptotically holomorphic methods for infinitely renormalizable
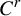 $C^r$ unimodal maps
$C^r$ unimodal maps
- Part of
-
- Journal:
- Ergodic Theory and Dynamical Systems / Volume 43 / Issue 11 / November 2023
- Published online by Cambridge University Press:
- 29 November 2022, pp. 3636-3684
- Print publication:
- November 2023
-
- Article
- Export citation
Escape components of McMullen maps
- Part of
-
- Journal:
- Ergodic Theory and Dynamical Systems / Volume 43 / Issue 11 / November 2023
- Published online by Cambridge University Press:
- 28 November 2022, pp. 3745-3775
- Print publication:
- November 2023
-
- Article
- Export citation
Iterates of meromorphic functions on escaping Fatou components
- Part of
-
- Journal:
- Proceedings of the Royal Society of Edinburgh. Section A: Mathematics / Volume 153 / Issue 6 / December 2023
- Published online by Cambridge University Press:
- 22 November 2022, pp. 1906-1928
- Print publication:
- December 2023
-
- Article
- Export citation
Topological dynamics of cosine maps
- Part of
-
- Journal:
- Mathematical Proceedings of the Cambridge Philosophical Society / Volume 174 / Issue 3 / May 2023
- Published online by Cambridge University Press:
- 23 September 2022, pp. 497-529
- Print publication:
- May 2023
-
- Article
-
- You have access
- Open access
- HTML
- Export citation
Perturbations of graphs for Newton maps I: bounded hyperbolic components
- Part of
-
- Journal:
- Ergodic Theory and Dynamical Systems / Volume 43 / Issue 9 / September 2023
- Published online by Cambridge University Press:
- 31 August 2022, pp. 2997-3025
- Print publication:
- September 2023
-
- Article
- Export citation
Accumulation set of critical points of the multipliers in the quadratic family
- Part of
-
- Journal:
- Ergodic Theory and Dynamical Systems / Volume 43 / Issue 5 / May 2023
- Published online by Cambridge University Press:
- 26 April 2022, pp. 1548-1569
- Print publication:
- May 2023
-
- Article
- Export citation