Article contents
Accumulation set of critical points of the multipliers in the quadratic family
Published online by Cambridge University Press: 26 April 2022
Abstract
A parameter
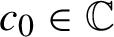 $c_{0}\in {\mathbb {C}}$
in the family of quadratic polynomials
$c_{0}\in {\mathbb {C}}$
in the family of quadratic polynomials
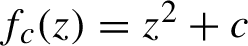 $f_{c}(z)=z^{2}+c$
is a critical point of a period n multiplier if the map
$f_{c}(z)=z^{2}+c$
is a critical point of a period n multiplier if the map
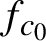 $f_{c_{0}}$
has a periodic orbit of period n, whose multiplier, viewed as a locally analytic function of c, has a vanishing derivative at
$f_{c_{0}}$
has a periodic orbit of period n, whose multiplier, viewed as a locally analytic function of c, has a vanishing derivative at
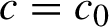 $c=c_{0}$
. We study the accumulation set
$c=c_{0}$
. We study the accumulation set
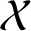 ${\mathcal X}$
of the critical points of the multipliers as
${\mathcal X}$
of the critical points of the multipliers as
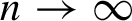 $n\to \infty $
. This study complements the equidistribution result for the critical points of the multipliers that was previously obtained by the authors. In particular, in the current paper, we prove that the accumulation set
$n\to \infty $
. This study complements the equidistribution result for the critical points of the multipliers that was previously obtained by the authors. In particular, in the current paper, we prove that the accumulation set
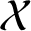 ${\mathcal X}$
is bounded, connected, and contains the Mandelbrot set as a proper subset. We also provide a necessary and sufficient condition for a parameter outside of the Mandelbrot set to be contained in the accumulation set
${\mathcal X}$
is bounded, connected, and contains the Mandelbrot set as a proper subset. We also provide a necessary and sufficient condition for a parameter outside of the Mandelbrot set to be contained in the accumulation set
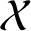 ${\mathcal X}$
and show that this condition is satisfied for an open set of parameters. Our condition is similar in flavor to one of the conditions that define the Mandelbrot set. As an application, we get that the function that sends c to the Hausdorff dimension of
${\mathcal X}$
and show that this condition is satisfied for an open set of parameters. Our condition is similar in flavor to one of the conditions that define the Mandelbrot set. As an application, we get that the function that sends c to the Hausdorff dimension of
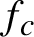 $f_{c}$
does not have critical points outside of the accumulation set
$f_{c}$
does not have critical points outside of the accumulation set
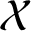 ${\mathcal X}$
.
${\mathcal X}$
.
MSC classification
- Type
- Original Article
- Information
- Copyright
- © The Author(s), 2022. Published by Cambridge University Press
References
- 1
- Cited by





