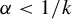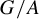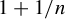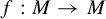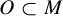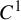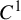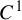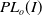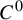207 results in 37Cxx
Global rigidity of smooth
 ${\mathbb{Z}}\ltimes _{\unicode{x3bb}}{\mathbb{R}}$-actions on
${\mathbb{Z}}\ltimes _{\unicode{x3bb}}{\mathbb{R}}$-actions on  ${\mathbb{T}}^{2}$
${\mathbb{T}}^{2}$
- Part of
-
- Journal:
- Ergodic Theory and Dynamical Systems , First View
- Published online by Cambridge University Press:
- 14 October 2024, pp. 1-16
-
- Article
-
- You have access
- HTML
- Export citation
Geometric properties of disintegration of measures
- Part of
-
- Journal:
- Ergodic Theory and Dynamical Systems , First View
- Published online by Cambridge University Press:
- 11 October 2024, pp. 1-30
-
- Article
-
- You have access
- HTML
- Export citation
Construction of smooth isomorphic and finite-to-one extensions of irrational rotations which are not almost automorphic
- Part of
-
- Journal:
- Ergodic Theory and Dynamical Systems , First View
- Published online by Cambridge University Press:
- 04 October 2024, pp. 1-22
-
- Article
-
- You have access
- Open access
- HTML
- Export citation
Birkhoff attractors of dissipative billiards
- Part of
-
- Journal:
- Ergodic Theory and Dynamical Systems , First View
- Published online by Cambridge University Press:
- 30 September 2024, pp. 1-59
-
- Article
-
- You have access
- Open access
- HTML
- Export citation
On the critical regularity of nilpotent groups acting on the interval: the metabelian case
- Part of
-
- Journal:
- Ergodic Theory and Dynamical Systems , First View
- Published online by Cambridge University Press:
- 24 September 2024, pp. 1-22
-
- Article
-
- You have access
- HTML
- Export citation
Shub’s example revisited
- Part of
-
- Journal:
- Ergodic Theory and Dynamical Systems , First View
- Published online by Cambridge University Press:
- 23 September 2024, pp. 1-21
-
- Article
-
- You have access
- HTML
- Export citation
Multifractal analysis of homological growth rates for hyperbolic surfaces
- Part of
-
- Journal:
- Ergodic Theory and Dynamical Systems , First View
- Published online by Cambridge University Press:
- 18 September 2024, pp. 1-35
-
- Article
-
- You have access
- HTML
- Export citation
Symbolic dynamics for pointwise hyperbolic systems on open regions
- Part of
-
- Journal:
- Ergodic Theory and Dynamical Systems , First View
- Published online by Cambridge University Press:
- 10 September 2024, pp. 1-54
-
- Article
-
- You have access
- HTML
- Export citation
Equilibrium measures for two-sided shift spaces via dimension theory
- Part of
-
- Journal:
- Ergodic Theory and Dynamical Systems , First View
- Published online by Cambridge University Press:
- 10 September 2024, pp. 1-40
-
- Article
-
- You have access
- HTML
- Export citation
Non-rigidity of partially hyperbolic abelian
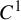 $C^1$-actions on tori
$C^1$-actions on tori
- Part of
-
- Journal:
- Ergodic Theory and Dynamical Systems , First View
- Published online by Cambridge University Press:
- 09 September 2024, pp. 1-22
-
- Article
-
- You have access
- Open access
- HTML
- Export citation
Bishop–Jones’ theorem and the ergodic limit set
- Part of
-
- Journal:
- Ergodic Theory and Dynamical Systems , First View
- Published online by Cambridge University Press:
- 09 September 2024, pp. 1-15
-
- Article
-
- You have access
- Open access
- HTML
- Export citation
Indistinguishable asymptotic pairs and multidimensional Sturmian configurations
- Part of
-
- Journal:
- Ergodic Theory and Dynamical Systems , First View
- Published online by Cambridge University Press:
- 31 May 2024, pp. 1-59
-
- Article
-
- You have access
- HTML
- Export citation
Distribution in homology classes and discrete fractal dimension
- Part of
-
- Journal:
- Proceedings of the Royal Society of Edinburgh. Section A: Mathematics , First View
- Published online by Cambridge University Press:
- 28 May 2024, pp. 1-8
-
- Article
-
- You have access
- Open access
- HTML
- Export citation
Partially hyperbolic endomorphisms with expanding linear part
- Part of
-
- Journal:
- Ergodic Theory and Dynamical Systems , First View
- Published online by Cambridge University Press:
- 28 May 2024, pp. 1-16
-
- Article
-
- You have access
- HTML
- Export citation
Girth Alternative for subgroups of
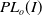 $PL_o(I)$
$PL_o(I)$
- Part of
-
- Journal:
- Glasgow Mathematical Journal , First View
- Published online by Cambridge University Press:
- 09 May 2024, pp. 1-10
-
- Article
-
- You have access
- HTML
- Export citation
Non-invertible planar self-affine sets
- Part of
-
- Journal:
- Mathematical Proceedings of the Cambridge Philosophical Society , First View
- Published online by Cambridge University Press:
- 08 May 2024, pp. 1-17
-
- Article
-
- You have access
- HTML
- Export citation
Weighted topological pressure revisited
- Part of
-
- Journal:
- Ergodic Theory and Dynamical Systems , First View
- Published online by Cambridge University Press:
- 08 May 2024, pp. 1-37
-
- Article
-
- You have access
- HTML
- Export citation
Similarities and differences between specification and non-uniform specification
- Part of
-
- Journal:
- Ergodic Theory and Dynamical Systems , First View
- Published online by Cambridge University Press:
- 15 April 2024, pp. 1-29
-
- Article
-
- You have access
- HTML
- Export citation
On the Hausdorff dimension of invariant measures of piecewise smooth circle homeomorphisms
- Part of
-
- Journal:
- Ergodic Theory and Dynamical Systems , First View
- Published online by Cambridge University Press:
- 11 April 2024, pp. 1-31
-
- Article
-
- You have access
- Open access
- HTML
- Export citation
Density of mode-locking property for quasi-periodically forced Arnold circle maps
- Part of
-
- Journal:
- Ergodic Theory and Dynamical Systems , First View
- Published online by Cambridge University Press:
- 04 April 2024, pp. 1-36
-
- Article
-
- You have access
- HTML
- Export citation