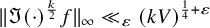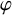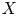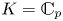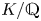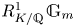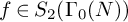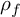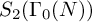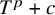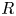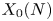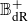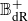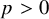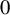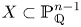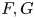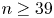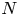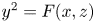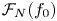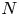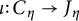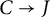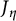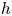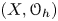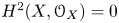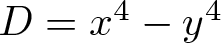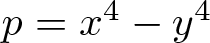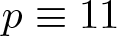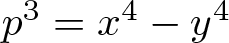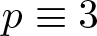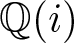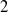320 results in 14Gxx
Theta functions, fourth moments of eigenforms and the sup-norm problem II
- Part of
-
- Journal:
- Forum of Mathematics, Pi / Volume 12 / 2024
- Published online by Cambridge University Press:
- 30 May 2024, e11
-
- Article
-
- You have access
- Open access
- HTML
- Export citation
A geometric p-adic Simpson correspondence in rank one
- Part of
-
- Journal:
- Compositio Mathematica / Volume 160 / Issue 7 / July 2024
- Published online by Cambridge University Press:
- 21 May 2024, pp. 1433-1466
- Print publication:
- July 2024
-
- Article
- Export citation
Weak approximation on the norm one torus
- Part of
-
- Journal:
- Compositio Mathematica / Volume 160 / Issue 6 / June 2024
- Published online by Cambridge University Press:
- 06 May 2024, pp. 1304-1348
- Print publication:
- June 2024
-
- Article
- Export citation
WILES DEFECT OF HECKE ALGEBRAS VIA LOCAL-GLOBAL ARGUMENTS: WITH AN APPENDIX BY NAJMUDDIN FAKHRUDDIN AND CHANDRASHEKHAR B. KHARE
- Part of
-
- Journal:
- Journal of the Institute of Mathematics of Jussieu , First View
- Published online by Cambridge University Press:
- 25 April 2024, pp. 1-81
-
- Article
-
- You have access
- Open access
- HTML
- Export citation
KOBAYASHI-OCHIAI’S FINITENESS THEOREM FOR ORBIFOLD PAIRS OF GENERAL TYPE
- Part of
-
- Journal:
- Journal of the Institute of Mathematics of Jussieu , First View
- Published online by Cambridge University Press:
- 17 April 2024, pp. 1-20
-
- Article
-
- You have access
- Open access
- HTML
- Export citation
GENERALISED QUADRATIC FORMS OVER TOTALLY REAL NUMBER FIELDS
- Part of
-
- Journal:
- Journal of the Institute of Mathematics of Jussieu , First View
- Published online by Cambridge University Press:
- 11 April 2024, pp. 1-54
-
- Article
-
- You have access
- Open access
- HTML
- Export citation
Lower Bounds for the Canonical Height of a Unicritical Polynomial and Capacity
- Part of
-
- Journal:
- Forum of Mathematics, Sigma / Volume 12 / 2024
- Published online by Cambridge University Press:
- 02 April 2024, e45
-
- Article
-
- You have access
- Open access
- HTML
- Export citation
Modular curves and Néron models of generalized Jacobians
- Part of
-
- Journal:
- Compositio Mathematica / Volume 160 / Issue 5 / May 2024
- Published online by Cambridge University Press:
- 26 March 2024, pp. 945-981
- Print publication:
- May 2024
-
- Article
-
- You have access
- Open access
- HTML
- Export citation
A note on Hodge–Tate spectral sequences
- Part of
-
- Journal:
- Mathematical Proceedings of the Cambridge Philosophical Society / Volume 176 / Issue 3 / May 2024
- Published online by Cambridge University Press:
- 22 March 2024, pp. 625-642
- Print publication:
- May 2024
-
- Article
- Export citation
Topology of moduli spaces of curves and anabelian geometry in positive characteristic
- Part of
-
- Journal:
- Forum of Mathematics, Sigma / Volume 12 / 2024
- Published online by Cambridge University Press:
- 14 March 2024, e33
-
- Article
-
- You have access
- Open access
- HTML
- Export citation
On the Hasse principle for complete intersections
- Part of
-
- Journal:
- Compositio Mathematica / Volume 160 / Issue 4 / April 2024
- Published online by Cambridge University Press:
- 05 March 2024, pp. 771-835
- Print publication:
- April 2024
-
- Article
-
- You have access
- Open access
- HTML
- Export citation
Most odd-degree binary forms fail to primitively represent a square
- Part of
-
- Journal:
- Compositio Mathematica / Volume 160 / Issue 3 / March 2024
- Published online by Cambridge University Press:
- 08 February 2024, pp. 481-517
- Print publication:
- March 2024
-
- Article
- Export citation
Heights and quantitative arithmetic on stacky curves
- Part of
-
- Journal:
- Canadian Journal of Mathematics , First View
- Published online by Cambridge University Press:
- 19 January 2024, pp. 1-54
-
- Article
-
- You have access
- Open access
- HTML
- Export citation
The Manin–Peyre conjecture for smooth spherical Fano varieties of semisimple rank one
- Part of
-
- Journal:
- Forum of Mathematics, Sigma / Volume 12 / 2024
- Published online by Cambridge University Press:
- 18 January 2024, e11
-
- Article
-
- You have access
- Open access
- HTML
- Export citation
A rigid analytic proof that the Abel–Jacobi map extends to compact-type models
- Part of
-
- Journal:
- Canadian Mathematical Bulletin , First View
- Published online by Cambridge University Press:
- 09 January 2024, pp. 1-7
-
- Article
- Export citation
On the Bezrukavnikov–Kaledin quantization of symplectic varieties in characteristic p
- Part of
-
- Journal:
- Compositio Mathematica / Volume 160 / Issue 2 / February 2024
- Published online by Cambridge University Press:
- 05 January 2024, pp. 411-450
- Print publication:
- February 2024
-
- Article
- Export citation
INTERSECTING THE TORSION OF ELLIPTIC CURVES
- Part of
-
- Journal:
- Bulletin of the Australian Mathematical Society , First View
- Published online by Cambridge University Press:
- 27 December 2023, pp. 1-8
-
- Article
- Export citation
ON A COMPARISON BETWEEN DWORK AND RIGID COHOMOLOGIES OF PROJECTIVE COMPLEMENTS
- Part of
-
- Journal:
- Nagoya Mathematical Journal / Volume 254 / June 2024
- Published online by Cambridge University Press:
- 01 December 2023, pp. 420-461
- Print publication:
- June 2024
-
- Article
-
- You have access
- Open access
- HTML
- Export citation
On the difference of two fourth powers
- Part of
-
- Journal:
- Proceedings of the Edinburgh Mathematical Society / Volume 67 / Issue 1 / February 2024
- Published online by Cambridge University Press:
- 10 November 2023, pp. 142-150
-
- Article
- Export citation
Notes on hyperelliptic mapping class groups
- Part of
-
- Journal:
- Glasgow Mathematical Journal / Volume 66 / Issue 1 / January 2024
- Published online by Cambridge University Press:
- 31 October 2023, pp. 126-161
- Print publication:
- January 2024
-
- Article
- Export citation