Introduction
In Chapter 8 I presented an overview of my vision of the long-term evolution of human societies with an emphasis on the transition from a biologically constrained cognitive evolution to a socially constrained one. In Chapter 9 I introduced the concept of dissipative flow structure as a tool to understand that information flow drives the coevolution between cognition, environment, and society. In Chapter 10, I drilled down into history and showed how technological advances in a region, made necessary by environmental circumstances and in interaction with the economy, transformed society and its institutions in a continuous back and forth between solutions and the challenges that these raised. Ultimately, they lead to the current landscape, technology, economy, and political organization of the Western Netherlands. In this chapter I want to step back again to a more general perspective and emphasize the nature of the principal, different system states that occurred in the second, sociocultural part of the long-term trajectory outlined in Chapter 8. This will show the role of changes in information processing structures that are responsible for such transitions.
Ever since the classic series of proposals by Sahlins and Service about the evolution of societal organization that appeared in the 1960s (Sahlins & Service Reference Sahlins and Service1960), it has generally been acknowledged that there have been a number of transitions in societal structure as societies grew in size and complexity, even though the details of these transitions have been open to much discussion. In the perspective that I am developing in this book, such transitions are essentially transformations of the structure of their information processing apparatus. In this chapter, I will look in some detail at these structures from an organization perspective.
Information Processing and Social Control
The wide literature on information-processing, communication, and control structures in very different domains presents us with (for the moment) three fundamentally different kinds of such structures. These differ notably in the form of control exerted over the information processing, regulating who has access to the information and who does not, but also determining to an important extent these structures’ efficiency in processing information and in adapting to changing circumstances, such as the growth of networks, or to various kinds of external disturbances. These differences have a number of consequences for the conditions under which each kind of communication structure operates best. I will first describe some of these consequences for each of these types of control structure.
Processing under Universal Control
When the universe of participating individuals is small enough that all know each other, messages can be sent between all participants. Even though, inevitably, some members of the society associate with each other more than others, the contacts between individual members are so frequent that information can spread in myriad ways between them. Communication therefore does not follow particular channels, except maybe in special situations. Moreover, because so many different channels link the members, there are no major delays in getting information from one individual to another. If a channel is temporarily blocked, a nearby channel, which is hardly longer, will convey the information immediately (Figure 11.1).
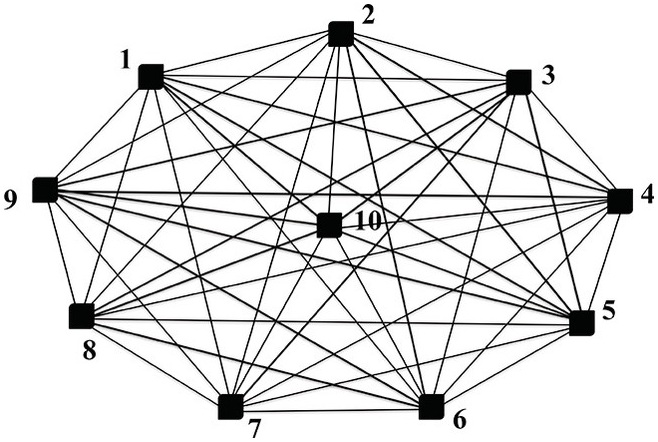
Figure 11.1 Graph of egalitarian information processing with universal control: all individuals are communicating with all others.
In addition, there is no control over information. Because each member of the group receives information from a number of different directions, and sends it on in different directions as well, there is ample opportunity to compare stories and thus correct for biases and errors. Although it takes time, groups in this situation usually manage eventually to have a highly homogeneous “information pool” on which to base their collective decisions.
The situation is that of small group interactions described by Mayhew and Levinger (Reference Mayhew and Levinger1976, Reference Mayhew and Levinger1977) in terms of the relationship between information flow, group size, and dominance of individuals in the group. It applies to egalitarian societies, in which control over information is very short lived and is accorded to specific individuals as a function of their aptitude to deal with specific kinds of situations, because these individuals have a particular know-how of the kind of problem faced. As a result, no single individual or group can ever gain longer-lasting control over such a society. In such situations, the homogeneity of the information pool is further aided by face-to-face contact. In such a contact situation, it is possible for the sender and the receiver of messages to communicate over many channels: words, tone of voice, gestures, eyes, body language, etc. Communication is therefore potentially very complete, detailed, and subtle. Mutual understanding can be subtle and can connect many cognitive dimensions, even though these remain relatively fuzzily defined.
Mayhew and Levinger (Reference Mayhew and Levinger1976, Reference Mayhew and Levinger1977) also show how the amount of time needed for each interaction between the members of the group effectively limits the size of such groups. The (logistic) information flow curve in a small group rises exponentially with the addition of members, until there is not enough time in the day to talk sufficiently long to everyone to keep the information pool homogeneous. Yet homogeneity is essential for the survival of the group because it keeps the incidence of conflict down. Increasing heterogeneity will immediately cause fission until the maximum sustainable group size is reached again. Johnson (Reference Johnson, Renfrew, Rowlands and Segraves1982) presents a large number of cases of societies organized along these lines. It should be noted that this kind of communication model is thus confined to very small-scale societies. It limits communication to what can be mastered by all individuals in the group and avoids the emergence of any specialized knowledge such as we see in more complex societies, thus also limiting the overall knowledge/information that can be shared. For an ethnographic study that highlights these dynamics, without using the terminology I have adopted, see Birdsell (Reference Birdsell1973).
Processing under Partial Control
When some participants know of all others, but others do not, some people can directly get messages to all concerned whereas others cannot do so. Such asymmetric situations arise when the group concerned is too large to maintain an egalitarian communication system or a homogeneous information pool. From ethnography and history, we know a wide range of societies that communicate and decide in this manner. They are extremely variable in overall size, as well as in the size of their component units, their communications, information processing structure, etc.
Processing under partial control is fundamentally different from universal control over communication and decision-making because it relies both on communication and on noncommunication between members. Members of the group usually communicate with some others, but not with the remainder of the group. The usual form that communications structures take in these societies is a hierarchical one (Figure 11.2), because it is the most efficient way to reduce the number of communications needed to (eventually) spread information from the center to the whole group (Mayhew & Levinger Reference Mayhew and Levinger1976, fig. 8).
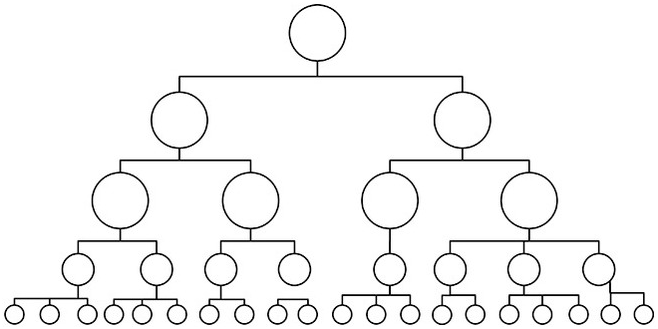
Figure 11.2 Graph of hierarchical organization with partial control: some people have more information at their disposal than others.
Evidently, such communication structures generate considerable heterogeneity in the information pool. As stories are transmitted they will inevitably change, and for most individual members of the society there is no way to correct this by comparing stories from a wide enough range of different sources.
But because there is relatively little communication crosscutting habitual channels, few are aware of that heterogeneity. This creates a potential problem: when information spreads in unusual ways, its heterogeneity is suddenly highlighted, causing explosive increases in conflict and strong fissionary tendencies. Suppression and control of information is therefore an essential characteristic of hierarchical systems.
As long as the society needs the communication capacity of its hierarchical control structure to remain intact, that structure is acceptable; but whenever the information flow either drops too low or exceeds channel capacity, the hierarchy will be under stress. In other words, as long as it is experienced as an enabling feature, the delegation of individual responsibility to those in control is acceptable. But as soon as the hierarchy is experienced as a constraint, the members of the group will try to forge links that circumvent the established channels. This starves the hierarchy of vital information and reduces its power and efficiency. Hence, frequent system stresses favor the implementation of hierarchical information flow structures, and such structures have a stake in maintaining the stresses concerned, but also in ensuring that they do not exceed certain levels that would tear the societal structure asunder.
Many essential communication channels in hierarchical systems are longer than in egalitarian ones, so that the risk that signals are lost is enhanced. Communications need a stronger signal-to-noise ratio. What is a signal in one cognitive dimension may be noise in relation to most other dimensions. One way in which to create a stronger signal is therefore to reduce the number of cognitive dimensions to which it refers. This can be achieved by strictly defining the contexts of interpretation, for example by imposing taboos or by ritual sanctioning. The establishment of such reduced-dimension cognitive structures manifests itself in the emergence of specialized knowledge in the group, thus widening the spectrum of knowledge, whether that is technological, commercial, religious, or other.
Processing without Central Control
When none of the participants know all the others, none can send any direct messages to all concerned (Figure 11.3). More importantly, in such a situation people necessarily send out messages without knowing whom they will reach or what the effect will be.
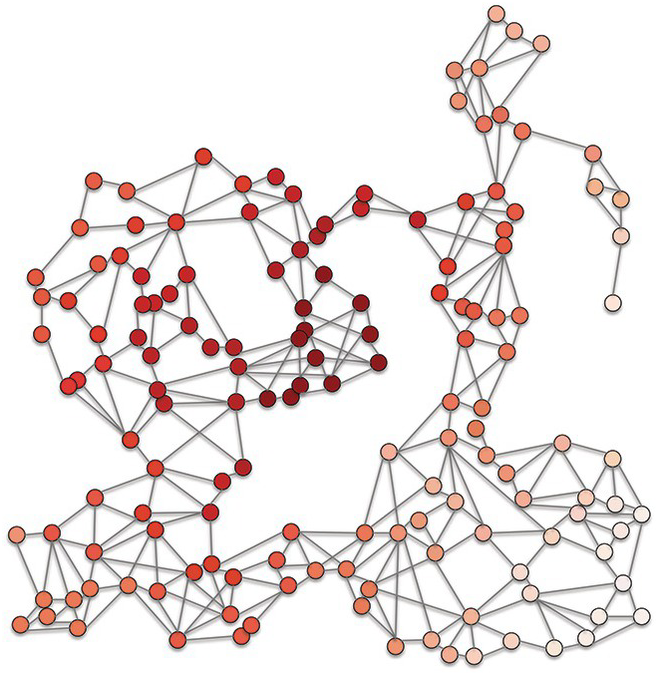
Figure 11.3 Graph of random communication network, without any control, in which all individuals have partial knowledge.
Whereas in our first example everyone was in the know and in our second one some were informed and some were not, in this case everyone is partly informed. People depend entirely on this partial information, which they cannot complete. Their information pool is much more heterogeneous, but because it is homogeneous in its heterogeneity, the situation is relatively stable.
In this situation, there are no set communication channels. Instead, there are multiple alternative channels if information stagnates anywhere or if it becomes too garbled. The system is thus more flexible and therefore more resistant to disruption from the outside; consequently it allows for a larger interactive group and a quantum increase in total amount of information processed. By the same token, no set individuals are in control of the whole information flow, which also makes the situation less vulnerable to individual incidents, such as those that regularly mar succession in hierarchical systems.
But on the other hand, more is demanded of the means of communication. More information needs to be passed, and more efficiently, between individuals who are less frequently and less directly in contact with one another. That is, paradoxically enough, facilitated when communications no longer depend on face-to-face situations in which communication occurs across a wide range of media or channels. Written communications can transcend space and time, and they become important because they fix a signal immutably on a material substrate, reducing down-the-line loss or deformation of the signal. But they also avoid transmitting certain dimensions that can be, and are, transmitted in face-to-face communication, and such communication can thus be more precise and avoid simultaneous transmission of contradictory signals.
This third mode of communication is the one that is generally present in (proto-) urban situations. But there it always occurs alongside universally controlled networks (families and other face-to-face groups) and often together with hierarchical communication networks. The different networks are connected via individuals who function in more than one of them. We will get back to such mixed or heterarchical networks in a later part of this chapter.
Phase Transitions in the Organization of Communication
To understand the differences in information processing dynamic that are responsible for these different kinds of social organization, it is useful to look at them from the perspective of a spreading activation network. That will allow us to begin to answer the following two questions:
How may these different communication structures have come into being?
How are they affected by changes in the size of the group and in the amount of information processed?
Such a spreading activation net consists of a set of randomly placed nodes (representing individuals) that have various potentially active (communicative) states (μ: the average number of connections leaving one node) with weighted links between them (Huberman & Hogg 1987). Their weight determines how much the activation (α) of a given node directly affects others (such as the degree to which messages get across and/or the degree to which people spread a message further, etc.). After a certain time, the action has run its course and the connection between the nodes lapses into “relaxation” (γ)
The behavior of such networks is thus controlled by two parameters, one specifying their shape or topology (μ) and the other describing local interactivity (α/γ: activation over relaxation), an estimate of the volume of information flow being processed. Visualization of the system is dependent on the transformative twists and turns of topology and the curving forms of dimensional nonlinearities to understand its statistical mechanics.
In assessing its dynamics, it is important to be aware of the fact that in such a model the interactivity (represented by α/γ) and the connectivity of the system (μ) are independent variables. In the two-dimensional graph of α/γ and μ, (Figure 11.4), different zones appear that one can identify as characterizing different types of information processing systems by combining different values for the two variables.
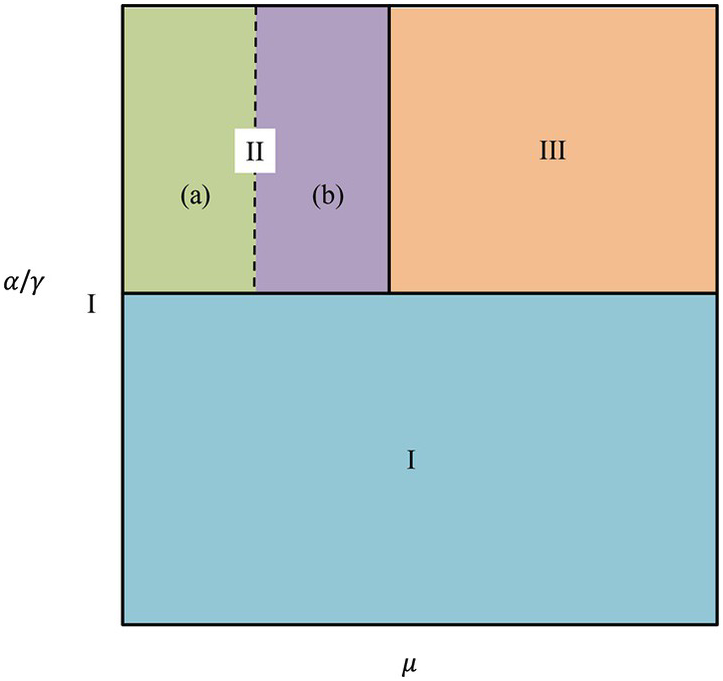
Figure 11.4 Phase diagram of a spreading activation net. The vertical axis represents the parameter α/γ and the horizontal axis represents the connectivity parameter μ. Phase space I represents localized activation in space and time; phase space II represents localized but continuous activation; phase space III represents infinite activation.
The precise nature of each state of the information processing system is the result of the interaction between these two parameters. We shall see that this only strengthens the implications of the model.
The behaviors of both an infinite and a finite case of such a system are represented in Figure 11.4. Essentially, for the two variables μ and α/γ there are three states of the system. In the first (state I), both are small and activation remains localized in time and space. One can think of such activation as taking place in finite clusters with little temporal continuity. This leads to a kind of balancing out. Hence, as long as the activation intervals of the different sources do not change much in relation to the overall relaxation time t, a net in which different nodes give different activation impulses will almost always remain near the point where activation started (state I in Figure 11.4). It is, moreover, remarkable that, in the finite case this stable state is, for very low α/γ, valid irrespective of the value of μ across its entire spectrum left to right. As we shall see, this is one of the key insights of the model.
As α/γ increases while μ is small (state II near 1; i.e., on average each node is connected to only one other node), relaxation becomes more and more sluggish. This initially causes the event horizon to grow in time but remain localized in space: the interactive clusters remain small but gain temporal continuity (state II in Figure 11.4). In a second step, with equally small μ and further increasing α/γ, the interactive nodes also expand in space: the clusters involve more and more nodes (state III in Figure 10.4). Under those conditions, “ancient history matters in determining the activation of any node, and […] since the activity keeps increasing, the assumption of an equilibrium between the net and the time variations at the source no longer holds” (Huberman & Hogg 1987, 27). A further peculiarity of the transition between states II and III is that, for μ near 1, the size of the clusters involved will know very large fluctuations.
For yet larger α/γ and higher μ, the amount of spreading grows indefinitely in both space and time, and therefore far regions of the net can significantly affect each other, another key insight. The transition to this state (state III in Figure 11.4) is abrupt: a large number of finite clusters is suddenly transformed into a single giant one as the number of nodes with values above this activation threshold grows explosively.
There are many interesting implications of this work for an information-processing approach to societal dynamics. For our immediate concerns, we are particularly interested in the following:
As long as the α/γ of the different nodes is much longer than the overall relaxation time t, all interaction in such a net remains localized, and the overall system remains in a stable state (state I). Moreover, the above is true irrespective of the number of people with which each individual interacts (the connectivity μ of the network). This might answer one of the most poignant questions of them all: “Why are the first 60,000 years of anatomically and cognitively modern man so particularly devoid of change?” The answer is that there was not enough interaction between the members of the sparse population to make information processing and communication take off. With so little information to process, the degree of interactivity of the people sharing that task does not seem to matter.
The fact that as α/γ increases while μ remains near 1, small clusters initially only gain in continuity (state IIa), and that only for even higher values of α/γ they spread in space (state IIb). Hence, when the quantity of information processed is only moderately increased, group size will remain small, but individual groups will exist longer in terms of travel through the graph. The quantity of information processed must increase considerably before larger groups of individuals can durably be drawn together in a network. I interpret this as a transition from rather unstable, short-lived, small groups to more stable, longer-living groups of people such as (small) tribes.
The fact that very large fluctuations in stability and size occur (for μ near 1) at the transition between states II and III; i.e., as the spatial extent of the activation network grows. According to the model, even as the information flow increases very considerably, provided the interactivity of the people drawn into the network remains limited, both the size range and the degree of permanence of the groups will vary wildly. This would indicate that at this point in development, groups of similar density and interactivity, which process similar volumes of information per capita, might exhibit spectacular differences in size, and that their interaction was far from durable. This would support the view that chiefdoms are unstable transitional organizations. It also applies to our understanding of the size differences in tribes and segmented lineages.
After this period of heavy instability, a third transition suddenly occurs from groups of very many different sizes (state IIb) to a continuous communication network (state III). This transition is attained by simultaneously increasing both α/γ and μ. In effect, as the volume of the information flow and the connectivity of the population grow, participation in one infinite network is inevitable. But the following particularities of this transition have interesting implications:
∘ If one introduces a measure of physical communication distance in the model, and imposes the constraint that the individuals in strongly interacting parts must physically be close to one another, the percolation model develops “clumpiness” in the spatial distribution of interaction in state II. This suggests that although theoretically very large rural social systems are a possibility, practical constraints make the emergence of spatial centers (such as villages or towns) highly probable in the absence of the equivalent of the Internet.
∘ The suddenness of the transition is explained by the exponential increase in interactivity and information flow as population density increases. This is compatible with the thesis that large-scale communications systems do not slowly spread from one center, but that a number of centers come about virtually simultaneously. This clearly is the case with urban systems, which always emerge as clusters of towns rather than as single towns.
∘ Long-range interactions emerge in state III. As soon as the whole of the system is in effect interactive, it is of course possible that interactions occur that link nodes in very distant parts of the system. This transition is reflected in the archaeological record in the form of long-distance trade.
∘ The model seems to indicate that an increase in the volume of information processed alone is not enough to really make the network develop long distance connectivity. In other words, it is a necessary condition but not a sufficient one: increasing interactivity between participant units is at least as important. Indeed, with low interactivity the effect of a unit increase in the volume of information flow on activation is at best linear, whereas the effect of a unit increase in connectivity is exponential, both on the volume of information flow and on activation.1
Modes of Communication in Early Societies
For this section, I am tentatively according the percolation model above the status of a metaphor applicable to the different observed forms of social organization and the changes between them. This metaphor distinguishes several different states of the percolation network and at least four important transitions.
The first state is a very stable state overall, though the individual interactive groups in it are small, very fluid, and ephemeral. The number of nodes in direct contact with any other node may vary. The anthropologist is, of course, immediately reminded of the very fluid and mobile social organization into small groups that was successfully maintained by gatherer-hunter-fisher societies for all of the Palaeolithic. It is generally estimated that such groups consisted of a few families, maybe up to about fifty people. In cases such as those of the Australian Aborigines, the Inuit, and the !Kung, individual members of such societies frequently move from band to band, while bands themselves frequently fuse or fission.
The first transition from this state that becomes visible in the percolation model, as α/γ is increased, transforms small ephemeral groups (state I) into groups of about the same size, but with communications channels that are stable for somewhat longer periods (state IIa). These groups may represent both “great men” and “big men” societies (Godelier Reference Godelier1982; Godelier & Strathern Reference Godelier and Strathern1991). In “great men” societies, typically consisting of a few hundred people, particular individuals come to play the upper hand in the context of a specific (set of) problem(s). Such individuals as achieve this are generally accorded that status because of their particular knowledge or capability to deal with a situation. As such their influence is delegated to them by the society. In the case of “big men” societies, the individuals who have come to the fore have done so by virtue of their wealth and their role in redistributing wealth among the members of the group. The groups would generally seem to be of about the same size. In neither case is there hereditary transmission of power, although it is easier to become a great (or big) man if your father was so. As far as the model is concerned, this state of the system would seem to include both mobile and sedentary groups.
As α/γ grows further, the percolation model predicts a second transition, from such small, periodically stable groups to groups that are stable over longer periods and exhibit a growing spatial presence (state IIb). I would associate this state of the model with a wide range of generally sedentary societies counting minimally a few hundred or a thousand members (tribes?). All acknowledge some sort of boss. As α/γ grows, these groups become larger and more enduring societies. In the process, μ may also be increasing, but much more slowly. These larger groups I tentatively propose to equate with what anthropologists such as Service (Reference Service1962, 1975) at one time called “segmentary lineages” and “chiefdoms,” more or less stable social formations that may include up to several tens of thousands of people.1
If this interpretation is correct, the small, mobile, and ephemeral groups of state I are generally egalitarian, those of state IIa alternate egalitarian information processing with occasional moments of hierarchical organization, particularly in times of stress, and the larger groups of state IIb are usually hierarchically organized. In many instances, crosscutting affiliations do to some extent mitigate the negative effects of a hierarchical organization among segmentary lineages and chiefdoms.
A detailed comparison between properties of small hierarchies as outlined above (Huberman & Hogg Reference Hogg, Huberman, Prigogine and Sanglier1987) and empirical observations, suggests (topological) answers to some aspects of the observed behavior of social systems documented by ethnographers (e.g., Johnson Reference Johnson, Renfrew, Rowlands and Segraves1982). First, it is interesting to note that cooperation between members of randomly interacting graph structures reduces the stability of such groups. This seems to indicate that fission among small face-to-face groups (“bands” in Service’s Reference Service1962 terms) in “empty space” must have had a very high incidence indeed, which undoubtedly contributed to the long absolute time span over which such groups dominated human social organization.
Next, if we take into account that in small face-to-face groups dominance relations develop with great frequency (Mayhew & Levinger, Reference Mayhew and Levinger1976, Reference Mayhew and Levinger1977), we may conclude from Hogg et al. (Reference Hogg, Huberman and McGlade1989) that the emergence of hierarchies can be argued to be statistically probable under a wide range of topological conditions. Hierarchies, therefore, need not have emerged under pressure. By implication, we must begin to ask why hierarchies did not develop much earlier in human history, rather than question how their development was possible at all. One possible answer seems to be that there was not enough information to go around to maintain the (much more efficient) hierarchical networks. Under those circumstances, the advantages of a homogeneous information pool may well have outweighed the potential gains in efficiency that hierarchy and stability could have offered. But we should also consider the possibility that such hierarchies emerged much more frequently than the ethnographic record seems to indicate. The speed with which information diffuses increases exponentially in a hierarchy that grows linearly in number of levels. Huberman and Kerzberg (Reference Huberman and Kerzberg1985) call this effect “ultradiffusion” (discussed here and in Appendix A). This could explain why, if scalar stress increases as a function of size, an increment in the response to stress could decrease with increments of group size (see Johnson Reference Johnson, Renfrew, Rowlands and Segraves1982, 413).
Indeed, ultradiffusion implies that with linear increases in the number of levels of a hierarchy, the size of the group that communicates by means of that hierarchy can grow exponentially. Ultradiffusion may thus explain the wide range of sizes (102–104 or more) of the groups that are organized along hierarchical lines, a fact that has long been noted in the study of what archaeologists and anthropologists call, following Service (1975) chiefdoms.
The percolation model predicts a very sudden third transition from spatially localized systems (state IIb) to infinite ones (state III), owing to an extension of the communications network to a (near) infinite number of individuals, with remarkable long-distance interactions. It essentially seems to represent what is known in archaeology and anthropology as the transition to states or even empires, which potentially include millions of people spread out over very large areas. As Wallerstein (Reference Wallerstein1974) has shown, such states and empires also activate large numbers of people outside their boundaries, so that the total number of people involved in their networks may be much larger than it seems.2
As I do not know of any enduring infinitely large purely hierarchical systems, I interpret this transition as leading to the introduction of distributed information processing alongside complex and large hierarchical organizations. The distortions and delays inherent in communicating through long hierarchical channels combined with the physical proximity of individuals belonging to different hierarchies will eventually have led to the formation of cross-links in and between hierarchies. This has the advantage that the individuals concerned can collect information received through many channels.
As soon as the average channel capacity can no longer cope with the amounts of information to be processed, the maintenance of the hierarchies concerned will then have become combined with other information processing avenues. We know that the information flows in both states and empires are maintained by both hierarchical (administrative) and distributed (market) systems. Such “complex societies” are the subject of the next part of this chapter.
Hierarchical, Distributed, and Heterarchical Systems
The remainder of this chapter will be devoted to answering questions about the dynamic properties of various forms of information-processing organization. For this I turn to the stretching and transforming capabilities of their topologies, which requires a rather technical discussion of the mathematical underpinnings of the behavior of these organizations, the details of which will not be of great interest to many readers. I will therefore attempt a summary of their main characteristics in this chapter and present some of the mathematical basis in Appendix A.
I begin this inquiry by distinguishing, with Simon (Reference Simon1962, Reference Simon1969), two fundamental processes that generate structure in complex systems: hierarchies and market systems. I have already presented a (simple) outline of the structure of a hierarchy in Figure 11.2. The essential thing to remember about hierarchies is that they have a central authority. The person or (small) group at the top of the hierarchy gathers all available information from people lower down, and then decides and instructs people lower down the hierarchy. Markets, on the other hand, are distributed horizontal organizations, without central control over information processing. An example is presented in Figure 11.3. Their collective behavior emerges from the interaction of individual and generally independent elements involved in the pursuit of different goals. All individuals participating in them have equal access to partial information, but the knowledge at each individual’s disposal differs. Examples of such market systems abound in biological, ecological, and physical systems, and their societal counterparts include the stock exchange, the global trade system, and local or regional markets.
Each of these two modes of information processing has different advantages and disadvantages, and these are fundamental for our understanding of the evolution of information processing in complex societies, as such societies combine features of both these kinds of dynamic structures. These differences concern the systems’ stability or instability, their efficiency, the oscillations they are subject to, the likelihood of transitions from one state to another, etc.
The first difference to be noted between hierarchies and market systems concerns their efficiency in information processing. In multilevel hierarchical structures each level is characterized by units that have a limited degree of autonomy and considerable internal coherence owing to the overall control at the top of the hierarchy. As the number of hierarchical levels increases linearly, the number of elements at the bottom (in technical language called leaves) increases geometrically (see the next section, point 1, and Appendix A for an explanation of this phenomenon). Under ideal conditions, the goal-seeking strategies of hierarchical structures maximize or optimize given resources, and can harness and process greater quantities of material, energy, and information per capita than market organizations.
An important feature of market systems is their inherently nonoptimizing behavior. There are two basic reasons for this. First, optimality in such structures would require that each actor have perfect information. But this is impossible since, as Simon (Reference Simon1969) points out, we inhabit a world of incomplete and erroneous information. As a consequence, the mode of operation of distributed systems is best defined as satisficing rather than optimizing. Second, rather than by hierarchical control, behaviors in market systems are constrained by their nonlinear structure. The strength of existing structures, for example, can prevent the emergence of competing structures in their nearby environment – even though these new structures may be more obviously efficient. A useful modern example is to be seen in the American motor industry, which continued the production of large, energy inefficient cars long after it was apparent that smaller cars were more fuel-efficient and less polluting. Overall therefore, market systems are less efficient than their hierarchical counterparts in processing matter, energy, and information. The differences between the market and hierarchical systems probably explain why, even in modern political systems such as those examined by Fukuyama (Reference Fukuyama2015), the best choice of government is a mix of the two (see also next section, point 1).
The next difference concerns the organizational stability of these two kinds of information processing structures. Since they operate on principles of competitive gain and self-interest, market systems are highly flexible and diverse. Political and legislative control in such systems is always difficult, as we see in our current democracies, because people in such distributed systems act on partial and different information and have more freedom to foster different perspectives. Such systems’ behaviors can therefore relatively easily become potentially disruptive and even destructive of the organizational stability of society.
This is, of course, not so in the case of hierarchical structures, whose main raison d’être lies in the efficiency with which authoritative control over decision-making is exercised at the top. But this means that the people lower down the hierarchy must sublimate many of their personal desires and aspirations for the good of the system. Autocratic and authoritarian rule systems may emerge to preserve the hierarchy’s pyramidal structure and maintain its organizational goals until they are no longer accepted by the base of society.
In view of these characteristics, it is highly improbable that either fully hierarchical or entirely market-based systems would have been able to provide a durable, coherent, structural organization for large societal systems. But the limitations of both hierarchical and market organizations can be avoided if they are coupled in complementary ways (Simon Reference Simon1969).3 Such societal structures that combine hierarchical and distributed processing are here called heterarchies.4 Their hybrid nature dampens or reduces the potential for runaway chaotic behavior and thus increases the information processing capacity of the system. Our next task is therefore to analyze in more detail the relationships between the structure and the information processing dynamics of hierarchies and market systems, and then to determine how they might interact in a heterarchy.
The first issue is the speed of information diffusion in hierarchical and market systems respectively.
Information Diffusion in Complex Hierarchical and Distributed Systems
Complex Hierarchies
Unfortunately, large hierarchies cannot be studied by observing the behavior of their parts (as one can do with small systems), nor can they be treated in a statistical manner, as if the individual components behave with infinite degrees of freedom. They are essentially hybrids of micro- and macrolevel structures, and need an approach of their own.5 That would involve treating the individual leaves at the lowest levels of a hierarchy statistically, by integrating over them, while considering those at the top static, as they constrain the intervening levels of the hierarchy everywhere in the same fashion (Huberman & Kerzberg Reference Huberman and Kerzberg1985; Bachas & Huberman Reference Bachas and Huberman1987). With that as a point of departure, Huberman’s team has developed a number of ideas about the information-processing characteristics of hierarchies that can be summarized as follows (see Appendix A):
1. Independent of the size of the population that a hierarchy integrates, there is an upper limit to the time it takes to diffuse information throughout it. For example, when expanding a hierarchy from five levels to six, the additional time needed to diffuse the information is a root of the time added upon expansion from four levels to five. There is a power-law involved, which relates the speed of information diffusion to the number of levels in the hierarchy. Hierarchies are therefore very efficient in passing information throughout a system and, although somewhat counterintuitive, the more levels the hierarchy has, the more rapidly information is (on average) distributed.
2. If a hierarchical tree is asymmetrical around a vertical axis, such as when the number of offspring is three per node on one side and two per node on the other, then overall diffusion is slower because it takes more time for the information to be diffused on one side than it does on the other side, and that may in turn garble information because, as all transfers pass in part through the same channels, interference and loss of signal will occur. Such constraints might lead one to predict that under unconstrained circumstances, fat and symmetrical trees would tend to develop. Evidence of asymmetrical ones or particularly narrow ones could therefore serve as pointers to such constraints.
3. This may be a major constraint on the hierarchy’s capacity to stably transfer undistorted information. To quantify this, we need to look at the overall complexity of the tree (again, for mathematical detail see Appendix A). It turns out that for large hierarchies, very complex trees will have a complexity that at most increases linearly with the number of its levels. That complexity is inversely proportional to the tree’s information diffusion capacity.
4. But is the number of levels unlimited? Theoretically, adding one more level to a hierarchy allows for an exponential increase in the number of individuals that it connects. If we assume a constant signal emission rate for leaves at the base of the hierarchy, it follows that the number of signals produced by the individuals at the base also increases exponentially. The diffusion of information through the whole system (see point 1) that permits this exponential increase, however, is achieved at the expense of reducing the increase in the amount of information that circulates to a linear one. This is done by “coarse-graining,” or suppressing detail every time a signal moves up to the next level. Thus, while the speed of diffusion of information increases, the precision of the information distributed decreases.
5. Defining adaptability as the ability to satisfy variations in constraints with minimal changes in the structure, Huberman and Hogg (1986, 381) argue that the most adaptable systems are the most complex, because such systems are the most diverse, whereas the most adapted systems tend to have a lower complexity than the adaptable ones, because the development of situation-specific connections will lower the diversity of the structure. Complexity seems to be lowered when a system adapts to more static constraints, thus lowering its adaptability and its potential rate of evolution.
The fact that these results are due to mathematical/topological properties of hierarchies, and are independent of the nature of the nodes or the connections between them, gives them wide implications, not only for computing systems, but also for social systems in which hierarchies play an important part.
Distributed Systems
Distributed systems are characterized by structural variables such as the degree of independence of the individual participants; the degree to which they compete or cooperate; the fact that knowledge about what happens in the remainder of the system is incomplete and/or that the individual actors are informed with considerable delays, and finally the ways in which finite resources are allocated within the system. Although a formal information processing structure is missing, distributed systems behave in some respects with considerable regularity, whereas in other respects their behavior is fundamentally unstable and irregular. The regularity is evident at the overall level, and is exemplified by the so-called Power-law of Learning (Anderson Reference Anderson1982; Huberman Reference Huberman2001), which states that those parts of a system that have started to perform a task first are more efficient at it. As a result, distributed systems structure themselves universally according to a Pareto distribution.6
Huberman and Hogg (Reference Huberman, Hogg and Huberman1988) study the behavior of such distributed systems by building a model that fits the following description:
The model consists of a number of agents engaging in various tasks, and free to choose among a number of strategies according to their perceived payoffs. Because of the lack of central controls, they make these choices asynchronously. Imperfect knowledge is modeled by assuming the perceived payoff to be a slightly inaccurate version of the actual payoff. Finally, in the case when the payoffs depend on what the other agents are doing, delays can be introduced in the evaluation of the payoffs by assuming each agent only has access to the relevant state of the system at earlier times.
After analyzing one by one the impact of a number of the variables mentioned above, their conclusions give us the following ideas about the behavior of distributed systems:
1. First, they calculate the number of agents engaged in each of the different strategies at any point in time. These strategies have different degrees of efficiency. Only in the case of complete independence of action and completely perfect knowledge by all actors do they achieve optimal overall efficiency. But if imperfect knowledge is introduced, the distributed system operates below optimality: never are all agents using the optimal strategy. In real life, distributed systems satisfice rather than optimize.
2. Where action depends in part on what other agents are doing, the payoff for each actor will also depend on how many others are choosing the same strategy and bidding for the same resources. Independent of the initial values chosen, with perfect knowledge the system will converge on the same suboptimal point attractor, which is the highest available given the constraints involved. That is evidently an entirely stable situation. With imperfect knowledge, however, an optimality gap develops of a size that is dependent on the uncertainty involved. The result is the same for competitive and co-operative strategies.
3. Time delays can also introduce oscillations into distributed systems. If the evaluation of payoff is delayed for a period shorter than the relaxation rate of the system the system evidently remains stable. But longer evaluation delays give rise to damped oscillations that signify initial alternate overshooting and undershooting of the optimal efficiency, and really long delays create persistent oscillations that grow until bounded by nonlinearities in the system. The oscillations depend on the degree of uncertainty in evaluating the payoff: large uncertainty means that the delays are less likely to push the system away from stability.
4. In a system of freely choosing agents, the reduced payoff due to competition for resources and the increase in efficiency resulting from cooperation will push the system in opposite directions. In that situation, a wide range of parameter values generates a chaotic and inherently unpredictable behavior of the system with few windows of regularity. Very narrowly different initial conditions will lead to vastly different developments, while rapid and random changes in the number of agents applying them make it impossible to determine optimal mixtures of strategies. In certain circumstances, regular and chaotic behaviors can alternate periodically so that the nature of our observations is directly determined by their duration.
5. Open distributed systems have a tendency not to optimize if they include long-range interactions. Under fairly general conditions the time it takes for a system to cross over from a local fixed point that is not optimal into a global one that is optimal can grow exponentially with the number of agents in the system. When such a crossover does occur, it happens extremely fast, giving rise to a phenomenon analogous to a punctuated equilibrium in biology.
6. A corollary of these results is that open systems with metastable strategies cannot spontaneously adapt to changing constraints, thereby “necessitating the introduction of globally coordinating agents to do so” (Huberman & Hogg Reference Huberman, Hogg and Huberman1988, 147, my italics). I will return to this point in discussing hybrid information-processing systems.
Instability and Differentiation
If a system is nonlinear and can undergo transitions into undesirable chaotic regimes, what are the conditions under which it can keep operating within desired constraints in the presence of strong perturbations? Glance and Huberman (Reference Glance, Huberman, van der Leeuw and McGlade1997) demonstrate (for the mathematical derivation, see Glance & Huberman 1997, 120–130) that:
1. In a purely competitive environment the payoff tends to decrease as more agents make use of it, but in a (partly) cooperative environment (agents exchanging information) the payoff increases up to a certain point with the number of agents that make use of a certain strategy. Increases beyond that point will not be rewarded.
2. In the case of a mixture of cooperative and competitive payoffs, as long as delays are limited the system converges to an equilibrium that is close to the optimum that a central controller could obtain without loss of information. But with increasing delays, as well as with increasing uncertainty, the number of agents using a particular resource continues to vary so that the overall performance is far from optimal. The system will eventually become unstable, leading to oscillation and potential chaos unless differential payoffs related to actual performance are accorded to actors.
3. Accordingly, such differential payoffs have the net effect of increasing the proportion of agents that perform successfully and decreasing the number of those that perform with less success, which will in turn modify the choices that each actor makes. Choices that may merit a reward at one point in time need no longer be rewarded at a later point in time, so that evolving diversity ensues. This has two effects (Glance & Huberman Reference Glance, Huberman, van der Leeuw and McGlade1997): (a) a diverse community of agents emerges out of an essentially homogeneous one and (b) a series of bifurcations will render chaos a transient phenomenon (see Appendix A for a more elaborate explanation).
In assessing the relevance of this work for the problems we are dealing with, we must first caution that as far as I know it has not (yet) been proven that one may generalize the conclusions at all. But if they can indeed be generalized, the results seem of direct relevance to societal systems. They seem to point to the fact that diversification is a necessary correlate of the stability of distributed systems. This certainly seems to be so in urban systems, which in all cases show considerable craft specialization as well as administrative differentiation, for example.
Heterarchical Systems
I argued earlier that urban systems are, in all probability, hybrid or mixed systems, consisting of egalitarian groups and small hierarchies as well as complex hierarchies and distributed systems. I call these mixed systems heterarchies.7 Unfortunately, we know even less about such heterarchical systems than we do about either distributed or hierarchical ones. Research in this area is badly needed, notably in order to quantify the values of the variables involved, as there is no overall approach to hybrid systems such as Huberman and Hogg have developed for complex hierarchies and distributed systems. I can therefore do no more than create a composite picture out of bits and pieces concerning each of the kinds of information processing systems we have discussed so far, and then ask some questions.
I will begin with mixtures of egalitarian and small-scale hierarchical communication networks. I conclude from Mayhew & Levinger’s (Reference Mayhew and Levinger1976, Reference Mayhew and Levinger1977) and Johnson’s (Reference Johnson, Renfrew, Rowlands and Segraves1982) arguments that there are substantial advantages to a hierarchical communications structure as soon as unit size exceeds four or five people. At the lowest level this implies hierarchization when more than five people are commonly involved in the same decisions, but at a higher level this also applies to hierarchization of lower-level units. This probably indicates a bottom up pressure for small- and intermediate-scale hierarchization in large, complex organizations.
Reynolds (Reference Reynolds1984), in an inspired response to early questions on the origins of small-group hierarchization posed by Wright (Reference Wright1977) and Johnson (Reference Johnson and Redman1978, Reference Johnson and van der Leeuw1981, Reference Johnson1983), studies the gain in efficiency that is achieved by subdividing problem-solving tasks, rather than treating them as a unit. Depending on whether it is the size of certain problems or their frequency that increases, greater efficiency gains are achieved by what he calls “divide and rule” (D&R) and “pipe-lining” (P) strategies (Reynolds Reference Reynolds1984, 180–182). In the divide and rule strategy, the lower-level units are kept independent, and the integrative part of the task is delegated to the lower-level units among themselves in a sequence of independent sub-processes, each of which is executed by a separate unit under overall process control from higher hierarchical levels.8
Pipe-lining (P) is a hybrid strategy that involves both horizontal and vertical movement in a hierarchy. It seems to be more efficient when increases in both size and frequency of problem-solving tasks occur, as it optimizes the amount of information flowing through each participating unit. It does so by regulating the balance between routine and nonroutine operations.
Unfortunately, once the systems considered are more complex, it is not so easy to generalize, as each different system may exhibit a range of very different kinds of behavior. One aspect of complex hybrid systems that may have general importance reminds us of pipe-lining. There is a need for reduction of error-making because in such systems many interfering communications pass through long lines of communication and do so with different frequencies. To reduce such error-making, higher-level units may compare information gathered from different sources at their own level with the information coming from sources lower down the hierarchy, and correct errors when they pass the information on to a node higher up. The disadvantage is that this also entails coarse-graining, generalizing by ignoring part of the total information content transmitted through the hierarchy.
Most other arguments in favor of heterarchical systems center on their efficiency and stability. We have seen in this chapter that Ceccato and Huberman (Reference Ceccato and Huberman1988) argue that after an initial period the complexity of hierarchical self-organizing systems is reduced, and their rate of evolution and their adaptability with it. The systems become adapted to the particular environment in which they operate. As a result, certain links are continuously activated whereas others are not. The unactivated, nonoptimal ones disappear, so that when circumstances change, new links need to be forged. That takes time and energy.
In distributed systems, on the other hand, nonoptimal strategies persist (Ceccato & Huberman Reference Ceccato and Huberman1988), which seems to affect very large market systems; these therefore also have difficulty adapting. Combining the two kinds of systems into hybrid systems has two advantages. First, the introduction of globally controlled (hierarchical) communications in distributed systems causes the latter to lose their penchant for retaining nonoptimal strategies. Secondly, the existence of distributed connections in the system increases the adaptability of the hybrid structure as well.
The next aspect of heterarchical systems we need to consider is their efficiency. Upon adopting a hybrid strategy, a system will have to deal with many new challenges. It would ideally need the optimum efficiency afforded by a hierarchical system and the optimum adaptability inherent in a distributed one. In practice, a hybrid structure will develop that is a best fit in the particular context involved. As it develops solutions to the specific problems that it faces, its hierarchically organized pathways will become simpler, reducing overall adaptability and possibly reducing efficiency as the original random hierarchy becomes more diverse. On the other hand, its distributed interactions may become better informed and/or improve their decision-making efficiency, and their adaptability will not necessarily be reduced.
Innovation introduces new resources into a system, and will therefore reduce competition or at least mitigate its negative effects. It will increase the efficiency of the distributed actors, which in turn will prompt more and more of them to cooperate, further increasing efficiency gains for a limited time until competition for resources becomes dominant again. This inherent fluctuation of the market aspect of the system is reduced by the much more stable efficiency of the hierarchy.
Similarly, in market systems both the time delays and their oscillations increase rapidly with increasing numbers of actors, whereas in hierarchical systems time delays proportionately decrease with each increase in the number of participants and oscillations are virtually nonexistent. Again, heterarchical systems seem to have the advantage.
Conclusion
The main point of this chapter is to argue that one can indeed make a coherent argument for considering the major societal transformations that we know from archaeology, history, and anthropology as due to an increase in knowledge and understanding, and thus an increase in the information processing capacity of human societies. Viewing this as part of a dissipative flow structure dynamic enables us to understand these transitions as being driven by the need to enable the communications structure of human groups to adapt to the growth in numbers that is in turn inherent in the increase in knowledge and understanding. It therefore presents us with an ultimate explanation for the different societal forms of organization that we encounter in the real world and the transitions between them, an explanation that does not need any other parameters (such as climate pressures, etc.). All these are subsumed under the variable “information-processing capacity.”





