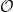 $\mathcal{O}$
$\mathcal{O}$
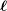 $\boldsymbol{\ell }$-independence
$\boldsymbol{\ell }$-independence

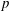 $p$-adic
$p$-adic 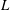 $L$-functions for
$L$-functions for 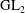 $\text{GL}_{2}$
$\text{GL}_{2}$
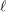 $\ell$-independence
$\ell$-independence