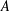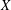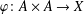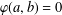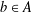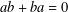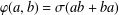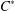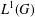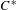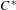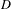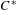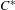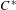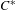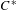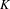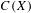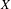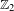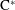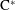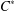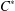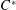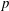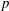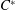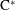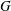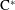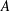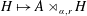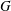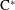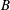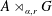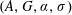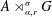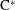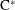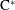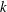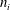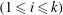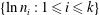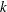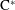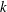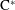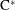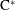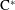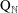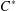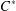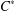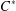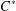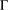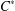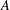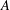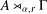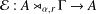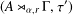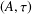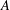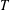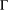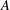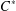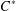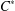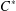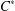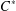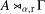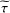12 results
ZERO JORDAN PRODUCT DETERMINED BANACH ALGEBRAS
- Part of
-
- Journal:
- Journal of the Australian Mathematical Society / Volume 111 / Issue 2 / October 2021
- Published online by Cambridge University Press:
- 08 January 2020, pp. 145-158
- Print publication:
- October 2021
-
- Article
- Export citation
ARENS PRODUCTS, ARENS REGULARITY AND RELATED PROBLEMS
- Part of
-
- Journal:
- Bulletin of the Australian Mathematical Society / Volume 102 / Issue 1 / August 2020
- Published online by Cambridge University Press:
- 04 December 2019, pp. 138-150
- Print publication:
- August 2020
-
- Article
- Export citation
Rokhlin dimension: duality, tracial properties, and crossed products
- Part of
-
- Journal:
- Ergodic Theory and Dynamical Systems / Volume 41 / Issue 2 / February 2021
- Published online by Cambridge University Press:
- 18 October 2019, pp. 408-460
- Print publication:
- February 2021
-
- Article
-
- You have access
- Open access
- Export citation
Corrigendum to: A Galois Correspondence for Reduced Crossed Products of Simple
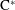 $\text{C}^{\ast }$-algebras by Discrete Groups
$\text{C}^{\ast }$-algebras by Discrete Groups
- Part of
-
- Journal:
- Canadian Journal of Mathematics / Volume 72 / Issue 2 / April 2020
- Published online by Cambridge University Press:
- 30 May 2019, pp. 557-562
- Print publication:
- April 2020
-
- Article
- Export citation
APPROXIMATIONS OF SUBHOMOGENEOUS ALGEBRAS
- Part of
-
- Journal:
- Bulletin of the Australian Mathematical Society / Volume 100 / Issue 2 / October 2019
- Published online by Cambridge University Press:
- 07 February 2019, pp. 328-337
- Print publication:
- October 2019
-
- Article
- Export citation
Maps on Quantum States in
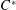 $C^{\ast }$-algebras Preserving von Neumann Entropy or Schatten
$C^{\ast }$-algebras Preserving von Neumann Entropy or Schatten 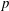 $p$-norm of Convex Combinations
$p$-norm of Convex Combinations
- Part of
-
- Journal:
- Canadian Mathematical Bulletin / Volume 62 / Issue 1 / March 2019
- Published online by Cambridge University Press:
- 09 January 2019, pp. 75-80
- Print publication:
- March 2019
-
- Article
-
- You have access
- Export citation
A Galois Correspondence for Reduced Crossed Products of Simple
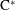 $\text{C}^{\ast }$-algebras by Discrete Groups
$\text{C}^{\ast }$-algebras by Discrete Groups
- Part of
-
- Journal:
- Canadian Journal of Mathematics / Volume 71 / Issue 5 / October 2019
- Published online by Cambridge University Press:
- 07 January 2019, pp. 1103-1125
- Print publication:
- October 2019
-
- Article
- Export citation
Boundary Quotient
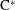 $\text{C}^{\ast }$-algebras of Products of Odometers
$\text{C}^{\ast }$-algebras of Products of Odometers
- Part of
-
- Journal:
- Canadian Journal of Mathematics / Volume 71 / Issue 1 / February 2019
- Published online by Cambridge University Press:
- 07 January 2019, pp. 183-212
- Print publication:
- February 2019
-
- Article
-
- You have access
- Export citation
A CHARACTERISATION OF CENTRAL ELEMENTS IN
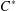 $C^{\ast }$-ALGEBRAS
$C^{\ast }$-ALGEBRAS
- Part of
-
- Journal:
- Bulletin of the Australian Mathematical Society / Volume 95 / Issue 1 / February 2017
- Published online by Cambridge University Press:
- 19 October 2016, pp. 138-143
- Print publication:
- February 2017
-
- Article
-
- You have access
- Export citation
HAAGERUP PROPERTY FOR
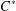 $C^{\ast }$-CROSSED PRODUCTS
$C^{\ast }$-CROSSED PRODUCTS
- Part of
-
- Journal:
- Bulletin of the Australian Mathematical Society / Volume 95 / Issue 1 / February 2017
- Published online by Cambridge University Press:
- 19 October 2016, pp. 144-148
- Print publication:
- February 2017
-
- Article
-
- You have access
- Export citation
A CHARACTERISATION OF 3-JORDAN HOMOMORPHISMS ON BANACH ALGEBRAS
- Part of
-
- Journal:
- Bulletin of the Australian Mathematical Society / Volume 93 / Issue 2 / April 2016
- Published online by Cambridge University Press:
- 04 September 2015, pp. 301-306
- Print publication:
- April 2016
-
- Article
-
- You have access
- Export citation
GROUP ACTION PRESERVING THE HAAGERUP PROPERTY OF
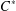 $C^{\ast }$-ALGEBRAS
$C^{\ast }$-ALGEBRAS
- Part of
-
- Journal:
- Bulletin of the Australian Mathematical Society / Volume 93 / Issue 2 / April 2016
- Published online by Cambridge University Press:
- 11 August 2015, pp. 295-300
- Print publication:
- April 2016
-
- Article
-
- You have access
- Export citation