This paper is about the connection between certain Banach-algebraic properties of a commutative Banach algebra E with unit and the associated commutative Banach algebra C(X, E) of all continuous functions from a compact Hausdorff space X into E. The properties concern Ditkin's condition and bounded relative units. We show that these properties are shared by E and C(X, E). We also consider the relationship between these properties in the algebras E, B and 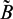$\~{B}$ that appear in the so-called admissible quadruples (X, E, B, 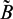$\~{B}$).

We study convergence in weighted convolution algebras ${{L}^{1}}\left( \omega \right)$ on ${{R}^{+}}$, with the weights chosen such that the corresponding weighted space $M\left( \omega \right)$ of measures is also a Banach algebra and is the dual space of a natural related space of continuous functions. We determine convergence factor $\eta $ for which weak$*$-convergence of $\left\{ {{\text{ }\!\!\lambda\!\!\text{ }}_{n}} \right\}$ to $\text{ }\!\!\lambda\!\!\text{ }$ in $M\left( \omega \right)$ implies norm convergence of ${{\text{ }\!\!\lambda\!\!\text{ }}_{n}}*f$ to $\text{ }\!\!\lambda\!\!\text{ *}f$ in ${{L}^{1}}\left( \omega \eta \right)$. We find necessary and sufficent conditions which depend on $\omega$ and $f$ and also find necessary and sufficent conditions for $\eta$ to be a convergence factor for all ${{L}^{1}}\left( \omega \right)$ and all $f$ in ${{L}^{1}}\left( \omega \right)$. We also give some applications to the structure of weighted convolution algebras. As a preliminary result we observe that $\eta$ is a convergence factor for $\omega$ and $f$ if and only if convolution by $f$ is a compact operator from $M\left( \omega \right)$ (or ${{L}^{1}}\left( \omega \right)$) to ${{L}^{1}}\left( \omega \eta \right)$.

A characterisation of the range of a homomorphism between two commutative group algebras is presented which implies, among other things, that this range is closed. The work relies mainly on the characterisation of such homomorphisms achieved by P. J. Cohen.

We consider the usual topological vector space H(G) of all functions holomorphic in a region G ⊂ ℂ. If G satisfies certain conditions, it is possible to introduce the Hadamard product as multiplication in H(G), and then H(G) turns out to be a commutative topological algebra. In [5] we characterized the invertible elements in H(G), and the aim of this paper is to study the closed ideals and some further questions.

It is proved that linear mappings of matrix algebras which preserve idempotents are Jordan homomorphisms. Applying this theorem we get some results concerning local derivations and local automorphisms. As an another application, the complete description of all weakly continuous linear surjective mappings on standard operator algebras which preserve projections is obtained. We also study local ring derivations on commutative semisimple Banach algebras.

We axiomatize the theory of real and complex numbers in Boolean-valued models of set theory, and prove that every Horn sentence true in the complex numbers is true in any complete Stonean algebra, and provable from its axioms.