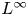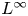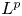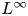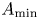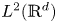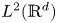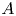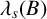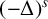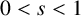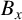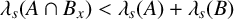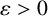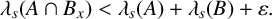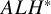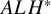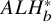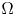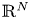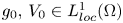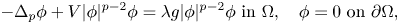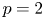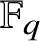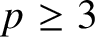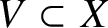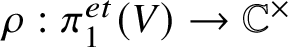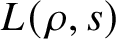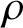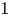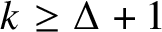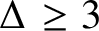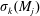37 results
Generalized second order vectorial ∞-eigenvalue problems
- Part of
-
- Journal:
- Proceedings of the Royal Society of Edinburgh. Section A: Mathematics , First View
- Published online by Cambridge University Press:
- 27 March 2024, pp. 1-21
-
- Article
-
- You have access
- Open access
- HTML
- Export citation
A universal inequality for Neumann eigenvalues of the Laplacian on a convex domain in Euclidean space
- Part of
-
- Journal:
- Canadian Mathematical Bulletin / Volume 67 / Issue 1 / March 2024
- Published online by Cambridge University Press:
- 19 September 2023, pp. 222-226
- Print publication:
- March 2024
-
- Article
- Export citation
General kernel estimates of Schrödinger-type operators with unbounded diffusion terms
- Part of
-
- Journal:
- Proceedings of the Royal Society of Edinburgh. Section A: Mathematics / Volume 154 / Issue 3 / June 2024
- Published online by Cambridge University Press:
- 19 May 2023, pp. 929-960
- Print publication:
- June 2024
-
- Article
-
- You have access
- Open access
- HTML
- Export citation
REILLY-TYPE UPPER BOUNDS FOR THE p-STEKLOV PROBLEM ON SUBMANIFOLDS
- Part of
-
- Journal:
- Bulletin of the Australian Mathematical Society / Volume 108 / Issue 3 / December 2023
- Published online by Cambridge University Press:
- 28 February 2023, pp. 492-503
- Print publication:
- December 2023
-
- Article
- Export citation
On Duclos–Exner’s conjecture about waveguides in strong uniform magnetic fields
- Part of
-
- Journal:
- Forum of Mathematics, Sigma / Volume 11 / 2023
- Published online by Cambridge University Press:
- 23 February 2023, e11
-
- Article
-
- You have access
- Open access
- HTML
- Export citation
Shape sensitivity of the Hardy constant involving the distance from a boundary submanifold
- Part of
-
- Journal:
- Proceedings of the Royal Society of Edinburgh. Section A: Mathematics / Volume 154 / Issue 2 / April 2024
- Published online by Cambridge University Press:
- 22 February 2023, pp. 408-423
- Print publication:
- April 2024
-
- Article
-
- You have access
- Open access
- HTML
- Export citation
Optimization of the anisotropic Cheeger constant with respect to the anisotropy
- Part of
-
- Journal:
- Canadian Mathematical Bulletin / Volume 66 / Issue 3 / September 2023
- Published online by Cambridge University Press:
- 17 February 2023, pp. 1030-1043
- Print publication:
- September 2023
-
- Article
-
- You have access
- Open access
- HTML
- Export citation
ON THE LOWEST EIGENVALUE OF THE FRACTIONAL LAPLACIAN FOR THE INTERSECTION OF TWO DOMAINS
- Part of
-
- Journal:
- Bulletin of the Australian Mathematical Society / Volume 108 / Issue 2 / October 2023
- Published online by Cambridge University Press:
- 02 December 2022, pp. 290-297
- Print publication:
- October 2023
-
- Article
- Export citation
The Torelli theorem for
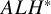 $ALH^*$
gravitational instantons
$ALH^*$
gravitational instantons
- Part of
-
- Journal:
- Forum of Mathematics, Sigma / Volume 10 / 2022
- Published online by Cambridge University Press:
- 15 September 2022, e79
-
- Article
-
- You have access
- Open access
- HTML
- Export citation
On the optimization of the first weighted eigenvalue
- Part of
-
- Journal:
- Proceedings of the Royal Society of Edinburgh. Section A: Mathematics / Volume 153 / Issue 6 / December 2023
- Published online by Cambridge University Press:
- 12 September 2022, pp. 1777-1804
- Print publication:
- December 2023
-
- Article
- Export citation
p-Adic estimates of abelian Artin L-functions on curves
- Part of
-
- Journal:
- Forum of Mathematics, Sigma / Volume 10 / 2022
- Published online by Cambridge University Press:
- 10 January 2022, e2
-
- Article
-
- You have access
- Open access
- HTML
- Export citation
Index estimates for closed minimal submanifolds of the sphere
- Part of
-
- Journal:
- Proceedings of the Royal Society of Edinburgh. Section A: Mathematics / Volume 152 / Issue 3 / June 2022
- Published online by Cambridge University Press:
- 17 December 2021, pp. 802-816
- Print publication:
- June 2022
-
- Article
- Export citation
Equitable colourings of Borel graphs
- Part of
-
- Journal:
- Forum of Mathematics, Pi / Volume 9 / 2021
- Published online by Cambridge University Press:
- 29 November 2021, e12
-
- Article
-
- You have access
- Open access
- HTML
- Export citation
Asymptotics of the principal eigenvalue of the Laplacian in 2D periodic domains with small traps
- Part of
-
- Journal:
- European Journal of Applied Mathematics / Volume 33 / Issue 4 / August 2022
- Published online by Cambridge University Press:
- 04 June 2021, pp. 646-673
-
- Article
- Export citation
Degenerating sequences of conformal classes and the conformal Steklov spectrum
- Part of
-
- Journal:
- Canadian Journal of Mathematics / Volume 74 / Issue 4 / August 2022
- Published online by Cambridge University Press:
- 05 March 2021, pp. 1093-1136
- Print publication:
- August 2022
-
- Article
- Export citation
On the first eigenvalue of the Laplace operator for compact spacelike submanifolds in Lorentz–Minkowski spacetime 𝕃m
- Part of
-
- Journal:
- Proceedings of the Royal Society of Edinburgh. Section A: Mathematics / Volume 152 / Issue 2 / April 2022
- Published online by Cambridge University Press:
- 11 February 2021, pp. 311-330
- Print publication:
- April 2022
-
- Article
- Export citation
Almost all Steiner triple systems are almost resolvable
- Part of
-
- Journal:
- Forum of Mathematics, Sigma / Volume 8 / 2020
- Published online by Cambridge University Press:
- 03 November 2020, e39
-
- Article
-
- You have access
- Open access
- Export citation
Bounded solutions for an ordinary differential system from the Ginzburg–Landau theory
- Part of
-
- Journal:
- Proceedings of the Royal Society of Edinburgh. Section A: Mathematics / Volume 150 / Issue 6 / December 2020
- Published online by Cambridge University Press:
- 14 August 2020, pp. 3378-3408
- Print publication:
- December 2020
-
- Article
- Export citation
Estimates for sums and gaps of eigenvalues of Laplacians on measure spaces
- Part of
-
- Journal:
- Proceedings of the Royal Society of Edinburgh. Section A: Mathematics / Volume 151 / Issue 2 / April 2021
- Published online by Cambridge University Press:
- 02 June 2020, pp. 842-861
- Print publication:
- April 2021
-
- Article
- Export citation
Hypersurfaces with Prescribed Boundary and Small Steklov Eigenvalues
- Part of
-
- Journal:
- Canadian Mathematical Bulletin / Volume 63 / Issue 1 / March 2020
- Published online by Cambridge University Press:
- 12 December 2019, pp. 46-57
- Print publication:
- March 2020
-
- Article
- Export citation