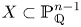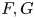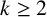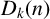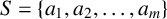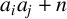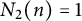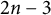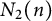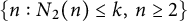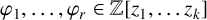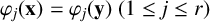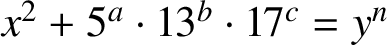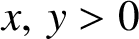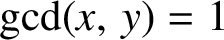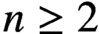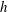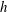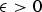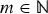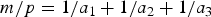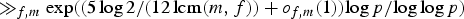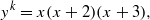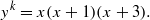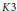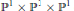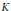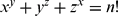21 results
On the Hasse principle for complete intersections
- Part of
-
- Journal:
- Compositio Mathematica / Volume 160 / Issue 4 / April 2024
- Published online by Cambridge University Press:
- 05 March 2024, pp. 771-835
- Print publication:
- April 2024
-
- Article
-
- You have access
- Open access
- HTML
- Export citation
AN EFFECTIVE BOUND FOR GENERALISED DIOPHANTINE m-TUPLES
- Part of
-
- Journal:
- Bulletin of the Australian Mathematical Society / Volume 109 / Issue 2 / April 2024
- Published online by Cambridge University Press:
- 06 November 2023, pp. 242-253
- Print publication:
- April 2024
-
- Article
- Export citation
Discrete restriction estimates for forms in many variables
- Part of
-
- Journal:
- Proceedings of the Edinburgh Mathematical Society / Volume 66 / Issue 4 / November 2023
- Published online by Cambridge University Press:
- 18 September 2023, pp. 923-939
-
- Article
-
- You have access
- Open access
- HTML
- Export citation
Equal-Sum-Product problem II
- Part of
-
- Journal:
- Canadian Mathematical Bulletin , First View
- Published online by Cambridge University Press:
- 13 September 2023, pp. 1-11
-
- Article
- Export citation
THE PAUCITY PROBLEM FOR CERTAIN SYMMETRIC DIOPHANTINE EQUATIONS
- Part of
-
- Journal:
- Bulletin of the Australian Mathematical Society / Volume 108 / Issue 1 / August 2023
- Published online by Cambridge University Press:
- 23 September 2022, pp. 29-39
- Print publication:
- August 2023
-
- Article
-
- You have access
- Open access
- HTML
- Export citation
SOLUTIONS TO A LEBESGUE–NAGELL EQUATION
- Part of
-
- Journal:
- Bulletin of the Australian Mathematical Society / Volume 105 / Issue 1 / February 2022
- Published online by Cambridge University Press:
- 24 May 2021, pp. 19-30
- Print publication:
- February 2022
-
- Article
- Export citation
NOTES ON THE K-RATIONAL DISTANCE PROBLEM
- Part of
-
- Journal:
- Bulletin of the Australian Mathematical Society / Volume 104 / Issue 1 / August 2021
- Published online by Cambridge University Press:
- 01 December 2020, pp. 40-44
- Print publication:
- August 2021
-
- Article
- Export citation
Rational lines on cubic hypersurfaces
- Part of
-
- Journal:
- Mathematical Proceedings of the Cambridge Philosophical Society / Volume 171 / Issue 1 / July 2021
- Published online by Cambridge University Press:
- 24 April 2020, pp. 99-112
- Print publication:
- July 2021
-
- Article
-
- You have access
- Open access
- Export citation
Zeroes of Polynomials With Prime Inputs and Schmidt’s
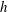 $h$-invariant
$h$-invariant
- Part of
-
- Journal:
- Canadian Journal of Mathematics / Volume 72 / Issue 3 / June 2020
- Published online by Cambridge University Press:
- 07 February 2019, pp. 805-833
- Print publication:
- June 2020
-
- Article
- Export citation
The number of solutions of the Erdős-Straus Equation and sums of k unit fractions
- Part of
-
- Journal:
- Proceedings of the Royal Society of Edinburgh. Section A: Mathematics / Volume 150 / Issue 3 / June 2020
- Published online by Cambridge University Press:
- 30 January 2019, pp. 1401-1427
- Print publication:
- June 2020
-
- Article
- Export citation
The Hermite–Joubert Problem and a Conjecture of Brassil and Reichstein
- Part of
-
- Journal:
- Canadian Mathematical Bulletin / Volume 62 / Issue 1 / March 2019
- Published online by Cambridge University Press:
- 04 January 2019, pp. 169-177
- Print publication:
- March 2019
-
- Article
-
- You have access
- Export citation
Simultaneous Additive Equations: Repeated and Differing Degrees
-
- Journal:
- Canadian Journal of Mathematics / Volume 69 / Issue 2 / 01 April 2017
- Published online by Cambridge University Press:
- 20 November 2018, pp. 258-283
- Print publication:
- 01 April 2017
-
- Article
-
- You have access
- Export citation
The Smallest Pisot Element in the Field of Formal Power Series Over a Finite Field
-
- Journal:
- Canadian Mathematical Bulletin / Volume 56 / Issue 2 / 01 June 2013
- Published online by Cambridge University Press:
- 20 November 2018, pp. 258-264
- Print publication:
- 01 June 2013
-
- Article
-
- You have access
- Export citation
HUA-TYPE ITERATION FOR MULTIDIMENSIONAL WEYL SUMS
- Part of
-
- Journal:
- Mathematika / Volume 58 / Issue 2 / July 2012
- Published online by Cambridge University Press:
- 27 March 2012, pp. 209-224
- Print publication:
- July 2012
-
- Article
- Export citation
RATIONAL POINTS ON THREE SUPERELLIPTIC CURVES
- Part of
-
- Journal:
- Bulletin of the Australian Mathematical Society / Volume 85 / Issue 1 / February 2012
- Published online by Cambridge University Press:
- 06 September 2011, pp. 105-113
- Print publication:
- February 2012
-
- Article
-
- You have access
- Export citation
The Ample Cone for a K3 Surface
-
- Journal:
- Canadian Journal of Mathematics / Volume 63 / Issue 3 / 01 June 2011
- Published online by Cambridge University Press:
- 20 November 2018, pp. 481-499
- Print publication:
- 01 June 2011
-
- Article
-
- You have access
- Export citation
Asymptotic Formulae for Pairs of Diagonal Cubic Equations
-
- Journal:
- Canadian Journal of Mathematics / Volume 63 / Issue 1 / 01 February 2011
- Published online by Cambridge University Press:
- 20 November 2018, pp. 38-54
- Print publication:
- 01 February 2011
-
- Article
-
- You have access
- Export citation
Zeros of systems of 𝔭-adic quadratic forms
- Part of
-
- Journal:
- Compositio Mathematica / Volume 146 / Issue 2 / March 2010
- Published online by Cambridge University Press:
- 22 January 2010, pp. 271-287
- Print publication:
- March 2010
-
- Article
-
- You have access
- Export citation
SOLUTIONS OF THE DIOPHANTINE EQUATION xy+yz+zx=n!
-
- Journal:
- Glasgow Mathematical Journal / Volume 50 / Issue 2 / May 2008
- Published online by Cambridge University Press:
- 01 May 2008, pp. 217-232
- Print publication:
- May 2008
-
- Article
-
- You have access
- Export citation
Conditions for the solvability of systems of two and three additive forms over p-adic fields
-
- Journal:
- Proceedings of the London Mathematical Society / Volume 91 / Issue 3 / November 2005
- Published online by Cambridge University Press:
- 19 October 2005, pp. 545-572
- Print publication:
- November 2005
-
- Article
- Export citation