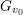39 results
Lower bounds for Maass forms on semisimple groups
- Part of
-
- Journal:
- Compositio Mathematica / Volume 156 / Issue 5 / May 2020
- Published online by Cambridge University Press:
- 17 April 2020, pp. 959-1003
- Print publication:
- May 2020
-
- Article
- Export citation
The case against distributed representations: Lack of evidence
-
- Journal:
- Behavioral and Brain Sciences / Volume 23 / Issue 4 / August 2000
- Published online by Cambridge University Press:
- 30 August 2019, pp. 476-477
-
- Article
- Export citation
Dedication
-
- Book:
- Computational Modeling of Cognition and Behavior
- Published online:
- 05 February 2018
- Print publication:
- 22 February 2018, pp v-vi
-
- Chapter
- Export citation
Preface
-
- Book:
- Computational Modeling of Cognition and Behavior
- Published online:
- 05 February 2018
- Print publication:
- 22 February 2018, pp xxi-xxii
-
- Chapter
- Export citation
Frontmatter
-
- Book:
- Computational Modeling of Cognition and Behavior
- Published online:
- 05 February 2018
- Print publication:
- 22 February 2018, pp i-iv
-
- Chapter
- Export citation
Index
-
- Book:
- Computational Modeling of Cognition and Behavior
- Published online:
- 05 February 2018
- Print publication:
- 22 February 2018, pp 455-461
-
- Chapter
- Export citation
Contents
-
- Book:
- Computational Modeling of Cognition and Behavior
- Published online:
- 05 February 2018
- Print publication:
- 22 February 2018, pp vii-xii
-
- Chapter
- Export citation
6 - Bayesian Parameter Estimation
- from Part II - Parameter Estimation
-
- Book:
- Computational Modeling of Cognition and Behavior
- Published online:
- 05 February 2018
- Print publication:
- 22 February 2018, pp 126-145
-
- Chapter
- Export citation
4 - Maximum Likelihood Parameter Estimation
- from Part II - Parameter Estimation
-
- Book:
- Computational Modeling of Cognition and Behavior
- Published online:
- 05 February 2018
- Print publication:
- 22 February 2018, pp 72-104
-
- Chapter
- Export citation
10 - Model Comparison
- from Part III - Model Comparison
-
- Book:
- Computational Modeling of Cognition and Behavior
- Published online:
- 05 February 2018
- Print publication:
- 22 February 2018, pp 241-272
-
- Chapter
- Export citation
References
-
- Book:
- Computational Modeling of Cognition and Behavior
- Published online:
- 05 February 2018
- Print publication:
- 22 February 2018, pp 427-454
-
- Chapter
- Export citation
13 - Neural Network Models
- from Part IV - Models in Psychology
-
- Book:
- Computational Modeling of Cognition and Behavior
- Published online:
- 05 February 2018
- Print publication:
- 22 February 2018, pp 334-368
-
- Chapter
- Export citation
3 - Basic Parameter Estimation Techniques
- from Part II - Parameter Estimation
-
- Book:
- Computational Modeling of Cognition and Behavior
- Published online:
- 05 February 2018
- Print publication:
- 22 February 2018, pp 47-71
-
- Chapter
- Export citation
11 - Bayesian Model Comparison Using Bayes Factors
- from Part III - Model Comparison
-
- Book:
- Computational Modeling of Cognition and Behavior
- Published online:
- 05 February 2018
- Print publication:
- 22 February 2018, pp 273-308
-
- Chapter
- Export citation
Part III - Model Comparison
-
- Book:
- Computational Modeling of Cognition and Behavior
- Published online:
- 05 February 2018
- Print publication:
- 22 February 2018, pp 239-240
-
- Chapter
- Export citation
Part I - Introduction to Modeling
-
- Book:
- Computational Modeling of Cognition and Behavior
- Published online:
- 05 February 2018
- Print publication:
- 22 February 2018, pp 1-2
-
- Chapter
- Export citation
15 - Models in Neuroscience
- from Part IV - Models in Psychology
-
- Book:
- Computational Modeling of Cognition and Behavior
- Published online:
- 05 February 2018
- Print publication:
- 22 February 2018, pp 395-423
-
- Chapter
- Export citation
Appendix B - Mathematical Terminology
-
- Book:
- Computational Modeling of Cognition and Behavior
- Published online:
- 05 February 2018
- Print publication:
- 22 February 2018, pp 425-426
-
- Chapter
- Export citation
2 - From Words to Models
- from Part I - Introduction to Modeling
-
- Book:
- Computational Modeling of Cognition and Behavior
- Published online:
- 05 February 2018
- Print publication:
- 22 February 2018, pp 24-44
-
- Chapter
- Export citation
List of Illustrations
-
- Book:
- Computational Modeling of Cognition and Behavior
- Published online:
- 05 February 2018
- Print publication:
- 22 February 2018, pp xiii-xvii
-
- Chapter
- Export citation