28 results
Attitudes toward automation and the demand for policies addressing job loss: the effects of information about trade-offs
-
- Journal:
- Political Science Research and Methods , First View
- Published online by Cambridge University Press:
- 15 February 2024, pp. 1-16
-
- Article
-
- You have access
- Open access
- HTML
- Export citation
On Littlewood Polynomials with Prescribed Number of Zeros Inside the Unit Disk
-
- Journal:
- Canadian Journal of Mathematics / Volume 67 / Issue 3 / 01 June 2015
- Published online by Cambridge University Press:
- 20 November 2018, pp. 507-526
- Print publication:
- 01 June 2015
-
- Article
-
- You have access
- Export citation
Wieferich pairs and Barker sequences, II
- Part of
-
- Journal:
- LMS Journal of Computation and Mathematics / Volume 17 / Issue 1 / 2014
- Published online by Cambridge University Press:
- 01 April 2014, pp. 24-32
-
- Article
-
- You have access
- Export citation
Sign Changes of the Liouville Function on Quadratics
-
- Journal:
- Canadian Mathematical Bulletin / Volume 56 / Issue 2 / 01 June 2013
- Published online by Cambridge University Press:
- 20 November 2018, pp. 251-257
- Print publication:
- 01 June 2013
-
- Article
-
- You have access
- Export citation
Lacunary Müntz systems
-
- Journal:
- Proceedings of the Edinburgh Mathematical Society / Volume 36 / Issue 3 / October 1993
- Published online by Cambridge University Press:
- 20 January 2009, pp. 361-374
-
- Article
-
- You have access
- Export citation
Expected Norms of Zero-One Polynomials
-
- Journal:
- Canadian Mathematical Bulletin / Volume 51 / Issue 4 / 01 December 2008
- Published online by Cambridge University Press:
- 20 November 2018, pp. 497-507
- Print publication:
- 01 December 2008
-
- Article
-
- You have access
- Export citation
The merit factor problem
-
-
- Book:
- Number Theory and Polynomials
- Published online:
- 04 May 2010
- Print publication:
- 08 May 2008, pp 52-70
-
- Chapter
- Export citation
Barker sequences and flat polynomials
-
-
- Book:
- Number Theory and Polynomials
- Published online:
- 04 May 2010
- Print publication:
- 08 May 2008, pp 71-88
-
- Chapter
- Export citation
Norms of cyclotomic Littlewood polynomials
-
- Journal:
- Mathematical Proceedings of the Cambridge Philosophical Society / Volume 138 / Issue 2 / March 2005
- Published online by Cambridge University Press:
- 24 February 2005, pp. 315-326
- Print publication:
- March 2005
-
- Article
- Export citation
THE MAHLER MEASURE OF POLYNOMIALS WITH ODD COEFFICIENTS
-
- Journal:
- Bulletin of the London Mathematical Society / Volume 36 / Issue 3 / May 2004
- Published online by Cambridge University Press:
- 28 April 2004, pp. 332-338
- Print publication:
- May 2004
-
- Article
- Export citation
TERRY SHEIL-SMALL: 428 pp., £65.00 (US$95.00), ISBN 0-521-40068-6 (Cambridge University Press, 2002)
-
- Journal:
- Bulletin of the London Mathematical Society / Volume 36 / Issue 1 / January 2004
- Published online by Cambridge University Press:
- 23 December 2003, pp. 134-135
- Print publication:
- January 2004
-
- Article
- Export citation
GENERAL FORMS FOR MINIMAL SPECTRAL VALUES FOR A CLASS OF QUADRATIC PISOT NUMBERS
-
- Journal:
- Bulletin of the London Mathematical Society / Volume 35 / Issue 1 / January 2003
- Published online by Cambridge University Press:
- 24 March 2003, pp. 47-54
- Print publication:
- January 2003
-
- Article
- Export citation
Merit Factors of Polynomials Formed by Jacobi Symbols
-
- Journal:
- Canadian Journal of Mathematics / Volume 53 / Issue 1 / 01 February 2001
- Published online by Cambridge University Press:
- 20 November 2018, pp. 33-50
- Print publication:
- 01 February 2001
-
- Article
-
- You have access
- Export citation
MERIT FACTORS OF CHARACTER POLYNOMIALS
-
- Journal:
- Journal of the London Mathematical Society / Volume 61 / Issue 3 / June 2000
- Published online by Cambridge University Press:
- 01 June 2000, pp. 706-720
- Print publication:
- June 2000
-
- Article
- Export citation
LITTLEWOOD-TYPE PROBLEMS ON [0,1]
-
- Journal:
- Proceedings of the London Mathematical Society / Volume 79 / Issue 1 / July 1999
- Published online by Cambridge University Press:
- 01 July 1999, pp. 22-46
- Print publication:
- July 1999
-
- Article
- Export citation
MULTIPLE ROOTS OF [−1, 1] POWER SERIES
-
- Journal:
- Journal of the London Mathematical Society / Volume 57 / Issue 1 / February 1998
- Published online by Cambridge University Press:
- 01 February 1998, pp. 135-147
- Print publication:
- February 1998
-
- Article
- Export citation
Polynomials With {0, +1, -1} Coefficients and a Root Close to a Given Point
-
- Journal:
- Canadian Journal of Mathematics / Volume 49 / Issue 5 / 01 October 1997
- Published online by Cambridge University Press:
- 20 November 2018, pp. 887-915
- Print publication:
- 01 October 1997
-
- Article
-
- You have access
- Export citation
Sharp extensions of Bernstein's inequality to rational spaces
- Part of
-
- Journal:
- Mathematika / Volume 43 / Issue 2 / December 1996
- Published online by Cambridge University Press:
- 26 February 2010, pp. 413-423
- Print publication:
- December 1996
-
- Article
- Export citation
Matrix transformations of series of orthogonal polynomials
- Part of
-
- Journal:
- Mathematika / Volume 42 / Issue 2 / December 1995
- Published online by Cambridge University Press:
- 26 February 2010, pp. 427-443
- Print publication:
- December 1995
-
- Article
- Export citation
Zeros of Iterated Integrals of Polynomials
-
- Journal:
- Canadian Journal of Mathematics / Volume 47 / Issue 1 / 01 February 1995
- Published online by Cambridge University Press:
- 20 November 2018, pp. 65-87
- Print publication:
- 01 February 1995
-
- Article
-
- You have access
- Export citation



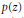
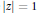
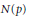
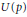
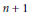
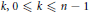
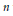
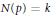
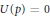
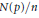
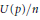
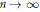
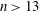

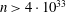
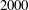
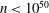
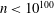

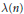

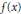

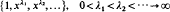
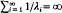 . We prove that, if {λ
. We prove that, if {λ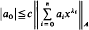
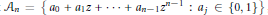

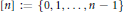
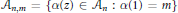
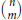

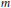
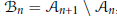

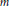
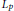

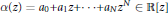
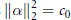
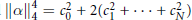

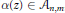

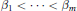
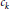

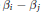
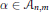
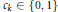
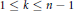
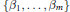
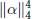
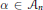
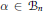

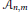
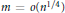
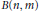
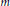

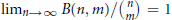
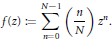
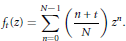
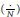
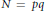
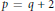
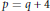
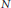
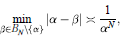
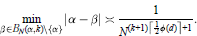
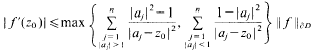
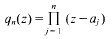
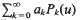 given by
given by 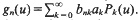 . We establish necessary and sufficient conditions on the matrix (
. We establish necessary and sufficient conditions on the matrix (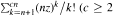 an integer) converge to pieces of a circle and of two "Szegö curves".
an integer) converge to pieces of a circle and of two "Szegö curves".