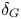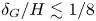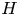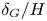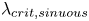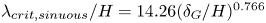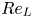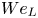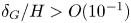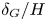Using a combination of mean flow spatial linear stability and two-dimensional volume-of-fluid (VoF) simulations, the physics governing the instability of high-speed liquid sheets being injected into a quiescent gas environment is studied. It is found that the gas shear layer thickness 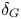 $\delta _G$ plays an influential role, where for values
$\delta _G$ plays an influential role, where for values 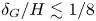 $\delta _G/H\lesssim 1/8$, the growth of sinuous and varicose modes is nearly indistinguishable. Here,
$\delta _G/H\lesssim 1/8$, the growth of sinuous and varicose modes is nearly indistinguishable. Here, 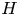 $H$ is the liquid sheet thickness. With larger values of
$H$ is the liquid sheet thickness. With larger values of 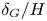 $\delta _G/H$, a second peak develops in the lower wavenumber region of the dispersion relation, and becomes increasingly dominant. This second peak corresponds to a large-scale sinuous mode, and its critical wavelength
$\delta _G/H$, a second peak develops in the lower wavenumber region of the dispersion relation, and becomes increasingly dominant. This second peak corresponds to a large-scale sinuous mode, and its critical wavelength 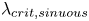 $\lambda _{crit,sinuous}$ is found to scale as
$\lambda _{crit,sinuous}$ is found to scale as 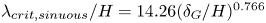 $\lambda _{crit,sinuous}/H = 14.26 (\delta _G/H)^{0.766}$. This scaling behaviour collapses onto a single curve for various combinations of the liquid-based Reynolds (
$\lambda _{crit,sinuous}/H = 14.26 (\delta _G/H)^{0.766}$. This scaling behaviour collapses onto a single curve for various combinations of the liquid-based Reynolds (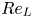 $Re_L$) and Weber (
$Re_L$) and Weber (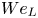 $We_L$) numbers, provided that
$We_L$) numbers, provided that 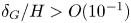 $\delta _G/H > O({10^{-1}})$. For the varicose modes, the shape of the dispersion relation does not change with variations in
$\delta _G/H > O({10^{-1}})$. For the varicose modes, the shape of the dispersion relation does not change with variations in 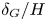 $\delta _G/H$, and the liquid shear layer thickness has an almost negligible influence on the growth of instabilities. Two-dimensional VoF simulations are employed to examine the validity of the linear stability assumptions. These simulations also show that the dominant sinuous mode remains active as the process transitions into the nonlinear regime, and that this mode is ultimately responsible for fragmenting the sheet. Based on an energy budget analysis, the most influential contributors to the growth of the sinuous mode are the gas Reynolds shear stress and the lateral working of pressure on the gas side.
$\delta _G/H$, and the liquid shear layer thickness has an almost negligible influence on the growth of instabilities. Two-dimensional VoF simulations are employed to examine the validity of the linear stability assumptions. These simulations also show that the dominant sinuous mode remains active as the process transitions into the nonlinear regime, and that this mode is ultimately responsible for fragmenting the sheet. Based on an energy budget analysis, the most influential contributors to the growth of the sinuous mode are the gas Reynolds shear stress and the lateral working of pressure on the gas side.