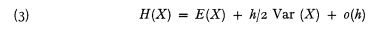20 results
EPA guidance on physical activity as a treatment for severe mental illness: a meta-review of the evidence and Position Statement from the European Psychiatric Association (EPA), supported by the International Organization of Physical Therapists in Mental Health (IOPTMH)
- Part of
-
- Journal:
- European Psychiatry / Volume 54 / October 2018
- Published online by Cambridge University Press:
- 18 July 2018, pp. 124-144
-
- Article
-
- You have access
- HTML
- Export citation
Optimal Dividends in the Dual Model with Diffusion
-
- Journal:
- ASTIN Bulletin: The Journal of the IAA / Volume 38 / Issue 2 / November 2008
- Published online by Cambridge University Press:
- 17 April 2015, pp. 653-667
- Print publication:
- November 2008
-
- Article
-
- You have access
- Export citation
A Note on the Dividends-Penalty Identity and the Optimal Dividend Barrier
-
- Journal:
- ASTIN Bulletin: The Journal of the IAA / Volume 36 / Issue 2 / November 2006
- Published online by Cambridge University Press:
- 17 April 2015, pp. 489-503
- Print publication:
- November 2006
-
- Article
-
- You have access
- Export citation
Maximizing Dividends without Bankruptcy
-
- Journal:
- ASTIN Bulletin: The Journal of the IAA / Volume 36 / Issue 1 / May 2006
- Published online by Cambridge University Press:
- 17 April 2015, pp. 5-23
- Print publication:
- May 2006
-
- Article
-
- You have access
- Export citation
D.R. Dannenburg, R. Kaas, M. J. Govaerts (1996): Practical Actuarial Credibility Models. IAE (Institute of Actuarial Science and Econometrics of the University of Amsterdam), 157 pages.
-
- Journal:
- ASTIN Bulletin: The Journal of the IAA / Volume 27 / Issue 2 / November 1997
- Published online by Cambridge University Press:
- 29 August 2014, p. 373
- Print publication:
- November 1997
-
- Article
-
- You have access
- Export citation
A Teacher's Remark on Exact Credibility
-
- Journal:
- ASTIN Bulletin: The Journal of the IAA / Volume 25 / Issue 2 / November 1995
- Published online by Cambridge University Press:
- 29 August 2014, pp. 189-192
- Print publication:
- November 1995
-
- Article
-
- You have access
- Export citation
Martingale Approach to Pricing Perpetual American Options
-
- Journal:
- ASTIN Bulletin: The Journal of the IAA / Volume 24 / Issue 2 / November 1994
- Published online by Cambridge University Press:
- 29 August 2014, pp. 195-220
- Print publication:
- November 1994
-
- Article
-
- You have access
- Export citation
Martingales and Tail Probabilities
-
- Journal:
- ASTIN Bulletin: The Journal of the IAA / Volume 24 / Issue 1 / May 1994
- Published online by Cambridge University Press:
- 29 August 2014, pp. 145-146
- Print publication:
- May 1994
-
- Article
-
- You have access
- Export citation
Risk Theory with the Gamma Process
-
- Journal:
- ASTIN Bulletin: The Journal of the IAA / Volume 21 / Issue 2 / November 1991
- Published online by Cambridge University Press:
- 29 August 2014, pp. 177-192
- Print publication:
- November 1991
-
- Article
-
- You have access
- Export citation
Three Methods to Calculate the Probability of Ruin
-
- Journal:
- ASTIN Bulletin: The Journal of the IAA / Volume 19 / Issue 1 / April 1989
- Published online by Cambridge University Press:
- 29 August 2014, pp. 71-90
- Print publication:
- April 1989
-
- Article
-
- You have access
- Export citation
Mathematical Fun with the Compound Binomial Process
-
- Journal:
- ASTIN Bulletin: The Journal of the IAA / Volume 18 / Issue 2 / November 1988
- Published online by Cambridge University Press:
- 29 August 2014, pp. 161-168
- Print publication:
- November 1988
-
- Article
-
- You have access
- Export citation
On the Probability and Severity of Ruin
-
- Journal:
- ASTIN Bulletin: The Journal of the IAA / Volume 17 / Issue 2 / November 1987
- Published online by Cambridge University Press:
- 29 August 2014, pp. 151-163
- Print publication:
- November 1987
-
- Article
-
- You have access
- Export citation
The Reinsurer's Monopoly and the Bowley Solution
-
- Journal:
- ASTIN Bulletin: The Journal of the IAA / Volume 15 / Issue 2 / November 1985
- Published online by Cambridge University Press:
- 29 August 2014, pp. 141-148
- Print publication:
- November 1985
-
- Article
-
- You have access
- Export citation
A Remark on the Principle of Zero Utility
-
- Journal:
- ASTIN Bulletin: The Journal of the IAA / Volume 13 / Issue 2 / December 1982
- Published online by Cambridge University Press:
- 29 August 2014, pp. 133-134
- Print publication:
- December 1982
-
- Article
-
- You have access
- Export citation
The Esscher Premium Principle: A Criticism. Comment.
-
- Journal:
- ASTIN Bulletin: The Journal of the IAA / Volume 12 / Issue 2 / December 1981
- Published online by Cambridge University Press:
- 29 August 2014, pp. 139-140
- Print publication:
- December 1981
-
- Article
-
- You have access
- Export citation
Risk Bearing and the Insurance Market
-
- Journal:
- ASTIN Bulletin: The Journal of the IAA / Volume 10 / Issue 1 / May 1978
- Published online by Cambridge University Press:
- 29 August 2014, pp. 12-24
- Print publication:
- May 1978
-
- Article
-
- You have access
- Export citation
Pareto-Optimal Risk Exchanges and Related Decision Problems
-
- Journal:
- ASTIN Bulletin: The Journal of the IAA / Volume 10 / Issue 1 / May 1978
- Published online by Cambridge University Press:
- 29 August 2014, pp. 25-33
- Print publication:
- May 1978
-
- Article
-
- You have access
- Export citation
On Optimal Cancellation of Policies
-
- Journal:
- ASTIN Bulletin: The Journal of the IAA / Volume 9 / Issue 1-2 / January 1977
- Published online by Cambridge University Press:
- 29 August 2014, pp. 125-138
- Print publication:
- January 1977
-
- Article
-
- You have access
- Export citation
The Surplus Process As A Fair Game—Utilitywise
-
- Journal:
- ASTIN Bulletin: The Journal of the IAA / Volume 8 / Issue 3 / September 1975
- Published online by Cambridge University Press:
- 29 August 2014, pp. 307-322
- Print publication:
- September 1975
-
- Article
-
- You have access
- Export citation
On Additive Premium Calculation Principles
-
- Journal:
- ASTIN Bulletin: The Journal of the IAA / Volume 7 / Issue 3 / March 1974
- Published online by Cambridge University Press:
- 29 August 2014, pp. 215-222
- Print publication:
- March 1974
-
- Article
-
- You have access
- Export citation



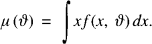
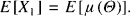
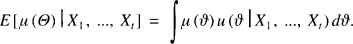
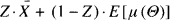
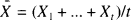 is the observed average. This is indeed the case for about half a dozen famous examples. Jewell (1974) has found an elegant and general approach to unify these examples, see also Goovaerts and Hoogstad (1987, chapter 2). The classical examples can be retrieved as special cases; however a preliminary reparameterization has to be performed on a case by case basis. The purpose of this note is to propose an alternative (but of course strongly related) formulation of the general model, from which the classical examples can be retrieved in a
is the observed average. This is indeed the case for about half a dozen famous examples. Jewell (1974) has found an elegant and general approach to unify these examples, see also Goovaerts and Hoogstad (1987, chapter 2). The classical examples can be retrieved as special cases; however a preliminary reparameterization has to be performed on a case by case basis. The purpose of this note is to propose an alternative (but of course strongly related) formulation of the general model, from which the classical examples can be retrieved in a