1. Introduction
In [Reference Gruszczyński and Pietruszczak16, Reference Gruszczyński and Pietruszczak18] we carried out an extensive analysis of one of the first systems of point-free topology by Grzegorczyk [Reference Grzegorczyk19], based on the notion of separation (the dual notion of contact). The two papers witnessed the formulation of representation and duality theorems for a subclass of so-called Grzegorczyk structures. In particular, we established an object duality between a class of Grzegorczyk structures that satisfy the countable chain condition and the concentric spaces (a subclass of the class of regular spaces), which satisfy the topological version of the same condition.
A particular idiosyncrasy of Grzegorczyk’s approach to point-free topology is his definition of a point, which is a formal reflection of the geometrical intuition of a point as a system of “shrinking” regions of space. We have devoted much attention to elucidating the idea in [14–16, Reference Gruszczyński and Pietruszczak18], so we refer the reader to these works if they want to familiarize themselves with an informal (yet precise) analysis of the notion.
One of the problems that occupied us in the aforementioned works was the relation of Grzegorczyk points to other classical point-like constructions, such as ultrafilters and maximal round filters. We have only scratched the surface of the problem, yet we demonstrated that the following two second-order sentences:
-
(a) Every Grzegorczyk point is an ultrafilter, and
-
(b) Every ultrafilter is a Grzegorczyk point
correspond to the following first-order and second-order sentences, respectively:
-
(a′) Each region is separated from its complement. (cf. Theorem 8.4)
-
(b′) The structure is finite. (cf. Theorem 9.1)
We proved as well that every Grzegorczyk point is a maximal round filter. For the sake of completeness of the presentation, some of these results are contained in this paper.
Here, we aim to examine how Grzegorczyk points behave and relate to filters and ultrafilters in atomless and atomic Boolean contact algebras, which in a very natural way relate to Grzegorczyk structures from the earlier works. To be more precise, previously we worked with mereological fields, which are structures that always lack the zero element and might lack the unity. In all other respects, they bear a very strong resemblance to Boolean algebras, thanks to the classical theorems to which we refer in Sections 6 and 7 of [Reference Gruszczyński and Pietruszczak16]. Thanks to these theorems, all results obtained in the earlier works are easily translatable into analogous results in the framework of Boolean algebras. We have also replaced the primitive binary relation of separation with its dual, the contact relation. The main reason to do so was the fact that since more or less the beginning of the twenty-first century and the seminal works of Stell [Reference Stell23], Düntsch & Winter [Reference Düntsch and Winter10, Reference Düntsch and Winter11] and Dimov & Vakarelov [Reference Dimov and Vakarelov8, Reference Dimov and Vakarelov9], Boolean contact algebras have been the standard framework for doing region-based topology. Thus, with technical results in focus and philosophical considerations aside, contact algebras are the most natural choice for the presentation of advances in the study of Grzegorczyk point-free topology.
2. Motivations
There are various reasons for doing region-based theories of space. Probably the main one is to describe spatial relations in terms of concepts that can be rooted in the sensory experience. Such were motivations for both Region Connection Calculus of Cohn et al. [Reference Cohn, Bennett, Gooday and Gotts5] and Boolean contact algebras. From the purely mathematical point of view, algebraic parts of these theories focused on finding suitable topological representations and duality theorems, most notably via the spaces of clusters as, among others, in the works of Düntsch & Winter [Reference Düntsch and Winter11] and Dimov & Vakarelov [Reference Dimov and Vakarelov8]. In closely related De Vries algebras from [Reference De Vries7] maximal round filters play a crucial role in algebraization of the topological notion of compactness.
The approach taken by Grzegorczyk [Reference Grzegorczyk19] seems to have yet another motivation—to find spatially satisfactory construction of points in terms of regions and separation (equivalently: contact) relation. Grzegorczyk points are, in a way, generalizations of Tarski’s points as sets of concentric balls from his geometry of solids [Reference Tarski and Corcoran25], and they embody the idea of a point as a system of shrinking regions of space.
From both philosophical and technical points of view, it is interesting (at least for us, as the authors of the paper) how second-order conditions expressing dependencies between various constructions of points relate to either first- or second-order properties of Boolean contact algebras. This line of research was initiated by Biacino & Gerla [Reference Biacino and Gerla3] with finding sufficient conditions for Grzegorczyk points and Whitehead points from [Reference Whitehead26] to coincide. We believe that further investigation of dependencies between various constructions of points can bring interesting results in region-based theories of space, even more so because it is very little examined fragment of such theories.
As pointed to in the introduction, in our previous works we showed certain correspondences between statements about points of contact algebras and their properties. In particular, we found it interesting how Grzegorczyk points relate to the standard filter constructions of Boolean contact algebras. Among these, the Fréchet filter plays a distinguished role in the class of atomic Boolean algebras, and, interestingly, its relation to Grzegorczyk points is independent from the axioms of Grzegorczyk contact algebras. We venture to say that this may be interpreted as the fact that the notion of Fréchet filter is independent from the spatial intuitions behind the definition of Grzegorczyk points. Investigating consequences of the statement “Fréchet filter is a Grzegorczyk point” may be interpreted philosophically as answering the question what are consequences of forcing our spatial intuitions about points into the notion of Fréchet filter? To us as the authors, logicians with a strong predilection toward philosophical aspects of mathematical theories, it seemed a very stimulating question which is faced and solved in the paper.
It is hard to say now what, if any, fruits bears the theory of correspondences between statements about points of Boolean contact algebras and their familiar properties. However, in our opinion, it is a path that is worth studying as it may lead to new perspectives on various—both mathematical and philosophical—aspects of region-based theories of space.
3. Boolean quasi-contact algebras
This section is a refresher of the standard notions, axioms and elementary properties of contact algebras that are essential for the key results of the paper.
A Boolean quasi-contact algebra (BQCA for short) is any pair
![]() $\mathfrak {R}=\langle \mathfrak {B},\mathbin {\mathsf {C}}\rangle $
, where
$\mathfrak {R}=\langle \mathfrak {B},\mathbin {\mathsf {C}}\rangle $
, where
![]() $\mathfrak {B}=\langle R, \mathord {\sqcap }, \mathord {\sqcup },-, \mathsf {0}, \mathsf {1}\rangle $
is a non-degenerate Boolean algebraFootnote
1
(BA for short) and
$\mathfrak {B}=\langle R, \mathord {\sqcap }, \mathord {\sqcup },-, \mathsf {0}, \mathsf {1}\rangle $
is a non-degenerate Boolean algebraFootnote
1
(BA for short) and
![]() $\mathord {\mathbin {\mathsf {C}}}$
is a binary contact relation on R which meets the following four axioms:Footnote
2
$\mathord {\mathbin {\mathsf {C}}}$
is a binary contact relation on R which meets the following four axioms:Footnote
2
 $$ \begin{align} \forall_{x,y\in R}\bigl(x\leq y\mathrel{\;\Longrightarrow\;}\forall_{z\in R}(z\mathbin{\mathsf{C}} x\mathrel{\Rightarrow} z \mathbin{\mathsf{C}} y)\bigr), \end{align} $$
$$ \begin{align} \forall_{x,y\in R}\bigl(x\leq y\mathrel{\;\Longrightarrow\;}\forall_{z\in R}(z\mathbin{\mathsf{C}} x\mathrel{\Rightarrow} z \mathbin{\mathsf{C}} y)\bigr), \end{align} $$
where
![]() is the complement of
is the complement of
![]() $\mathbin {\mathsf {C}}$
,
$\mathbin {\mathsf {C}}$
,
![]() $R^{+}:= R\setminus \{\mathsf {0}\}$
and
$R^{+}:= R\setminus \{\mathsf {0}\}$
and
![]() $\leq $
is the standard partial order defined by:
$\leq $
is the standard partial order defined by:
Furthermore, we will use the standard strict partial order defined by:
All elements of the domain R will be called regions; the region
![]() $\mathsf {0}$
will be called empty; and all regions from
$\mathsf {0}$
will be called empty; and all regions from
![]() $R^{+}$
will be called non-empty. In the case
$R^{+}$
will be called non-empty. In the case
![]() $x\mathbin {\mathsf {C}} y$
(resp.
$x\mathbin {\mathsf {C}} y$
(resp.
![]() ;
;
![]() $x\leq y$
;
$x\leq y$
;
![]() $x\lneq y$
) we will say that x is in contact with y (resp. x is separated from y; x is part of y; x is a proper part of y). Axioms (C0)–(C3) say, respectively:
$x\lneq y$
) we will say that x is in contact with y (resp. x is separated from y; x is part of y; x is a proper part of y). Axioms (C0)–(C3) say, respectively:
![]() $\mathsf {0}$
is separated from any region;
$\mathsf {0}$
is separated from any region;
![]() $\mathbin {\mathsf {C}}$
is symmetric and reflexive on
$\mathbin {\mathsf {C}}$
is symmetric and reflexive on
![]() $R^{+}$
; and if one region is part of another, then each region in contact with the first is also in contact with the other. In BAs condition (C3) is equivalent to
$R^{+}$
; and if one region is part of another, then each region in contact with the first is also in contact with the other. In BAs condition (C3) is equivalent to
From (C3) and the reflexivity of
![]() $\leq $
we obtain that in place of (C2) we can assume that
$\leq $
we obtain that in place of (C2) we can assume that
![]() $\mathbin {\mathsf {C}}$
includes
$\mathbin {\mathsf {C}}$
includes
![]() $\leq $
limited to non-empty regions:
$\leq $
limited to non-empty regions:
 $$\begin{align} \forall_{x,y\in R^+}(x\leq y\mathrel{\Longrightarrow} x\mathbin{\mathsf{C}} y). \end{align}$$
$$\begin{align} \forall_{x,y\in R^+}(x\leq y\mathrel{\Longrightarrow} x\mathbin{\mathsf{C}} y). \end{align}$$
So every non-empty region is in contact with
![]() $\mathsf {1}$
:
$\mathsf {1}$
:
We will also use two auxiliary binary relations on R:
![]() and
and
![]() $\mathord {\bot }$
. We define the first by:
$\mathord {\bot }$
. We define the first by:
and we let the second be the complement of
![]() . In the case
. In the case
![]() (resp.
(resp.
![]() $x\bot y$
) we will say that x overlaps y (resp.
$x\bot y$
) we will say that x overlaps y (resp.
![]() $x$
is disjoint from y). From (C3), (C1) and (≤|R+
⊆C
) we have:
$x$
is disjoint from y). From (C3), (C1) and (≤|R+
⊆C
) we have:
 $$ \begin{align} \forall_{x,y\in R}\bigl(x\mathbin{\mathsf{C}}\mathop{-}y \iff \exists_{z\in R}(x\mathbin{\mathsf{C}} z \mathrel{\wedge} z\bot y)\bigr), \end{align} $$
$$ \begin{align} \forall_{x,y\in R}\bigl(x\mathbin{\mathsf{C}}\mathop{-}y \iff \exists_{z\in R}(x\mathbin{\mathsf{C}} z \mathrel{\wedge} z\bot y)\bigr), \end{align} $$
Yet another auxiliary standard relation of non-tangential inclusion is defined by:
In the case
![]() $x\ll y$
we say that x is a non-tangential part of y. From (3.3) it follows that:
$x\ll y$
we say that x is a non-tangential part of y. From (3.3) it follows that:
From (C0), (C1), (≤|R+
⊆C
), (df′≪) we obtain that every region is a non-tangential part of
![]() $\mathsf {1}$
and each non-tangential part of a given region is its (ordinary) part:
$\mathsf {1}$
and each non-tangential part of a given region is its (ordinary) part:
From (df′≪), (df ◯) and the transitivity of
![]() $\leq $
we have:
$\leq $
we have:
Furthermore, we have the following property of
![]() $\ll \,$
:
$\ll \,$
:
It—together with (≪⊆≤) and the reflexivity of
![]() $\leq $
—gives the transitivity of
$\leq $
—gives the transitivity of
![]() $\ll \,$
:
$\ll \,$
:
We will use three families of filters in BAs. The first one will be the family
![]() $\textbf {Ult}$
of all ultrafilters, i.e., proper maximal filters. The second one will be the family of principal filters of the form
$\textbf {Ult}$
of all ultrafilters, i.e., proper maximal filters. The second one will be the family of principal filters of the form
![]() $\operatorname {\mathrm {\uparrow }} x := \{u\in R \mid x\leq u\}$
for an
$\operatorname {\mathrm {\uparrow }} x := \{u\in R \mid x\leq u\}$
for an
![]() $x\in R$
(the set
$x\in R$
(the set
![]() $\operatorname {\mathrm {\uparrow }} x$
is called a principal filter generated by x). Let
$\operatorname {\mathrm {\uparrow }} x$
is called a principal filter generated by x). Let
![]() $\textbf {PF}$
and
$\textbf {PF}$
and
![]() $\textbf {PF}_{\!\text {At}}$
be families of all principal filters and of principal filters generated by atoms, respectively. The third family will be the family of free filters which satisfy the following condition: there is no
$\textbf {PF}_{\!\text {At}}$
be families of all principal filters and of principal filters generated by atoms, respectively. The third family will be the family of free filters which satisfy the following condition: there is no
![]() $x\in R$
such that for any
$x\in R$
such that for any
![]() $y\in F$
we have
$y\in F$
we have
![]() $x\leq y$
. Every ultrafilter is free or belongs to
$x\leq y$
. Every ultrafilter is free or belongs to
![]() $\textbf {PF}_{\!\text {At}}$
.
$\textbf {PF}_{\!\text {At}}$
.
Moreover, two families of filters in BQCAs will play special roles in the sequel. The first one will be the family
![]() $\textbf {Rnd}$
of so-called round (or contracting) filters which are proper filters satisfying:
$\textbf {Rnd}$
of so-called round (or contracting) filters which are proper filters satisfying:
-
• for any
 $x\in F$
there is a
$x\in F$
there is a
 $y\in F$
such that
$y\in F$
such that
 $y\ll x$
.
$y\ll x$
.
From (◯⊆C ), (df′≪) and (≪⊆≤) we obtain:
Lemma 3.1. For any round filter F we have:
![]() .
.
The second one is the family
![]() ${\textbf {M.Rnd}}$
of all proper maximal filters in the family
${\textbf {M.Rnd}}$
of all proper maximal filters in the family
![]() $\textbf {Rnd}$
.Footnote
3
$\textbf {Rnd}$
.Footnote
3
Lemma 3.2 [Reference Gruszczyński and Pietruszczak18, lemma 10.6]
If a round filter F satisfies the condition
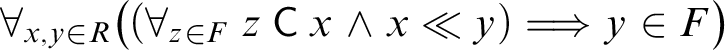 $\forall _{x,y\in R}\bigl ((\forall _{z\in F}\: z\mathbin {\mathsf {C}} x \mathrel {\wedge } x\ll y) \mathrel {\Longrightarrow } y\in F\bigr )$
, then F belongs to
$\forall _{x,y\in R}\bigl ((\forall _{z\in F}\: z\mathbin {\mathsf {C}} x \mathrel {\wedge } x\ll y) \mathrel {\Longrightarrow } y\in F\bigr )$
, then F belongs to
![]() ${\textbf {M.Rnd}}$
.
${\textbf {M.Rnd}}$
.
It is easy to check that the structures
![]() and
and
![]() $\langle \mathfrak {B},R^+\times R^+\rangle $
are BQCAs. We will call them trivial BQCAs. The relation
$\langle \mathfrak {B},R^+\times R^+\rangle $
are BQCAs. We will call them trivial BQCAs. The relation
![]() is the smallest contact relation on
is the smallest contact relation on
![]() $\mathfrak {B}$
(cf. [Reference Düntsch and Winter10, proposition 2.2(1)]. From (df′≪), (◯⊆C
) and (C2) we obtain:
$\mathfrak {B}$
(cf. [Reference Düntsch and Winter10, proposition 2.2(1)]. From (df′≪), (◯⊆C
) and (C2) we obtain:
Hence all filters in
![]() are round; and so
are round; and so
![]() $\textbf {Ult}={\textbf {M.Rnd}}$
.
$\textbf {Ult}={\textbf {M.Rnd}}$
.
4. Boolean contact algebras
After [Reference Düntsch and Winter10], we will call a Boolean contact algebra (BCA for short) any BQCA satisfying
By means of (3.5), (df≪), (C3), (≪⊆≤), (≤|R+
⊆C
), (C1), (3.2) and the antisymmetry of
![]() $\leq $
, we can prove:
$\leq $
, we can prove:
Lemma 4.1. In BQCAs condition (C5) is equivalent to each of the following:
 $$\begin{align} \forall_{x,y\in R}\bigl(\forall_{z\in R}(z\mathbin{\mathsf{C}} x\Rightarrow z\mathbin{\mathsf{C}} y)\:\Longrightarrow\: x\leq y\bigr), \end{align}$$
$$\begin{align} \forall_{x,y\in R}\bigl(\forall_{z\in R}(z\mathbin{\mathsf{C}} x\Rightarrow z\mathbin{\mathsf{C}} y)\:\Longrightarrow\: x\leq y\bigr), \end{align}$$
 $$\begin{align} \forall_{x,y\in R}\bigl(x\leq y\iff\forall_{z\in R}(z\mathbin{\mathsf{C}} x\mathrel{\;\Rightarrow\;} z\mathbin{\mathsf{C}} y)\bigr), \end{align}$$
$$\begin{align} \forall_{x,y\in R}\bigl(x\leq y\iff\forall_{z\in R}(z\mathbin{\mathsf{C}} x\mathrel{\;\Rightarrow\;} z\mathbin{\mathsf{C}} y)\bigr), \end{align}$$
 $$\begin{align} \forall_{x,y\in R}\bigl(\forall_{z\in R}(z\mathbin{\mathsf{C}} x\:\Leftrightarrow\: z\mathbin{\mathsf{C}} y)\:\Longrightarrow\: x=y \bigr). \end{align}$$
$$\begin{align} \forall_{x,y\in R}\bigl(\forall_{z\in R}(z\mathbin{\mathsf{C}} x\:\Leftrightarrow\: z\mathbin{\mathsf{C}} y)\:\Longrightarrow\: x=y \bigr). \end{align}$$
Remark 4.2. Dimov & Vakarelov [Reference Dimov and Vakarelov8, p. 213] analyzed contact algebras as structures of the form
![]() $\langle \mathfrak {B}, \mathbin {\mathsf {C}}\rangle $
satisfying (C0)–(C2) and (4.1). The algebras that additionally satisfy (ext
C
) are named by them as extensional contact algebras (p. 215). In Lemma 2.2 of [Reference Dimov and Vakarelov8] the authors demonstrate that conditions (ext
C
), (C5), (∃≪
) and (C3c
) are equivalent in any contact algebra. But, as the above lemma shows, BQCAs are enough for this, i.e., the condition (C4) can be omitted in the proofs.
$\langle \mathfrak {B}, \mathbin {\mathsf {C}}\rangle $
satisfying (C0)–(C2) and (4.1). The algebras that additionally satisfy (ext
C
) are named by them as extensional contact algebras (p. 215). In Lemma 2.2 of [Reference Dimov and Vakarelov8] the authors demonstrate that conditions (ext
C
), (C5), (∃≪
) and (C3c
) are equivalent in any contact algebra. But, as the above lemma shows, BQCAs are enough for this, i.e., the condition (C4) can be omitted in the proofs.
Düntsch & Winter [Reference Düntsch and Winter11] treated Boolean contact algebras as structures of the form
![]() $\langle \mathfrak {B}, \mathbin {\mathsf {C}}\rangle $
satisfying (C0)–(C4) and (C3c
). They showed that these conditions entail (C5) and (3.1) (Lemma 3.2).
$\langle \mathfrak {B}, \mathbin {\mathsf {C}}\rangle $
satisfying (C0)–(C4) and (C3c
). They showed that these conditions entail (C5) and (3.1) (Lemma 3.2).
It is easy to check that trivial BQCAs of the form
![]() (see p. 21) are BCAs. In the sequel we will use ‘
(see p. 21) are BCAs. In the sequel we will use ‘
![]() ’ as a general name for all BCAs with
’ as a general name for all BCAs with
![]() . The BQCAs of the form
. The BQCAs of the form
![]() $\langle \mathfrak {B},R^+\times R^+\rangle $
are BCAs iff
$\langle \mathfrak {B},R^+\times R^+\rangle $
are BCAs iff
![]() $R^{+}=\{\mathsf {1}\}$
iff
$R^{+}=\{\mathsf {1}\}$
iff
![]() iff
iff
![]() . So all trivial examples of BCAs are
. So all trivial examples of BCAs are
![]() s.
s.
Let
![]() $\text {At}$
be the set of atoms of a given BA. Directly from (∃≪
) and (≪⊆≤) we have:
$\text {At}$
be the set of atoms of a given BA. Directly from (∃≪
) and (≪⊆≤) we have:
Hence, using (◯⊆C ), (df′≪) and (3.7), we obtain:

From this and (df′≪), (C1), and (4.1), we get a generalization of (4.2):
For any
![]() $x\in R$
we put:
$x\in R$
we put:
![]() $\text {At}_x := \{a\in \text {At} \mid a\leq x\}$
and
$\text {At}_x := \{a\in \text {At} \mid a\leq x\}$
and
![]() $\text {At}_x^{\bot } := \{a\in \text {At} \mid a\bot x\}$
. It is clear that the atomicity of a given BA implies that
$\text {At}_x^{\bot } := \{a\in \text {At} \mid a\bot x\}$
. It is clear that the atomicity of a given BA implies that
![]() $x=\sup \text {At}_x$
. A BQCA is atomic iff it is based on an atomic BA. The following fact will be used in the proof of Theorem 7.8.
$x=\sup \text {At}_x$
. A BQCA is atomic iff it is based on an atomic BA. The following fact will be used in the proof of Theorem 7.8.
Lemma 4.3. In any atomic BCA we have:
 $$ \begin{align*} \forall_{x,y\in R}\bigl(x\mathbin{\mathsf{C}} y \mathrel{\wedge} x\bot y\mathrel{\Longrightarrow} \text{both } \text{At}_x \text{ and } \text{At}_y \text{ are infinite} \bigr). \end{align*} $$
$$ \begin{align*} \forall_{x,y\in R}\bigl(x\mathbin{\mathsf{C}} y \mathrel{\wedge} x\bot y\mathrel{\Longrightarrow} \text{both } \text{At}_x \text{ and } \text{At}_y \text{ are infinite} \bigr). \end{align*} $$
Proof. Assume for a contradiction that
![]() $x\mathbin {\mathsf {C}} y$
,
$x\mathbin {\mathsf {C}} y$
,
![]() $x\bot y$
and
$x\bot y$
and
![]() $\text {At}_x$
is finite. Then for some atoms
$\text {At}_x$
is finite. Then for some atoms
![]() $a_1$
, …,
$a_1$
, …,
![]() $a_n$
we have
$a_n$
we have
![]() $x=a_1\sqcup \dots \sqcup a_n$
. So, by (C1), (4.1) and (4.3), we have:
$x=a_1\sqcup \dots \sqcup a_n$
. So, by (C1), (4.1) and (4.3), we have:
![]() $x\mathbin {\mathsf {C}} y$
iff
$x\mathbin {\mathsf {C}} y$
iff
![]() $a_1\mathbin {\mathsf {C}} y$
or … or
$a_1\mathbin {\mathsf {C}} y$
or … or
![]() $a_n\mathbin {\mathsf {C}} y$
iff
$a_n\mathbin {\mathsf {C}} y$
iff
![]() $a_1\leq y$
or … or
$a_1\leq y$
or … or
![]() $a_n\leq y$
. Therefore
$a_n\leq y$
. Therefore
![]() , a contradiction.□
, a contradiction.□
We say that a BA is finite–cofinite iff for any
![]() $x\in R$
either
$x\in R$
either
![]() $x\in \{\mathsf {0},\mathsf {1}\}$
or there are
$x\in \{\mathsf {0},\mathsf {1}\}$
or there are
![]() $n>0$
and
$n>0$
and
![]() $a_1, \ldots , a_n\in \text {At}$
such that either
$a_1, \ldots , a_n\in \text {At}$
such that either
![]() $x=a_1\sqcup \cdots \sqcup a_n$
or
$x=a_1\sqcup \cdots \sqcup a_n$
or
![]() $x=-(a_1\sqcup \cdots \sqcup a_n)$
. Clearly, all finite BAs are finite–cofinite. Düntsch & Winter [Reference Düntsch and Winter10] showed that the only BCAs that can be obtained from finite–cofinite BAs are the trivial
$x=-(a_1\sqcup \cdots \sqcup a_n)$
. Clearly, all finite BAs are finite–cofinite. Düntsch & Winter [Reference Düntsch and Winter10] showed that the only BCAs that can be obtained from finite–cofinite BAs are the trivial
![]() .
.
Proposition 4.4 [Reference Düntsch and Winter10, proposition 2.2(2)]
If
![]() $\mathfrak {B}$
is finite–cofinite, then
$\mathfrak {B}$
is finite–cofinite, then
![]() is the only BCA based on
is the only BCA based on
![]() $\mathfrak {B}$
.
$\mathfrak {B}$
.
Notice that every non-empty region which is not an atom has at least two non-tangential non-empty proper parts which are separated from each other:

Indeed, assume that
![]() $x\in R^+\setminus \text {At}$
. Then there are
$x\in R^+\setminus \text {At}$
. Then there are
![]() $y,z\in R^+$
such that
$y,z\in R^+$
such that
![]() $y\bot z$
and
$y\bot z$
and
![]() $x=y\sqcup z$
. Hence, by (∃≪
), there are
$x=y\sqcup z$
. Hence, by (∃≪
), there are
![]() $u,v\in R^+$
such that
$u,v\in R^+$
such that
![]() $u\ll y\lneq x$
and
$u\ll y\lneq x$
and
![]() $v\ll z\lneq x$
. So, by (3.6) and (≪⊆≤), we have
$v\ll z\lneq x$
. So, by (3.6) and (≪⊆≤), we have
![]() . Moreover, by (3.7), we have
. Moreover, by (3.7), we have
![]() $u\ll x$
,
$u\ll x$
,
![]() $v\ll x$
and
$v\ll x$
and
![]() $u\ne x\ne v$
.
$u\ne x\ne v$
.
A BQCA is atomless iff it is based on an atomless BA.
Remark 4.5. (i) Dimov & Vakarelov [Reference Dimov and Vakarelov8, definition 3.3] define another type of filters. Namely, a filter F is an end iff F is a round filter satisfying the following condition:
They show (Lemma 3.2(viii)) that all end filters belong to
![]() ${\textbf {M.Rnd}}$
. Moreover, they prove (Proposition 3.1(iii)) that in any BCA satisfying the so-called interpolation axiom
${\textbf {M.Rnd}}$
. Moreover, they prove (Proposition 3.1(iii)) that in any BCA satisfying the so-called interpolation axiom
every filter from
![]() ${\textbf {M.Rnd}}$
is an end.
${\textbf {M.Rnd}}$
is an end.
(ii) Gruszczyński [Reference Gruszczyński14] proves that in any BCA satisfying (IA), a filter F belongs to
![]() ${\textbf {M.Rnd}}$
if and only if F satisfies the following condition:
${\textbf {M.Rnd}}$
if and only if F satisfies the following condition:
 $$ \begin{align} \forall_{x,y\in R}\bigl(\forall_{z\in F}(x\mathbin{\mathsf{C}} z\mathrel{\wedge} y\mathbin{\mathsf{C}} z)\mathrel{\Longrightarrow} x\mathbin{\mathsf{C}} y\bigr). \end{align} $$
$$ \begin{align} \forall_{x,y\in R}\bigl(\forall_{z\in F}(x\mathbin{\mathsf{C}} z\mathrel{\wedge} y\mathbin{\mathsf{C}} z)\mathrel{\Longrightarrow} x\mathbin{\mathsf{C}} y\bigr). \end{align} $$
The following lemma will be used to obtain Proposition 4.8.
Lemma 4.6. In any atomless BCA, any filter F satisfying the following condition is free:
 $$ \begin{align*} \forall_{x,y\in R^{+}}\bigl(\forall_{z\in F}(x\leq z\mathrel{\wedge} y\leq z)\mathrel{\Longrightarrow} x\mathbin{\mathsf{C}} y \bigr). \end{align*} $$
$$ \begin{align*} \forall_{x,y\in R^{+}}\bigl(\forall_{z\in F}(x\leq z\mathrel{\wedge} y\leq z)\mathrel{\Longrightarrow} x\mathbin{\mathsf{C}} y \bigr). \end{align*} $$
Proposition 4.7. In any atomless BCA, if
![]() $F\in \textbf {Ult}\cup {\textbf {M.Rnd}}$
then F satisfies the following condition:
$F\in \textbf {Ult}\cup {\textbf {M.Rnd}}$
then F satisfies the following condition:

Proof. Suppose that in an atomless BCA for a filter F there are
![]() $x,y\in R^{+}$
such that (a)
$x,y\in R^{+}$
such that (a)
![]() $x\bot y$
and (b) for any
$x\bot y$
and (b) for any
![]() $z\in F$
:
$z\in F$
:
![]() $x\leq z$
and
$x\leq z$
and
![]() $y\leq z$
. Then, by (a), either x or y does not belong to F. Assume the first possibility holds: (c)
$y\leq z$
. Then, by (a), either x or y does not belong to F. Assume the first possibility holds: (c)
![]() $x\notin F$
. By (4.5), for some
$x\notin F$
. By (4.5), for some
![]() $u_1\in R^{+}$
we have
$u_1\in R^{+}$
we have
![]() $u_1\ll x$
and
$u_1\ll x$
and
![]() $u_1\ne x$
. Observe that by (b) and (3.7),
$u_1\ne x$
. Observe that by (b) and (3.7),
![]() $u_1$
is a non-tangential part of any
$u_1$
is a non-tangential part of any
![]() $z\in F$
. By means of (4.5) and the axiom of dependent choices we produce a sequence
$z\in F$
. By means of (4.5) and the axiom of dependent choices we produce a sequence
![]() $\langle u_n\mid n<\omega \rangle $
such that
$\langle u_n\mid n<\omega \rangle $
such that
![]() $u_0:= x$
,
$u_0:= x$
,
![]() $u_{i+1}\ll u_i$
and
$u_{i+1}\ll u_i$
and
![]() $u_{i+1}\neq u_i$
. The filter
$u_{i+1}\neq u_i$
. The filter
![]() $\operatorname {\mathrm {\uparrow }} X$
generated by the set of the terms of the sequence is obviously round, and by (b) and (c) it is the case that
$\operatorname {\mathrm {\uparrow }} X$
generated by the set of the terms of the sequence is obviously round, and by (b) and (c) it is the case that
![]() $F\subsetneq \operatorname {\mathrm {\uparrow }} X$
. Therefore,
$F\subsetneq \operatorname {\mathrm {\uparrow }} X$
. Therefore,
![]() $F\notin \textbf {Ult}$
and
$F\notin \textbf {Ult}$
and
![]() $F\notin {\textbf {M.Rnd}}$
.□
$F\notin {\textbf {M.Rnd}}$
.□
Finally, from Lemma 4.6, Proposition 4.7 and (◯⊆C ) we obtain:
Proposition 4.8. In any atomless BCA, all filters from
![]() ${\textbf {M.Rnd}}$
are free.Footnote
4
${\textbf {M.Rnd}}$
are free.Footnote
4
5. Pre-points
Let
![]() $\mathfrak {R}$
be a BQCA based on a BA
$\mathfrak {R}$
be a BQCA based on a BA
![]() $\mathfrak {B}$
. A pre-point of
$\mathfrak {B}$
. A pre-point of
![]() $\mathfrak {R}$
is any non-empty set Q of non-empty regions which satisfies the following conditions:
$\mathfrak {R}$
is any non-empty set Q of non-empty regions which satisfies the following conditions:

The purpose of this definition is to formally grasp the intuition that a point is a system of diminishing regions determining a unique location in space. We call it a pre-point, since if we understand a point as a perfect representation of some location in space, then it may happen that two different sets of regions represent one and the same location. Further, we will identify such pre-points to act as one point. Let
![]() $\textbf {Q}$
be the set of all pre-points of
$\textbf {Q}$
be the set of all pre-points of
![]() $\mathfrak {R}$
.
$\mathfrak {R}$
.
Notice that by (≪⊆≤), all pre-points are chains with respect to the part of relation. Furthermore, by (r1), (≪⊆≤) and (df≤), all pre-points have the finite intersection property. So each pre-point Q generates the filter
![]() $\operatorname {\mathrm {\uparrow }} Q:= \{x\in R\mid \exists _{u_1,\ldots ,u_n\in Q}\: u_1\sqcap \cdots \sqcap u_n\leq x\}$
. From (r1) we have
$\operatorname {\mathrm {\uparrow }} Q:= \{x\in R\mid \exists _{u_1,\ldots ,u_n\in Q}\: u_1\sqcap \cdots \sqcap u_n\leq x\}$
. From (r1) we have
![]() $\operatorname {\mathrm {\uparrow }} Q=\{x\in R\mid \exists _{u\in Q} \: u\leq x\}$
.
$\operatorname {\mathrm {\uparrow }} Q=\{x\in R\mid \exists _{u\in Q} \: u\leq x\}$
.
By (4.2) and (◯⊆C ), all singletons composed of atoms are pre-points in all BCAs:
Lemma 5.1. In any BCA, for any
![]() $a\in \text {At}$
the singleton
$a\in \text {At}$
the singleton
![]() $\{a\}$
is a pre-point.
$\{a\}$
is a pre-point.
6. Grzegorczyk points
6.1. Grzegorczyk points of BQCAs
Let
![]() $\mathfrak {R}$
be a BQCA based on a BA
$\mathfrak {R}$
be a BQCA based on a BA
![]() $\mathfrak {B}$
. By a Grzegorczyk point (G-point for short) of
$\mathfrak {B}$
. By a Grzegorczyk point (G-point for short) of
![]() $\mathfrak {R}$
we will mean any filter generated by a pre-point of
$\mathfrak {R}$
we will mean any filter generated by a pre-point of
![]() $\mathfrak {R}$
. Thus, for any filter F we have:
$\mathfrak {R}$
. Thus, for any filter F we have:
Let
![]() $\textbf {Gpt}$
be the set of all G-points of
$\textbf {Gpt}$
be the set of all G-points of
![]() $\mathfrak {R}$
. Its elements will be denoted by small gothic letters ‘
$\mathfrak {R}$
. Its elements will be denoted by small gothic letters ‘
![]() $\mathfrak {p}$
’ and ‘
$\mathfrak {p}$
’ and ‘
![]() $\mathfrak {q}$
’.
$\mathfrak {q}$
’.
Every G-point is a maximal filter in
![]() $\textbf {Gpt}$
(see [Reference Gruszczyński and Pietruszczak16]):
$\textbf {Gpt}$
(see [Reference Gruszczyński and Pietruszczak16]):
Furthermore, in [Reference Gruszczyński and Pietruszczak18] we proved that in all BQCAs:

 $$ \begin{align} \forall_{x,y\in R}\bigl(x\ll y \mathrel{\Longrightarrow} \forall_{\mathfrak{p}\in\textbf{Gpt}}(y\in\mathfrak{p}\mathrel{\vee}\exists_{z\in\mathfrak{p}}\: z\bot x) \bigr). \end{align} $$
$$ \begin{align} \forall_{x,y\in R}\bigl(x\ll y \mathrel{\Longrightarrow} \forall_{\mathfrak{p}\in\textbf{Gpt}}(y\in\mathfrak{p}\mathrel{\vee}\exists_{z\in\mathfrak{p}}\: z\bot x) \bigr). \end{align} $$
For Grzegorczyk contact algebras, which are presented in Section 8 and which are BCAs, we obtain the converse implications (8.2) and (8.3).
In the light of (r2) and (3.7) we have
![]() $\textbf {Gpt}\subseteq \textbf {Rnd}$
. Hence, by (6.2) and Lemmas 3.1 and 3.2, for any BQCA we obtain the following fact:
$\textbf {Gpt}\subseteq \textbf {Rnd}$
. Hence, by (6.2) and Lemmas 3.1 and 3.2, for any BQCA we obtain the following fact:
Proposition 6.1. Every G-point in a BQCA belongs to
![]() ${\textbf {M.Rnd}}$
.Footnote
5
${\textbf {M.Rnd}}$
.Footnote
5
Hence, in the light of Lemma 3.1, condition (6.1) is equivalent to the following (cf. condition (%)):
 $$ \begin{align} \forall_{\mathfrak{p}\in\textbf{Gpt}}\forall_{x,y\in R}\bigl(\forall_{z\in\mathfrak{p}}(x\mathbin{\mathsf{C}} z \wedge y\mathbin{\mathsf{C}} z)\mathrel{\Longrightarrow} x\mathbin{\mathsf{C}} y \bigr). \end{align} $$
$$ \begin{align} \forall_{\mathfrak{p}\in\textbf{Gpt}}\forall_{x,y\in R}\bigl(\forall_{z\in\mathfrak{p}}(x\mathbin{\mathsf{C}} z \wedge y\mathbin{\mathsf{C}} z)\mathrel{\Longrightarrow} x\mathbin{\mathsf{C}} y \bigr). \end{align} $$
Now we will consider BQCAs which are complete.
Proposition 6.2.
-
1. In any complete BQCA, every G-point being an ultrafilter is principal and generated by an atom, i.e.,
 $\textbf {Gpt}\cap \textbf {Ult}\subseteq \textbf {PF}_{\!\text {At}}$
.
$\textbf {Gpt}\cap \textbf {Ult}\subseteq \textbf {PF}_{\!\text {At}}$
. -
2. In any atomless complete BQCA, no G-point is an ultrafilter, i.e.,
 $\textbf {Gpt}\cap \textbf {Ult}=\emptyset $
.
$\textbf {Gpt}\cap \textbf {Ult}=\emptyset $
.
Proof.
Ad 1. Every ultrafilter is free or belongs to
![]() $\textbf {PF}_{\!\text {At}}$
. Every G-point is generated by a chain. But no free ultrafilter in a complete BA is generated by a chain (see, e.g., [Reference Hamkins and Seabold21, lemma 43]). Ad 2. Directly from point 1.□
$\textbf {PF}_{\!\text {At}}$
. Every G-point is generated by a chain. But no free ultrafilter in a complete BA is generated by a chain (see, e.g., [Reference Hamkins and Seabold21, lemma 43]). Ad 2. Directly from point 1.□
6.2. G-points of BCAs
In the general case of BCAs, from Lemma 5.1 and Proposition 6.1 we obtain:
Proposition 6.3. In any BCA, every principal filter generated by an atom is a G-point being an ultrafilter and belongs to
![]() ${\textbf {M.Rnd}}$
, i.e.,
${\textbf {M.Rnd}}$
, i.e.,
![]() $\textbf {PF}_{\!\text {At}}\subseteq \textbf {Gpt}\cap \textbf {Ult}\cap {\textbf {M.Rnd}} = \textbf {Gpt}\cap \textbf {Ult}$
.
$\textbf {PF}_{\!\text {At}}\subseteq \textbf {Gpt}\cap \textbf {Ult}\cap {\textbf {M.Rnd}} = \textbf {Gpt}\cap \textbf {Ult}$
.
Hence we have:
Corollary 6.4. In any BCA, every principal ultrafilter is a G-point generated by an atom, i.e.,
![]() $\textbf {PF}\cap \textbf {Ult}\subseteq \textbf {Gpt}\cap \textbf {PF}_{\!\text {At}}$
.
$\textbf {PF}\cap \textbf {Ult}\subseteq \textbf {Gpt}\cap \textbf {PF}_{\!\text {At}}$
.
Moreover, by Propositions 6.2(1) and 6.3, for complete BCAs we have:
Corollary 6.5. In any complete BCA,
![]() $\textbf {Gpt}\cap \textbf {Ult}=\textbf {PF}_{\!\text {At}}= \textbf {Gpt}\cap \textbf {Ult}\cap {\textbf {M.Rnd}}$
.
$\textbf {Gpt}\cap \textbf {Ult}=\textbf {PF}_{\!\text {At}}= \textbf {Gpt}\cap \textbf {Ult}\cap {\textbf {M.Rnd}}$
.
From Propositions 6.1 and 6.3 for atomic BCAs we obtain:
Proposition 6.6. In any atomic BCA, every G-point being a principal filter is generated by an atom, i.e.,
![]() $\textbf {Gpt}\cap \textbf {PF}\subseteq \textbf {PF}_{\!\text {At}}$
.
$\textbf {Gpt}\cap \textbf {PF}\subseteq \textbf {PF}_{\!\text {At}}$
.
Proof. By Proposition 6.1, if
![]() $\operatorname {\mathrm {\uparrow }} x\in \textbf {Gpt}$
then
$\operatorname {\mathrm {\uparrow }} x\in \textbf {Gpt}$
then
![]() $\operatorname {\mathrm {\uparrow }} x\in {\textbf {M.Rnd}}$
. Moreover, for some
$\operatorname {\mathrm {\uparrow }} x\in {\textbf {M.Rnd}}$
. Moreover, for some
![]() $a\in \text {At}$
we have
$a\in \text {At}$
we have
![]() $a\leq x$
. Hence
$a\leq x$
. Hence
![]() $\operatorname {\mathrm {\uparrow }} x \subseteq \operatorname {\mathrm {\uparrow }} a$
. But,
$\operatorname {\mathrm {\uparrow }} x \subseteq \operatorname {\mathrm {\uparrow }} a$
. But,
![]() $\operatorname {\mathrm {\uparrow }} a\in \textbf {Gpt}$
, by Proposition 6.3. Therefore
$\operatorname {\mathrm {\uparrow }} a\in \textbf {Gpt}$
, by Proposition 6.3. Therefore
![]() $x=a$
.□
$x=a$
.□
For atomless BCAs, by Propositions 6.3 and 4.8, we obtain:Footnote 6
Theorem 6.7. Every G-point of an atomless BCA is a free filter.
Finally, we consider the case of
![]() . Firstly, since all filters in
. Firstly, since all filters in
![]() are round, from Proposition 6.1 we get:
are round, from Proposition 6.1 we get:
Lemma 6.8. In any
![]() ,
,
![]() $\textbf {Gpt}\subseteq {\textbf {M.Rnd}}=\textbf {Ult}$
.
$\textbf {Gpt}\subseteq {\textbf {M.Rnd}}=\textbf {Ult}$
.
Secondly, there are, however,
![]() s in which
s in which
![]() $\textbf {Gpt}\subsetneq {\textbf {M.Rnd}}$
:
$\textbf {Gpt}\subsetneq {\textbf {M.Rnd}}$
:
Proposition 6.9. In any infinite complete atomic
![]() ,
,
![]() $\textbf {Gpt}\subsetneq {\textbf {M.Rnd}}=\textbf {Ult}$
.
$\textbf {Gpt}\subsetneq {\textbf {M.Rnd}}=\textbf {Ult}$
.
Proof. Every infinite complete atomic BA has a free ultrafilter. But, by Proposition 6.2(1), no free ultrafilter is a G-point. Hence
![]() $\textbf {Gpt}\subsetneq \textbf {Ult}={\textbf {M.Rnd}}$
, by Lemma 6.8.□
$\textbf {Gpt}\subsetneq \textbf {Ult}={\textbf {M.Rnd}}$
, by Lemma 6.8.□
From finite–cofinite BAs we only get
![]() (see Proposition 4.4). Hence from Propositions 6.3 and 6.9, Corollary 6.5 and Lemma 6.8, respectively, we get:
(see Proposition 4.4). Hence from Propositions 6.3 and 6.9, Corollary 6.5 and Lemma 6.8, respectively, we get:
Corollary 6.10.
-
1. In any finite BCA,
 $\textbf {Gpt} = \textbf {PF}_{\!\text {At}} = \textbf {Ult} = {\textbf {M.Rnd}}$
.
$\textbf {Gpt} = \textbf {PF}_{\!\text {At}} = \textbf {Ult} = {\textbf {M.Rnd}}$
. -
2. In any infinite finite–cofinite BCA,
 $\textbf {PF}_{\!\text {At}}\subseteq \textbf {Gpt}\subseteq \textbf {Ult}={\textbf {M.Rnd}}$
.
$\textbf {PF}_{\!\text {At}}\subseteq \textbf {Gpt}\subseteq \textbf {Ult}={\textbf {M.Rnd}}$
.
7. The Fréchet filter vs. G-points
As we have seen in any BCA each principal ultrafilter is a G-point generated by an atom (cf. Corollary 6.4). In the case of finite BCAs we have
![]() $\textbf {Gpt}=\textbf {PF}_{\!\text {At}}=\textbf {Ult}$
(cf. Corollary 6.10.(1)). We will now answer the following two questions: Are there any other G-points than principal ultrafilters in infinite atomic algebras? and In which infinite atomic BCAs the Fréchet filter can or cannot be a G-point? The subclass of BCAs which will serve to answer those question corresponds to a certain subclass of GCAs.
$\textbf {Gpt}=\textbf {PF}_{\!\text {At}}=\textbf {Ult}$
(cf. Corollary 6.10.(1)). We will now answer the following two questions: Are there any other G-points than principal ultrafilters in infinite atomic algebras? and In which infinite atomic BCAs the Fréchet filter can or cannot be a G-point? The subclass of BCAs which will serve to answer those question corresponds to a certain subclass of GCAs.
Let
![]() $\mathfrak {B}$
be an infinite atomic BA. Then the set
$\mathfrak {B}$
be an infinite atomic BA. Then the set
![]() $\text {cAt}$
of all coatoms has a finite intersection property and generates the so-called Fréchet (or cofinite) filter
$\text {cAt}$
of all coatoms has a finite intersection property and generates the so-called Fréchet (or cofinite) filter
![]() $\text {F}_{\text {c}}$
, which is free. We will use the following properties of
$\text {F}_{\text {c}}$
, which is free. We will use the following properties of
![]() $\text {F}_{\text {c}}$
.
$\text {F}_{\text {c}}$
.
Lemma 7.1. For any
![]() $x\in \text {F}_{\text {c}}$
there are
$x\in \text {F}_{\text {c}}$
there are
![]() $a_1, \ldots , a_n\in \text {At}$
(
$a_1, \ldots , a_n\in \text {At}$
(
![]() $n>0$
) such that
$n>0$
) such that
![]() $x=-(a_1\sqcup \cdots \sqcup a_n)$
.
$x=-(a_1\sqcup \cdots \sqcup a_n)$
.
From Lemma 7.1 and Proposition 4.4 we obtain:
Corollary 7.2. If
![]() $\text {F}_{\text {c}}\in \textbf {Ult}$
, then
$\text {F}_{\text {c}}\in \textbf {Ult}$
, then
![]() $\mathfrak {B}$
is finite–cofinite, and so
$\mathfrak {B}$
is finite–cofinite, and so
![]() is the only BCA based on
is the only BCA based on
![]() $\mathfrak {B}$
.
$\mathfrak {B}$
.
The following two lemmas are analogous to the facts given in [Reference Blass4], where the completeness of a Boolean algebra
![]() $\mathfrak {B}$
is assumed and the fact that
$\mathfrak {B}$
is assumed and the fact that
![]() $\mathfrak {B}$
is isomorphic to the algebra of sets over
$\mathfrak {B}$
is isomorphic to the algebra of sets over
![]() $\text {At}$
is used.
$\text {At}$
is used.
Lemma 7.3. Let
![]() $\mathfrak {B}$
have countably many atoms:
$\mathfrak {B}$
have countably many atoms:
![]() $\textit {a}_1$
,
$\textit {a}_1$
,
![]() $\textit {a}_2$
, …. Then
$\textit {a}_2$
, …. Then
![]() $\text {F}_{\text {c}}$
is generated by the chain
$\text {F}_{\text {c}}$
is generated by the chain
![]() $\text {C}_{\text {c}}:= \{-\textit {a}_1\sqcap \cdots \sqcap - \textit {a}_n \mid n\in \unicode{x3c9} \}$
.
$\text {C}_{\text {c}}:= \{-\textit {a}_1\sqcap \cdots \sqcap - \textit {a}_n \mid n\in \unicode{x3c9} \}$
.
Proof. If
![]() $x\in \text {F}_{\text {c}}$
then for some
$x\in \text {F}_{\text {c}}$
then for some
![]() $k>0$
and
$k>0$
and
![]() $\textit {a}_{i_1}$
, …,
$\textit {a}_{i_1}$
, …,
![]() $\textit {a}_{i_k}\in \text {At}$
we have
$\textit {a}_{i_k}\in \text {At}$
we have
![]() $- \textit {a}_{i_1}\sqcap \cdots \sqcap - \textit {a}_{i_k}\leq x$
. Hence
$- \textit {a}_{i_1}\sqcap \cdots \sqcap - \textit {a}_{i_k}\leq x$
. Hence
![]() $\text {C}_{\text {c}}\ni -\textit {a}_1\sqcap \cdots \sqcap - \textit {a}_{\max \{i_1, \ldots , i_k\}} \leq - \textit {a}_{i_1}\sqcap \cdots \sqcap - \textit {a}_{i_k}\leq x$
. So
$\text {C}_{\text {c}}\ni -\textit {a}_1\sqcap \cdots \sqcap - \textit {a}_{\max \{i_1, \ldots , i_k\}} \leq - \textit {a}_{i_1}\sqcap \cdots \sqcap - \textit {a}_{i_k}\leq x$
. So
![]() $\text {F}_{\text {c}}\subseteq \operatorname {\mathrm {\uparrow }}\text {C}_{\text {c}}$
. Furthermore, if for some
$\text {F}_{\text {c}}\subseteq \operatorname {\mathrm {\uparrow }}\text {C}_{\text {c}}$
. Furthermore, if for some
![]() $n\in \unicode{x3c9} $
we have
$n\in \unicode{x3c9} $
we have
![]() $-\textit {a}_1\sqcap \cdots \sqcap - \textit {a}_n\leq x$
, then
$-\textit {a}_1\sqcap \cdots \sqcap - \textit {a}_n\leq x$
, then
![]() $-x\leq \textit {a}_1\sqcup \cdots \sqcup \textit {a}_n$
, which means that
$-x\leq \textit {a}_1\sqcup \cdots \sqcup \textit {a}_n$
, which means that
![]() $-x$
is composed of finitely many atoms, i.e.,
$-x$
is composed of finitely many atoms, i.e.,
![]() $x\in \text {F}_{\text {c}}$
. So also
$x\in \text {F}_{\text {c}}$
. So also
![]() $\operatorname {\mathrm {\uparrow }} \text {C}_{\text {c}}\subseteq \text {F}_{\text {c}}$
.□
$\operatorname {\mathrm {\uparrow }} \text {C}_{\text {c}}\subseteq \text {F}_{\text {c}}$
.□
The proof of the lemma below is after [Reference Blass4], yet omits the completeness assumption.
Lemma 7.4. If
![]() $\mathfrak {B}$
has uncountably many atoms, then
$\mathfrak {B}$
has uncountably many atoms, then
![]() $\text {F}_{\text {c}}$
is not generated by a chain.
$\text {F}_{\text {c}}$
is not generated by a chain.
Proof. Assume for a contradiction that
![]() $\text {F}_{\text {c}}$
is generated by a chain C. Then
$\text {F}_{\text {c}}$
is generated by a chain C. Then
![]() $C\subseteq \text {F}_{\text {c}}$
. Hence, by Lemma 7.1, for any
$C\subseteq \text {F}_{\text {c}}$
. Hence, by Lemma 7.1, for any
![]() $x\in C$
there are
$x\in C$
there are
![]() $n>0$
and
$n>0$
and
![]() $a_1,\ldots ,a_n\in \text {At}$
such that
$a_1,\ldots ,a_n\in \text {At}$
such that
![]() $-x= a_1\sqcup \cdots \sqcup a_n$
. Therefore the set
$-x= a_1\sqcup \cdots \sqcup a_n$
. Therefore the set
![]() $\text {At}_x^{\bot }$
is finite.
$\text {At}_x^{\bot }$
is finite.
Furthermore, since C is a chain, for all
![]() $x,y\in C$
such that
$x,y\in C$
such that
![]() $x\ne y$
either
$x\ne y$
either
 $\text {At}_x^{\bot }\subsetneq \text {At}_{y}^{\bot }$
or
$\text {At}_x^{\bot }\subsetneq \text {At}_{y}^{\bot }$
or
 $\text {At}_{y}^{\bot }\subsetneq \text {At}_x^{\bot }$
. Thus, the function
$\text {At}_{y}^{\bot }\subsetneq \text {At}_x^{\bot }$
. Thus, the function
![]() $C\ni x\mapsto \text {Card}(\text {At}_x^{\bot }) \in \unicode{x3c9} $
is injective; and so C and
$C\ni x\mapsto \text {Card}(\text {At}_x^{\bot }) \in \unicode{x3c9} $
is injective; and so C and
 $\bigcup _{x\in C}\: \text {At}_x^{\bot }$
are countable. Hence for some
$\bigcup _{x\in C}\: \text {At}_x^{\bot }$
are countable. Hence for some
![]() $a_0\in \text {At}$
we have
$a_0\in \text {At}$
we have
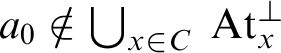 $a_0\notin \bigcup _{x\in C}\: \text {At}_x^{\bot }$
, i.e., for any
$a_0\notin \bigcup _{x\in C}\: \text {At}_x^{\bot }$
, i.e., for any
![]() $x\in C$
we have
$x\in C$
we have
![]() $x\nleq -a_0$
. However, for all
$x\nleq -a_0$
. However, for all
![]() $a\in \text {At}$
it is the case that
$a\in \text {At}$
it is the case that
![]() $-a\in \text {F}_{\text {c}}$
. Therefore, since
$-a\in \text {F}_{\text {c}}$
. Therefore, since
![]() $\text {F}_{\text {c}}$
is generated by C, for some
$\text {F}_{\text {c}}$
is generated by C, for some
![]() $x_a\in C$
we have
$x_a\in C$
we have
![]() $x_a\leq -a$
; a contradiction.□
$x_a\leq -a$
; a contradiction.□
Furthermore, let us remind that:
Lemma 7.5.
![]() $\text {F}_{\text {c}}$
is included in any free filter in
$\text {F}_{\text {c}}$
is included in any free filter in
![]() $\mathfrak {B}$
.
$\mathfrak {B}$
.
Now we will show two classes of BCAs in which
![]() $\text {F}_{\text {c}}$
is not a G-point. From them we will also get two classes of GCAs in which
$\text {F}_{\text {c}}$
is not a G-point. From them we will also get two classes of GCAs in which
![]() $\text {F}_{\text {c}}\notin \textbf {Gpt}$
(see Section 10). Keep in mind that whether
$\text {F}_{\text {c}}\notin \textbf {Gpt}$
(see Section 10). Keep in mind that whether
![]() $\text {F}_{\text {c}}$
is generated by the chain depends on whether
$\text {F}_{\text {c}}$
is generated by the chain depends on whether
![]() $\mathfrak {B}$
has countably many atoms.
$\mathfrak {B}$
has countably many atoms.
Because all G-points are generated by chains, in the light of Lemma 7.4 we obtain:
Proposition 7.6. There is no atomic BQCA with uncountably many atoms such that:
Moreover, we have the following generalization of model 6.18 from [Reference Gruszczyński14]:
Proposition 7.7. There is no infinite complete atomic
![]() that satisfies (
pF
c
).
that satisfies (
pF
c
).
Proof. Let
![]() be based on an infinite complete atomic BA. If
be based on an infinite complete atomic BA. If
![]() $\mathfrak {R}$
has uncountably many atoms, then we use Proposition 7.6. Otherwise,
$\mathfrak {R}$
has uncountably many atoms, then we use Proposition 7.6. Otherwise,
![]() $\text {F}_{\text {c}}$
is free and generated by a chain, by Lemma 7.3. Hence
$\text {F}_{\text {c}}$
is free and generated by a chain, by Lemma 7.3. Hence
![]() $\text {F}_{\text {c}}\notin \textbf {Ult}$
, because no free ultrafilter in a complete BA is generated by a chain (see, e.g., [Reference Hamkins and Seabold21, lemma 43]). But
$\text {F}_{\text {c}}\notin \textbf {Ult}$
, because no free ultrafilter in a complete BA is generated by a chain (see, e.g., [Reference Hamkins and Seabold21, lemma 43]). But
![]() $\textbf {Gpt}\subseteq \textbf {Ult}$
, by Lemma 6.8. Thus, we have
$\textbf {Gpt}\subseteq \textbf {Ult}$
, by Lemma 6.8. Thus, we have
![]() $\text {F}_{\text {c}}\notin \textbf {Gpt}$
.□
$\text {F}_{\text {c}}\notin \textbf {Gpt}$
.□
In consequence, there are BCAs that do not satisfy (
pF
c
). In Theorem 7.9 we will construct a certain class of BCAs satisfying (
pF
c
). Moreover, in Theorem 10.1 we will show that elements of the class are also GCAs. Now we will focus on some properties of infinite atomic BCAs in which
![]() $\text {F}_{\text {c}}$
is a G-point.
$\text {F}_{\text {c}}$
is a G-point.
Theorem 7.8. Let
![]() $\mathfrak {R}$
be an infinite atomic BCA satisfying (
pF
c
). Then:
$\mathfrak {R}$
be an infinite atomic BCA satisfying (
pF
c
). Then:
-
1.
 $\mathfrak {R}$
has countably many atoms.
$\mathfrak {R}$
has countably many atoms. -
2. For all
 $x,y\in R$
:
$x,y\in R$
:
 $x\mathbin {\mathsf {C}} y$
iff either
$x\mathbin {\mathsf {C}} y$
iff either
 or both
or both
 $\text {At}_x$
and
$\text {At}_x$
and
 $\text {At}_y$
are infinite.Footnote
7
$\text {At}_y$
are infinite.Footnote
7
-
3.
 $\text {F}_{\text {c}}$
is the only G-point of
$\text {F}_{\text {c}}$
is the only G-point of
 $\mathfrak {R}$
being a free filter.
$\mathfrak {R}$
being a free filter. -
4.
 $\textbf {Gpt}=\textbf {PF}_{\!\text {At}}\cup \{\text {F}_{\text {c}}\}$
and
$\textbf {Gpt}=\textbf {PF}_{\!\text {At}}\cup \{\text {F}_{\text {c}}\}$
and
 $\textbf {Gpt}$
is countable.
$\textbf {Gpt}$
is countable. -
5.
 $\text {F}_{\text {c}}\in \textbf {Ult}$
iff
$\text {F}_{\text {c}}\in \textbf {Ult}$
iff
 $\textbf {Gpt}\subseteq \textbf {Ult}$
iff
$\textbf {Gpt}\subseteq \textbf {Ult}$
iff
 $\mathfrak {R}$
is a
$\mathfrak {R}$
is a
 .
. -
6. If
 $\text {F}_{\text {c}}\in \textbf {Ult}\,$
, then
$\text {F}_{\text {c}}\in \textbf {Ult}\,$
, then
 $\textbf {Gpt}=\textbf {Ult}$
and
$\textbf {Gpt}=\textbf {Ult}$
and
 $\mathfrak {R}$
is incomplete and finite–cofinite.
$\mathfrak {R}$
is incomplete and finite–cofinite.
Proof. Ad 1. Directly from Proposition 7.6.
Ad 2. The “
![]() $\Rightarrow $
”-part we obtain directly from Lemma 4.3. For the “
$\Rightarrow $
”-part we obtain directly from Lemma 4.3. For the “
![]() $\Leftarrow $
”-part assume that
$\Leftarrow $
”-part assume that
![]() $\text {At}_x$
and
$\text {At}_x$
and
![]() $\text {At}_y$
are infinite. Then, by Lemma 7.1, for any
$\text {At}_y$
are infinite. Then, by Lemma 7.1, for any
![]() $z\in \text {F}_{\text {c}}$
we have:
$z\in \text {F}_{\text {c}}$
we have:
![]() and
and
![]() . Hence, since
. Hence, since
![]() $\text {F}_{\text {c}}\in \textbf {Gpt}$
, by condition (r3), we have
$\text {F}_{\text {c}}\in \textbf {Gpt}$
, by condition (r3), we have
![]() $x\mathbin {\mathsf {C}} y$
.
$x\mathbin {\mathsf {C}} y$
.
Ad 3. By Lemma 7.5,
![]() $\text {F}_{\text {c}}$
is included in any free filter. In consequence, if
$\text {F}_{\text {c}}$
is included in any free filter. In consequence, if
![]() $\text {F}_{\text {c}}$
belongs to
$\text {F}_{\text {c}}$
belongs to
![]() $\textbf {Gpt}$
, then its maximality in the set of G-points excludes any free filter from the set
$\textbf {Gpt}$
, then its maximality in the set of G-points excludes any free filter from the set
![]() $\textbf {Gpt}\,$
. In other words, none of the other G-points is a free filter.
$\textbf {Gpt}\,$
. In other words, none of the other G-points is a free filter.
Ad 4. By our assumption and Proposition 6.3, we have
![]() $\textbf {PF}_{\!\text {At}}\cup \{\text {F}_{\text {c}}\}\subseteq \textbf {Gpt}$
. In virtue of point 2, since
$\textbf {PF}_{\!\text {At}}\cup \{\text {F}_{\text {c}}\}\subseteq \textbf {Gpt}$
. In virtue of point 2, since
![]() $\mathfrak {R}$
is atomic, all G-points different from
$\mathfrak {R}$
is atomic, all G-points different from
![]() $\text {F}_{\text {c}}$
belong to
$\text {F}_{\text {c}}$
belong to
![]() $\textbf {PF}_{\!\text {At}}$
. Thus, also
$\textbf {PF}_{\!\text {At}}$
. Thus, also
![]() $\textbf {Gpt}\subseteq \textbf {PF}_{\!\text {At}}\cup \{\text {F}_{\text {c}}\}$
. So, by point 1,
$\textbf {Gpt}\subseteq \textbf {PF}_{\!\text {At}}\cup \{\text {F}_{\text {c}}\}$
. So, by point 1,
![]() $\textbf {Gpt}$
is countable.
$\textbf {Gpt}$
is countable.
Ad 5. It is obvious that
![]() $\textbf {PF}_{\!\text {At}}\subseteq \textbf {Ult}$
. So if
$\textbf {PF}_{\!\text {At}}\subseteq \textbf {Ult}$
. So if
![]() $\text {F}_{\text {c}}\in \textbf {Ult}$
then
$\text {F}_{\text {c}}\in \textbf {Ult}$
then
![]() $\textbf {Gpt}\subseteq \textbf {Ult}$
, by point 3. Moreover, if
$\textbf {Gpt}\subseteq \textbf {Ult}$
, by point 3. Moreover, if
![]() $\textbf {Gpt}\subseteq \textbf {Ult}$
then
$\textbf {Gpt}\subseteq \textbf {Ult}$
then
![]() $\text {F}_{\text {c}}\in \textbf {Ult}$
, also by point 3. Hence
$\text {F}_{\text {c}}\in \textbf {Ult}$
, also by point 3. Hence
![]() $\mathfrak {R}$
is a
$\mathfrak {R}$
is a
![]() , by Corollary 7.2. Finally, if
, by Corollary 7.2. Finally, if
![]() $\mathfrak {R}$
is a
$\mathfrak {R}$
is a
![]() then
then
![]() $\textbf {Gpt}\subseteq \textbf {Ult}\,$
, by Lemma 6.8. So
$\textbf {Gpt}\subseteq \textbf {Ult}\,$
, by Lemma 6.8. So
![]() $\text {F}_{\text {c}}\in \textbf {Ult}\,$
, by our assumption.
$\text {F}_{\text {c}}\in \textbf {Ult}\,$
, by our assumption.
Ad 6. Suppose that
![]() $\text {F}_{\text {c}}\in \textbf {Ult}$
. Then
$\text {F}_{\text {c}}\in \textbf {Ult}$
. Then
![]() $\textbf {Gpt}\subseteq \textbf {Ult}$
, by point 5. For the converse inclusion assume that
$\textbf {Gpt}\subseteq \textbf {Ult}$
, by point 5. For the converse inclusion assume that
![]() $U\in \textbf {Ult}$
. But each ultrafilter in a given BA either belongs to
$U\in \textbf {Ult}$
. But each ultrafilter in a given BA either belongs to
![]() $\textbf {PF}_{\!\text {At}}$
or is free. In the first case,
$\textbf {PF}_{\!\text {At}}$
or is free. In the first case,
![]() $U\in \textbf {Gpt}$
, by point 3. In the second case, by Lemma 7.5, we have
$U\in \textbf {Gpt}$
, by point 3. In the second case, by Lemma 7.5, we have
![]() $\text {F}_{\text {c}}\subseteq U$
. So
$\text {F}_{\text {c}}\subseteq U$
. So
![]() $U=\text {F}_{\text {c}}\in \textbf {Gpt}$
. Thus, we also obtain that
$U=\text {F}_{\text {c}}\in \textbf {Gpt}$
. Thus, we also obtain that
![]() $\textbf {Ult}\subseteq \textbf {Gpt}$
.
$\textbf {Ult}\subseteq \textbf {Gpt}$
.
Finally, since
![]() $\text {F}_{\text {c}}\in \textbf {Gpt}\cap \textbf {Ult}$
, by Proposition 6.2(1),
$\text {F}_{\text {c}}\in \textbf {Gpt}\cap \textbf {Ult}$
, by Proposition 6.2(1),
![]() $\mathfrak {R}$
is incomplete (we can also use point 5 and Proposition 7.7). Furthermore,
$\mathfrak {R}$
is incomplete (we can also use point 5 and Proposition 7.7). Furthermore,
![]() $\mathfrak {R}$
is finite–cofinite, by Corollary 7.2.□
$\mathfrak {R}$
is finite–cofinite, by Corollary 7.2.□
Below we describe a construction of BCAs which satisfy ( pF c ). The construction is a generalization of model 6.19 from [Reference Gruszczyński14].
Theorem 7.9. Let
![]() $\mathfrak {B}$
be an infinite atomic BA with countably many atoms. For all
$\mathfrak {B}$
be an infinite atomic BA with countably many atoms. For all
![]() $x,y\in R$
we put:
$x,y\in R$
we put:
Then:
-
1. For all
 $x,y\in R$
we have:
$x,y\in R$
we have:  $$ \begin{align*} x\ll y\iff (x\leq y\mathrel{\wedge} \textit{At}_x \textit{ is finite}) \mathrel{\vee} (x\leq y\: \mathrel{\wedge}\: \textit{At}_{-y} \textit{ is finite}). \end{align*} $$
$$ \begin{align*} x\ll y\iff (x\leq y\mathrel{\wedge} \textit{At}_x \textit{ is finite}) \mathrel{\vee} (x\leq y\: \mathrel{\wedge}\: \textit{At}_{-y} \textit{ is finite}). \end{align*} $$
-
2.
 $\langle \mathfrak {B},\mathbin {\mathsf {C}}\rangle $
is a BCA.
$\langle \mathfrak {B},\mathbin {\mathsf {C}}\rangle $
is a BCA. -
3. For the chain
 $\text {C}_{\text {c}}$
from Lemma 7.3 and
$\text {C}_{\text {c}}$
from Lemma 7.3 and
 $x\in R$
we have: (†)
$x\in R$
we have: (†) $$ \begin{align} x \textit{ overlaps with each member of } \text {C}_{\text {c}}\iff \textit{ At}_x \textit{ is infinite.} \end{align} $$
$$ \begin{align} x \textit{ overlaps with each member of } \text {C}_{\text {c}}\iff \textit{ At}_x \textit{ is infinite.} \end{align} $$
-
4.
 $\text {C}_{\text {c}}$
is a pre-point and
$\text {C}_{\text {c}}$
is a pre-point and
 $\text {F}_{\text {c}}$
is a G-point of
$\text {F}_{\text {c}}$
is a G-point of
 $\langle \mathfrak {B},\mathord {\mathbin {\mathsf {C}}}\rangle $
.
$\langle \mathfrak {B},\mathord {\mathbin {\mathsf {C}}}\rangle $
.
Proof.
Ad 1. For all
![]() $x,y\in R$
:
$x,y\in R$
:
![]() $x\ll y$
iff
$x\ll y$
iff
![]() iff
iff
![]() $x\bot - y$
and either
$x\bot - y$
and either
![]() $\text {At}_x$
or
$\text {At}_x$
or
![]() $\text {At}_{-y}$
is finite iff either both
$\text {At}_{-y}$
is finite iff either both
![]() $x\leq y$
and
$x\leq y$
and
![]() $\text {At}_x$
is finite, or both
$\text {At}_x$
is finite, or both
![]() $x\leq y$
and
$x\leq y$
and
![]() $\text {At}_{-y}$
is finite.
$\text {At}_{-y}$
is finite.
Ad 2. It is obvious that
![]() $\langle \mathfrak {B},\mathbin {\mathsf {C}}\rangle $
satisfies (C0)–(C2) and (C4). Moreover, from point 1 we have (∃≪
). For (C3) suppose that
$\langle \mathfrak {B},\mathbin {\mathsf {C}}\rangle $
satisfies (C0)–(C2) and (C4). Moreover, from point 1 we have (∃≪
). For (C3) suppose that
![]() $x\leq y$
and
$x\leq y$
and
![]() $z\mathbin {\mathsf {C}} x$
. If
$z\mathbin {\mathsf {C}} x$
. If
![]() , then
, then
![]() . If both
. If both
![]() $\text {At}_z$
and
$\text {At}_z$
and
![]() $\text {At}_x$
are infinite, then
$\text {At}_x$
are infinite, then
![]() $\text {At}_y$
is also infinite; and so
$\text {At}_y$
is also infinite; and so
![]() $z\mathbin {\mathsf {C}} y$
.
$z\mathbin {\mathsf {C}} y$
.
Ad 3. Condition (†) is obvious.
Ad 4. Let
![]() $\text {At}:= \{\textit {a}_1, \textit {a}_2, \ldots \}$
. For any
$\text {At}:= \{\textit {a}_1, \textit {a}_2, \ldots \}$
. For any
![]() $x\in \text {C}_{\text {c}}$
the set
$x\in \text {C}_{\text {c}}$
the set
![]() $\text {At}_{-x}$
is finite, since for some
$\text {At}_{-x}$
is finite, since for some
![]() $n\in \unicode{x3c9} $
we have
$n\in \unicode{x3c9} $
we have
![]() $-x=\textit {a}_{0}\sqcup \cdots \sqcup \textit {a}_{n}$
. For (r1) suppose that
$-x=\textit {a}_{0}\sqcup \cdots \sqcup \textit {a}_{n}$
. For (r1) suppose that
![]() $u,v\in \text {C}_{\text {c}}$
and
$u,v\in \text {C}_{\text {c}}$
and
![]() $u\neq v$
. Then
$u\neq v$
. Then
![]() $u\leq v$
or
$u\leq v$
or
![]() $v\leq u$
. Thus
$v\leq u$
. Thus
![]() $u\ll v$
or
$u\ll v$
or
![]() $v\ll u$
, by point 1. For (r2) notice that in the case
$v\ll u$
, by point 1. For (r2) notice that in the case
![]() $u\in \text {C}_{\text {c}}$
for some
$u\in \text {C}_{\text {c}}$
for some
![]() $n\in \unicode{x3c9} $
we have:
$n\in \unicode{x3c9} $
we have:
![]() $v:= -\textit {a}_1\sqcap \cdots \sqcap - \textit {a}_n\sqcap - \textit {a}_{n+1}\leq -\textit {a}_1\sqcap \cdots \sqcap - \textit {a}_n=u$
. So
$v:= -\textit {a}_1\sqcap \cdots \sqcap - \textit {a}_n\sqcap - \textit {a}_{n+1}\leq -\textit {a}_1\sqcap \cdots \sqcap - \textit {a}_n=u$
. So
![]() $v\in \text {C}_{\text {c}}$
and
$v\in \text {C}_{\text {c}}$
and
![]() $v\ll u$
, by point 1. For (r3) suppose that x and y overlap with each element of
$v\ll u$
, by point 1. For (r3) suppose that x and y overlap with each element of
![]() $\text {C}_{\text {c}}$
. Then, by (†),
$\text {C}_{\text {c}}$
. Then, by (†),
![]() $\text {At}_x$
and
$\text {At}_x$
and
![]() $\text {At}_y$
are infinite. So
$\text {At}_y$
are infinite. So
![]() $x\mathbin {\mathsf {C}} y$
.
$x\mathbin {\mathsf {C}} y$
.
To round off the proof we use Lemma 7.3.□
Thus, directly from Theorems 7.8 and 7.9 we obtain the following characterization of infinite atomic BCAs having the Fréchet filter as a G-point:
Corollary 7.10. Let
![]() $\langle \mathfrak {B},\mathbin {\mathsf {C}}\rangle $
be an infinite atomic BCA. Then
$\langle \mathfrak {B},\mathbin {\mathsf {C}}\rangle $
be an infinite atomic BCA. Then
![]() $\text {F}_{\text {c}}\in \textbf {Gpt}$
if and only if
$\text {F}_{\text {c}}\in \textbf {Gpt}$
if and only if
![]() $\mathfrak {B}$
has countably many atoms and for all
$\mathfrak {B}$
has countably many atoms and for all
![]() $x,y\in R$
:
$x,y\in R$
:
Remark 7.11. (i) For any set X, let
![]() $\text {P}(X)$
be the power set algebra of X. Any given atomic BA is monomorphic to
$\text {P}(X)$
be the power set algebra of X. Any given atomic BA is monomorphic to
![]() $\text {P}(\text {At})$
. Namely, it is isomorphic to the field of sets
$\text {P}(\text {At})$
. Namely, it is isomorphic to the field of sets
![]() $\{\text {At}_x \mid x\in R\}$
. If a BA is complete, it is isomorphic to
$\{\text {At}_x \mid x\in R\}$
. If a BA is complete, it is isomorphic to
![]() $\text {P}(\text {At})$
. Thus, any atomic BA with countably infinitely many atoms is isomorphic to a dense subalgebra of
$\text {P}(\text {At})$
. Thus, any atomic BA with countably infinitely many atoms is isomorphic to a dense subalgebra of
![]() $\text {P}(\unicode{x3c9} )$
. Moreover, if such a BA is complete, then it is isomorphic to
$\text {P}(\unicode{x3c9} )$
. Moreover, if such a BA is complete, then it is isomorphic to
![]() $\text {P}(\unicode{x3c9} )$
.
$\text {P}(\unicode{x3c9} )$
.
(ii) With reference to Theorems 7.8 and 7.9, let us observe that we can distinguish three kinds of infinite atomic BAs with countably many atoms:
-
1. finite–cofinite—they are incomplete and isomorphic to the finite–cofinite algebra of sets on
 $\unicode{x3c9} $
(shortly:
$\unicode{x3c9} $
(shortly:
 $\text {FC}(\unicode{x3c9} )$
);
$\text {FC}(\unicode{x3c9} )$
); -
2. complete—they are isomorphic to
 $\text {P}(\unicode{x3c9} )$
;
$\text {P}(\unicode{x3c9} )$
; -
3. incomplete, but not finite–cofinite—each is isomorphic to a dense subalgebra of
 $\text {P}(\unicode{x3c9} )$
. This type includes, for example, the Borel algebra of the space of rational numbers with the standard topology (see, e.g., [Reference Koppelberg, Monk and Bonnet22, p. 21]).
$\text {P}(\unicode{x3c9} )$
. This type includes, for example, the Borel algebra of the space of rational numbers with the standard topology (see, e.g., [Reference Koppelberg, Monk and Bonnet22, p. 21]).
If in such BAs we introduce the relation
![]() $\mathbin {\mathsf {C}}$
from Theorem 7.9, we obtain BCAs in which
$\mathbin {\mathsf {C}}$
from Theorem 7.9, we obtain BCAs in which
![]() $\text {F}_{\text {c}}$
is a G-point. For the first type of BAs, we get
$\text {F}_{\text {c}}$
is a G-point. For the first type of BAs, we get
![]() ,
,
![]() $\text {F}_{\text {c}}\in \textbf {Ult}$
and
$\text {F}_{\text {c}}\in \textbf {Ult}$
and
![]() $\textbf {Gpt}=\textbf {Ult}$
; but for the other two types,
$\textbf {Gpt}=\textbf {Ult}$
; but for the other two types,
![]() and
and
![]() $\text {F}_{\text {c}}\notin \textbf {Ult}$
(cf. Proposition 4.4 and Theorem 7.8).
$\text {F}_{\text {c}}\notin \textbf {Ult}$
(cf. Proposition 4.4 and Theorem 7.8).
By Theorems 7.8 and 7.9, the above three types of BAs constitute all infinite atomic BAs satisfying ( pF c ).
It is often walking on thin ice when trying to infer philosophical conclusions from mathematical results. Nevertheless, we venture to sketch a spatial perspective on Corollary 7.10. The notion of Fréchet filter is one of the central concepts of the theory of atomic Boolean algebras. As is well-known, there are algebras whose Stone spaces of points contain the filter, and in the case a BA has the Fréchet filter, it is a subset of every point (ultrafilter) of the Stone space. The notion of a Grzegorczyk point is motivated by geometrical intuitions about the pre-theoretical concept of point. Thus, the sentence “the Fréchet filter is a Grzegorczyk point” might be viewed as saying that the Fréchet filter of a BA satisfies the geometrical intuitions about points. Corollary 7.10 shows that the class of algebras whose Fréchet filter meets those intuitions is relatively narrow, and as such, it testifies to a kind of limitation result about the dependency between the spatial, region-based motivations and purely algebraic constructions. Most of the Boolean algebras have Fréchet filters that do not follow the idea of a point embodied in the definition of Grzegorczyk’s.
8. Grzegorczyk contact algebras
We extend the axioms for the class of BQCAs with the following second-order postulates:

called Grzegorczyk axioms, introduced in [Reference Gruszczyński and Pietruszczak16, Proposition 6.1] and equivalent to the single axiom from [Reference Grzegorczyk19]. Every BQCA which satisfies (G◯ ) and (G⊥ ) is called a Grzegorczyk contact algebra (GCA in short).
It has been demonstrated in [Reference Gruszczyński and Pietruszczak16, Theorem 6.4] that (C0)–(C3) together with (G◯
) and (G⊥
) entail (C4) and (C3c
).Footnote
8
All other conditions from Lemma 4.1, i.e., (C5), (∃≪
), (ext≤
) and (ext
C
), hold as well. (We also get (∃≪
) from the reflexivity of
![]() on
on
![]() $R^+$
, (G◯
), (r2) and (3.7).) Therefore,
$R^+$
, (G◯
), (r2) and (3.7).) Therefore,
Proposition 8.1. Every GCA is a BCA.
Notice that in virtue of Lemma 5.1, we have that:
Lemma 8.2. All atomic BCAs satisfy ( G ◯ ).
All GCAs with
![]() will be called
will be called
![]() . In this case we get (G⊥
) in a trivial way. Thus, we obtain:
. In this case we get (G⊥
) in a trivial way. Thus, we obtain:
Proposition 8.3. Every atomic
![]() is a
is a
![]() and vice versa.
and vice versa.
Thanks to Proposition 6.9 we obtain examples of
![]() in which
in which
![]() $\textbf {Gpt}\subsetneq {\textbf {M.Rnd}}$
(all infinite complete atomic
$\textbf {Gpt}\subsetneq {\textbf {M.Rnd}}$
(all infinite complete atomic
![]() ).Footnote
9
).Footnote
9
In any GCA, by (G◯
), the definition of
![]() $\textbf {Gpt}$
and the reflexivity of
$\textbf {Gpt}$
and the reflexivity of
on
![]() $R^+$
, we have:
$R^+$
, we have:
The following properties of G-points of
![]() $\mathfrak {R}$
play an important role in the analysis of GCAs (see [Reference Gruszczyński14, Reference Gruszczyński and Pietruszczak18]):
$\mathfrak {R}$
play an important role in the analysis of GCAs (see [Reference Gruszczyński14, Reference Gruszczyński and Pietruszczak18]):


 $$ \begin{align} &\!\forall_{x,y\in R}\bigl(x\ll y \iff \forall_{\mathfrak{p}\in\textbf{Gpt}}(y\in\mathfrak{p}\mathrel{\vee}\exists_{z\in\mathfrak{p}}\: z\bot x)\bigr), \end{align} $$
$$ \begin{align} &\!\forall_{x,y\in R}\bigl(x\ll y \iff \forall_{\mathfrak{p}\in\textbf{Gpt}}(y\in\mathfrak{p}\mathrel{\vee}\exists_{z\in\mathfrak{p}}\: z\bot x)\bigr), \end{align} $$
 $$ \begin{align} &\!\!\!\!\!\!\!\!\!\forall_{x,y\in R}\bigl(x\ll y \iff\forall_{\mathfrak{p}\in\textbf{Gpt}}(y\in\mathfrak{p} \mathrel{\vee} -x\in\mathfrak{p})\bigr). \end{align} $$
$$ \begin{align} &\!\!\!\!\!\!\!\!\!\forall_{x,y\in R}\bigl(x\ll y \iff\forall_{\mathfrak{p}\in\textbf{Gpt}}(y\in\mathfrak{p} \mathrel{\vee} -x\in\mathfrak{p})\bigr). \end{align} $$
We get that all points of a given GCA are ultrafilters if and only if it is trivial (and so each of its region is separated from its complement):
Theorem 8.4. In any GCA:
9. G-points, ultrafilters, principal filters and atoms of GCAs
Due to the seminal duality established by Stone [Reference Stone24] for BAs, ultrafilters are candidates for points of GCAs and therefore a question how they relate to G-points comes to mind in a natural way. A partial answer, formulated in [Reference Gruszczyński14, Reference Gruszczyński and Pietruszczak18], boils down to the following theorem which is closely related to Corollary 6.10.(1). The proof of the theorem refers to two non-trivial properties of BAs: any infinite BA has a free ultrafilter and an infinite antichain and no free ultrafilter in a complete BA is generated by a chain (for the latter see, e.g., [Reference Hamkins and Seabold21, Lemma 43]).
Theorem 9.1. If
![]() $\mathfrak {R}$
is a complete GCA, the following conditions are equivalent:
$\mathfrak {R}$
is a complete GCA, the following conditions are equivalent:
-
a.
 $\mathfrak R$
is finite,
$\mathfrak R$
is finite, -
b.
 $\textbf {Gpt}$
is finite,
$\textbf {Gpt}$
is finite, -
c.
 $\textbf {Ult}\subseteq \textbf {Gpt}$
,
$\textbf {Ult}\subseteq \textbf {Gpt}$
, -
d.
 $\textbf {Ult}=\textbf {Gpt}$
.
$\textbf {Ult}=\textbf {Gpt}$
.
In Remark 7.11, we showed that
![]() is an example of an infinite incomplete atomic
is an example of an infinite incomplete atomic
![]() (and so also
(and so also
![]() ) in which we have
) in which we have
![]() $\textbf {Gpt}=\textbf {Ult}$
.
$\textbf {Gpt}=\textbf {Ult}$
.
In the sequel, we will consider the relationship between atoms and principal filters in GCAs. To begin with, we show that we can strengthen Proposition 6.3.
Lemma 9.2. For any
![]() $x\in R$
:
$x\in R$
:
![]() $x\in \text {At}$
iff
$x\in \text {At}$
iff
![]() $\operatorname {\mathrm {\uparrow }} x\in {\textbf {M.Rnd}}$
.
$\operatorname {\mathrm {\uparrow }} x\in {\textbf {M.Rnd}}$
.
Proof. The “
![]() $\Rightarrow $
”-part we obtain directly from Propositions 6.3 and 8.1. For the “
$\Rightarrow $
”-part we obtain directly from Propositions 6.3 and 8.1. For the “
![]() $\Leftarrow $
”-part, assume that
$\Leftarrow $
”-part, assume that
![]() $x\notin \text {At}$
. Then for some
$x\notin \text {At}$
. Then for some
![]() $y\in R^{+}$
we have
$y\in R^{+}$
we have
![]() $y\lneq x$
. Moreover, by (8.1), for some
$y\lneq x$
. Moreover, by (8.1), for some
![]() $\mathfrak {p}_0\in \textbf {Gpt}$
we have
$\mathfrak {p}_0\in \textbf {Gpt}$
we have
![]() $y\in \mathfrak {p}_0$
. Hence
$y\in \mathfrak {p}_0$
. Hence
![]() $\operatorname {\mathrm {\uparrow }} x\subsetneq \mathfrak {p}_0$
. Therefore,
$\operatorname {\mathrm {\uparrow }} x\subsetneq \mathfrak {p}_0$
. Therefore,
![]() $\operatorname {\mathrm {\uparrow }} x$
is not maximal in the family of all round filters, since
$\operatorname {\mathrm {\uparrow }} x$
is not maximal in the family of all round filters, since
![]() $\mathfrak {p}_0\in \textbf {Rnd}$
. Thus, we have
$\mathfrak {p}_0\in \textbf {Rnd}$
. Thus, we have
![]() $\operatorname {\mathrm {\uparrow }} x\notin {\textbf {M.Rnd}}$
.□
$\operatorname {\mathrm {\uparrow }} x\notin {\textbf {M.Rnd}}$
.□
Furthermore, we obtain the following theorem which previously appeared in [Reference Gruszczyński14, Reference Gruszczyński and Pietruszczak18] and which is a strengthening of Proposition 6.3 and Corollary 6.4 for GCAs:
Theorem 9.3. In any GCA, for any
![]() $x\in R$
:
$x\in R$
:
![]() $x\in \text {At}$
iff
$x\in \text {At}$
iff
![]() $\, \operatorname {\mathrm {\uparrow }} x\in \textbf {Gpt}$
iff
$\, \operatorname {\mathrm {\uparrow }} x\in \textbf {Gpt}$
iff
![]() $\, \operatorname {\mathrm {\uparrow }} x\in \textbf {Ult}$
.
$\, \operatorname {\mathrm {\uparrow }} x\in \textbf {Ult}$
.
Proof. Obviously:
![]() $x\in \text {At}$
iff
$x\in \text {At}$
iff
![]() $\operatorname {\mathrm {\uparrow }} x\in \textbf {Ult}$
. From Propositions 6.3 and 8.1 for any
$\operatorname {\mathrm {\uparrow }} x\in \textbf {Ult}$
. From Propositions 6.3 and 8.1 for any
![]() $x\in \text {At}$
we have
$x\in \text {At}$
we have
![]() $\operatorname {\mathrm {\uparrow }} x\in \textbf {Gpt}$
. So if
$\operatorname {\mathrm {\uparrow }} x\in \textbf {Gpt}$
. So if
![]() $\operatorname {\mathrm {\uparrow }} x\in \textbf {Ult}$
then
$\operatorname {\mathrm {\uparrow }} x\in \textbf {Ult}$
then
![]() $\operatorname {\mathrm {\uparrow }} x\in \textbf {Gpt}$
. Let
$\operatorname {\mathrm {\uparrow }} x\in \textbf {Gpt}$
. Let
![]() $\operatorname {\mathrm {\uparrow }} x\in \textbf {Gpt}$
. Then
$\operatorname {\mathrm {\uparrow }} x\in \textbf {Gpt}$
. Then
![]() $\operatorname {\mathrm {\uparrow }} x\in {\textbf {M.Rnd}}$
, by Proposition 6.1. Hence
$\operatorname {\mathrm {\uparrow }} x\in {\textbf {M.Rnd}}$
, by Proposition 6.1. Hence
![]() $x\in \text {At}$
, by Lemma 9.2. So also
$x\in \text {At}$
, by Lemma 9.2. So also
![]() $\operatorname {\mathrm {\uparrow }} x\in \textbf {Ult}$
.□
$\operatorname {\mathrm {\uparrow }} x\in \textbf {Ult}$
.□
From the above theorem we have the following generalization of Proposition 6.6:
Corollary 9.4. In any GCA,
![]() $\textbf {PF}\cap \textbf {Ult}=\textbf {PF}_{\!\text {At}}=\textbf {Gpt}\cap \textbf {PF}$
.
$\textbf {PF}\cap \textbf {Ult}=\textbf {PF}_{\!\text {At}}=\textbf {Gpt}\cap \textbf {PF}$
.
10. G-points and free filters in infinite atomic GCAs
This section is devoted to GCAs based on an infinite atomic BAs. In this case condition ( pF c ) is independent from the axioms of GCAs.
Firstly, there are GCAs that do not satisfy (
pF
c
). Indeed, in the light of Proposition 8.1 and Propositions 7.6 and 7.7, respectively, we get that: no atomic GCA with uncountably many atoms or complete atomic
![]() with infinitely many atoms fulfills (
pF
c
).
with infinitely many atoms fulfills (
pF
c
).
Secondly, we show that there are GCAs satisfying ( pF c ). They are given by the construction we used in Theorem 7.9.
Theorem 10.1. Let
![]() $\mathfrak {B}$
be an infinite atomic BA with countably many atoms. For all
$\mathfrak {B}$
be an infinite atomic BA with countably many atoms. For all
![]() $x,y\in R$
we put:
$x,y\in R$
we put:
Then
![]() $\langle \mathfrak {B},\mathbin {\mathsf {C}}\rangle $
satisfies conditions 1–4 from Theorem 7.9 and moreover:
$\langle \mathfrak {B},\mathbin {\mathsf {C}}\rangle $
satisfies conditions 1–4 from Theorem 7.9 and moreover:
-
5.
 $\langle \mathfrak {B},\mathbin {\mathsf {C}}\rangle $
is a GCA satisfying (
pF
c
).
$\langle \mathfrak {B},\mathbin {\mathsf {C}}\rangle $
is a GCA satisfying (
pF
c
).
Proof. From point 2 and Lemma 8.2 we have that
![]() $\langle \mathfrak {B},\mathbin {\mathsf {C}}\rangle $
satisfies (G◯
). For (G⊥
), if
$\langle \mathfrak {B},\mathbin {\mathsf {C}}\rangle $
satisfies (G◯
). For (G⊥
), if
![]() $x\mathbin {\mathsf {C}} y$
and
$x\mathbin {\mathsf {C}} y$
and
![]() $x\bot y$
, then
$x\bot y$
, then
![]() $\text {At}_x$
and
$\text {At}_x$
and
![]() $\text {At}_y$
are infinite, by point 2 and Lemma 4.3. Now we use (†).□
$\text {At}_y$
are infinite, by point 2 and Lemma 4.3. Now we use (†).□
Finally, notice that in any infinite atomic GCAs in which (
pF
c
) holds, the filter
![]() $\text {F}_{\text {c}}$
has all properties from Theorem 7.8.
$\text {F}_{\text {c}}$
has all properties from Theorem 7.8.
11. Topological spaces of G-points for infinite atomic GCAs
This section shows how the relation between G-points and ultrafilters influences the topological spaces of G-points.
Let
![]() $\mathfrak {R}=\langle \mathfrak {B},\mathbin {\mathsf {C}}\rangle $
be a GCA. For any region x of
$\mathfrak {R}=\langle \mathfrak {B},\mathbin {\mathsf {C}}\rangle $
be a GCA. For any region x of
![]() $\mathfrak {R}$
we put
$\mathfrak {R}$
we put
![]() $\textbf {Ult}(x):= \{U\in \textbf {Ult}\mid x\in U\}$
. It is well-known that the family
$\textbf {Ult}(x):= \{U\in \textbf {Ult}\mid x\in U\}$
. It is well-known that the family
![]() $\{\textbf {Ult}(x)\mid x\in R\}$
is a topological basis on
$\{\textbf {Ult}(x)\mid x\in R\}$
is a topological basis on
![]() $\textbf {Ult}$
. By the Stone space of
$\textbf {Ult}$
. By the Stone space of
![]() $\mathfrak {B}$
we mean—in the standard way—the topological space
$\mathfrak {B}$
we mean—in the standard way—the topological space
![]() $\mathcal {S}(\mathfrak {B})$
in which points are ultrafilters of
$\mathcal {S}(\mathfrak {B})$
in which points are ultrafilters of
![]() $\mathfrak {B}$
and the topology is introduced via the basis
$\mathfrak {B}$
and the topology is introduced via the basis
![]() $\{\textbf {Ult}(x)\mid x\in R\}$
.Footnote
10
$\{\textbf {Ult}(x)\mid x\in R\}$
.Footnote
10
Furthermore, for any region x of
![]() $\mathfrak {R}$
we define the set of all its internal G-points:
$\mathfrak {R}$
we define the set of all its internal G-points:
Of course,
![]() $\operatorname {\mathrm {\textbf {Irl}}}(\mathsf {0})=\emptyset $
and
$\operatorname {\mathrm {\textbf {Irl}}}(\mathsf {0})=\emptyset $
and
![]() $\operatorname {\mathrm {\textbf {Irl}}}(\mathsf {1})=\textbf {Gpt}$
. Moreover, for all
$\operatorname {\mathrm {\textbf {Irl}}}(\mathsf {1})=\textbf {Gpt}$
. Moreover, for all
![]() $x,y\in R$
: if
$x,y\in R$
: if
![]() , then
, then
![]() $\operatorname {\mathrm {\textbf {Irl}}}(x\sqcap y)=\operatorname {\mathrm {\textbf {Irl}}}(x)\cap \operatorname {\mathrm {\textbf {Irl}}}(y)$
;
$\operatorname {\mathrm {\textbf {Irl}}}(x\sqcap y)=\operatorname {\mathrm {\textbf {Irl}}}(x)\cap \operatorname {\mathrm {\textbf {Irl}}}(y)$
;
![]() $x\leq y$
iff
$x\leq y$
iff
![]() $\operatorname {\mathrm {\textbf {Irl}}}(x)\subseteq \operatorname {\mathrm {\textbf {Irl}}}(y)$
(see [Reference Gruszczyński and Pietruszczak18, p. 826]). It is routine to verify that the family
$\operatorname {\mathrm {\textbf {Irl}}}(x)\subseteq \operatorname {\mathrm {\textbf {Irl}}}(y)$
(see [Reference Gruszczyński and Pietruszczak18, p. 826]). It is routine to verify that the family
![]() $\mathscr {B}_{\mathfrak {R}}:= \{\operatorname {\mathrm {\textbf {Irl}}}(x)\mid x\in R\}$
is a topological basis on
$\mathscr {B}_{\mathfrak {R}}:= \{\operatorname {\mathrm {\textbf {Irl}}}(x)\mid x\in R\}$
is a topological basis on
![]() $\textbf {Gpt}\,$
. Let
$\textbf {Gpt}\,$
. Let
![]() $\mathcal {T}_{\!\mathfrak {R}}:= \langle \textbf {Gpt},\mathscr {O}_{\mathfrak {R}}\rangle $
be the topological space introduced via
$\mathcal {T}_{\!\mathfrak {R}}:= \langle \textbf {Gpt},\mathscr {O}_{\mathfrak {R}}\rangle $
be the topological space introduced via
![]() $\mathscr {B}_{\mathfrak {R}}$
. One can prove that every set from
$\mathscr {B}_{\mathfrak {R}}$
. One can prove that every set from
![]() $\mathscr {B}_{\mathfrak {R}}$
is regular open in
$\mathscr {B}_{\mathfrak {R}}$
is regular open in
![]() $\mathcal {T}_{\!\mathfrak {R}}$
, and so
$\mathcal {T}_{\!\mathfrak {R}}$
, and so
![]() $\mathcal {T}_{\!\mathfrak {R}}$
is semi-regular. Moreover,
$\mathcal {T}_{\!\mathfrak {R}}$
is semi-regular. Moreover,
![]() $\mathcal {T}_{\!\mathfrak {R}}$
is concentric, i.e., it is a T
$\mathcal {T}_{\!\mathfrak {R}}$
is concentric, i.e., it is a T
![]() $_1$
-space and each point
$_1$
-space and each point
![]() $\mathfrak {p}\in \textbf {Gpt}$
has a local basis
$\mathfrak {p}\in \textbf {Gpt}$
has a local basis
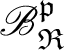 $\mathscr {B}_{\mathfrak {R}}^{\mathfrak {p}}$
satisfying the following condition:
$\mathscr {B}_{\mathfrak {R}}^{\mathfrak {p}}$
satisfying the following condition:
 $$ \begin{align} \forall_{U,V\in\mathscr{B}_{\mathfrak{R}}^{\mathfrak{p}}}\bigl(U=V\vee\operatorname{\mathrm{Cl}} U\subseteq V \vee \operatorname{\mathrm{Cl}} V\subseteq U\bigr). \end{align} $$
$$ \begin{align} \forall_{U,V\in\mathscr{B}_{\mathfrak{R}}^{\mathfrak{p}}}\bigl(U=V\vee\operatorname{\mathrm{Cl}} U\subseteq V \vee \operatorname{\mathrm{Cl}} V\subseteq U\bigr). \end{align} $$
It is known that every topological space having the same properties as
![]() $\mathcal {T}_{\!\mathfrak {R}}$
is also a regular space (see [Reference Gruszczyński14, Reference Gruszczyński and Pietruszczak16, Reference Gruszczyński and Pietruszczak18] for details).Footnote
11
$\mathcal {T}_{\!\mathfrak {R}}$
is also a regular space (see [Reference Gruszczyński14, Reference Gruszczyński and Pietruszczak16, Reference Gruszczyński and Pietruszczak18] for details).Footnote
11
In [Reference Gruszczyński and Pietruszczak18, p. 839] it is shown that: the base
![]() $\mathscr {B}_{\mathfrak {R}}$
consists of clopen sets if and only if
$\mathscr {B}_{\mathfrak {R}}$
consists of clopen sets if and only if
![]() $\mathfrak {R}$
is a
$\mathfrak {R}$
is a
![]() . Thus, in the general case, the base of
. Thus, in the general case, the base of
![]() $\mathcal {T}_{\!\mathfrak {R}}$
does not have to consist of clopen sets. However, below in Proposition 11.3 we can prove that for any infinite atomic GCA
$\mathcal {T}_{\!\mathfrak {R}}$
does not have to consist of clopen sets. However, below in Proposition 11.3 we can prove that for any infinite atomic GCA
![]() $\mathfrak {R}$
satisfying (
pF
c
),
$\mathfrak {R}$
satisfying (
pF
c
),
![]() $\mathcal {T}_{\!\mathfrak {R}}$
is a continuous image of a certain Boolean space (i.e., a Hausdorff, compact and zero-dimensional space).
$\mathcal {T}_{\!\mathfrak {R}}$
is a continuous image of a certain Boolean space (i.e., a Hausdorff, compact and zero-dimensional space).
Given a topological space
![]() $\mathcal {T}=\langle S,\mathscr {O}\rangle $
, its compactification is a pair
$\mathcal {T}=\langle S,\mathscr {O}\rangle $
, its compactification is a pair
![]() $\langle \mathcal {K},e\rangle $
such that:
$\langle \mathcal {K},e\rangle $
such that:
![]() $\mathcal {K}=\langle K,\mathscr {K}\rangle $
is a compact space,
$\mathcal {K}=\langle K,\mathscr {K}\rangle $
is a compact space,
![]() $e\colon S\to K$
is an embedding (an injective continuous map) of
$e\colon S\to K$
is an embedding (an injective continuous map) of
![]() $\mathcal {T}$
into
$\mathcal {T}$
into
![]() $\mathcal {K}$
(so e is a homeomorphism between S and
$\mathcal {K}$
(so e is a homeomorphism between S and
![]() $e[S]$
) and the set
$e[S]$
) and the set
![]() $e[S]$
is dense in
$e[S]$
is dense in
![]() $\mathcal {K}$
. Moreover, we say that
$\mathcal {K}$
. Moreover, we say that
![]() $\mathcal {K}$
is a compactification of
$\mathcal {K}$
is a compactification of
![]() $\mathcal {T}$
iff e is the identity map.
$\mathcal {T}$
iff e is the identity map.
The following lemma will be used in the proof of the last theorem of the paper.
Lemma 11.1. Let
![]() $\mathcal {T}_1=\langle S_1,\mathscr {O}_1\rangle $
,
$\mathcal {T}_1=\langle S_1,\mathscr {O}_1\rangle $
,
![]() $\mathcal {T}_2=\langle S_2,\mathscr {O}_2\rangle $
and
$\mathcal {T}_2=\langle S_2,\mathscr {O}_2\rangle $
and
![]() $\mathcal {K}=\langle K,\mathscr {K}\rangle $
be topological spaces such that:
$\mathcal {K}=\langle K,\mathscr {K}\rangle $
be topological spaces such that:
-
•
 $\!\langle \mathcal {K},e\rangle $
is a compactification of
$\!\langle \mathcal {K},e\rangle $
is a compactification of
 $\mathcal {T}_1$
for some
$\mathcal {T}_1$
for some
 $e\colon S_1\to K$
,
$e\colon S_1\to K$
, -
•
 $\!e'\colon S_1\to S_2$
is an embedding of
$\!e'\colon S_1\to S_2$
is an embedding of
 $\mathcal {T}_1$
into
$\mathcal {T}_1$
into
 $\mathcal {T}_2$
,
$\mathcal {T}_2$
, -
•
 $\!f\colon K\to S_2$
is a continuous surjection such that for any
$\!f\colon K\to S_2$
is a continuous surjection such that for any
 $p\in S_1$
,
$p\in S_1$
,
 $f(e(p))=e'(p)$
.
$f(e(p))=e'(p)$
.
Then
![]() $\langle \mathcal {T}_2,e'\rangle $
is a compactification of
$\langle \mathcal {T}_2,e'\rangle $
is a compactification of
![]() $\mathcal {T}_1$
.
$\mathcal {T}_1$
.
Proof.
![]() $\mathcal {T}_2$
is compact as a continuous image of the compact space
$\mathcal {T}_2$
is compact as a continuous image of the compact space
![]() $\mathcal {K}$
. Therefore, it remains to show that
$\mathcal {K}$
. Therefore, it remains to show that
![]() $e'[S_1]$
is dense in
$e'[S_1]$
is dense in
![]() $\mathcal {T}_2$
. Let
$\mathcal {T}_2$
. Let
![]() $p\in S_2\setminus e'[S_1]$
,
$p\in S_2\setminus e'[S_1]$
,
![]() $V\in \mathscr {O}_2$
and
$V\in \mathscr {O}_2$
and
![]() $p\in V$
. Thus, for some
$p\in V$
. Thus, for some
![]() $k\in K\setminus e[S_1]$
we have
$k\in K\setminus e[S_1]$
we have
![]() $f(k)=p$
and
$f(k)=p$
and
![]() $f^{-1}[V]\in \mathscr {K}$
. So,
$f^{-1}[V]\in \mathscr {K}$
. So,
![]() $f^{-1}[V]\cap e[S_1]\neq \emptyset $
and
$f^{-1}[V]\cap e[S_1]\neq \emptyset $
and
![]() $\emptyset \neq f[f^{-1}[V]\cap e[S_1]]\subseteq f[f^{-1}[V]]\cap f[e[S_1]]\subseteq V\cap e'[S_1]$
.□
$\emptyset \neq f[f^{-1}[V]\cap e[S_1]]\subseteq f[f^{-1}[V]]\cap f[e[S_1]]\subseteq V\cap e'[S_1]$
.□
The following proposition is standard:
Proposition 11.2. If
![]() $\mathfrak {R}$
is infinite and atomic, then
$\mathfrak {R}$
is infinite and atomic, then
![]() $\mathcal {S}(\mathfrak {B})$
is
$\mathcal {S}(\mathfrak {B})$
is
![]() $($
unique up to homeomorphism
$($
unique up to homeomorphism
![]() $)$
the Stone–Čech compactification of
$)$
the Stone–Čech compactification of
![]() $\langle \textbf {PF}_{\!\text {At}}, \wp (\textbf {PF}_{\!\text {At}})\rangle $
.
$\langle \textbf {PF}_{\!\text {At}}, \wp (\textbf {PF}_{\!\text {At}})\rangle $
.
Now we prove:
Proposition 11.3. Let
![]() $\mathfrak R=\langle B,\mathbin {\mathsf {C}}\rangle $
be an infinite atomic GCA satisfying (
pF
c
). Then
$\mathfrak R=\langle B,\mathbin {\mathsf {C}}\rangle $
be an infinite atomic GCA satisfying (
pF
c
). Then
![]() $\mathcal {T}_{\!\mathfrak {R}}$
is a continuous image of
$\mathcal {T}_{\!\mathfrak {R}}$
is a continuous image of
![]() $\mathcal {S}(\mathfrak {B})$
under the function
$\mathcal {S}(\mathfrak {B})$
under the function
![]() $\text {f}\colon \textbf {Ult}\to \textbf {Gpt} \ (= \textbf {PF}_{\!\text {At}} \cup \{\text {F}_{\text {c}}\})$
defined via:
$\text {f}\colon \textbf {Ult}\to \textbf {Gpt} \ (= \textbf {PF}_{\!\text {At}} \cup \{\text {F}_{\text {c}}\})$
defined via:
 $$ \begin{align*} \text{f}(U):= \begin{cases} U & \text{if } U\in\textbf{PF}_{\!\text{At}},\\ \text{F}_{\text{c}} & \text{if } U \text{ is free.} \end{cases} \end{align*} $$
$$ \begin{align*} \text{f}(U):= \begin{cases} U & \text{if } U\in\textbf{PF}_{\!\text{At}},\\ \text{F}_{\text{c}} & \text{if } U \text{ is free.} \end{cases} \end{align*} $$
Furthermore, if
![]() $\text {F}_{\text {c}}\in \textbf {Ult}$
, then
$\text {F}_{\text {c}}\in \textbf {Ult}$
, then
![]() $\text {f}$
is the identity map.
$\text {f}$
is the identity map.
Proof. The proof is trivial if
![]() $\text {F}_{\text {c}}\in \textbf {Ult}$
, because then we have
$\text {F}_{\text {c}}\in \textbf {Ult}$
, because then we have
![]() $\textbf {Gpt}=\textbf {Ult}$
, and so
$\textbf {Gpt}=\textbf {Ult}$
, and so
![]() $\text {f}(U)=U$
for any
$\text {f}(U)=U$
for any
![]() $U\in \textbf {Ult}$
. In other cases, to show that
$U\in \textbf {Ult}$
. In other cases, to show that
![]() $\text {f}$
is continuous it is enough to prove that for any
$\text {f}$
is continuous it is enough to prove that for any
![]() $x\in R$
, the set
$x\in R$
, the set
 $\text {f}^{-1}[\operatorname {\mathrm {\textbf {Irl}}}(x)]$
is open in
$\text {f}^{-1}[\operatorname {\mathrm {\textbf {Irl}}}(x)]$
is open in
![]() $\mathcal {S}_{\mathfrak {R}}$
. We consider three cases.
$\mathcal {S}_{\mathfrak {R}}$
. We consider three cases.
Let x be finite, i.e.,
![]() $x=a_1\sqcup \cdots \sqcup a_n$
, for some
$x=a_1\sqcup \cdots \sqcup a_n$
, for some
![]() $a_1,\ldots ,a_n\in \text {At}$
. Then
$a_1,\ldots ,a_n\in \text {At}$
. Then
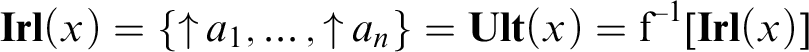 $\operatorname {\mathrm {\textbf {Irl}}}(x)=\{\operatorname {\mathrm {\uparrow }} a_1, \ldots , \operatorname {\mathrm {\uparrow }} a_n\}=\textbf {Ult}(x)=\text {f}^{-1}[\operatorname {\mathrm {\textbf {Irl}}}(x)]$
.
$\operatorname {\mathrm {\textbf {Irl}}}(x)=\{\operatorname {\mathrm {\uparrow }} a_1, \ldots , \operatorname {\mathrm {\uparrow }} a_n\}=\textbf {Ult}(x)=\text {f}^{-1}[\operatorname {\mathrm {\textbf {Irl}}}(x)]$
.
Let x be cofinite, i.e.,
![]() $x=-(a_1\sqcup \cdots \sqcup a_n)$
, for some
$x=-(a_1\sqcup \cdots \sqcup a_n)$
, for some
![]() $a_1,\ldots ,a_n\in \text {At}$
. Then again we have
$a_1,\ldots ,a_n\in \text {At}$
. Then again we have
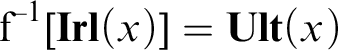 $\text {f}^{-1}[\operatorname {\mathrm {\textbf {Irl}}}(x)]=\textbf {Ult}(x)$
, since for any free ultrafilter U we have:
$\text {f}^{-1}[\operatorname {\mathrm {\textbf {Irl}}}(x)]=\textbf {Ult}(x)$
, since for any free ultrafilter U we have:
 $U\in \text {f}^{-1}[\operatorname {\mathrm {\textbf {Irl}}}(x)]$
iff
$U\in \text {f}^{-1}[\operatorname {\mathrm {\textbf {Irl}}}(x)]$
iff
![]() $U\in \textbf {Ult}(x)$
. Indeed, assume that
$U\in \textbf {Ult}(x)$
. Indeed, assume that
 $U\in \text {f}^{-1}[\operatorname {\mathrm {\textbf {Irl}}}(x)]$
, i.e., for some
$U\in \text {f}^{-1}[\operatorname {\mathrm {\textbf {Irl}}}(x)]$
, i.e., for some
![]() $\mathfrak {p}\in \operatorname {\mathrm {\textbf {Irl}}}(x)$
:
$\mathfrak {p}\in \operatorname {\mathrm {\textbf {Irl}}}(x)$
:
![]() $\mathfrak {p}=\text {f}(U)$
. Then
$\mathfrak {p}=\text {f}(U)$
. Then
![]() $x\in \textrm{f}(U)$
. Furthermore,
$x\in \textrm{f}(U)$
. Furthermore,
![]() $\text {f}(U)=\text {F}_{\text {c}}$
, since U is free. So
$\text {f}(U)=\text {F}_{\text {c}}$
, since U is free. So
![]() $\text {f}(U)\in \operatorname {\mathrm {\textbf {Irl}}}(x)$
. The other way round, if
$\text {f}(U)\in \operatorname {\mathrm {\textbf {Irl}}}(x)$
. The other way round, if
![]() $\text {f}(U)\in \operatorname {\mathrm {\textbf {Irl}}}(x)$
, then
$\text {f}(U)\in \operatorname {\mathrm {\textbf {Irl}}}(x)$
, then
![]() $x\in \text {f}(U)=\text {F}_{\text {c}}$
, since U is free. Finally, because
$x\in \text {f}(U)=\text {F}_{\text {c}}$
, since U is free. Finally, because
![]() $\text {F}_{\text {c}}\subseteq U$
(see Lemma 7.5), we have
$\text {F}_{\text {c}}\subseteq U$
(see Lemma 7.5), we have
![]() $x\in U$
, as required.
$x\in U$
, as required.
Let x be neither finite nor cofinite. Then
![]() $\text {F}_{\text {c}}\notin \textbf {Ult}$
and
$\text {F}_{\text {c}}\notin \textbf {Ult}$
and
![]() $\operatorname {\mathrm {\textbf {Irl}}}(x)=\{\operatorname {\mathrm {\uparrow }} a\mid a\in \text {At}_x\}$
, because
$\operatorname {\mathrm {\textbf {Irl}}}(x)=\{\operatorname {\mathrm {\uparrow }} a\mid a\in \text {At}_x\}$
, because
![]() $x\notin \text {F}_{\text {c}}$
(see Lemma 7.5). Therefore,
$x\notin \text {F}_{\text {c}}$
(see Lemma 7.5). Therefore,
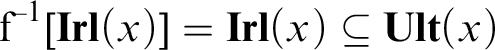 $\text {f}^{-1}[\operatorname {\mathrm {\textbf {Irl}}}(x)]=\operatorname {\mathrm {\textbf {Irl}}}(x)\subseteq \textbf {Ult}(x)$
. Yet the principal ultrafilters correspond to isolated points of
$\text {f}^{-1}[\operatorname {\mathrm {\textbf {Irl}}}(x)]=\operatorname {\mathrm {\textbf {Irl}}}(x)\subseteq \textbf {Ult}(x)$
. Yet the principal ultrafilters correspond to isolated points of
![]() $\mathcal {S}_{\mathfrak {R}}$
; and so
$\mathcal {S}_{\mathfrak {R}}$
; and so
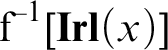 $\text {f}^{-1}[\operatorname {\mathrm {\textbf {Irl}}}(x)]$
must be open in
$\text {f}^{-1}[\operatorname {\mathrm {\textbf {Irl}}}(x)]$
must be open in
![]() $\mathcal {S}(\mathfrak {B})$
.□
$\mathcal {S}(\mathfrak {B})$
.□
Thanks to Lemma 11.1 and Propositions 11.2 and 11.3 we have the following theorem which is a stronger version of Theorem 6.33 from [Reference Gruszczyński14]:
Theorem 11.4. Let
![]() $\mathfrak {R}=\langle \mathfrak {B},\mathbin {\mathsf {C}}\rangle $
be an infinite atomic GCA satisfying (
pF
c
). Then:
$\mathfrak {R}=\langle \mathfrak {B},\mathbin {\mathsf {C}}\rangle $
be an infinite atomic GCA satisfying (
pF
c
). Then:
-
1.
 $\mathcal {T}_{\!\mathfrak {R}}$
is compact.
$\mathcal {T}_{\!\mathfrak {R}}$
is compact. -
2.
 $\mathcal {T}_{\!\mathfrak {R}}$
is the one-point compactification of the discrete space
$\mathcal {T}_{\!\mathfrak {R}}$
is the one-point compactification of the discrete space
 $\langle \textbf {PF}_{\!\text {At}}, \wp (\textbf {PF}_{\!\text {At}})\rangle $
with
$\langle \textbf {PF}_{\!\text {At}}, \wp (\textbf {PF}_{\!\text {At}})\rangle $
with
 $\text {F}_{\text {c}}$
as the “point at infinity.”
$\text {F}_{\text {c}}$
as the “point at infinity.” -
3.
 $\mathscr {O}_{\mathfrak {R}}=\wp (\textbf {PF}_{\!\text {At}})\cup \{X\cup \{\text {F}_{\text {c}}\} \mid X\subseteq \textbf {PF}_{\!\text {At}}$
and
$\mathscr {O}_{\mathfrak {R}}=\wp (\textbf {PF}_{\!\text {At}})\cup \{X\cup \{\text {F}_{\text {c}}\} \mid X\subseteq \textbf {PF}_{\!\text {At}}$
and
 $\textbf {PF}_{\!\text {At}}\setminus X \text { is finite}\}$
.
$\textbf {PF}_{\!\text {At}}\setminus X \text { is finite}\}$
. -
4.
 $\mathcal {T}_{\!\mathfrak {R}}$
is homeomorphic to the Stone space
$\mathcal {T}_{\!\mathfrak {R}}$
is homeomorphic to the Stone space
 $\mathcal {S}(\text {FC}(\mathfrak {B}))$
of the subalgebra
$\mathcal {S}(\text {FC}(\mathfrak {B}))$
of the subalgebra
 $\text {FC}(\mathfrak {B})$
of
$\text {FC}(\mathfrak {B})$
of
 $\mathfrak {B}$
composed of all its finite–cofinite elements.Footnote
12
$\mathfrak {B}$
composed of all its finite–cofinite elements.Footnote
12
Proof.
Ad 1. In the light of Proposition 11.3,
![]() $\mathcal {T}_{\!\mathfrak {R}}$
is compact as a continuous image of the compact space
$\mathcal {T}_{\!\mathfrak {R}}$
is compact as a continuous image of the compact space
![]() $\mathcal {S}(\mathfrak {B})$
.
$\mathcal {S}(\mathfrak {B})$
.
Ad 2. Of course,
![]() $\text {id}\colon \textbf {PF}_{\!\text {At}}\to \textbf {Gpt}$
is an embedding of
$\text {id}\colon \textbf {PF}_{\!\text {At}}\to \textbf {Gpt}$
is an embedding of
![]() $\langle \textbf {PF}_{\!\text {At}}, \wp (\textbf {PF}_{\!\text {At}})\rangle $
into
$\langle \textbf {PF}_{\!\text {At}}, \wp (\textbf {PF}_{\!\text {At}})\rangle $
into
![]() $\mathcal {T}_{\!\mathfrak {R}}$
. By Proposition 11.2,
$\mathcal {T}_{\!\mathfrak {R}}$
. By Proposition 11.2,
![]() $\mathcal {S}(\mathfrak {B})$
is a compactification of
$\mathcal {S}(\mathfrak {B})$
is a compactification of
![]() $\langle \textbf {PF}_{\!\text {At}}, \wp (\textbf {PF}_{\!\text {At}})\rangle $
. By Proposition 11.3,
$\langle \textbf {PF}_{\!\text {At}}, \wp (\textbf {PF}_{\!\text {At}})\rangle $
. By Proposition 11.3,
![]() $\mathcal {T}_{\!\mathfrak {R}}$
is a continuous image of
$\mathcal {T}_{\!\mathfrak {R}}$
is a continuous image of
![]() $\mathcal {S}(\mathfrak {B})$
under the function
$\mathcal {S}(\mathfrak {B})$
under the function
![]() $\text {f}\colon \textbf {Ult}\to \textbf {Gpt}$
. Thus, since f is the identity map on
$\text {f}\colon \textbf {Ult}\to \textbf {Gpt}$
. Thus, since f is the identity map on
![]() $\textbf {PF}_{\!\text {At}}$
,
$\textbf {PF}_{\!\text {At}}$
,
![]() $\mathcal {T}_{\!\mathfrak {R}}$
is a compactification of
$\mathcal {T}_{\!\mathfrak {R}}$
is a compactification of
![]() $\langle \textbf {PF}_{\!\text {At}}, \wp (\textbf {PF}_{\!\text {At}})\rangle $
, by Lemma 11.1.
$\langle \textbf {PF}_{\!\text {At}}, \wp (\textbf {PF}_{\!\text {At}})\rangle $
, by Lemma 11.1.
Furthermore,
![]() $\mathcal {T}_{\!\mathfrak {R}}$
has the unique G-point
$\mathcal {T}_{\!\mathfrak {R}}$
has the unique G-point
![]() $\text {F}_{\text {c}}$
which does not belong to
$\text {F}_{\text {c}}$
which does not belong to
![]() $\textbf {PF}_{\!\text {At}}$
, and therefore
$\textbf {PF}_{\!\text {At}}$
, and therefore
![]() $\mathcal {T}_{\!\mathfrak {R}} $
must be the one-point compactification of
$\mathcal {T}_{\!\mathfrak {R}} $
must be the one-point compactification of
![]() $\langle \textbf {PF}_{\!\text {At}}, \wp (\textbf {PF}_{\!\text {At}})\rangle $
.
$\langle \textbf {PF}_{\!\text {At}}, \wp (\textbf {PF}_{\!\text {At}})\rangle $
.
Ad 4.
![]() $\text {F}_{\text {c}}$
is the only free ultrafilter in
$\text {F}_{\text {c}}$
is the only free ultrafilter in
![]() $\text {FC}(\mathfrak {B})$
, which entails that
$\text {FC}(\mathfrak {B})$
, which entails that
![]() $\mathcal {S}(\text {FC}(\mathfrak {B}))$
is exactly the one-point compactification of
$\mathcal {S}(\text {FC}(\mathfrak {B}))$
is exactly the one-point compactification of
![]() $\langle \textbf {PF}_{\!\text {At}}, \wp (\textbf {PF}_{\!\text {At}})\rangle $
. See also point 3.□
$\langle \textbf {PF}_{\!\text {At}}, \wp (\textbf {PF}_{\!\text {At}})\rangle $
. See also point 3.□
With respect to Remark 7.11(ii), note that in the light of Theorem 11.4(4), there are non-isomorphic GCAs
![]() $\mathfrak {R}_1$
and
$\mathfrak {R}_1$
and
![]() $\mathfrak {R}_2$
which have homeomorphic spaces
$\mathfrak {R}_2$
which have homeomorphic spaces
![]() $\mathcal {T}_{\mathfrak {R}_1}$
and
$\mathcal {T}_{\mathfrak {R}_1}$
and
![]() $\mathcal {T}_{\mathfrak {R}_2}$
, respectively. For example, it is true for
$\mathcal {T}_{\mathfrak {R}_2}$
, respectively. For example, it is true for
![]() and
and
![]() $\langle \text {P}(\unicode{x3c9} ),\mathbin {\mathsf {C}}\rangle $
, where
$\langle \text {P}(\unicode{x3c9} ),\mathbin {\mathsf {C}}\rangle $
, where
![]() $\mathbin {\mathsf {C}}$
is such as in Theorem 7.9 (see Proposition 8.3 and Theorem 10.1). Namely, in both cases, the dual spaces are homeomorphic to
$\mathbin {\mathsf {C}}$
is such as in Theorem 7.9 (see Proposition 8.3 and Theorem 10.1). Namely, in both cases, the dual spaces are homeomorphic to
![]() $\mathcal {S}(\text {FC}(\unicode{x3c9} ))$
. This may be a reason to question the usefulness of the theorem. However, the primary objective of representation theorems is to find a familiar set-theoretical construction to which the initial structure can be reduced. Concerning this, the theorem does a good job, so to say. The representation theorems in the spirit of Stone [Reference Stone24], Düntsch & Winter [Reference Düntsch and Winter11] and Dimov & Vakarelov [Reference Dimov and Vakarelov8] were presented by us in our earlier works [Reference Gruszczyński and Pietruszczak16, Reference Gruszczyński and Pietruszczak18] where we produced object duality theorems for the class of Grzegorczyk contact algebras that satisfy an algebraic version of the countable chain condition.Footnote
13
In the context of this paper, we are only interested in the much narrower class of Grzegorczyk contact algebras. The results obtained, including the representation theorem above, broaden the understanding of Grzegorczyk point-free topology, so far a largely neglected system of a region-based theory of space.
$\mathcal {S}(\text {FC}(\unicode{x3c9} ))$
. This may be a reason to question the usefulness of the theorem. However, the primary objective of representation theorems is to find a familiar set-theoretical construction to which the initial structure can be reduced. Concerning this, the theorem does a good job, so to say. The representation theorems in the spirit of Stone [Reference Stone24], Düntsch & Winter [Reference Düntsch and Winter11] and Dimov & Vakarelov [Reference Dimov and Vakarelov8] were presented by us in our earlier works [Reference Gruszczyński and Pietruszczak16, Reference Gruszczyński and Pietruszczak18] where we produced object duality theorems for the class of Grzegorczyk contact algebras that satisfy an algebraic version of the countable chain condition.Footnote
13
In the context of this paper, we are only interested in the much narrower class of Grzegorczyk contact algebras. The results obtained, including the representation theorem above, broaden the understanding of Grzegorczyk point-free topology, so far a largely neglected system of a region-based theory of space.
A. Appendix: concentric topological spaces and lob-spaces
In this appendix, we prove that all regular lob-spaces are concentric, and in consequence, a topological space is concentric if and only if it is a regular lob-space.
Let
![]() $\mathcal {T}=\langle S,\mathscr {O}\rangle $
be a topological space. We call
$\mathcal {T}=\langle S,\mathscr {O}\rangle $
be a topological space. We call
![]() $\mathcal {T}$
a lob-space provided that for each
$\mathcal {T}$
a lob-space provided that for each
![]() $p\in S$
there is a linearly ordered base
$p\in S$
there is a linearly ordered base
![]() $\mathscr {B}^p$
at p (see, e.g., [Reference Davis6, definition 1.1]), i.e.,
$\mathscr {B}^p$
at p (see, e.g., [Reference Davis6, definition 1.1]), i.e.,
![]() $\mathscr {B}^p$
satisfies the trichotomy condition:
$\mathscr {B}^p$
satisfies the trichotomy condition:
 $$ \begin{align*} \forall_{U,V\in\mathscr{B}^p}\bigl(U=V \vee U\subsetneq V \vee V\subsetneq U\bigr). \end{align*} $$
$$ \begin{align*} \forall_{U,V\in\mathscr{B}^p}\bigl(U=V \vee U\subsetneq V \vee V\subsetneq U\bigr). \end{align*} $$
Furthermore,
![]() $\mathcal {T}$
is concentric iff it is a
$\mathcal {T}$
is concentric iff it is a
![]() $\text {T}_1$
-space and for any
$\text {T}_1$
-space and for any
![]() $p\in S$
there is a base
$p\in S$
there is a base
![]() $\mathscr {B}^p$
at p such that:
$\mathscr {B}^p$
at p such that:
 $$ \begin{align} \forall_{U,V\in\mathscr{B}^p}\bigl(U=V\vee\operatorname{\mathrm{Cl}} U\subseteq V \vee \operatorname{\mathrm{Cl}} V\subseteq U\bigr). \end{align} $$
$$ \begin{align} \forall_{U,V\in\mathscr{B}^p}\bigl(U=V\vee\operatorname{\mathrm{Cl}} U\subseteq V \vee \operatorname{\mathrm{Cl}} V\subseteq U\bigr). \end{align} $$
Obviously, all concentric spaces are lob-spaces. Now we prove that all regular lob-spaces are concentric.
Theorem A.1 A topological space is concentric if and only if it is a regular lob-space.
Proof. For the “
![]() $\Rightarrow $
”-part see Lemma A2 in [Reference Gruszczyński and Pietruszczak16].
$\Rightarrow $
”-part see Lemma A2 in [Reference Gruszczyński and Pietruszczak16].
For the “
![]() $\Leftarrow $
”-part suppose that
$\Leftarrow $
”-part suppose that
![]() $\mathcal {T}=\langle S,\mathscr {O}\rangle $
is a regular lob-space and
$\mathcal {T}=\langle S,\mathscr {O}\rangle $
is a regular lob-space and
![]() $p\in S$
. Then
$p\in S$
. Then
![]() $\mathcal {T}$
is a
$\mathcal {T}$
is a
![]() $\text {T}_1$
-space and there is a base
$\text {T}_1$
-space and there is a base
![]() $\mathscr {B}^p$
at p satisfying the trichotomy condition and such that for any
$\mathscr {B}^p$
at p satisfying the trichotomy condition and such that for any
![]() $B\in \mathscr {B}^p$
there is a
$B\in \mathscr {B}^p$
there is a
![]() $U\in \mathscr {O}$
such that
$U\in \mathscr {O}$
such that
![]() $p\in U\subseteq \operatorname {\mathrm {Cl}} U\subseteq B$
.
$p\in U\subseteq \operatorname {\mathrm {Cl}} U\subseteq B$
.
For some ordinal
![]() $\alpha $
, let
$\alpha $
, let
![]() $\langle W_\beta \mid \beta <\alpha \rangle $
be a coinitial subset of
$\langle W_\beta \mid \beta <\alpha \rangle $
be a coinitial subset of
![]() $\langle \mathscr {B}^p,\mathord {\subseteq }\rangle $
such that for all
$\langle \mathscr {B}^p,\mathord {\subseteq }\rangle $
such that for all
![]() $\beta <\delta <\alpha $
we have
$\beta <\delta <\alpha $
we have
![]() $W_\delta \subsetneq W_\beta $
.Footnote
14
For every
$W_\delta \subsetneq W_\beta $
.Footnote
14
For every
![]() $\beta <\alpha $
there is a
$\beta <\alpha $
there is a
![]() $\delta $
such that
$\delta $
such that
![]() $\beta \leqslant \delta <\alpha $
and
$\beta \leqslant \delta <\alpha $
and
![]() $\operatorname {\mathrm {Cl}} W_\delta \subseteq W_\beta $
. Indeed, for
$\operatorname {\mathrm {Cl}} W_\delta \subseteq W_\beta $
. Indeed, for
![]() $W_\beta $
there is an open set U such that
$W_\beta $
there is an open set U such that
![]() $p\in U\subseteq \operatorname {\mathrm {Cl}} U\subseteq W_\beta $
. Yet
$p\in U\subseteq \operatorname {\mathrm {Cl}} U\subseteq W_\beta $
. Yet
![]() $\langle W_\beta \mid \beta <\alpha \rangle $
is a base at p, so there is a
$\langle W_\beta \mid \beta <\alpha \rangle $
is a base at p, so there is a
![]() $\delta <\alpha $
such that
$\delta <\alpha $
such that
![]() $W_\delta \subseteq U$
, and in consequence
$W_\delta \subseteq U$
, and in consequence
![]() $\operatorname {\mathrm {Cl}} W_\delta \subseteq W_\beta $
, so
$\operatorname {\mathrm {Cl}} W_\delta \subseteq W_\beta $
, so
![]() $\beta \leqslant \delta $
. Thus, there is a monotone coinitial subsequence of
$\beta \leqslant \delta $
. Thus, there is a monotone coinitial subsequence of
![]() $\langle W_\beta \mid \beta <\alpha \rangle $
that satisfies (C), as required.□
$\langle W_\beta \mid \beta <\alpha \rangle $
that satisfies (C), as required.□
Acknowledgements
We would like to thank anonymous referees whose apt and valuable remarks helped us improve the paper.
This research was funded in part by the National Science Center (Poland), grant number 2020/39/B/HS1/00216 “Logico-philosophical foundations of geometry and topology.”





