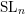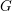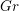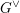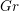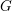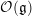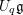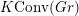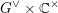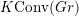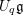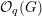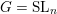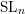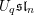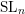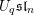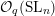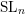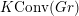1 Introduction
1.1 The geometric Satake correspondence
Let
![]() $G$
be a semisimple complex group. Let
$G$
be a semisimple complex group. Let
![]() $G^{\vee }$
be its Langlands dual group and let
$G^{\vee }$
be its Langlands dual group and let
 $Gr=G^{\vee }((t))/G^{\vee }[[t]]$
be the affine Grassmannian. Let
$Gr=G^{\vee }((t))/G^{\vee }[[t]]$
be the affine Grassmannian. Let
![]() $P(Gr)$
denote the abelian category of perverse sheaves on
$P(Gr)$
denote the abelian category of perverse sheaves on
![]() $Gr$
which are constructible with respect to the stratification by
$Gr$
which are constructible with respect to the stratification by
![]() $G^{\vee }[[t]]$
-orbits. This category is naturally equipped with a monoidal structure using convolution. The geometric Satake correspondence of Mirković and Vybornov [Reference Mirković and VilonenMV07] gives the following result.
$G^{\vee }[[t]]$
-orbits. This category is naturally equipped with a monoidal structure using convolution. The geometric Satake correspondence of Mirković and Vybornov [Reference Mirković and VilonenMV07] gives the following result.
Theorem 1.1. There is an equivalence of monoidal categories
 $$\begin{eqnarray}P(Gr)\cong {\mathcal{R}}\text{ep}(G).\end{eqnarray}$$
$$\begin{eqnarray}P(Gr)\cong {\mathcal{R}}\text{ep}(G).\end{eqnarray}$$
Let
 $D_{G^{\vee }}(Gr)$
and
$D_{G^{\vee }}(Gr)$
and
 $D_{G^{\vee }\times \mathbb{C}^{\times }}(Gr)$
denote the
$D_{G^{\vee }\times \mathbb{C}^{\times }}(Gr)$
denote the
![]() $G^{\vee }$
-equivariant and
$G^{\vee }$
-equivariant and
 $G^{\vee }\times \mathbb{C}^{\times }$
-equivariant derived categories of constructible sheaves on
$G^{\vee }\times \mathbb{C}^{\times }$
-equivariant derived categories of constructible sheaves on
![]() $Gr$
. Here
$Gr$
. Here
![]() $G^{\vee }$
acts naturally on
$G^{\vee }$
acts naturally on
![]() $Gr$
by left multiplication and
$Gr$
by left multiplication and
![]() $\mathbb{C}^{\times }$
acts by loop rotation.
$\mathbb{C}^{\times }$
acts by loop rotation.
The derived geometric Satake correspondence describes these categories of sheaves in terms of representation theory/geometry of the group
![]() $G$
. Let
$G$
. Let
 $\operatorname{Coh}^{G\times \mathbb{C}^{\times }}(\mathfrak{g})={\mathcal{O}}(\frac{\mathfrak{g}}{G})\operatorname{ - mod}$
denote the category of
$\operatorname{Coh}^{G\times \mathbb{C}^{\times }}(\mathfrak{g})={\mathcal{O}}(\frac{\mathfrak{g}}{G})\operatorname{ - mod}$
denote the category of
![]() $G$
-equivariant
$G$
-equivariant
![]() $\mathbb{Z}$
-graded
$\mathbb{Z}$
-graded
![]() ${\mathcal{O}}(\mathfrak{g})$
-modules and likewise let
${\mathcal{O}}(\mathfrak{g})$
-modules and likewise let
 $U_{\hbar }(\frac{\mathfrak{g}}{G})\operatorname{ - mod}$
denote the category of
$U_{\hbar }(\frac{\mathfrak{g}}{G})\operatorname{ - mod}$
denote the category of
![]() $G$
-equivariant graded
$G$
-equivariant graded
![]() $U_{\hbar }(\mathfrak{g})$
-modules. Here
$U_{\hbar }(\mathfrak{g})$
-modules. Here
![]() $U_{\hbar }(\mathfrak{g})$
denotes the Rees algebra of the universal enveloping algebra
$U_{\hbar }(\mathfrak{g})$
denotes the Rees algebra of the universal enveloping algebra
![]() $U\mathfrak{g}$
with respect to the Poincaré–Birkhoff–Witt (PBW) filtration (
$U\mathfrak{g}$
with respect to the Poincaré–Birkhoff–Witt (PBW) filtration (
![]() $U_{\hbar }(\mathfrak{g})$
is sometimes called the asymptotic universal enveloping algebra; it should not be confused with the quantum group
$U_{\hbar }(\mathfrak{g})$
is sometimes called the asymptotic universal enveloping algebra; it should not be confused with the quantum group
![]() $U_{q}\mathfrak{g}$
). The
$U_{q}\mathfrak{g}$
). The
![]() $\mathbb{C}^{\times }$
action on
$\mathbb{C}^{\times }$
action on
![]() $\mathfrak{g}$
is by scaling, which means that in the induced
$\mathfrak{g}$
is by scaling, which means that in the induced
![]() $\mathbb{Z}$
-grading on
$\mathbb{Z}$
-grading on
![]() ${\mathcal{O}}(\mathfrak{g})$
and
${\mathcal{O}}(\mathfrak{g})$
and
![]() $U_{\hbar }(\mathfrak{g})$
, elements of
$U_{\hbar }(\mathfrak{g})$
, elements of
![]() $\mathfrak{g}$
as well as
$\mathfrak{g}$
as well as
![]() $\hbar$
have degree
$\hbar$
have degree
![]() $1$
. As usual, we will write
$1$
. As usual, we will write
![]() $\{1\}$
for a shift in the
$\{1\}$
for a shift in the
![]() $\mathbb{Z}$
-grading. Typical objects of
$\mathbb{Z}$
-grading. Typical objects of
 ${\mathcal{O}}(\frac{\mathfrak{g}}{G})\operatorname{ - mod}$
and
${\mathcal{O}}(\frac{\mathfrak{g}}{G})\operatorname{ - mod}$
and
 $U_{\hbar }(\frac{\mathfrak{g}}{G})\operatorname{ - mod}$
are
$U_{\hbar }(\frac{\mathfrak{g}}{G})\operatorname{ - mod}$
are
 ${\mathcal{O}}(\mathfrak{g})\otimes V$
and
${\mathcal{O}}(\mathfrak{g})\otimes V$
and
 $U_{\hbar }(\mathfrak{g})\otimes V$
where
$U_{\hbar }(\mathfrak{g})\otimes V$
where
![]() $V$
is a finite-dimensional representation of
$V$
is a finite-dimensional representation of
![]() $G$
.
$G$
.
The following result is due to Bezrukavnikov and Finkelberg [Reference Bezrukavnikov and FinkelbergBF08, Corollary 1].
Theorem 1.2. There are monoidal functors
 $$\begin{eqnarray}\displaystyle & F:D({\mathcal{O}}({\textstyle \frac{\mathfrak{g}}{G}})\operatorname{ - mod})\rightarrow D_{G^{\vee }}(Gr), & \displaystyle \nonumber\\ \displaystyle & F:D(U_{\hbar }({\textstyle \frac{\mathfrak{g}}{G}})\operatorname{ - mod})\rightarrow D_{G^{\vee }\times \mathbb{C}^{\times }}(Gr) & \displaystyle \nonumber\end{eqnarray}$$
$$\begin{eqnarray}\displaystyle & F:D({\mathcal{O}}({\textstyle \frac{\mathfrak{g}}{G}})\operatorname{ - mod})\rightarrow D_{G^{\vee }}(Gr), & \displaystyle \nonumber\\ \displaystyle & F:D(U_{\hbar }({\textstyle \frac{\mathfrak{g}}{G}})\operatorname{ - mod})\rightarrow D_{G^{\vee }\times \mathbb{C}^{\times }}(Gr) & \displaystyle \nonumber\end{eqnarray}$$
such that for any two objects
 $A,B\in {\mathcal{O}}(\frac{\mathfrak{g}}{G})\operatorname{ - mod}$
,
$A,B\in {\mathcal{O}}(\frac{\mathfrak{g}}{G})\operatorname{ - mod}$
,
![]() $F$
gives an isomorphism
$F$
gives an isomorphism
 $$\begin{eqnarray}\bigoplus _{n,m}\operatorname{Ext}^{m}(A,B\{n\})\cong \bigoplus _{k}\operatorname{Ext}^{k}(F(A),F(B))\end{eqnarray}$$
$$\begin{eqnarray}\bigoplus _{n,m}\operatorname{Ext}^{m}(A,B\{n\})\cong \bigoplus _{k}\operatorname{Ext}^{k}(F(A),F(B))\end{eqnarray}$$
(and similarly for
 $A,B\in U_{\hbar }(\frac{\mathfrak{g}}{G})\operatorname{ - mod}$
).
$A,B\in U_{\hbar }(\frac{\mathfrak{g}}{G})\operatorname{ - mod}$
).
Using a standard result of Ginzburg [Reference Chriss and GinzburgCG97, Theorem 8.6.7] (see § 3.4 below), we can translate this into a statement about homology of certain fibre products. Suppose that
 $\text{}\underline{\unicode[STIX]{x1D706}}=(\unicode[STIX]{x1D706}_{1},\ldots ,\unicode[STIX]{x1D706}_{m})$
and
$\text{}\underline{\unicode[STIX]{x1D706}}=(\unicode[STIX]{x1D706}_{1},\ldots ,\unicode[STIX]{x1D706}_{m})$
and
 $\text{}\underline{\unicode[STIX]{x1D707}}=(\unicode[STIX]{x1D707}_{1},\ldots ,\unicode[STIX]{x1D707}_{m^{\prime }})$
are two sequences of minuscule dominant weights for
$\text{}\underline{\unicode[STIX]{x1D707}}=(\unicode[STIX]{x1D707}_{1},\ldots ,\unicode[STIX]{x1D707}_{m^{\prime }})$
are two sequences of minuscule dominant weights for
![]() $G$
. Then the geometric Satake equivalence and its derived version (Theorem 1.2) imply the following isomorphisms.
$G$
. Then the geometric Satake equivalence and its derived version (Theorem 1.2) imply the following isomorphisms.
Theorem 1.3. There are canonical isomorphisms
 $$\begin{eqnarray}\displaystyle H_{\text{top}}(Z(\text{}\underline{\unicode[STIX]{x1D706}},\text{}\underline{\unicode[STIX]{x1D707}})) & \cong & \displaystyle \operatorname{Hom}_{G}(V(\text{}\underline{\unicode[STIX]{x1D706}}),V(\text{}\underline{\unicode[STIX]{x1D707}})),\nonumber\\ \displaystyle H_{\ast }^{G^{\vee }}(Z(\text{}\underline{\unicode[STIX]{x1D706}},\text{}\underline{\unicode[STIX]{x1D707}})) & \cong & \displaystyle \operatorname{Hom}_{{\mathcal{O}}(\frac{\mathfrak{g}}{G})\operatorname{-mod}}({\mathcal{O}}(\mathfrak{g})\otimes V(\text{}\underline{\unicode[STIX]{x1D706}}),{\mathcal{O}}(\mathfrak{g})\otimes V(\text{}\underline{\unicode[STIX]{x1D707}})),\nonumber\\ \displaystyle H_{\ast }^{G^{\vee }\times \mathbb{C}^{\times }}(Z(\text{}\underline{\unicode[STIX]{x1D706}},\text{}\underline{\unicode[STIX]{x1D707}})) & \cong & \displaystyle \operatorname{Hom}_{U_{\hbar }(\frac{\mathfrak{g}}{G})\operatorname{-mod}}(U_{\hbar }(\mathfrak{g})\otimes V(\text{}\underline{\unicode[STIX]{x1D706}}),U_{\hbar }(\mathfrak{g})\otimes V(\text{}\underline{\unicode[STIX]{x1D707}})).\nonumber\end{eqnarray}$$
$$\begin{eqnarray}\displaystyle H_{\text{top}}(Z(\text{}\underline{\unicode[STIX]{x1D706}},\text{}\underline{\unicode[STIX]{x1D707}})) & \cong & \displaystyle \operatorname{Hom}_{G}(V(\text{}\underline{\unicode[STIX]{x1D706}}),V(\text{}\underline{\unicode[STIX]{x1D707}})),\nonumber\\ \displaystyle H_{\ast }^{G^{\vee }}(Z(\text{}\underline{\unicode[STIX]{x1D706}},\text{}\underline{\unicode[STIX]{x1D707}})) & \cong & \displaystyle \operatorname{Hom}_{{\mathcal{O}}(\frac{\mathfrak{g}}{G})\operatorname{-mod}}({\mathcal{O}}(\mathfrak{g})\otimes V(\text{}\underline{\unicode[STIX]{x1D706}}),{\mathcal{O}}(\mathfrak{g})\otimes V(\text{}\underline{\unicode[STIX]{x1D707}})),\nonumber\\ \displaystyle H_{\ast }^{G^{\vee }\times \mathbb{C}^{\times }}(Z(\text{}\underline{\unicode[STIX]{x1D706}},\text{}\underline{\unicode[STIX]{x1D707}})) & \cong & \displaystyle \operatorname{Hom}_{U_{\hbar }(\frac{\mathfrak{g}}{G})\operatorname{-mod}}(U_{\hbar }(\mathfrak{g})\otimes V(\text{}\underline{\unicode[STIX]{x1D706}}),U_{\hbar }(\mathfrak{g})\otimes V(\text{}\underline{\unicode[STIX]{x1D707}})).\nonumber\end{eqnarray}$$
Here
![]() $Z(\text{}\underline{\unicode[STIX]{x1D706}},\text{}\underline{\unicode[STIX]{x1D707}})$
is a certain fibre product defined using
$Z(\text{}\underline{\unicode[STIX]{x1D706}},\text{}\underline{\unicode[STIX]{x1D707}})$
is a certain fibre product defined using
![]() $Gr$
(see § 3.4), and
$Gr$
(see § 3.4), and
 $V(\text{}\underline{\unicode[STIX]{x1D706}})=V(\unicode[STIX]{x1D706}_{1})\otimes \cdots \otimes V(\unicode[STIX]{x1D706}_{m})$
is a tensor product of irreducible representations.
$V(\text{}\underline{\unicode[STIX]{x1D706}})=V(\unicode[STIX]{x1D706}_{1})\otimes \cdots \otimes V(\unicode[STIX]{x1D706}_{m})$
is a tensor product of irreducible representations.
1.2 A conjectural K-theoretic version
One goal in this paper is to extend the geometric Satake correspondence and the isomorphisms from Theorem 1.3 to the quantum group
![]() $U_{q}\mathfrak{g}$
. We will introduce the quantum parameter
$U_{q}\mathfrak{g}$
. We will introduce the quantum parameter
![]() $q$
by replacing homology with
$q$
by replacing homology with
![]() $\mathbb{C}^{\times }$
-equivariant
$\mathbb{C}^{\times }$
-equivariant
![]() $K$
-theory.Footnote
1
We begin with the ansatz that passing from homology to K-theory on the left-hand sides on Theorem 1.3 corresponds to passing from
$K$
-theory.Footnote
1
We begin with the ansatz that passing from homology to K-theory on the left-hand sides on Theorem 1.3 corresponds to passing from
![]() ${\mathcal{O}}(\mathfrak{g})$
to
${\mathcal{O}}(\mathfrak{g})$
to
![]() ${\mathcal{O}}(G)$
on the right-hand sides. Let
${\mathcal{O}}(G)$
on the right-hand sides. Let
![]() ${\mathcal{O}}_{q}(G)$
be the braided quantum function algebra, which is a quantization of
${\mathcal{O}}_{q}(G)$
be the braided quantum function algebra, which is a quantization of
![]() ${\mathcal{O}}(G)$
. This leads us to the following conjecture.
${\mathcal{O}}(G)$
. This leads us to the following conjecture.
Conjecture 1.4. Let
![]() $\text{}\underline{\unicode[STIX]{x1D706}}$
and
$\text{}\underline{\unicode[STIX]{x1D706}}$
and
![]() $\text{}\underline{\unicode[STIX]{x1D707}}$
be two sequences of minuscule dominant weights. Up to appropriate localizations, there are canonical isomorphisms
$\text{}\underline{\unicode[STIX]{x1D707}}$
be two sequences of minuscule dominant weights. Up to appropriate localizations, there are canonical isomorphisms
 $$\begin{eqnarray}\displaystyle & K^{G^{\vee }}(Z(\text{}\underline{\unicode[STIX]{x1D706}},\text{}\underline{\unicode[STIX]{x1D707}}))\cong \operatorname{Hom}_{{\mathcal{O}}({\textstyle \frac{G}{G}})\operatorname{-mod}}({\mathcal{O}}(G)\otimes V(\text{}\underline{\unicode[STIX]{x1D706}}),{\mathcal{O}}(G)\otimes V(\text{}\underline{\unicode[STIX]{x1D707}})), & \displaystyle \nonumber\\ \displaystyle & K^{G^{\vee }\times \mathbb{C}^{\times }}(Z(\text{}\underline{\unicode[STIX]{x1D706}},\text{}\underline{\unicode[STIX]{x1D707}}))\cong \operatorname{Hom}_{{\mathcal{O}}_{q}({\textstyle \frac{G}{G}})\operatorname{-mod}}({\mathcal{O}}_{q}(G)\otimes V(\text{}\underline{\unicode[STIX]{x1D706}}),{\mathcal{O}}_{q}(G)\otimes V(\text{}\underline{\unicode[STIX]{x1D707}})), & \displaystyle \nonumber\end{eqnarray}$$
$$\begin{eqnarray}\displaystyle & K^{G^{\vee }}(Z(\text{}\underline{\unicode[STIX]{x1D706}},\text{}\underline{\unicode[STIX]{x1D707}}))\cong \operatorname{Hom}_{{\mathcal{O}}({\textstyle \frac{G}{G}})\operatorname{-mod}}({\mathcal{O}}(G)\otimes V(\text{}\underline{\unicode[STIX]{x1D706}}),{\mathcal{O}}(G)\otimes V(\text{}\underline{\unicode[STIX]{x1D707}})), & \displaystyle \nonumber\\ \displaystyle & K^{G^{\vee }\times \mathbb{C}^{\times }}(Z(\text{}\underline{\unicode[STIX]{x1D706}},\text{}\underline{\unicode[STIX]{x1D707}}))\cong \operatorname{Hom}_{{\mathcal{O}}_{q}({\textstyle \frac{G}{G}})\operatorname{-mod}}({\mathcal{O}}_{q}(G)\otimes V(\text{}\underline{\unicode[STIX]{x1D706}}),{\mathcal{O}}_{q}(G)\otimes V(\text{}\underline{\unicode[STIX]{x1D707}})), & \displaystyle \nonumber\end{eqnarray}$$
where
 ${\mathcal{O}}({\textstyle \frac{G}{G}})\operatorname{ - mod}$
is the category of
${\mathcal{O}}({\textstyle \frac{G}{G}})\operatorname{ - mod}$
is the category of
![]() $G$
-equivariant
$G$
-equivariant
![]() ${\mathcal{O}}(G)$
-modules and
${\mathcal{O}}(G)$
-modules and
 ${\mathcal{O}}_{q}({\textstyle \frac{G}{G}})\operatorname{ - mod}$
the category of
${\mathcal{O}}_{q}({\textstyle \frac{G}{G}})\operatorname{ - mod}$
the category of
![]() $U_{q}\mathfrak{g}$
-equivariant
$U_{q}\mathfrak{g}$
-equivariant
![]() ${\mathcal{O}}_{q}(G)$
-modules.
${\mathcal{O}}_{q}(G)$
-modules.
Notice that we do not make any statement concerning
 $\operatorname{Hom}_{U_{q}\mathfrak{g}}(V(\text{}\underline{\unicode[STIX]{x1D706}}),V(\text{}\underline{\unicode[STIX]{x1D707}}))$
. This is because we do not have an analog of ‘top homology’ within the world of
$\operatorname{Hom}_{U_{q}\mathfrak{g}}(V(\text{}\underline{\unicode[STIX]{x1D706}}),V(\text{}\underline{\unicode[STIX]{x1D707}}))$
. This is because we do not have an analog of ‘top homology’ within the world of
![]() $\mathbb{C}^{\times }$
-equivariant K-theory.
$\mathbb{C}^{\times }$
-equivariant K-theory.
In § 3.5, we define a category
 $K\operatorname{Conv}^{G^{\vee }\times \mathbb{C}^{\times }}(Gr)$
whose objects are sequences of minuscule dominant weights and whose morphisms are given by
$K\operatorname{Conv}^{G^{\vee }\times \mathbb{C}^{\times }}(Gr)$
whose objects are sequences of minuscule dominant weights and whose morphisms are given by
 $K^{G^{\vee }\times \mathbb{C}^{\times }}(Z(\text{}\underline{\unicode[STIX]{x1D706}},\text{}\underline{\unicode[STIX]{x1D707}}))$
(and similarly without the
$K^{G^{\vee }\times \mathbb{C}^{\times }}(Z(\text{}\underline{\unicode[STIX]{x1D706}},\text{}\underline{\unicode[STIX]{x1D707}}))$
(and similarly without the
![]() $\mathbb{C}^{\times }$
). Then Conjecture 1.4 can be reformulated as the existence of full embeddings
$\mathbb{C}^{\times }$
). Then Conjecture 1.4 can be reformulated as the existence of full embeddings
 $$\begin{eqnarray}\displaystyle K\operatorname{Conv}^{G^{\vee }}(Gr) & \rightarrow & \displaystyle {\mathcal{O}}({\textstyle \frac{G}{G}})\operatorname{ - mod},\nonumber\\ \displaystyle K\operatorname{Conv}^{G^{\vee }\times \mathbb{C}^{\times }}(Gr) & \rightarrow & \displaystyle {\mathcal{O}}_{q}({\textstyle \frac{G}{G}})\operatorname{ - mod}\nonumber\end{eqnarray}$$
$$\begin{eqnarray}\displaystyle K\operatorname{Conv}^{G^{\vee }}(Gr) & \rightarrow & \displaystyle {\mathcal{O}}({\textstyle \frac{G}{G}})\operatorname{ - mod},\nonumber\\ \displaystyle K\operatorname{Conv}^{G^{\vee }\times \mathbb{C}^{\times }}(Gr) & \rightarrow & \displaystyle {\mathcal{O}}_{q}({\textstyle \frac{G}{G}})\operatorname{ - mod}\nonumber\end{eqnarray}$$
(see Conjecture 3.4).
There are two explanations for the appearances of the categories
 ${\mathcal{O}}({\textstyle \frac{G}{G}})\operatorname{ - mod}$
and
${\mathcal{O}}({\textstyle \frac{G}{G}})\operatorname{ - mod}$
and
 ${\mathcal{O}}_{q}({\textstyle \frac{G}{G}})\operatorname{ - mod}$
. On the one hand, they are the natural ‘multiplicative’ analogs of the categories
${\mathcal{O}}_{q}({\textstyle \frac{G}{G}})\operatorname{ - mod}$
. On the one hand, they are the natural ‘multiplicative’ analogs of the categories
 ${\mathcal{O}}(\frac{\mathfrak{g}}{G})\operatorname{ - mod}$
and
${\mathcal{O}}(\frac{\mathfrak{g}}{G})\operatorname{ - mod}$
and
 $U_{\hbar }(\frac{\mathfrak{g}}{G})\operatorname{ - mod}$
from the work of Bezrukavnikov and Finkelberg [Reference Bezrukavnikov and FinkelbergBF08]. On the other hand, as we will recall in § 2.4, they are the horizontal traces of the monoidal categories
$U_{\hbar }(\frac{\mathfrak{g}}{G})\operatorname{ - mod}$
from the work of Bezrukavnikov and Finkelberg [Reference Bezrukavnikov and FinkelbergBF08]. On the other hand, as we will recall in § 2.4, they are the horizontal traces of the monoidal categories
 ${\mathcal{R}}\text{ep}(G)$
and
${\mathcal{R}}\text{ep}(G)$
and
 ${\mathcal{R}}\text{ep}_{q}(G)$
. Both perspectives will play a role in this paper.
${\mathcal{R}}\text{ep}_{q}(G)$
. Both perspectives will play a role in this paper.
The algebras
 ${\mathcal{O}}(\mathfrak{g}),U_{\hbar }(\mathfrak{g}),{\mathcal{O}}(G),{\mathcal{O}}_{q}(G)$
fit into a natural ‘diamond’, which we learnt from Jordan [Reference JordanJor14].Footnote
2
${\mathcal{O}}(\mathfrak{g}),U_{\hbar }(\mathfrak{g}),{\mathcal{O}}(G),{\mathcal{O}}_{q}(G)$
fit into a natural ‘diamond’, which we learnt from Jordan [Reference JordanJor14].Footnote
2

This leads to a diagram of categories.

Conjecture 1.4 can then be formulated as saying that this diagram of ‘algebraic’ categories is related to the following diagram of ‘topological’ categories.

1.3 Proof in type A
Most of this paper is devoted to proving the above conjecture for
 $G=\operatorname{SL}_{n}$
.
$G=\operatorname{SL}_{n}$
.
Let
 ${\mathcal{O}}_{q}^{\min }({\textstyle \frac{\operatorname{SL}_{n}}{\operatorname{SL}_{n}}})\operatorname{ - mod}$
be the full subcategory of
${\mathcal{O}}_{q}^{\min }({\textstyle \frac{\operatorname{SL}_{n}}{\operatorname{SL}_{n}}})\operatorname{ - mod}$
be the full subcategory of
![]() $U_{q}\mathfrak{s}\mathfrak{l}_{n}$
-equivariant
$U_{q}\mathfrak{s}\mathfrak{l}_{n}$
-equivariant
 ${\mathcal{O}}_{q}(\operatorname{SL}_{n})$
-modules of the form
${\mathcal{O}}_{q}(\operatorname{SL}_{n})$
-modules of the form
 ${\mathcal{O}}_{q}(\operatorname{SL}_{n})\otimes V$
, where
${\mathcal{O}}_{q}(\operatorname{SL}_{n})\otimes V$
, where
![]() $V$
is a tensor product of fundamental representations. Our strategy is to give a combinatorial/diagrammatic presentation of both categories
$V$
is a tensor product of fundamental representations. Our strategy is to give a combinatorial/diagrammatic presentation of both categories
 ${\mathcal{O}}_{q}^{\min }({\textstyle \frac{\operatorname{SL}_{n}}{\operatorname{SL}_{n}}})\operatorname{ - mod}$
and
${\mathcal{O}}_{q}^{\min }({\textstyle \frac{\operatorname{SL}_{n}}{\operatorname{SL}_{n}}})\operatorname{ - mod}$
and
 $K\operatorname{Conv}^{\operatorname{SL}_{n}\times \mathbb{C}^{\times }}(Gr)$
using the annular
$K\operatorname{Conv}^{\operatorname{SL}_{n}\times \mathbb{C}^{\times }}(Gr)$
using the annular
![]() $\operatorname{SL}_{n}$
spider. We believe that these presentations are of their own independent interest.
$\operatorname{SL}_{n}$
spider. We believe that these presentations are of their own independent interest.
Our strategy involves a series of functors and categories summarized in the commutative diagram (1). We now briefly discuss these categories and functors.

1.3.1 Annular spiders
The
![]() $\operatorname{SL}_{n}$
spider category
$\operatorname{SL}_{n}$
spider category
![]() ${\mathcal{S}}p_{n}$
is a combinatorial/diagrammatic presentation of the representation category of
${\mathcal{S}}p_{n}$
is a combinatorial/diagrammatic presentation of the representation category of
![]() $\operatorname{SL}_{n}$
due to the authors and Morrison [Reference Cautis, Kamnitzer and MorrisonCKM14].Footnote
3
In this paper, we use the annular version
$\operatorname{SL}_{n}$
due to the authors and Morrison [Reference Cautis, Kamnitzer and MorrisonCKM14].Footnote
3
In this paper, we use the annular version
![]() ${\mathcal{A}}{\mathcal{S}}p_{n}$
of this category, where morphisms are linear combination of webs (with boundary) in an annulus modulo the same local relations as in
${\mathcal{A}}{\mathcal{S}}p_{n}$
of this category, where morphisms are linear combination of webs (with boundary) in an annulus modulo the same local relations as in
![]() ${\mathcal{S}}p_{n}$
. Using the machinery of horizontal trace and the main result in [Reference Cautis, Kamnitzer and MorrisonCKM14], we obtain the following.
${\mathcal{S}}p_{n}$
. Using the machinery of horizontal trace and the main result in [Reference Cautis, Kamnitzer and MorrisonCKM14], we obtain the following.
Theorem 1.5. There is an equivalence of categories
 $$\begin{eqnarray}A\unicode[STIX]{x1D6E4}:{\mathcal{A}}{\mathcal{S}}p_{n}(q)\xrightarrow[{}]{{\sim}}{\mathcal{O}}_{q}^{\min }({\textstyle \frac{\operatorname{SL}_{n}}{\operatorname{SL}_{n}}})\text{-}\text{mod}.\end{eqnarray}$$
$$\begin{eqnarray}A\unicode[STIX]{x1D6E4}:{\mathcal{A}}{\mathcal{S}}p_{n}(q)\xrightarrow[{}]{{\sim}}{\mathcal{O}}_{q}^{\min }({\textstyle \frac{\operatorname{SL}_{n}}{\operatorname{SL}_{n}}})\text{-}\text{mod}.\end{eqnarray}$$
1.3.2 Quantum loop algebras
The main tool in [Reference Cautis, Kamnitzer and MorrisonCKM14] was the realization that via skew-Howe duality,
 ${\mathcal{R}}\text{ep}_{q}(\operatorname{SL}_{n})$
(and thus
${\mathcal{R}}\text{ep}_{q}(\operatorname{SL}_{n})$
(and thus
![]() ${\mathcal{S}}p_{n}(q)$
) is the limit as
${\mathcal{S}}p_{n}(q)$
) is the limit as
 $m\rightarrow \infty$
of truncations
$m\rightarrow \infty$
of truncations
 $(\dot{U}_{q}\mathfrak{g}\mathfrak{l}_{m})^{n}$
of the idempotented version of quantum groups. In this paper, we will use that
$(\dot{U}_{q}\mathfrak{g}\mathfrak{l}_{m})^{n}$
of the idempotented version of quantum groups. In this paper, we will use that
 ${\mathcal{A}}{\mathcal{S}}p_{n}(q)$
is the limit of truncations
${\mathcal{A}}{\mathcal{S}}p_{n}(q)$
is the limit of truncations
 $(\dot{U}_{q}L\mathfrak{g}\mathfrak{l}_{m})^{n}$
of idempotented quantum loop algebras. This is achieved by defining an annular ‘ladder-formation’ functor
$(\dot{U}_{q}L\mathfrak{g}\mathfrak{l}_{m})^{n}$
of idempotented quantum loop algebras. This is achieved by defining an annular ‘ladder-formation’ functor
 $A\unicode[STIX]{x1D6F9}_{m}:(\dot{U}_{q}L\mathfrak{g}\mathfrak{l}_{m})^{n}\rightarrow {\mathcal{A}}{\mathcal{S}}p_{n}(q)$
.
$A\unicode[STIX]{x1D6F9}_{m}:(\dot{U}_{q}L\mathfrak{g}\mathfrak{l}_{m})^{n}\rightarrow {\mathcal{A}}{\mathcal{S}}p_{n}(q)$
.
On the other hand, Nakajima [Reference NakajimaNak01] (following Ginzburg and Vasserot) constructed actions of quantum loop algebras on the K-theory of quiver varieties. In type A, the varieties
![]() $Z(\text{}\underline{\unicode[STIX]{x1D706}},\text{}\underline{\unicode[STIX]{x1D707}})$
are closely related to Steinberg varieties of quiver varieties. Motivated by this connection and by our earlier work [Reference Cautis, Kamnitzer and LicataCKL10, Reference CautisCau05, Reference Cautis and KamnitzerCK17], we construct functors
$Z(\text{}\underline{\unicode[STIX]{x1D706}},\text{}\underline{\unicode[STIX]{x1D707}})$
are closely related to Steinberg varieties of quiver varieties. Motivated by this connection and by our earlier work [Reference Cautis, Kamnitzer and LicataCKL10, Reference CautisCau05, Reference Cautis and KamnitzerCK17], we construct functors
 $$\begin{eqnarray}\unicode[STIX]{x1D6F7}_{m}:(\dot{U}_{q}L\mathfrak{g}\mathfrak{l}_{m})^{n}\rightarrow K\operatorname{Conv}^{\operatorname{SL}_{n}\times \mathbb{C}^{\times }}(Gr)\end{eqnarray}$$
$$\begin{eqnarray}\unicode[STIX]{x1D6F7}_{m}:(\dot{U}_{q}L\mathfrak{g}\mathfrak{l}_{m})^{n}\rightarrow K\operatorname{Conv}^{\operatorname{SL}_{n}\times \mathbb{C}^{\times }}(Gr)\end{eqnarray}$$
for each
![]() $m$
. These functors are compatible with the inclusion of
$m$
. These functors are compatible with the inclusion of
 $(\dot{U}_{q}L\mathfrak{g}\mathfrak{l}_{m})^{n}$
into
$(\dot{U}_{q}L\mathfrak{g}\mathfrak{l}_{m})^{n}$
into
 $(\dot{U}_{q}L\mathfrak{g}\mathfrak{l}_{m+1})^{n}$
and thus induce a functor
$(\dot{U}_{q}L\mathfrak{g}\mathfrak{l}_{m+1})^{n}$
and thus induce a functor
 $$\begin{eqnarray}\unicode[STIX]{x1D6F7}:{\mathcal{A}}{\mathcal{S}}p_{n}(q)\rightarrow K\operatorname{Conv}^{\operatorname{SL}_{n}\times \mathbb{C}^{\times }}(Gr).\end{eqnarray}$$
$$\begin{eqnarray}\unicode[STIX]{x1D6F7}:{\mathcal{A}}{\mathcal{S}}p_{n}(q)\rightarrow K\operatorname{Conv}^{\operatorname{SL}_{n}\times \mathbb{C}^{\times }}(Gr).\end{eqnarray}$$
1.3.3 The proof
Since we have an equivalence
 $A\unicode[STIX]{x1D6E4}:{\mathcal{A}}{\mathcal{S}}p_{n}(q)\xrightarrow[{}]{{\sim}}{\mathcal{O}}_{q}^{\min }({\textstyle \frac{\operatorname{SL}_{n}}{\operatorname{SL}_{n}}})\operatorname{ - mod}$
, it suffices to show that
$A\unicode[STIX]{x1D6E4}:{\mathcal{A}}{\mathcal{S}}p_{n}(q)\xrightarrow[{}]{{\sim}}{\mathcal{O}}_{q}^{\min }({\textstyle \frac{\operatorname{SL}_{n}}{\operatorname{SL}_{n}}})\operatorname{ - mod}$
, it suffices to show that
 $\unicode[STIX]{x1D6F7}:{\mathcal{A}}{\mathcal{S}}p_{n}(q)\rightarrow K\operatorname{Conv}^{\operatorname{SL}_{n}\times \mathbb{C}^{\times }}(Gr)$
is an equivalence. Using a simple trick, this can be reduced to showing that the map
$\unicode[STIX]{x1D6F7}:{\mathcal{A}}{\mathcal{S}}p_{n}(q)\rightarrow K\operatorname{Conv}^{\operatorname{SL}_{n}\times \mathbb{C}^{\times }}(Gr)$
is an equivalence. Using a simple trick, this can be reduced to showing that the map
 $\unicode[STIX]{x1D6F7}:\operatorname{End}_{{\mathcal{A}}{\mathcal{S}}p_{n}(q)}(1^{m})\rightarrow K^{\operatorname{SL}_{n}\times \mathbb{C}^{\times }}(Z(1^{m},1^{m}))$
is an isomorphism (where
$\unicode[STIX]{x1D6F7}:\operatorname{End}_{{\mathcal{A}}{\mathcal{S}}p_{n}(q)}(1^{m})\rightarrow K^{\operatorname{SL}_{n}\times \mathbb{C}^{\times }}(Z(1^{m},1^{m}))$
is an isomorphism (where
 $1^{m}=(1,\ldots ,1)$
). To do this we consider the composition
$1^{m}=(1,\ldots ,1)$
). To do this we consider the composition
 $$\begin{eqnarray}\operatorname{End}_{{\mathcal{A}}{\mathcal{S}}p_{n}(q)}(1^{m})\rightarrow K^{\operatorname{SL}_{n}\times \mathbb{C}^{\times }}(Z(1^{m},1^{m}))\rightarrow \operatorname{End}(K^{\operatorname{SL}_{n}\times \mathbb{C}^{\times }}(Y(1^{m})))\end{eqnarray}$$
$$\begin{eqnarray}\operatorname{End}_{{\mathcal{A}}{\mathcal{S}}p_{n}(q)}(1^{m})\rightarrow K^{\operatorname{SL}_{n}\times \mathbb{C}^{\times }}(Z(1^{m},1^{m}))\rightarrow \operatorname{End}(K^{\operatorname{SL}_{n}\times \mathbb{C}^{\times }}(Y(1^{m})))\end{eqnarray}$$
and compute explicitly the images of everything inside the right-hand term.
Here
![]() $Y(1^{m})$
is an iterated fibre product of
$Y(1^{m})$
is an iterated fibre product of
![]() $m$
copies of
$m$
copies of
![]() $\mathbb{P}^{n-1}$
which is defined using the affine Grassmannian. To do this computation, we study a certain ring
$\mathbb{P}^{n-1}$
which is defined using the affine Grassmannian. To do this computation, we study a certain ring
![]() $R_{n,[q^{\pm }]}^{m}$
(see § 7.3 for the definition) which we identify with the equivariant K-theory of
$R_{n,[q^{\pm }]}^{m}$
(see § 7.3 for the definition) which we identify with the equivariant K-theory of
![]() $Y(1^{m})$
(Lemma 8.14). We also study certain endomorphisms of this ring which give us an algebra closely related to cyclotomic affine Hecke algebras (we discuss this in § 10). All these rings are quite explicit and may be of independent interest.
$Y(1^{m})$
(Lemma 8.14). We also study certain endomorphisms of this ring which give us an algebra closely related to cyclotomic affine Hecke algebras (we discuss this in § 10). All these rings are quite explicit and may be of independent interest.
1.4 Relationship to other work
1.4.1 Betti geometric Langlands
The work of Kapustin and Witten [Reference Kapustin and WittenKW07], and more recent work of Ben-Zvi and Nadler (in progress), describes a Betti version of the geometric Langlands program. In this setup one has a (partially defined) four-dimensional topological field theory. To a surface this theory associates a category. These categories were studied recently in [Reference Ben-Zvi, Brochier and JordanBBJ15]. In the case when the surface is an annulus the theory gives
 ${\mathcal{O}}_{q}({\textstyle \frac{G}{G}})\operatorname{ - mod}$
. This category along with the category associated to a pair of pants form the building blocks of this topological field theory (TFT).
${\mathcal{O}}_{q}({\textstyle \frac{G}{G}})\operatorname{ - mod}$
. This category along with the category associated to a pair of pants form the building blocks of this topological field theory (TFT).
The results in this paper relate
 ${\mathcal{O}}_{q}({\textstyle \frac{G}{G}})\operatorname{ - mod}$
with the
${\mathcal{O}}_{q}({\textstyle \frac{G}{G}})\operatorname{ - mod}$
with the
![]() $K$
-theoretic convolution category of the affine Grassmannian for the Langlands dual group. It would be interesting to obtain a similar result for the category associated to a pair of pants. We hope that our results will be an important step towards the Betti geometric Langlands program.
$K$
-theoretic convolution category of the affine Grassmannian for the Langlands dual group. It would be interesting to obtain a similar result for the category associated to a pair of pants. We hope that our results will be an important step towards the Betti geometric Langlands program.
1.4.2 Gaitsgory’s work
There is already a quantum version of the geometric Satake correspondence due to Gaitsgory [Reference GaitsgoryGai08]. In his work, the category of representations of the quantum group is realized as the category of twisted Whittaker sheaves on the affine Grassmannian. The relationship between Gaitsgory’s result and the present work is not at all clear. In particular, it follows that the horizontal trace of the category of twisted Whittaker sheaves is equivalent to our category
 $K\operatorname{Conv}^{\operatorname{SL}_{n}\times \mathbb{C}^{\times }}(Gr)$
; we do not have a geometric explanation for this fact.
$K\operatorname{Conv}^{\operatorname{SL}_{n}\times \mathbb{C}^{\times }}(Gr)$
; we do not have a geometric explanation for this fact.
1.4.3 Elias’ work
Our work can also be compared with a recent paper by Elias [Reference EliasEli17]. Analogous to the category
 $K\operatorname{Conv}^{G^{\vee }}(Gr)$
, one may also define
$K\operatorname{Conv}^{G^{\vee }}(Gr)$
, one may also define
 $h\operatorname{Conv}^{G^{\vee }}(Gr)$
(see § 3.4), which is equivalent to a full subcategory of
$h\operatorname{Conv}^{G^{\vee }}(Gr)$
(see § 3.4), which is equivalent to a full subcategory of
 $D_{G^{\vee }}(Gr)$
. Via the work of Soergel and others (see [Reference EliasEli17, § 6]), the category
$D_{G^{\vee }}(Gr)$
. Via the work of Soergel and others (see [Reference EliasEli17, § 6]), the category
 $h\operatorname{Conv}^{G^{\vee }}(Gr)$
is equivalent to the category of maximally singular Bott–Samelson bimodules
$h\operatorname{Conv}^{G^{\vee }}(Gr)$
is equivalent to the category of maximally singular Bott–Samelson bimodules
 $mSBSBim$
for the corresponding affine Weyl group.
$mSBSBim$
for the corresponding affine Weyl group.
Assume now
 $G=\operatorname{SL}_{n}$
. By combinatorial/algebraic methods, Elias has constructed an equivalence between
$G=\operatorname{SL}_{n}$
. By combinatorial/algebraic methods, Elias has constructed an equivalence between
![]() ${\mathcal{S}}p_{n}$
and the degree-0 part of
${\mathcal{S}}p_{n}$
and the degree-0 part of
 $mSBSBim$
(in [Reference EliasEli17] this is done for
$mSBSBim$
(in [Reference EliasEli17] this is done for
 $n=2,3$
and the general case will appear in a future work). This reproves the original abelian geometric Satake equivalence in this case. This should be compared with our equivalence
$n=2,3$
and the general case will appear in a future work). This reproves the original abelian geometric Satake equivalence in this case. This should be compared with our equivalence
 ${\mathcal{A}}{\mathcal{S}}p_{n}\cong K\operatorname{Conv}^{G^{\vee }}(Gr)$
. (Our work gives an equivalence between
${\mathcal{A}}{\mathcal{S}}p_{n}\cong K\operatorname{Conv}^{G^{\vee }}(Gr)$
. (Our work gives an equivalence between
![]() ${\mathcal{S}}p_{n}$
and a subcategory of
${\mathcal{S}}p_{n}$
and a subcategory of
 $K\operatorname{Conv}^{G^{\vee }}(Gr)$
, but it is not clear whether this reproves the original abelian geometric Satake equivalence.)
$K\operatorname{Conv}^{G^{\vee }}(Gr)$
, but it is not clear whether this reproves the original abelian geometric Satake equivalence.)
Moreover, Elias gives a
![]() $q$
-deformation
$q$
-deformation
 $mSBSBim_{q}$
which he proves is degree-0 equivalent to
$mSBSBim_{q}$
which he proves is degree-0 equivalent to
![]() ${\mathcal{S}}p_{n}(q)$
. We do not know how this
${\mathcal{S}}p_{n}(q)$
. We do not know how this
![]() $q$
-deformation is related to our equivalence
$q$
-deformation is related to our equivalence
 ${\mathcal{A}}{\mathcal{S}}p_{n}(q)\cong K\operatorname{Conv}^{\operatorname{SL}_{n}\times \mathbb{C}^{\times }}(Gr)$
.
${\mathcal{A}}{\mathcal{S}}p_{n}(q)\cong K\operatorname{Conv}^{\operatorname{SL}_{n}\times \mathbb{C}^{\times }}(Gr)$
.
1.4.4 Categorification
In our previous work [Reference Cautis, Kamnitzer and MorrisonCKM14], we suggested that the equivalence
 ${\mathcal{S}}p_{n}(q)\cong {\mathcal{R}}\text{ep}_{q}(\operatorname{SL}_{n})$
could be used to define a categorification of
${\mathcal{S}}p_{n}(q)\cong {\mathcal{R}}\text{ep}_{q}(\operatorname{SL}_{n})$
could be used to define a categorification of
 ${\mathcal{R}}\text{ep}_{q}(\operatorname{SL}_{n})$
, called
${\mathcal{R}}\text{ep}_{q}(\operatorname{SL}_{n})$
, called
![]() $\operatorname{Foam}_{n}$
, as the a limit of categorifications of
$\operatorname{Foam}_{n}$
, as the a limit of categorifications of
 $(\dot{U}_{q}\mathfrak{g}\mathfrak{l}_{m})^{n}$
$(\dot{U}_{q}\mathfrak{g}\mathfrak{l}_{m})^{n}$
 $$\begin{eqnarray}\lim _{m\rightarrow \infty }(\dot{{\mathcal{U}}}_{q}\mathfrak{g}\mathfrak{l}_{m})^{n}\cong \operatorname{Foam}_{n}\!.\end{eqnarray}$$
$$\begin{eqnarray}\lim _{m\rightarrow \infty }(\dot{{\mathcal{U}}}_{q}\mathfrak{g}\mathfrak{l}_{m})^{n}\cong \operatorname{Foam}_{n}\!.\end{eqnarray}$$
This program was carried out by Queffelec and Rose [Reference Queffelec and RoseQR16]. The foam category
![]() $\operatorname{Foam}_{n}$
has objects sequences from
$\operatorname{Foam}_{n}$
has objects sequences from
 $\{1,\ldots ,n-1\}$
, 1-morphisms given by webs, and 2-morphisms given by certain bordisms with seams, called foams.
$\{1,\ldots ,n-1\}$
, 1-morphisms given by webs, and 2-morphisms given by certain bordisms with seams, called foams.
In our current paper, we have functors
 $$\begin{eqnarray}(\dot{U}_{q}L\mathfrak{g}\mathfrak{l}_{m})^{n}\rightarrow {\mathcal{A}}{\mathcal{S}}p_{n}\rightarrow K\operatorname{Conv}^{\operatorname{SL}_{n}\times \mathbb{C}^{\times }}(Gr)\end{eqnarray}$$
$$\begin{eqnarray}(\dot{U}_{q}L\mathfrak{g}\mathfrak{l}_{m})^{n}\rightarrow {\mathcal{A}}{\mathcal{S}}p_{n}\rightarrow K\operatorname{Conv}^{\operatorname{SL}_{n}\times \mathbb{C}^{\times }}(Gr)\end{eqnarray}$$
and it is natural to look for categorifications of each of these categories. One expects that
 $(\dot{U}_{q}L\mathfrak{g}\mathfrak{l}_{m})^{n}$
can be categorified by some 2-category
$(\dot{U}_{q}L\mathfrak{g}\mathfrak{l}_{m})^{n}$
can be categorified by some 2-category
 $(\dot{{\mathcal{U}}}_{q}L\mathfrak{g}\mathfrak{l}_{m})^{n}$
analogous to
$(\dot{{\mathcal{U}}}_{q}L\mathfrak{g}\mathfrak{l}_{m})^{n}$
analogous to
 $(\dot{{\mathcal{U}}}_{q}\mathfrak{g}\mathfrak{l}_{m})^{n}$
(though this has not been done as far as we know).
$(\dot{{\mathcal{U}}}_{q}\mathfrak{g}\mathfrak{l}_{m})^{n}$
(though this has not been done as far as we know).
![]() ${\mathcal{A}}{\mathcal{S}}p_{n}$
can be categorified by
${\mathcal{A}}{\mathcal{S}}p_{n}$
can be categorified by
 $A\operatorname{Foam}_{n}$
, the category whose objects are the same as
$A\operatorname{Foam}_{n}$
, the category whose objects are the same as
![]() $\operatorname{Foam}_{n}$
, whose 1-morphisms are webs in the annulus (with boundary) and whose 2-morphisms are annular foams. In a recent paper [Reference Queffelec and RoseQR15], Queffelec and Rose study the endomorphisms of the trivial object in this category. Finally,
$\operatorname{Foam}_{n}$
, whose 1-morphisms are webs in the annulus (with boundary) and whose 2-morphisms are annular foams. In a recent paper [Reference Queffelec and RoseQR15], Queffelec and Rose study the endomorphisms of the trivial object in this category. Finally,
 $K\operatorname{Conv}^{\operatorname{SL}_{n}\times \mathbb{C}^{\times }}(Gr)$
has a natural categorification
$K\operatorname{Conv}^{\operatorname{SL}_{n}\times \mathbb{C}^{\times }}(Gr)$
has a natural categorification
 $\operatorname{CohConv}^{\operatorname{SL}_{n}\times \mathbb{C}^{\times }}(Gr)$
, where the morphism categories are given by derived categories of coherent sheaves on the fibre products
$\operatorname{CohConv}^{\operatorname{SL}_{n}\times \mathbb{C}^{\times }}(Gr)$
, where the morphism categories are given by derived categories of coherent sheaves on the fibre products
![]() $Z(\text{}\underline{\unicode[STIX]{x1D706}},\text{}\underline{\unicode[STIX]{x1D707}})$
.
$Z(\text{}\underline{\unicode[STIX]{x1D706}},\text{}\underline{\unicode[STIX]{x1D707}})$
.
Thus it is natural to expect that we should have 2-functors
 $$\begin{eqnarray}\lim _{m\rightarrow \infty }(\dot{{\mathcal{U}}}_{q}L\mathfrak{g}\mathfrak{l}_{m})^{n}\rightarrow A\operatorname{Foam}_{n}\rightarrow \operatorname{CohConv}^{\operatorname{SL}_{n}\times \mathbb{C}^{\times }}(Gr).\end{eqnarray}$$
$$\begin{eqnarray}\lim _{m\rightarrow \infty }(\dot{{\mathcal{U}}}_{q}L\mathfrak{g}\mathfrak{l}_{m})^{n}\rightarrow A\operatorname{Foam}_{n}\rightarrow \operatorname{CohConv}^{\operatorname{SL}_{n}\times \mathbb{C}^{\times }}(Gr).\end{eqnarray}$$
The composition of these 2-functors is understood to some extent, based on this paper and earlier work by the authors. We expect the first 2-functor to be an equivalence while the second 2-functor is more mysterious.
1.4.5 Knot invariants
The spider category
![]() ${\mathcal{S}}p_{n}(q)$
can be used to define Reshetikhin–Turaev (RT) invariants of type A for links in the ball. Similarly, the categorification
${\mathcal{S}}p_{n}(q)$
can be used to define Reshetikhin–Turaev (RT) invariants of type A for links in the ball. Similarly, the categorification
![]() $\operatorname{Foam}_{n}$
can be used to define homological link invariants (this was done in [Reference Queffelec and RoseQR16] following the original approach due to Khovanov [Reference KhovanovKho04]).
$\operatorname{Foam}_{n}$
can be used to define homological link invariants (this was done in [Reference Queffelec and RoseQR16] following the original approach due to Khovanov [Reference KhovanovKho04]).
The results of this paper show that
![]() ${\mathcal{S}}p_{n}(q)$
embeds into
${\mathcal{S}}p_{n}(q)$
embeds into
 $K\operatorname{Conv}^{\operatorname{SL}_{n}\times \mathbb{C}^{\times }}(Gr)$
and thus the category
$K\operatorname{Conv}^{\operatorname{SL}_{n}\times \mathbb{C}^{\times }}(Gr)$
and thus the category
 $K\operatorname{Conv}^{\operatorname{SL}_{n}\times \mathbb{C}^{\times }}(Gr)$
can be used to define Reshetikhin–Turaev invariants. This suggests that the 2-category
$K\operatorname{Conv}^{\operatorname{SL}_{n}\times \mathbb{C}^{\times }}(Gr)$
can be used to define Reshetikhin–Turaev invariants. This suggests that the 2-category
 $\operatorname{CohConv}^{\operatorname{SL}_{n}\times \mathbb{C}^{\times }}(Gr)$
can be used to define homological knot invariants. This is essentially the approach used in our previous papers [Reference Cautis and KamnitzerCK08a, Reference Cautis and KamnitzerCK08b, Reference CautisCau05]. Our current work gives a little more perspective to these papers.
$\operatorname{CohConv}^{\operatorname{SL}_{n}\times \mathbb{C}^{\times }}(Gr)$
can be used to define homological knot invariants. This is essentially the approach used in our previous papers [Reference Cautis and KamnitzerCK08a, Reference Cautis and KamnitzerCK08b, Reference CautisCau05]. Our current work gives a little more perspective to these papers.
Moreover, the results of this paper show that
 $K\operatorname{Conv}^{\operatorname{SL}_{n}\times \mathbb{C}^{\times }}(Gr)$
can be used to define RT-invariants for links in the annulus. This suggests that
$K\operatorname{Conv}^{\operatorname{SL}_{n}\times \mathbb{C}^{\times }}(Gr)$
can be used to define RT-invariants for links in the annulus. This suggests that
 $\operatorname{CohConv}^{\operatorname{SL}_{n}\times \mathbb{C}^{\times }}(Gr)$
can be used to obtain homological invariants of links in the annulus. The case
$\operatorname{CohConv}^{\operatorname{SL}_{n}\times \mathbb{C}^{\times }}(Gr)$
can be used to obtain homological invariants of links in the annulus. The case
 $G=\operatorname{SL}_{2}$
should correspond to sutured Khovanov homology. Using this approach, we immediately obtain an action of
$G=\operatorname{SL}_{2}$
should correspond to sutured Khovanov homology. Using this approach, we immediately obtain an action of
![]() $\operatorname{SL}_{n}$
on the
$\operatorname{SL}_{n}$
on the
![]() $\operatorname{SL}_{n}$
-homology of links in the annulus. This is because the resulting invariant lies in the
$\operatorname{SL}_{n}$
-homology of links in the annulus. This is because the resulting invariant lies in the
 $\operatorname{SL}_{n}\times \mathbb{C}^{\times }$
-equivariant derived category of a point (in the case
$\operatorname{SL}_{n}\times \mathbb{C}^{\times }$
-equivariant derived category of a point (in the case
![]() $n=2$
, such an action was studied by Grigsby et al. [Reference Grigsby, Licata and WehrliGLW15]). This construction is compatible with the recent work of Queffelec and Rose [Reference Queffelec and RoseQR15]. More details will appear in a future paper.
$n=2$
, such an action was studied by Grigsby et al. [Reference Grigsby, Licata and WehrliGLW15]). This construction is compatible with the recent work of Queffelec and Rose [Reference Queffelec and RoseQR15]. More details will appear in a future paper.
2 Representation categories
2.1 Notation
Let
![]() $G$
be a simply connected semisimple group. Let
$G$
be a simply connected semisimple group. Let
![]() $T$
be a maximal torus of
$T$
be a maximal torus of
![]() $G$
, let
$G$
, let
![]() $\unicode[STIX]{x1D6EC}$
denote its weight lattice and let
$\unicode[STIX]{x1D6EC}$
denote its weight lattice and let
![]() $W$
denote the Weyl group. Let
$W$
denote the Weyl group. Let
![]() $\unicode[STIX]{x1D6EC}_{+}$
denote the set of dominant weights and
$\unicode[STIX]{x1D6EC}_{+}$
denote the set of dominant weights and
![]() $\unicode[STIX]{x1D70C}^{\vee }$
half the sum of the fundamental coroots. For
$\unicode[STIX]{x1D70C}^{\vee }$
half the sum of the fundamental coroots. For
![]() $\unicode[STIX]{x1D706}\in \unicode[STIX]{x1D6EC}_{+}$
, let
$\unicode[STIX]{x1D706}\in \unicode[STIX]{x1D6EC}_{+}$
, let
![]() $V(\unicode[STIX]{x1D706})$
denote the irreducible representation of highest weight
$V(\unicode[STIX]{x1D706})$
denote the irreducible representation of highest weight
![]() $\unicode[STIX]{x1D706}$
.
$\unicode[STIX]{x1D706}$
.
Recall that we have an isomorphism
 ${\mathcal{O}}(G)^{G}\cong {\mathcal{O}}(T)^{W}$
where
${\mathcal{O}}(G)^{G}\cong {\mathcal{O}}(T)^{W}$
where
![]() $G$
acts on
$G$
acts on
![]() $G$
by the adjoint action. Let
$G$
by the adjoint action. Let
 $E={\mathcal{O}}(T)^{W}\cong \mathbb{C}[\unicode[STIX]{x1D6EC}]^{W}$
. Recall that
$E={\mathcal{O}}(T)^{W}\cong \mathbb{C}[\unicode[STIX]{x1D6EC}]^{W}$
. Recall that
![]() $E$
is a polynomial ring in
$E$
is a polynomial ring in
![]() $r$
variables, where
$r$
variables, where
![]() $r$
is the rank of
$r$
is the rank of
![]() $G$
. We also have an isomorphism
$G$
. We also have an isomorphism
 $R(G)\cong E$
, where
$R(G)\cong E$
, where
![]() $R(G)$
denotes the (complexified) representation ring of
$R(G)$
denotes the (complexified) representation ring of
![]() $G$
.
$G$
.
Let
![]() $G^{\vee }$
denote the Langlands dual group to
$G^{\vee }$
denote the Langlands dual group to
![]() $G$
and let
$G$
and let
![]() $\widetilde{G^{\vee }}$
be its simply connected cover. Let
$\widetilde{G^{\vee }}$
be its simply connected cover. Let
![]() $\unicode[STIX]{x1D6EC}^{\vee }$
be the weight lattice of
$\unicode[STIX]{x1D6EC}^{\vee }$
be the weight lattice of
![]() $\widetilde{G^{\vee }}$
and let
$\widetilde{G^{\vee }}$
and let
 $E^{\vee }=R(\widetilde{G^{\vee }})=\mathbb{C}[\unicode[STIX]{x1D6EC}^{\vee }]^{W}$
.
$E^{\vee }=R(\widetilde{G^{\vee }})=\mathbb{C}[\unicode[STIX]{x1D6EC}^{\vee }]^{W}$
.
Let
![]() $(\,,)$
be the
$(\,,)$
be the
![]() $W$
-invariant bilinear form on
$W$
-invariant bilinear form on
![]() $\mathfrak{t}^{\ast }$
(the dual of the Lie algebra of
$\mathfrak{t}^{\ast }$
(the dual of the Lie algebra of
![]() $T$
), such that
$T$
), such that
 $(\unicode[STIX]{x1D6FC},\unicode[STIX]{x1D6FC})=2$
for all short roots
$(\unicode[STIX]{x1D6FC},\unicode[STIX]{x1D6FC})=2$
for all short roots
![]() $\unicode[STIX]{x1D6FC}$
. This bilinear form gives an isomorphism
$\unicode[STIX]{x1D6FC}$
. This bilinear form gives an isomorphism
 $\unicode[STIX]{x1D704}:\mathfrak{t}^{\ast }\rightarrow \mathfrak{t}$
. From the
$\unicode[STIX]{x1D704}:\mathfrak{t}^{\ast }\rightarrow \mathfrak{t}$
. From the
![]() $W$
-invariance, it follows that
$W$
-invariance, it follows that
 $\unicode[STIX]{x1D704}(\unicode[STIX]{x1D6EC})\subset \unicode[STIX]{x1D6EC}^{\vee }$
(with equality if
$\unicode[STIX]{x1D704}(\unicode[STIX]{x1D6EC})\subset \unicode[STIX]{x1D6EC}^{\vee }$
(with equality if
![]() $G$
is simply laced). Thus
$G$
is simply laced). Thus
![]() $\unicode[STIX]{x1D704}$
gives us an inclusion
$\unicode[STIX]{x1D704}$
gives us an inclusion
 $E{\hookrightarrow}E^{\vee }$
(which is an isomorphism when
$E{\hookrightarrow}E^{\vee }$
(which is an isomorphism when
![]() $G$
is simply laced).
$G$
is simply laced).
2.2 Classical representation categories
Let
 ${\mathcal{R}}\text{ep}(G)$
denote the usual category of finite-dimensional representations of
${\mathcal{R}}\text{ep}(G)$
denote the usual category of finite-dimensional representations of
![]() $G$
. We will be interested in various enhancements/modifications of
$G$
. We will be interested in various enhancements/modifications of
 ${\mathcal{R}}\text{ep}(G)$
.
${\mathcal{R}}\text{ep}(G)$
.
We have the adjoint actions of
![]() $G$
on
$G$
on
![]() $\mathfrak{g}$
and
$\mathfrak{g}$
and
![]() $G$
. This makes
$G$
. This makes
![]() ${\mathcal{O}}(\mathfrak{g})$
and
${\mathcal{O}}(\mathfrak{g})$
and
![]() ${\mathcal{O}}(G)$
into (infinite-dimensional)
${\mathcal{O}}(G)$
into (infinite-dimensional)
![]() $G$
representations. Let
$G$
representations. Let
 ${\mathcal{O}}(\frac{\mathfrak{g}}{G})\operatorname{ - mod}$
denote the full subcategory of
${\mathcal{O}}(\frac{\mathfrak{g}}{G})\operatorname{ - mod}$
denote the full subcategory of
![]() $G$
-equivariant
$G$
-equivariant
![]() ${\mathcal{O}}(\mathfrak{g})$
-modules which are of the form
${\mathcal{O}}(\mathfrak{g})$
-modules which are of the form
 ${\mathcal{O}}(\mathfrak{g})\otimes V$
, for
${\mathcal{O}}(\mathfrak{g})\otimes V$
, for
![]() $V$
in
$V$
in
 ${\mathcal{R}}\text{ep}(G)$
. Here
${\mathcal{R}}\text{ep}(G)$
. Here
![]() $G$
acts diagonally on
$G$
acts diagonally on
 ${\mathcal{O}}(\mathfrak{g})\otimes V$
and
${\mathcal{O}}(\mathfrak{g})\otimes V$
and
![]() ${\mathcal{O}}(\mathfrak{g})$
acts on the left tensor factor. Similarly we define
${\mathcal{O}}(\mathfrak{g})$
acts on the left tensor factor. Similarly we define
 ${\mathcal{O}}({\textstyle \frac{G}{G}})\operatorname{ - mod}$
to be the full subcategory of
${\mathcal{O}}({\textstyle \frac{G}{G}})\operatorname{ - mod}$
to be the full subcategory of
![]() $G$
-equivariant
$G$
-equivariant
![]() ${\mathcal{O}}(G)$
-modules which are of the form
${\mathcal{O}}(G)$
-modules which are of the form
 ${\mathcal{O}}(G)\otimes V$
. Note that we can think of
${\mathcal{O}}(G)\otimes V$
. Note that we can think of
 ${\mathcal{O}}(\frac{\mathfrak{g}}{G})\operatorname{ - mod}$
as the full subcategory of
${\mathcal{O}}(\frac{\mathfrak{g}}{G})\operatorname{ - mod}$
as the full subcategory of
![]() $G$
-equivariant coherent sheaves of
$G$
-equivariant coherent sheaves of
![]() $\mathfrak{g}$
consisting of trivial vector bundles with
$\mathfrak{g}$
consisting of trivial vector bundles with
![]() $G$
-action (and similarly for
$G$
-action (and similarly for
 ${\mathcal{O}}({\textstyle \frac{G}{G}})\operatorname{ - mod}$
).
${\mathcal{O}}({\textstyle \frac{G}{G}})\operatorname{ - mod}$
).
2.3 Quantum representation categories
2.3.1 Quantum group and quantum function algebra
We will denote by
![]() $[n]$
the quantum integer
$[n]$
the quantum integer
 $q^{n-1}+q^{n-3}+\cdots +q^{-n+3}+q^{-n+1}$
. More generally, we have quantum binomial coefficients
$q^{n-1}+q^{n-3}+\cdots +q^{-n+3}+q^{-n+1}$
. More generally, we have quantum binomial coefficients
 $$\begin{eqnarray}\left[\begin{array}{@{}c@{}}n\\ k\\ \end{array}\right]:=\frac{[n]\ldots [1]}{([n-k]\ldots [1])([k]\ldots [1])}.\end{eqnarray}$$
$$\begin{eqnarray}\left[\begin{array}{@{}c@{}}n\\ k\\ \end{array}\right]:=\frac{[n]\ldots [1]}{([n-k]\ldots [1])([k]\ldots [1])}.\end{eqnarray}$$
Let
![]() $U_{q}\mathfrak{g}$
denote the quantum group over
$U_{q}\mathfrak{g}$
denote the quantum group over
![]() $\mathbb{C}(q)$
. Let
$\mathbb{C}(q)$
. Let
 ${\mathcal{R}}\text{ep}_{q}(G)$
denote the category of finite-dimensional representations of
${\mathcal{R}}\text{ep}_{q}(G)$
denote the category of finite-dimensional representations of
![]() $U_{q}\mathfrak{g}$
. For each
$U_{q}\mathfrak{g}$
. For each
![]() $\unicode[STIX]{x1D706}\in \unicode[STIX]{x1D6EC}_{+}$
, we have an irreducible representation
$\unicode[STIX]{x1D706}\in \unicode[STIX]{x1D6EC}_{+}$
, we have an irreducible representation
![]() $V(\unicode[STIX]{x1D706})$
. Recall that the representation ring
$V(\unicode[STIX]{x1D706})$
. Recall that the representation ring
![]() $R_{q}(G)$
of
$R_{q}(G)$
of
![]() $U_{q}\mathfrak{g}$
coincides with the representation ring of
$U_{q}\mathfrak{g}$
coincides with the representation ring of
![]() $G$
, so
$G$
, so
 $R_{q}(G)\cong E$
. Also recall that for any two representations
$R_{q}(G)\cong E$
. Also recall that for any two representations
![]() $V,W$
of
$V,W$
of
![]() $U_{q}\mathfrak{g}$
, we have a braiding map
$U_{q}\mathfrak{g}$
, we have a braiding map
 $\unicode[STIX]{x1D6FD}_{V,W}:V\otimes W\rightarrow W\otimes V$
.
$\unicode[STIX]{x1D6FD}_{V,W}:V\otimes W\rightarrow W\otimes V$
.
We consider the quantum function algebra
![]() ${\mathcal{O}}_{q}(G)$
. There are (at least) two versions of
${\mathcal{O}}_{q}(G)$
. There are (at least) two versions of
![]() ${\mathcal{O}}_{q}(G)$
in the literature. We will need the version introduced by Majid, which sometimes goes under the name ‘reflection equation algebra’. We define
${\mathcal{O}}_{q}(G)$
in the literature. We will need the version introduced by Majid, which sometimes goes under the name ‘reflection equation algebra’. We define
![]() ${\mathcal{O}}_{q}(G)$
to be the subspace of
${\mathcal{O}}_{q}(G)$
to be the subspace of
![]() $(U_{q}\mathfrak{g})^{\ast }$
spanned by matrix coefficients
$(U_{q}\mathfrak{g})^{\ast }$
spanned by matrix coefficients
![]() $V\otimes V^{\ast }$
of finite-dimensional representations
$V\otimes V^{\ast }$
of finite-dimensional representations
![]() $V$
. From this we see that as a vector space
$V$
. From this we see that as a vector space
 ${\mathcal{O}}_{q}(G)=\bigoplus _{\unicode[STIX]{x1D706}}V(\unicode[STIX]{x1D706})\otimes V(\unicode[STIX]{x1D706})^{\ast }$
and we have a map
${\mathcal{O}}_{q}(G)=\bigoplus _{\unicode[STIX]{x1D706}}V(\unicode[STIX]{x1D706})\otimes V(\unicode[STIX]{x1D706})^{\ast }$
and we have a map
 $r_{V}:V\otimes V^{\ast }\rightarrow {\mathcal{O}}_{q}(G)$
.
$r_{V}:V\otimes V^{\ast }\rightarrow {\mathcal{O}}_{q}(G)$
.
There is an action of
![]() $U_{q}\mathfrak{g}$
on
$U_{q}\mathfrak{g}$
on
![]() ${\mathcal{O}}_{q}(G)$
such that for all
${\mathcal{O}}_{q}(G)$
such that for all
![]() $V$
,
$V$
,
 $r_{V}:V\otimes V^{\ast }\rightarrow {\mathcal{O}}_{q}(G)$
is
$r_{V}:V\otimes V^{\ast }\rightarrow {\mathcal{O}}_{q}(G)$
is
![]() $U_{q}\mathfrak{g}$
-equivariant.
$U_{q}\mathfrak{g}$
-equivariant.
The multiplication on
![]() ${\mathcal{O}}_{q}(G)$
is defined so that for any
${\mathcal{O}}_{q}(G)$
is defined so that for any
![]() $V,W$
the diagram
$V,W$
the diagram

commutes.
Since the upper horizontal line in this diagram is a map of
![]() $U_{q}\mathfrak{g}$
modules, we see that multiplication in
$U_{q}\mathfrak{g}$
modules, we see that multiplication in
![]() ${\mathcal{O}}_{q}(G)$
is equivariant for this action.
${\mathcal{O}}_{q}(G)$
is equivariant for this action.
Let
 ${\mathcal{O}}_{q}({\textstyle \frac{G}{G}})\operatorname{ - mod}$
denote the full subcategory of
${\mathcal{O}}_{q}({\textstyle \frac{G}{G}})\operatorname{ - mod}$
denote the full subcategory of
![]() $U_{q}\mathfrak{g}$
-equivariant
$U_{q}\mathfrak{g}$
-equivariant
![]() ${\mathcal{O}}_{q}(G)$
-modules which are of the form
${\mathcal{O}}_{q}(G)$
-modules which are of the form
 ${\mathcal{O}}_{q}(G)\otimes V$
, where
${\mathcal{O}}_{q}(G)\otimes V$
, where
![]() $V$
is a representation
$V$
is a representation
![]() $U_{q}\mathfrak{g}$
. Here
$U_{q}\mathfrak{g}$
. Here
![]() $U_{q}\mathfrak{g}$
acts on
$U_{q}\mathfrak{g}$
acts on
 ${\mathcal{O}}_{q}(G)\otimes V$
by the diagonal action and
${\mathcal{O}}_{q}(G)\otimes V$
by the diagonal action and
![]() ${\mathcal{O}}_{q}(G)$
acts by left multiplication.
${\mathcal{O}}_{q}(G)$
acts by left multiplication.
2.3.2 Central elements and enrichment
For any representation
![]() $V$
, let
$V$
, let
 $t_{V}\in {\mathcal{O}}_{q}(G)$
denote the image of the canonical element of
$t_{V}\in {\mathcal{O}}_{q}(G)$
denote the image of the canonical element of
![]() $V\otimes V^{\ast }$
under the map
$V\otimes V^{\ast }$
under the map
![]() $r_{V}$
(so interpreted as an element of
$r_{V}$
(so interpreted as an element of
![]() $(U_{q}\mathfrak{g})^{\ast }$
,
$(U_{q}\mathfrak{g})^{\ast }$
,
![]() $t_{V}$
is the trace along the representation
$t_{V}$
is the trace along the representation
![]() $V$
).
$V$
).
Proposition 2.1. The elements
![]() $t_{V}$
are central and the map
$t_{V}$
are central and the map
 $[V]\mapsto t_{V}$
defines an algebra isomorphism between
$[V]\mapsto t_{V}$
defines an algebra isomorphism between
 $E(q)\cong R_{q}(G)$
and
$E(q)\cong R_{q}(G)$
and
 $({\mathcal{O}}_{q}(G))^{U_{q}\mathfrak{g}}$
.
$({\mathcal{O}}_{q}(G))^{U_{q}\mathfrak{g}}$
.
Proof. To prove that
![]() $t_{V}$
is central, let us write the canonical element of
$t_{V}$
is central, let us write the canonical element of
![]() $V\otimes V^{\ast }$
as
$V\otimes V^{\ast }$
as
 $\sum _{i}x_{i}\otimes x^{i}$
where
$\sum _{i}x_{i}\otimes x^{i}$
where
![]() $x_{i}$
is a basis for
$x_{i}$
is a basis for
![]() $V$
and
$V$
and
![]() $x^{i}$
is the dual basis. Consider some element
$x^{i}$
is the dual basis. Consider some element
 $r_{W}(w\otimes w^{\prime })\in {\mathcal{O}}_{q}(G)$
for some
$r_{W}(w\otimes w^{\prime })\in {\mathcal{O}}_{q}(G)$
for some
 $w\in W,w^{\prime }\in W^{\ast }$
. Then we have
$w\in W,w^{\prime }\in W^{\ast }$
. Then we have
 $$\begin{eqnarray}\displaystyle t_{V}r_{W}(w\otimes w^{\prime }) & = & \displaystyle \mathop{\sum }_{i}r_{V\otimes W}(x_{i}\otimes \unicode[STIX]{x1D6FD}_{W\otimes W^{\ast },V^{\ast }}^{-1}(x^{i}\otimes (w\otimes w^{\prime })))\nonumber\\ \displaystyle & = & \displaystyle \mathop{\sum }_{i}r_{V\otimes W}((1\otimes 1\otimes \unicode[STIX]{x1D6FD}_{W^{\ast },V^{\ast }}^{-1})(x_{i}\otimes \unicode[STIX]{x1D6FD}_{W,V^{\ast }}^{-1}(x^{i}\otimes w)\otimes w^{\prime }))\nonumber\\ \displaystyle & = & \displaystyle \mathop{\sum }_{i}r_{V\otimes W}((\unicode[STIX]{x1D6FD}_{W,V}\otimes \unicode[STIX]{x1D6FD}_{W^{\ast },V^{\ast }}^{-1})(w\otimes x_{i}\otimes x^{i}\otimes w^{\prime }))\nonumber\\ \displaystyle & = & \displaystyle \mathop{\sum }_{i}r_{V\otimes W}(x_{i}\otimes w\otimes w^{\prime }\otimes x^{i}),\nonumber\end{eqnarray}$$
$$\begin{eqnarray}\displaystyle t_{V}r_{W}(w\otimes w^{\prime }) & = & \displaystyle \mathop{\sum }_{i}r_{V\otimes W}(x_{i}\otimes \unicode[STIX]{x1D6FD}_{W\otimes W^{\ast },V^{\ast }}^{-1}(x^{i}\otimes (w\otimes w^{\prime })))\nonumber\\ \displaystyle & = & \displaystyle \mathop{\sum }_{i}r_{V\otimes W}((1\otimes 1\otimes \unicode[STIX]{x1D6FD}_{W^{\ast },V^{\ast }}^{-1})(x_{i}\otimes \unicode[STIX]{x1D6FD}_{W,V^{\ast }}^{-1}(x^{i}\otimes w)\otimes w^{\prime }))\nonumber\\ \displaystyle & = & \displaystyle \mathop{\sum }_{i}r_{V\otimes W}((\unicode[STIX]{x1D6FD}_{W,V}\otimes \unicode[STIX]{x1D6FD}_{W^{\ast },V^{\ast }}^{-1})(w\otimes x_{i}\otimes x^{i}\otimes w^{\prime }))\nonumber\\ \displaystyle & = & \displaystyle \mathop{\sum }_{i}r_{V\otimes W}(x_{i}\otimes w\otimes w^{\prime }\otimes x^{i}),\nonumber\end{eqnarray}$$
where the last line follows from the fact that
![]() $\unicode[STIX]{x1D6FD}_{W,V}$
and
$\unicode[STIX]{x1D6FD}_{W,V}$
and
![]() $\unicode[STIX]{x1D6FD}_{W^{\ast },V^{\ast }}$
are dual to each other. A similar (but simpler) calculation shows that
$\unicode[STIX]{x1D6FD}_{W^{\ast },V^{\ast }}$
are dual to each other. A similar (but simpler) calculation shows that
 $r_{W}(w\otimes w^{\prime })t_{V}$
is given by the same formula. Thus
$r_{W}(w\otimes w^{\prime })t_{V}$
is given by the same formula. Thus
![]() $t_{V}$
is central.
$t_{V}$
is central.
Next note that
![]() $t_{V}$
is clearly
$t_{V}$
is clearly
![]() $U_{q}\mathfrak{g}$
-invariant. Since
$U_{q}\mathfrak{g}$
-invariant. Since
 $t_{V\otimes W}=t_{V}t_{W}$
, we see that the map is an algebra morphism. It is clearly injective. Finally, to show that it is surjective, we just use the
$t_{V\otimes W}=t_{V}t_{W}$
, we see that the map is an algebra morphism. It is clearly injective. Finally, to show that it is surjective, we just use the
![]() $U_{q}\mathfrak{g}$
-equivariant isomorphism
$U_{q}\mathfrak{g}$
-equivariant isomorphism
 ${\mathcal{O}}_{q}(G)\cong \bigoplus _{\unicode[STIX]{x1D706}}V(\unicode[STIX]{x1D706})\otimes V(\unicode[STIX]{x1D706})^{\ast }$
.◻
${\mathcal{O}}_{q}(G)\cong \bigoplus _{\unicode[STIX]{x1D706}}V(\unicode[STIX]{x1D706})\otimes V(\unicode[STIX]{x1D706})^{\ast }$
.◻
Remark 2.2. We believe that these
![]() $t_{V}$
generate the centre of
$t_{V}$
generate the centre of
![]() ${\mathcal{O}}_{q}(G)$
and thus the centre is isomorphic to
${\mathcal{O}}_{q}(G)$
and thus the centre is isomorphic to
![]() $E(q)$
. We were not able to find a reference for this fact.
$E(q)$
. We were not able to find a reference for this fact.
Using these elements
![]() $t_{V}$
, we can see that the category
$t_{V}$
, we can see that the category
 ${\mathcal{O}}_{q}({\textstyle \frac{G}{G}})\operatorname{ - mod}$
is enriched over
${\mathcal{O}}_{q}({\textstyle \frac{G}{G}})\operatorname{ - mod}$
is enriched over
![]() $E(q)$
(the hom spaces are
$E(q)$
(the hom spaces are
![]() $E(q)$
-modules). Equivalently, we have a map from
$E(q)$
-modules). Equivalently, we have a map from
![]() $E(q)$
to endomorphisms of the identity functor in
$E(q)$
to endomorphisms of the identity functor in
 ${\mathcal{O}}_{q}({\textstyle \frac{G}{G}})\operatorname{ - mod}$
given by sending an element of
${\mathcal{O}}_{q}({\textstyle \frac{G}{G}})\operatorname{ - mod}$
given by sending an element of
 $E(q)\cong ({\mathcal{O}}_{q}(G))^{U_{q}\mathfrak{g}}$
to its action on
$E(q)\cong ({\mathcal{O}}_{q}(G))^{U_{q}\mathfrak{g}}$
to its action on
 ${\mathcal{O}}_{q}(G)\otimes V$
given by multiplication on the
${\mathcal{O}}_{q}(G)\otimes V$
given by multiplication on the
![]() ${\mathcal{O}}_{q}(G)$
factor.
${\mathcal{O}}_{q}(G)$
factor.
2.3.3 Coaction and canonical automorphism
For any representation
![]() $V$
of
$V$
of
![]() $U_{q}\mathfrak{g}$
, we have a coaction map
$U_{q}\mathfrak{g}$
, we have a coaction map
 $C_{V}:V\rightarrow {\mathcal{O}}_{q}(G)\otimes V$
defined by
$C_{V}:V\rightarrow {\mathcal{O}}_{q}(G)\otimes V$
defined by
 $$\begin{eqnarray}V\rightarrow V\otimes V^{\ast }\otimes V\xrightarrow[{}]{r_{V}\otimes I}{\mathcal{O}}_{q}(G)\otimes V,\end{eqnarray}$$
$$\begin{eqnarray}V\rightarrow V\otimes V^{\ast }\otimes V\xrightarrow[{}]{r_{V}\otimes I}{\mathcal{O}}_{q}(G)\otimes V,\end{eqnarray}$$
where the first map is the canonical coevaluation (creating the second two tensor factors). This coaction map is a
![]() $U_{q}\mathfrak{g}$
-module map.
$U_{q}\mathfrak{g}$
-module map.
Using the coaction, the category
 ${\mathcal{O}}_{q}({\textstyle \frac{G}{G}})\operatorname{ - mod}$
comes with an automorphism
${\mathcal{O}}_{q}({\textstyle \frac{G}{G}})\operatorname{ - mod}$
comes with an automorphism
![]() $X$
of the identity functor. For
$X$
of the identity functor. For
 $V\in {\mathcal{R}}\text{ep}_{q}(G)$
, we define
$V\in {\mathcal{R}}\text{ep}_{q}(G)$
, we define
![]() $X_{V}$
as the composition
$X_{V}$
as the composition
 $$\begin{eqnarray}{\mathcal{O}}_{q}(G)\otimes V\xrightarrow[{}]{I\otimes C_{V}}{\mathcal{O}}_{q}(G)\otimes {\mathcal{O}}_{q}(G)\otimes V\xrightarrow[{}]{m\otimes \unicode[STIX]{x1D703}_{V}}{\mathcal{O}}_{q}(G)\otimes V,\end{eqnarray}$$
$$\begin{eqnarray}{\mathcal{O}}_{q}(G)\otimes V\xrightarrow[{}]{I\otimes C_{V}}{\mathcal{O}}_{q}(G)\otimes {\mathcal{O}}_{q}(G)\otimes V\xrightarrow[{}]{m\otimes \unicode[STIX]{x1D703}_{V}}{\mathcal{O}}_{q}(G)\otimes V,\end{eqnarray}$$
where
 $m:{\mathcal{O}}_{q}(G)\otimes {\mathcal{O}}_{q}(G)\rightarrow {\mathcal{O}}_{q}(G)$
is the multiplication, and where
$m:{\mathcal{O}}_{q}(G)\otimes {\mathcal{O}}_{q}(G)\rightarrow {\mathcal{O}}_{q}(G)$
is the multiplication, and where
![]() $\unicode[STIX]{x1D703}_{V}$
is the balancing isomorphism (which acts by a power of
$\unicode[STIX]{x1D703}_{V}$
is the balancing isomorphism (which acts by a power of
![]() $q$
on each irreducible representation, see [Reference Bakalov and KirillovBK01, § 2.2]). Since each arrow is a map of
$q$
on each irreducible representation, see [Reference Bakalov and KirillovBK01, § 2.2]). Since each arrow is a map of
![]() $U_{q}\mathfrak{g}$
-modules, so is the composite.
$U_{q}\mathfrak{g}$
-modules, so is the composite.
Remark 2.3. If we work with
 ${\mathcal{O}}({\textstyle \frac{G}{G}})\operatorname{ - mod}$
, this definition also makes sense. In this case,
${\mathcal{O}}({\textstyle \frac{G}{G}})\operatorname{ - mod}$
, this definition also makes sense. In this case,
![]() $X_{V}$
is the automorphism of the trivial vector bundle over
$X_{V}$
is the automorphism of the trivial vector bundle over
![]() $G$
with fibre
$G$
with fibre
![]() $V$
, given by acting by
$V$
, given by acting by
![]() $g$
in the fibre over
$g$
in the fibre over
![]() $g$
.
$g$
.
2.4 Horizontal trace and
 ${\mathcal{O}}_{q}({\textstyle \frac{G}{G}})\operatorname{ - mod}$
${\mathcal{O}}_{q}({\textstyle \frac{G}{G}})\operatorname{ - mod}$
One reason why these categories
 ${\mathcal{O}}_{q}({\textstyle \frac{G}{G}})\operatorname{ - mod}$
are important for us is because they arise as horizontal traces. We now explain this construction. The results in this section seem to be known to experts, but we were not able to find an adequate reference.
${\mathcal{O}}_{q}({\textstyle \frac{G}{G}})\operatorname{ - mod}$
are important for us is because they arise as horizontal traces. We now explain this construction. The results in this section seem to be known to experts, but we were not able to find an adequate reference.
2.4.1 Definition of horizontal trace
Given a skeletally small monoidal category
![]() ${\mathcal{C}}$
, we define its horizontal trace
${\mathcal{C}}$
, we define its horizontal trace
![]() ${\mathcal{C}}(S^{1})$
to have the some objects as
${\mathcal{C}}(S^{1})$
to have the some objects as
![]() ${\mathcal{C}}$
but with morphisms defined as follows. Fix two objects
${\mathcal{C}}$
but with morphisms defined as follows. Fix two objects
![]() $A,B$
in
$A,B$
in
![]() ${\mathcal{C}}$
. We consider pairs
${\mathcal{C}}$
. We consider pairs
![]() $(Z,\unicode[STIX]{x1D719})$
where
$(Z,\unicode[STIX]{x1D719})$
where
![]() $Z$
is an object of
$Z$
is an object of
![]() ${\mathcal{C}}$
and
${\mathcal{C}}$
and
![]() $\unicode[STIX]{x1D719}$
is a morphism
$\unicode[STIX]{x1D719}$
is a morphism
 $$\begin{eqnarray}\unicode[STIX]{x1D719}:A\otimes Z\rightarrow Z\otimes B\end{eqnarray}$$
$$\begin{eqnarray}\unicode[STIX]{x1D719}:A\otimes Z\rightarrow Z\otimes B\end{eqnarray}$$
in
![]() ${\mathcal{C}}$
.
${\mathcal{C}}$
.
We define an equivalence relation on these pairs as follows. Suppose that
![]() $Z,Z^{\prime }$
are objects of
$Z,Z^{\prime }$
are objects of
![]() ${\mathcal{C}}$
,
${\mathcal{C}}$
,
 $\unicode[STIX]{x1D6FC}:Z\rightarrow Z^{\prime }$
is a morphism in
$\unicode[STIX]{x1D6FC}:Z\rightarrow Z^{\prime }$
is a morphism in
![]() ${\mathcal{C}}$
, and
${\mathcal{C}}$
, and
 $\unicode[STIX]{x1D713}:A\otimes Z^{\prime }\rightarrow Z\otimes B$
is a morphism in
$\unicode[STIX]{x1D713}:A\otimes Z^{\prime }\rightarrow Z\otimes B$
is a morphism in
![]() ${\mathcal{C}}$
, then we can form two pairs
${\mathcal{C}}$
, then we can form two pairs
 $(Z,\unicode[STIX]{x1D713}\circ 1\otimes \unicode[STIX]{x1D6FC})$
and
$(Z,\unicode[STIX]{x1D713}\circ 1\otimes \unicode[STIX]{x1D6FC})$
and
 $(Z^{\prime },\unicode[STIX]{x1D6FC}\otimes 1\circ \unicode[STIX]{x1D713})$
. Under this circumstance, we say
$(Z^{\prime },\unicode[STIX]{x1D6FC}\otimes 1\circ \unicode[STIX]{x1D713})$
. Under this circumstance, we say
 $(Z,\unicode[STIX]{x1D713}\circ 1\otimes \unicode[STIX]{x1D6FC})$
and
$(Z,\unicode[STIX]{x1D713}\circ 1\otimes \unicode[STIX]{x1D6FC})$
and
 $(Z^{\prime },\unicode[STIX]{x1D6FC}\otimes 1\circ \unicode[STIX]{x1D713})$
are related and we consider the equivalence relation generated by these relations. Then we define the set
$(Z^{\prime },\unicode[STIX]{x1D6FC}\otimes 1\circ \unicode[STIX]{x1D713})$
are related and we consider the equivalence relation generated by these relations. Then we define the set
 $\operatorname{Hom}_{{\mathcal{C}}(S^{1})}(A,B)$
to be the set of equivalence classes of these pairs. Composition of morphisms is defined in the natural way.
$\operatorname{Hom}_{{\mathcal{C}}(S^{1})}(A,B)$
to be the set of equivalence classes of these pairs. Composition of morphisms is defined in the natural way.
Remark 2.4. We learned of the definition of horizontal trace from Scott Morrison. This definition was introduced by Walker [Reference WalkerWal06] under the name ‘annularization’. The name ‘horizontal trace’ appears in the paper [Reference Beliakova, Habiro, Lauda and ZivkovićBHLZ17]. Finally, in the paper [Reference Ben-Zvi, Brochier and JordanBBJ15], the same concept is defined under the name ‘zeroth Hochschild homology’.
2.4.2 Monoidal structure
In general the category
![]() ${\mathcal{C}}(S^{1})$
has no monoidal structure. However, if
${\mathcal{C}}(S^{1})$
has no monoidal structure. However, if
![]() ${\mathcal{C}}$
is a braided monoidal category with braiding
${\mathcal{C}}$
is a braided monoidal category with braiding
![]() $\unicode[STIX]{x1D6FD}$
, then
$\unicode[STIX]{x1D6FD}$
, then
![]() ${\mathcal{C}}(S^{1})$
has a natural monoidal structure, where tensor product of objects is the same as in
${\mathcal{C}}(S^{1})$
has a natural monoidal structure, where tensor product of objects is the same as in
![]() ${\mathcal{C}}$
and tensor product of morphism is given by
${\mathcal{C}}$
and tensor product of morphism is given by
 $$\begin{eqnarray}[Z_{1},\unicode[STIX]{x1D719}_{1}]\otimes [Z_{2},\unicode[STIX]{x1D719}_{2}]=[Z_{1}\otimes Z_{2},I\otimes \unicode[STIX]{x1D6FD}_{B_{1},Z_{2}}\otimes I\circ \unicode[STIX]{x1D719}_{1}\otimes \unicode[STIX]{x1D719}_{2}\circ I\otimes \unicode[STIX]{x1D6FD}_{A_{2},Z_{1}}\otimes I]\end{eqnarray}$$
$$\begin{eqnarray}[Z_{1},\unicode[STIX]{x1D719}_{1}]\otimes [Z_{2},\unicode[STIX]{x1D719}_{2}]=[Z_{1}\otimes Z_{2},I\otimes \unicode[STIX]{x1D6FD}_{B_{1},Z_{2}}\otimes I\circ \unicode[STIX]{x1D719}_{1}\otimes \unicode[STIX]{x1D719}_{2}\circ I\otimes \unicode[STIX]{x1D6FD}_{A_{2},Z_{1}}\otimes I]\end{eqnarray}$$
where
 $[Z_{1},\unicode[STIX]{x1D719}_{1}]\in \operatorname{Hom}_{{\mathcal{C}}(S^{1})}(A_{1},B_{1})$
and
$[Z_{1},\unicode[STIX]{x1D719}_{1}]\in \operatorname{Hom}_{{\mathcal{C}}(S^{1})}(A_{1},B_{1})$
and
 $(Z_{2},\unicode[STIX]{x1D719}_{2})\in \operatorname{Hom}_{{\mathcal{C}}(S^{1})}(A_{2},B_{2})$
.
$(Z_{2},\unicode[STIX]{x1D719}_{2})\in \operatorname{Hom}_{{\mathcal{C}}(S^{1})}(A_{2},B_{2})$
.
2.4.3 Semisimple case
If
![]() ${\mathcal{C}}$
is semisimple, then we can get a simpler description of morphisms in
${\mathcal{C}}$
is semisimple, then we can get a simpler description of morphisms in
![]() ${\mathcal{C}}(S^{1})$
.
${\mathcal{C}}(S^{1})$
.
Lemma 2.5. Suppose that
![]() ${\mathcal{C}}$
is a semisimple abelian category, with simple objects
${\mathcal{C}}$
is a semisimple abelian category, with simple objects
![]() $\{V_{i}\}_{i\in I}$
. Then we have an isomorphism
$\{V_{i}\}_{i\in I}$
. Then we have an isomorphism
 $$\begin{eqnarray}\operatorname{Hom}_{{\mathcal{C}}(S^{1})}(A,B)\cong \bigoplus _{i\in I}\operatorname{Hom}_{{\mathcal{C}}}(A\otimes V_{i},V_{i}\otimes B).\end{eqnarray}$$
$$\begin{eqnarray}\operatorname{Hom}_{{\mathcal{C}}(S^{1})}(A,B)\cong \bigoplus _{i\in I}\operatorname{Hom}_{{\mathcal{C}}}(A\otimes V_{i},V_{i}\otimes B).\end{eqnarray}$$
Proof. Fix
![]() $A,B$
objects of
$A,B$
objects of
![]() ${\mathcal{C}}$
. First, we define an abelian group structure on
${\mathcal{C}}$
. First, we define an abelian group structure on
 $\operatorname{Hom}_{{\mathcal{C}}(S^{1})}(A,B)$
as follows.
$\operatorname{Hom}_{{\mathcal{C}}(S^{1})}(A,B)$
as follows.
Given
![]() $[Z_{1},\unicode[STIX]{x1D719}_{1}]$
and
$[Z_{1},\unicode[STIX]{x1D719}_{1}]$
and
![]() $[Z_{2},\unicode[STIX]{x1D719}_{2}]$
in
$[Z_{2},\unicode[STIX]{x1D719}_{2}]$
in
 $\operatorname{Hom}_{{\mathcal{C}}(S^{1})}(A,B)$
, we define
$\operatorname{Hom}_{{\mathcal{C}}(S^{1})}(A,B)$
, we define
 $$\begin{eqnarray}[Z_{1},\unicode[STIX]{x1D719}_{1}]+[Z_{2},\unicode[STIX]{x1D719}_{2}]=\left[Z_{1}\oplus Z_{2},\left[\begin{array}{@{}cc@{}}\unicode[STIX]{x1D719}_{1} & 0\\ 0 & \unicode[STIX]{x1D719}_{2}\end{array}\right]\right],\end{eqnarray}$$
$$\begin{eqnarray}[Z_{1},\unicode[STIX]{x1D719}_{1}]+[Z_{2},\unicode[STIX]{x1D719}_{2}]=\left[Z_{1}\oplus Z_{2},\left[\begin{array}{@{}cc@{}}\unicode[STIX]{x1D719}_{1} & 0\\ 0 & \unicode[STIX]{x1D719}_{2}\end{array}\right]\right],\end{eqnarray}$$
where the matrix represents a morphism
 $A\otimes (Z_{1}\oplus Z_{2})=(A\otimes Z_{1})\oplus (A\otimes Z_{2})\rightarrow (Z_{1}\otimes B)\oplus (Z_{2}\otimes B)=(Z_{1}\oplus Z_{2})\otimes B$
. This extends the usual addition of morphisms; if
$A\otimes (Z_{1}\oplus Z_{2})=(A\otimes Z_{1})\oplus (A\otimes Z_{2})\rightarrow (Z_{1}\otimes B)\oplus (Z_{2}\otimes B)=(Z_{1}\oplus Z_{2})\otimes B$
. This extends the usual addition of morphisms; if
 $Z_{1}=Z_{2}=Z$
then the diagonal map
$Z_{1}=Z_{2}=Z$
then the diagonal map
 $Z\rightarrow Z\oplus Z$
gives an equivalence between
$Z\rightarrow Z\oplus Z$
gives an equivalence between
 $(Z,\unicode[STIX]{x1D719}_{1})+(Z,\unicode[STIX]{x1D719}_{2})$
and
$(Z,\unicode[STIX]{x1D719}_{1})+(Z,\unicode[STIX]{x1D719}_{2})$
and
 $(Z,\unicode[STIX]{x1D719}_{1}+\unicode[STIX]{x1D719}_{2})$
.
$(Z,\unicode[STIX]{x1D719}_{1}+\unicode[STIX]{x1D719}_{2})$
.
Along with the usual scaling of morphisms, we obtain a
![]() $\mathbb{C}$
-vector space structure on
$\mathbb{C}$
-vector space structure on
 $\operatorname{Hom}_{{\mathcal{C}}(S^{1})}(A,B)$
.
$\operatorname{Hom}_{{\mathcal{C}}(S^{1})}(A,B)$
.
This gives us a map
 $$\begin{eqnarray}\bigoplus _{i\in I}\operatorname{Hom}_{{\mathcal{C}}}(A\otimes V_{i},V_{i}\otimes B)\rightarrow \operatorname{Hom}_{{\mathcal{C}}(S^{1})}(A,B).\end{eqnarray}$$
$$\begin{eqnarray}\bigoplus _{i\in I}\operatorname{Hom}_{{\mathcal{C}}}(A\otimes V_{i},V_{i}\otimes B)\rightarrow \operatorname{Hom}_{{\mathcal{C}}(S^{1})}(A,B).\end{eqnarray}$$
On the other hand, suppose that
 $Z=Z_{1}\oplus Z_{2}$
and
$Z=Z_{1}\oplus Z_{2}$
and
 $[Z,\unicode[STIX]{x1D719}]\in \operatorname{Hom}_{{\mathcal{C}}(S^{1})}(A,B)$
. Then we can write
$[Z,\unicode[STIX]{x1D719}]\in \operatorname{Hom}_{{\mathcal{C}}(S^{1})}(A,B)$
. Then we can write
 $$\begin{eqnarray}\unicode[STIX]{x1D719}=\left[\begin{array}{@{}cc@{}}\unicode[STIX]{x1D719}_{11} & \unicode[STIX]{x1D719}_{12}\\ \unicode[STIX]{x1D719}_{21} & \unicode[STIX]{x1D719}_{22}\end{array}\right]=\left[\begin{array}{@{}cc@{}}\unicode[STIX]{x1D719}_{11} & \unicode[STIX]{x1D719}_{12}\\ 0 & 0\end{array}\right]+\left[\begin{array}{@{}cc@{}}0 & 0\\ \unicode[STIX]{x1D719}_{21} & \unicode[STIX]{x1D719}_{22}\end{array}\right].\end{eqnarray}$$
$$\begin{eqnarray}\unicode[STIX]{x1D719}=\left[\begin{array}{@{}cc@{}}\unicode[STIX]{x1D719}_{11} & \unicode[STIX]{x1D719}_{12}\\ \unicode[STIX]{x1D719}_{21} & \unicode[STIX]{x1D719}_{22}\end{array}\right]=\left[\begin{array}{@{}cc@{}}\unicode[STIX]{x1D719}_{11} & \unicode[STIX]{x1D719}_{12}\\ 0 & 0\end{array}\right]+\left[\begin{array}{@{}cc@{}}0 & 0\\ \unicode[STIX]{x1D719}_{21} & \unicode[STIX]{x1D719}_{22}\end{array}\right].\end{eqnarray}$$
Consider the inclusion map
 $\unicode[STIX]{x1D6FC}:Z_{1}\rightarrow Z_{1}\oplus Z_{2}$
. Using this map, we can see that
$\unicode[STIX]{x1D6FC}:Z_{1}\rightarrow Z_{1}\oplus Z_{2}$
. Using this map, we can see that
 $\left[Z,\left[\begin{smallmatrix}\unicode[STIX]{x1D719}_{11} & \unicode[STIX]{x1D719}_{12}\\ 0 & 0\end{smallmatrix}\right]\right]=[Z_{1},\unicode[STIX]{x1D719}_{11}]$
. Similarly,
$\left[Z,\left[\begin{smallmatrix}\unicode[STIX]{x1D719}_{11} & \unicode[STIX]{x1D719}_{12}\\ 0 & 0\end{smallmatrix}\right]\right]=[Z_{1},\unicode[STIX]{x1D719}_{11}]$
. Similarly,
 $\left[Z,\left[\begin{smallmatrix}0 & 0\\ \unicode[STIX]{x1D719}_{21} & \unicode[STIX]{x1D719}_{22}\end{smallmatrix}\right]\right]=[Z_{2},\unicode[STIX]{x1D719}_{22}]$
. Thus
$\left[Z,\left[\begin{smallmatrix}0 & 0\\ \unicode[STIX]{x1D719}_{21} & \unicode[STIX]{x1D719}_{22}\end{smallmatrix}\right]\right]=[Z_{2},\unicode[STIX]{x1D719}_{22}]$
. Thus
 $[Z,\unicode[STIX]{x1D719}]=[Z_{1},\unicode[STIX]{x1D719}_{11}]+[Z_{2},\unicode[STIX]{x1D719}_{22}]$
. Applying this repeatedly leads to an inverse to (3).◻
$[Z,\unicode[STIX]{x1D719}]=[Z_{1},\unicode[STIX]{x1D719}_{11}]+[Z_{2},\unicode[STIX]{x1D719}_{22}]$
. Applying this repeatedly leads to an inverse to (3).◻
When
 ${\mathcal{C}}={\mathcal{R}}\text{ep}_{q}(G)$
, then
${\mathcal{C}}={\mathcal{R}}\text{ep}_{q}(G)$
, then
![]() ${\mathcal{C}}(S^{1})$
is quite familiar. (This result also appears as [Reference Ben-Zvi, Brochier and JordanBBJ15, Theorem 4.16].)
${\mathcal{C}}(S^{1})$
is quite familiar. (This result also appears as [Reference Ben-Zvi, Brochier and JordanBBJ15, Theorem 4.16].)
Proposition 2.6. We have an equivalence of categories
 ${\mathcal{R}}\text{ep}_{q}(G)(S^{1})\cong {\mathcal{O}}_{q}({\textstyle \frac{G}{G}})\operatorname{ - mod}$
.
${\mathcal{R}}\text{ep}_{q}(G)(S^{1})\cong {\mathcal{O}}_{q}({\textstyle \frac{G}{G}})\operatorname{ - mod}$
.
Proof. Let
 $V,W\in {\mathcal{R}}\text{ep}_{q}(G)$
. Then,
$V,W\in {\mathcal{R}}\text{ep}_{q}(G)$
. Then,
 $$\begin{eqnarray}\displaystyle \operatorname{Hom}_{{\mathcal{R}}\text{ep}_{q}(G)(S^{1})}(A,B) & \cong & \displaystyle \bigoplus _{\unicode[STIX]{x1D706}\in \unicode[STIX]{x1D6EC}_{+}}\operatorname{Hom}_{{\mathcal{R}}\text{ep}_{q}(G)}(A\otimes V(\unicode[STIX]{x1D706}),V(\unicode[STIX]{x1D706})\otimes B)\nonumber\\ \displaystyle & \cong & \displaystyle \bigoplus _{\unicode[STIX]{x1D706}\in \unicode[STIX]{x1D6EC}_{+}}\operatorname{Hom}_{{\mathcal{R}}\text{ep}_{q}(G)}(A,V(\unicode[STIX]{x1D706})\otimes B\otimes V(\unicode[STIX]{x1D706})^{\ast })\nonumber\\ \displaystyle & \cong & \displaystyle \bigoplus _{\unicode[STIX]{x1D706}\in \unicode[STIX]{x1D6EC}_{+}}\operatorname{Hom}_{{\mathcal{R}}\text{ep}_{q}(G)}(A,V(\unicode[STIX]{x1D706})\otimes V(\unicode[STIX]{x1D706})^{\ast }\otimes B)\nonumber\\ \displaystyle & \cong & \displaystyle \operatorname{Hom}_{{\mathcal{R}}\text{ep}_{q}(G)}(A,{\mathcal{O}}_{q}(G)\otimes B)\nonumber\\ \displaystyle & \cong & \displaystyle \operatorname{Hom}_{{\mathcal{O}}_{q}({\textstyle \frac{G}{G}})\operatorname{-mod}}({\mathcal{O}}_{q}(G)\otimes A,{\mathcal{O}}_{q}(G)\otimes B).\nonumber\end{eqnarray}$$
$$\begin{eqnarray}\displaystyle \operatorname{Hom}_{{\mathcal{R}}\text{ep}_{q}(G)(S^{1})}(A,B) & \cong & \displaystyle \bigoplus _{\unicode[STIX]{x1D706}\in \unicode[STIX]{x1D6EC}_{+}}\operatorname{Hom}_{{\mathcal{R}}\text{ep}_{q}(G)}(A\otimes V(\unicode[STIX]{x1D706}),V(\unicode[STIX]{x1D706})\otimes B)\nonumber\\ \displaystyle & \cong & \displaystyle \bigoplus _{\unicode[STIX]{x1D706}\in \unicode[STIX]{x1D6EC}_{+}}\operatorname{Hom}_{{\mathcal{R}}\text{ep}_{q}(G)}(A,V(\unicode[STIX]{x1D706})\otimes B\otimes V(\unicode[STIX]{x1D706})^{\ast })\nonumber\\ \displaystyle & \cong & \displaystyle \bigoplus _{\unicode[STIX]{x1D706}\in \unicode[STIX]{x1D6EC}_{+}}\operatorname{Hom}_{{\mathcal{R}}\text{ep}_{q}(G)}(A,V(\unicode[STIX]{x1D706})\otimes V(\unicode[STIX]{x1D706})^{\ast }\otimes B)\nonumber\\ \displaystyle & \cong & \displaystyle \operatorname{Hom}_{{\mathcal{R}}\text{ep}_{q}(G)}(A,{\mathcal{O}}_{q}(G)\otimes B)\nonumber\\ \displaystyle & \cong & \displaystyle \operatorname{Hom}_{{\mathcal{O}}_{q}({\textstyle \frac{G}{G}})\operatorname{-mod}}({\mathcal{O}}_{q}(G)\otimes A,{\mathcal{O}}_{q}(G)\otimes B).\nonumber\end{eqnarray}$$
Here in the third line we use the inverse braiding
 $\unicode[STIX]{x1D6FD}_{V(\unicode[STIX]{x1D706})^{\ast },B}^{-1}$
and in the last line, we use that
$\unicode[STIX]{x1D6FD}_{V(\unicode[STIX]{x1D706})^{\ast },B}^{-1}$
and in the last line, we use that
 ${\mathcal{O}}_{q}(G)\otimes A$
is free as an
${\mathcal{O}}_{q}(G)\otimes A$
is free as an
![]() ${\mathcal{O}}_{q}(G)$
-module.
${\mathcal{O}}_{q}(G)$
-module.
Moreover, these isomorphisms are compatible with composition on both sides. ◻
2.4.4 Idempotent completion
Finally, we will need to examine the behaviour of horizontal trace under idempotent completion.
Proposition 2.7. Let
![]() ${\mathcal{C}}$
be a monoidal category and let
${\mathcal{C}}$
be a monoidal category and let
![]() $\overline{{\mathcal{C}}}$
be its idempotent completion. Then the functor
$\overline{{\mathcal{C}}}$
be its idempotent completion. Then the functor
 ${\mathcal{C}}(S^{1})\rightarrow \overline{{\mathcal{C}}}(S^{1})$
is fully faithful.
${\mathcal{C}}(S^{1})\rightarrow \overline{{\mathcal{C}}}(S^{1})$
is fully faithful.
Proof. By general results, we know that the functor
![]() ${\mathcal{C}}\rightarrow \overline{{\mathcal{C}}}$
is fully faithful.
${\mathcal{C}}\rightarrow \overline{{\mathcal{C}}}$
is fully faithful.
Let
![]() $A,B$
be objects of
$A,B$
be objects of
![]() ${\mathcal{C}}$
. We would like to show that the map
${\mathcal{C}}$
. We would like to show that the map
 $$\begin{eqnarray}\operatorname{Hom}_{{\mathcal{C}}(S^{1})}(A,B)\rightarrow \operatorname{Hom}_{\overline{{\mathcal{C}}}(S^{1})}(A,B)\end{eqnarray}$$
$$\begin{eqnarray}\operatorname{Hom}_{{\mathcal{C}}(S^{1})}(A,B)\rightarrow \operatorname{Hom}_{\overline{{\mathcal{C}}}(S^{1})}(A,B)\end{eqnarray}$$
is an isomorphism.
To show surjectivity, let
![]() $[Z,\unicode[STIX]{x1D719}]$
be a morphism in
$[Z,\unicode[STIX]{x1D719}]$
be a morphism in
![]() $\overline{{\mathcal{C}}}(S^{1})$
. Then there is an object
$\overline{{\mathcal{C}}}(S^{1})$
. Then there is an object
![]() $Y$
of
$Y$
of
![]() ${\mathcal{C}}$
and an isomorphism
${\mathcal{C}}$
and an isomorphism
 $Y=Z\oplus Z^{\prime }$
in
$Y=Z\oplus Z^{\prime }$
in
![]() $\overline{{\mathcal{C}}}$
. Then consider
$\overline{{\mathcal{C}}}$
. Then consider
 $\unicode[STIX]{x1D713}:A\otimes (Z\oplus Z^{\prime })\rightarrow (Z\oplus Z^{\prime })\otimes B$
defined by the matrix
$\unicode[STIX]{x1D713}:A\otimes (Z\oplus Z^{\prime })\rightarrow (Z\oplus Z^{\prime })\otimes B$
defined by the matrix
![]() $\left[\begin{smallmatrix}\unicode[STIX]{x1D719} & 0\\ 0 & 0\end{smallmatrix}\right]$
; it is a morphism in
$\left[\begin{smallmatrix}\unicode[STIX]{x1D719} & 0\\ 0 & 0\end{smallmatrix}\right]$
; it is a morphism in
![]() ${\mathcal{C}}$
. Then
${\mathcal{C}}$
. Then
![]() $[Y,\unicode[STIX]{x1D713}]$
is a morphism in
$[Y,\unicode[STIX]{x1D713}]$
is a morphism in
![]() ${\mathcal{C}}(S^{1})$
and the image of
${\mathcal{C}}(S^{1})$
and the image of
![]() $[Y,\unicode[STIX]{x1D713}]$
in
$[Y,\unicode[STIX]{x1D713}]$
in
 $\operatorname{Hom}_{\overline{{\mathcal{C}}}(S^{1})}(A,B)$
will be
$\operatorname{Hom}_{\overline{{\mathcal{C}}}(S^{1})}(A,B)$
will be
![]() $[Z,\unicode[STIX]{x1D719}]$
.
$[Z,\unicode[STIX]{x1D719}]$
.
The proof of injectivity is similar. ◻
2.5 Action of annular braids
As mentioned above, the procedure of horizontal trace is closely related to the circle or annulus. In particular, if
![]() ${\mathcal{C}}$
is braided monoidal, then the annular braid group acts on tensor products in
${\mathcal{C}}$
is braided monoidal, then the annular braid group acts on tensor products in
![]() ${\mathcal{C}}(S^{1})$
. Let us formulate this fact in a precise fashion in the case of
${\mathcal{C}}(S^{1})$
. Let us formulate this fact in a precise fashion in the case of
 ${\mathcal{R}}\text{ep}_{q}(G)$
.
${\mathcal{R}}\text{ep}_{q}(G)$
.
2.5.1 The annular braid group
Consider the annular braid group
![]() $AB_{m}$
(sometimes it is also called the extended affine braid group). It has generators
$AB_{m}$
(sometimes it is also called the extended affine braid group). It has generators
 $X_{1},\ldots ,X_{m}$
and
$X_{1},\ldots ,X_{m}$
and
 $T_{1},\ldots ,T_{m-1}$
subject to the following relations:
$T_{1},\ldots ,T_{m-1}$
subject to the following relations:
-
(i)
 $T_{i}T_{j}=T_{j}T_{i}$
if
$T_{i}T_{j}=T_{j}T_{i}$
if
 $|i-j|>1$
and
$|i-j|>1$
and
 $T_{i}T_{j}T_{i}=T_{j}T_{i}T_{j}$
if
$T_{i}T_{j}T_{i}=T_{j}T_{i}T_{j}$
if
 $|i-j|=1$
;
$|i-j|=1$
; -
(ii)
 $T_{i}X_{j}=X_{j}T_{i}$
if
$T_{i}X_{j}=X_{j}T_{i}$
if
 $j\neq i,i+1$
;
$j\neq i,i+1$
; -
(iii)
 $T_{i}X_{i}T_{i}=X_{i+1}$
for
$T_{i}X_{i}T_{i}=X_{i+1}$
for
 $i=1,\ldots ,m-1$
;
$i=1,\ldots ,m-1$
; -
(iv)
 $X_{i}X_{j}=X_{j}X_{i}$
.
$X_{i}X_{j}=X_{j}X_{i}$
.
These can be viewed as braids with
![]() $m$
strands lying on an annulus. More precisely
$m$
strands lying on an annulus. More precisely
 $AB_{m}=\unicode[STIX]{x1D70B}_{1}(A^{m}\smallsetminus \unicode[STIX]{x1D6E5}/S_{m})$
, where
$AB_{m}=\unicode[STIX]{x1D70B}_{1}(A^{m}\smallsetminus \unicode[STIX]{x1D6E5}/S_{m})$
, where
![]() $A$
is the annulus. The
$A$
is the annulus. The
![]() $T_{i}$
corresponds to strand
$T_{i}$
corresponds to strand
![]() $i$
crossing over strand
$i$
crossing over strand
![]() $i+1$
, while
$i+1$
, while
![]() $X_{i}$
is the braid where the
$X_{i}$
is the braid where the
![]() $i$
th strand curls itself once counterclockwise around the annulus, passing under strands
$i$
th strand curls itself once counterclockwise around the annulus, passing under strands
 $1,\ldots ,i-1$
and over strands
$1,\ldots ,i-1$
and over strands
 $i+1,\ldots ,m$
(from this description it is clear why
$i+1,\ldots ,m$
(from this description it is clear why
 $X_{i}X_{j}=X_{j}X_{i}$
).
$X_{i}X_{j}=X_{j}X_{i}$
).
Another common description of
![]() $AB_{m}$
is using generators
$AB_{m}$
is using generators
 $T_{0},T_{1},\ldots ,T_{m-1}$
and
$T_{0},T_{1},\ldots ,T_{m-1}$
and
![]() $R$
where the
$R$
where the
![]() $T_{i}$
satisfy the same relations as above while
$T_{i}$
satisfy the same relations as above while
![]() $R$
satisfies
$R$
satisfies
 $RT_{i}=T_{i-1}R$
(modulo
$RT_{i}=T_{i-1}R$
(modulo
![]() $m$
). Here
$m$
). Here
![]() $R$
is the braid where each strand moves to the counterclockwise one position (see Figure 1). From this description it is clear that
$R$
is the braid where each strand moves to the counterclockwise one position (see Figure 1). From this description it is clear that
 $R^{m}=X_{1}\ldots X_{m}$
while an easy exercise shows that
$R^{m}=X_{1}\ldots X_{m}$
while an easy exercise shows that
 $R=T_{m-1}\cdots T_{1}X_{1}$
.
$R=T_{m-1}\cdots T_{1}X_{1}$
.

Figure 1. Some generators of
![]() $AB_{5}$
.
$AB_{5}$
.
Given any set
![]() $S$
, we can form the groupoid of annular braids labelled by
$S$
, we can form the groupoid of annular braids labelled by
![]() $S$
,
$S$
,
 ${\mathcal{A}}{\mathcal{B}}_{m}(S)$
. This is a groupoid whose set of objects is
${\mathcal{A}}{\mathcal{B}}_{m}(S)$
. This is a groupoid whose set of objects is
![]() $S^{m}$
with generators
$S^{m}$
with generators
 $$\begin{eqnarray}T_{i}:(s_{1},\ldots ,s_{m})\rightarrow (s_{1},\ldots ,s_{i+1},s_{i},\ldots ,s_{m}),\quad X_{i}:(s_{1},\ldots ,s_{m})\rightarrow (s_{1},\ldots ,s_{m})\end{eqnarray}$$
$$\begin{eqnarray}T_{i}:(s_{1},\ldots ,s_{m})\rightarrow (s_{1},\ldots ,s_{i+1},s_{i},\ldots ,s_{m}),\quad X_{i}:(s_{1},\ldots ,s_{m})\rightarrow (s_{1},\ldots ,s_{m})\end{eqnarray}$$
for all
 $s_{1},\ldots ,s_{m}\in S$
. These generators satisfy the same relations as in
$s_{1},\ldots ,s_{m}\in S$
. These generators satisfy the same relations as in
![]() $AB_{m}$
. In other words,
$AB_{m}$
. In other words,
 ${\mathcal{A}}{\mathcal{B}}_{m}(S)$
is the fundamental groupoid of the space
${\mathcal{A}}{\mathcal{B}}_{m}(S)$
is the fundamental groupoid of the space
 $(A\times S)^{m}\setminus \unicode[STIX]{x1D6E5}/S_{m}$
(where
$(A\times S)^{m}\setminus \unicode[STIX]{x1D6E5}/S_{m}$
(where
![]() $\unicode[STIX]{x1D6E5}$
is the pullback of the usual fat diagonal in
$\unicode[STIX]{x1D6E5}$
is the pullback of the usual fat diagonal in
![]() $A^{m}$
).
$A^{m}$
).
We can also consider the usual braid group
![]() $B_{m}$
(the subgroup generated by the elements
$B_{m}$
(the subgroup generated by the elements
![]() $T_{i}$
) and the groupoid
$T_{i}$
) and the groupoid
![]() ${\mathcal{B}}_{m}(S)$
.
${\mathcal{B}}_{m}(S)$
.
2.5.2 Action on
 ${\mathcal{O}}_{q}({\textstyle \frac{G}{G}})\operatorname{ - mod}$
${\mathcal{O}}_{q}({\textstyle \frac{G}{G}})\operatorname{ - mod}$
Since
 ${\mathcal{R}}\text{ep}_{q}(G)$
is a braided monoidal category, then we have a functor
${\mathcal{R}}\text{ep}_{q}(G)$
is a braided monoidal category, then we have a functor
 ${\mathcal{B}}_{m}({\mathcal{R}}\text{ep}_{q}(G))\rightarrow {\mathcal{R}}\text{ep}_{q}(G)$
where the elements
${\mathcal{B}}_{m}({\mathcal{R}}\text{ep}_{q}(G))\rightarrow {\mathcal{R}}\text{ep}_{q}(G)$
where the elements
![]() $T_{i}$
act by the usual braiding of adjacent tensor factors. This can be extended to the annular braid groupoid as follows.
$T_{i}$
act by the usual braiding of adjacent tensor factors. This can be extended to the annular braid groupoid as follows.
Now, suppose that we have representations
 $V_{1},\ldots ,V_{m}$
of
$V_{1},\ldots ,V_{m}$
of
![]() $U_{q}\mathfrak{g}$
. Then we can form
$U_{q}\mathfrak{g}$
. Then we can form
 ${\mathcal{O}}_{q}(G)\otimes V_{1}\otimes \cdots \otimes V_{m}$
. We can braid the representations
${\mathcal{O}}_{q}(G)\otimes V_{1}\otimes \cdots \otimes V_{m}$
. We can braid the representations
 $V_{1},\ldots ,V_{m}$
using the braiding in
$V_{1},\ldots ,V_{m}$
using the braiding in
 ${\mathcal{R}}\text{ep}_{q}(G)$
which gives us isomorphisms
${\mathcal{R}}\text{ep}_{q}(G)$
which gives us isomorphisms
 $T_{1},\ldots ,T_{m-1}$
satisfying the braid relations.
$T_{1},\ldots ,T_{m-1}$
satisfying the braid relations.
We define the automorphism
![]() $X_{j}$
by placing the automorphism
$X_{j}$
by placing the automorphism
![]() $X$
(from § 2.3.3) in the
$X$
(from § 2.3.3) in the
![]() $j$
th position using the monoidal structure defined in § 2.4.2. In other words,
$j$
th position using the monoidal structure defined in § 2.4.2. In other words,
![]() $X_{j}$
is given by the composition
$X_{j}$
is given by the composition
 $$\begin{eqnarray}\displaystyle & {\mathcal{O}}_{q}(G)\otimes V_{1}\otimes \cdots \otimes V_{m}\xrightarrow[{}]{I\otimes \unicode[STIX]{x1D6FD}_{V_{1}\otimes \cdots \otimes V_{j-1},V_{j}}\otimes I}{\mathcal{O}}_{q}(G)\otimes V_{j}\otimes V_{1}\cdots V_{m} & \displaystyle \nonumber\\ \displaystyle & \xrightarrow[{}]{X\otimes I}{\mathcal{O}}_{q}(G)\otimes V_{j}\otimes V_{1}\cdots V_{m}\xrightarrow[{}]{I\otimes \unicode[STIX]{x1D6FD}_{V_{j},V_{1}\otimes \cdots \otimes V_{j-1}}\otimes I}{\mathcal{O}}_{q}(G)\otimes V_{1}\otimes \cdots \otimes V_{m}. & \displaystyle \nonumber\end{eqnarray}$$
$$\begin{eqnarray}\displaystyle & {\mathcal{O}}_{q}(G)\otimes V_{1}\otimes \cdots \otimes V_{m}\xrightarrow[{}]{I\otimes \unicode[STIX]{x1D6FD}_{V_{1}\otimes \cdots \otimes V_{j-1},V_{j}}\otimes I}{\mathcal{O}}_{q}(G)\otimes V_{j}\otimes V_{1}\cdots V_{m} & \displaystyle \nonumber\\ \displaystyle & \xrightarrow[{}]{X\otimes I}{\mathcal{O}}_{q}(G)\otimes V_{j}\otimes V_{1}\cdots V_{m}\xrightarrow[{}]{I\otimes \unicode[STIX]{x1D6FD}_{V_{j},V_{1}\otimes \cdots \otimes V_{j-1}}\otimes I}{\mathcal{O}}_{q}(G)\otimes V_{1}\otimes \cdots \otimes V_{m}. & \displaystyle \nonumber\end{eqnarray}$$
Because they come from the monoidal structure,
 $X_{1},\ldots ,X_{m}$
commute. The following result is due to Lyubashenko and Majid [Reference Lyubashenko and MajidLM94]. The proof is straightforward.
$X_{1},\ldots ,X_{m}$
commute. The following result is due to Lyubashenko and Majid [Reference Lyubashenko and MajidLM94]. The proof is straightforward.
Proposition 2.8. The above
![]() $T_{i},X_{j}$
satisfy the annular braid group relations and thus define a functor
$T_{i},X_{j}$
satisfy the annular braid group relations and thus define a functor
 $AB({\mathcal{R}}\text{ep}_{q}(G))\rightarrow {\mathcal{O}}_{q}({\textstyle \frac{G}{G}})\operatorname{ - mod}$
.
$AB({\mathcal{R}}\text{ep}_{q}(G))\rightarrow {\mathcal{O}}_{q}({\textstyle \frac{G}{G}})\operatorname{ - mod}$
.
An object of
 ${\mathcal{O}}_{q}({\textstyle \frac{G}{G}})\operatorname{ - mod}$
of the form
${\mathcal{O}}_{q}({\textstyle \frac{G}{G}})\operatorname{ - mod}$
of the form
 ${\mathcal{O}}_{q}(G)\otimes V_{1}\otimes \cdots \otimes V_{m}$
will be called an object of length
${\mathcal{O}}_{q}(G)\otimes V_{1}\otimes \cdots \otimes V_{m}$
will be called an object of length
![]() $m$
. As a special case of Proposition 2.8, we see that
$m$
. As a special case of Proposition 2.8, we see that
![]() $\mathbb{Z}^{m}$
acts on objects of length
$\mathbb{Z}^{m}$
acts on objects of length
![]() $m$
in
$m$
in
 ${\mathcal{O}}_{q}({\textstyle \frac{G}{G}})\operatorname{ - mod}$
.
${\mathcal{O}}_{q}({\textstyle \frac{G}{G}})\operatorname{ - mod}$
.
2.6 Kostant slice functor
In [Reference Bezrukavnikov and FinkelbergBF08], an important role is played by the Kostant slice functor. In their setting of
 ${\mathcal{O}}(\frac{\mathfrak{g}}{G})\operatorname{ - mod}$
, they considered the Kostant slice
${\mathcal{O}}(\frac{\mathfrak{g}}{G})\operatorname{ - mod}$
, they considered the Kostant slice
 $\mathfrak{t}/W{\hookrightarrow}\mathfrak{g}$
. Pulling back along the Kostant slice gives rise to a fully faithful functor
$\mathfrak{t}/W{\hookrightarrow}\mathfrak{g}$
. Pulling back along the Kostant slice gives rise to a fully faithful functor
 $S:{\mathcal{O}}(\frac{\mathfrak{g}}{G})\operatorname{ - mod}\rightarrow Z_{\mathfrak{g}}\operatorname{ - mod}$
where
$S:{\mathcal{O}}(\frac{\mathfrak{g}}{G})\operatorname{ - mod}\rightarrow Z_{\mathfrak{g}}\operatorname{ - mod}$
where
![]() $Z_{\mathfrak{g}}$
is the group scheme of regular centralizers regarded as a group scheme over
$Z_{\mathfrak{g}}$
is the group scheme of regular centralizers regarded as a group scheme over
![]() $\mathfrak{t}/W$
.
$\mathfrak{t}/W$
.
In our situation, we have a Steinberg slice
 $T/W{\hookrightarrow}G$
. As in the Lie algebra case, the image of this Steinberg slice meets every regular
$T/W{\hookrightarrow}G$
. As in the Lie algebra case, the image of this Steinberg slice meets every regular
![]() $G$
-orbit once. Moreover, the set
$G$
-orbit once. Moreover, the set
![]() $G^{\text{reg}}$
of regular elements of
$G^{\text{reg}}$
of regular elements of
![]() $G$
is dense and its complement has codimension 2. Thus we see that the resulting functor
$G$
is dense and its complement has codimension 2. Thus we see that the resulting functor
 $S:{\mathcal{O}}({\textstyle \frac{G}{G}})\operatorname{ - mod}\rightarrow Z_{G}\operatorname{ - mod}$
given by
$S:{\mathcal{O}}({\textstyle \frac{G}{G}})\operatorname{ - mod}\rightarrow Z_{G}\operatorname{ - mod}$
given by
 $M\mapsto M\otimes _{{\mathcal{O}}(G)}{\mathcal{O}}(T/W)$
is an equivalence, where
$M\mapsto M\otimes _{{\mathcal{O}}(G)}{\mathcal{O}}(T/W)$
is an equivalence, where
![]() $Z_{G}$
is the group scheme of group regular centralizers regarded as a group scheme over
$Z_{G}$
is the group scheme of group regular centralizers regarded as a group scheme over
![]() $T/W$
. This functor (as in the work of [Reference Bezrukavnikov and FinkelbergBF08]) can and will be used to give a more algebraic description of the category
$T/W$
. This functor (as in the work of [Reference Bezrukavnikov and FinkelbergBF08]) can and will be used to give a more algebraic description of the category
 ${\mathcal{O}}({\textstyle \frac{G}{G}})\operatorname{ - mod}$
.
${\mathcal{O}}({\textstyle \frac{G}{G}})\operatorname{ - mod}$
.
Unfortunately, in the quantum group situation we do not seem to have an analogous map
 ${\mathcal{O}}_{q}(G)\rightarrow E(q)$
(nor an analog of the group scheme of regular centralizers). However, it should be possible to construct a version of the Kostant slice functor by relating
${\mathcal{O}}_{q}(G)\rightarrow E(q)$
(nor an analog of the group scheme of regular centralizers). However, it should be possible to construct a version of the Kostant slice functor by relating
 ${\mathcal{O}}_{q}({\textstyle \frac{G}{G}})\operatorname{ - mod}$
to a category of Harish-Chandra modules and using the work of Sevostyanov [Reference SevostyanovSev00].
${\mathcal{O}}_{q}({\textstyle \frac{G}{G}})\operatorname{ - mod}$
to a category of Harish-Chandra modules and using the work of Sevostyanov [Reference SevostyanovSev00].
2.7 Minuscule versions
A non-trivial irreducible representation
![]() $V$
of
$V$
of
![]() $G$
is called minuscule, if all weights of
$G$
is called minuscule, if all weights of
![]() $V$
lie in single Weyl orbit. Equivalently
$V$
lie in single Weyl orbit. Equivalently
![]() $V(\unicode[STIX]{x1D706})$
is minuscule if and only if
$V(\unicode[STIX]{x1D706})$
is minuscule if and only if
![]() $\unicode[STIX]{x1D706}$
is a non-zero minimal element of
$\unicode[STIX]{x1D706}$
is a non-zero minimal element of
![]() $\unicode[STIX]{x1D6EC}_{+}$
(with respect to the usual partial order on
$\unicode[STIX]{x1D6EC}_{+}$
(with respect to the usual partial order on
![]() $\unicode[STIX]{x1D6EC}_{+}$
).
$\unicode[STIX]{x1D6EC}_{+}$
).
We consider the full subcategory
 ${\mathcal{R}}\text{ep}_{q}^{\min }(G)$
of
${\mathcal{R}}\text{ep}_{q}^{\min }(G)$
of
 ${\mathcal{R}}\text{ep}_{q}(G)$
consisting of tensor products of minuscule representations. Similarly, we consider
${\mathcal{R}}\text{ep}_{q}(G)$
consisting of tensor products of minuscule representations. Similarly, we consider
 ${\mathcal{O}}_{q}^{\min }({\textstyle \frac{G}{G}})\operatorname{ - mod}$
to be the subcategory of
${\mathcal{O}}_{q}^{\min }({\textstyle \frac{G}{G}})\operatorname{ - mod}$
to be the subcategory of
 ${\mathcal{O}}_{q}({\textstyle \frac{G}{G}})\operatorname{ - mod}$
consisting of objects of the form
${\mathcal{O}}_{q}({\textstyle \frac{G}{G}})\operatorname{ - mod}$
consisting of objects of the form
 ${\mathcal{O}}_{q}(G)\otimes V$
for
${\mathcal{O}}_{q}(G)\otimes V$
for
 $V\in {\mathcal{R}}\text{ep}_{q}^{\min }(G)$
.
$V\in {\mathcal{R}}\text{ep}_{q}^{\min }(G)$
.
When
 $G=\operatorname{SL}_{n}$
, the minuscule representations coincide with the fundamental representations
$G=\operatorname{SL}_{n}$
, the minuscule representations coincide with the fundamental representations
![]() $\bigwedge ^{k}\mathbb{C}^{n}$
for
$\bigwedge ^{k}\mathbb{C}^{n}$
for
 $k=1,\ldots ,n-1$
. In this case, the idempotent completion of
$k=1,\ldots ,n-1$
. In this case, the idempotent completion of
 ${\mathcal{R}}\text{ep}_{q}^{\min }(\operatorname{SL}_{n})$
is
${\mathcal{R}}\text{ep}_{q}^{\min }(\operatorname{SL}_{n})$
is
 ${\mathcal{R}}\text{ep}_{q}(\operatorname{SL}_{n})$
. From Propositions 2.6 and 2.7, we deduce the following.
${\mathcal{R}}\text{ep}_{q}(\operatorname{SL}_{n})$
. From Propositions 2.6 and 2.7, we deduce the following.
Corollary 2.9. There is an equivalence
 ${\mathcal{R}}\text{ep}_{q}^{\min }(\operatorname{SL}_{n})(S^{1})\cong {\mathcal{O}}_{q}^{\min }({\textstyle \frac{\operatorname{SL}_{n}}{\operatorname{SL}_{n}}})\operatorname{ - mod}$
.
${\mathcal{R}}\text{ep}_{q}^{\min }(\operatorname{SL}_{n})(S^{1})\cong {\mathcal{O}}_{q}^{\min }({\textstyle \frac{\operatorname{SL}_{n}}{\operatorname{SL}_{n}}})\operatorname{ - mod}$
.
3 Geometry of affine Grassmannians
3.1 The affine Grassmannian
Let
 ${\mathcal{K}}=\mathbb{C}((t)),{\mathcal{O}}=\mathbb{C}[[t]]$
and let
${\mathcal{K}}=\mathbb{C}((t)),{\mathcal{O}}=\mathbb{C}[[t]]$
and let
 $Gr=G^{\vee }({\mathcal{K}})/G^{\vee }({\mathcal{O}})$
denote the affine Grassmannian of the Langlands dual group. See Zhu [Reference ZhuZhu16] for a thorough discussion about affine Grassmannians.
$Gr=G^{\vee }({\mathcal{K}})/G^{\vee }({\mathcal{O}})$
denote the affine Grassmannian of the Langlands dual group. See Zhu [Reference ZhuZhu16] for a thorough discussion about affine Grassmannians.
For every weight
![]() $\unicode[STIX]{x1D706}\in \unicode[STIX]{x1D6EC}$
, there is a point
$\unicode[STIX]{x1D706}\in \unicode[STIX]{x1D6EC}$
, there is a point
 $t^{\unicode[STIX]{x1D706}}\in Gr$
. For each
$t^{\unicode[STIX]{x1D706}}\in Gr$
. For each
![]() $\unicode[STIX]{x1D706}\in \unicode[STIX]{x1D6EC}_{+}$
, let
$\unicode[STIX]{x1D706}\in \unicode[STIX]{x1D6EC}_{+}$
, let
 $Gr^{\unicode[STIX]{x1D706}}=G^{\vee }({\mathcal{O}})t^{\unicode[STIX]{x1D706}}$
. We have
$Gr^{\unicode[STIX]{x1D706}}=G^{\vee }({\mathcal{O}})t^{\unicode[STIX]{x1D706}}$
. We have
 $\dim Gr^{\unicode[STIX]{x1D706}}=2\unicode[STIX]{x1D70C}^{\vee }(\unicode[STIX]{x1D706})$
. We have the stratification
$\dim Gr^{\unicode[STIX]{x1D706}}=2\unicode[STIX]{x1D70C}^{\vee }(\unicode[STIX]{x1D706})$
. We have the stratification
 $Gr=\bigcup _{\unicode[STIX]{x1D706}\in \unicode[STIX]{x1D6EC}_{+}}Gr^{\unicode[STIX]{x1D706}}$
. Moreover, given any two points
$Gr=\bigcup _{\unicode[STIX]{x1D706}\in \unicode[STIX]{x1D6EC}_{+}}Gr^{\unicode[STIX]{x1D706}}$
. Moreover, given any two points
 $L_{1},L_{2}\in Gr$
, there exists
$L_{1},L_{2}\in Gr$
, there exists
 $g\in G^{\vee }({\mathcal{K}})$
such that
$g\in G^{\vee }({\mathcal{K}})$
such that
 $(gL_{1},gL_{2})=(t^{0},t^{\unicode[STIX]{x1D706}})$
for a unique dominant weight
$(gL_{1},gL_{2})=(t^{0},t^{\unicode[STIX]{x1D706}})$
for a unique dominant weight
![]() $\unicode[STIX]{x1D706}\in \unicode[STIX]{x1D6EC}_{+}$
. In this case, we say that
$\unicode[STIX]{x1D706}\in \unicode[STIX]{x1D6EC}_{+}$
. In this case, we say that
![]() $L_{2}$
is distance
$L_{2}$
is distance
![]() $\unicode[STIX]{x1D706}$
from
$\unicode[STIX]{x1D706}$
from
![]() $L_{1}$
and we write
$L_{1}$
and we write
 $d(L_{1},L_{2})=\unicode[STIX]{x1D706}$
. With this definition,
$d(L_{1},L_{2})=\unicode[STIX]{x1D706}$
. With this definition,
![]() $Gr^{\unicode[STIX]{x1D706}}$
is the set of points of distance
$Gr^{\unicode[STIX]{x1D706}}$
is the set of points of distance
![]() $\unicode[STIX]{x1D706}$
from
$\unicode[STIX]{x1D706}$
from
![]() $t^{0}$
.
$t^{0}$
.
The following well-known result explains the geometric significance of minuscule weights.
Lemma 3.1. The following are equivalent:
-
(i)
 $Gr^{\unicode[STIX]{x1D706}}$
is projective;
$Gr^{\unicode[STIX]{x1D706}}$
is projective; -
(ii)
 $\overline{Gr^{\unicode[STIX]{x1D706}}}$
is smooth;
$\overline{Gr^{\unicode[STIX]{x1D706}}}$
is smooth; -
(iii)
 $\unicode[STIX]{x1D706}$
is minuscule.
$\unicode[STIX]{x1D706}$
is minuscule.
Given a sequence
 $\text{}\underline{\unicode[STIX]{x1D706}}=(\unicode[STIX]{x1D706}_{1},\ldots ,\unicode[STIX]{x1D706}_{m})$
of minuscule dominant weights, we can consider the variety
$\text{}\underline{\unicode[STIX]{x1D706}}=(\unicode[STIX]{x1D706}_{1},\ldots ,\unicode[STIX]{x1D706}_{m})$
of minuscule dominant weights, we can consider the variety
 $$\begin{eqnarray}Gr^{\text{}\underline{\unicode[STIX]{x1D706}}}:=\{(t^{0}=L_{0},L_{1},\ldots ,L_{m})\in Gr^{m}:d(L_{i-1},L_{i})=\unicode[STIX]{x1D706}_{i}\}\end{eqnarray}$$
$$\begin{eqnarray}Gr^{\text{}\underline{\unicode[STIX]{x1D706}}}:=\{(t^{0}=L_{0},L_{1},\ldots ,L_{m})\in Gr^{m}:d(L_{i-1},L_{i})=\unicode[STIX]{x1D706}_{i}\}\end{eqnarray}$$
which comes with a morphism
 $p_{\text{}\underline{\unicode[STIX]{x1D706}}}:Gr^{\text{}\underline{\unicode[STIX]{x1D706}}}\rightarrow Gr$
given by
$p_{\text{}\underline{\unicode[STIX]{x1D706}}}:Gr^{\text{}\underline{\unicode[STIX]{x1D706}}}\rightarrow Gr$
given by
 $(L_{1},\ldots ,L_{m})\mapsto L_{m}$
. Note that
$(L_{1},\ldots ,L_{m})\mapsto L_{m}$
. Note that
![]() $Gr^{\text{}\underline{\unicode[STIX]{x1D706}}}$
is an iterated bundle of
$Gr^{\text{}\underline{\unicode[STIX]{x1D706}}}$
is an iterated bundle of
![]() $Gr^{\unicode[STIX]{x1D706}_{i}}$
; there is a obvious map
$Gr^{\unicode[STIX]{x1D706}_{i}}$
; there is a obvious map
 $Gr^{\text{}\underline{\unicode[STIX]{x1D706}}}\rightarrow Gr^{(\unicode[STIX]{x1D706}_{1},\ldots ,\unicode[STIX]{x1D706}_{m-1})}$
which is a
$Gr^{\text{}\underline{\unicode[STIX]{x1D706}}}\rightarrow Gr^{(\unicode[STIX]{x1D706}_{1},\ldots ,\unicode[STIX]{x1D706}_{m-1})}$
which is a
![]() $Gr^{\unicode[STIX]{x1D706}_{m}}$
-bundle.
$Gr^{\unicode[STIX]{x1D706}_{m}}$
-bundle.
There is an action of
![]() $G^{\vee }$
on
$G^{\vee }$
on
![]() $Gr$
by left multiplication. Also there is an action of
$Gr$
by left multiplication. Also there is an action of
![]() $\mathbb{C}^{\times }$
on
$\mathbb{C}^{\times }$
on
![]() $Gr$
by ‘loop rotation’; this comes from the action of
$Gr$
by ‘loop rotation’; this comes from the action of
![]() $\mathbb{C}^{\times }$
on
$\mathbb{C}^{\times }$
on
![]() ${\mathcal{O}}$
given by
${\mathcal{O}}$
given by
 $s\cdot p(t)=p(st)$
.
$s\cdot p(t)=p(st)$
.
3.2 Line bundles on the affine Grassmannian
Recall that the connected components of
![]() $Gr$
are labelled by the finite set
$Gr$
are labelled by the finite set
![]() $\unicode[STIX]{x1D6EC}/\mathbb{Z}\unicode[STIX]{x1D6E5}$
, where
$\unicode[STIX]{x1D6EC}/\mathbb{Z}\unicode[STIX]{x1D6E5}$
, where
![]() $\unicode[STIX]{x1D6E5}$
is the set of roots of
$\unicode[STIX]{x1D6E5}$
is the set of roots of
![]() $G$
. Each connected component has Picard group
$G$
. Each connected component has Picard group
![]() $\mathbb{Z}$
and we define a line bundle
$\mathbb{Z}$
and we define a line bundle
![]() ${\mathcal{L}}$
on
${\mathcal{L}}$
on
![]() $Gr$
to be the positive generator of the Picard group on each connected component (see for example [Reference ZhuZhu16, § 2.4]).
$Gr$
to be the positive generator of the Picard group on each connected component (see for example [Reference ZhuZhu16, § 2.4]).
Unfortunately, the line bundle
![]() ${\mathcal{L}}$
is not always
${\mathcal{L}}$
is not always
![]() $G^{\vee }$
-equivariant. It is however
$G^{\vee }$
-equivariant. It is however
![]() $\widetilde{G^{\vee }}$
-equivariant (since each connected component is isomorphic to the quotient of
$\widetilde{G^{\vee }}$
-equivariant (since each connected component is isomorphic to the quotient of
![]() $\widehat{\widetilde{G^{\vee }}}$
(the affine Kac–Moody group) by a hyperspecial parahoric subgroup). In fact
$\widehat{\widetilde{G^{\vee }}}$
(the affine Kac–Moody group) by a hyperspecial parahoric subgroup). In fact
![]() ${\mathcal{L}}$
carries a
${\mathcal{L}}$
carries a
 $\widetilde{G^{\vee }}\times \mathbb{C}^{\times }$
-equivariant structure where the action of
$\widetilde{G^{\vee }}\times \mathbb{C}^{\times }$
-equivariant structure where the action of
![]() $\widetilde{T^{\vee }}$
on the fibre over
$\widetilde{T^{\vee }}$
on the fibre over
![]() $t^{\unicode[STIX]{x1D707}}$
is given by the weight
$t^{\unicode[STIX]{x1D707}}$
is given by the weight
![]() $\unicode[STIX]{x1D704}(\unicode[STIX]{x1D707})$
and the action of
$\unicode[STIX]{x1D704}(\unicode[STIX]{x1D707})$
and the action of
![]() $\mathbb{C}^{\times }$
on the same fibre over
$\mathbb{C}^{\times }$
on the same fibre over
![]() $t^{\unicode[STIX]{x1D707}}$
is given by the pairing
$t^{\unicode[STIX]{x1D707}}$
is given by the pairing
![]() $(\unicode[STIX]{x1D707},\unicode[STIX]{x1D707})$
.
$(\unicode[STIX]{x1D707},\unicode[STIX]{x1D707})$
.
3.3 The equivariant Satake category
Consider the Satake category
![]() $P(Gr)$
of perverse sheaves on
$P(Gr)$
of perverse sheaves on
![]() $Gr$
constructible with respect to the stratification by
$Gr$
constructible with respect to the stratification by
![]() $G^{\vee }({\mathcal{O}})$
orbits.
$G^{\vee }({\mathcal{O}})$
orbits.
We will need an equivariant version of this category. Note that we have an action of
![]() $G^{\vee }$
on
$G^{\vee }$
on
![]() $Gr$
which preserves the
$Gr$
which preserves the
![]() $G^{\vee }({\mathcal{O}})$
-orbits. Using the
$G^{\vee }({\mathcal{O}})$
-orbits. Using the
![]() $W$
-invariant bilinear form, we may identify
$W$
-invariant bilinear form, we may identify
 $H_{G^{\vee }}(\operatorname{pt})={\mathcal{O}}(\mathfrak{t}^{\vee })^{W}\cong {\mathcal{O}}(\mathfrak{t})^{W}$
.
$H_{G^{\vee }}(\operatorname{pt})={\mathcal{O}}(\mathfrak{t}^{\vee })^{W}\cong {\mathcal{O}}(\mathfrak{t})^{W}$
.
Let
 $D_{G^{\vee }}(Gr)$
denote the equivariant derived category of
$D_{G^{\vee }}(Gr)$
denote the equivariant derived category of
![]() $Gr$
for this action. We consider
$Gr$
for this action. We consider
 $D_{G^{\vee }}(Gr)$
with morphisms given by total
$D_{G^{\vee }}(Gr)$
with morphisms given by total
![]() $\text{Ext}$
. Thus the category
$\text{Ext}$
. Thus the category
 $D_{G^{\vee }}(Gr)$
is enriched over graded
$D_{G^{\vee }}(Gr)$
is enriched over graded
![]() ${\mathcal{O}}(\mathfrak{t})^{W}$
-modules.
${\mathcal{O}}(\mathfrak{t})^{W}$
-modules.
We have a global section functor
 $$\begin{eqnarray}D_{G^{\vee }}(Gr)\rightarrow H_{G^{\vee }}^{\ast }(Gr)\operatorname{ - mod}\!.\end{eqnarray}$$
$$\begin{eqnarray}D_{G^{\vee }}(Gr)\rightarrow H_{G^{\vee }}^{\ast }(Gr)\operatorname{ - mod}\!.\end{eqnarray}$$
By a theorem of Ginzburg (see [Reference Bezrukavnikov and FinkelbergBF08, Lemma 13]), this functor is fully faithful.
Since
![]() $Gr^{\text{}\underline{\unicode[STIX]{x1D706}}}$
is smooth and
$Gr^{\text{}\underline{\unicode[STIX]{x1D706}}}$
is smooth and
![]() $p_{\text{}\underline{\unicode[STIX]{x1D706}}}$
is semismall, we can consider the perverse sheaf
$p_{\text{}\underline{\unicode[STIX]{x1D706}}}$
is semismall, we can consider the perverse sheaf
 ${p_{\text{}\underline{\unicode[STIX]{x1D706}}}}_{\ast }\mathbb{C}_{Gr^{\text{}\underline{\unicode[STIX]{x1D706}}}}[2\unicode[STIX]{x1D70C}^{\vee }(\sum _{k}\unicode[STIX]{x1D706}_{k})]\in P(Gr)$
. It is the tensor product of the objects
${p_{\text{}\underline{\unicode[STIX]{x1D706}}}}_{\ast }\mathbb{C}_{Gr^{\text{}\underline{\unicode[STIX]{x1D706}}}}[2\unicode[STIX]{x1D70C}^{\vee }(\sum _{k}\unicode[STIX]{x1D706}_{k})]\in P(Gr)$
. It is the tensor product of the objects
 $\mathbb{C}_{Gr^{\unicode[STIX]{x1D706}_{k}}}[2\unicode[STIX]{x1D70C}^{\vee }(\unicode[STIX]{x1D706}_{k})]$
with respect to the usual monoidal structure on
$\mathbb{C}_{Gr^{\unicode[STIX]{x1D706}_{k}}}[2\unicode[STIX]{x1D70C}^{\vee }(\unicode[STIX]{x1D706}_{k})]$
with respect to the usual monoidal structure on
![]() $P(Gr)$
. We let
$P(Gr)$
. We let
 $D_{G^{\vee }}^{\min }(Gr)$
denote the full subcategory of
$D_{G^{\vee }}^{\min }(Gr)$
denote the full subcategory of
 $D_{G^{\vee }}(Gr)$
consisting of these objects.
$D_{G^{\vee }}(Gr)$
consisting of these objects.
3.4 Homology convolution categories
Recall convolution in homology following Chriss and Ginzburg [Reference Chriss and GinzburgCG97]. Let
![]() $I$
be an index set and let
$I$
be an index set and let
![]() $\{Y_{i}\}_{i\in I}$
be a collection of smooth varieties along with proper maps
$\{Y_{i}\}_{i\in I}$
be a collection of smooth varieties along with proper maps
 $p_{i}:Y_{i}\rightarrow Y$
to some fixed variety
$p_{i}:Y_{i}\rightarrow Y$
to some fixed variety
![]() $Y$
. Form the fibre products
$Y$
. Form the fibre products
 $Z_{ij}=Y_{i}\times _{Y}Y_{j}$
.
$Z_{ij}=Y_{i}\times _{Y}Y_{j}$
.
We can use this data to define a category
 $h\operatorname{Conv}(Y)$
(this category depends on more than just
$h\operatorname{Conv}(Y)$
(this category depends on more than just
![]() $Y$
, but we suppress the rest of the data in the notation). The objects in
$Y$
, but we suppress the rest of the data in the notation). The objects in
 $h\operatorname{Conv}(Y)$
consist of the elements of the set
$h\operatorname{Conv}(Y)$
consist of the elements of the set
![]() $I$
. The morphisms are defined as
$I$
. The morphisms are defined as
 $$\begin{eqnarray}\operatorname{Hom}_{h\operatorname{Conv}(Y)}(i,j)=H_{\ast }(Z_{ij})\end{eqnarray}$$
$$\begin{eqnarray}\operatorname{Hom}_{h\operatorname{Conv}(Y)}(i,j)=H_{\ast }(Z_{ij})\end{eqnarray}$$
where
 $H_{\ast }(Z_{ij})$
denotes the total Borel–Moore homology of
$H_{\ast }(Z_{ij})$
denotes the total Borel–Moore homology of
![]() $Z_{ij}$
(with coefficients in
$Z_{ij}$
(with coefficients in
![]() $\mathbb{C}$
). The composition operation in
$\mathbb{C}$
). The composition operation in
 $h\operatorname{Conv}(Y)$
is defined by the convolution product
$h\operatorname{Conv}(Y)$
is defined by the convolution product
 $$\begin{eqnarray}H_{\ast }(Z_{ij})\otimes H_{\ast }(Z_{jk})\rightarrow H_{\ast }(Z_{ik})\end{eqnarray}$$
$$\begin{eqnarray}H_{\ast }(Z_{ij})\otimes H_{\ast }(Z_{jk})\rightarrow H_{\ast }(Z_{ik})\end{eqnarray}$$
which is given by the formula
 $$\begin{eqnarray}c_{1}\ast c_{2}=(\unicode[STIX]{x1D70B}_{13})_{\ast }(\unicode[STIX]{x1D70B}_{12}^{\ast }(c_{1})\cap \unicode[STIX]{x1D70B}_{23}^{\ast }(c_{2})),\end{eqnarray}$$
$$\begin{eqnarray}c_{1}\ast c_{2}=(\unicode[STIX]{x1D70B}_{13})_{\ast }(\unicode[STIX]{x1D70B}_{12}^{\ast }(c_{1})\cap \unicode[STIX]{x1D70B}_{23}^{\ast }(c_{2})),\end{eqnarray}$$
where ‘
![]() $\cap$
’ denotes the intersection product (with support), relative to the ambient manifold
$\cap$
’ denotes the intersection product (with support), relative to the ambient manifold
 $Y_{i}\times Y_{j}\times Y_{k}$
and
$Y_{i}\times Y_{j}\times Y_{k}$
and
 $\unicode[STIX]{x1D70B}_{12}:Y_{i}\times Y_{j}\times Y_{k}\rightarrow Y_{i}\times Y_{j}$
, etc. For more details about this construction see [Reference Chriss and GinzburgCG97, § 2.7].
$\unicode[STIX]{x1D70B}_{12}:Y_{i}\times Y_{j}\times Y_{k}\rightarrow Y_{i}\times Y_{j}$
, etc. For more details about this construction see [Reference Chriss and GinzburgCG97, § 2.7].
The following result of Chriss and Ginzburg shows the importance of these categories. Consider the derived category of constructible sheaves on
![]() $Y$
,
$Y$
,
![]() $D_{c}(Y)$
, which we regard as a category enriched over graded vector spaces by taking total
$D_{c}(Y)$
, which we regard as a category enriched over graded vector spaces by taking total
![]() $Ext$
.
$Ext$
.
Theorem 3.2 [Reference Chriss and GinzburgCG97, Theorem 8.6.7].
The category
 $h\operatorname{Conv}(Y)$
is equivalent to the full subcategory of
$h\operatorname{Conv}(Y)$
is equivalent to the full subcategory of
![]() $D_{c}(Y)$
whose objects are
$D_{c}(Y)$
whose objects are
![]() ${p_{i}}_{\ast }\mathbb{C}_{Y_{i}}$
.
${p_{i}}_{\ast }\mathbb{C}_{Y_{i}}$
.
If the varieties
![]() $Y_{i},Y$
all carry compatible actions of some group
$Y_{i},Y$
all carry compatible actions of some group
![]() $H$
, we may consider the corresponding equivariant category
$H$
, we may consider the corresponding equivariant category
 $h\operatorname{Conv}^{H}(Y)$
where the morphisms are defined by equivariant homology.
$h\operatorname{Conv}^{H}(Y)$
where the morphisms are defined by equivariant homology.
We now apply this framework to obtain the category
 $h\operatorname{Conv}(Gr)$
where the base variety is
$h\operatorname{Conv}(Gr)$
where the base variety is
![]() $Gr$
and the mapping varieties are given by
$Gr$
and the mapping varieties are given by
 $p_{\text{}\underline{\unicode[STIX]{x1D706}}}:Gr^{\text{}\underline{\unicode[STIX]{x1D706}}}\rightarrow Gr$
, where
$p_{\text{}\underline{\unicode[STIX]{x1D706}}}:Gr^{\text{}\underline{\unicode[STIX]{x1D706}}}\rightarrow Gr$
, where
![]() $\text{}\underline{\unicode[STIX]{x1D706}}$
ranges over all sequence of minuscule dominant weights. The category
$\text{}\underline{\unicode[STIX]{x1D706}}$
ranges over all sequence of minuscule dominant weights. The category
 $h\operatorname{Conv}(Gr)$
was first considered by the second author with Fontaine and Kuperberg in [Reference Fontaine, Kamnitzer and KuperbergFKK13]. The fibre products
$h\operatorname{Conv}(Gr)$
was first considered by the second author with Fontaine and Kuperberg in [Reference Fontaine, Kamnitzer and KuperbergFKK13]. The fibre products
![]() $Z(\text{}\underline{\unicode[STIX]{x1D706}},\text{}\underline{\unicode[STIX]{x1D707}})$
appearing in
$Z(\text{}\underline{\unicode[STIX]{x1D706}},\text{}\underline{\unicode[STIX]{x1D707}})$
appearing in
 $h\operatorname{Conv}(Gr)$
are the ‘Steinberg-like’ varieties
$h\operatorname{Conv}(Gr)$
are the ‘Steinberg-like’ varieties
 $$\begin{eqnarray}Z(\text{}\underline{\unicode[STIX]{x1D706}},\text{}\underline{\unicode[STIX]{x1D707}})=\{(L_{1},\ldots ,L_{m}),(L_{1}^{\prime },\ldots ,L_{m^{\prime }}^{\prime })\in Gr^{\text{}\underline{\unicode[STIX]{x1D706}}}\times Gr^{\text{}\underline{\unicode[STIX]{x1D707}}}:L_{m}=L_{m^{\prime }}^{\prime }\}.\end{eqnarray}$$
$$\begin{eqnarray}Z(\text{}\underline{\unicode[STIX]{x1D706}},\text{}\underline{\unicode[STIX]{x1D707}})=\{(L_{1},\ldots ,L_{m}),(L_{1}^{\prime },\ldots ,L_{m^{\prime }}^{\prime })\in Gr^{\text{}\underline{\unicode[STIX]{x1D706}}}\times Gr^{\text{}\underline{\unicode[STIX]{x1D707}}}:L_{m}=L_{m^{\prime }}^{\prime }\}.\end{eqnarray}$$
Using the action of
![]() $G^{\vee }$
we may also define
$G^{\vee }$
we may also define
 $h\operatorname{Conv}^{G^{\vee }}(Gr)$
. Applying Theorem 3.2 we deduce the following.
$h\operatorname{Conv}^{G^{\vee }}(Gr)$
. Applying Theorem 3.2 we deduce the following.
Theorem 3.3. We have an equivalence
 $$\begin{eqnarray}D_{G^{\vee }}^{\min }(Gr)\cong h\operatorname{Conv}^{G^{\vee }}(Gr).\end{eqnarray}$$
$$\begin{eqnarray}D_{G^{\vee }}^{\min }(Gr)\cong h\operatorname{Conv}^{G^{\vee }}(Gr).\end{eqnarray}$$
In other words, we can model
 $D_{G^{\vee }}^{\min }(Gr)$
using this homology convolution category. This motivates us to introduce a K-theory convolution category.
$D_{G^{\vee }}^{\min }(Gr)$
using this homology convolution category. This motivates us to introduce a K-theory convolution category.
3.5 The category
 $K\operatorname{Conv}(Gr)$
$K\operatorname{Conv}(Gr)$
The convolution formalism in homology from § 3.4 can be repeated in K-theory. More precisely, given a collection
 $Y_{i}\rightarrow Y$
as above, the objects in
$Y_{i}\rightarrow Y$
as above, the objects in
 $K\operatorname{Conv}(Y)$
are still indexed by the set
$K\operatorname{Conv}(Y)$
are still indexed by the set
![]() $I$
but the morphisms are now defined as
$I$
but the morphisms are now defined as
 $$\begin{eqnarray}\operatorname{Hom}_{K\operatorname{Conv}(Y)}(i,j)=K(Z_{ij})\end{eqnarray}$$
$$\begin{eqnarray}\operatorname{Hom}_{K\operatorname{Conv}(Y)}(i,j)=K(Z_{ij})\end{eqnarray}$$
where
![]() $K(Z_{ij})$
denotes the complexified Grothendieck group of coherent sheaves on
$K(Z_{ij})$
denotes the complexified Grothendieck group of coherent sheaves on
![]() $Z_{ij}$
. The composition operation in
$Z_{ij}$
. The composition operation in
 $K\operatorname{Conv}(Y)$
is defined by a similar formula, namely
$K\operatorname{Conv}(Y)$
is defined by a similar formula, namely
 $$\begin{eqnarray}\displaystyle K(Z_{ij})\otimes K(Z_{jk}) & \rightarrow & \displaystyle K(Z_{ik})\nonumber\\ \displaystyle \text{}[{\mathcal{F}}_{1}]\otimes [{\mathcal{F}}_{2}] & \mapsto & \displaystyle [\unicode[STIX]{x1D70B}_{13\ast }(\unicode[STIX]{x1D70B}_{12}^{\ast }({\mathcal{F}}_{1})\otimes \unicode[STIX]{x1D70B}_{23}^{\ast }({\mathcal{F}}_{2}))].\nonumber\end{eqnarray}$$
$$\begin{eqnarray}\displaystyle K(Z_{ij})\otimes K(Z_{jk}) & \rightarrow & \displaystyle K(Z_{ik})\nonumber\\ \displaystyle \text{}[{\mathcal{F}}_{1}]\otimes [{\mathcal{F}}_{2}] & \mapsto & \displaystyle [\unicode[STIX]{x1D70B}_{13\ast }(\unicode[STIX]{x1D70B}_{12}^{\ast }({\mathcal{F}}_{1})\otimes \unicode[STIX]{x1D70B}_{23}^{\ast }({\mathcal{F}}_{2}))].\nonumber\end{eqnarray}$$
For more details about this construction see [Reference Chriss and GinzburgCG97, § 5.2]. As before, given a compatible action of a group
![]() $H$
we can work with equivariant K-theory
$H$
we can work with equivariant K-theory
![]() $K^{H}(\cdot )$
to define the category
$K^{H}(\cdot )$
to define the category
 $K\operatorname{Conv}^{H}(Y)$
.
$K\operatorname{Conv}^{H}(Y)$
.
Applying this construction to the collection
 $Gr^{\text{}\underline{\unicode[STIX]{x1D706}}}\rightarrow Gr$
, we obtain the categories
$Gr^{\text{}\underline{\unicode[STIX]{x1D706}}}\rightarrow Gr$
, we obtain the categories
 $K\operatorname{Conv}^{\widetilde{G^{\vee }}}(Gr)$
and
$K\operatorname{Conv}^{\widetilde{G^{\vee }}}(Gr)$
and
 $K\operatorname{Conv}^{\widetilde{G^{\vee }}\times \mathbb{C}^{\times }}(Gr)$
where
$K\operatorname{Conv}^{\widetilde{G^{\vee }}\times \mathbb{C}^{\times }}(Gr)$
where
![]() $\widetilde{G^{\vee }}$
acts as before and
$\widetilde{G^{\vee }}$
acts as before and
![]() $\mathbb{C}^{\times }$
acts by loop rotation. (Here we are using
$\mathbb{C}^{\times }$
acts by loop rotation. (Here we are using
![]() $\widetilde{G^{\vee }}$
rather than
$\widetilde{G^{\vee }}$
rather than
![]() $G^{\vee }$
, since our line bundles are only
$G^{\vee }$
, since our line bundles are only
![]() $\widetilde{G^{\vee }}$
-equivariant.) In these categories, the objects are sequences
$\widetilde{G^{\vee }}$
-equivariant.) In these categories, the objects are sequences
 $(\unicode[STIX]{x1D706}_{1},\ldots ,\unicode[STIX]{x1D706}_{m})$
(we will say that this object has length
$(\unicode[STIX]{x1D706}_{1},\ldots ,\unicode[STIX]{x1D706}_{m})$
(we will say that this object has length
![]() $m$
).
$m$
).
On the variety
![]() $Gr^{\text{}\underline{\unicode[STIX]{x1D706}}}$
we have
$Gr^{\text{}\underline{\unicode[STIX]{x1D706}}}$
we have
![]() $m$
line bundles
$m$
line bundles
 ${\mathcal{L}}_{1},\ldots ,{\mathcal{L}}_{m}$
, where
${\mathcal{L}}_{1},\ldots ,{\mathcal{L}}_{m}$
, where
![]() ${\mathcal{L}}_{k}$
is defined as
${\mathcal{L}}_{k}$
is defined as
 $p_{k}^{\ast }{\mathcal{L}}\otimes p_{k-1}^{\ast }{\mathcal{L}}^{\vee }$
, where
$p_{k}^{\ast }{\mathcal{L}}\otimes p_{k-1}^{\ast }{\mathcal{L}}^{\vee }$
, where
 $p_{k}:Gr^{\text{}\underline{\unicode[STIX]{x1D706}}}\rightarrow Gr$
is given by
$p_{k}:Gr^{\text{}\underline{\unicode[STIX]{x1D706}}}\rightarrow Gr$
is given by
 $p_{k}(L_{1},\ldots ,L_{m})=L_{k}$
. For
$p_{k}(L_{1},\ldots ,L_{m})=L_{k}$
. For
 $i=1,\ldots ,m$
we define
$i=1,\ldots ,m$
we define
 $$\begin{eqnarray}X_{i}\in \operatorname{End}_{K\operatorname{Conv}^{\widetilde{G^{\vee }}\times \mathbb{C}^{\times }}}(\text{}\underline{\unicode[STIX]{x1D706}})=K^{\widetilde{G^{\vee }}\times \mathbb{C}^{\times }}(Z(\text{}\underline{\unicode[STIX]{x1D706}},\text{}\underline{\unicode[STIX]{x1D706}}))\end{eqnarray}$$
$$\begin{eqnarray}X_{i}\in \operatorname{End}_{K\operatorname{Conv}^{\widetilde{G^{\vee }}\times \mathbb{C}^{\times }}}(\text{}\underline{\unicode[STIX]{x1D706}})=K^{\widetilde{G^{\vee }}\times \mathbb{C}^{\times }}(Z(\text{}\underline{\unicode[STIX]{x1D706}},\text{}\underline{\unicode[STIX]{x1D706}}))\end{eqnarray}$$
as
 $X_{i}:=\unicode[STIX]{x1D6E5}_{\ast }[{\mathcal{L}}_{i}]$
where
$X_{i}:=\unicode[STIX]{x1D6E5}_{\ast }[{\mathcal{L}}_{i}]$
where
 $\unicode[STIX]{x1D6E5}:Gr^{\text{}\underline{\unicode[STIX]{x1D706}}}\rightarrow Z(\text{}\underline{\unicode[STIX]{x1D706}},\text{}\underline{\unicode[STIX]{x1D706}})$
is the diagonal inclusion. These
$\unicode[STIX]{x1D6E5}:Gr^{\text{}\underline{\unicode[STIX]{x1D706}}}\rightarrow Z(\text{}\underline{\unicode[STIX]{x1D706}},\text{}\underline{\unicode[STIX]{x1D706}})$
is the diagonal inclusion. These
![]() $X_{i}$
are invertible and so they define a map
$X_{i}$
are invertible and so they define a map
 $\mathbb{Z}^{m}\rightarrow \operatorname{End}_{K\operatorname{Conv}^{\widetilde{G^{\vee }}\times \mathbb{C}^{\times }}}(\text{}\underline{\unicode[STIX]{x1D706}})$
. Thus, we see that
$\mathbb{Z}^{m}\rightarrow \operatorname{End}_{K\operatorname{Conv}^{\widetilde{G^{\vee }}\times \mathbb{C}^{\times }}}(\text{}\underline{\unicode[STIX]{x1D706}})$
. Thus, we see that
![]() $\mathbb{Z}^{m}$
acts on objects of length
$\mathbb{Z}^{m}$
acts on objects of length
![]() $m$
in
$m$
in
 $K\operatorname{Conv}^{\widetilde{G^{\vee }}}(Gr)$
and
$K\operatorname{Conv}^{\widetilde{G^{\vee }}}(Gr)$
and
 $K\operatorname{Conv}^{\widetilde{G^{\vee }}\times \mathbb{C}^{\times }}(Gr)$
.
$K\operatorname{Conv}^{\widetilde{G^{\vee }}\times \mathbb{C}^{\times }}(Gr)$
.
3.6 Main conjecture
Motivated by Theorem 3.3 and the discussion in the introduction, we now formulate the following main conjecture.
Conjecture 3.4. We have equivalences
 $$\begin{eqnarray}\displaystyle {\mathcal{O}}^{\min }({\textstyle \frac{G}{G}})\operatorname{ - mod}\otimes _{E}E^{\vee } & \cong & \displaystyle K\operatorname{Conv}^{\widetilde{G^{\vee }}}(Gr),\end{eqnarray}$$
$$\begin{eqnarray}\displaystyle {\mathcal{O}}^{\min }({\textstyle \frac{G}{G}})\operatorname{ - mod}\otimes _{E}E^{\vee } & \cong & \displaystyle K\operatorname{Conv}^{\widetilde{G^{\vee }}}(Gr),\end{eqnarray}$$
 $$\begin{eqnarray}\displaystyle {\mathcal{O}}_{q}^{\min }({\textstyle \frac{G}{G}})\operatorname{ - mod}\otimes _{E}E^{\vee } & \cong & \displaystyle K\operatorname{Conv}^{\widetilde{G^{\vee }}\times \mathbb{C}^{\times }}(Gr)\otimes _{\mathbb{C}[q^{\pm }]}\mathbb{C}(q)\end{eqnarray}$$
$$\begin{eqnarray}\displaystyle {\mathcal{O}}_{q}^{\min }({\textstyle \frac{G}{G}})\operatorname{ - mod}\otimes _{E}E^{\vee } & \cong & \displaystyle K\operatorname{Conv}^{\widetilde{G^{\vee }}\times \mathbb{C}^{\times }}(Gr)\otimes _{\mathbb{C}[q^{\pm }]}\mathbb{C}(q)\end{eqnarray}$$
of
 $E^{\vee }\operatorname{- mod}$
and
$E^{\vee }\operatorname{- mod}$
and
 $E^{\vee }(q)\operatorname{ - mod}$
enriched categories respectively.
$E^{\vee }(q)\operatorname{ - mod}$
enriched categories respectively.
Moreover, these equivalences should be compatible with the actions of
![]() $\mathbb{Z}^{m}$
on objects of length
$\mathbb{Z}^{m}$
on objects of length
![]() $m$
on each side of the equivalence.
$m$
on each side of the equivalence.
By an equivalence of
 $E^{\vee }\operatorname{- mod}$
enriched categories, we mean that the map on Hom spaces should be an
$E^{\vee }\operatorname{- mod}$
enriched categories, we mean that the map on Hom spaces should be an
![]() $E^{\vee }$
-module morphism map. On the left-hand side the
$E^{\vee }$
-module morphism map. On the left-hand side the
![]() $E^{\vee }$
-module structure comes from tensoring (and the
$E^{\vee }$
-module structure comes from tensoring (and the
![]() $E$
-module structure was explained in § 2.6), while on the right-hand side it comes from
$E$
-module structure was explained in § 2.6), while on the right-hand side it comes from
 $K^{\widetilde{G^{\vee }}}(pt)=E^{\vee }$
.
$K^{\widetilde{G^{\vee }}}(pt)=E^{\vee }$
.
The compatibility between the actions of
![]() $\mathbb{Z}^{m}$
should be viewed as a partial substitute for the commutative diagram appearing in [Reference Bezrukavnikov and FinkelbergBF08] which involves the Kostant slice functor. The action of
$\mathbb{Z}^{m}$
should be viewed as a partial substitute for the commutative diagram appearing in [Reference Bezrukavnikov and FinkelbergBF08] which involves the Kostant slice functor. The action of
![]() $\mathbb{Z}^{m}$
on the left-hand side is defined in § 2.5 and the action of
$\mathbb{Z}^{m}$
on the left-hand side is defined in § 2.5 and the action of
![]() $\mathbb{Z}^{m}$
on the right-hand side is defined in § 3.5.
$\mathbb{Z}^{m}$
on the right-hand side is defined in § 3.5.
Remark 3.5. The base change from
![]() $E$
to
$E$
to
![]() $E^{\vee }$
on the left-hand side seems to be necessary to get the endomorphisms of the trivial objects to match. Note that in the simply laced case, we have an isomorphism
$E^{\vee }$
on the left-hand side seems to be necessary to get the endomorphisms of the trivial objects to match. Note that in the simply laced case, we have an isomorphism
 $E\cong E^{\vee }$
, so the base change is unnecessary.
$E\cong E^{\vee }$
, so the base change is unnecessary.
4 Spiders and annular spiders
4.1 Some
 $\operatorname{SL}_{n}$
notation
$\operatorname{SL}_{n}$
notation
The remainder of the paper will be devoted to the proof of Conjecture 3.4 for the case
 $G=\operatorname{SL}_{n}$
.
$G=\operatorname{SL}_{n}$
.
The weight lattice of
![]() $\operatorname{SL}_{n}$
is
$\operatorname{SL}_{n}$
is
 $\unicode[STIX]{x1D6EC}=\mathbb{Z}^{n}/\mathbb{Z}(1,\ldots ,1)$
and
$\unicode[STIX]{x1D6EC}=\mathbb{Z}^{n}/\mathbb{Z}(1,\ldots ,1)$
and
![]() $\unicode[STIX]{x1D6EC}_{+}$
is the subset consisting of those
$\unicode[STIX]{x1D6EC}_{+}$
is the subset consisting of those
 $\unicode[STIX]{x1D706}=(a_{1},\ldots ,a_{n})$
such that
$\unicode[STIX]{x1D706}=(a_{1},\ldots ,a_{n})$
such that
 $a_{1}\geqslant \ldots \geqslant a_{n}$
. The minuscule dominant weights are
$a_{1}\geqslant \ldots \geqslant a_{n}$
. The minuscule dominant weights are
 $\unicode[STIX]{x1D714}_{k}=(1,\ldots ,1,0,\ldots ,0)$
, for
$\unicode[STIX]{x1D714}_{k}=(1,\ldots ,1,0,\ldots ,0)$
, for
 $k=1,\ldots ,n-1$
. The corresponding representation of
$k=1,\ldots ,n-1$
. The corresponding representation of
![]() $U_{q}\mathfrak{s}\mathfrak{l}_{n}$
is
$U_{q}\mathfrak{s}\mathfrak{l}_{n}$
is
 $V(\unicode[STIX]{x1D714}_{k})=\bigwedge _{q}^{k}\mathbb{C}_{q}^{n}$
.
$V(\unicode[STIX]{x1D714}_{k})=\bigwedge _{q}^{k}\mathbb{C}_{q}^{n}$
.
A sequence of minuscule dominant weights
 $\text{}\underline{\unicode[STIX]{x1D706}}=(\unicode[STIX]{x1D706}_{1},\ldots ,\unicode[STIX]{x1D706}_{m})$
will be encoded by a sequence
$\text{}\underline{\unicode[STIX]{x1D706}}=(\unicode[STIX]{x1D706}_{1},\ldots ,\unicode[STIX]{x1D706}_{m})$
will be encoded by a sequence
 $\text{}\underline{k}=(k_{1},\ldots ,k_{m})$
, where
$\text{}\underline{k}=(k_{1},\ldots ,k_{m})$
, where
 $\unicode[STIX]{x1D706}_{j}=\unicode[STIX]{x1D714}_{k_{j}}$
. Note that
$\unicode[STIX]{x1D706}_{j}=\unicode[STIX]{x1D714}_{k_{j}}$
. Note that
 $G^{\vee }=PGL_{n}$
and
$G^{\vee }=PGL_{n}$
and
 $\widetilde{G^{\vee }}=\operatorname{SL}_{n}$
. We write
$\widetilde{G^{\vee }}=\operatorname{SL}_{n}$
. We write
 $$\begin{eqnarray}E=(\mathbb{C}[t_{1}^{\pm },\ldots ,t_{n}^{\pm }]/(t_{1}\ldots t_{n}-1))^{S_{n}}=\mathbb{C}[e_{1},\ldots ,e_{n-1}],\end{eqnarray}$$
$$\begin{eqnarray}E=(\mathbb{C}[t_{1}^{\pm },\ldots ,t_{n}^{\pm }]/(t_{1}\ldots t_{n}-1))^{S_{n}}=\mathbb{C}[e_{1},\ldots ,e_{n-1}],\end{eqnarray}$$
where
![]() $e_{k}$
is the usual
$e_{k}$
is the usual
![]() $k$
th elementary symmetric function.
$k$
th elementary symmetric function.
4.2 The spider
Our main tool for proving the conjecture in the
![]() $\operatorname{SL}_{n}$
case will be a combinatorially defined category called the annular spider.
$\operatorname{SL}_{n}$
case will be a combinatorially defined category called the annular spider.
We begin by recalling the definition of the spider category
 ${\mathcal{S}}p_{n}[q^{\pm }]$
from [Reference Cautis, Kamnitzer and MorrisonCKM14].
${\mathcal{S}}p_{n}[q^{\pm }]$
from [Reference Cautis, Kamnitzer and MorrisonCKM14].
 ${\mathcal{S}}p_{n}[q^{\pm }]$
has as objects sequences
${\mathcal{S}}p_{n}[q^{\pm }]$
has as objects sequences
![]() $\text{}\underline{k}$
in
$\text{}\underline{k}$
in
 $\{1^{\pm },\ldots ,(n-1)^{\pm }\}$
, and as morphisms
$\{1^{\pm },\ldots ,(n-1)^{\pm }\}$
, and as morphisms
![]() $\mathbb{C}[q^{\pm }]$
-linear combinations of oriented planar graphs by the following four types of vertices:
$\mathbb{C}[q^{\pm }]$
-linear combinations of oriented planar graphs by the following four types of vertices:

with all labels drawn from the set
 $\{1,\ldots ,n-1\}$
. The third and fourth graphs depict bivalent vertices, called ‘tags’, which are not rotationally symmetric, meaning that the tag provides a distinguished side. The bottom boundary of any planar graph in
$\{1,\ldots ,n-1\}$
. The third and fourth graphs depict bivalent vertices, called ‘tags’, which are not rotationally symmetric, meaning that the tag provides a distinguished side. The bottom boundary of any planar graph in
 $\operatorname{Hom}(\text{}\underline{k},\text{}\underline{l})$
is
$\operatorname{Hom}(\text{}\underline{k},\text{}\underline{l})$
is
![]() $\text{}\underline{k}$
with the strand oriented up for each positive entry, and the strand oriented down for each negative entry. Similarly, the top boundary is determined by
$\text{}\underline{k}$
with the strand oriented up for each positive entry, and the strand oriented down for each negative entry. Similarly, the top boundary is determined by
![]() $\text{}\underline{l}$
in the same way.
$\text{}\underline{l}$
in the same way.
On these diagrams, we impose the following relations, together with the mirror reflections and the arrow reversals of these.








Remark 4.1. In the relations above we allow strands to be labelled by
![]() $0$
and
$0$
and
![]() $n$
. This means that
$n$
. This means that
![]() $0$
-strands should be deleted and
$0$
-strands should be deleted and
![]() $n$
-strands replaced by tags. On the other hand, any diagram containing a strand whose label is less than
$n$
-strands replaced by tags. On the other hand, any diagram containing a strand whose label is less than
![]() $0$
or greater than
$0$
or greater than
![]() $n$
should be interpreted as the 0 morphism.
$n$
should be interpreted as the 0 morphism.
The category
 ${\mathcal{S}}p_{n}[q^{\pm }]$
is a monoidal category with tensor product given on objects by concatenation of sequences and on morphisms by concatenation in the vertical direction. It also has a natural pivotal structure by the usual graphical calculus. We will denote by
${\mathcal{S}}p_{n}[q^{\pm }]$
is a monoidal category with tensor product given on objects by concatenation of sequences and on morphisms by concatenation in the vertical direction. It also has a natural pivotal structure by the usual graphical calculus. We will denote by
![]() ${\mathcal{S}}p_{n}(q)$
the same category but over
${\mathcal{S}}p_{n}(q)$
the same category but over
![]() $\mathbb{C}(q)$
rather than
$\mathbb{C}(q)$
rather than
![]() $\mathbb{C}[q^{\pm }]$
. We also denote by
$\mathbb{C}[q^{\pm }]$
. We also denote by
![]() ${\mathcal{S}}p_{n}$
the category specialized to
${\mathcal{S}}p_{n}$
the category specialized to
![]() $q=1$
.
$q=1$
.
It will be useful for us to add crossings to the spider. As in [Reference Cautis, Kamnitzer and MorrisonCKM14], we define a crossing of a strand labelled
![]() $k$
with a strand labelled
$k$
with a strand labelled
![]() $l$
to be a sum of webs.
$l$
to be a sum of webs.

This defines a functor
 ${\mathcal{B}}_{m}(\{1,\ldots ,n\})\rightarrow {\mathcal{S}}p_{n}$
which we can regard as giving a braiding on the category
${\mathcal{B}}_{m}(\{1,\ldots ,n\})\rightarrow {\mathcal{S}}p_{n}$
which we can regard as giving a braiding on the category
![]() ${\mathcal{S}}p_{n}$
.
${\mathcal{S}}p_{n}$
.

Figure 2. An example of an annular web with source
 $(3,2,5,-4)$
and target
$(3,2,5,-4)$
and target
 $(1,2,3,-4,3,1)$
.
$(1,2,3,-4,3,1)$
.
4.3 The annular spider
We now define the annular spider
 ${\mathcal{A}}{\mathcal{S}}p_{n}[q^{\pm }]$
. The objects are the same as in
${\mathcal{A}}{\mathcal{S}}p_{n}[q^{\pm }]$
. The objects are the same as in
 ${\mathcal{S}}p_{n}[q^{\pm }]$
. For the morphisms, we consider webs with the same kinds of vertices, except that the webs are now embedded in an annulus
${\mathcal{S}}p_{n}[q^{\pm }]$
. For the morphisms, we consider webs with the same kinds of vertices, except that the webs are now embedded in an annulus
 $A=S^{1}\times [0,1]$
. We consider the same local generating relations as in
$A=S^{1}\times [0,1]$
. We consider the same local generating relations as in
 ${\mathcal{S}}p_{n}[q^{\pm }]$
. The inner boundary of the annulus is regarded as the source of the morphism and the outer boundary is the target. Let
${\mathcal{S}}p_{n}[q^{\pm }]$
. The inner boundary of the annulus is regarded as the source of the morphism and the outer boundary is the target. Let
![]() $\ast \in S^{1}$
denote the bottom of the circle. We do not allow strands to start or end at
$\ast \in S^{1}$
denote the bottom of the circle. We do not allow strands to start or end at
![]() $\ast$
. Given a web
$\ast$
. Given a web
![]() $w$
, its source (respectively target) is found by reading the inner (respectively outer) circle clockwise starting at the
$w$
, its source (respectively target) is found by reading the inner (respectively outer) circle clockwise starting at the
![]() $\ast$
(see Figure 2 for an example).
$\ast$
(see Figure 2 for an example).
As before, we denote by
 ${\mathcal{A}}{\mathcal{S}}p_{n}(q)$
the same category but with the space of morphisms defined over
${\mathcal{A}}{\mathcal{S}}p_{n}(q)$
the same category but with the space of morphisms defined over
![]() $\mathbb{C}(q)$
rather than
$\mathbb{C}(q)$
rather than
![]() $\mathbb{C}[q^{\pm }]$
. We can also consider the
$\mathbb{C}[q^{\pm }]$
. We can also consider the
![]() $q=1$
version of
$q=1$
version of
 ${\mathcal{A}}{\mathcal{S}}p_{n}[q^{\pm }]$
, which we denote
${\mathcal{A}}{\mathcal{S}}p_{n}[q^{\pm }]$
, which we denote
![]() ${\mathcal{A}}{\mathcal{S}}p_{n}$
.
${\mathcal{A}}{\mathcal{S}}p_{n}$
.
4.4 The functor
 $\unicode[STIX]{x1D6E4}$
$\unicode[STIX]{x1D6E4}$
We begin by defining a functor
 $$\begin{eqnarray}\unicode[STIX]{x1D6E4}:{\mathcal{S}}p_{n}(q)\rightarrow {\mathcal{R}}\text{ep}_{q}^{\min }(\operatorname{SL}_{n})\end{eqnarray}$$
$$\begin{eqnarray}\unicode[STIX]{x1D6E4}:{\mathcal{S}}p_{n}(q)\rightarrow {\mathcal{R}}\text{ep}_{q}^{\min }(\operatorname{SL}_{n})\end{eqnarray}$$
following [Reference Cautis, Kamnitzer and MorrisonCKM14] (this functor was called
![]() $\unicode[STIX]{x1D6E4}_{n}$
in [Reference Cautis, Kamnitzer and MorrisonCKM14]). At the level of objects we take
$\unicode[STIX]{x1D6E4}_{n}$
in [Reference Cautis, Kamnitzer and MorrisonCKM14]). At the level of objects we take
 $$\begin{eqnarray}(k_{1}^{\unicode[STIX]{x1D700}_{1}},\ldots ,k_{m}^{\unicode[STIX]{x1D700}_{m}})\mapsto \biggl(\bigwedge _{q}^{k_{1}}\mathbb{C}_{q}^{n}\biggr)^{\unicode[STIX]{x1D700}_{1}}\otimes \cdots \otimes \biggl(\bigwedge _{q}^{k_{m}}\mathbb{C}_{q}^{n}\biggr)^{\unicode[STIX]{x1D700}_{m}}\end{eqnarray}$$
$$\begin{eqnarray}(k_{1}^{\unicode[STIX]{x1D700}_{1}},\ldots ,k_{m}^{\unicode[STIX]{x1D700}_{m}})\mapsto \biggl(\bigwedge _{q}^{k_{1}}\mathbb{C}_{q}^{n}\biggr)^{\unicode[STIX]{x1D700}_{1}}\otimes \cdots \otimes \biggl(\bigwedge _{q}^{k_{m}}\mathbb{C}_{q}^{n}\biggr)^{\unicode[STIX]{x1D700}_{m}}\end{eqnarray}$$
(where
 $\unicode[STIX]{x1D700}_{i}\in \{+,-\}$
).
$\unicode[STIX]{x1D700}_{i}\in \{+,-\}$
).
The morphisms are mapped as

where
 $M_{k,l}:\bigwedge _{q}^{k}(\mathbb{C}_{q}^{n})\otimes \bigwedge _{q}^{l}(\mathbb{C}_{q}^{n})\rightarrow \bigwedge _{q}^{k+l}(\mathbb{C}_{q}^{n})$
is defined by
$M_{k,l}:\bigwedge _{q}^{k}(\mathbb{C}_{q}^{n})\otimes \bigwedge _{q}^{l}(\mathbb{C}_{q}^{n})\rightarrow \bigwedge _{q}^{k+l}(\mathbb{C}_{q}^{n})$
is defined by
 $$\begin{eqnarray}M_{k,l}(x_{S}\otimes x_{T})=x_{S}\wedge _{q}x_{T}=\left\{\begin{array}{@{}ll@{}}(-q)^{\ell (S,T)}x_{S\cup T}\quad & \text{if }S\cap T=\emptyset ,\\ 0\quad & \text{otherwise},\end{array}\right.\end{eqnarray}$$
$$\begin{eqnarray}M_{k,l}(x_{S}\otimes x_{T})=x_{S}\wedge _{q}x_{T}=\left\{\begin{array}{@{}ll@{}}(-q)^{\ell (S,T)}x_{S\cup T}\quad & \text{if }S\cap T=\emptyset ,\\ 0\quad & \text{otherwise},\end{array}\right.\end{eqnarray}$$
while
 $M_{k,l}^{\prime }:\bigwedge _{q}^{k+l}(\mathbb{C}_{q}^{n})\rightarrow \bigwedge _{q}^{k}(\mathbb{C}_{q}^{n})\otimes \bigwedge _{q}^{l}(\mathbb{C}_{q}^{n})$
is defined by
$M_{k,l}^{\prime }:\bigwedge _{q}^{k+l}(\mathbb{C}_{q}^{n})\rightarrow \bigwedge _{q}^{k}(\mathbb{C}_{q}^{n})\otimes \bigwedge _{q}^{l}(\mathbb{C}_{q}^{n})$
is defined by
 $$\begin{eqnarray}\displaystyle M_{k,l}^{\prime }(x_{S})=(-1)^{kl}\mathop{\sum }_{T\subset S}(-q)^{-\ell (S\smallsetminus T,T)}x_{T}\otimes x_{S\smallsetminus T}. & & \displaystyle \nonumber\end{eqnarray}$$
$$\begin{eqnarray}\displaystyle M_{k,l}^{\prime }(x_{S})=(-1)^{kl}\mathop{\sum }_{T\subset S}(-q)^{-\ell (S\smallsetminus T,T)}x_{T}\otimes x_{S\smallsetminus T}. & & \displaystyle \nonumber\end{eqnarray}$$
Here, if
 $S=\{k_{1},\ldots ,k_{a}\}\subset \{1,\ldots ,n\}$
, with
$S=\{k_{1},\ldots ,k_{a}\}\subset \{1,\ldots ,n\}$
, with
 $k_{1}>\cdots >k_{a}$
, we write
$k_{1}>\cdots >k_{a}$
, we write
 $x_{S}=x_{k_{1}}\wedge _{q}\cdots \wedge _{q}x_{k_{a}}\in \bigwedge _{q}^{a}(\mathbb{C}_{q}^{n})$
and likewise for
$x_{S}=x_{k_{1}}\wedge _{q}\cdots \wedge _{q}x_{k_{a}}\in \bigwedge _{q}^{a}(\mathbb{C}_{q}^{n})$
and likewise for
![]() $x_{T}$
. Moreover, if
$x_{T}$
. Moreover, if
![]() $S,T$
are disjoint subsets of
$S,T$
are disjoint subsets of
 $\{1,\ldots ,n\}$
we define
$\{1,\ldots ,n\}$
we define
 $$\begin{eqnarray}\ell (S,T)=|\{(i,j):i\in S,j\in T\text{ and }i<j\}|.\end{eqnarray}$$
$$\begin{eqnarray}\ell (S,T)=|\{(i,j):i\in S,j\in T\text{ and }i<j\}|.\end{eqnarray}$$
The maps in (15) then force upon us the definition for tags. The main result from [Reference Cautis, Kamnitzer and MorrisonCKM14] can be stated as follows.
Theorem 4.2. The functor
 $\unicode[STIX]{x1D6E4}:{\mathcal{S}}p_{n}(q)\rightarrow {\mathcal{R}}\text{ep}_{q}^{\min }(\operatorname{SL}_{n})$
is an equivalence of braided monoidal categories.
$\unicode[STIX]{x1D6E4}:{\mathcal{S}}p_{n}(q)\rightarrow {\mathcal{R}}\text{ep}_{q}^{\min }(\operatorname{SL}_{n})$
is an equivalence of braided monoidal categories.
Remark 4.3. The argument in [Reference Cautis, Kamnitzer and MorrisonCKM14] implies that the functor
![]() $\unicode[STIX]{x1D6E4}$
is also an equivalence when
$\unicode[STIX]{x1D6E4}$
is also an equivalence when
![]() $q=1$
.
$q=1$
.
4.5 Horizontal trace and the annular spider category
We will now identify the annular spider category as the horizontal trace of the usual spider category. We define a functor
 ${\mathcal{S}}p_{n}(q)(S^{1})\rightarrow {\mathcal{A}}{\mathcal{S}}p_{n}(q)$
as follows. On objects it is the identity.
${\mathcal{S}}p_{n}(q)(S^{1})\rightarrow {\mathcal{A}}{\mathcal{S}}p_{n}(q)$
as follows. On objects it is the identity.
For morphisms, let
![]() $\text{}\underline{k},\text{}\underline{l}$
be two objects in
$\text{}\underline{k},\text{}\underline{l}$
be two objects in
![]() ${\mathcal{S}}p_{n}(q)$
. Suppose that we have a morphism
${\mathcal{S}}p_{n}(q)$
. Suppose that we have a morphism
![]() $[\text{}\underline{r},\unicode[STIX]{x1D719}]$
in
$[\text{}\underline{r},\unicode[STIX]{x1D719}]$
in
 ${\mathcal{S}}p_{n}(q)(S^{1})$
, where
${\mathcal{S}}p_{n}(q)(S^{1})$
, where
![]() $\unicode[STIX]{x1D719}$
is a web with bottom boundary
$\unicode[STIX]{x1D719}$
is a web with bottom boundary
![]() $\text{}\underline{k}\sqcup \text{}\underline{r}$
and top boundary
$\text{}\underline{k}\sqcup \text{}\underline{r}$
and top boundary
![]() $\text{}\underline{r}\sqcup \text{}\underline{l}$
. From
$\text{}\underline{r}\sqcup \text{}\underline{l}$
. From
![]() $(\text{}\underline{r},\unicode[STIX]{x1D719})$
we can get a morphism
$(\text{}\underline{r},\unicode[STIX]{x1D719})$
we can get a morphism
![]() $\overline{(r,\unicode[STIX]{x1D719})}$
in
$\overline{(r,\unicode[STIX]{x1D719})}$
in
 ${\mathcal{A}}{\mathcal{S}}p_{n}(q)$
by sending
${\mathcal{A}}{\mathcal{S}}p_{n}(q)$
by sending
![]() $\text{}\underline{r}$
around the circle as follows.
$\text{}\underline{r}$
around the circle as follows.

Proposition 4.4. For any two objects
![]() $\text{}\underline{k},\text{}\underline{l}$
, this gives an isomorphism
$\text{}\underline{k},\text{}\underline{l}$
, this gives an isomorphism
 $$\begin{eqnarray}\operatorname{Hom}_{{\mathcal{S}}p_{n}(q)(S^{1})}(\text{}\underline{k},\text{}\underline{l})\xrightarrow[{}]{{\sim}}\operatorname{Hom}_{{\mathcal{A}}{\mathcal{S}}p_{n}(q)}(\text{}\underline{k},\text{}\underline{l}).\end{eqnarray}$$
$$\begin{eqnarray}\operatorname{Hom}_{{\mathcal{S}}p_{n}(q)(S^{1})}(\text{}\underline{k},\text{}\underline{l})\xrightarrow[{}]{{\sim}}\operatorname{Hom}_{{\mathcal{A}}{\mathcal{S}}p_{n}(q)}(\text{}\underline{k},\text{}\underline{l}).\end{eqnarray}$$
This implies
 ${\mathcal{A}}{\mathcal{S}}p_{n}(q)\cong {\mathcal{S}}p_{n}(q)(S^{1})$
.
${\mathcal{A}}{\mathcal{S}}p_{n}(q)\cong {\mathcal{S}}p_{n}(q)(S^{1})$
.
Proof. First we check that the map is well defined. Suppose that we have a morphism
 $\unicode[STIX]{x1D6FC}:\text{}\underline{r}\rightarrow \text{}\underline{r}^{\prime }$
and a morphism
$\unicode[STIX]{x1D6FC}:\text{}\underline{r}\rightarrow \text{}\underline{r}^{\prime }$
and a morphism
 $\unicode[STIX]{x1D713}:\text{}\underline{k}\sqcup \text{}\underline{r}^{\prime }\rightarrow \text{}\underline{r}\sqcup \text{}\underline{l}$
. Then we need to know that
$\unicode[STIX]{x1D713}:\text{}\underline{k}\sqcup \text{}\underline{r}^{\prime }\rightarrow \text{}\underline{r}\sqcup \text{}\underline{l}$
. Then we need to know that
 $(\text{}\underline{r},\unicode[STIX]{x1D713}\circ I\sqcup \unicode[STIX]{x1D6FC})$
and
$(\text{}\underline{r},\unicode[STIX]{x1D713}\circ I\sqcup \unicode[STIX]{x1D6FC})$
and
 $(\text{}\underline{r}^{\prime },\unicode[STIX]{x1D6FC}\sqcup I\circ \unicode[STIX]{x1D713})$
give rise to the same annular web. This follows since the following two annular webs are isotopic.
$(\text{}\underline{r}^{\prime },\unicode[STIX]{x1D6FC}\sqcup I\circ \unicode[STIX]{x1D713})$
give rise to the same annular web. This follows since the following two annular webs are isotopic.

Let
![]() $\text{}\underline{k},\text{}\underline{l}$
be objects of
$\text{}\underline{k},\text{}\underline{l}$
be objects of
 ${\mathcal{A}}{\mathcal{S}}p_{n}(q)$
. Suppose that we have an annular web
${\mathcal{A}}{\mathcal{S}}p_{n}(q)$
. Suppose that we have an annular web
![]() $\unicode[STIX]{x1D713}$
which gives a morphism between
$\unicode[STIX]{x1D713}$
which gives a morphism between
![]() $\text{}\underline{k}$
and
$\text{}\underline{k}$
and
![]() $\text{}\underline{l}$
in
$\text{}\underline{l}$
in
 ${\mathcal{A}}{\mathcal{S}}p_{n}(q)$
. Draw a cut line from the inner boundary to the outer boundary (connecting the bottoms) and let
${\mathcal{A}}{\mathcal{S}}p_{n}(q)$
. Draw a cut line from the inner boundary to the outer boundary (connecting the bottoms) and let
![]() $\text{}\underline{r}$
be the labels on the strands cutting this line. Then unfold
$\text{}\underline{r}$
be the labels on the strands cutting this line. Then unfold
![]() $\unicode[STIX]{x1D713}$
to give a web
$\unicode[STIX]{x1D713}$
to give a web
![]() $\unicode[STIX]{x1D713}^{\prime }$
with bottom boundary
$\unicode[STIX]{x1D713}^{\prime }$
with bottom boundary
![]() $\text{}\underline{k}\sqcup \text{}\underline{r}$
and top boundary
$\text{}\underline{k}\sqcup \text{}\underline{r}$
and top boundary
![]() $\text{}\underline{r}\sqcup \text{}\underline{l}$
(see Figure 3). It is easy to see that this map
$\text{}\underline{r}\sqcup \text{}\underline{l}$
(see Figure 3). It is easy to see that this map
 $\unicode[STIX]{x1D713}\mapsto \unicode[STIX]{x1D713}^{\prime }$
provides an inverse to the above construction and thus the map
$\unicode[STIX]{x1D713}\mapsto \unicode[STIX]{x1D713}^{\prime }$
provides an inverse to the above construction and thus the map
 $$\begin{eqnarray}\operatorname{Hom}_{{\mathcal{S}}p_{n}(q)(S^{1})}(\text{}\underline{k},\text{}\underline{l})\rightarrow \operatorname{Hom}_{{\mathcal{A}}{\mathcal{S}}p_{n}(q)}(\text{}\underline{k},\text{}\underline{l})\end{eqnarray}$$
$$\begin{eqnarray}\operatorname{Hom}_{{\mathcal{S}}p_{n}(q)(S^{1})}(\text{}\underline{k},\text{}\underline{l})\rightarrow \operatorname{Hom}_{{\mathcal{A}}{\mathcal{S}}p_{n}(q)}(\text{}\underline{k},\text{}\underline{l})\end{eqnarray}$$
is an isomorphism. ◻

Figure 3. An annular web
![]() $\unicode[STIX]{x1D713}$
and its unfolding
$\unicode[STIX]{x1D713}$
and its unfolding
![]() $\unicode[STIX]{x1D713}^{\prime }$
. In this example
$\unicode[STIX]{x1D713}^{\prime }$
. In this example
 $\text{}\underline{k}=(3,2,5,4^{-})$
,
$\text{}\underline{k}=(3,2,5,4^{-})$
,
 $\text{}\underline{l}=(1,2,3,4^{-},3,1)$
and
$\text{}\underline{l}=(1,2,3,4^{-},3,1)$
and
 $\text{}\underline{r}=(3,1)$
.
$\text{}\underline{r}=(3,1)$
.
Because
![]() ${\mathcal{S}}p_{n}(q)$
is a braided monoidal category,
${\mathcal{S}}p_{n}(q)$
is a braided monoidal category,
 ${\mathcal{S}}p_{n}(q)(S^{1})$
carries a monoidal structure and thus
${\mathcal{S}}p_{n}(q)(S^{1})$
carries a monoidal structure and thus
 ${\mathcal{A}}{\mathcal{S}}p_{n}(q)$
acquires a monoidal structure. Diagrammatically, the tensor product of two morphisms
${\mathcal{A}}{\mathcal{S}}p_{n}(q)$
acquires a monoidal structure. Diagrammatically, the tensor product of two morphisms
![]() $\unicode[STIX]{x1D719}_{1}$
and
$\unicode[STIX]{x1D719}_{1}$
and
![]() $\unicode[STIX]{x1D719}_{2}$
is given by placing the source and target of
$\unicode[STIX]{x1D719}_{2}$
is given by placing the source and target of
![]() $\unicode[STIX]{x1D719}_{1}$
to the left of those of
$\unicode[STIX]{x1D719}_{1}$
to the left of those of
![]() $\unicode[STIX]{x1D719}_{2}$
and having the strands of
$\unicode[STIX]{x1D719}_{2}$
and having the strands of
![]() $\unicode[STIX]{x1D719}_{1}$
cross over those of
$\unicode[STIX]{x1D719}_{1}$
cross over those of
![]() $\unicode[STIX]{x1D719}_{2}$
.
$\unicode[STIX]{x1D719}_{2}$
.
Corollary 4.5. The functor
![]() $\unicode[STIX]{x1D6E4}$
induces an equivalence
$\unicode[STIX]{x1D6E4}$
induces an equivalence
 $$\begin{eqnarray}A\unicode[STIX]{x1D6E4}:{\mathcal{A}}{\mathcal{S}}p_{n}(q)\rightarrow {\mathcal{O}}_{q}^{\min }({\textstyle \frac{\operatorname{SL}_{n}}{\operatorname{SL}_{n}}})\text{-}\text{mod}.\end{eqnarray}$$
$$\begin{eqnarray}A\unicode[STIX]{x1D6E4}:{\mathcal{A}}{\mathcal{S}}p_{n}(q)\rightarrow {\mathcal{O}}_{q}^{\min }({\textstyle \frac{\operatorname{SL}_{n}}{\operatorname{SL}_{n}}})\text{-}\text{mod}.\end{eqnarray}$$
Proof. By Proposition 4.4 and Theorem 4.2, we have
 $$\begin{eqnarray}{\mathcal{A}}{\mathcal{S}}p_{n}(q)\cong {\mathcal{S}}p_{n}(q)(S^{1})\cong {\mathcal{R}}\text{ep}_{q}^{\min }(\operatorname{SL}_{n})(S^{1}).\end{eqnarray}$$
$$\begin{eqnarray}{\mathcal{A}}{\mathcal{S}}p_{n}(q)\cong {\mathcal{S}}p_{n}(q)(S^{1})\cong {\mathcal{R}}\text{ep}_{q}^{\min }(\operatorname{SL}_{n})(S^{1}).\end{eqnarray}$$
On the other hand, Corollary 2.9 gives an equivalence between
 ${\mathcal{R}}\text{ep}_{q}^{\min }(\operatorname{SL}_{n})(S^{1})$
and
${\mathcal{R}}\text{ep}_{q}^{\min }(\operatorname{SL}_{n})(S^{1})$
and
 ${\mathcal{O}}_{q}^{\min }({\textstyle \frac{\operatorname{SL}_{n}}{\operatorname{SL}_{n}}})\operatorname{ - mod}$
.◻
${\mathcal{O}}_{q}^{\min }({\textstyle \frac{\operatorname{SL}_{n}}{\operatorname{SL}_{n}}})\operatorname{ - mod}$
.◻
4.6 Action of annular braids and loops
Suppose we have an annular braid with strands labelled from
 $1,\ldots ,n-1$
. Since we have crossings in
$1,\ldots ,n-1$
. Since we have crossings in
 ${\mathcal{A}}{\mathcal{S}}p_{n}(q)$
, we can interpret this annular braid as a morphism in
${\mathcal{A}}{\mathcal{S}}p_{n}(q)$
, we can interpret this annular braid as a morphism in
 ${\mathcal{A}}{\mathcal{S}}p_{n}(q)$
. Thus we get a functor
${\mathcal{A}}{\mathcal{S}}p_{n}(q)$
. Thus we get a functor
 $$\begin{eqnarray}{\mathcal{A}}{\mathcal{B}}_{m}(\{1,\ldots ,n-1\})\rightarrow {\mathcal{A}}{\mathcal{S}}p_{n}(q).\end{eqnarray}$$
$$\begin{eqnarray}{\mathcal{A}}{\mathcal{B}}_{m}(\{1,\ldots ,n-1\})\rightarrow {\mathcal{A}}{\mathcal{S}}p_{n}(q).\end{eqnarray}$$
Proposition 4.7. The functor
 ${\mathcal{A}}{\mathcal{B}}_{m}(\{1,\ldots ,n-1\})\rightarrow {\mathcal{O}}_{q}^{\min }({\textstyle \frac{\operatorname{SL}_{n}}{\operatorname{SL}_{n}}})\operatorname{ - mod}$
defined in § 2.5 factors as
${\mathcal{A}}{\mathcal{B}}_{m}(\{1,\ldots ,n-1\})\rightarrow {\mathcal{O}}_{q}^{\min }({\textstyle \frac{\operatorname{SL}_{n}}{\operatorname{SL}_{n}}})\operatorname{ - mod}$
defined in § 2.5 factors as
 $$\begin{eqnarray}{\mathcal{A}}{\mathcal{B}}_{m}(\{1,\ldots ,n-1\})\rightarrow {\mathcal{A}}{\mathcal{S}}p_{n}(q)\xrightarrow[{}]{A\unicode[STIX]{x1D6E4}}{\mathcal{O}}_{q}^{\min }({\textstyle \frac{\operatorname{SL}_{n}}{\operatorname{SL}_{n}}})\operatorname{ - mod}\end{eqnarray}$$
$$\begin{eqnarray}{\mathcal{A}}{\mathcal{B}}_{m}(\{1,\ldots ,n-1\})\rightarrow {\mathcal{A}}{\mathcal{S}}p_{n}(q)\xrightarrow[{}]{A\unicode[STIX]{x1D6E4}}{\mathcal{O}}_{q}^{\min }({\textstyle \frac{\operatorname{SL}_{n}}{\operatorname{SL}_{n}}})\operatorname{ - mod}\end{eqnarray}$$
up to a factor of
![]() $q$
as in Remark 4.8.
$q$
as in Remark 4.8.
Proof. Since annular braids are generated by the
![]() $T_{i}$
and
$T_{i}$
and
![]() $X_{1}$
, it suffices to check the result on these generators. For
$X_{1}$
, it suffices to check the result on these generators. For
![]() $T_{i}$
the result is proved in [Reference Cautis, Kamnitzer and MorrisonCKM14, Corollary 6.2.3].
$T_{i}$
the result is proved in [Reference Cautis, Kamnitzer and MorrisonCKM14, Corollary 6.2.3].
Remark 4.8. Unfortunately this is not entirely correct as the two images of
![]() $T_{i}$
actually differ by a factor of
$T_{i}$
actually differ by a factor of
![]() $q$
. More precisely, the two
$q$
. More precisely, the two
![]() $T_{i}$
acting on
$T_{i}$
acting on
 $\wedge ^{k}(\mathbb{C}^{n})\otimes \wedge ^{l}(\mathbb{C}^{n})$
differ by a factor of
$\wedge ^{k}(\mathbb{C}^{n})\otimes \wedge ^{l}(\mathbb{C}^{n})$
differ by a factor of
![]() $q^{kl/n}$
. This is because of the usual conventions for defining the braiding in
$q^{kl/n}$
. This is because of the usual conventions for defining the braiding in
 ${\mathcal{R}}\text{ep}_{q}(G)$
. We chose to overlook this small discrepancy rather than adding this factor to the definition in (14) which would also mean having to work over
${\mathcal{R}}\text{ep}_{q}(G)$
. We chose to overlook this small discrepancy rather than adding this factor to the definition in (14) which would also mean having to work over
![]() $\mathbb{C}(q^{1/n})$
throughout.
$\mathbb{C}(q^{1/n})$
throughout.
For
![]() $X_{1}$
, we consider some object
$X_{1}$
, we consider some object
 $\text{}\underline{k}=(k_{1},\ldots ,k_{m})$
and then we use the construction from the proof of Proposition 4.4 to unfold
$\text{}\underline{k}=(k_{1},\ldots ,k_{m})$
and then we use the construction from the proof of Proposition 4.4 to unfold
![]() $X_{1}$
(see Figure 4) and produce a morphism
$X_{1}$
(see Figure 4) and produce a morphism
 $\text{}\underline{k}\sqcup \{k_{1}\}\rightarrow \{k_{1}\}\sqcup \text{}\underline{k}$
.
$\text{}\underline{k}\sqcup \{k_{1}\}\rightarrow \{k_{1}\}\sqcup \text{}\underline{k}$
.

Figure 4.
![]() $X_{1}$
and its unfolded version.
$X_{1}$
and its unfolded version.
Applying
![]() $\unicode[STIX]{x1D6E4}$
we get the map
$\unicode[STIX]{x1D6E4}$
we get the map
 $$\begin{eqnarray}V\otimes W\otimes V\xrightarrow[{}]{I\otimes \unicode[STIX]{x1D6FD}_{W,V}^{-1}}V\otimes V\otimes W,\end{eqnarray}$$
$$\begin{eqnarray}V\otimes W\otimes V\xrightarrow[{}]{I\otimes \unicode[STIX]{x1D6FD}_{W,V}^{-1}}V\otimes V\otimes W,\end{eqnarray}$$
where
 $V=\bigwedge _{q}^{k_{1}}(\mathbb{C}_{q}^{n})$
and
$V=\bigwedge _{q}^{k_{1}}(\mathbb{C}_{q}^{n})$
and
 $W=\bigwedge _{q}^{k_{2}}(\mathbb{C}_{q}^{n})\otimes \cdots \otimes \bigwedge _{q}^{k_{m}}(\mathbb{C}_{q}^{n})$
.
$W=\bigwedge _{q}^{k_{2}}(\mathbb{C}_{q}^{n})\otimes \cdots \otimes \bigwedge _{q}^{k_{m}}(\mathbb{C}_{q}^{n})$
.
If we apply the identification between
 ${\mathcal{R}}\text{ep}_{q}(\operatorname{SL}_{n})$
and
${\mathcal{R}}\text{ep}_{q}(\operatorname{SL}_{n})$
and
 ${\mathcal{O}}_{q}^{\min }({\textstyle \frac{\operatorname{SL}_{n}}{\operatorname{SL}_{n}}})\operatorname{ - mod}$
given by Proposition 2.6, we see that this map corresponds to the map in
${\mathcal{O}}_{q}^{\min }({\textstyle \frac{\operatorname{SL}_{n}}{\operatorname{SL}_{n}}})\operatorname{ - mod}$
given by Proposition 2.6, we see that this map corresponds to the map in
 ${\mathcal{O}}_{q}^{\min }({\textstyle \frac{\operatorname{SL}_{n}}{\operatorname{SL}_{n}}})\operatorname{ - mod}$
given by
${\mathcal{O}}_{q}^{\min }({\textstyle \frac{\operatorname{SL}_{n}}{\operatorname{SL}_{n}}})\operatorname{ - mod}$
given by
 $$\begin{eqnarray}\displaystyle {\mathcal{O}}_{q}(\operatorname{SL}_{n})\otimes V\otimes W & & \displaystyle \rightarrow {\mathcal{O}}_{q}(\operatorname{SL}_{n})\otimes V\otimes W\otimes V\otimes V^{\ast }\nonumber\\ \displaystyle & & \displaystyle \xrightarrow[{}]{\unicode[STIX]{x1D6FD}_{V,W}^{-1}}{\mathcal{O}}_{q}(\operatorname{SL}_{n})\otimes V\otimes V\otimes W\otimes V^{\ast }\nonumber\\ \displaystyle & & \displaystyle \xrightarrow[{}]{\unicode[STIX]{x1D6FD}_{V^{\ast },V\otimes W}^{-1}}{\mathcal{O}}_{q}(\operatorname{SL}_{n})\otimes V\otimes V^{\ast }\otimes V\otimes W\rightarrow {\mathcal{O}}_{q}(\operatorname{SL}_{n})\otimes V\otimes W\nonumber\end{eqnarray}$$
$$\begin{eqnarray}\displaystyle {\mathcal{O}}_{q}(\operatorname{SL}_{n})\otimes V\otimes W & & \displaystyle \rightarrow {\mathcal{O}}_{q}(\operatorname{SL}_{n})\otimes V\otimes W\otimes V\otimes V^{\ast }\nonumber\\ \displaystyle & & \displaystyle \xrightarrow[{}]{\unicode[STIX]{x1D6FD}_{V,W}^{-1}}{\mathcal{O}}_{q}(\operatorname{SL}_{n})\otimes V\otimes V\otimes W\otimes V^{\ast }\nonumber\\ \displaystyle & & \displaystyle \xrightarrow[{}]{\unicode[STIX]{x1D6FD}_{V^{\ast },V\otimes W}^{-1}}{\mathcal{O}}_{q}(\operatorname{SL}_{n})\otimes V\otimes V^{\ast }\otimes V\otimes W\rightarrow {\mathcal{O}}_{q}(\operatorname{SL}_{n})\otimes V\otimes W\nonumber\end{eqnarray}$$
which is the same as the map
![]() $X_{1}$
defined in § 2.5, because the composition
$X_{1}$
defined in § 2.5, because the composition
 $$\begin{eqnarray}\mathbb{C}(q)\rightarrow V\otimes V^{\ast }\xrightarrow[{}]{\unicode[STIX]{x1D6FD}_{V^{\ast },V}^{-1}}V^{\ast }\otimes V\end{eqnarray}$$
$$\begin{eqnarray}\mathbb{C}(q)\rightarrow V\otimes V^{\ast }\xrightarrow[{}]{\unicode[STIX]{x1D6FD}_{V^{\ast },V}^{-1}}V^{\ast }\otimes V\end{eqnarray}$$
agrees with the composition
 $$\begin{eqnarray}\mathbb{C}(q)\rightarrow V^{\ast }\otimes V\xrightarrow[{}]{I\otimes \unicode[STIX]{x1D703}_{V}}V^{\ast }\otimes V.\Box\end{eqnarray}$$
$$\begin{eqnarray}\mathbb{C}(q)\rightarrow V^{\ast }\otimes V\xrightarrow[{}]{I\otimes \unicode[STIX]{x1D703}_{V}}V^{\ast }\otimes V.\Box\end{eqnarray}$$
4.7 The action of
 $E$
$E$
One can define a map
 $E[q^{\pm }]\rightarrow \operatorname{End}_{{\mathcal{A}}{\mathcal{S}}p_{n}[q^{\pm }]}(\text{}\underline{k})$
by taking
$E[q^{\pm }]\rightarrow \operatorname{End}_{{\mathcal{A}}{\mathcal{S}}p_{n}[q^{\pm }]}(\text{}\underline{k})$
by taking
![]() $e_{k}$
to a counterclockwise loop labelled
$e_{k}$
to a counterclockwise loop labelled
![]() $k$
passing over all the strands.
$k$
passing over all the strands.

Such maps commute with all morphisms in
 ${\mathcal{A}}{\mathcal{S}}p_{n}[q^{\pm }]$
and hence give a map
${\mathcal{A}}{\mathcal{S}}p_{n}[q^{\pm }]$
and hence give a map
 $E[q^{\pm }]\rightarrow \operatorname{End}_{{\mathcal{A}}{\mathcal{S}}p_{n}[q^{\pm }]}(\operatorname{id})$
to the endomorphisms of the identity functor.
$E[q^{\pm }]\rightarrow \operatorname{End}_{{\mathcal{A}}{\mathcal{S}}p_{n}[q^{\pm }]}(\operatorname{id})$
to the endomorphisms of the identity functor.
On the other hand, by the construction in § 2.3.2, we have a map
 $$\begin{eqnarray}E(q)\rightarrow \operatorname{End}_{{\mathcal{O}}_{q}^{\min }({\textstyle \frac{\operatorname{SL}_{n}}{\operatorname{SL}_{n}}})\operatorname{-mod}}(\operatorname{id}).\end{eqnarray}$$
$$\begin{eqnarray}E(q)\rightarrow \operatorname{End}_{{\mathcal{O}}_{q}^{\min }({\textstyle \frac{\operatorname{SL}_{n}}{\operatorname{SL}_{n}}})\operatorname{-mod}}(\operatorname{id}).\end{eqnarray}$$
By a similar argument as in the proof of Proposition 4.7, we deduce the following.
Proposition 4.9. The composition
 $$\begin{eqnarray}E(q)\rightarrow \operatorname{End}_{{\mathcal{A}}{\mathcal{S}}p_{n}(q)}(\operatorname{id})\xrightarrow[{}]{A\unicode[STIX]{x1D6E4}}\operatorname{End}_{{\mathcal{O}}_{q}^{\min }({\textstyle \frac{\operatorname{SL}_{n}}{\operatorname{SL}_{n}}})\operatorname{-mod}}(\operatorname{id})\end{eqnarray}$$
$$\begin{eqnarray}E(q)\rightarrow \operatorname{End}_{{\mathcal{A}}{\mathcal{S}}p_{n}(q)}(\operatorname{id})\xrightarrow[{}]{A\unicode[STIX]{x1D6E4}}\operatorname{End}_{{\mathcal{O}}_{q}^{\min }({\textstyle \frac{\operatorname{SL}_{n}}{\operatorname{SL}_{n}}})\operatorname{-mod}}(\operatorname{id})\end{eqnarray}$$
equals the map defined in § 2.3.2. In other words if we have a counterclockwise loop labelled
![]() $k$
, then we get the morphism
$k$
, then we get the morphism
 ${\mathcal{O}}_{q}(\operatorname{SL}_{n})\otimes V\rightarrow {\mathcal{O}}_{q}(\operatorname{SL}_{n})\otimes V$
given by left multiplication by
${\mathcal{O}}_{q}(\operatorname{SL}_{n})\otimes V\rightarrow {\mathcal{O}}_{q}(\operatorname{SL}_{n})\otimes V$
given by left multiplication by
![]() $e_{k}$
.
$e_{k}$
.
5 Quantum loop algebras and annular spiders
It turns out that
 ${\mathcal{A}}{\mathcal{S}}p_{n}[q^{\pm }]$
is closely related to quantum loop algebras of
${\mathcal{A}}{\mathcal{S}}p_{n}[q^{\pm }]$
is closely related to quantum loop algebras of
![]() $\mathfrak{g}\mathfrak{l}_{m}$
for varying
$\mathfrak{g}\mathfrak{l}_{m}$
for varying
![]() $m$
(a similar relationship between
$m$
(a similar relationship between
 ${\mathcal{S}}p_{n}[q^{\pm }]$
and usual quantum
${\mathcal{S}}p_{n}[q^{\pm }]$
and usual quantum
![]() $\mathfrak{g}\mathfrak{l}_{m}$
was studied in [Reference Cautis, Kamnitzer and MorrisonCKM14]).
$\mathfrak{g}\mathfrak{l}_{m}$
was studied in [Reference Cautis, Kamnitzer and MorrisonCKM14]).
5.1 The quantum loop algebra
We first recall the integral, idempotent form
 $\dot{U}_{[q^{\pm }]}L\mathfrak{g}\mathfrak{l}_{m}$
of the quantum loop algebra of
$\dot{U}_{[q^{\pm }]}L\mathfrak{g}\mathfrak{l}_{m}$
of the quantum loop algebra of
![]() $\mathfrak{g}\mathfrak{l}_{m}$
. This is a category whose objects are indexed by
$\mathfrak{g}\mathfrak{l}_{m}$
. This is a category whose objects are indexed by
 $\text{}\underline{k}=(k_{1},\ldots ,k_{m})\in \mathbb{Z}^{m}$
. For
$\text{}\underline{k}=(k_{1},\ldots ,k_{m})\in \mathbb{Z}^{m}$
. For
 $i=1,\ldots ,m-1$
we denote
$i=1,\ldots ,m-1$
we denote
 $\unicode[STIX]{x1D6FC}_{i}=(0,\ldots ,1,-1,\ldots ,0)$
where the
$\unicode[STIX]{x1D6FC}_{i}=(0,\ldots ,1,-1,\ldots ,0)$
where the
![]() $1$
is in position
$1$
is in position
![]() $i$
. Moreover, we denote
$i$
. Moreover, we denote
 $\unicode[STIX]{x1D6FC}_{0}=(-1,0,\ldots ,0,1)$
.
$\unicode[STIX]{x1D6FC}_{0}=(-1,0,\ldots ,0,1)$
.
As usual, we will write
![]() $1_{\text{}\underline{k}}$
for the identity morphism of
$1_{\text{}\underline{k}}$
for the identity morphism of
![]() $\text{}\underline{k}$
. The morphisms in
$\text{}\underline{k}$
. The morphisms in
 $\dot{U}_{[q^{\pm }]}L\mathfrak{g}\mathfrak{l}_{m}$
are further generated over
$\dot{U}_{[q^{\pm }]}L\mathfrak{g}\mathfrak{l}_{m}$
are further generated over
![]() $\mathbb{C}[q^{\pm }]$
by
$\mathbb{C}[q^{\pm }]$
by
 $E_{i}^{(s)},F_{i}^{(s)}$
, for
$E_{i}^{(s)},F_{i}^{(s)}$
, for
 $i=0,\ldots ,m-1$
,
$i=0,\ldots ,m-1$
,
![]() $s\in \mathbb{N}$
and by
$s\in \mathbb{N}$
and by
![]() $R$
. These satisfy the following relations:
$R$
. These satisfy the following relations:
-
(i)
 $1_{\text{}\underline{k}+s\unicode[STIX]{x1D6FC}_{i}}E_{i}^{(s)}=1_{\text{}\underline{k}+s\unicode[STIX]{x1D6FC}_{i}}E_{i}^{(s)}1_{\text{}\underline{k}}=E_{i}^{(s)}1_{\text{}\underline{k}}$
and
$1_{\text{}\underline{k}+s\unicode[STIX]{x1D6FC}_{i}}E_{i}^{(s)}=1_{\text{}\underline{k}+s\unicode[STIX]{x1D6FC}_{i}}E_{i}^{(s)}1_{\text{}\underline{k}}=E_{i}^{(s)}1_{\text{}\underline{k}}$
and
 $1_{\text{}\underline{k}}F_{i}^{(s)}=1_{\text{}\underline{k}}F_{i}^{(s)}1_{\text{}\underline{k}+s\unicode[STIX]{x1D6FC}_{i}}=F_{i}^{(s)}1_{\text{}\underline{k}+s\unicode[STIX]{x1D6FC}_{i}}$
;
$1_{\text{}\underline{k}}F_{i}^{(s)}=1_{\text{}\underline{k}}F_{i}^{(s)}1_{\text{}\underline{k}+s\unicode[STIX]{x1D6FC}_{i}}=F_{i}^{(s)}1_{\text{}\underline{k}+s\unicode[STIX]{x1D6FC}_{i}}$
; -
(ii)
 $R1_{\text{}\underline{k}}=1_{r\cdot \text{}\underline{k}}R$
where
$R1_{\text{}\underline{k}}=1_{r\cdot \text{}\underline{k}}R$
where
 $r\cdot (k_{1},\ldots ,k_{m})=(k_{m},k_{1},\ldots ,k_{m-1})$
is ‘rotation’ of the weights;
$r\cdot (k_{1},\ldots ,k_{m})=(k_{m},k_{1},\ldots ,k_{m-1})$
is ‘rotation’ of the weights; -
(iii)
 $[E_{i}^{(s)},F_{i}^{(t)}]1_{\text{}\underline{k}}=\sum _{j\geqslant 0}\left[\begin{smallmatrix}\langle \text{}\underline{k},\unicode[STIX]{x1D6FC}_{i}\rangle -t+s\\ j\\ \end{smallmatrix}\right]F_{i}^{(t-j)}E_{i}^{(s-j)}1_{\text{}\underline{k}}$
where
$[E_{i}^{(s)},F_{i}^{(t)}]1_{\text{}\underline{k}}=\sum _{j\geqslant 0}\left[\begin{smallmatrix}\langle \text{}\underline{k},\unicode[STIX]{x1D6FC}_{i}\rangle -t+s\\ j\\ \end{smallmatrix}\right]F_{i}^{(t-j)}E_{i}^{(s-j)}1_{\text{}\underline{k}}$
where
 $\langle \cdot ,\cdot \rangle$
is the standard inner product (here by convention
$\langle \cdot ,\cdot \rangle$
is the standard inner product (here by convention
 $F^{(r)}=E^{(r)}=0$
if
$F^{(r)}=E^{(r)}=0$
if
 $r<0$
, so this is actually a finite sum);
$r<0$
, so this is actually a finite sum); -
(iv)
 $[E_{i}^{(s)},F_{j}^{(t)}]=0$
if
$[E_{i}^{(s)},F_{j}^{(t)}]=0$
if
 $i\neq j$
;
$i\neq j$
; -
(v) if
 $|i-j|=1$
(modulo
$|i-j|=1$
(modulo
 $m$
) then
$m$
) then
 $E_{i}E_{j}E_{i}=E_{i}^{(2)}E_{j}+E_{j}E_{i}^{(2)}$
and similarly where the generators
$E_{i}E_{j}E_{i}=E_{i}^{(2)}E_{j}+E_{j}E_{i}^{(2)}$
and similarly where the generators
 $E_{i}$
are replaced by the generators
$E_{i}$
are replaced by the generators
 $F_{i}$
;
$F_{i}$
; -
(vi) if
 $|i-j|>1$
(modulo
$|i-j|>1$
(modulo
 $m$
) then
$m$
) then
 $[E_{i}^{(r)},E_{j}^{(s)}]=0=[F_{i}^{(r)},F_{j}^{(s)}]$
;
$[E_{i}^{(r)},E_{j}^{(s)}]=0=[F_{i}^{(r)},F_{j}^{(s)}]$
; -
(vii)
 $RE_{i}^{(s)}=E_{i+1}^{(s)}R$
(modulo
$RE_{i}^{(s)}=E_{i+1}^{(s)}R$
(modulo
 $m$
) and similarly
$m$
) and similarly
 $RF_{i}^{(s)}=F_{i+1}^{(s)}R$
(modulo
$RF_{i}^{(s)}=F_{i+1}^{(s)}R$
(modulo
 $m$
).
$m$
).
Remark 5.1. The above definition of
 $\dot{U}_{[q^{\pm }]}L\mathfrak{g}\mathfrak{l}_{m}$
is the integral, idempotent form of [Reference GreenGre99, Definition 3.1.1]. Sometimes a slightly smaller algebra is defined without using the
$\dot{U}_{[q^{\pm }]}L\mathfrak{g}\mathfrak{l}_{m}$
is the integral, idempotent form of [Reference GreenGre99, Definition 3.1.1]. Sometimes a slightly smaller algebra is defined without using the
![]() $R$
generator. For a comparison of the two definitions, see [Reference Doty and GreenDG07, § 1.4].
$R$
generator. For a comparison of the two definitions, see [Reference Doty and GreenDG07, § 1.4].
We will denote by
 $(\dot{U}_{[q^{\pm }]}L\mathfrak{g}\mathfrak{l}_{m})^{n}$
the quotient of
$(\dot{U}_{[q^{\pm }]}L\mathfrak{g}\mathfrak{l}_{m})^{n}$
the quotient of
 $\dot{U}_{[q^{\pm }]}L\mathfrak{g}\mathfrak{l}_{m}$
obtained by killing any object not of the form
$\dot{U}_{[q^{\pm }]}L\mathfrak{g}\mathfrak{l}_{m}$
obtained by killing any object not of the form
 $(k_{1},\ldots ,k_{m})$
with
$(k_{1},\ldots ,k_{m})$
with
 $0\leqslant k_{i}\leqslant n$
. We will also denote by
$0\leqslant k_{i}\leqslant n$
. We will also denote by
 $\dot{U}_{[q^{\pm }]}\mathfrak{g}\mathfrak{l}_{m}$
the subcategory generated by
$\dot{U}_{[q^{\pm }]}\mathfrak{g}\mathfrak{l}_{m}$
the subcategory generated by
![]() $E_{i}$
and
$E_{i}$
and
![]() $F_{i}$
for
$F_{i}$
for
 $i=1,\ldots ,m-1$
and by
$i=1,\ldots ,m-1$
and by
 $(\dot{U}_{[q^{\pm }]}\mathfrak{g}\mathfrak{l}_{m})^{n}$
the corresponding quotient.
$(\dot{U}_{[q^{\pm }]}\mathfrak{g}\mathfrak{l}_{m})^{n}$
the corresponding quotient.
The category
 $(\dot{U}_{[q^{\pm }]}L\mathfrak{g}\mathfrak{l}_{m})^{n}$
(or more precisely the direct sum of all Hom spaces in this category) is a special case of an affine generalized
$(\dot{U}_{[q^{\pm }]}L\mathfrak{g}\mathfrak{l}_{m})^{n}$
(or more precisely the direct sum of all Hom spaces in this category) is a special case of an affine generalized
![]() $q$
-Schur algebra (or Beilinson–Lusztig–MacPherson (BLM) algebra), as defined in [Reference McGertyMcG07, § 6.1]. As explained by McGerty [Reference McGertyMcG07, Proposition 6.4], the following result is a consequence of the work of Beck and Nakajima [Reference Beck and NakajimaBN04].
$q$
-Schur algebra (or Beilinson–Lusztig–MacPherson (BLM) algebra), as defined in [Reference McGertyMcG07, § 6.1]. As explained by McGerty [Reference McGertyMcG07, Proposition 6.4], the following result is a consequence of the work of Beck and Nakajima [Reference Beck and NakajimaBN04].
Lemma 5.2. All Hom sets in
 $(\dot{U}_{[q^{\pm }]}L\mathfrak{g}\mathfrak{l}_{m})^{n}$
are free over
$(\dot{U}_{[q^{\pm }]}L\mathfrak{g}\mathfrak{l}_{m})^{n}$
are free over
![]() $\mathbb{C}[q^{\pm }]$
.
$\mathbb{C}[q^{\pm }]$
.
5.2 The braiding functor
Like the braiding structure (14) in
![]() ${\mathcal{S}}p_{n}$
we can define a functor
${\mathcal{S}}p_{n}$
we can define a functor
 ${\mathcal{B}}_{m}(\{0,\ldots ,n\})\rightarrow (\dot{U}_{[q^{\pm }]}\mathfrak{g}\mathfrak{l}_{m})^{n}$
as follows (following [Reference LusztigLus93, 5.2.1]). On objects it takes
${\mathcal{B}}_{m}(\{0,\ldots ,n\})\rightarrow (\dot{U}_{[q^{\pm }]}\mathfrak{g}\mathfrak{l}_{m})^{n}$
as follows (following [Reference LusztigLus93, 5.2.1]). On objects it takes
![]() $\text{}\underline{k}\mapsto \text{}\underline{k}$
. On morphisms it takes
$\text{}\underline{k}\mapsto \text{}\underline{k}$
. On morphisms it takes
 $$\begin{eqnarray}T_{i}1_{\text{}\underline{k}}\mapsto (-1)^{k_{i}k_{i+1}}(-q)^{k_{i}}\mathop{\sum }_{\substack{ a,b\geqslant 0 \\ b-a=k_{i}-k_{i+1}}}(-q)^{-b}E_{i}^{(a)}F_{i}^{(b)}1_{\text{}\underline{k}}.\end{eqnarray}$$
$$\begin{eqnarray}T_{i}1_{\text{}\underline{k}}\mapsto (-1)^{k_{i}k_{i+1}}(-q)^{k_{i}}\mathop{\sum }_{\substack{ a,b\geqslant 0 \\ b-a=k_{i}-k_{i+1}}}(-q)^{-b}E_{i}^{(a)}F_{i}^{(b)}1_{\text{}\underline{k}}.\end{eqnarray}$$
Remark 5.3. If
 $k_{i}=k_{i+1}=1$
, the formula for the braiding simplifies to give
$k_{i}=k_{i+1}=1$
, the formula for the braiding simplifies to give
 $$\begin{eqnarray}T_{i}1_{\text{}\underline{k}}\mapsto q1_{\text{}\underline{k}}-E_{i}F_{i}1_{\text{}\underline{k}}.\end{eqnarray}$$
$$\begin{eqnarray}T_{i}1_{\text{}\underline{k}}\mapsto q1_{\text{}\underline{k}}-E_{i}F_{i}1_{\text{}\underline{k}}.\end{eqnarray}$$
Lemma 5.4. For
 $i,j\in \{1,\ldots ,m-1\}$
we have, inside
$i,j\in \{1,\ldots ,m-1\}$
we have, inside
 $(\dot{U}_{[q^{\pm }]}\mathfrak{g}\mathfrak{l}_{m})^{n}$
,
$(\dot{U}_{[q^{\pm }]}\mathfrak{g}\mathfrak{l}_{m})^{n}$
,
 $T_{j}E_{i}^{(s)}=E_{i}^{(s)}T_{j}$
if
$T_{j}E_{i}^{(s)}=E_{i}^{(s)}T_{j}$
if
 $|i-j|>1$
and
$|i-j|>1$
and
 $T_{i}T_{j}E_{i}^{(s)}=E_{j}^{(s)}T_{i}T_{j}$
if
$T_{i}T_{j}E_{i}^{(s)}=E_{j}^{(s)}T_{i}T_{j}$
if
 $|i-j|=1$
, where the definition of the elements
$|i-j|=1$
, where the definition of the elements
![]() $T_{i}$
are given by (16).
$T_{i}$
are given by (16).
Proof. This follows from [Reference LusztigLus93, § 39.2.4] (see also [Reference Cautis, Kamnitzer and MorrisonCKM14, Lemma 6.1.3]). ◻
5.3 Representations of
 $(\dot{U}_{[q^{\pm }]}L\mathfrak{g}\mathfrak{l}_{m})^{n}$
$(\dot{U}_{[q^{\pm }]}L\mathfrak{g}\mathfrak{l}_{m})^{n}$
The description above gives
 $\dot{U}_{[q^{\pm }]}L\mathfrak{g}\mathfrak{l}_{m}$
in its Kac–Moody form rather than its more common loop form. In the latter form, one also considers generators
$\dot{U}_{[q^{\pm }]}L\mathfrak{g}\mathfrak{l}_{m}$
in its Kac–Moody form rather than its more common loop form. In the latter form, one also considers generators
 $E_{i}\otimes t^{r},F_{i}\otimes t^{r}$
, for
$E_{i}\otimes t^{r},F_{i}\otimes t^{r}$
, for
![]() $r\in \mathbb{Z}$
, but no
$r\in \mathbb{Z}$
, but no
![]() $E_{0}$
or
$E_{0}$
or
![]() $F_{0}$
.
$F_{0}$
.
The advantage of the Kac–Moody presentation of
 $\dot{U}_{[q^{\pm }]}L\mathfrak{g}\mathfrak{l}_{m}$
is that it is more closely related to the annular spider category
$\dot{U}_{[q^{\pm }]}L\mathfrak{g}\mathfrak{l}_{m}$
is that it is more closely related to the annular spider category
![]() ${\mathcal{A}}{\mathcal{S}}p_{n}$
. However, we will need to define representations of
${\mathcal{A}}{\mathcal{S}}p_{n}$
. However, we will need to define representations of
 $(\dot{U}_{[q^{\pm }]}L\mathfrak{g}\mathfrak{l}_{m})^{n}$
which are more naturally defined in the loop presentation. The following technical lemma tells us how to deal with this issue. It shows that it suffices to define the functor on
$(\dot{U}_{[q^{\pm }]}L\mathfrak{g}\mathfrak{l}_{m})^{n}$
which are more naturally defined in the loop presentation. The following technical lemma tells us how to deal with this issue. It shows that it suffices to define the functor on
 $(\dot{U}_{[q^{\pm }]}\mathfrak{g}\mathfrak{l}_{m})^{n}$
together with a compatible functor from the annular braid groupoid.
$(\dot{U}_{[q^{\pm }]}\mathfrak{g}\mathfrak{l}_{m})^{n}$
together with a compatible functor from the annular braid groupoid.
Lemma 5.5. Let
![]() ${\mathcal{C}}$
be any
${\mathcal{C}}$
be any
![]() $\mathbb{C}$
-linear category.
$\mathbb{C}$
-linear category.
Suppose you have a
![]() $\mathbb{C}$
-linear functor
$\mathbb{C}$
-linear functor
 $\unicode[STIX]{x1D719}\,:\,(\dot{U}_{[q^{\pm }]}\mathfrak{g}\mathfrak{l}_{m})^{n}\,\rightarrow \,{\mathcal{C}}$
and a functor
$\unicode[STIX]{x1D719}\,:\,(\dot{U}_{[q^{\pm }]}\mathfrak{g}\mathfrak{l}_{m})^{n}\,\rightarrow \,{\mathcal{C}}$
and a functor
 $\unicode[STIX]{x1D6FD}\,:\,{\mathcal{A}}{\mathcal{B}}_{m}(\{0,\ldots ,n\})\rightarrow {\mathcal{C}}$
satisfying the following:
$\unicode[STIX]{x1D6FD}\,:\,{\mathcal{A}}{\mathcal{B}}_{m}(\{0,\ldots ,n\})\rightarrow {\mathcal{C}}$
satisfying the following:
-
(i)
 $\unicode[STIX]{x1D6FD}(T_{i})=\unicode[STIX]{x1D719}(T_{i})$
for all
$\unicode[STIX]{x1D6FD}(T_{i})=\unicode[STIX]{x1D719}(T_{i})$
for all
 $i=1,\ldots ,m-1$
where in the case of
$i=1,\ldots ,m-1$
where in the case of
 $\unicode[STIX]{x1D719}(T_{i})$
we regard
$\unicode[STIX]{x1D719}(T_{i})$
we regard
 $T_{i}$
as a morphism in
$T_{i}$
as a morphism in
 $(\dot{U}_{[q^{\pm }]}\mathfrak{g}\mathfrak{l}_{m})^{n}$
via (16);
$(\dot{U}_{[q^{\pm }]}\mathfrak{g}\mathfrak{l}_{m})^{n}$
via (16); -
(ii)
 $\unicode[STIX]{x1D6FD}(X_{1})$
commutes with
$\unicode[STIX]{x1D6FD}(X_{1})$
commutes with
 $\unicode[STIX]{x1D719}(E_{i}^{(s)})$
and
$\unicode[STIX]{x1D719}(E_{i}^{(s)})$
and
 $\unicode[STIX]{x1D719}(F_{i}^{(s)})$
for
$\unicode[STIX]{x1D719}(F_{i}^{(s)})$
for
 $i=2,\ldots ,m-1$
;
$i=2,\ldots ,m-1$
; -
(iii)
 $\unicode[STIX]{x1D6FD}(X_{1}\ldots X_{m})$
commutes with everything in the image of
$\unicode[STIX]{x1D6FD}(X_{1}\ldots X_{m})$
commutes with everything in the image of
 $\unicode[STIX]{x1D719}$
.
$\unicode[STIX]{x1D719}$
.
Then
![]() $\unicode[STIX]{x1D719}$
and
$\unicode[STIX]{x1D719}$
and
![]() $\unicode[STIX]{x1D6FD}$
extend to a
$\unicode[STIX]{x1D6FD}$
extend to a
![]() $\mathbb{C}$
-linear functor
$\mathbb{C}$
-linear functor
 $\unicode[STIX]{x1D6F7}:(\dot{U}_{[q^{\pm }]}L\mathfrak{g}\mathfrak{l}_{m})^{n}\rightarrow {\mathcal{C}}$
.
$\unicode[STIX]{x1D6F7}:(\dot{U}_{[q^{\pm }]}L\mathfrak{g}\mathfrak{l}_{m})^{n}\rightarrow {\mathcal{C}}$
.
Proof. Since
![]() $\unicode[STIX]{x1D719}$
already tells us where to map
$\unicode[STIX]{x1D719}$
already tells us where to map
 $E_{i}^{(s)},F_{i}^{(s)}$
, for
$E_{i}^{(s)},F_{i}^{(s)}$
, for
 $i=1,\ldots ,m-1$
and all
$i=1,\ldots ,m-1$
and all
![]() $s\in \mathbb{N}$
, we only need to say where
$s\in \mathbb{N}$
, we only need to say where
 $E_{0}^{(s)},F_{0}^{(s)}$
and
$E_{0}^{(s)},F_{0}^{(s)}$
and
![]() $R$
are mapped. We define
$R$
are mapped. We define
 $$\begin{eqnarray}\unicode[STIX]{x1D6F7}(R1_{\text{}\underline{k}}):=\unicode[STIX]{x1D6FD}(X_{1}T_{1}\cdots T_{m-1}1_{\text{}\underline{k}})\end{eqnarray}$$
$$\begin{eqnarray}\unicode[STIX]{x1D6F7}(R1_{\text{}\underline{k}}):=\unicode[STIX]{x1D6FD}(X_{1}T_{1}\cdots T_{m-1}1_{\text{}\underline{k}})\end{eqnarray}$$
and then
 $\unicode[STIX]{x1D6F7}(E_{0}^{(s)}):=\unicode[STIX]{x1D6F7}(R)\unicode[STIX]{x1D6F7}(E_{m-1}^{(s)})\unicode[STIX]{x1D6F7}(R^{-1})$
and similarly for
$\unicode[STIX]{x1D6F7}(E_{0}^{(s)}):=\unicode[STIX]{x1D6F7}(R)\unicode[STIX]{x1D6F7}(E_{m-1}^{(s)})\unicode[STIX]{x1D6F7}(R^{-1})$
and similarly for
![]() $F_{0}^{(s)}$
.
$F_{0}^{(s)}$
.
Now we need to show that
 $\unicode[STIX]{x1D6F7}(R)\unicode[STIX]{x1D6F7}(E_{i}^{(s)})=\unicode[STIX]{x1D6F7}(E_{i+1}^{(s)})\unicode[STIX]{x1D6F7}(R)$
holds (the analogous results for the generators
$\unicode[STIX]{x1D6F7}(R)\unicode[STIX]{x1D6F7}(E_{i}^{(s)})=\unicode[STIX]{x1D6F7}(E_{i+1}^{(s)})\unicode[STIX]{x1D6F7}(R)$
holds (the analogous results for the generators
![]() $F_{i}$
follow similarly). For
$F_{i}$
follow similarly). For
 $i=1,\ldots ,m-2$
, we have
$i=1,\ldots ,m-2$
, we have
 $$\begin{eqnarray}\displaystyle \unicode[STIX]{x1D6F7}(R)\unicode[STIX]{x1D6F7}(E_{i}^{(s)}) & = & \displaystyle \unicode[STIX]{x1D6FD}(X_{1})\unicode[STIX]{x1D6F7}(T_{1}\cdots T_{m-1}E_{i}^{(s)})\nonumber\\ \displaystyle & = & \displaystyle \unicode[STIX]{x1D6FD}(X_{1})\unicode[STIX]{x1D6F7}(E_{i+1}^{(s)}T_{1}\cdots T_{m-1})\nonumber\\ \displaystyle & = & \displaystyle \unicode[STIX]{x1D6F7}(E_{i+1}^{(s)})\unicode[STIX]{x1D6FD}(X_{1})\unicode[STIX]{x1D6FD}(T_{1}\cdots T_{m-1})\nonumber\\ \displaystyle & = & \displaystyle \unicode[STIX]{x1D6F7}(E_{i+1}^{(s)})\unicode[STIX]{x1D6F7}(R),\end{eqnarray}$$
$$\begin{eqnarray}\displaystyle \unicode[STIX]{x1D6F7}(R)\unicode[STIX]{x1D6F7}(E_{i}^{(s)}) & = & \displaystyle \unicode[STIX]{x1D6FD}(X_{1})\unicode[STIX]{x1D6F7}(T_{1}\cdots T_{m-1}E_{i}^{(s)})\nonumber\\ \displaystyle & = & \displaystyle \unicode[STIX]{x1D6FD}(X_{1})\unicode[STIX]{x1D6F7}(E_{i+1}^{(s)}T_{1}\cdots T_{m-1})\nonumber\\ \displaystyle & = & \displaystyle \unicode[STIX]{x1D6F7}(E_{i+1}^{(s)})\unicode[STIX]{x1D6FD}(X_{1})\unicode[STIX]{x1D6FD}(T_{1}\cdots T_{m-1})\nonumber\\ \displaystyle & = & \displaystyle \unicode[STIX]{x1D6F7}(E_{i+1}^{(s)})\unicode[STIX]{x1D6F7}(R),\end{eqnarray}$$
where the second equality follows using Lemma 5.4 repeatedly, while the third follows by condition (i).
Now, we check the cases
 $m=0,m-1$
. The case
$m=0,m-1$
. The case
 $i=m-1$
holds by definition. For the case
$i=m-1$
holds by definition. For the case
![]() $i=0$
, we must show that
$i=0$
, we must show that
 $\unicode[STIX]{x1D6F7}(R)\unicode[STIX]{x1D6F7}(E_{0}^{(s)})=\unicode[STIX]{x1D6F7}(E_{1}^{(s)})\unicode[STIX]{x1D6F7}(R)$
. This follows by writing
$\unicode[STIX]{x1D6F7}(R)\unicode[STIX]{x1D6F7}(E_{0}^{(s)})=\unicode[STIX]{x1D6F7}(E_{1}^{(s)})\unicode[STIX]{x1D6F7}(R)$
. This follows by writing
 $\unicode[STIX]{x1D6F7}(E_{0}^{(s)})=\unicode[STIX]{x1D6F7}(R)\unicode[STIX]{x1D6F7}(E_{m-1}^{(s)})\unicode[STIX]{x1D6F7}(R^{-1})$
and then using (17) repeatedly, together with the fact that
$\unicode[STIX]{x1D6F7}(E_{0}^{(s)})=\unicode[STIX]{x1D6F7}(R)\unicode[STIX]{x1D6F7}(E_{m-1}^{(s)})\unicode[STIX]{x1D6F7}(R^{-1})$
and then using (17) repeatedly, together with the fact that
 $\unicode[STIX]{x1D6F7}(R)^{m}=\unicode[STIX]{x1D6F7}(R^{m})=\unicode[STIX]{x1D6FD}(X_{1}\ldots X_{m})$
commutes with everything (condition (iii)). This completes the proof.◻
$\unicode[STIX]{x1D6F7}(R)^{m}=\unicode[STIX]{x1D6F7}(R^{m})=\unicode[STIX]{x1D6FD}(X_{1}\ldots X_{m})$
commutes with everything (condition (iii)). This completes the proof.◻
5.4 Embeddings
Observe that we have
 $2(m+1)$
faithful functors
$2(m+1)$
faithful functors
 $(\dot{U}_{[q^{\pm }]}L\mathfrak{g}\mathfrak{l}_{m})^{n}\rightarrow (\dot{U}_{[q^{\pm }]}L\mathfrak{g}\mathfrak{l}_{m+1})^{n}$
, given by adding either a
$(\dot{U}_{[q^{\pm }]}L\mathfrak{g}\mathfrak{l}_{m})^{n}\rightarrow (\dot{U}_{[q^{\pm }]}L\mathfrak{g}\mathfrak{l}_{m+1})^{n}$
, given by adding either a
![]() $0$
or an
$0$
or an
![]() $n$
in some slot. For concreteness let us describe the functor of adding a
$n$
in some slot. For concreteness let us describe the functor of adding a
![]() $0$
at the end. On objects it is given by
$0$
at the end. On objects it is given by
 $(k_{1},\ldots ,k_{m})\mapsto (k_{1},\ldots ,k_{m},0)$
. On morphisms it is given by
$(k_{1},\ldots ,k_{m})\mapsto (k_{1},\ldots ,k_{m},0)$
. On morphisms it is given by
 $$\begin{eqnarray}\displaystyle R & \mapsto & \displaystyle R,\nonumber\\ \displaystyle E_{i}^{(s)} & \mapsto & \displaystyle E_{i}^{(s)}\quad \text{and}\quad F_{i}^{(s)}\mapsto F_{i}^{(s)}\quad \text{if }i\neq 0,\nonumber\\ \displaystyle E_{0}^{(s)} & \mapsto & \displaystyle E_{m}^{(s)}E_{0}^{(s)}\quad \text{and}\quad F_{0}^{(s)}\mapsto F_{0}^{(s)}F_{m}^{(s)}.\nonumber\end{eqnarray}$$
$$\begin{eqnarray}\displaystyle R & \mapsto & \displaystyle R,\nonumber\\ \displaystyle E_{i}^{(s)} & \mapsto & \displaystyle E_{i}^{(s)}\quad \text{and}\quad F_{i}^{(s)}\mapsto F_{i}^{(s)}\quad \text{if }i\neq 0,\nonumber\\ \displaystyle E_{0}^{(s)} & \mapsto & \displaystyle E_{m}^{(s)}E_{0}^{(s)}\quad \text{and}\quad F_{0}^{(s)}\mapsto F_{0}^{(s)}F_{m}^{(s)}.\nonumber\end{eqnarray}$$
Proposition 5.6. The functor
 $(\dot{U}_{[q^{\pm }]}L\mathfrak{g}\mathfrak{l}_{m})^{n}\rightarrow (\dot{U}_{[q^{\pm }]}L\mathfrak{g}\mathfrak{l}_{m+1})^{n}$
is faithful.
$(\dot{U}_{[q^{\pm }]}L\mathfrak{g}\mathfrak{l}_{m})^{n}\rightarrow (\dot{U}_{[q^{\pm }]}L\mathfrak{g}\mathfrak{l}_{m+1})^{n}$
is faithful.
Proof. For the purposes of this proof, we will use
 $(U_{[q^{\pm }]}L\mathfrak{g}\mathfrak{l}_{m})^{n}$
to denote the ‘algebra version’ of the category
$(U_{[q^{\pm }]}L\mathfrak{g}\mathfrak{l}_{m})^{n}$
to denote the ‘algebra version’ of the category
 $(\dot{U}_{[q^{\pm }]}L\mathfrak{g}\mathfrak{l}_{m})^{n}$
(i.e. the algebra obtained as the direct sum of all Hom spaces in the category). Then we must prove that the (non-unital) map of algebras
$(\dot{U}_{[q^{\pm }]}L\mathfrak{g}\mathfrak{l}_{m})^{n}$
(i.e. the algebra obtained as the direct sum of all Hom spaces in the category). Then we must prove that the (non-unital) map of algebras
 $(U_{[q^{\pm }]}L\mathfrak{g}\mathfrak{l}_{m})^{n}\rightarrow (U_{[q^{\pm }]}L\mathfrak{g}\mathfrak{l}_{m+1})^{n}$
is injective.
$(U_{[q^{\pm }]}L\mathfrak{g}\mathfrak{l}_{m})^{n}\rightarrow (U_{[q^{\pm }]}L\mathfrak{g}\mathfrak{l}_{m+1})^{n}$
is injective.
For any
 $\unicode[STIX]{x1D706}=(\unicode[STIX]{x1D706}_{1},\ldots ,\unicode[STIX]{x1D706}_{m})$
with
$\unicode[STIX]{x1D706}=(\unicode[STIX]{x1D706}_{1},\ldots ,\unicode[STIX]{x1D706}_{m})$
with
 $\unicode[STIX]{x1D706}_{1}\geqslant \ldots \geqslant \unicode[STIX]{x1D706}_{m}$
, let
$\unicode[STIX]{x1D706}_{1}\geqslant \ldots \geqslant \unicode[STIX]{x1D706}_{m}$
, let
![]() $V(\unicode[STIX]{x1D706})$
denote the extremal weight module for
$V(\unicode[STIX]{x1D706})$
denote the extremal weight module for
 $U_{[q^{\pm }]}L\mathfrak{g}\mathfrak{l}_{m}$
. Let
$U_{[q^{\pm }]}L\mathfrak{g}\mathfrak{l}_{m}$
. Let
 $P_{n,m}=\{(\unicode[STIX]{x1D706}_{1},\ldots ,\unicode[STIX]{x1D706}_{m}):n\geqslant \unicode[STIX]{x1D706}_{1}\ldots \geqslant \unicode[STIX]{x1D706}_{m}\geqslant 0\}$
. By Proposition 6.4 of [Reference McGertyMcG07], we know that
$P_{n,m}=\{(\unicode[STIX]{x1D706}_{1},\ldots ,\unicode[STIX]{x1D706}_{m}):n\geqslant \unicode[STIX]{x1D706}_{1}\ldots \geqslant \unicode[STIX]{x1D706}_{m}\geqslant 0\}$
. By Proposition 6.4 of [Reference McGertyMcG07], we know that
 $(U_{[q^{\pm }]}L\mathfrak{g}\mathfrak{l}_{m})^{n}$
is the image of
$(U_{[q^{\pm }]}L\mathfrak{g}\mathfrak{l}_{m})^{n}$
is the image of
 $U_{[q^{\pm }]}L\mathfrak{g}\mathfrak{l}_{m}$
inside
$U_{[q^{\pm }]}L\mathfrak{g}\mathfrak{l}_{m}$
inside
 $\bigoplus _{\unicode[STIX]{x1D706}\in P_{n,m}}\operatorname{End}V(\unicode[STIX]{x1D706})$
.
$\bigoplus _{\unicode[STIX]{x1D706}\in P_{n,m}}\operatorname{End}V(\unicode[STIX]{x1D706})$
.
If
 $\unicode[STIX]{x1D706}\in P_{n,m}$
, then we can add a
$\unicode[STIX]{x1D706}\in P_{n,m}$
, then we can add a
![]() $0$
to this sequence to produce
$0$
to this sequence to produce
 $(\unicode[STIX]{x1D706},0)\in P_{n,m+1}$
. By the lemma below, the restriction of
$(\unicode[STIX]{x1D706},0)\in P_{n,m+1}$
. By the lemma below, the restriction of
![]() $V(\unicode[STIX]{x1D706},0)$
to
$V(\unicode[STIX]{x1D706},0)$
to
 $U_{[q^{\pm }]}L\mathfrak{g}\mathfrak{l}_{m}$
contains
$U_{[q^{\pm }]}L\mathfrak{g}\mathfrak{l}_{m}$
contains
![]() $V(\unicode[STIX]{x1D706})$
. Thus the composite map
$V(\unicode[STIX]{x1D706})$
. Thus the composite map
 $$\begin{eqnarray}(U_{[q^{\pm }]}L\mathfrak{g}\mathfrak{l}_{m})^{n}\rightarrow (U_{[q^{\pm }]}L\mathfrak{g}\mathfrak{l}_{m+1})^{n}\rightarrow \bigoplus _{\unicode[STIX]{x1D706}\in P_{n,m}}\operatorname{End}(V(\unicode[STIX]{x1D706},0))\end{eqnarray}$$
$$\begin{eqnarray}(U_{[q^{\pm }]}L\mathfrak{g}\mathfrak{l}_{m})^{n}\rightarrow (U_{[q^{\pm }]}L\mathfrak{g}\mathfrak{l}_{m+1})^{n}\rightarrow \bigoplus _{\unicode[STIX]{x1D706}\in P_{n,m}}\operatorname{End}(V(\unicode[STIX]{x1D706},0))\end{eqnarray}$$
is injective. Thus,
 $(U_{[q^{\pm }]}L\mathfrak{g}\mathfrak{l}_{m})^{n}\rightarrow (U_{[q^{\pm }]}L\mathfrak{g}\mathfrak{l}_{m+1})^{n}$
is injective as desired.◻
$(U_{[q^{\pm }]}L\mathfrak{g}\mathfrak{l}_{m})^{n}\rightarrow (U_{[q^{\pm }]}L\mathfrak{g}\mathfrak{l}_{m+1})^{n}$
is injective as desired.◻
Lemma 5.7. Let
 $\unicode[STIX]{x1D706}\in P_{n,m}$
and let
$\unicode[STIX]{x1D706}\in P_{n,m}$
and let
![]() $v_{\unicode[STIX]{x1D706},0}$
be the generating vector of
$v_{\unicode[STIX]{x1D706},0}$
be the generating vector of
![]() $V(\unicode[STIX]{x1D706},0)$
. Then
$V(\unicode[STIX]{x1D706},0)$
. Then
![]() $v_{\unicode[STIX]{x1D706},0}$
generates
$v_{\unicode[STIX]{x1D706},0}$
generates
![]() $V(\unicode[STIX]{x1D706})$
as a
$V(\unicode[STIX]{x1D706})$
as a
 $\dot{U}_{[q^{\pm }]}L\mathfrak{g}\mathfrak{l}_{m}$
-module.
$\dot{U}_{[q^{\pm }]}L\mathfrak{g}\mathfrak{l}_{m}$
-module.
Proof. Let us write
 $\unicode[STIX]{x1D706}=\sum _{i=1}^{m}w_{i}\unicode[STIX]{x1D714}_{i}$
where
$\unicode[STIX]{x1D706}=\sum _{i=1}^{m}w_{i}\unicode[STIX]{x1D714}_{i}$
where
 $\unicode[STIX]{x1D714}_{i}=(1,\ldots ,1,0,\ldots ,0)$
has length
$\unicode[STIX]{x1D714}_{i}=(1,\ldots ,1,0,\ldots ,0)$
has length
![]() $m$
. By [Reference Beck and NakajimaBN04, Corollary 4.15], we know that there is an injective map
$m$
. By [Reference Beck and NakajimaBN04, Corollary 4.15], we know that there is an injective map
 $V(\unicode[STIX]{x1D706},0)\rightarrow \bigotimes _{i\in I}V(\unicode[STIX]{x1D714}_{i},0)^{\otimes w_{i}}$
taking
$V(\unicode[STIX]{x1D706},0)\rightarrow \bigotimes _{i\in I}V(\unicode[STIX]{x1D714}_{i},0)^{\otimes w_{i}}$
taking
![]() $v_{\unicode[STIX]{x1D706},0}$
to the tensor products
$v_{\unicode[STIX]{x1D706},0}$
to the tensor products
![]() $\otimes v_{\unicode[STIX]{x1D714}_{i},0}^{\otimes w_{i}}$
of the generating vectors.
$\otimes v_{\unicode[STIX]{x1D714}_{i},0}^{\otimes w_{i}}$
of the generating vectors.
We also know that
 $V(\unicode[STIX]{x1D714}_{i},0)$
is isomorphic to
$V(\unicode[STIX]{x1D714}_{i},0)$
is isomorphic to
 $\bigwedge _{q}^{i}\mathbb{C}^{m+1}\otimes \mathbb{C}[t,t^{-1}]$
. Thus, upon restriction to
$\bigwedge _{q}^{i}\mathbb{C}^{m+1}\otimes \mathbb{C}[t,t^{-1}]$
. Thus, upon restriction to
 $\dot{U}_{[q^{\pm }]}L\mathfrak{g}\mathfrak{l}_{m}$
it is easy to see that the highest weight vector of
$\dot{U}_{[q^{\pm }]}L\mathfrak{g}\mathfrak{l}_{m}$
it is easy to see that the highest weight vector of
 $V(\unicode[STIX]{x1D714}_{i},0)$
generates a copy of
$V(\unicode[STIX]{x1D714}_{i},0)$
generates a copy of
![]() $V(\unicode[STIX]{x1D714}_{i})$
.
$V(\unicode[STIX]{x1D714}_{i})$
.
Thus, we see that as a
 $\dot{U}_{[q^{\pm }]}L\mathfrak{g}\mathfrak{l}_{m}$
-module,
$\dot{U}_{[q^{\pm }]}L\mathfrak{g}\mathfrak{l}_{m}$
-module,
![]() $v_{\unicode[STIX]{x1D706},0}$
generates the same module as does
$v_{\unicode[STIX]{x1D706},0}$
generates the same module as does
![]() $\otimes v_{\unicode[STIX]{x1D714}_{i}}^{\otimes w_{i}}$
inside
$\otimes v_{\unicode[STIX]{x1D714}_{i}}^{\otimes w_{i}}$
inside
 $\otimes V(\unicode[STIX]{x1D714}_{i})^{\otimes w_{i}}$
and hence the lemma follows.◻
$\otimes V(\unicode[STIX]{x1D714}_{i})^{\otimes w_{i}}$
and hence the lemma follows.◻
5.5 From quantum loop algebras to annular spiders
In [Reference Cautis, Kamnitzer and MorrisonCKM14] we studied the spider category
 ${\mathcal{S}}p_{n}[q^{\pm }]$
by defining a functor
${\mathcal{S}}p_{n}[q^{\pm }]$
by defining a functor
 $\unicode[STIX]{x1D6F9}_{m}:(\dot{U}_{[q^{\pm }]}\mathfrak{g}\mathfrak{l}_{m})^{n}\rightarrow {\mathcal{S}}p_{n}[q^{\pm }]$
for each
$\unicode[STIX]{x1D6F9}_{m}:(\dot{U}_{[q^{\pm }]}\mathfrak{g}\mathfrak{l}_{m})^{n}\rightarrow {\mathcal{S}}p_{n}[q^{\pm }]$
for each
![]() $m$
. In exactly the same way one can define a functor
$m$
. In exactly the same way one can define a functor
 $$\begin{eqnarray}A\unicode[STIX]{x1D6F9}_{m}:(\dot{U}_{[q^{\pm }]}L\mathfrak{g}\mathfrak{l}_{m})^{n}\rightarrow {\mathcal{A}}{\mathcal{S}}p_{n}[q^{\pm }].\end{eqnarray}$$
$$\begin{eqnarray}A\unicode[STIX]{x1D6F9}_{m}:(\dot{U}_{[q^{\pm }]}L\mathfrak{g}\mathfrak{l}_{m})^{n}\rightarrow {\mathcal{A}}{\mathcal{S}}p_{n}[q^{\pm }].\end{eqnarray}$$
More precisely, on objects it takes
![]() $\text{}\underline{k}$
to
$\text{}\underline{k}$
to
![]() $\overline{\text{}\underline{k}}$
where
$\overline{\text{}\underline{k}}$
where
![]() $\overline{\text{}\underline{k}}$
is the sequence obtained from
$\overline{\text{}\underline{k}}$
is the sequence obtained from
![]() $\text{}\underline{k}$
by deleting all
$\text{}\underline{k}$
by deleting all
![]() $0,n$
. On morphisms we define
$0,n$
. On morphisms we define
![]() $A\unicode[STIX]{x1D6F9}_{m}$
by forming ‘ladder-like’ webs, as in [Reference Cautis, Kamnitzer and MorrisonCKM14], the only difference being that
$A\unicode[STIX]{x1D6F9}_{m}$
by forming ‘ladder-like’ webs, as in [Reference Cautis, Kamnitzer and MorrisonCKM14], the only difference being that
 $E_{0}^{(s)},F_{0}^{(s)}$
are sent to webs which ‘wrap-around’ the annulus crossing the cut line, as illustrated in (18) with
$E_{0}^{(s)},F_{0}^{(s)}$
are sent to webs which ‘wrap-around’ the annulus crossing the cut line, as illustrated in (18) with
![]() $E_{0}^{(s)}$
. Note that this functor was also defined in [Reference QueffelecQue15, § 2.3].
$E_{0}^{(s)}$
. Note that this functor was also defined in [Reference QueffelecQue15, § 2.3].

Theorem 5.8. The functor
 $A\unicode[STIX]{x1D6F9}_{m}:(\dot{U}_{[q^{\pm }]}L\mathfrak{g}\mathfrak{l}_{m})^{n}\rightarrow {\mathcal{A}}{\mathcal{S}}p_{n}[q^{\pm }]$
is faithful.
$A\unicode[STIX]{x1D6F9}_{m}:(\dot{U}_{[q^{\pm }]}L\mathfrak{g}\mathfrak{l}_{m})^{n}\rightarrow {\mathcal{A}}{\mathcal{S}}p_{n}[q^{\pm }]$
is faithful.
Moreover, suppose that
![]() $\text{}\underline{k},\text{}\underline{k}^{\prime }$
are two sequences drawn from
$\text{}\underline{k},\text{}\underline{k}^{\prime }$
are two sequences drawn from
 $\{1,\ldots ,n-1\}$
. Given a morphism
$\{1,\ldots ,n-1\}$
. Given a morphism
 $w\in \operatorname{Hom}_{{\mathcal{A}}{\mathcal{S}}p_{n}[q^{\pm }]}(\text{}\underline{k},\text{}\underline{k}^{\prime })$
, there exists some
$w\in \operatorname{Hom}_{{\mathcal{A}}{\mathcal{S}}p_{n}[q^{\pm }]}(\text{}\underline{k},\text{}\underline{k}^{\prime })$
, there exists some
![]() $m$
and a way to add
$m$
and a way to add
![]() $0$
s and
$0$
s and
![]() $n$
s to
$n$
s to
![]() $\text{}\underline{k},\text{}\underline{k}^{\prime }$
to form
$\text{}\underline{k},\text{}\underline{k}^{\prime }$
to form
![]() $\text{}\underline{l},\text{}\underline{l}^{\prime }$
of length
$\text{}\underline{l},\text{}\underline{l}^{\prime }$
of length
![]() $m$
such that
$m$
such that
![]() $w$
lies in the image of
$w$
lies in the image of
 $$\begin{eqnarray}A\unicode[STIX]{x1D6F9}_{m}:\operatorname{Hom}_{(\dot{U}_{[q^{\pm }]}L\mathfrak{g}\mathfrak{l}_{m})^{n}}(\text{}\underline{l},\text{}\underline{l}^{\prime })\rightarrow \operatorname{Hom}_{{\mathcal{A}}{\mathcal{S}}p_{n}[q^{\pm }]}(\text{}\underline{k},\text{}\underline{k}^{\prime }).\end{eqnarray}$$
$$\begin{eqnarray}A\unicode[STIX]{x1D6F9}_{m}:\operatorname{Hom}_{(\dot{U}_{[q^{\pm }]}L\mathfrak{g}\mathfrak{l}_{m})^{n}}(\text{}\underline{l},\text{}\underline{l}^{\prime })\rightarrow \operatorname{Hom}_{{\mathcal{A}}{\mathcal{S}}p_{n}[q^{\pm }]}(\text{}\underline{k},\text{}\underline{k}^{\prime }).\end{eqnarray}$$
Proof. We begin with the surjectivity part of the statement. Note that is suffices to prove this for the case when
![]() $w$
is an annular web (rather than a linear combination). If we have any annular web
$w$
is an annular web (rather than a linear combination). If we have any annular web
![]() $w$
between two objects
$w$
between two objects
![]() $\text{}\underline{k},\text{}\underline{k}^{\prime }$
, then we can turn
$\text{}\underline{k},\text{}\underline{k}^{\prime }$
, then we can turn
![]() $w$
into a ladder-like web as follows.
$w$
into a ladder-like web as follows.
We will call the radial coordinate on the annulus, time. Let
 $t_{1},\ldots ,t_{p-1}$
be the times at which
$t_{1},\ldots ,t_{p-1}$
be the times at which
![]() $w$
crosses the cut line. Then we can write
$w$
crosses the cut line. Then we can write
![]() $w$
as the composition
$w$
as the composition
 $w=w_{p}R^{\pm }\cdots R^{\pm }w_{2}R^{\pm }w_{1}$
where
$w=w_{p}R^{\pm }\cdots R^{\pm }w_{2}R^{\pm }w_{1}$
where
![]() $w_{i}$
denotes the part of
$w_{i}$
denotes the part of
![]() $w$
between times
$w$
between times
![]() $t_{i-1}$
and
$t_{i-1}$
and
![]() $t_{i}$
(we write
$t_{i}$
(we write
![]() $t_{0}$
for the inside and
$t_{0}$
for the inside and
![]() $t_{p}$
for the outside). In this composition, we see
$t_{p}$
for the outside). In this composition, we see
![]() $R$
if the cut line is cut with a right-pointing strand and
$R$
if the cut line is cut with a right-pointing strand and
![]() $R^{-1}$
if the cut line is cut with a left-pointing strand. Each web
$R^{-1}$
if the cut line is cut with a left-pointing strand. Each web
![]() $w_{i}$
is a web which does not cross the cut line and thus is a planar web.
$w_{i}$
is a web which does not cross the cut line and thus is a planar web.
In order to apply [Reference Cautis, Kamnitzer and MorrisonCKM14, Theorem 5.3.1] we need each web
![]() $w_{i}$
to have their starting and ending strands pointing outwards (up in the terminology of [Reference Cautis, Kamnitzer and MorrisonCKM14]). To achieve this, we can insert pairs of cancelling tags everywhere we have downward pointing strands at some time
$w_{i}$
to have their starting and ending strands pointing outwards (up in the terminology of [Reference Cautis, Kamnitzer and MorrisonCKM14]). To achieve this, we can insert pairs of cancelling tags everywhere we have downward pointing strands at some time
![]() $t_{i}$
. Abusing notation slightly, we continue to use
$t_{i}$
. Abusing notation slightly, we continue to use
 $w_{1},\ldots ,w_{p}$
to denote the webs obtained by this procedure.
$w_{1},\ldots ,w_{p}$
to denote the webs obtained by this procedure.
Now, for each
![]() $i$
we can apply [Reference Cautis, Kamnitzer and MorrisonCKM14, Theorem 5.3.1] to find
$i$
we can apply [Reference Cautis, Kamnitzer and MorrisonCKM14, Theorem 5.3.1] to find
![]() $m_{i}$
and an element
$m_{i}$
and an element
![]() $a_{i}$
such that
$a_{i}$
such that
 $\unicode[STIX]{x1D6F9}_{m_{i}}(a_{i})=w_{i}$
. Moreover, note that
$\unicode[STIX]{x1D6F9}_{m_{i}}(a_{i})=w_{i}$
. Moreover, note that
 $$\begin{eqnarray}\operatorname{Hom}((k_{1},\ldots ,k_{m}),(k_{2},\ldots ,k_{m},k_{1}))\ni R=A\unicode[STIX]{x1D6F9}_{m+1}(E_{0}^{(k_{1})}),\end{eqnarray}$$
$$\begin{eqnarray}\operatorname{Hom}((k_{1},\ldots ,k_{m}),(k_{2},\ldots ,k_{m},k_{1}))\ni R=A\unicode[STIX]{x1D6F9}_{m+1}(E_{0}^{(k_{1})}),\end{eqnarray}$$
where
 $E_{0}^{(k_{1})}\in \operatorname{Hom}((k_{1},\ldots ,k_{m},0),(0,k_{2},\ldots ,k_{m},k_{1}))$
and similarly for
$E_{0}^{(k_{1})}\in \operatorname{Hom}((k_{1},\ldots ,k_{m},0),(0,k_{2},\ldots ,k_{m},k_{1}))$
and similarly for
![]() $R^{-1}$
. Combining all this together (by inserting as many
$R^{-1}$
. Combining all this together (by inserting as many
![]() $0$
s and
$0$
s and
![]() $n$
s as necessary) we get the desired statement.
$n$
s as necessary) we get the desired statement.
It remains to show that
![]() $A\unicode[STIX]{x1D6F9}_{m}$
is faithful. For this, let us note that both categories
$A\unicode[STIX]{x1D6F9}_{m}$
is faithful. For this, let us note that both categories
 $(\dot{U}_{[q^{\pm }]}L\mathfrak{g}\mathfrak{l}_{m})^{n}$
and
$(\dot{U}_{[q^{\pm }]}L\mathfrak{g}\mathfrak{l}_{m})^{n}$
and
 ${\mathcal{A}}{\mathcal{S}}p_{n}[q^{\pm }]$
are defined by generators and relations. Let
${\mathcal{A}}{\mathcal{S}}p_{n}[q^{\pm }]$
are defined by generators and relations. Let
![]() $\text{}\underline{l},\text{}\underline{l}^{\prime }$
be two objects in
$\text{}\underline{l},\text{}\underline{l}^{\prime }$
be two objects in
 $(\dot{U}_{[q^{\pm }]}L\mathfrak{g}\mathfrak{l}_{m})^{n}$
and let
$(\dot{U}_{[q^{\pm }]}L\mathfrak{g}\mathfrak{l}_{m})^{n}$
and let
![]() $\text{}\underline{k},\text{}\underline{k}^{\prime }$
denote the result of removing all
$\text{}\underline{k},\text{}\underline{k}^{\prime }$
denote the result of removing all
![]() $0,n$
from them.
$0,n$
from them.
Let
 $F_{(\dot{U}_{[q^{\pm }]}L\mathfrak{g}\mathfrak{l}_{m})^{n}}(\text{}\underline{l},\text{}\underline{l}^{\prime })$
denote the space of morphisms between these two objects in the free category with the same generators as
$F_{(\dot{U}_{[q^{\pm }]}L\mathfrak{g}\mathfrak{l}_{m})^{n}}(\text{}\underline{l},\text{}\underline{l}^{\prime })$
denote the space of morphisms between these two objects in the free category with the same generators as
 $(\dot{U}_{[q^{\pm }]}L\mathfrak{g}\mathfrak{l}_{m})^{n}$
and let
$(\dot{U}_{[q^{\pm }]}L\mathfrak{g}\mathfrak{l}_{m})^{n}$
and let
 $R_{(\dot{U}_{[q^{\pm }]}L\mathfrak{g}\mathfrak{l}_{m})^{n}}(\text{}\underline{l},\text{}\underline{l}^{\prime })$
denote the relations, so that
$R_{(\dot{U}_{[q^{\pm }]}L\mathfrak{g}\mathfrak{l}_{m})^{n}}(\text{}\underline{l},\text{}\underline{l}^{\prime })$
denote the relations, so that
 $$\begin{eqnarray}\operatorname{Hom}_{(\dot{U}_{[q^{\pm }]}L\mathfrak{g}\mathfrak{l}_{m})^{n}}(\text{}\underline{l},\text{}\underline{l}^{\prime })=F_{(\dot{U}_{[q^{\pm }]}L\mathfrak{g}\mathfrak{l}_{m})^{n}}(\text{}\underline{l},\text{}\underline{l}^{\prime })/R_{(\dot{U}_{[q^{\pm }]}L\mathfrak{g}\mathfrak{l}_{m})^{n}}(\text{}\underline{l},\text{}\underline{l}^{\prime }).\end{eqnarray}$$
$$\begin{eqnarray}\operatorname{Hom}_{(\dot{U}_{[q^{\pm }]}L\mathfrak{g}\mathfrak{l}_{m})^{n}}(\text{}\underline{l},\text{}\underline{l}^{\prime })=F_{(\dot{U}_{[q^{\pm }]}L\mathfrak{g}\mathfrak{l}_{m})^{n}}(\text{}\underline{l},\text{}\underline{l}^{\prime })/R_{(\dot{U}_{[q^{\pm }]}L\mathfrak{g}\mathfrak{l}_{m})^{n}}(\text{}\underline{l},\text{}\underline{l}^{\prime }).\end{eqnarray}$$
Similarly, we can define
 $F_{{\mathcal{A}}{\mathcal{S}}p_{n}[q^{\pm }]}(\text{}\underline{k},\text{}\underline{k}^{\prime })$
and
$F_{{\mathcal{A}}{\mathcal{S}}p_{n}[q^{\pm }]}(\text{}\underline{k},\text{}\underline{k}^{\prime })$
and
 $R_{{\mathcal{A}}{\mathcal{S}}p_{n}[q^{\pm }]}(\text{}\underline{k},\text{}\underline{k}^{\prime })$
and we have
$R_{{\mathcal{A}}{\mathcal{S}}p_{n}[q^{\pm }]}(\text{}\underline{k},\text{}\underline{k}^{\prime })$
and we have
 $$\begin{eqnarray}\operatorname{Hom}_{{\mathcal{A}}{\mathcal{S}}p_{n}[q^{\pm }]}(\text{}\underline{k},\text{}\underline{k}^{\prime })=F_{{\mathcal{A}}{\mathcal{S}}p_{n}[q^{\pm }]}(\text{}\underline{k},\text{}\underline{k}^{\prime })/R_{{\mathcal{A}}{\mathcal{S}}p_{n}[q^{\pm }]}(\text{}\underline{k},\text{}\underline{k}^{\prime }).\end{eqnarray}$$
$$\begin{eqnarray}\operatorname{Hom}_{{\mathcal{A}}{\mathcal{S}}p_{n}[q^{\pm }]}(\text{}\underline{k},\text{}\underline{k}^{\prime })=F_{{\mathcal{A}}{\mathcal{S}}p_{n}[q^{\pm }]}(\text{}\underline{k},\text{}\underline{k}^{\prime })/R_{{\mathcal{A}}{\mathcal{S}}p_{n}[q^{\pm }]}(\text{}\underline{k},\text{}\underline{k}^{\prime }).\end{eqnarray}$$
Now, suppose that
 $a\in \operatorname{Hom}_{(\dot{U}_{[q^{\pm }]}L\mathfrak{g}\mathfrak{l}_{m})^{n}}(\text{}\underline{l},\text{}\underline{l}^{\prime })$
and
$a\in \operatorname{Hom}_{(\dot{U}_{[q^{\pm }]}L\mathfrak{g}\mathfrak{l}_{m})^{n}}(\text{}\underline{l},\text{}\underline{l}^{\prime })$
and
 $A\unicode[STIX]{x1D6F9}_{m}(a)=0$
in
$A\unicode[STIX]{x1D6F9}_{m}(a)=0$
in
 $\operatorname{Hom}_{{\mathcal{A}}{\mathcal{S}}p_{n}[q^{\pm }]}(\text{}\underline{k},\text{}\underline{k}^{\prime })$
. This means that we have an element
$\operatorname{Hom}_{{\mathcal{A}}{\mathcal{S}}p_{n}[q^{\pm }]}(\text{}\underline{k},\text{}\underline{k}^{\prime })$
. This means that we have an element
 $a\in F_{(\dot{U}_{[q^{\pm }]}L\mathfrak{g}\mathfrak{l}_{m})^{n}}(\text{}\underline{l},\text{}\underline{l}^{\prime })$
and that
$a\in F_{(\dot{U}_{[q^{\pm }]}L\mathfrak{g}\mathfrak{l}_{m})^{n}}(\text{}\underline{l},\text{}\underline{l}^{\prime })$
and that
 $A\unicode[STIX]{x1D6F9}_{m}(a)\in R_{{\mathcal{A}}{\mathcal{S}}p_{n}[q^{\pm }]}(\text{}\underline{k},\text{}\underline{k}^{\prime })$
. This means that
$A\unicode[STIX]{x1D6F9}_{m}(a)\in R_{{\mathcal{A}}{\mathcal{S}}p_{n}[q^{\pm }]}(\text{}\underline{k},\text{}\underline{k}^{\prime })$
. This means that
![]() $a$
can be written as a linear combination of compositions of a generating relation in
$a$
can be written as a linear combination of compositions of a generating relation in
 ${\mathcal{A}}{\mathcal{S}}p_{n}[q^{\pm }]$
with elements of
${\mathcal{A}}{\mathcal{S}}p_{n}[q^{\pm }]$
with elements of
 ${\mathcal{A}}{\mathcal{S}}p_{n}[q^{\pm }]$
.
${\mathcal{A}}{\mathcal{S}}p_{n}[q^{\pm }]$
.
However, by inspection, we see that each generating relation (given in § 4.2) in
 ${\mathcal{A}}{\mathcal{S}}p_{n}[q^{\pm }]$
comes from a relation in some
${\mathcal{A}}{\mathcal{S}}p_{n}[q^{\pm }]$
comes from a relation in some
 $\dot{U}_{[q^{\pm }]}L\mathfrak{g}\mathfrak{l}_{p}$
. This observation, combined with the surjectivity proven above, shows that there exists
$\dot{U}_{[q^{\pm }]}L\mathfrak{g}\mathfrak{l}_{p}$
. This observation, combined with the surjectivity proven above, shows that there exists
![]() $M$
and sequences
$M$
and sequences
![]() $\text{}\underline{L},\text{}\underline{L^{\prime }}$
obtained by adding
$\text{}\underline{L},\text{}\underline{L^{\prime }}$
obtained by adding
![]() $0,n$
to
$0,n$
to
![]() $\text{}\underline{k},\text{}\underline{k}^{\prime }$
, and
$\text{}\underline{k},\text{}\underline{k}^{\prime }$
, and
 $b\in R_{(\dot{U}_{[q^{\pm }]}L\mathfrak{g}\mathfrak{l}_{M})^{n}}(\text{}\underline{L},\text{}\underline{L^{\prime }})$
such that
$b\in R_{(\dot{U}_{[q^{\pm }]}L\mathfrak{g}\mathfrak{l}_{M})^{n}}(\text{}\underline{L},\text{}\underline{L^{\prime }})$
such that
 $A\unicode[STIX]{x1D6F9}_{M}(b)=A\unicode[STIX]{x1D6F9}_{m}(a)$
. This means that
$A\unicode[STIX]{x1D6F9}_{M}(b)=A\unicode[STIX]{x1D6F9}_{m}(a)$
. This means that
![]() $a$
becomes 0 in
$a$
becomes 0 in
 $\operatorname{Hom}_{(\dot{U}_{[q^{\pm }]}L\mathfrak{g}\mathfrak{l}_{M})^{n}}(\text{}\underline{L},\text{}\underline{L^{\prime }})$
. However, by Proposition 5.6, the functor
$\operatorname{Hom}_{(\dot{U}_{[q^{\pm }]}L\mathfrak{g}\mathfrak{l}_{M})^{n}}(\text{}\underline{L},\text{}\underline{L^{\prime }})$
. However, by Proposition 5.6, the functor
 $(\dot{U}_{[q^{\pm }]}L\mathfrak{g}\mathfrak{l}_{m})^{n}\rightarrow (\dot{U}_{[q^{\pm }]}L\mathfrak{g}\mathfrak{l}_{M})^{n}$
is faithful, which means that
$(\dot{U}_{[q^{\pm }]}L\mathfrak{g}\mathfrak{l}_{m})^{n}\rightarrow (\dot{U}_{[q^{\pm }]}L\mathfrak{g}\mathfrak{l}_{M})^{n}$
is faithful, which means that
![]() $a=0$
in
$a=0$
in
 $\operatorname{Hom}_{(\dot{U}_{[q^{\pm }]}L\mathfrak{g}\mathfrak{l}_{m})^{n}}(\text{}\underline{l},\text{}\underline{l}^{\prime })$
as desired.◻
$\operatorname{Hom}_{(\dot{U}_{[q^{\pm }]}L\mathfrak{g}\mathfrak{l}_{m})^{n}}(\text{}\underline{l},\text{}\underline{l}^{\prime })$
as desired.◻
Remark 5.9. Theorem 5.8 explains that one should think of the category
 ${\mathcal{A}}{\mathcal{S}}p_{n}[q^{\pm }]$
as the directed limit as
${\mathcal{A}}{\mathcal{S}}p_{n}[q^{\pm }]$
as the directed limit as
 $m\rightarrow \infty$
$m\rightarrow \infty$
 $$\begin{eqnarray}(\dot{U}_{[q^{\pm }]}L\mathfrak{g}\mathfrak{l}_{\infty })^{n}:=\varinjlim (\dot{U}_{[q^{\pm }]}L\mathfrak{g}\mathfrak{l}_{m})^{n}\end{eqnarray}$$
$$\begin{eqnarray}(\dot{U}_{[q^{\pm }]}L\mathfrak{g}\mathfrak{l}_{\infty })^{n}:=\varinjlim (\dot{U}_{[q^{\pm }]}L\mathfrak{g}\mathfrak{l}_{m})^{n}\end{eqnarray}$$
via the functors discussed in § 5.4. One could make this precise but we do not actually require this stronger result.
6 From the annular spider to
 $K\operatorname{Conv}$
$K\operatorname{Conv}$
In this section we define a functor
 $$\begin{eqnarray}\unicode[STIX]{x1D6F7}_{m}:(\dot{U}_{[q^{\pm }]}L\mathfrak{g}\mathfrak{l}_{m})^{n}\rightarrow K\operatorname{Conv}^{\operatorname{SL}_{n}\times \mathbb{C}^{\times }}(Gr)\end{eqnarray}$$
$$\begin{eqnarray}\unicode[STIX]{x1D6F7}_{m}:(\dot{U}_{[q^{\pm }]}L\mathfrak{g}\mathfrak{l}_{m})^{n}\rightarrow K\operatorname{Conv}^{\operatorname{SL}_{n}\times \mathbb{C}^{\times }}(Gr)\end{eqnarray}$$
which follows our earlier constructions from [Reference Cautis, Kamnitzer and LicataCKL10, Reference CautisCau05, Reference Cautis and KamnitzerCK17] but descended from derived categories to K-theory. This in turn induces a functor
 $$\begin{eqnarray}\unicode[STIX]{x1D6F7}:{\mathcal{A}}{\mathcal{S}}p_{n}[q^{\pm }]\rightarrow K\operatorname{Conv}^{\operatorname{SL}_{n}\times \mathbb{C}^{\times }}(Gr)\end{eqnarray}$$
$$\begin{eqnarray}\unicode[STIX]{x1D6F7}:{\mathcal{A}}{\mathcal{S}}p_{n}[q^{\pm }]\rightarrow K\operatorname{Conv}^{\operatorname{SL}_{n}\times \mathbb{C}^{\times }}(Gr)\end{eqnarray}$$
which we will prove is an equivalence after tensoring with
![]() $\mathbb{C}(q)$
.
$\mathbb{C}(q)$
.
6.1 The varieties
We work with the lattice description of
 $Gr=Gr_{P\operatorname{GL}_{n}}\!$
. This means that we identify
$Gr=Gr_{P\operatorname{GL}_{n}}\!$
. This means that we identify
![]() $Gr$
with the space of
$Gr$
with the space of
![]() ${\mathcal{O}}$
-lattices in the vector space
${\mathcal{O}}$
-lattices in the vector space
![]() ${\mathcal{K}}^{n}$
(where
${\mathcal{K}}^{n}$
(where
 ${\mathcal{O}}=\mathbb{C}[[z]]$
and
${\mathcal{O}}=\mathbb{C}[[z]]$
and
 ${\mathcal{K}}=\mathbb{C}((z))$
) modulo the equivalence relation of homothety, i.e.
${\mathcal{K}}=\mathbb{C}((z))$
) modulo the equivalence relation of homothety, i.e.
 $L_{1}\sim L_{2}$
if and only if
$L_{1}\sim L_{2}$
if and only if
 $z^{k}L_{1}=L_{2}$
for some
$z^{k}L_{1}=L_{2}$
for some
![]() $k\in \mathbb{Z}$
.
$k\in \mathbb{Z}$
.
Note that under this identification, if
 $\unicode[STIX]{x1D706}\in \unicode[STIX]{x1D6EC}_{+}\subset \mathbb{Z}^{n}/\mathbb{Z}(1,\ldots ,1)$
, then we have
$\unicode[STIX]{x1D706}\in \unicode[STIX]{x1D6EC}_{+}\subset \mathbb{Z}^{n}/\mathbb{Z}(1,\ldots ,1)$
, then we have
 $$\begin{eqnarray}Gr^{\unicode[STIX]{x1D706}}=\{L\in Gr:{\mathcal{O}}^{n}=L_{0}\subset L\text{ and }z|_{L/L_{0}}\text{ has Jordan type }\unicode[STIX]{x1D706}\},\end{eqnarray}$$
$$\begin{eqnarray}Gr^{\unicode[STIX]{x1D706}}=\{L\in Gr:{\mathcal{O}}^{n}=L_{0}\subset L\text{ and }z|_{L/L_{0}}\text{ has Jordan type }\unicode[STIX]{x1D706}\},\end{eqnarray}$$
where we regard
![]() $z|_{L/L_{0}}$
as a nilpotent linear operator on a finite-dimensional vector space and consider its Jordan type to be the length of blocks in its Jordan form. (Note that
$z|_{L/L_{0}}$
as a nilpotent linear operator on a finite-dimensional vector space and consider its Jordan type to be the length of blocks in its Jordan form. (Note that
![]() $\unicode[STIX]{x1D706}$
is only defined up to shift by a constant sequence; this matches the fact that
$\unicode[STIX]{x1D706}$
is only defined up to shift by a constant sequence; this matches the fact that
![]() $L$
is only defined up to homothety.)
$L$
is only defined up to homothety.)
As before, we encode of sequence of minuscule dominant weights
![]() $\text{}\underline{\unicode[STIX]{x1D706}}$
by a sequence
$\text{}\underline{\unicode[STIX]{x1D706}}$
by a sequence
 $\text{}\underline{k}=(k_{1},\ldots ,k_{m})$
with
$\text{}\underline{k}=(k_{1},\ldots ,k_{m})$
with
 $1\leqslant k_{i}\leqslant n-1$
. Let us introduce the notation
$1\leqslant k_{i}\leqslant n-1$
. Let us introduce the notation
 $Y(\text{}\underline{k}):=Gr^{\text{}\underline{\unicode[STIX]{x1D706}}}$
. The varieties
$Y(\text{}\underline{k}):=Gr^{\text{}\underline{\unicode[STIX]{x1D706}}}$
. The varieties
![]() $Y(\text{}\underline{k})$
can be described explicitly as sequences of lattices (not considered up to homothety).
$Y(\text{}\underline{k})$
can be described explicitly as sequences of lattices (not considered up to homothety).
Lemma 6.1. We have
 $$\begin{eqnarray}\displaystyle Y(\text{}\underline{k})=\{(L_{1},\ldots ,L_{m}) & : & \displaystyle L_{i}\subset {\mathcal{K}}^{n},~{\mathcal{O}}^{n}=L_{0}\subset L_{1}\subset L_{2}\subset \cdots \subset L_{m},\nonumber\\ \displaystyle & & \displaystyle \quad \dim (L_{i}/L_{i-1})=k_{i}\text{ and }zL_{i}\subset L_{i-1}\}.\nonumber\end{eqnarray}$$
$$\begin{eqnarray}\displaystyle Y(\text{}\underline{k})=\{(L_{1},\ldots ,L_{m}) & : & \displaystyle L_{i}\subset {\mathcal{K}}^{n},~{\mathcal{O}}^{n}=L_{0}\subset L_{1}\subset L_{2}\subset \cdots \subset L_{m},\nonumber\\ \displaystyle & & \displaystyle \quad \dim (L_{i}/L_{i-1})=k_{i}\text{ and }zL_{i}\subset L_{i-1}\}.\nonumber\end{eqnarray}$$
Moreover, the projection map
 $Y(\text{}\underline{k})\rightarrow Gr$
is given by sending
$Y(\text{}\underline{k})\rightarrow Gr$
is given by sending
 $(L_{1},\ldots ,L_{m})$
to
$(L_{1},\ldots ,L_{m})$
to
![]() $[L_{m}]$
.
$[L_{m}]$
.
For convenience of notation, we also allow sequences
![]() $\text{}\underline{k}$
containing
$\text{}\underline{k}$
containing
![]() $0,n$
. We have a canonical identification
$0,n$
. We have a canonical identification
 $Y(\text{}\underline{k})=Y(\overline{\text{}\underline{k}})$
where
$Y(\text{}\underline{k})=Y(\overline{\text{}\underline{k}})$
where
![]() $\overline{\text{}\underline{k}}$
is defined by removing all
$\overline{\text{}\underline{k}}$
is defined by removing all
![]() $0,n$
.
$0,n$
.
Assume that
 $\text{}\underline{k}=(k_{1},\ldots ,k_{m})$
and
$\text{}\underline{k}=(k_{1},\ldots ,k_{m})$
and
 $\text{}\underline{k}^{\prime }=(k_{1}^{\prime },\ldots ,k_{m^{\prime }}^{\prime })$
are two sequences with the same sum,
$\text{}\underline{k}^{\prime }=(k_{1}^{\prime },\ldots ,k_{m^{\prime }}^{\prime })$
are two sequences with the same sum,
 $k_{1}+\cdots +k_{m}=k_{1}^{\prime }+\cdots +k_{m^{\prime }}^{\prime }$
. From the lemma, we reach a simple description of the varieties
$k_{1}+\cdots +k_{m}=k_{1}^{\prime }+\cdots +k_{m^{\prime }}^{\prime }$
. From the lemma, we reach a simple description of the varieties
 $$\begin{eqnarray}Z(\text{}\underline{k},\text{}\underline{k}^{\prime }):=\{(L_{1},\ldots ,L_{m}),(L_{1}^{\prime },\ldots ,L_{m^{\prime }}^{\prime })\in Y(\text{}\underline{k})\times Y(\text{}\underline{k}^{\prime }):L_{m}=L_{m^{\prime }}^{\prime }\}.\end{eqnarray}$$
$$\begin{eqnarray}Z(\text{}\underline{k},\text{}\underline{k}^{\prime }):=\{(L_{1},\ldots ,L_{m}),(L_{1}^{\prime },\ldots ,L_{m^{\prime }}^{\prime })\in Y(\text{}\underline{k})\times Y(\text{}\underline{k}^{\prime }):L_{m}=L_{m^{\prime }}^{\prime }\}.\end{eqnarray}$$
We consider the action of
 $\operatorname{SL}_{n}\times \mathbb{C}^{\times }$
on
$\operatorname{SL}_{n}\times \mathbb{C}^{\times }$
on
 ${\mathcal{K}}^{n}=\mathbb{C}^{n}\otimes {\mathcal{K}}$
where
${\mathcal{K}}^{n}=\mathbb{C}^{n}\otimes {\mathcal{K}}$
where
![]() $\operatorname{SL}_{n}$
acts on
$\operatorname{SL}_{n}$
acts on
![]() $\mathbb{C}^{n}$
and
$\mathbb{C}^{n}$
and
![]() $\mathbb{C}^{\times }$
acts on
$\mathbb{C}^{\times }$
acts on
![]() ${\mathcal{K}}$
by
${\mathcal{K}}$
by
 $s\cdot z^{k}=s^{k}z^{k}$
. This gives us an action of
$s\cdot z^{k}=s^{k}z^{k}$
. This gives us an action of
 $\operatorname{SL}_{n}\times \mathbb{C}^{\times }$
on
$\operatorname{SL}_{n}\times \mathbb{C}^{\times }$
on
![]() $Gr$
and on each
$Gr$
and on each
![]() $Y(\text{}\underline{k})$
.
$Y(\text{}\underline{k})$
.
Remark 6.2. Given a sheaf
![]() ${\mathcal{F}}$
we denote by
${\mathcal{F}}$
we denote by
![]() ${\mathcal{F}}\{1\}$
the same sheaf but shifted equivariantly with respect to the
${\mathcal{F}}\{1\}$
the same sheaf but shifted equivariantly with respect to the
![]() $\mathbb{C}^{\times }$
action. At the level of K-theory we use the convention that
$\mathbb{C}^{\times }$
action. At the level of K-theory we use the convention that
![]() $\{1\}$
is multiplication by
$\{1\}$
is multiplication by
![]() $-q^{-1}$
. This matches our previous conventions from [Reference Cautis, Kamnitzer and LicataCKL10, Reference CautisCau05].
$-q^{-1}$
. This matches our previous conventions from [Reference Cautis, Kamnitzer and LicataCKL10, Reference CautisCau05].
6.2 The action of
 $(\dot{U}_{[q^{\pm }]}\mathfrak{g}\mathfrak{l}_{m})^{n}$
$(\dot{U}_{[q^{\pm }]}\mathfrak{g}\mathfrak{l}_{m})^{n}$
We first define a functor
 $$\begin{eqnarray}\unicode[STIX]{x1D719}_{m}:(\dot{U}_{[q^{\pm }]}\mathfrak{g}\mathfrak{l}_{m})^{n}\rightarrow K\operatorname{Conv}^{\operatorname{SL}_{n}\times \mathbb{C}^{\times }}(Gr).\end{eqnarray}$$
$$\begin{eqnarray}\unicode[STIX]{x1D719}_{m}:(\dot{U}_{[q^{\pm }]}\mathfrak{g}\mathfrak{l}_{m})^{n}\rightarrow K\operatorname{Conv}^{\operatorname{SL}_{n}\times \mathbb{C}^{\times }}(Gr).\end{eqnarray}$$
On objects
![]() $\unicode[STIX]{x1D719}_{m}$
takes
$\unicode[STIX]{x1D719}_{m}$
takes
![]() $\text{}\underline{k}$
to
$\text{}\underline{k}$
to
![]() $\overline{\text{}\underline{k}}$
where
$\overline{\text{}\underline{k}}$
where
![]() $\overline{\text{}\underline{k}}$
is obtained from
$\overline{\text{}\underline{k}}$
is obtained from
![]() $\text{}\underline{k}$
by removing all
$\text{}\underline{k}$
by removing all
![]() $0,n$
. To define it on morphisms, we must define maps
$0,n$
. To define it on morphisms, we must define maps
 $$\begin{eqnarray}\unicode[STIX]{x1D719}_{m}:\operatorname{Hom}_{(\dot{U}_{[q^{\pm }]}\mathfrak{g}\mathfrak{l}_{m})^{n}}(\text{}\underline{k},\text{}\underline{k}^{\prime })\rightarrow K^{\operatorname{SL}_{n}\times \mathbb{C}^{\times }}(Z(\overline{\text{}\underline{k}},\overline{\text{}\underline{k}^{\prime }}))\end{eqnarray}$$
$$\begin{eqnarray}\unicode[STIX]{x1D719}_{m}:\operatorname{Hom}_{(\dot{U}_{[q^{\pm }]}\mathfrak{g}\mathfrak{l}_{m})^{n}}(\text{}\underline{k},\text{}\underline{k}^{\prime })\rightarrow K^{\operatorname{SL}_{n}\times \mathbb{C}^{\times }}(Z(\overline{\text{}\underline{k}},\overline{\text{}\underline{k}^{\prime }}))\end{eqnarray}$$
for every
![]() $\text{}\underline{k},\text{}\underline{k}^{\prime }$
. Since
$\text{}\underline{k},\text{}\underline{k}^{\prime }$
. Since
 $(\dot{U}_{[q^{\pm }]}\mathfrak{g}\mathfrak{l}_{m})^{n}$
is defined by generators and relations, we will define
$(\dot{U}_{[q^{\pm }]}\mathfrak{g}\mathfrak{l}_{m})^{n}$
is defined by generators and relations, we will define
![]() $\unicode[STIX]{x1D719}_{m}$
on the generators
$\unicode[STIX]{x1D719}_{m}$
on the generators
![]() $E_{i}^{(s)}$
and
$E_{i}^{(s)}$
and
![]() $F_{i}^{(s)}$
for
$F_{i}^{(s)}$
for
 $i=1,\ldots ,m-1$
. To do this we use the varieties
$i=1,\ldots ,m-1$
. To do this we use the varieties
 $$\begin{eqnarray}W_{i}^{s}(\text{}\underline{k})=\{(L_{\bullet },L_{\bullet }^{\prime })\in Y(\text{}\underline{k})\times Y(\text{}\underline{k}-s\unicode[STIX]{x1D6FC}_{i}):L_{j}=L_{j}^{\prime }\text{if }j\neq i,L_{i}^{\prime }\subset L_{i}\}.\end{eqnarray}$$
$$\begin{eqnarray}W_{i}^{s}(\text{}\underline{k})=\{(L_{\bullet },L_{\bullet }^{\prime })\in Y(\text{}\underline{k})\times Y(\text{}\underline{k}-s\unicode[STIX]{x1D6FC}_{i}):L_{j}=L_{j}^{\prime }\text{if }j\neq i,L_{i}^{\prime }\subset L_{i}\}.\end{eqnarray}$$
Note that these varieties are actually supported on
 $Z(\text{}\underline{k},\text{}\underline{k}-s\unicode[STIX]{x1D6FC}_{i})$
. Then we define
$Z(\text{}\underline{k},\text{}\underline{k}-s\unicode[STIX]{x1D6FC}_{i})$
. Then we define
 $$\begin{eqnarray}\displaystyle \unicode[STIX]{x1D719}_{m}(1_{\text{}\underline{k}}E_{i}^{(s)}) & = & \displaystyle (-q)^{-sk_{i+1}}[{\mathcal{O}}_{W_{i}^{s}(\text{}\underline{k})}\otimes \det (L_{i}^{\prime }/L_{i})^{k_{i+1}-k_{i}+s}],\end{eqnarray}$$
$$\begin{eqnarray}\displaystyle \unicode[STIX]{x1D719}_{m}(1_{\text{}\underline{k}}E_{i}^{(s)}) & = & \displaystyle (-q)^{-sk_{i+1}}[{\mathcal{O}}_{W_{i}^{s}(\text{}\underline{k})}\otimes \det (L_{i}^{\prime }/L_{i})^{k_{i+1}-k_{i}+s}],\end{eqnarray}$$
 $$\begin{eqnarray}\displaystyle \unicode[STIX]{x1D719}_{m}(F_{i}^{(s)}1_{\text{}\underline{k}}) & = & \displaystyle (-q)^{-s(k_{i}-s)}[{\mathcal{O}}_{W_{i}^{s}(\text{}\underline{k})}\otimes \det (L_{i+1}/L_{i}^{\prime })^{-s}\otimes \det (L_{i}/L_{i-1})^{s}],\end{eqnarray}$$
$$\begin{eqnarray}\displaystyle \unicode[STIX]{x1D719}_{m}(F_{i}^{(s)}1_{\text{}\underline{k}}) & = & \displaystyle (-q)^{-s(k_{i}-s)}[{\mathcal{O}}_{W_{i}^{s}(\text{}\underline{k})}\otimes \det (L_{i+1}/L_{i}^{\prime })^{-s}\otimes \det (L_{i}/L_{i-1})^{s}],\end{eqnarray}$$
where the prime denotes the corresponding bundle pulled back from the second factor. (These kernels live in
 $K^{\operatorname{SL}_{n}\times \mathbb{C}^{\times }}(Z(\text{}\underline{k}-s\unicode[STIX]{x1D6FC}_{i},\text{}\underline{k}))$
and
$K^{\operatorname{SL}_{n}\times \mathbb{C}^{\times }}(Z(\text{}\underline{k}-s\unicode[STIX]{x1D6FC}_{i},\text{}\underline{k}))$
and
 $K^{\operatorname{SL}_{n}\times \mathbb{C}^{\times }}(Z(\text{}\underline{k},\text{}\underline{k}-s\unicode[STIX]{x1D6FC}_{i}))$
respectively.) It follows from the calculations in [Reference Cautis, Kamnitzer and LicataCKL10, Reference CautisCau05] that these satisfy the relations of
$K^{\operatorname{SL}_{n}\times \mathbb{C}^{\times }}(Z(\text{}\underline{k},\text{}\underline{k}-s\unicode[STIX]{x1D6FC}_{i}))$
respectively.) It follows from the calculations in [Reference Cautis, Kamnitzer and LicataCKL10, Reference CautisCau05] that these satisfy the relations of
 $\dot{U}_{[q^{\pm }]}\mathfrak{g}\mathfrak{l}_{m}$
(see for instance [Reference CautisCau05, Theorem 8.2]).
$\dot{U}_{[q^{\pm }]}\mathfrak{g}\mathfrak{l}_{m}$
(see for instance [Reference CautisCau05, Theorem 8.2]).
Remark 6.3. These definitions differ from those in [Reference Cautis, Kamnitzer and LicataCKL10, Reference CautisCau05, Reference Cautis and KamnitzerCK17] in two ways. First we have reversed the roles of
![]() $E_{i},F_{i}$
and negated weights (this procedure actually defines an involution of
$E_{i},F_{i}$
and negated weights (this procedure actually defines an involution of
 $(\dot{U}_{[q^{\pm }]}\mathfrak{g}\mathfrak{l}_{m})^{n}$
). We do this in order to use the standard definition of
$(\dot{U}_{[q^{\pm }]}\mathfrak{g}\mathfrak{l}_{m})^{n}$
). We do this in order to use the standard definition of
 $\unicode[STIX]{x1D6FC}_{i}=(0,\ldots ,1,-1,\ldots ,0)$
and thereby match the previous sections of this paper. Second, the choice of line bundles matches that in [Reference Cautis, Kamnitzer and LicataCKL10] but not [Reference CautisCau05, Reference Cautis and KamnitzerCK17]. The difference is just conjugation by a line bundle (denoted by
$\unicode[STIX]{x1D6FC}_{i}=(0,\ldots ,1,-1,\ldots ,0)$
and thereby match the previous sections of this paper. Second, the choice of line bundles matches that in [Reference Cautis, Kamnitzer and LicataCKL10] but not [Reference CautisCau05, Reference Cautis and KamnitzerCK17]. The difference is just conjugation by a line bundle (denoted by
![]() $\unicode[STIX]{x1D70C}$
in [Reference Cautis and KamnitzerCK17]). The reason for choosing the line bundles from [Reference Cautis, Kamnitzer and LicataCKL10] rather than [Reference CautisCau05, Reference Cautis and KamnitzerCK17] is that they make the diagrams in § 9 commute on the nose without having to conjugate by line bundles.
$\unicode[STIX]{x1D70C}$
in [Reference Cautis and KamnitzerCK17]). The reason for choosing the line bundles from [Reference Cautis, Kamnitzer and LicataCKL10] rather than [Reference CautisCau05, Reference Cautis and KamnitzerCK17] is that they make the diagrams in § 9 commute on the nose without having to conjugate by line bundles.
6.3 Extending to an action of
 $(\dot{U}_{[q^{\pm }]}L\mathfrak{g}\mathfrak{l}_{m})^{n}$
$(\dot{U}_{[q^{\pm }]}L\mathfrak{g}\mathfrak{l}_{m})^{n}$
To extend the action above we first define an action of the annular braid group on
 $K\operatorname{Conv}^{\operatorname{SL}_{n}\times \mathbb{C}^{\times }}(Gr)$
and then use Lemma 5.5.
$K\operatorname{Conv}^{\operatorname{SL}_{n}\times \mathbb{C}^{\times }}(Gr)$
and then use Lemma 5.5.
Proposition 6.4. There exists a functor
 $$\begin{eqnarray}\unicode[STIX]{x1D6FD}:{\mathcal{A}}{\mathcal{B}}_{m}(\{0,\ldots ,n\})\rightarrow K\operatorname{Conv}^{\operatorname{SL}_{n}\times \mathbb{C}^{\times }}(Gr),\end{eqnarray}$$
$$\begin{eqnarray}\unicode[STIX]{x1D6FD}:{\mathcal{A}}{\mathcal{B}}_{m}(\{0,\ldots ,n\})\rightarrow K\operatorname{Conv}^{\operatorname{SL}_{n}\times \mathbb{C}^{\times }}(Gr),\end{eqnarray}$$
where
![]() $\unicode[STIX]{x1D6FD}(T_{i}1_{\text{}\underline{k}})$
is defined using (16) and
$\unicode[STIX]{x1D6FD}(T_{i}1_{\text{}\underline{k}})$
is defined using (16) and
 $\unicode[STIX]{x1D6FD}(X_{i}1_{\text{}\underline{k}}):=\unicode[STIX]{x1D6E5}_{\ast }\det (L_{i}/L_{i-1})^{\vee }$
where
$\unicode[STIX]{x1D6FD}(X_{i}1_{\text{}\underline{k}}):=\unicode[STIX]{x1D6E5}_{\ast }\det (L_{i}/L_{i-1})^{\vee }$
where
![]() $\unicode[STIX]{x1D6E5}$
is the diagonal embedding
$\unicode[STIX]{x1D6E5}$
is the diagonal embedding
 $Y(\text{}\underline{k})\rightarrow Z(\text{}\underline{k},\text{}\underline{k})$
.
$Y(\text{}\underline{k})\rightarrow Z(\text{}\underline{k},\text{}\underline{k})$
.
Proof. We need to show the last three relations of
![]() $AB_{m}$
. The relations
$AB_{m}$
. The relations
 $T_{i}X_{j}=X_{j}T_{i}$
and
$T_{i}X_{j}=X_{j}T_{i}$
and
 $X_{i}X_{j}=X_{j}X_{i}$
are easy. The final relation
$X_{i}X_{j}=X_{j}X_{i}$
are easy. The final relation
 $T_{i}X_{i}T_{i}=X_{i+1}$
follows from [Reference Cautis and KamnitzerCK17, Corollary A.14].◻
$T_{i}X_{i}T_{i}=X_{i+1}$
follows from [Reference Cautis and KamnitzerCK17, Corollary A.14].◻
In order to apply Lemma 5.5 we need to check the following two conditions:
-
(i)
 $\unicode[STIX]{x1D6FD}(X_{1})$
commutes with
$\unicode[STIX]{x1D6FD}(X_{1})$
commutes with
 $\unicode[STIX]{x1D719}_{m}(E_{i}^{(s)})$
and
$\unicode[STIX]{x1D719}_{m}(E_{i}^{(s)})$
and
 $\unicode[STIX]{x1D719}_{m}(F_{i}^{(s)})$
for
$\unicode[STIX]{x1D719}_{m}(F_{i}^{(s)})$
for
 $i=2,\ldots ,m-1$
;
$i=2,\ldots ,m-1$
; -
(ii)
 $\unicode[STIX]{x1D6FD}(X_{1}\ldots X_{m})$
commutes with everything in the image of
$\unicode[STIX]{x1D6FD}(X_{1}\ldots X_{m})$
commutes with everything in the image of
 $\unicode[STIX]{x1D719}_{m}$
.
$\unicode[STIX]{x1D719}_{m}$
.
The first condition follows since
![]() $\unicode[STIX]{x1D6FD}(X_{1})$
only involves the line bundle
$\unicode[STIX]{x1D6FD}(X_{1})$
only involves the line bundle
 $\det (L_{1}/L_{0})$
while
$\det (L_{1}/L_{0})$
while
 $\unicode[STIX]{x1D719}_{m}(E_{i}^{(s)})$
only involves changing the flag
$\unicode[STIX]{x1D719}_{m}(E_{i}^{(s)})$
only involves changing the flag
![]() $L_{i}$
. The second condition follows since
$L_{i}$
. The second condition follows since
 $\unicode[STIX]{x1D6FD}(X_{1}\ldots X_{m})$
is given by
$\unicode[STIX]{x1D6FD}(X_{1}\ldots X_{m})$
is given by
 $\unicode[STIX]{x1D6E5}_{\ast }\det (L_{m}/L_{0})^{\vee }$
which clearly commutes with the image of every
$\unicode[STIX]{x1D6E5}_{\ast }\det (L_{m}/L_{0})^{\vee }$
which clearly commutes with the image of every
![]() $E_{i}^{(s)}$
and
$E_{i}^{(s)}$
and
![]() $F_{i}^{(s)}$
. Thus, by Lemma 5.5,
$F_{i}^{(s)}$
. Thus, by Lemma 5.5,
![]() $\unicode[STIX]{x1D719}_{m}$
extends to a functor
$\unicode[STIX]{x1D719}_{m}$
extends to a functor
 $$\begin{eqnarray}\unicode[STIX]{x1D6F7}_{m}:(\dot{U}_{[q^{\pm }]}L\mathfrak{g}\mathfrak{l}_{m})^{n}\rightarrow K\operatorname{Conv}^{\operatorname{SL}_{n}\times \mathbb{C}^{\times }}(Gr).\end{eqnarray}$$
$$\begin{eqnarray}\unicode[STIX]{x1D6F7}_{m}:(\dot{U}_{[q^{\pm }]}L\mathfrak{g}\mathfrak{l}_{m})^{n}\rightarrow K\operatorname{Conv}^{\operatorname{SL}_{n}\times \mathbb{C}^{\times }}(Gr).\end{eqnarray}$$
Remark 6.5. It is easy to see that the functors
![]() $\unicode[STIX]{x1D6F7}_{m}$
are compatible with the functors
$\unicode[STIX]{x1D6F7}_{m}$
are compatible with the functors
 $(\dot{U}_{[q^{\pm }]}L\mathfrak{g}\mathfrak{l}_{m})^{n}\rightarrow (\dot{U}_{[q^{\pm }]}L\mathfrak{g}\mathfrak{l}_{m+1})^{n}$
discussed in the proof of Theorem 5.8.
$(\dot{U}_{[q^{\pm }]}L\mathfrak{g}\mathfrak{l}_{m})^{n}\rightarrow (\dot{U}_{[q^{\pm }]}L\mathfrak{g}\mathfrak{l}_{m+1})^{n}$
discussed in the proof of Theorem 5.8.
6.4 The functor
 $\unicode[STIX]{x1D6F7}$
$\unicode[STIX]{x1D6F7}$
Proposition 6.6. There exists a unique functor
 $$\begin{eqnarray}\unicode[STIX]{x1D6F7}:{\mathcal{A}}{\mathcal{S}}p_{n}[q^{\pm }]\rightarrow K\operatorname{Conv}^{\operatorname{SL}_{n}\times \mathbb{C}^{\times }}(Gr)\end{eqnarray}$$
$$\begin{eqnarray}\unicode[STIX]{x1D6F7}:{\mathcal{A}}{\mathcal{S}}p_{n}[q^{\pm }]\rightarrow K\operatorname{Conv}^{\operatorname{SL}_{n}\times \mathbb{C}^{\times }}(Gr)\end{eqnarray}$$
such that for each
![]() $m$
we have
$m$
we have
 $\unicode[STIX]{x1D6F7}_{m}=\unicode[STIX]{x1D6F7}\circ A\unicode[STIX]{x1D6F9}_{m}$
.
$\unicode[STIX]{x1D6F7}_{m}=\unicode[STIX]{x1D6F7}\circ A\unicode[STIX]{x1D6F9}_{m}$
.
Proof. Consider the full subcategory of
 ${\mathcal{A}}{\mathcal{S}}p_{n}[q^{\pm }]$
consisting of objects
${\mathcal{A}}{\mathcal{S}}p_{n}[q^{\pm }]$
consisting of objects
 $(k_{1},\ldots ,k_{m})$
with
$(k_{1},\ldots ,k_{m})$
with
 $k_{i}\in \{1,\ldots ,n-1\}$
(in other words, we are considering webs where the strands point away from the inner circle and into the outer circle). Because of the tags, every object in
$k_{i}\in \{1,\ldots ,n-1\}$
(in other words, we are considering webs where the strands point away from the inner circle and into the outer circle). Because of the tags, every object in
 ${\mathcal{A}}{\mathcal{S}}p_{n}[q^{\pm }]$
is equivalent to an object in this subcategory. Thus, it suffices to define
${\mathcal{A}}{\mathcal{S}}p_{n}[q^{\pm }]$
is equivalent to an object in this subcategory. Thus, it suffices to define
![]() $\unicode[STIX]{x1D6F7}$
on this subcategory.
$\unicode[STIX]{x1D6F7}$
on this subcategory.
On objects, we define
![]() $\unicode[STIX]{x1D6F7}$
to take
$\unicode[STIX]{x1D6F7}$
to take
![]() $\text{}\underline{k}$
to
$\text{}\underline{k}$
to
![]() $\text{}\underline{k}$
. Now consider objects
$\text{}\underline{k}$
. Now consider objects
![]() $\text{}\underline{k},\text{}\underline{k}^{\prime }$
in
$\text{}\underline{k},\text{}\underline{k}^{\prime }$
in
 ${\mathcal{A}}{\mathcal{S}}p_{n}[q^{\pm }]$
(with all
${\mathcal{A}}{\mathcal{S}}p_{n}[q^{\pm }]$
(with all
 $k_{i},k_{i}^{\prime }>0$
) and let
$k_{i},k_{i}^{\prime }>0$
) and let
 $a\in \operatorname{Hom}_{{\mathcal{A}}{\mathcal{S}}p_{n}[q^{\pm }]}(\text{}\underline{k},\text{}\underline{k}^{\prime })$
. We wish to define
$a\in \operatorname{Hom}_{{\mathcal{A}}{\mathcal{S}}p_{n}[q^{\pm }]}(\text{}\underline{k},\text{}\underline{k}^{\prime })$
. We wish to define
![]() $\unicode[STIX]{x1D6F7}(a)$
. By Theorem 5.8, we know that there exists
$\unicode[STIX]{x1D6F7}(a)$
. By Theorem 5.8, we know that there exists
![]() $m$
and
$m$
and
![]() $\text{}\underline{l},\text{}\underline{l}^{\prime }$
(such that
$\text{}\underline{l},\text{}\underline{l}^{\prime }$
(such that
![]() $\text{}\underline{l},\text{}\underline{l}^{\prime }$
are obtained by adding to
$\text{}\underline{l},\text{}\underline{l}^{\prime }$
are obtained by adding to
![]() $0$
s and
$0$
s and
![]() $n$
s to
$n$
s to
![]() $\text{}\underline{k},\text{}\underline{k}^{\prime }$
) and
$\text{}\underline{k},\text{}\underline{k}^{\prime }$
) and
 $b\in \operatorname{Hom}_{\dot{U}_{q}L\mathfrak{g}\mathfrak{l}_{m}}(\text{}\underline{l},\text{}\underline{l}^{\prime })$
with
$b\in \operatorname{Hom}_{\dot{U}_{q}L\mathfrak{g}\mathfrak{l}_{m}}(\text{}\underline{l},\text{}\underline{l}^{\prime })$
with
 $A\unicode[STIX]{x1D6F9}_{m}(b)=a$
. Then we define
$A\unicode[STIX]{x1D6F9}_{m}(b)=a$
. Then we define
 $\unicode[STIX]{x1D6F7}(a):=\unicode[STIX]{x1D6F7}_{m}(b)$
.
$\unicode[STIX]{x1D6F7}(a):=\unicode[STIX]{x1D6F7}_{m}(b)$
.
Finally, we must check that this is well defined. Suppose we have two choices of
 $m_{1},\text{}\underline{l}_{1},\text{}\underline{l}_{1}^{\prime },b_{1}$
and
$m_{1},\text{}\underline{l}_{1},\text{}\underline{l}_{1}^{\prime },b_{1}$
and
 $m_{2},\text{}\underline{l}_{2},\text{}\underline{l}_{2}^{\prime },b_{2}$
as above. Since both
$m_{2},\text{}\underline{l}_{2},\text{}\underline{l}_{2}^{\prime },b_{2}$
as above. Since both
![]() $\text{}\underline{l}_{1}$
(respectively
$\text{}\underline{l}_{1}$
(respectively
![]() $\text{}\underline{l}_{1}^{\prime }$
) and
$\text{}\underline{l}_{1}^{\prime }$
) and
![]() $\text{}\underline{l}_{2}$
(respectively
$\text{}\underline{l}_{2}$
(respectively
![]() $\text{}\underline{l}_{2}^{\prime }$
) are obtained by adding
$\text{}\underline{l}_{2}^{\prime }$
) are obtained by adding
![]() $0,n$
to
$0,n$
to
![]() $\text{}\underline{k}$
(respectively
$\text{}\underline{k}$
(respectively
![]() $\text{}\underline{k}^{\prime }$
), we can find a third
$\text{}\underline{k}^{\prime }$
), we can find a third
![]() $\text{}\underline{l}_{3}$
(respectively
$\text{}\underline{l}_{3}$
(respectively
![]() $\text{}\underline{l}_{3}^{\prime }$
) which is obtained by adding
$\text{}\underline{l}_{3}^{\prime }$
) which is obtained by adding
![]() $0,n$
to both
$0,n$
to both
![]() $\text{}\underline{l}_{1}$
and
$\text{}\underline{l}_{1}$
and
![]() $\text{}\underline{l}_{2}$
(respectively
$\text{}\underline{l}_{2}$
(respectively
![]() $\text{}\underline{l}_{1}^{\prime },\text{}\underline{l}_{2}^{\prime }$
).
$\text{}\underline{l}_{1}^{\prime },\text{}\underline{l}_{2}^{\prime }$
).
Using the functors
 $(\dot{U}_{[q^{\pm }]}L\mathfrak{g}\mathfrak{l}_{m})^{n}\rightarrow (\dot{U}_{[q^{\pm }]}L\mathfrak{g}\mathfrak{l}_{m+1})^{n}$
defined in the proof of Theorem 5.8, we can regard
$(\dot{U}_{[q^{\pm }]}L\mathfrak{g}\mathfrak{l}_{m})^{n}\rightarrow (\dot{U}_{[q^{\pm }]}L\mathfrak{g}\mathfrak{l}_{m+1})^{n}$
defined in the proof of Theorem 5.8, we can regard
![]() $b_{1},b_{2}$
inside
$b_{1},b_{2}$
inside
 $\operatorname{Hom}_{(\dot{U}_{[q^{\pm }]}L\mathfrak{g}\mathfrak{l}_{m_{3}})^{n}}(\text{}\underline{l}_{3},\text{}\underline{l}_{3}^{\prime })$
. We have
$\operatorname{Hom}_{(\dot{U}_{[q^{\pm }]}L\mathfrak{g}\mathfrak{l}_{m_{3}})^{n}}(\text{}\underline{l}_{3},\text{}\underline{l}_{3}^{\prime })$
. We have
 $A\unicode[STIX]{x1D6F9}_{m_{3}}(b_{1})=A\unicode[STIX]{x1D6F9}_{m_{3}}(b_{2})=a$
and thus
$A\unicode[STIX]{x1D6F9}_{m_{3}}(b_{1})=A\unicode[STIX]{x1D6F9}_{m_{3}}(b_{2})=a$
and thus
![]() $b_{1}=b_{2}$
by Theorem 5.8. Since the functors
$b_{1}=b_{2}$
by Theorem 5.8. Since the functors
![]() $\unicode[STIX]{x1D6F7}_{m}$
are compatible with the inclusion functors
$\unicode[STIX]{x1D6F7}_{m}$
are compatible with the inclusion functors
 $(\dot{U}_{[q^{\pm }]}L\mathfrak{g}\mathfrak{l}_{m})^{n}\rightarrow (\dot{U}_{[q^{\pm }]}L\mathfrak{g}\mathfrak{l}_{m+1})^{n}$
, this completes the proof of existence and uniqueness is clear by construction.◻
$(\dot{U}_{[q^{\pm }]}L\mathfrak{g}\mathfrak{l}_{m})^{n}\rightarrow (\dot{U}_{[q^{\pm }]}L\mathfrak{g}\mathfrak{l}_{m+1})^{n}$
, this completes the proof of existence and uniqueness is clear by construction.◻
The remainder of the paper will be devoted to proving the following result which combined with Corollary 4.5 completes the proof of Conjecture 3.4 in the case
 $G=\operatorname{SL}_{n}$
.
$G=\operatorname{SL}_{n}$
.
Theorem 6.7. The functor
![]() $\unicode[STIX]{x1D6F7}$
induces equivalences
$\unicode[STIX]{x1D6F7}$
induces equivalences
 $$\begin{eqnarray}\displaystyle {\mathcal{A}}{\mathcal{S}}p_{n} & \xrightarrow[{}]{{\sim}} & \displaystyle K\operatorname{Conv}^{\operatorname{SL}_{n}}(Gr),\nonumber\\ \displaystyle {\mathcal{A}}{\mathcal{S}}p_{n}(q) & \xrightarrow[{}]{{\sim}} & \displaystyle K\operatorname{Conv}^{\operatorname{SL}_{n}\times \mathbb{C}^{\times }}(Gr)\otimes _{\mathbb{C}[q^{\pm }]}\mathbb{C}(q).\nonumber\end{eqnarray}$$
$$\begin{eqnarray}\displaystyle {\mathcal{A}}{\mathcal{S}}p_{n} & \xrightarrow[{}]{{\sim}} & \displaystyle K\operatorname{Conv}^{\operatorname{SL}_{n}}(Gr),\nonumber\\ \displaystyle {\mathcal{A}}{\mathcal{S}}p_{n}(q) & \xrightarrow[{}]{{\sim}} & \displaystyle K\operatorname{Conv}^{\operatorname{SL}_{n}\times \mathbb{C}^{\times }}(Gr)\otimes _{\mathbb{C}[q^{\pm }]}\mathbb{C}(q).\nonumber\end{eqnarray}$$
6.5 Compatibility with
 $E$
-action
$E$
-action
Recall that inside
 ${\mathcal{A}}{\mathcal{S}}p_{n}[q^{\pm }]$
we have the elements
${\mathcal{A}}{\mathcal{S}}p_{n}[q^{\pm }]$
we have the elements
![]() $e_{j}$
corresponding to counterclockwise loops. This was used to define a
$e_{j}$
corresponding to counterclockwise loops. This was used to define a
![]() $E[q^{\pm }]$
-module structure to the Hom spaces in
$E[q^{\pm }]$
-module structure to the Hom spaces in
 ${\mathcal{A}}{\mathcal{S}}p_{n}[q^{\pm }]$
. The following result determines the image of
${\mathcal{A}}{\mathcal{S}}p_{n}[q^{\pm }]$
. The following result determines the image of
![]() $e_{j}$
under
$e_{j}$
under
![]() $\unicode[STIX]{x1D6F7}$
.
$\unicode[STIX]{x1D6F7}$
.
Lemma 6.8. For any
![]() $\text{}\underline{k}$
, the image of
$\text{}\underline{k}$
, the image of
 $e_{j}\in \operatorname{End}_{{\mathcal{A}}{\mathcal{S}}p_{n}[q^{\pm }]}(\text{}\underline{k})$
inside
$e_{j}\in \operatorname{End}_{{\mathcal{A}}{\mathcal{S}}p_{n}[q^{\pm }]}(\text{}\underline{k})$
inside
 $K^{\operatorname{SL}_{n}\times \mathbb{C}^{\times }}(Z(\text{}\underline{k},\text{}\underline{k}))$
is
$K^{\operatorname{SL}_{n}\times \mathbb{C}^{\times }}(Z(\text{}\underline{k},\text{}\underline{k}))$
is
 $\unicode[STIX]{x1D6E5}_{\ast }\wedge ^{n-j}(\mathbb{C}^{n})$
where
$\unicode[STIX]{x1D6E5}_{\ast }\wedge ^{n-j}(\mathbb{C}^{n})$
where
![]() $\unicode[STIX]{x1D6E5}$
is the embedding of
$\unicode[STIX]{x1D6E5}$
is the embedding of
![]() $Y(\text{}\underline{k})$
as the diagonal and
$Y(\text{}\underline{k})$
as the diagonal and
 $\wedge ^{n-j}(\mathbb{C}^{n})$
is the natural
$\wedge ^{n-j}(\mathbb{C}^{n})$
is the natural
![]() $\operatorname{SL}_{n}$
-equivariant vector bundle on
$\operatorname{SL}_{n}$
-equivariant vector bundle on
![]() $Y(\text{}\underline{k})$
.
$Y(\text{}\underline{k})$
.
Proof. To simplify notation we prove the case
![]() $\text{}\underline{k}=\emptyset$
(the general case is no different). Consider the composition
$\text{}\underline{k}=\emptyset$
(the general case is no different). Consider the composition
 $$\begin{eqnarray}\emptyset \xrightarrow[{}]{\text{cup}}(j,n-j)\xrightarrow[{}]{X_{1}}(j,n-j)\xrightarrow[{}]{\text{cap}}\emptyset\end{eqnarray}$$
$$\begin{eqnarray}\emptyset \xrightarrow[{}]{\text{cup}}(j,n-j)\xrightarrow[{}]{X_{1}}(j,n-j)\xrightarrow[{}]{\text{cap}}\emptyset\end{eqnarray}$$
inside
 ${\mathcal{A}}{\mathcal{S}}p_{n}[q^{\pm }]$
where the first map is a
${\mathcal{A}}{\mathcal{S}}p_{n}[q^{\pm }]$
where the first map is a
![]() $j$
-cup and the last map is a
$j$
-cup and the last map is a
![]() $j$
-cap. This composition recovers
$j$
-cap. This composition recovers
![]() $e_{j}$
up to a positive twist involving the
$e_{j}$
up to a positive twist involving the
![]() $j$
-strand. Since such a positive twist can be undone at the cost of a factor of
$j$
-strand. Since such a positive twist can be undone at the cost of a factor of
 $(-q)^{-j(n-j)}$
, the composition in (21) is equal to the image of
$(-q)^{-j(n-j)}$
, the composition in (21) is equal to the image of
 $(-q)^{j(n-j)}e_{j}$
.
$(-q)^{j(n-j)}e_{j}$
.
On the other hand, the composition in (21) is equivalent to the composition
 $$\begin{eqnarray}(0,n)\xrightarrow[{}]{E_{1}^{(j)}}(j,n-j)\xrightarrow[{}]{X_{1}}(j,n-j)\xrightarrow[{}]{F_{1}^{(j)}}(0,n).\end{eqnarray}$$
$$\begin{eqnarray}(0,n)\xrightarrow[{}]{E_{1}^{(j)}}(j,n-j)\xrightarrow[{}]{X_{1}}(j,n-j)\xrightarrow[{}]{F_{1}^{(j)}}(0,n).\end{eqnarray}$$
Let us first consider what happens to this composition without the middle map
![]() $X_{1}$
. We will need the natural projection and inclusion maps
$X_{1}$
. We will need the natural projection and inclusion maps
 $$\begin{eqnarray}Y(0,n)\xleftarrow[{}]{\unicode[STIX]{x1D70B}}X(j,n-j)\xrightarrow[{}]{i}Y(j,n-j),\end{eqnarray}$$
$$\begin{eqnarray}Y(0,n)\xleftarrow[{}]{\unicode[STIX]{x1D70B}}X(j,n-j)\xrightarrow[{}]{i}Y(j,n-j),\end{eqnarray}$$
where
 $$\begin{eqnarray}X(j,n-j):=\{L_{0}\subset L_{1}\subset L_{2}=z^{-1}(L_{0}):\dim (L_{1}/L_{0})=j,\dim (L_{2}/L_{1})=n-j\}\end{eqnarray}$$
$$\begin{eqnarray}X(j,n-j):=\{L_{0}\subset L_{1}\subset L_{2}=z^{-1}(L_{0}):\dim (L_{1}/L_{0})=j,\dim (L_{2}/L_{1})=n-j\}\end{eqnarray}$$
can be identified with the Grassmannian
![]() $\mathbb{G}(j,n)$
. Then
$\mathbb{G}(j,n)$
. Then
 $F_{1}^{(j)}E_{1}^{(j)}$
is given by the composition
$F_{1}^{(j)}E_{1}^{(j)}$
is given by the composition
 $$\begin{eqnarray}(-q)^{-j(n-j)}\unicode[STIX]{x1D70B}_{\ast }(i^{\ast }i_{\ast }\unicode[STIX]{x1D70B}^{\ast }(\cdot )\cdot [\det (L_{1}/L_{0})]^{n-j}\cdot [\det (L_{2}/L_{1})]^{-j}).\end{eqnarray}$$
$$\begin{eqnarray}(-q)^{-j(n-j)}\unicode[STIX]{x1D70B}_{\ast }(i^{\ast }i_{\ast }\unicode[STIX]{x1D70B}^{\ast }(\cdot )\cdot [\det (L_{1}/L_{0})]^{n-j}\cdot [\det (L_{2}/L_{1})]^{-j}).\end{eqnarray}$$
Notice that
 $\unicode[STIX]{x1D6FA}_{X(j,n-j)}\cong (L_{2}/L_{1})^{\vee }\otimes (L_{1}/L_{0})$
which means that
$\unicode[STIX]{x1D6FA}_{X(j,n-j)}\cong (L_{2}/L_{1})^{\vee }\otimes (L_{1}/L_{0})$
which means that
 $$\begin{eqnarray}\unicode[STIX]{x1D714}_{X(j,n-j)}\cong \det (L_{1}/L_{0})^{n-j}\otimes \det (L_{2}/L_{1})^{-j}.\end{eqnarray}$$
$$\begin{eqnarray}\unicode[STIX]{x1D714}_{X(j,n-j)}\cong \det (L_{1}/L_{0})^{n-j}\otimes \det (L_{2}/L_{1})^{-j}.\end{eqnarray}$$
So the composition above is just
 $$\begin{eqnarray}(-q)^{-d}\unicode[STIX]{x1D70B}_{\ast }(i^{\ast }i_{\ast }\unicode[STIX]{x1D70B}^{\ast }(\cdot )\cdot [\unicode[STIX]{x1D714}_{X(j,n-j)}])\end{eqnarray}$$
$$\begin{eqnarray}(-q)^{-d}\unicode[STIX]{x1D70B}_{\ast }(i^{\ast }i_{\ast }\unicode[STIX]{x1D70B}^{\ast }(\cdot )\cdot [\unicode[STIX]{x1D714}_{X(j,n-j)}])\end{eqnarray}$$
where
 $d=j(n-j)=\dim X(j,n-j)$
. Now, to compute
$d=j(n-j)=\dim X(j,n-j)$
. Now, to compute
![]() $i^{\ast }i_{\ast }$
notice that
$i^{\ast }i_{\ast }$
notice that
 $X(j,n-j)\subset Y(j,n-j)$
is carved out as the zero section of
$X(j,n-j)\subset Y(j,n-j)$
is carved out as the zero section of
 $$\begin{eqnarray}z:L_{2}/L_{1}\rightarrow L_{1}/L_{0}\{2\},\end{eqnarray}$$
$$\begin{eqnarray}z:L_{2}/L_{1}\rightarrow L_{1}/L_{0}\{2\},\end{eqnarray}$$
where the
![]() $\{2\}$
shift is because of the
$\{2\}$
shift is because of the
![]() $\mathbb{C}^{\times }$
action on
$\mathbb{C}^{\times }$
action on
![]() $z$
. This means that we have a Koszul resolution
$z$
. This means that we have a Koszul resolution
 $$\begin{eqnarray}\ldots \rightarrow \bigwedge ^{2}V\rightarrow V\rightarrow {\mathcal{O}}_{Y(j,n-j)}\rightarrow {\mathcal{O}}_{X(j,n-j)},\end{eqnarray}$$
$$\begin{eqnarray}\ldots \rightarrow \bigwedge ^{2}V\rightarrow V\rightarrow {\mathcal{O}}_{Y(j,n-j)}\rightarrow {\mathcal{O}}_{X(j,n-j)},\end{eqnarray}$$
where
 $V=(L_{2}/L_{1})\otimes (L_{1}/L_{0})^{\vee }\{-2\}$
. But
$V=(L_{2}/L_{1})\otimes (L_{1}/L_{0})^{\vee }\{-2\}$
. But
![]() $V$
restricted to
$V$
restricted to
 $X(j,n-j)$
is just
$X(j,n-j)$
is just
 $\unicode[STIX]{x1D6FA}_{X(j,n-j)}^{\vee }\{-2\}$
and
$\unicode[STIX]{x1D6FA}_{X(j,n-j)}^{\vee }\{-2\}$
and
 $$\begin{eqnarray}\bigwedge ^{i}(\unicode[STIX]{x1D6FA}_{X(j,n-j)}^{\vee }\{-2\})\otimes \unicode[STIX]{x1D714}_{X(j,n-j)}\cong \unicode[STIX]{x1D6FA}_{X(n-j)}^{d-i}\{-2i\}.\end{eqnarray}$$
$$\begin{eqnarray}\bigwedge ^{i}(\unicode[STIX]{x1D6FA}_{X(j,n-j)}^{\vee }\{-2\})\otimes \unicode[STIX]{x1D714}_{X(j,n-j)}\cong \unicode[STIX]{x1D6FA}_{X(n-j)}^{d-i}\{-2i\}.\end{eqnarray}$$
Hence the composition in (23) simplifies to give
 $$\begin{eqnarray}(-q)^{-d}\mathop{\sum }_{i\geqslant 0}\unicode[STIX]{x1D70B}_{\ast }((\cdot )\cdot (-1)^{i}q^{2i}[\unicode[STIX]{x1D6FA}_{X(j,n-j)}^{d-i}])=\mathop{\sum }_{i\geqslant 0}(-1)^{d+i}q^{d-2i}\unicode[STIX]{x1D70B}_{\ast }[\unicode[STIX]{x1D6FA}_{X(j,n-j)}^{i}]\cdot (\cdot ).\end{eqnarray}$$
$$\begin{eqnarray}(-q)^{-d}\mathop{\sum }_{i\geqslant 0}\unicode[STIX]{x1D70B}_{\ast }((\cdot )\cdot (-1)^{i}q^{2i}[\unicode[STIX]{x1D6FA}_{X(j,n-j)}^{d-i}])=\mathop{\sum }_{i\geqslant 0}(-1)^{d+i}q^{d-2i}\unicode[STIX]{x1D70B}_{\ast }[\unicode[STIX]{x1D6FA}_{X(j,n-j)}^{i}]\cdot (\cdot ).\end{eqnarray}$$
Since
 $X(j,n-j)\cong \mathbb{G}(j,n)$
, it is a standard fact that this evaluates to multiplication by
$X(j,n-j)\cong \mathbb{G}(j,n)$
, it is a standard fact that this evaluates to multiplication by
 $(-1)^{d}\left[\begin{smallmatrix}n\\ j\\ \end{smallmatrix}\right]$
.
$(-1)^{d}\left[\begin{smallmatrix}n\\ j\\ \end{smallmatrix}\right]$
.
We now need to reintroduce
![]() $X_{1}$
. Since
$X_{1}$
. Since
![]() $X_{1}$
is tensoring with
$X_{1}$
is tensoring with
 $\det (L_{1}/L_{0})^{\vee }$
, the composition in (22) simplifies to give
$\det (L_{1}/L_{0})^{\vee }$
, the composition in (22) simplifies to give
 $$\begin{eqnarray}\mathop{\sum }_{i\geqslant 0}(-1)^{d+i}q^{d-2i}\unicode[STIX]{x1D70B}_{\ast }([\unicode[STIX]{x1D6FA}_{X(j,n-j)}^{i}]\cdot [\det (L_{1}/L_{0})^{\vee }])\cdot (\cdot ).\end{eqnarray}$$
$$\begin{eqnarray}\mathop{\sum }_{i\geqslant 0}(-1)^{d+i}q^{d-2i}\unicode[STIX]{x1D70B}_{\ast }([\unicode[STIX]{x1D6FA}_{X(j,n-j)}^{i}]\cdot [\det (L_{1}/L_{0})^{\vee }])\cdot (\cdot ).\end{eqnarray}$$
Since
 ${\mathcal{O}}_{X(j,n-j)}\otimes \det (L_{1}/L_{0})^{\vee }\cong {\mathcal{O}}_{\mathbb{G}(j,n)}(1)$
, all these terms vanish except the lowest degree term
${\mathcal{O}}_{X(j,n-j)}\otimes \det (L_{1}/L_{0})^{\vee }\cong {\mathcal{O}}_{\mathbb{G}(j,n)}(1)$
, all these terms vanish except the lowest degree term
![]() $i=0$
which gives
$i=0$
which gives
 $$\begin{eqnarray}(-q)^{d}\unicode[STIX]{x1D70B}_{\ast }([{\mathcal{O}}_{X(j,n-j)}]\cdot [\det (L_{1}/L_{0})^{\vee }])\cdot (\cdot ).\end{eqnarray}$$
$$\begin{eqnarray}(-q)^{d}\unicode[STIX]{x1D70B}_{\ast }([{\mathcal{O}}_{X(j,n-j)}]\cdot [\det (L_{1}/L_{0})^{\vee }])\cdot (\cdot ).\end{eqnarray}$$
This is equivalent to multiplication by
 $(-q)^{d}[\wedge ^{n-j}(\mathbb{C}^{n})]$
. It follows that
$(-q)^{d}[\wedge ^{n-j}(\mathbb{C}^{n})]$
. It follows that
 $e_{j}\in \operatorname{End}_{{\mathcal{A}}{\mathcal{S}}p_{n}[q^{\pm }]}(\emptyset )$
is mapped to multiplication by
$e_{j}\in \operatorname{End}_{{\mathcal{A}}{\mathcal{S}}p_{n}[q^{\pm }]}(\emptyset )$
is mapped to multiplication by
 $[\wedge ^{n-j}(\mathbb{C}^{n})]$
. The result follows.◻
$[\wedge ^{n-j}(\mathbb{C}^{n})]$
. The result follows.◻
Corollary 6.9. The functor
![]() $\unicode[STIX]{x1D6F7}$
is a
$\unicode[STIX]{x1D6F7}$
is a
![]() $E[q^{\pm }]$
-linear functor where the following hold:
$E[q^{\pm }]$
-linear functor where the following hold:
-
–
 $e_{j}\in {\mathcal{A}}{\mathcal{S}}p_{n}[q^{\pm }]$
acts as a counterclockwise loop labelled
$e_{j}\in {\mathcal{A}}{\mathcal{S}}p_{n}[q^{\pm }]$
acts as a counterclockwise loop labelled
 $j$
;
$j$
; -
–
 $e_{j}\in K\operatorname{Conv}^{\operatorname{SL}_{n}\times \mathbb{C}^{\times }}(Gr)$
acts by tensoring with the vector bundle
$e_{j}\in K\operatorname{Conv}^{\operatorname{SL}_{n}\times \mathbb{C}^{\times }}(Gr)$
acts by tensoring with the vector bundle
 $\wedge ^{n-j}(\mathbb{C}^{n})$
.
$\wedge ^{n-j}(\mathbb{C}^{n})$
.
6.6 Reduction to
 $1^{m}$
$1^{m}$
Lemma 6.10. To show that
![]() $\unicode[STIX]{x1D6F7}$
is an equivalence it suffices to check that for each
$\unicode[STIX]{x1D6F7}$
is an equivalence it suffices to check that for each
![]() $m$
,
$m$
,
![]() $\unicode[STIX]{x1D6F7}$
induces an isomorphism
$\unicode[STIX]{x1D6F7}$
induces an isomorphism
 $$\begin{eqnarray}\operatorname{End}_{{\mathcal{A}}{\mathcal{S}}p_{n}(q)}(1^{m})\xrightarrow[{}]{{\sim}}\operatorname{End}_{K\operatorname{Conv}^{\operatorname{SL}_{n}\times \mathbb{C}^{\times }}(Gr)}(1^{m})\otimes _{\mathbb{ C}[q^{\pm }]}\mathbb{C}(q).\end{eqnarray}$$
$$\begin{eqnarray}\operatorname{End}_{{\mathcal{A}}{\mathcal{S}}p_{n}(q)}(1^{m})\xrightarrow[{}]{{\sim}}\operatorname{End}_{K\operatorname{Conv}^{\operatorname{SL}_{n}\times \mathbb{C}^{\times }}(Gr)}(1^{m})\otimes _{\mathbb{ C}[q^{\pm }]}\mathbb{C}(q).\end{eqnarray}$$
Proof. By a ‘fork’ we mean a map
![]() $1^{k}\rightarrow k$
(or its mirror
$1^{k}\rightarrow k$
(or its mirror
![]() $k\rightarrow 1^{k}$
) depicted in Figure 5 when
$k\rightarrow 1^{k}$
) depicted in Figure 5 when
![]() $k=3$
.
$k=3$
.

Figure 5. The two equal forks
 $(1,1,1)\rightarrow 3$
.
$(1,1,1)\rightarrow 3$
.
By attaching forks to the bottom and top of a morphism we get maps
 $$\begin{eqnarray}\displaystyle & & \displaystyle u:\operatorname{End}_{{\mathcal{A}}{\mathcal{S}}p_{n}(q)}(1^{m})\rightarrow \operatorname{Hom}_{{\mathcal{A}}{\mathcal{S}}p_{n}(q)}(\text{}\underline{k},\text{}\underline{l}),\nonumber\\ \displaystyle & & \displaystyle v:\operatorname{Hom}_{{\mathcal{A}}{\mathcal{S}}p_{n}(q)}(\text{}\underline{k},\text{}\underline{l})\rightarrow \operatorname{End}_{{\mathcal{A}}{\mathcal{S}}p_{n}(q)}(1^{m}),\nonumber\end{eqnarray}$$
$$\begin{eqnarray}\displaystyle & & \displaystyle u:\operatorname{End}_{{\mathcal{A}}{\mathcal{S}}p_{n}(q)}(1^{m})\rightarrow \operatorname{Hom}_{{\mathcal{A}}{\mathcal{S}}p_{n}(q)}(\text{}\underline{k},\text{}\underline{l}),\nonumber\\ \displaystyle & & \displaystyle v:\operatorname{Hom}_{{\mathcal{A}}{\mathcal{S}}p_{n}(q)}(\text{}\underline{k},\text{}\underline{l})\rightarrow \operatorname{End}_{{\mathcal{A}}{\mathcal{S}}p_{n}(q)}(1^{m}),\nonumber\end{eqnarray}$$
where
 $m=\sum _{i}k_{i}=\sum _{i}l_{i}$
. Note that we have
$m=\sum _{i}k_{i}=\sum _{i}l_{i}$
. Note that we have
 $$\begin{eqnarray}uv=\mathop{\prod }_{i}[k_{i}]![l_{i}]!\cdot \operatorname{id}\end{eqnarray}$$
$$\begin{eqnarray}uv=\mathop{\prod }_{i}[k_{i}]![l_{i}]!\cdot \operatorname{id}\end{eqnarray}$$
since the composition (prong to prong) of two forks with
![]() $k$
prongs is
$k$
prongs is
![]() $[k]!$
times the identity. We also get similar maps for
$[k]!$
times the identity. We also get similar maps for
![]() $K\operatorname{Conv}$
instead of
$K\operatorname{Conv}$
instead of
![]() ${\mathcal{A}}{\mathcal{S}}p_{n}$
.
${\mathcal{A}}{\mathcal{S}}p_{n}$
.
To simplify notation we write
 $$\begin{eqnarray}\operatorname{Hom}_{K\operatorname{Conv}(q)}(\text{}\underline{k},\text{}\underline{l}):=\operatorname{Hom}_{K\operatorname{Conv}^{\operatorname{SL}_{n}\times \mathbb{C}^{\times }}(Gr)}(\text{}\underline{k},\text{}\underline{l})\otimes _{\mathbb{C}[q^{\pm }]}\mathbb{C}(q).\end{eqnarray}$$
$$\begin{eqnarray}\operatorname{Hom}_{K\operatorname{Conv}(q)}(\text{}\underline{k},\text{}\underline{l}):=\operatorname{Hom}_{K\operatorname{Conv}^{\operatorname{SL}_{n}\times \mathbb{C}^{\times }}(Gr)}(\text{}\underline{k},\text{}\underline{l})\otimes _{\mathbb{C}[q^{\pm }]}\mathbb{C}(q).\end{eqnarray}$$
Now consider the following commutative diagram.

We assume that the left and right vertical maps
![]() $\unicode[STIX]{x1D6F7}^{\prime }$
(which are the same) are isomorphisms. Now consider
$\unicode[STIX]{x1D6F7}^{\prime }$
(which are the same) are isomorphisms. Now consider
 $\unicode[STIX]{x1D6FC}\in \operatorname{Hom}_{{\mathcal{A}}{\mathcal{S}}p_{n}(q)}(\text{}\underline{k},\text{}\underline{l})$
and suppose
$\unicode[STIX]{x1D6FC}\in \operatorname{Hom}_{{\mathcal{A}}{\mathcal{S}}p_{n}(q)}(\text{}\underline{k},\text{}\underline{l})$
and suppose
 $\unicode[STIX]{x1D6F7}(\unicode[STIX]{x1D6FC})=0$
. Then
$\unicode[STIX]{x1D6F7}(\unicode[STIX]{x1D6FC})=0$
. Then
 $\unicode[STIX]{x1D6F7}^{\prime }\circ v(\unicode[STIX]{x1D6FC})=v\circ \unicode[STIX]{x1D6F7}(\unicode[STIX]{x1D6FC})=0$
. Since
$\unicode[STIX]{x1D6F7}^{\prime }\circ v(\unicode[STIX]{x1D6FC})=v\circ \unicode[STIX]{x1D6F7}(\unicode[STIX]{x1D6FC})=0$
. Since
![]() $\unicode[STIX]{x1D6F7}^{\prime }$
is injective, this means
$\unicode[STIX]{x1D6F7}^{\prime }$
is injective, this means
 $v(\unicode[STIX]{x1D6FC})=0$
. It follows from (25) that
$v(\unicode[STIX]{x1D6FC})=0$
. It follows from (25) that
![]() $\unicode[STIX]{x1D6FC}=0$
. Thus the middle
$\unicode[STIX]{x1D6FC}=0$
. Thus the middle
![]() $\unicode[STIX]{x1D6F7}$
is injective. (Note that we are using here that we are over
$\unicode[STIX]{x1D6F7}$
is injective. (Note that we are using here that we are over
![]() $\mathbb{C}(q)$
so the product of the corresponding quantum integers is invertible.)
$\mathbb{C}(q)$
so the product of the corresponding quantum integers is invertible.)
On the other hand, consider
 $\unicode[STIX]{x1D6FD}\in \operatorname{Hom}_{K\operatorname{Conv}(q)}(\text{}\underline{k},\text{}\underline{l})$
. From (25) we know that
$\unicode[STIX]{x1D6FD}\in \operatorname{Hom}_{K\operatorname{Conv}(q)}(\text{}\underline{k},\text{}\underline{l})$
. From (25) we know that
![]() $u$
is surjective so choose
$u$
is surjective so choose
![]() $\unicode[STIX]{x1D6FD}^{\prime }$
so that
$\unicode[STIX]{x1D6FD}^{\prime }$
so that
 $u(\unicode[STIX]{x1D6FD}^{\prime })=\unicode[STIX]{x1D6FD}$
. Since
$u(\unicode[STIX]{x1D6FD}^{\prime })=\unicode[STIX]{x1D6FD}$
. Since
![]() $\unicode[STIX]{x1D6F7}^{\prime }$
is surjective, take
$\unicode[STIX]{x1D6F7}^{\prime }$
is surjective, take
![]() $\unicode[STIX]{x1D6FD}^{\prime \prime }$
so that
$\unicode[STIX]{x1D6FD}^{\prime \prime }$
so that
 $\unicode[STIX]{x1D6F7}^{\prime }(\unicode[STIX]{x1D6FD}^{\prime \prime })=\unicode[STIX]{x1D6FD}^{\prime }$
. Then
$\unicode[STIX]{x1D6F7}^{\prime }(\unicode[STIX]{x1D6FD}^{\prime \prime })=\unicode[STIX]{x1D6FD}^{\prime }$
. Then
 $\unicode[STIX]{x1D6F7}\circ u(\unicode[STIX]{x1D6FD}^{\prime \prime })=u\circ \unicode[STIX]{x1D6F7}^{\prime }(\unicode[STIX]{x1D6FD}^{\prime \prime })=u(\unicode[STIX]{x1D6FD}^{\prime })=\unicode[STIX]{x1D6FD}$
which means that
$\unicode[STIX]{x1D6F7}\circ u(\unicode[STIX]{x1D6FD}^{\prime \prime })=u\circ \unicode[STIX]{x1D6F7}^{\prime }(\unicode[STIX]{x1D6FD}^{\prime \prime })=u(\unicode[STIX]{x1D6FD}^{\prime })=\unicode[STIX]{x1D6FD}$
which means that
![]() $\unicode[STIX]{x1D6F7}$
is also surjective. This completes the proof.◻
$\unicode[STIX]{x1D6F7}$
is also surjective. This completes the proof.◻
7 Algebraic study
In order to prove that the map
 $$\begin{eqnarray}\operatorname{End}_{{\mathcal{A}}{\mathcal{S}}p_{n}(q)}(1^{m})\rightarrow \operatorname{End}_{K\operatorname{Conv}^{\operatorname{SL}_{n}\times \mathbb{C}^{\times }}(Gr)}(1^{m})\otimes _{\mathbb{ C}[q^{\pm }]}\mathbb{C}(q)\end{eqnarray}$$
$$\begin{eqnarray}\operatorname{End}_{{\mathcal{A}}{\mathcal{S}}p_{n}(q)}(1^{m})\rightarrow \operatorname{End}_{K\operatorname{Conv}^{\operatorname{SL}_{n}\times \mathbb{C}^{\times }}(Gr)}(1^{m})\otimes _{\mathbb{ C}[q^{\pm }]}\mathbb{C}(q)\end{eqnarray}$$
is an isomorphism, we will need to undertake a more detailed study of each side. We begin with
 $\operatorname{End}_{{\mathcal{A}}{\mathcal{S}}p_{n}(q)}(1^{m})$
and in particular
$\operatorname{End}_{{\mathcal{A}}{\mathcal{S}}p_{n}(q)}(1^{m})$
and in particular
 $\operatorname{End}_{{\mathcal{A}}{\mathcal{S}}p_{n}}(1^{m})$
which we study using Corollary 4.5 which tells us that
$\operatorname{End}_{{\mathcal{A}}{\mathcal{S}}p_{n}}(1^{m})$
which we study using Corollary 4.5 which tells us that
 $$\begin{eqnarray}\operatorname{End}_{{\mathcal{A}}{\mathcal{S}}p_{n}}(1^{m})\cong \operatorname{End}_{{\mathcal{O}}({\textstyle \frac{\operatorname{SL}_{n}}{\operatorname{SL}_{n}}})\operatorname{-mod}}({\mathcal{O}}(\operatorname{SL}_{n})\otimes (\mathbb{C}^{n})^{\otimes m}).\end{eqnarray}$$
$$\begin{eqnarray}\operatorname{End}_{{\mathcal{A}}{\mathcal{S}}p_{n}}(1^{m})\cong \operatorname{End}_{{\mathcal{O}}({\textstyle \frac{\operatorname{SL}_{n}}{\operatorname{SL}_{n}}})\operatorname{-mod}}({\mathcal{O}}(\operatorname{SL}_{n})\otimes (\mathbb{C}^{n})^{\otimes m}).\end{eqnarray}$$
7.1 Endomorphisms in equivariant coherent sheaves
Note that the right-hand side of (27) is the space of
![]() $\operatorname{SL}_{n}$
-equivariant endomorphisms of the trivial bundle with fibre
$\operatorname{SL}_{n}$
-equivariant endomorphisms of the trivial bundle with fibre
 $(\mathbb{C}^{n})^{\otimes m}$
. Thus we can identify
$(\mathbb{C}^{n})^{\otimes m}$
. Thus we can identify
 $$\begin{eqnarray}\operatorname{End}_{{\mathcal{O}}({\textstyle \frac{\operatorname{SL}_{n}}{\operatorname{SL}_{n}}})\operatorname{-mod}}({\mathcal{O}}(\operatorname{SL}_{n})\otimes (\mathbb{C}^{n})^{\otimes m})=\operatorname{Maps}_{\operatorname{ SL}_{n}}(\operatorname{SL}_{n},\operatorname{End}((\mathbb{C}^{n})^{\otimes m}))\end{eqnarray}$$
$$\begin{eqnarray}\operatorname{End}_{{\mathcal{O}}({\textstyle \frac{\operatorname{SL}_{n}}{\operatorname{SL}_{n}}})\operatorname{-mod}}({\mathcal{O}}(\operatorname{SL}_{n})\otimes (\mathbb{C}^{n})^{\otimes m})=\operatorname{Maps}_{\operatorname{ SL}_{n}}(\operatorname{SL}_{n},\operatorname{End}((\mathbb{C}^{n})^{\otimes m}))\end{eqnarray}$$
where the right side is the space of
![]() $\operatorname{SL}_{n}$
-equivariant maps of algebraic varieties from
$\operatorname{SL}_{n}$
-equivariant maps of algebraic varieties from
![]() $\operatorname{SL}_{n}$
to
$\operatorname{SL}_{n}$
to
 $\operatorname{End}(\mathbb{C}^{n})^{\otimes m}$
.
$\operatorname{End}(\mathbb{C}^{n})^{\otimes m}$
.
From Proposition 2.8 at
![]() $q=1$
, we have an action of the affine symmetric group
$q=1$
, we have an action of the affine symmetric group
 $AS_{m}=\mathbb{Z}^{m}\rtimes S_{m}$
on
$AS_{m}=\mathbb{Z}^{m}\rtimes S_{m}$
on
 ${\mathcal{O}}(\operatorname{SL}_{n})\otimes (\mathbb{C}^{n})^{\otimes m}$
and thus a map
${\mathcal{O}}(\operatorname{SL}_{n})\otimes (\mathbb{C}^{n})^{\otimes m}$
and thus a map
 $$\begin{eqnarray}E[AS_{m}]\rightarrow \operatorname{Maps}_{\operatorname{SL}_{n}}(\operatorname{SL}_{n},\operatorname{End}((\mathbb{C}^{n})^{\otimes m})).\end{eqnarray}$$
$$\begin{eqnarray}E[AS_{m}]\rightarrow \operatorname{Maps}_{\operatorname{SL}_{n}}(\operatorname{SL}_{n},\operatorname{End}((\mathbb{C}^{n})^{\otimes m})).\end{eqnarray}$$
We will temporarily study a slight variant of this construction, involving
 $$\begin{eqnarray}\operatorname{Maps}_{\operatorname{GL}_{n}}(\mathfrak{g}\mathfrak{l}_{n},\operatorname{End}((\mathbb{C}^{n})^{\otimes m})).\end{eqnarray}$$
$$\begin{eqnarray}\operatorname{Maps}_{\operatorname{GL}_{n}}(\mathfrak{g}\mathfrak{l}_{n},\operatorname{End}((\mathbb{C}^{n})^{\otimes m})).\end{eqnarray}$$
Let
 $\overline{E}=\mathbb{C}[e_{1},\ldots ,e_{n}]={\mathcal{O}}(\mathfrak{g}\mathfrak{l}_{n})^{\operatorname{GL}_{n}}$
, where
$\overline{E}=\mathbb{C}[e_{1},\ldots ,e_{n}]={\mathcal{O}}(\mathfrak{g}\mathfrak{l}_{n})^{\operatorname{GL}_{n}}$
, where
![]() $e_{k}(A)$
is the
$e_{k}(A)$
is the
![]() $k$
th elementary symmetric function in the eigenvalues of
$k$
th elementary symmetric function in the eigenvalues of
![]() $A$
. We have a surjection
$A$
. We have a surjection
 $\overline{E}\rightarrow E$
sending
$\overline{E}\rightarrow E$
sending
![]() $e_{n}\mapsto 1$
; this corresponds to the inclusion
$e_{n}\mapsto 1$
; this corresponds to the inclusion
 $\operatorname{SL}_{n}\rightarrow \mathfrak{g}\mathfrak{l}_{n}$
. Let
$\operatorname{SL}_{n}\rightarrow \mathfrak{g}\mathfrak{l}_{n}$
. Let
![]() $AS_{m}^{+}$
be the monoid
$AS_{m}^{+}$
be the monoid
 $\mathbb{N}^{m}\rtimes S_{m}$
. We write the generators of
$\mathbb{N}^{m}\rtimes S_{m}$
. We write the generators of
![]() $AS_{m}^{+}$
as
$AS_{m}^{+}$
as
![]() $X_{i},T_{i}$
, where
$X_{i},T_{i}$
, where
 $X_{i}=(0,\ldots ,1,\ldots 0)\in \mathbb{N}^{m}$
and
$X_{i}=(0,\ldots ,1,\ldots 0)\in \mathbb{N}^{m}$
and
![]() $T_{i}$
is the usual generator of
$T_{i}$
is the usual generator of
![]() $S_{m}$
.
$S_{m}$
.
We define a map
 $$\begin{eqnarray}\overline{E}[AS_{m}^{+}]\rightarrow \operatorname{Maps}_{\operatorname{ GL}_{n}}(\mathfrak{g}\mathfrak{l}_{n},\operatorname{End}((\mathbb{C}^{n})^{\otimes m}))=\operatorname{End}_{{\mathcal{O}}({\textstyle \frac{\mathfrak{g}\mathfrak{l}_{n}}{\operatorname{GL}_{n}}})\operatorname{-mod}}({\mathcal{O}}(\mathfrak{g}\mathfrak{l}_{n})\otimes (\mathbb{C}^{n})^{\otimes m})\end{eqnarray}$$
$$\begin{eqnarray}\overline{E}[AS_{m}^{+}]\rightarrow \operatorname{Maps}_{\operatorname{ GL}_{n}}(\mathfrak{g}\mathfrak{l}_{n},\operatorname{End}((\mathbb{C}^{n})^{\otimes m}))=\operatorname{End}_{{\mathcal{O}}({\textstyle \frac{\mathfrak{g}\mathfrak{l}_{n}}{\operatorname{GL}_{n}}})\operatorname{-mod}}({\mathcal{O}}(\mathfrak{g}\mathfrak{l}_{n})\otimes (\mathbb{C}^{n})^{\otimes m})\end{eqnarray}$$
by sending:
-
–
 $e_{k}\in \overline{E}$
to the map which takes
$e_{k}\in \overline{E}$
to the map which takes
 $X\in \mathfrak{g}\mathfrak{l}_{n}$
to multiplication by
$X\in \mathfrak{g}\mathfrak{l}_{n}$
to multiplication by
 $e_{k}(X)$
;
$e_{k}(X)$
; -
–
 $X_{i}\in AS_{m}^{+}$
to the map which takes
$X_{i}\in AS_{m}^{+}$
to the map which takes
 $A$
to
$A$
to
 $I\otimes \cdots \otimes A\otimes \cdots \otimes I$
(where
$I\otimes \cdots \otimes A\otimes \cdots \otimes I$
(where
 $A$
occurs on the
$A$
occurs on the
 $i$
th tensor factor);
$i$
th tensor factor); -
–
 $T_{i}$
to the constant map giving the endomorphism switching the
$T_{i}$
to the constant map giving the endomorphism switching the
 $i$
and
$i$
and
 $i+1$
tensor factors.
$i+1$
tensor factors.
This is very similar to the construction from Proposition 2.8, except that
![]() $X_{i}$
are not acting invertibly, so the domain of this map involves the monoid
$X_{i}$
are not acting invertibly, so the domain of this map involves the monoid
![]() $AS_{m}^{+}$
.
$AS_{m}^{+}$
.
Because this construction matches the one from Proposition 2.8, the inclusion
 $\operatorname{SL}_{n}\rightarrow \mathfrak{g}\mathfrak{l}_{n}$
gives rise to the following commutative diagram.
$\operatorname{SL}_{n}\rightarrow \mathfrak{g}\mathfrak{l}_{n}$
gives rise to the following commutative diagram.

The following result (essentially due to Kraft and Procesi [Reference Kraft and ProcesiKP79]) will be quite helpful for us.
Theorem 7.1. In the above commutative diagram all the arrows are surjective.
Proof. The surjectivity
 $\overline{E}[AS_{m}^{+}]\rightarrow E[AS_{m}^{+}]$
is obvious.
$\overline{E}[AS_{m}^{+}]\rightarrow E[AS_{m}^{+}]$
is obvious.
The surjectivity of
 $$\begin{eqnarray}\operatorname{Maps}_{\operatorname{GL}_{n}}(\mathfrak{g}\mathfrak{l}_{n},\operatorname{End}((\mathbb{C}^{n})^{\otimes m}))\rightarrow \operatorname{Maps}_{\operatorname{ SL}_{n}}(\operatorname{SL}_{n},\operatorname{End}((\mathbb{C}^{n})^{\otimes m}))\end{eqnarray}$$
$$\begin{eqnarray}\operatorname{Maps}_{\operatorname{GL}_{n}}(\mathfrak{g}\mathfrak{l}_{n},\operatorname{End}((\mathbb{C}^{n})^{\otimes m}))\rightarrow \operatorname{Maps}_{\operatorname{ SL}_{n}}(\operatorname{SL}_{n},\operatorname{End}((\mathbb{C}^{n})^{\otimes m}))\end{eqnarray}$$
is a special case of [Reference Kraft and ProcesiKP79, Lemma 6.2]. (Note that the actions of
 $\operatorname{GL}_{n},\operatorname{SL}_{n}$
factor through
$\operatorname{GL}_{n},\operatorname{SL}_{n}$
factor through
![]() $P\operatorname{GL}_{n}$
, so on both sides we can consider
$P\operatorname{GL}_{n}$
, so on both sides we can consider
![]() $\operatorname{GL}_{n}$
-equivariant maps.)
$\operatorname{GL}_{n}$
-equivariant maps.)
The surjectivity
 $$\begin{eqnarray}\overline{E}[AS_{m}^{+}]\rightarrow \operatorname{Maps}_{\operatorname{ GL}_{n}}(\mathfrak{g}\mathfrak{l}_{n},\operatorname{End}((\mathbb{C}^{n})^{\otimes m}))\end{eqnarray}$$
$$\begin{eqnarray}\overline{E}[AS_{m}^{+}]\rightarrow \operatorname{Maps}_{\operatorname{ GL}_{n}}(\mathfrak{g}\mathfrak{l}_{n},\operatorname{End}((\mathbb{C}^{n})^{\otimes m}))\end{eqnarray}$$
is [Reference Kraft and ProcesiKP79, Proposition 6.5].
Finally, the other three surjectivities imply that
 $$\begin{eqnarray}E[AS_{m}]\rightarrow \operatorname{Maps}_{\operatorname{SL}_{n}}(\operatorname{SL}_{n},\operatorname{End}((\mathbb{C}^{n})^{\otimes m}))\end{eqnarray}$$
$$\begin{eqnarray}E[AS_{m}]\rightarrow \operatorname{Maps}_{\operatorname{SL}_{n}}(\operatorname{SL}_{n},\operatorname{End}((\mathbb{C}^{n})^{\otimes m}))\end{eqnarray}$$
is surjective. ◻
7.2 An algebraic model
Define the ring
 $$\begin{eqnarray}\overline{R}_{n}^{m}:=\overline{E}[x_{1},\ldots ,x_{m}]/(x_{i}^{n}-e_{1}x_{i}^{n-1}+\cdots \pm e_{n-1}x_{i}\mp e_{n})\end{eqnarray}$$
$$\begin{eqnarray}\overline{R}_{n}^{m}:=\overline{E}[x_{1},\ldots ,x_{m}]/(x_{i}^{n}-e_{1}x_{i}^{n-1}+\cdots \pm e_{n-1}x_{i}\mp e_{n})\end{eqnarray}$$
and let
 $R_{n}^{m}=\overline{R}_{n}^{m}\otimes _{\overline{E}}E$
. In other words,
$R_{n}^{m}=\overline{R}_{n}^{m}\otimes _{\overline{E}}E$
. In other words,
![]() $R_{n}^{m}$
is obtained from
$R_{n}^{m}$
is obtained from
![]() $\overline{R}_{n}^{m}$
by setting
$\overline{R}_{n}^{m}$
by setting
![]() $e_{n}=1$
. In the next section, we will see that
$e_{n}=1$
. In the next section, we will see that
 $R_{n}^{m}\cong K_{\operatorname{SL}_{n}}((\mathbb{P}^{n-1})^{m})$
, the equivariant cohomology of the product of
$R_{n}^{m}\cong K_{\operatorname{SL}_{n}}((\mathbb{P}^{n-1})^{m})$
, the equivariant cohomology of the product of
![]() $m$
copies of
$m$
copies of
![]() $\mathbb{P}^{n-1}$
.
$\mathbb{P}^{n-1}$
.
Let
 $\operatorname{Sym}(\text{}\underline{x})\subset \operatorname{End}_{\overline{E}}(\overline{R}_{n}^{m})$
denote the
$\operatorname{Sym}(\text{}\underline{x})\subset \operatorname{End}_{\overline{E}}(\overline{R}_{n}^{m})$
denote the
![]() $\overline{E}$
-subalgebra generated by multiplication by symmetric functions in
$\overline{E}$
-subalgebra generated by multiplication by symmetric functions in
 $x_{1},\ldots ,x_{m}$
.
$x_{1},\ldots ,x_{m}$
.
Theorem 7.2. We have an isomorphism
 $$\begin{eqnarray}\operatorname{Maps}_{\operatorname{GL}_{n}}(\operatorname{End}(\mathbb{C}^{n}),\operatorname{End}((\mathbb{C}^{n})^{\otimes m}))\xrightarrow[{}]{{\sim}}\operatorname{End}_{\operatorname{ Sym}(\text{}\underline{x})}(\overline{R}_{n}^{m}).\end{eqnarray}$$
$$\begin{eqnarray}\operatorname{Maps}_{\operatorname{GL}_{n}}(\operatorname{End}(\mathbb{C}^{n}),\operatorname{End}((\mathbb{C}^{n})^{\otimes m}))\xrightarrow[{}]{{\sim}}\operatorname{End}_{\operatorname{ Sym}(\text{}\underline{x})}(\overline{R}_{n}^{m}).\end{eqnarray}$$
Proof. Consider the inclusion
 $s:\operatorname{Spec}(\overline{E})\rightarrow \operatorname{End}(\mathbb{C}^{n})$
given by
$s:\operatorname{Spec}(\overline{E})\rightarrow \operatorname{End}(\mathbb{C}^{n})$
given by
 $$\begin{eqnarray}s(e_{1},\ldots ,e_{n})=\left[\begin{array}{@{}cccccc@{}}0 & 0 & 0 & \ldots \, & 0 & (-1)^{n-1}e_{n}\\ 1 & 0 & 0 & \ldots \, & 0 & (-1)^{n-2}e_{n-1}\\ 0 & 1 & 0 & \ldots \, & 0 & (-1)^{n-3}e_{n-2}\\ \ldots \, & \ldots \, & \ldots \, & \ldots \, & \ldots \, & \ldots \\ 0 & 0 & 0 & \ldots \, & 0 & -e_{2}\\ 0 & 0 & 0 & \ldots \, & 1 & e_{1}\end{array}\right].\end{eqnarray}$$
$$\begin{eqnarray}s(e_{1},\ldots ,e_{n})=\left[\begin{array}{@{}cccccc@{}}0 & 0 & 0 & \ldots \, & 0 & (-1)^{n-1}e_{n}\\ 1 & 0 & 0 & \ldots \, & 0 & (-1)^{n-2}e_{n-1}\\ 0 & 1 & 0 & \ldots \, & 0 & (-1)^{n-3}e_{n-2}\\ \ldots \, & \ldots \, & \ldots \, & \ldots \, & \ldots \, & \ldots \\ 0 & 0 & 0 & \ldots \, & 0 & -e_{2}\\ 0 & 0 & 0 & \ldots \, & 1 & e_{1}\end{array}\right].\end{eqnarray}$$
This is a variant of the Kostant section and gives us an isomorphism
 $$\begin{eqnarray}\operatorname{End}_{{\mathcal{O}}({\textstyle \frac{\mathfrak{g}\mathfrak{l}_{n}}{\operatorname{GL}_{n}}})\operatorname{-mod}}({\mathcal{O}}(\mathfrak{g}\mathfrak{l}_{n})\otimes (\mathbb{C}^{n})^{\otimes m})\rightarrow \operatorname{End}_{\overline{Z}}(\overline{E}\otimes _{{\mathcal{O}}(\mathfrak{g}\mathfrak{l}_{n})}{\mathcal{O}}(\mathfrak{g}\mathfrak{l}_{n})\otimes (\mathbb{C}^{n})^{\otimes m})\end{eqnarray}$$
$$\begin{eqnarray}\operatorname{End}_{{\mathcal{O}}({\textstyle \frac{\mathfrak{g}\mathfrak{l}_{n}}{\operatorname{GL}_{n}}})\operatorname{-mod}}({\mathcal{O}}(\mathfrak{g}\mathfrak{l}_{n})\otimes (\mathbb{C}^{n})^{\otimes m})\rightarrow \operatorname{End}_{\overline{Z}}(\overline{E}\otimes _{{\mathcal{O}}(\mathfrak{g}\mathfrak{l}_{n})}{\mathcal{O}}(\mathfrak{g}\mathfrak{l}_{n})\otimes (\mathbb{C}^{n})^{\otimes m})\end{eqnarray}$$
where
![]() $\overline{Z}$
is the group scheme over
$\overline{Z}$
is the group scheme over
 $\operatorname{Spec}(\overline{E})$
whose fibre at a point
$\operatorname{Spec}(\overline{E})$
whose fibre at a point
![]() $e$
is the centralizer in
$e$
is the centralizer in
![]() $\operatorname{GL}_{n}$
of
$\operatorname{GL}_{n}$
of
![]() $s(e)$
.
$s(e)$
.
If
 $e\in \operatorname{Spec}(\overline{E})$
, then for any
$e\in \operatorname{Spec}(\overline{E})$
, then for any
![]() $k$
,
$k$
,
![]() $s(e)^{k}$
lies in the centralizer in
$s(e)^{k}$
lies in the centralizer in
![]() $\mathfrak{g}\mathfrak{l}_{n}$
of
$\mathfrak{g}\mathfrak{l}_{n}$
of
![]() $s(e)$
. It is easy to see that
$s(e)$
. It is easy to see that
 $I,s(e),\ldots ,s(e)^{n-1}$
gives a basis for this centralizer. Thus for each
$I,s(e),\ldots ,s(e)^{n-1}$
gives a basis for this centralizer. Thus for each
![]() $k$
, we define a map
$k$
, we define a map
 $P_{k}:\operatorname{Spec}(\overline{E})\rightarrow \operatorname{Lie}(\overline{Z})$
taking
$P_{k}:\operatorname{Spec}(\overline{E})\rightarrow \operatorname{Lie}(\overline{Z})$
taking
![]() $e$
to
$e$
to
![]() $s(e)^{k}$
, where
$s(e)^{k}$
, where
![]() $\operatorname{Lie}(\overline{Z})$
denotes the total space bundle of Lie algebras over
$\operatorname{Lie}(\overline{Z})$
denotes the total space bundle of Lie algebras over
 $\operatorname{Spec}(\overline{E})$
coming from the group scheme
$\operatorname{Spec}(\overline{E})$
coming from the group scheme
![]() $\overline{Z}$
. Thus
$\overline{Z}$
. Thus
 $P_{0},\ldots ,P_{n-1}$
give a basis for
$P_{0},\ldots ,P_{n-1}$
give a basis for
![]() $\operatorname{Lie}(\overline{Z})$
as a Lie algebra over
$\operatorname{Lie}(\overline{Z})$
as a Lie algebra over
![]() $\overline{E}$
. Hence considering endomorphisms of
$\overline{E}$
. Hence considering endomorphisms of
 $\overline{E}\otimes _{{\mathcal{O}}(\mathfrak{g}\mathfrak{l}_{n})}{\mathcal{O}}(\mathfrak{g}\mathfrak{l}_{n})\otimes (\mathbb{C}^{n})^{\otimes m}$
over
$\overline{E}\otimes _{{\mathcal{O}}(\mathfrak{g}\mathfrak{l}_{n})}{\mathcal{O}}(\mathfrak{g}\mathfrak{l}_{n})\otimes (\mathbb{C}^{n})^{\otimes m}$
over
![]() $\overline{Z}$
is the same as considering endomorphisms of this
$\overline{Z}$
is the same as considering endomorphisms of this
![]() $\overline{E}$
-module over the action of
$\overline{E}$
-module over the action of
 $P_{0},\ldots ,P_{n-1}$
.
$P_{0},\ldots ,P_{n-1}$
.
For each
![]() $k$
, the action of
$k$
, the action of
![]() $P_{k}$
on
$P_{k}$
on
 $\overline{E}\otimes _{{\mathcal{O}}(\mathfrak{g}\mathfrak{l}_{n})}{\mathcal{O}}(\mathfrak{g}\mathfrak{l}_{n})\otimes (\mathbb{C}^{n})^{\otimes m}$
is given by
$\overline{E}\otimes _{{\mathcal{O}}(\mathfrak{g}\mathfrak{l}_{n})}{\mathcal{O}}(\mathfrak{g}\mathfrak{l}_{n})\otimes (\mathbb{C}^{n})^{\otimes m}$
is given by
 $\sum _{i=1}^{m}X_{i}^{k}$
, where
$\sum _{i=1}^{m}X_{i}^{k}$
, where
![]() $X_{i}$
is the endomorphism coming from
$X_{i}$
is the endomorphism coming from
 $X_{i}\in AS_{m}^{+}$
by the construction in the previous section. Thus,
$X_{i}\in AS_{m}^{+}$
by the construction in the previous section. Thus,
 $\operatorname{End}_{\overline{Z}}(\overline{E}\otimes _{{\mathcal{O}}(\mathfrak{g}\mathfrak{l}_{n})}{\mathcal{O}}(\mathfrak{g}\mathfrak{l}_{n})\otimes (\mathbb{C}^{n})^{\otimes m})$
is the same thing as endomorphisms over the
$\operatorname{End}_{\overline{Z}}(\overline{E}\otimes _{{\mathcal{O}}(\mathfrak{g}\mathfrak{l}_{n})}{\mathcal{O}}(\mathfrak{g}\mathfrak{l}_{n})\otimes (\mathbb{C}^{n})^{\otimes m})$
is the same thing as endomorphisms over the
![]() $\overline{E}$
-algebra generated by symmetric functions in the
$\overline{E}$
-algebra generated by symmetric functions in the
 $X_{1},\ldots ,X_{m}$
.
$X_{1},\ldots ,X_{m}$
.
We now identify
 $\overline{E}\otimes _{{\mathcal{O}}(\mathfrak{g}\mathfrak{l}_{n})}{\mathcal{O}}(\mathfrak{g}\mathfrak{l}_{n})\otimes (\mathbb{C}^{n})^{\otimes m}$
with
$\overline{E}\otimes _{{\mathcal{O}}(\mathfrak{g}\mathfrak{l}_{n})}{\mathcal{O}}(\mathfrak{g}\mathfrak{l}_{n})\otimes (\mathbb{C}^{n})^{\otimes m}$
with
![]() $\overline{R}_{n}^{m}$
(both are free
$\overline{R}_{n}^{m}$
(both are free
![]() $\overline{E}$
-modules of rank
$\overline{E}$
-modules of rank
![]() $n^{m}$
) via the map
$n^{m}$
) via the map
 $$\begin{eqnarray}1\otimes 1\otimes v_{k_{1}}\otimes \cdots \otimes v_{k_{m}}\mapsto x_{1}^{k_{1}-1}\cdots x_{m}^{k_{m}-1},\end{eqnarray}$$
$$\begin{eqnarray}1\otimes 1\otimes v_{k_{1}}\otimes \cdots \otimes v_{k_{m}}\mapsto x_{1}^{k_{1}-1}\cdots x_{m}^{k_{m}-1},\end{eqnarray}$$
where
 $v_{1},\ldots ,v_{n}$
denotes the standard basis for
$v_{1},\ldots ,v_{n}$
denotes the standard basis for
![]() $\mathbb{C}^{n}$
.
$\mathbb{C}^{n}$
.
We claim that under this identification,
![]() $X_{i}$
corresponds to multiplication by
$X_{i}$
corresponds to multiplication by
![]() $x_{i}$
. To see this, let us assume for simplicity that
$x_{i}$
. To see this, let us assume for simplicity that
![]() $m=1$
. Then
$m=1$
. Then
![]() $X$
as an element of
$X$
as an element of
 $\operatorname{End}_{{\mathcal{O}}({\textstyle \frac{\mathfrak{g}\mathfrak{l}_{n}}{\operatorname{GL}_{n}}})\operatorname{-mod}}({\mathcal{O}}(\mathfrak{g}\mathfrak{l}_{n})\otimes \mathbb{C}^{n})$
is given by
$\operatorname{End}_{{\mathcal{O}}({\textstyle \frac{\mathfrak{g}\mathfrak{l}_{n}}{\operatorname{GL}_{n}}})\operatorname{-mod}}({\mathcal{O}}(\mathfrak{g}\mathfrak{l}_{n})\otimes \mathbb{C}^{n})$
is given by
 $$\begin{eqnarray}1\otimes v_{k}\mapsto \unicode[STIX]{x1D719}_{k},\end{eqnarray}$$
$$\begin{eqnarray}1\otimes v_{k}\mapsto \unicode[STIX]{x1D719}_{k},\end{eqnarray}$$
where
![]() $\unicode[STIX]{x1D719}_{k}$
is the
$\unicode[STIX]{x1D719}_{k}$
is the
![]() $\mathbb{C}^{n}$
valued function on
$\mathbb{C}^{n}$
valued function on
![]() $\mathfrak{g}\mathfrak{l}_{n}$
given by
$\mathfrak{g}\mathfrak{l}_{n}$
given by
 $\unicode[STIX]{x1D719}_{k}(g)=g(v_{k})$
. Now, if
$\unicode[STIX]{x1D719}_{k}(g)=g(v_{k})$
. Now, if
 $g=s(e_{1},\ldots ,e_{n})$
, then we have
$g=s(e_{1},\ldots ,e_{n})$
, then we have
 $$\begin{eqnarray}g(v_{k})=\left\{\begin{array}{@{}ll@{}}v_{k+1}\quad & \text{if }k\neq n,\\ (-1)^{n-1}e_{n}v_{1}+(-1)^{n-2}e_{n-1}v_{2}+\cdots +e_{1}v_{n}\quad & \text{if }k=n.\end{array}\right.\end{eqnarray}$$
$$\begin{eqnarray}g(v_{k})=\left\{\begin{array}{@{}ll@{}}v_{k+1}\quad & \text{if }k\neq n,\\ (-1)^{n-1}e_{n}v_{1}+(-1)^{n-2}e_{n-1}v_{2}+\cdots +e_{1}v_{n}\quad & \text{if }k=n.\end{array}\right.\end{eqnarray}$$
Thus under the above identification
 $\overline{E}\otimes _{{\mathcal{O}}(\mathfrak{g}\mathfrak{l}_{n})}{\mathcal{O}}(\mathfrak{g}\mathfrak{l}_{n})\otimes \mathbb{C}^{n}\rightarrow \overline{R}_{n}$
, we see that the image of
$\overline{E}\otimes _{{\mathcal{O}}(\mathfrak{g}\mathfrak{l}_{n})}{\mathcal{O}}(\mathfrak{g}\mathfrak{l}_{n})\otimes \mathbb{C}^{n}\rightarrow \overline{R}_{n}$
, we see that the image of
![]() $X$
is given by
$X$
is given by
 $$\begin{eqnarray}x^{k-1}\mapsto \left\{\begin{array}{@{}ll@{}}x^{k}\quad & \text{if }k\neq n,\\ (-1)^{n-1}e_{n}+(-1)^{n-2}e_{n-1}x+\cdots +e_{1}x^{n-1}\quad & \text{if }k=n,\end{array}\right.\end{eqnarray}$$
$$\begin{eqnarray}x^{k-1}\mapsto \left\{\begin{array}{@{}ll@{}}x^{k}\quad & \text{if }k\neq n,\\ (-1)^{n-1}e_{n}+(-1)^{n-2}e_{n-1}x+\cdots +e_{1}x^{n-1}\quad & \text{if }k=n,\end{array}\right.\end{eqnarray}$$
which matches multiplication by
![]() $x$
acting on
$x$
acting on
![]() $\overline{R}_{n}$
.
$\overline{R}_{n}$
.
Combining all this, we see that we have an isomorphism
 $$\begin{eqnarray}\operatorname{End}_{{\mathcal{O}}({\textstyle \frac{\mathfrak{g}\mathfrak{l}_{n}}{\operatorname{GL}_{n}}})\operatorname{-mod}}({\mathcal{O}}(\mathfrak{g}\mathfrak{l}_{n})\otimes (\mathbb{C}^{n})^{\otimes m})\cong \operatorname{End}_{\operatorname{ Sym}(\text{}\underline{x})}(\overline{R}_{n}^{m})\end{eqnarray}$$
$$\begin{eqnarray}\operatorname{End}_{{\mathcal{O}}({\textstyle \frac{\mathfrak{g}\mathfrak{l}_{n}}{\operatorname{GL}_{n}}})\operatorname{-mod}}({\mathcal{O}}(\mathfrak{g}\mathfrak{l}_{n})\otimes (\mathbb{C}^{n})^{\otimes m})\cong \operatorname{End}_{\operatorname{ Sym}(\text{}\underline{x})}(\overline{R}_{n}^{m})\end{eqnarray}$$
as desired. ◻
As a consequence of Theorems 7.1 and 7.2 we deduce the following.
Corollary 7.3. There is a surjective
![]() $\overline{E}$
-algebra map
$\overline{E}$
-algebra map
 $$\begin{eqnarray}\overline{\unicode[STIX]{x1D712}}:\overline{E}[AS_{m}]\rightarrow \operatorname{End}_{\operatorname{Sym}(\text{}\underline{x})}(\overline{R}_{n}^{m})\end{eqnarray}$$
$$\begin{eqnarray}\overline{\unicode[STIX]{x1D712}}:\overline{E}[AS_{m}]\rightarrow \operatorname{End}_{\operatorname{Sym}(\text{}\underline{x})}(\overline{R}_{n}^{m})\end{eqnarray}$$
such that
![]() $\overline{\unicode[STIX]{x1D712}}(X_{i})$
is multiplication by
$\overline{\unicode[STIX]{x1D712}}(X_{i})$
is multiplication by
![]() $x_{i}$
and
$x_{i}$
and
![]() $\overline{\unicode[STIX]{x1D712}}(T_{i})$
permutes the variables
$\overline{\unicode[STIX]{x1D712}}(T_{i})$
permutes the variables
![]() $x_{i}$
and
$x_{i}$
and
![]() $x_{i+1}$
.
$x_{i+1}$
.
7.3 A
 $q$
-deformation
$q$
-deformation
We now introduce a
![]() $q$
-deformation of the ring
$q$
-deformation of the ring
![]() $\overline{R}_{n}^{m}$
.
$\overline{R}_{n}^{m}$
.
We define
 $$\begin{eqnarray}\overline{R}_{n,[q^{\pm }]}^{m}:=\overline{E}[q^{\pm }][x_{1},\ldots ,x_{m}]/(x_{i}^{n}-e_{1}^{(i)}x_{i}^{n-1}+e_{2}^{(i)}x_{i}^{n-2}-\cdots +(-1)^{n}e_{n}^{(i)}),\end{eqnarray}$$
$$\begin{eqnarray}\overline{R}_{n,[q^{\pm }]}^{m}:=\overline{E}[q^{\pm }][x_{1},\ldots ,x_{m}]/(x_{i}^{n}-e_{1}^{(i)}x_{i}^{n-1}+e_{2}^{(i)}x_{i}^{n-2}-\cdots +(-1)^{n}e_{n}^{(i)}),\end{eqnarray}$$
where the elements
![]() $e_{j}^{(i)}$
are defined recursively by
$e_{j}^{(i)}$
are defined recursively by
 $e_{j}^{(1)}=e_{j}$
and
$e_{j}^{(1)}=e_{j}$
and
 $$\begin{eqnarray}e_{j}^{(i)}:=e_{j}^{(i-1)}+(q^{2}-1)[x_{i-1}e_{j-1}^{(i-1)}-x_{i-1}^{2}e_{j-2}^{(i-1)}+x_{i-1}^{3}e_{j-3}^{(i-1)}-\cdots \,].\end{eqnarray}$$
$$\begin{eqnarray}e_{j}^{(i)}:=e_{j}^{(i-1)}+(q^{2}-1)[x_{i-1}e_{j-1}^{(i-1)}-x_{i-1}^{2}e_{j-2}^{(i-1)}+x_{i-1}^{3}e_{j-3}^{(i-1)}-\cdots \,].\end{eqnarray}$$
This definition is motivated by computations in
 $K\operatorname{Conv}^{\operatorname{SL}_{n}\times \mathbb{C}^{\times }}(Gr)$
as we will explain in the next section. Again, we consider the
$K\operatorname{Conv}^{\operatorname{SL}_{n}\times \mathbb{C}^{\times }}(Gr)$
as we will explain in the next section. Again, we consider the
![]() $\overline{E}$
subalgebra
$\overline{E}$
subalgebra
![]() $\operatorname{Sym}(\text{}\underline{x})$
of
$\operatorname{Sym}(\text{}\underline{x})$
of
![]() $\overline{R}_{n,[q^{\pm }]}^{m}$
generated by multiplication by symmetric functions in the
$\overline{R}_{n,[q^{\pm }]}^{m}$
generated by multiplication by symmetric functions in the
![]() $x_{i}$
. Similarly, we can define
$x_{i}$
. Similarly, we can define
![]() $\overline{R}_{n,(q)}^{m}$
by tensoring with
$\overline{R}_{n,(q)}^{m}$
by tensoring with
![]() $\mathbb{C}(q)$
, and we define
$\mathbb{C}(q)$
, and we define
![]() $R_{n,[q^{\pm }]}^{m}$
and
$R_{n,[q^{\pm }]}^{m}$
and
![]() $R_{n,(q)}^{m}$
by setting
$R_{n,(q)}^{m}$
by setting
![]() $e_{n}=1$
.
$e_{n}=1$
.
Remark 7.4. It will follow from our later results that there is an isomorphism
 $$\begin{eqnarray}\operatorname{End}_{{\mathcal{O}}_{q}({\textstyle \frac{\operatorname{SL}_{n}}{\operatorname{SL}_{n}}})\operatorname{-mod}}({\mathcal{O}}_{q}(\operatorname{SL}_{n})\otimes (\mathbb{C}_{q}^{n})^{\otimes m})\cong \operatorname{End}_{\operatorname{ Sym}(\text{}\underline{x})}(R_{n,(q)}^{m})\end{eqnarray}$$
$$\begin{eqnarray}\operatorname{End}_{{\mathcal{O}}_{q}({\textstyle \frac{\operatorname{SL}_{n}}{\operatorname{SL}_{n}}})\operatorname{-mod}}({\mathcal{O}}_{q}(\operatorname{SL}_{n})\otimes (\mathbb{C}_{q}^{n})^{\otimes m})\cong \operatorname{End}_{\operatorname{ Sym}(\text{}\underline{x})}(R_{n,(q)}^{m})\end{eqnarray}$$
but we do not know how to prove this directly. We also suspect that
 $$\begin{eqnarray}\operatorname{End}_{{\mathcal{O}}_{q}({\textstyle \frac{\mathfrak{g}\mathfrak{l}_{n}}{\operatorname{GL}_{n}}})}({\mathcal{O}}_{q}(\mathfrak{g}\mathfrak{l}_{n})\otimes (\mathbb{C}_{q}^{n})^{\otimes m})\cong \operatorname{End}_{\operatorname{ Sym}(\text{}\underline{x})}(\overline{R}_{n,(q)}^{m}),\end{eqnarray}$$
$$\begin{eqnarray}\operatorname{End}_{{\mathcal{O}}_{q}({\textstyle \frac{\mathfrak{g}\mathfrak{l}_{n}}{\operatorname{GL}_{n}}})}({\mathcal{O}}_{q}(\mathfrak{g}\mathfrak{l}_{n})\otimes (\mathbb{C}_{q}^{n})^{\otimes m})\cong \operatorname{End}_{\operatorname{ Sym}(\text{}\underline{x})}(\overline{R}_{n,(q)}^{m}),\end{eqnarray}$$
where
![]() ${\mathcal{O}}_{q}(\mathfrak{g}\mathfrak{l}_{n})$
is the quantum matrix algebra as defined in, for example, [Reference Berenstein and ZwicknaglBZ08, Appendix A].
${\mathcal{O}}_{q}(\mathfrak{g}\mathfrak{l}_{n})$
is the quantum matrix algebra as defined in, for example, [Reference Berenstein and ZwicknaglBZ08, Appendix A].
Let
![]() $AB_{m}^{+}$
be the submonoid of
$AB_{m}^{+}$
be the submonoid of
![]() $AB_{m}$
generated by
$AB_{m}$
generated by
![]() $X_{i}$
,
$X_{i}$
,
 $i=1,\ldots ,m$
and
$i=1,\ldots ,m$
and
![]() $T_{i},T_{i}^{-1}$
for
$T_{i},T_{i}^{-1}$
for
 $i=1,\ldots ,m-1$
. This is useful for us since it allows us to consider ‘representations’ of the annular braid group such that the
$i=1,\ldots ,m-1$
. This is useful for us since it allows us to consider ‘representations’ of the annular braid group such that the
![]() $X_{i}$
do not act invertibly.
$X_{i}$
do not act invertibly.
We define the
![]() $\overline{E}[q^{\pm }]$
-linear map
$\overline{E}[q^{\pm }]$
-linear map
 $$\begin{eqnarray}\overline{\unicode[STIX]{x1D712}}:\overline{E}[q^{\pm }][AB_{m}^{+}]\rightarrow \operatorname{End}_{\operatorname{ Sym}(\text{}\underline{x})}(\overline{R}_{n,[q^{\pm }]}^{m})\end{eqnarray}$$
$$\begin{eqnarray}\overline{\unicode[STIX]{x1D712}}:\overline{E}[q^{\pm }][AB_{m}^{+}]\rightarrow \operatorname{End}_{\operatorname{ Sym}(\text{}\underline{x})}(\overline{R}_{n,[q^{\pm }]}^{m})\end{eqnarray}$$
by taking
![]() $X_{i}$
to multiplication by
$X_{i}$
to multiplication by
![]() $x_{i}$
and
$x_{i}$
and
![]() $T_{i}$
to the unique map which:
$T_{i}$
to the unique map which:
-
(i) is linear over
 $\overline{E}[q^{\pm }][x_{1},\ldots ,x_{n}]^{s_{i}}$
where
$\overline{E}[q^{\pm }][x_{1},\ldots ,x_{n}]^{s_{i}}$
where
 $s_{i}$
acts by exchanging
$s_{i}$
acts by exchanging
 $x_{i}$
and
$x_{i}$
and
 $x_{i+1}$
;
$x_{i+1}$
; -
(ii) satisfies
 $T_{i}(1)=q$
and
$T_{i}(1)=q$
and
 $T_{i}(x_{i})=q^{-1}x_{i+1}$
.
$T_{i}(x_{i})=q^{-1}x_{i+1}$
.
Remark 7.5. At
![]() $q=1$
, the map
$q=1$
, the map
![]() $\overline{\unicode[STIX]{x1D712}}$
from (28) specializes to
$\overline{\unicode[STIX]{x1D712}}$
from (28) specializes to
![]() $\overline{\unicode[STIX]{x1D712}}$
from Corollary 7.3.
$\overline{\unicode[STIX]{x1D712}}$
from Corollary 7.3.
Proposition 7.6. The map
![]() $\overline{\unicode[STIX]{x1D712}}$
from (28) is well defined.
$\overline{\unicode[STIX]{x1D712}}$
from (28) is well defined.
Proof. Although not trivial, one can check this directly by hand. Alternatively the result follows from Lemmas 8.14 and 9.3. More precisely, in Lemma 8.14 we identify
![]() $R_{n,[q^{\pm }]}^{m}$
with
$R_{n,[q^{\pm }]}^{m}$
with
 $K^{\operatorname{SL}_{n}\times \mathbb{C}^{\times }}(Y(1^{m}))$
while Lemma 9.3 shows that there is an action of
$K^{\operatorname{SL}_{n}\times \mathbb{C}^{\times }}(Y(1^{m}))$
while Lemma 9.3 shows that there is an action of
 $E[q^{\pm }][AB_{m}]$
on
$E[q^{\pm }][AB_{m}]$
on
 $K^{\operatorname{SL}_{n}\times \mathbb{C}^{\times }}(Y(1^{m}))$
which satisfies properties (i) and (ii) from above. It then follows that this action induces an action of
$K^{\operatorname{SL}_{n}\times \mathbb{C}^{\times }}(Y(1^{m}))$
which satisfies properties (i) and (ii) from above. It then follows that this action induces an action of
 $\overline{E}[q^{\pm }][AB_{m}^{+}]$
on
$\overline{E}[q^{\pm }][AB_{m}^{+}]$
on
![]() $\overline{R}_{n,[q^{\pm }]}^{m}$
satisfying these same properties.◻
$\overline{R}_{n,[q^{\pm }]}^{m}$
satisfying these same properties.◻
7.4 Surjectivity
The reason for introducing
![]() $\overline{E}$
and
$\overline{E}$
and
![]() $\overline{R}_{n}^{m}$
(rather than working with
$\overline{R}_{n}^{m}$
(rather than working with
![]() $E$
and
$E$
and
![]() $R_{n}^{m}$
) is because they carry an
$R_{n}^{m}$
) is because they carry an
![]() $\mathbb{N}$
-grading. This means that they can be used to extend surjectivity from
$\mathbb{N}$
-grading. This means that they can be used to extend surjectivity from
![]() $q=1$
to generic
$q=1$
to generic
![]() $q$
. This grading is defined by setting
$q$
. This grading is defined by setting
 $\deg (e_{j})=j,\deg (q)=0,\deg (x_{i})=1$
.
$\deg (e_{j})=j,\deg (q)=0,\deg (x_{i})=1$
.
Proposition 7.7. The map
 $\overline{\unicode[STIX]{x1D712}}:\overline{E}(q)[AB_{m}^{+}]\rightarrow \operatorname{End}_{\operatorname{Sym}(\text{}\underline{x})}(\overline{R}_{n,(q)}^{m})$
is surjective. This means that the induced map
$\overline{\unicode[STIX]{x1D712}}:\overline{E}(q)[AB_{m}^{+}]\rightarrow \operatorname{End}_{\operatorname{Sym}(\text{}\underline{x})}(\overline{R}_{n,(q)}^{m})$
is surjective. This means that the induced map
 $\unicode[STIX]{x1D712}:E(q)[AB_{m}]\rightarrow \operatorname{End}_{\operatorname{Sym}(\text{}\underline{x})}(R_{n,(q)}^{m})$
is surjective.
$\unicode[STIX]{x1D712}:E(q)[AB_{m}]\rightarrow \operatorname{End}_{\operatorname{Sym}(\text{}\underline{x})}(R_{n,(q)}^{m})$
is surjective.
Proof. Note that
 $\operatorname{End}_{\operatorname{Sym}(\text{}\underline{x})}(\overline{R}_{n,[q^{\pm }]}^{m})$
is a finitely generated graded
$\operatorname{End}_{\operatorname{Sym}(\text{}\underline{x})}(\overline{R}_{n,[q^{\pm }]}^{m})$
is a finitely generated graded
![]() $\overline{E}[q^{\pm }]$
-module. Define an
$\overline{E}[q^{\pm }]$
-module. Define an
![]() $\mathbb{N}$
-grading on
$\mathbb{N}$
-grading on
 $\overline{E}[AB_{m}^{+}]$
with
$\overline{E}[AB_{m}^{+}]$
with
 $\deg (X_{i})=1$
and
$\deg (X_{i})=1$
and
 $\deg (T_{i})=0$
. Then using Corollary 7.3, the map
$\deg (T_{i})=0$
. Then using Corollary 7.3, the map
 $\overline{\unicode[STIX]{x1D712}}:\overline{E}[q^{\pm }][AB_{m}^{+}]\rightarrow \operatorname{End}_{\operatorname{Sym}(\text{}\underline{x})}(\overline{R}_{n,[q^{\pm }]}^{m})$
fits into the framework of Lemma 7.8. The result follows.◻
$\overline{\unicode[STIX]{x1D712}}:\overline{E}[q^{\pm }][AB_{m}^{+}]\rightarrow \operatorname{End}_{\operatorname{Sym}(\text{}\underline{x})}(\overline{R}_{n,[q^{\pm }]}^{m})$
fits into the framework of Lemma 7.8. The result follows.◻
Lemma 7.8. Suppose
 $f:A\rightarrow B$
is a map of graded
$f:A\rightarrow B$
is a map of graded
![]() $\overline{E}[q^{\pm }]$
-modules, and that
$\overline{E}[q^{\pm }]$
-modules, and that
![]() $B$
is finitely generated over
$B$
is finitely generated over
![]() $\overline{E}[q^{\pm }]$
. If
$\overline{E}[q^{\pm }]$
. If
![]() $f|_{q=1}$
is surjective then the induced map
$f|_{q=1}$
is surjective then the induced map
 $$\begin{eqnarray}f\otimes _{\mathbb{C}[q^{\pm }]}\mathbb{C}(q):A\otimes _{\mathbb{C}[q^{\pm }]}\mathbb{C}(q)\rightarrow B\otimes _{\mathbb{C}[q^{\pm }]}\mathbb{C}(q)\end{eqnarray}$$
$$\begin{eqnarray}f\otimes _{\mathbb{C}[q^{\pm }]}\mathbb{C}(q):A\otimes _{\mathbb{C}[q^{\pm }]}\mathbb{C}(q)\rightarrow B\otimes _{\mathbb{C}[q^{\pm }]}\mathbb{C}(q)\end{eqnarray}$$
is surjective.
Proof. Consider the cokernel
 $C:=\operatorname{coker}(f)$
. Since
$C:=\operatorname{coker}(f)$
. Since
![]() $f|_{q=1}$
is surjective, this means
$f|_{q=1}$
is surjective, this means
 $C\otimes _{\mathbb{C}[q^{\pm }]}\mathbb{C}_{1}=0$
. On the other hand,
$C\otimes _{\mathbb{C}[q^{\pm }]}\mathbb{C}_{1}=0$
. On the other hand,
![]() $C$
is a finitely generated, graded
$C$
is a finitely generated, graded
![]() $\overline{E}[q^{\pm }]$
-module so we can consider its support
$\overline{E}[q^{\pm }]$
-module so we can consider its support
 $$\begin{eqnarray}\operatorname{supp}(C)\subset \operatorname{Spec}(\mathbb{C}[q^{\pm }])\times \operatorname{Proj}(\overline{E})\xrightarrow[{}]{\unicode[STIX]{x1D70B}}\operatorname{Spec}(\mathbb{C}[q^{\pm }]).\end{eqnarray}$$
$$\begin{eqnarray}\operatorname{supp}(C)\subset \operatorname{Spec}(\mathbb{C}[q^{\pm }])\times \operatorname{Proj}(\overline{E})\xrightarrow[{}]{\unicode[STIX]{x1D70B}}\operatorname{Spec}(\mathbb{C}[q^{\pm }]).\end{eqnarray}$$
Since
![]() $\unicode[STIX]{x1D70B}$
is proper, this means that
$\unicode[STIX]{x1D70B}$
is proper, this means that
 $\unicode[STIX]{x1D70B}(\operatorname{supp}(C))\subset \operatorname{Spec}(\mathbb{C}[q^{\pm }])$
is a closed subvariety. On the other hand, since
$\unicode[STIX]{x1D70B}(\operatorname{supp}(C))\subset \operatorname{Spec}(\mathbb{C}[q^{\pm }])$
is a closed subvariety. On the other hand, since
 $C\otimes _{\mathbb{C}[q^{\pm }]}\mathbb{C}_{1}=0$
this means that
$C\otimes _{\mathbb{C}[q^{\pm }]}\mathbb{C}_{1}=0$
this means that
 $\unicode[STIX]{x1D70B}(\operatorname{supp}(C))$
does not contain the point
$\unicode[STIX]{x1D70B}(\operatorname{supp}(C))$
does not contain the point
![]() $q=1$
. Thus
$q=1$
. Thus
 $\unicode[STIX]{x1D70B}(\operatorname{supp}(C))$
must be the union of a finite number of points and thus
$\unicode[STIX]{x1D70B}(\operatorname{supp}(C))$
must be the union of a finite number of points and thus
 $C\otimes _{\mathbb{C}[q^{\pm }]}\mathbb{C}(q)=0$
. This implies that
$C\otimes _{\mathbb{C}[q^{\pm }]}\mathbb{C}(q)=0$
. This implies that
 $f\otimes _{\mathbb{C}[q^{\pm }]}\mathbb{C}(q)$
is surjective.◻
$f\otimes _{\mathbb{C}[q^{\pm }]}\mathbb{C}(q)$
is surjective.◻
8 Geometric study
We now study the right-hand side of the isomorphism
 $$\begin{eqnarray}\operatorname{End}_{{\mathcal{A}}{\mathcal{S}}p_{n}(q)}(1^{m})\rightarrow \operatorname{End}_{K\operatorname{Conv}^{\operatorname{SL}_{n}\times \mathbb{C}^{\times }}(Gr)}(1^{m})\otimes _{\mathbb{ C}[q^{\pm }]}\mathbb{C}(q)\end{eqnarray}$$
$$\begin{eqnarray}\operatorname{End}_{{\mathcal{A}}{\mathcal{S}}p_{n}(q)}(1^{m})\rightarrow \operatorname{End}_{K\operatorname{Conv}^{\operatorname{SL}_{n}\times \mathbb{C}^{\times }}(Gr)}(1^{m})\otimes _{\mathbb{ C}[q^{\pm }]}\mathbb{C}(q)\end{eqnarray}$$
which means investigating the K-theory of the variety
 $Z(1^{m},1^{m})$
.
$Z(1^{m},1^{m})$
.
8.1 Property
 $T_{A}$
$T_{A}$
The first step is to prove that
 $K^{\operatorname{SL}_{n}\times \mathbb{C}^{\times }}(Z(1^{m},1^{m}))$
is a free
$K^{\operatorname{SL}_{n}\times \mathbb{C}^{\times }}(Z(1^{m},1^{m}))$
is a free
![]() $E[q^{\pm }]$
-module (Corollary 8.11). To do this we will prove that this space satisfies a certain property, called property
$E[q^{\pm }]$
-module (Corollary 8.11). To do this we will prove that this space satisfies a certain property, called property
![]() $T_{A}$
, as discussed below.
$T_{A}$
, as discussed below.
Let
![]() $A$
be an algebraic group and let
$A$
be an algebraic group and let
 $R_{A}=K^{A}(\operatorname{pt})$
be the representation ring of
$R_{A}=K^{A}(\operatorname{pt})$
be the representation ring of
![]() $A$
. Suppose that
$A$
. Suppose that
![]() $X$
is an algebraic variety equipped with an action of
$X$
is an algebraic variety equipped with an action of
![]() $A$
. We write
$A$
. We write
 $K_{i,\text{top}}^{A}(X)$
for the (higher)
$K_{i,\text{top}}^{A}(X)$
for the (higher)
![]() $A$
-equivariant topological K-theory of
$A$
-equivariant topological K-theory of
![]() $X$
. Following [Reference NakajimaNak01, § 7] we say that
$X$
. Following [Reference NakajimaNak01, § 7] we say that
![]() $X$
has property
$X$
has property
![]() $T_{A}$
if the following hold:
$T_{A}$
if the following hold:
-
(i)
 $K_{1,\text{top}}^{A}(X)=0$
and
$K_{1,\text{top}}^{A}(X)=0$
and
 $K_{\text{top}}^{A}(X)=K_{0,\text{top}}^{A}(X)$
is a free
$K_{\text{top}}^{A}(X)=K_{0,\text{top}}^{A}(X)$
is a free
 $R_{A}$
-module;
$R_{A}$
-module; -
(ii) the map
 $K^{A}(X)\rightarrow K_{\text{top}}^{A}(X)$
is an isomorphism;
$K^{A}(X)\rightarrow K_{\text{top}}^{A}(X)$
is an isomorphism; -
(iii) for any closed algebraic subgroup
 $A^{\prime }\subset A$
the
$A^{\prime }\subset A$
the
 $A^{\prime }$
-equivariant K-theories satisfy the two properties above and moreover the map
$A^{\prime }$
-equivariant K-theories satisfy the two properties above and moreover the map
 $K^{A}(X)\otimes _{R_{A}}R_{A^{\prime }}\rightarrow K^{A^{\prime }}(X)$
is an isomorphism.
$K^{A}(X)\otimes _{R_{A}}R_{A^{\prime }}\rightarrow K^{A^{\prime }}(X)$
is an isomorphism.
Now consider a finite collection of
![]() $A$
-invariant, locally closed subvarieties
$A$
-invariant, locally closed subvarieties
 $\{X_{i}\}_{i\in I}$
of
$\{X_{i}\}_{i\in I}$
of
![]() $X$
. Suppose
$X$
. Suppose
 $\bigcup _{i\in I}X_{i}=X$
and that
$\bigcup _{i\in I}X_{i}=X$
and that
![]() $I$
is equipped with a partial order
$I$
is equipped with a partial order
![]() ${\leqslant}$
so that for each
${\leqslant}$
so that for each
![]() $i\in I$
the union
$i\in I$
the union
 $\bigcup _{j\leqslant i}X_{j}$
is closed in
$\bigcup _{j\leqslant i}X_{j}$
is closed in
![]() $X$
. Then we say
$X$
. Then we say
 $\{X_{i}\}_{i\in I}$
forms an
$\{X_{i}\}_{i\in I}$
forms an
![]() $\unicode[STIX]{x1D6FC}$
-partition of
$\unicode[STIX]{x1D6FC}$
-partition of
![]() $X$
.
$X$
.
Lemma 8.1 [Reference NakajimaNak01, Lemma 7.1.3].
If
![]() $X$
has an
$X$
has an
![]() $\unicode[STIX]{x1D6FC}$
-partition
$\unicode[STIX]{x1D6FC}$
-partition
 $X_{1},\ldots ,X_{k}$
where each
$X_{1},\ldots ,X_{k}$
where each
![]() $X_{i}$
satisfies property
$X_{i}$
satisfies property
![]() $T_{A}$
then
$T_{A}$
then
![]() $X$
satisfies property
$X$
satisfies property
![]() $T_{A}$
.
$T_{A}$
.
Remark 8.2. The actual definition of an
![]() $\unicode[STIX]{x1D6FC}$
-partition from [Reference NakajimaNak01] assumes that
$\unicode[STIX]{x1D6FC}$
-partition from [Reference NakajimaNak01] assumes that
![]() ${\leqslant}$
is a total ordering of
${\leqslant}$
is a total ordering of
![]() $I$
. However, the lemma above holds because we can always refine a partial order to a total ordering. We use the definition above because in our case a particular partial order shows up and it does not seem natural to refine it arbitrarily.
$I$
. However, the lemma above holds because we can always refine a partial order to a total ordering. We use the definition above because in our case a particular partial order shows up and it does not seem natural to refine it arbitrarily.
Lemma 8.3. Suppose that
![]() $V,W$
are two
$V,W$
are two
![]() $A$
-equivariant vector bundles over
$A$
-equivariant vector bundles over
![]() $X$
equipped with an equivariant vector bundle inclusion
$X$
equipped with an equivariant vector bundle inclusion
 $V\rightarrow W$
. If
$V\rightarrow W$
. If
![]() $X$
has property
$X$
has property
![]() $T_{A}$
, then so does
$T_{A}$
, then so does
 $\mathbb{P}(W)\smallsetminus \mathbb{P}(V)$
.
$\mathbb{P}(W)\smallsetminus \mathbb{P}(V)$
.
Remark 8.4. Our stratification of
 $Z(1^{m},1^{m})$
has pieces of the form
$Z(1^{m},1^{m})$
has pieces of the form
 $\mathbb{P}(W)\smallsetminus \mathbb{P}(V)$
which is why we need this lemma. Unfortunately this result does not appear in [Reference NakajimaNak01] so we include a proof based on [Reference Chriss and GinzburgCG97].
$\mathbb{P}(W)\smallsetminus \mathbb{P}(V)$
which is why we need this lemma. Unfortunately this result does not appear in [Reference NakajimaNak01] so we include a proof based on [Reference Chriss and GinzburgCG97].
Proof. Let us denote the inclusion
 $i:\mathbb{P}(V)\rightarrow \mathbb{P}(W)$
and the projections
$i:\mathbb{P}(V)\rightarrow \mathbb{P}(W)$
and the projections
 $\unicode[STIX]{x1D70B}_{1}:\mathbb{P}(V)\rightarrow X$
and
$\unicode[STIX]{x1D70B}_{1}:\mathbb{P}(V)\rightarrow X$
and
 $\unicode[STIX]{x1D70B}_{2}:\mathbb{P}(W)\rightarrow X$
. First we show that the map
$\unicode[STIX]{x1D70B}_{2}:\mathbb{P}(W)\rightarrow X$
. First we show that the map
 $i_{\ast }:K_{0}^{A}(\mathbb{P}(V))\rightarrow K_{0}^{A}(\mathbb{P}(W))$
is injective. By Theorem 8.5 a general element
$i_{\ast }:K_{0}^{A}(\mathbb{P}(V))\rightarrow K_{0}^{A}(\mathbb{P}(W))$
is injective. By Theorem 8.5 a general element
 $b\in K_{0}^{A}(\mathbb{P}(V))$
is of the form
$b\in K_{0}^{A}(\mathbb{P}(V))$
is of the form
 $$\begin{eqnarray}b=\mathop{\sum }_{j=0}^{\operatorname{rk}(V)-1}[\unicode[STIX]{x1D70B}_{1}^{\ast }(a_{j})]\cdot [{\mathcal{O}}_{\mathbb{P}(V)}(-j)]\end{eqnarray}$$
$$\begin{eqnarray}b=\mathop{\sum }_{j=0}^{\operatorname{rk}(V)-1}[\unicode[STIX]{x1D70B}_{1}^{\ast }(a_{j})]\cdot [{\mathcal{O}}_{\mathbb{P}(V)}(-j)]\end{eqnarray}$$
for some
 $a_{j}\in K_{0}^{A}(X)$
. Now suppose
$a_{j}\in K_{0}^{A}(X)$
. Now suppose
 $i_{\ast }(b)=0$
. Then by the projection formula together with the fact that
$i_{\ast }(b)=0$
. Then by the projection formula together with the fact that
 $\unicode[STIX]{x1D70B}_{1}^{\ast }(a_{j})=i^{\ast }\unicode[STIX]{x1D70B}_{2}^{\ast }(a_{j})$
we get
$\unicode[STIX]{x1D70B}_{1}^{\ast }(a_{j})=i^{\ast }\unicode[STIX]{x1D70B}_{2}^{\ast }(a_{j})$
we get
 $$\begin{eqnarray}\mathop{\sum }_{j=0}^{\operatorname{rk}(V)-1}[\unicode[STIX]{x1D70B}_{2}^{\ast }(a_{j})]\cdot [i_{\ast }{\mathcal{O}}_{\mathbb{P}(V)}(-j)]=0.\end{eqnarray}$$
$$\begin{eqnarray}\mathop{\sum }_{j=0}^{\operatorname{rk}(V)-1}[\unicode[STIX]{x1D70B}_{2}^{\ast }(a_{j})]\cdot [i_{\ast }{\mathcal{O}}_{\mathbb{P}(V)}(-j)]=0.\end{eqnarray}$$
On the other hand, we have the Koszul resolution
 $$\begin{eqnarray}\ldots \rightarrow {\mathcal{O}}_{\mathbb{P}(W)}(-2)\otimes \unicode[STIX]{x1D70B}_{2}^{\ast }\wedge ^{2}Q\rightarrow {\mathcal{O}}_{\mathbb{ P}(W)}(-1)\otimes \unicode[STIX]{x1D70B}_{2}^{\ast }Q\rightarrow {\mathcal{O}}_{\mathbb{ P}(W)}\rightarrow {\mathcal{O}}_{\mathbb{P}(V)},\end{eqnarray}$$
$$\begin{eqnarray}\ldots \rightarrow {\mathcal{O}}_{\mathbb{P}(W)}(-2)\otimes \unicode[STIX]{x1D70B}_{2}^{\ast }\wedge ^{2}Q\rightarrow {\mathcal{O}}_{\mathbb{ P}(W)}(-1)\otimes \unicode[STIX]{x1D70B}_{2}^{\ast }Q\rightarrow {\mathcal{O}}_{\mathbb{ P}(W)}\rightarrow {\mathcal{O}}_{\mathbb{P}(V)},\end{eqnarray}$$
where
 $Q=(W/V)^{\vee }$
. Substituting this into the relation above we get
$Q=(W/V)^{\vee }$
. Substituting this into the relation above we get
 $$\begin{eqnarray}\mathop{\sum }_{j=0}^{\operatorname{rk}(V)-1}[\unicode[STIX]{x1D70B}_{2}^{\ast }(a_{j})]\cdot \biggl(\mathop{\sum }_{k=0}^{\operatorname{rk}(W)-\operatorname{rk}(V)}(-1)^{k}[{\mathcal{O}}_{\mathbb{ P}(W)}(-j-k)]\cdot [\unicode[STIX]{x1D70B}_{2}^{\ast }\wedge ^{k}Q]\biggr)=0\end{eqnarray}$$
$$\begin{eqnarray}\mathop{\sum }_{j=0}^{\operatorname{rk}(V)-1}[\unicode[STIX]{x1D70B}_{2}^{\ast }(a_{j})]\cdot \biggl(\mathop{\sum }_{k=0}^{\operatorname{rk}(W)-\operatorname{rk}(V)}(-1)^{k}[{\mathcal{O}}_{\mathbb{ P}(W)}(-j-k)]\cdot [\unicode[STIX]{x1D70B}_{2}^{\ast }\wedge ^{k}Q]\biggr)=0\end{eqnarray}$$
or equivalently
 $$\begin{eqnarray}\mathop{\sum }_{l=0}^{\operatorname{rk}(W)-1}[{\mathcal{O}}_{\mathbb{ P}(W)}(-l)]\cdot \biggl(\mathop{\sum }_{j+k=l}(-1)^{k}[\unicode[STIX]{x1D70B}_{2}^{\ast }(a_{j}\otimes \wedge ^{k}Q)]\biggr)=0.\end{eqnarray}$$
$$\begin{eqnarray}\mathop{\sum }_{l=0}^{\operatorname{rk}(W)-1}[{\mathcal{O}}_{\mathbb{ P}(W)}(-l)]\cdot \biggl(\mathop{\sum }_{j+k=l}(-1)^{k}[\unicode[STIX]{x1D70B}_{2}^{\ast }(a_{j}\otimes \wedge ^{k}Q)]\biggr)=0.\end{eqnarray}$$
Since
 $[{\mathcal{O}}_{\mathbb{P}(W)}(-l)]$
are linearly independent for
$[{\mathcal{O}}_{\mathbb{P}(W)}(-l)]$
are linearly independent for
 $l=0,\ldots ,\operatorname{rk}(W)-1$
, we see that
$l=0,\ldots ,\operatorname{rk}(W)-1$
, we see that
 $\sum _{j+k=l}(-1)^{k}[\unicode[STIX]{x1D70B}_{2}^{\ast }(a_{j}\otimes \wedge ^{k}Q)]=0$
for all
$\sum _{j+k=l}(-1)^{k}[\unicode[STIX]{x1D70B}_{2}^{\ast }(a_{j}\otimes \wedge ^{k}Q)]=0$
for all
![]() $l$
. From this one can show inductively that
$l$
. From this one can show inductively that
 $\unicode[STIX]{x1D70B}_{2}^{\ast }(a_{j})=0$
for all
$\unicode[STIX]{x1D70B}_{2}^{\ast }(a_{j})=0$
for all
![]() $j$
(starting with
$j$
(starting with
![]() $j=0$
). Hence
$j=0$
). Hence
![]() $b=0$
which shows that
$b=0$
which shows that
![]() $i_{\ast }$
is injective.
$i_{\ast }$
is injective.
The same argument shows that
![]() $i_{\ast }$
is also injective on topological K-theory. Now, by Corollary 8.7 we know that
$i_{\ast }$
is also injective on topological K-theory. Now, by Corollary 8.7 we know that
 $K_{1,\text{top}}^{A}(\mathbb{P}(V))=K_{1,\text{top}}^{A}(\mathbb{P}(W))=0$
. It follows from the long exact sequence
$K_{1,\text{top}}^{A}(\mathbb{P}(V))=K_{1,\text{top}}^{A}(\mathbb{P}(W))=0$
. It follows from the long exact sequence
 $$\begin{eqnarray}K_{1,\text{top}}^{A}(\mathbb{P}(W))\rightarrow K_{1,\text{top}}^{A}(\mathbb{P}(W)\smallsetminus \mathbb{P}(V))\rightarrow K_{0,\text{top}}^{A}(\mathbb{P}(V))\xrightarrow[{}]{i_{\ast }}K_{0,\text{top}}^{A}(\mathbb{P}(W))\end{eqnarray}$$
$$\begin{eqnarray}K_{1,\text{top}}^{A}(\mathbb{P}(W))\rightarrow K_{1,\text{top}}^{A}(\mathbb{P}(W)\smallsetminus \mathbb{P}(V))\rightarrow K_{0,\text{top}}^{A}(\mathbb{P}(V))\xrightarrow[{}]{i_{\ast }}K_{0,\text{top}}^{A}(\mathbb{P}(W))\end{eqnarray}$$
that
 $K_{1,\text{top}}^{A}(\mathbb{P}(W)\smallsetminus \mathbb{P}(V))=0$
.
$K_{1,\text{top}}^{A}(\mathbb{P}(W)\smallsetminus \mathbb{P}(V))=0$
.
Next, consider the following commutative diagram.

The first two vertical maps are isomorphisms by Corollary 8.7. It follows that the rightmost vertical map is also an isomorphism.
Finally, it remains to show that
 $K_{0,\text{top}}^{A}(\mathbb{P}(W)\smallsetminus \mathbb{P}(V))$
is a free
$K_{0,\text{top}}^{A}(\mathbb{P}(W)\smallsetminus \mathbb{P}(V))$
is a free
![]() $R_{A}$
-module. Consider the short exact sequence
$R_{A}$
-module. Consider the short exact sequence
 $$\begin{eqnarray}0\rightarrow K_{0,\text{top}}^{A}(\mathbb{P}(V))\xrightarrow[{}]{i_{\ast }}K_{0,\text{top}}^{A}(\mathbb{P}(W))\rightarrow K_{0,\text{top}}^{A}(\mathbb{P}(W)\smallsetminus \mathbb{P}(V))\rightarrow 0.\end{eqnarray}$$
$$\begin{eqnarray}0\rightarrow K_{0,\text{top}}^{A}(\mathbb{P}(V))\xrightarrow[{}]{i_{\ast }}K_{0,\text{top}}^{A}(\mathbb{P}(W))\rightarrow K_{0,\text{top}}^{A}(\mathbb{P}(W)\smallsetminus \mathbb{P}(V))\rightarrow 0.\end{eqnarray}$$
The image of
![]() $i_{\ast }$
are elements of the form
$i_{\ast }$
are elements of the form
 $b\cdot [i_{\ast }{\mathcal{O}}_{\mathbb{P}(V)}]$
for
$b\cdot [i_{\ast }{\mathcal{O}}_{\mathbb{P}(V)}]$
for
 $b\in K_{0,\text{top}}^{A}(\mathbb{P}(W))$
. Using the Koszul resolution (29) for
$b\in K_{0,\text{top}}^{A}(\mathbb{P}(W))$
. Using the Koszul resolution (29) for
![]() ${\mathcal{O}}_{\mathbb{P}(V)}$
it is not hard to see that this means
${\mathcal{O}}_{\mathbb{P}(V)}$
it is not hard to see that this means
 $K_{0,\text{top}}^{A}(\mathbb{P}(W))$
is generated, as a
$K_{0,\text{top}}^{A}(\mathbb{P}(W))$
is generated, as a
 $K_{0,\text{top}}^{A}(X)$
-module, by the image of
$K_{0,\text{top}}^{A}(X)$
-module, by the image of
![]() $i_{\ast }$
and by
$i_{\ast }$
and by
 ${\mathcal{O}}_{\mathbb{P}(W)}(-k)$
for
${\mathcal{O}}_{\mathbb{P}(W)}(-k)$
for
 $k=\operatorname{rk}(V),\ldots ,\operatorname{rk}(W)-1$
. Since
$k=\operatorname{rk}(V),\ldots ,\operatorname{rk}(W)-1$
. Since
 $K_{0,\text{top}}^{A}(\mathbb{P}(V))$
and
$K_{0,\text{top}}^{A}(\mathbb{P}(V))$
and
 $K_{0,\text{top}}^{A}(\mathbb{P}(W))$
are free
$K_{0,\text{top}}^{A}(\mathbb{P}(W))$
are free
 $K_{0,\text{top}}^{A}(X)$
-modules of rank
$K_{0,\text{top}}^{A}(X)$
-modules of rank
![]() $\operatorname{rk}(V)$
and
$\operatorname{rk}(V)$
and
![]() $\operatorname{rk}(W)$
respectively, this means that
$\operatorname{rk}(W)$
respectively, this means that
 $K_{0,\text{top}}^{A}(\mathbb{P}(W)\smallsetminus \mathbb{P}(V))$
is freely generated over
$K_{0,\text{top}}^{A}(\mathbb{P}(W)\smallsetminus \mathbb{P}(V))$
is freely generated over
 $K_{0,\text{top}}^{A}(X)$
by
$K_{0,\text{top}}^{A}(X)$
by
 ${\mathcal{O}}_{\mathbb{P}(W)}(-k)$
for
${\mathcal{O}}_{\mathbb{P}(W)}(-k)$
for
 $k=\operatorname{rk}(V),\ldots ,\operatorname{rk}(W)-1$
. This completes the proof.◻
$k=\operatorname{rk}(V),\ldots ,\operatorname{rk}(W)-1$
. This completes the proof.◻
Theorem 8.5 [Reference Chriss and GinzburgCG97, Theorem 5.2.31].
Consider an
![]() $A$
-equivariant vector bundle
$A$
-equivariant vector bundle
 $E\rightarrow X$
and let
$E\rightarrow X$
and let
 $\unicode[STIX]{x1D70B}:\mathbb{P}(E)\rightarrow X$
be the associated vector bundle. Then for
$\unicode[STIX]{x1D70B}:\mathbb{P}(E)\rightarrow X$
be the associated vector bundle. Then for
![]() $j\geqslant 0$
the groups
$j\geqslant 0$
the groups
 $K_{j}^{A}(\mathbb{P}(E))$
are freely generated over
$K_{j}^{A}(\mathbb{P}(E))$
are freely generated over
![]() $K_{j}^{A}(X)$
by the classes
$K_{j}^{A}(X)$
by the classes
 $[{\mathcal{O}}_{\mathbb{P}(E)}(-k)]$
,
$[{\mathcal{O}}_{\mathbb{P}(E)}(-k)]$
,
 $k=0,1,\ldots ,\operatorname{rk}(E)-1$
.
$k=0,1,\ldots ,\operatorname{rk}(E)-1$
.
Remark 8.6. The actual statement in [Reference Chriss and GinzburgCG97] uses
 $[{\mathcal{O}}_{\mathbb{P}(E)}(k)]$
but one could equally well use
$[{\mathcal{O}}_{\mathbb{P}(E)}(k)]$
but one could equally well use
 $[{\mathcal{O}}_{\mathbb{P}(E)}(-k)]$
.
$[{\mathcal{O}}_{\mathbb{P}(E)}(-k)]$
.
The argument in [Reference Chriss and GinzburgCG97] can also be used to prove the same result for topological K-theory. The following is then immediate.
Corollary 8.7. Suppose
 $E\rightarrow X$
is an
$E\rightarrow X$
is an
![]() $A$
-equivariant vector bundle on
$A$
-equivariant vector bundle on
![]() $X$
. If
$X$
. If
![]() $X$
satisfies property
$X$
satisfies property
![]() $T_{A}$
then
$T_{A}$
then
![]() $\mathbb{P}(E)$
satisfies property
$\mathbb{P}(E)$
satisfies property
![]() $T_{A}$
.
$T_{A}$
.
8.2 Property
 $T_{A}$
for
$T_{A}$
for
 $Z(1^{m},1^{m})$
$Z(1^{m},1^{m})$
Our current goal is to establish the following result.
Theorem 8.8. The varieties
![]() $Y(1^{m})$
and
$Y(1^{m})$
and
 $Z(1^{m},1^{m})$
satisfy property
$Z(1^{m},1^{m})$
satisfy property
 $T_{\operatorname{SL}_{n}\times \mathbb{C}^{\times }}$
.
$T_{\operatorname{SL}_{n}\times \mathbb{C}^{\times }}$
.
For
![]() $Y(1^{m})$
this is immediate from Lemma 8.3, since it is an iterated bundle of projective spaces. For
$Y(1^{m})$
this is immediate from Lemma 8.3, since it is an iterated bundle of projective spaces. For
 $Z(1^{m},1^{m})$
the proof is more involved and will occupy the rest of this section.
$Z(1^{m},1^{m})$
the proof is more involved and will occupy the rest of this section.
The main idea is to partition the variety
 $Z=Z(1^{m},1^{m})$
into pieces and then apply Lemma 8.3. This partition is a special case of the one considered in [Reference Fontaine, Kamnitzer and KuperbergFKK13, § 4.1] which in turn was inspired by the proof of Theorem 3.1 from [Reference HainesHai06].
$Z=Z(1^{m},1^{m})$
into pieces and then apply Lemma 8.3. This partition is a special case of the one considered in [Reference Fontaine, Kamnitzer and KuperbergFKK13, § 4.1] which in turn was inspired by the proof of Theorem 3.1 from [Reference HainesHai06].
Let
![]() $T$
be a standard Young tableau with
$T$
be a standard Young tableau with
![]() $m$
boxes and at most
$m$
boxes and at most
![]() $n$
rows. Then we write
$n$
rows. Then we write
 $\unicode[STIX]{x1D706}^{(i)}(T)=T|_{1,\ldots ,i}$
for the shape made by using only the boxes filled with
$\unicode[STIX]{x1D706}^{(i)}(T)=T|_{1,\ldots ,i}$
for the shape made by using only the boxes filled with
![]() $1,\ldots ,i$
. We regard
$1,\ldots ,i$
. We regard
![]() $\unicode[STIX]{x1D706}^{(i)}(T)$
as an element of
$\unicode[STIX]{x1D706}^{(i)}(T)$
as an element of
![]() $\unicode[STIX]{x1D6EC}_{+}$
.
$\unicode[STIX]{x1D6EC}_{+}$
.
Let
![]() ${\mathcal{P}}$
be the set of pairs
${\mathcal{P}}$
be the set of pairs
![]() $(T,T^{\prime })$
of standard Young tableaux (SYT) of the same shape, each with
$(T,T^{\prime })$
of standard Young tableaux (SYT) of the same shape, each with
![]() $m$
boxes and at most
$m$
boxes and at most
![]() $n$
rows. We define a partial order on
$n$
rows. We define a partial order on
![]() ${\mathcal{P}}$
by
${\mathcal{P}}$
by
 $$\begin{eqnarray}(U,U^{\prime })\leqslant (T,T^{\prime })\text{ if, for all }i,\unicode[STIX]{x1D706}^{(i)}(U)\leqslant \unicode[STIX]{x1D706}^{(i)}(T)\text{ and }\unicode[STIX]{x1D706}^{(i)}(U^{\prime })\leqslant \unicode[STIX]{x1D706}^{(i)}(T^{\prime }).\end{eqnarray}$$
$$\begin{eqnarray}(U,U^{\prime })\leqslant (T,T^{\prime })\text{ if, for all }i,\unicode[STIX]{x1D706}^{(i)}(U)\leqslant \unicode[STIX]{x1D706}^{(i)}(T)\text{ and }\unicode[STIX]{x1D706}^{(i)}(U^{\prime })\leqslant \unicode[STIX]{x1D706}^{(i)}(T^{\prime }).\end{eqnarray}$$
With this partial order, the pair
![]() $(T_{0},T_{0})$
where
$(T_{0},T_{0})$
where
![]() $T_{0}$
is the unique SYT with one row and
$T_{0}$
is the unique SYT with one row and
![]() $m$
boxes is the maximal element. We define
$m$
boxes is the maximal element. We define
 $$\begin{eqnarray}Z(T,T^{\prime })=\{(L_{\bullet },L_{\bullet }^{\prime })\in Z:L_{i}\in Gr^{\unicode[STIX]{x1D706}^{(i)}(T)},L_{i}^{\prime }\in Gr^{\unicode[STIX]{x1D706}^{(i)}(T^{\prime })},\text{ for }i=1,\ldots ,m\},\end{eqnarray}$$
$$\begin{eqnarray}Z(T,T^{\prime })=\{(L_{\bullet },L_{\bullet }^{\prime })\in Z:L_{i}\in Gr^{\unicode[STIX]{x1D706}^{(i)}(T)},L_{i}^{\prime }\in Gr^{\unicode[STIX]{x1D706}^{(i)}(T^{\prime })},\text{ for }i=1,\ldots ,m\},\end{eqnarray}$$
where we recall (from § 6.1) that for
 $\unicode[STIX]{x1D706}=(\unicode[STIX]{x1D706}_{1},\ldots ,\unicode[STIX]{x1D706}_{n})\in \unicode[STIX]{x1D6EC}_{+}$
,
$\unicode[STIX]{x1D706}=(\unicode[STIX]{x1D706}_{1},\ldots ,\unicode[STIX]{x1D706}_{n})\in \unicode[STIX]{x1D6EC}_{+}$
,
![]() $Gr^{\unicode[STIX]{x1D706}}$
consists of those lattices such that
$Gr^{\unicode[STIX]{x1D706}}$
consists of those lattices such that
![]() $z|_{L/L_{0}}$
has Jordan type
$z|_{L/L_{0}}$
has Jordan type
![]() $\unicode[STIX]{x1D706}$
.
$\unicode[STIX]{x1D706}$
.
Proposition 8.9. The closures
 $\{\overline{Z(T,T^{\prime })}\}_{(T,T^{\prime })\in {\mathcal{P}}}$
are the irreducible components of
$\{\overline{Z(T,T^{\prime })}\}_{(T,T^{\prime })\in {\mathcal{P}}}$
are the irreducible components of
![]() $Z$
. Moreover, the collection
$Z$
. Moreover, the collection
 $\{Z(T,T^{\prime })\}_{(T,T^{\prime })\in {\mathcal{P}}}$
forms an
$\{Z(T,T^{\prime })\}_{(T,T^{\prime })\in {\mathcal{P}}}$
forms an
![]() $\unicode[STIX]{x1D6FC}$
-partition of
$\unicode[STIX]{x1D6FC}$
-partition of
![]() $Z$
.
$Z$
.
Proof. The first claim is a special case of [Reference Fontaine, Kamnitzer and KuperbergFKK13, Theorem 4.1]. To see the second claim it is clear that each
 $Z(T,T^{\prime })$
is
$Z(T,T^{\prime })$
is
 $\operatorname{SL}_{n}\times \mathbb{C}^{\times }$
-invariant and that they give a partition of
$\operatorname{SL}_{n}\times \mathbb{C}^{\times }$
-invariant and that they give a partition of
![]() $Z$
. From the closure relation among the strata of the affine Grassmannian, we see that, for each
$Z$
. From the closure relation among the strata of the affine Grassmannian, we see that, for each
![]() $(T,T^{\prime })$
, we have
$(T,T^{\prime })$
, we have
 $$\begin{eqnarray}\overline{Z(T,T^{\prime })}\subset \mathop{\bigcup }_{(U,U^{\prime })\leqslant (T,T^{\prime })}Z(U,U^{\prime }).\end{eqnarray}$$
$$\begin{eqnarray}\overline{Z(T,T^{\prime })}\subset \mathop{\bigcup }_{(U,U^{\prime })\leqslant (T,T^{\prime })}Z(U,U^{\prime }).\end{eqnarray}$$
This implies the necessary closedness property for having an
![]() $\unicode[STIX]{x1D6FC}$
-partition.◻
$\unicode[STIX]{x1D6FC}$
-partition.◻
Theorem 8.8 now follows from the Proposition above and the following result.
Lemma 8.10. For each
 $(T,T^{\prime })\in {\mathcal{P}}$
,
$(T,T^{\prime })\in {\mathcal{P}}$
,
 $Z(T,T^{\prime })$
satisfies property
$Z(T,T^{\prime })$
satisfies property
 $T_{\operatorname{SL}_{n}\times \mathbb{C}^{\times }}$
.
$T_{\operatorname{SL}_{n}\times \mathbb{C}^{\times }}$
.
Proof. For each
 $k=1,\ldots ,2m-1$
, we define varieties
$k=1,\ldots ,2m-1$
, we define varieties
 $Z(T,T^{\prime })_{k}$
which contain only part of the data of
$Z(T,T^{\prime })_{k}$
which contain only part of the data of
 $Z(T,T^{\prime })$
. Increasing
$Z(T,T^{\prime })$
. Increasing
![]() $k$
remembers more data about the flags
$k$
remembers more data about the flags
 $(L_{\bullet },L_{\bullet }^{\prime })$
. Roughly speaking, we remember the lattices
$(L_{\bullet },L_{\bullet }^{\prime })$
. Roughly speaking, we remember the lattices
![]() $L_{i}$
one by one starting with
$L_{i}$
one by one starting with
![]() $L_{1}$
and working up until
$L_{1}$
and working up until
![]() $L_{m}$
(
$L_{m}$
(
![]() $k=m$
). We then remember the
$k=m$
). We then remember the
![]() $L_{i}^{\prime }$
starting with
$L_{i}^{\prime }$
starting with
![]() $L_{m-1}^{\prime }$
and working back down to
$L_{m-1}^{\prime }$
and working back down to
![]() $L_{1}^{\prime }$
.
$L_{1}^{\prime }$
.
More precisely, for
 $k=1,\ldots ,m$
we define
$k=1,\ldots ,m$
we define
 $$\begin{eqnarray}Z(T,T^{\prime })_{k}=\{(L_{1},\ldots ,L_{k}):L_{0}\subset L_{1}\subset \cdots \subset L_{k},zL_{i}\subset L_{i-1},L_{i}\in Gr^{\unicode[STIX]{x1D706}^{(i)}(T)}\text{ for }i\}.\end{eqnarray}$$
$$\begin{eqnarray}Z(T,T^{\prime })_{k}=\{(L_{1},\ldots ,L_{k}):L_{0}\subset L_{1}\subset \cdots \subset L_{k},zL_{i}\subset L_{i-1},L_{i}\in Gr^{\unicode[STIX]{x1D706}^{(i)}(T)}\text{ for }i\}.\end{eqnarray}$$
On the other hand, for
 $k=m,\ldots ,2m-1$
, we define
$k=m,\ldots ,2m-1$
, we define
 $Z(T,T^{\prime })_{k}$
as
$Z(T,T^{\prime })_{k}$
as
 $$\begin{eqnarray}\displaystyle & & \displaystyle \{(L_{1},\ldots ,L_{m}),(L_{2m-k}^{\prime },\ldots ,L_{m}^{\prime }):L_{m}=L_{m}^{\prime }\text{and }\nonumber\\ \displaystyle & & \displaystyle \quad L_{i-1}\subset L_{i},\dim L_{i}/L_{i-1}=1,zL_{i}\subset L_{i-1},L_{i}\in Gr^{\unicode[STIX]{x1D706}^{(i)}(T)}\text{ for }i=1,\ldots ,m,\nonumber\\ \displaystyle & & \displaystyle \quad L_{i-1}^{\prime }\subset L_{i}^{\prime },\dim L_{i}^{\prime }/L_{i-1}^{\prime }=1,zL_{i}^{\prime }\subset L_{i-1}^{\prime },L_{i}^{\prime }\in Gr^{\unicode[STIX]{x1D706}^{(i)}(T^{\prime })}\text{ for }i=2m-k+1,\ldots ,m\!\}\!.\nonumber\end{eqnarray}$$
$$\begin{eqnarray}\displaystyle & & \displaystyle \{(L_{1},\ldots ,L_{m}),(L_{2m-k}^{\prime },\ldots ,L_{m}^{\prime }):L_{m}=L_{m}^{\prime }\text{and }\nonumber\\ \displaystyle & & \displaystyle \quad L_{i-1}\subset L_{i},\dim L_{i}/L_{i-1}=1,zL_{i}\subset L_{i-1},L_{i}\in Gr^{\unicode[STIX]{x1D706}^{(i)}(T)}\text{ for }i=1,\ldots ,m,\nonumber\\ \displaystyle & & \displaystyle \quad L_{i-1}^{\prime }\subset L_{i}^{\prime },\dim L_{i}^{\prime }/L_{i-1}^{\prime }=1,zL_{i}^{\prime }\subset L_{i-1}^{\prime },L_{i}^{\prime }\in Gr^{\unicode[STIX]{x1D706}^{(i)}(T^{\prime })}\text{ for }i=2m-k+1,\ldots ,m\!\}\!.\nonumber\end{eqnarray}$$
Notice that
 $Z(T,T^{\prime })=Z(T,T^{\prime })_{2m-1}$
.
$Z(T,T^{\prime })=Z(T,T^{\prime })_{2m-1}$
.
We will now prove the lemma by induction on
![]() $k$
. Let us suppose the conclusions of the lemma are true for
$k$
. Let us suppose the conclusions of the lemma are true for
 $Z(T,T^{\prime })_{k-1}$
. We have a map
$Z(T,T^{\prime })_{k-1}$
. We have a map
 $\unicode[STIX]{x1D70B}_{k}:Z(T,T^{\prime })_{k}\rightarrow Z(T,T^{\prime })_{k-1}$
given by forgetting the last piece of data. We claim that this map satisfies the hypotheses of Lemma 8.3.
$\unicode[STIX]{x1D70B}_{k}:Z(T,T^{\prime })_{k}\rightarrow Z(T,T^{\prime })_{k-1}$
given by forgetting the last piece of data. We claim that this map satisfies the hypotheses of Lemma 8.3.
To see this, we examine the fibres of
![]() $\unicode[STIX]{x1D70B}_{k}$
. If
$\unicode[STIX]{x1D70B}_{k}$
. If
![]() $k\leqslant m$
the fibre over of point
$k\leqslant m$
the fibre over of point
 $L_{\bullet }\in Z(T,T^{\prime })_{k-1}$
is
$L_{\bullet }\in Z(T,T^{\prime })_{k-1}$
is
 $$\begin{eqnarray}\unicode[STIX]{x1D70B}_{k}^{-1}(L_{\bullet })=\{L_{k-1}\subset L_{k}\subset z^{-1}L_{k-1},z|_{L_{i}/L_{0}}\text{ has Jordan type }\unicode[STIX]{x1D706}^{(k)}(T)\}.\end{eqnarray}$$
$$\begin{eqnarray}\unicode[STIX]{x1D70B}_{k}^{-1}(L_{\bullet })=\{L_{k-1}\subset L_{k}\subset z^{-1}L_{k-1},z|_{L_{i}/L_{0}}\text{ has Jordan type }\unicode[STIX]{x1D706}^{(k)}(T)\}.\end{eqnarray}$$
Now the condition on the Jordan type of
![]() $z|_{L_{i}/L_{0}}$
is equivalent to a condition on the intersections of
$z|_{L_{i}/L_{0}}$
is equivalent to a condition on the intersections of
![]() $L_{k}$
with the subspaces
$L_{k}$
with the subspaces
![]() $z^{-j}L_{0}$
for various
$z^{-j}L_{0}$
for various
![]() $j$
. More precisely, if the box labelled
$j$
. More precisely, if the box labelled
![]() $k$
is on the
$k$
is on the
![]() $j$
th column of
$j$
th column of
![]() $T$
, then the condition on the Jordan type is equivalent to the condition that
$T$
, then the condition on the Jordan type is equivalent to the condition that
 $$\begin{eqnarray}\dim (L_{k}\cap z^{-j}L_{0})=\dim (L_{k-1}\cap z^{-j}L_{0})+1\quad \text{and}\quad L_{k}\cap z^{-(j-1)}L_{0}=L_{k-1}\cap z^{-(j-1)}L_{0}.\end{eqnarray}$$
$$\begin{eqnarray}\dim (L_{k}\cap z^{-j}L_{0})=\dim (L_{k-1}\cap z^{-j}L_{0})+1\quad \text{and}\quad L_{k}\cap z^{-(j-1)}L_{0}=L_{k-1}\cap z^{-(j-1)}L_{0}.\end{eqnarray}$$
Thus we can identify the fibre with the space
 $$\begin{eqnarray}\mathbb{P}((z^{-1}L_{k-1}\cap z^{-j}L_{0})/(L_{k-1}\cap z^{-j}L_{0}))\smallsetminus \mathbb{P}((z^{-1}L_{k-1}\cap z^{-(j-1)}L_{0})/(L_{k-1}\cap z^{-(j-1)}L_{0}))\end{eqnarray}$$
$$\begin{eqnarray}\mathbb{P}((z^{-1}L_{k-1}\cap z^{-j}L_{0})/(L_{k-1}\cap z^{-j}L_{0}))\smallsetminus \mathbb{P}((z^{-1}L_{k-1}\cap z^{-(j-1)}L_{0})/(L_{k-1}\cap z^{-(j-1)}L_{0}))\end{eqnarray}$$
and thus the hypotheses of Lemma 8.3 are satisfied. The case
![]() $k>m$
is similar. This proves that
$k>m$
is similar. This proves that
 $Z(T,T^{\prime })_{k}$
satisfies property
$Z(T,T^{\prime })_{k}$
satisfies property
 $T_{\operatorname{SL}_{n}\times \mathbb{C}^{\times }}$
.◻
$T_{\operatorname{SL}_{n}\times \mathbb{C}^{\times }}$
.◻
Corollary 8.11.
 $K^{\operatorname{SL}_{n}\times \mathbb{C}^{\times }}(Z(1^{m},1^{m}))$
is a free
$K^{\operatorname{SL}_{n}\times \mathbb{C}^{\times }}(Z(1^{m},1^{m}))$
is a free
![]() $E[q^{\pm }]$
-module.
$E[q^{\pm }]$
-module.
8.3 Localization
Suppose
![]() $T$
is an abelian reductive group and
$T$
is an abelian reductive group and
![]() $Y$
an algebraic variety equipped with an action of
$Y$
an algebraic variety equipped with an action of
![]() $T$
. As before, we write
$T$
. As before, we write
 $R_{T}=K^{T}(\operatorname{pt})$
and denote by
$R_{T}=K^{T}(\operatorname{pt})$
and denote by
![]() $F_{T}$
the fraction field of
$F_{T}$
the fraction field of
![]() $R_{T}$
. For
$R_{T}$
. For
![]() $t\in T$
we denote by
$t\in T$
we denote by
![]() $Y^{t}$
the fixed point locus of
$Y^{t}$
the fixed point locus of
![]() $t$
.
$t$
.
It was proved by Thomason [Reference ThomasonTho83, Reference ThomasonTho86] that the inclusion
 $i^{t}:Y^{t}\rightarrow Y$
induces an isomorphism
$i^{t}:Y^{t}\rightarrow Y$
induces an isomorphism
 $$\begin{eqnarray}i_{\ast }^{t}:K^{T}(Y^{t})\otimes _{R_{T}}F_{T}\xrightarrow[{}]{{\sim}}K^{T}(Y)\otimes _{R_{T}}F_{T}.\end{eqnarray}$$
$$\begin{eqnarray}i_{\ast }^{t}:K^{T}(Y^{t})\otimes _{R_{T}}F_{T}\xrightarrow[{}]{{\sim}}K^{T}(Y)\otimes _{R_{T}}F_{T}.\end{eqnarray}$$
Lemma 8.12. If
 $i:Z(1^{m},1^{m})\rightarrow Y(1^{m})\times Y(1^{m})$
is the natural inclusion, then
$i:Z(1^{m},1^{m})\rightarrow Y(1^{m})\times Y(1^{m})$
is the natural inclusion, then
 $$\begin{eqnarray}i_{\ast }:K^{\operatorname{SL}_{n}\times \mathbb{C}^{\times }}(Z(1^{m},1^{m}))\rightarrow K^{\operatorname{SL}_{n}\times \mathbb{C}^{\times }}(Y(1^{m})\times Y(1^{m}))\end{eqnarray}$$
$$\begin{eqnarray}i_{\ast }:K^{\operatorname{SL}_{n}\times \mathbb{C}^{\times }}(Z(1^{m},1^{m}))\rightarrow K^{\operatorname{SL}_{n}\times \mathbb{C}^{\times }}(Y(1^{m})\times Y(1^{m}))\end{eqnarray}$$
is injective.
Proof. We write
![]() $Y\times Y$
for
$Y\times Y$
for
 $Y(1^{m})\times Y(1^{m})$
and
$Y(1^{m})\times Y(1^{m})$
and
![]() $Z$
for
$Z$
for
 $Z(1^{m},1^{m})$
. Choose
$Z(1^{m},1^{m})$
. Choose
 $T\subset A:=\operatorname{SL}_{n}\times \mathbb{C}^{\times }$
to be the maximal torus in
$T\subset A:=\operatorname{SL}_{n}\times \mathbb{C}^{\times }$
to be the maximal torus in
![]() $\operatorname{SL}_{n}$
cross
$\operatorname{SL}_{n}$
cross
![]() $\mathbb{C}^{\times }$
and
$\mathbb{C}^{\times }$
and
![]() $t$
a generic element in
$t$
a generic element in
![]() $T$
. This means that
$T$
. This means that
 $(Y\times Y)^{t}$
consists of a finite number of isolated points.
$(Y\times Y)^{t}$
consists of a finite number of isolated points.
Next, consider the commutative diagram

where the vertical maps are the natural inclusions. The vertical maps are isomorphisms by Thomason’s result while
![]() $i_{\ast }^{t}$
is induced by an inclusion of isolated fixed points and thus injective. This means that the map
$i_{\ast }^{t}$
is induced by an inclusion of isolated fixed points and thus injective. This means that the map
 $$\begin{eqnarray}i_{\ast }:K^{T}(Z)\otimes _{R_{T}}F_{T}\rightarrow K^{T}(Y\times Y)\otimes _{R_{T}}F_{T}\end{eqnarray}$$
$$\begin{eqnarray}i_{\ast }:K^{T}(Z)\otimes _{R_{T}}F_{T}\rightarrow K^{T}(Y\times Y)\otimes _{R_{T}}F_{T}\end{eqnarray}$$
is injective.
On the other hand, since
![]() $Z$
and
$Z$
and
![]() $Y\times Y$
have property
$Y\times Y$
have property
![]() $T_{A}$
both
$T_{A}$
both
![]() $K^{T}(Z)$
and
$K^{T}(Z)$
and
 $K^{T}(Y\times Y)$
are free
$K^{T}(Y\times Y)$
are free
![]() $R_{T}$
-modules. Thus we have the commutative diagram
$R_{T}$
-modules. Thus we have the commutative diagram

where the vertical maps are injective since
![]() $R_{T}$
embeds into
$R_{T}$
embeds into
![]() $F_{T}$
and the bottom horizontal map is injective by (30). This means that the map
$F_{T}$
and the bottom horizontal map is injective by (30). This means that the map
 $$\begin{eqnarray}i_{\ast }:K^{T}(Z)\rightarrow K^{T}(Y\times Y)\end{eqnarray}$$
$$\begin{eqnarray}i_{\ast }:K^{T}(Z)\rightarrow K^{T}(Y\times Y)\end{eqnarray}$$
is injective. But
 $K^{T}(Z)\cong K^{A}(Z)\otimes _{R_{A}}R_{T}$
and likewise for
$K^{T}(Z)\cong K^{A}(Z)\otimes _{R_{A}}R_{T}$
and likewise for
 $K^{T}(Y\times Y)$
. Since
$K^{T}(Y\times Y)$
. Since
![]() $R_{T}$
is a free
$R_{T}$
is a free
![]() $R_{A}$
module, this implies that
$R_{A}$
module, this implies that
 $i_{\ast }:K^{A}(Z)\rightarrow K^{A}(Y\times Y)$
is injective as a consequence of the injectivity of (31).◻
$i_{\ast }:K^{A}(Z)\rightarrow K^{A}(Y\times Y)$
is injective as a consequence of the injectivity of (31).◻
8.4 K-theory of
 $Y(1^{m})$
$Y(1^{m})$
Recall that
 $K^{\operatorname{SL}_{n}\times \mathbb{C}^{\times }}(\operatorname{pt})\cong E[q^{\pm }]$
where
$K^{\operatorname{SL}_{n}\times \mathbb{C}^{\times }}(\operatorname{pt})\cong E[q^{\pm }]$
where
![]() $e_{j}\in E$
denotes
$e_{j}\in E$
denotes
 $\wedge ^{n-j}(\mathbb{C}^{n})$
and
$\wedge ^{n-j}(\mathbb{C}^{n})$
and
![]() $-q^{-1}$
keeps track of the shift
$-q^{-1}$
keeps track of the shift
![]() $\{1\}$
(cf. Remark 6.2). Note that
$\{1\}$
(cf. Remark 6.2). Note that
![]() $e_{n}=1$
. Since
$e_{n}=1$
. Since
![]() $Y(1^{m})$
is an iterated
$Y(1^{m})$
is an iterated
![]() $\mathbb{P}^{n-1}$
-bundle,
$\mathbb{P}^{n-1}$
-bundle,
 $K^{\operatorname{SL}_{n}\times \mathbb{C}^{\times }}(Y(1^{m}))$
is generated, over
$K^{\operatorname{SL}_{n}\times \mathbb{C}^{\times }}(Y(1^{m}))$
is generated, over
![]() $E[q^{\pm }]$
, by
$E[q^{\pm }]$
, by
 $x_{1},\ldots ,x_{m}$
where
$x_{1},\ldots ,x_{m}$
where
![]() $x_{i}$
is the line bundle
$x_{i}$
is the line bundle
 $[(L_{i}/L_{i-1})^{\vee }]$
. We will also write
$[(L_{i}/L_{i-1})^{\vee }]$
. We will also write
 $e_{j}^{(i)}:=[\bigwedge ^{j}(z^{-1}L_{i-1}/L_{i-1})^{\vee }]$
. Note that
$e_{j}^{(i)}:=[\bigwedge ^{j}(z^{-1}L_{i-1}/L_{i-1})^{\vee }]$
. Note that
 $e_{j}^{(1)}=e_{j}$
and, by convention,
$e_{j}^{(1)}=e_{j}$
and, by convention,
![]() $e_{0}^{(i)}=1$
and
$e_{0}^{(i)}=1$
and
![]() $e_{j}^{(i)}=0$
if
$e_{j}^{(i)}=0$
if
![]() $j<0$
.
$j<0$
.
Lemma 8.13. The
![]() $e_{j}^{(i)}$
are related to each other via the relations
$e_{j}^{(i)}$
are related to each other via the relations
 $$\begin{eqnarray}\displaystyle & e_{j}^{(i+1)}=e_{j}^{(i)}+(q^{2}-1)[x_{i}e_{j-1}^{(i)}-x_{i}^{2}e_{j-2}^{(i)}+x_{i}^{3}e_{j-3}^{(i)}-\cdots \,], & \displaystyle\end{eqnarray}$$
$$\begin{eqnarray}\displaystyle & e_{j}^{(i+1)}=e_{j}^{(i)}+(q^{2}-1)[x_{i}e_{j-1}^{(i)}-x_{i}^{2}e_{j-2}^{(i)}+x_{i}^{3}e_{j-3}^{(i)}-\cdots \,], & \displaystyle\end{eqnarray}$$
 $$\begin{eqnarray}\displaystyle & e_{j}^{(i+1)}+x_{i}e_{j-1}^{(i+1)}=e_{j}^{(i)}+q^{2}x_{i}e_{j-1}^{(i)}. & \displaystyle\end{eqnarray}$$
$$\begin{eqnarray}\displaystyle & e_{j}^{(i+1)}+x_{i}e_{j-1}^{(i+1)}=e_{j}^{(i)}+q^{2}x_{i}e_{j-1}^{(i)}. & \displaystyle\end{eqnarray}$$
Proof. We will prove this by induction on
![]() $j$
. The base case
$j$
. The base case
![]() $j=0$
is obvious.
$j=0$
is obvious.
Now, let us write
 $V_{i}=(z^{-1}L_{i-1}/L_{i-1})^{\vee }$
. From the following two standard exact sequences
$V_{i}=(z^{-1}L_{i-1}/L_{i-1})^{\vee }$
. From the following two standard exact sequences
 $$\begin{eqnarray}\displaystyle & 0\rightarrow L_{i}/L_{i-1}\rightarrow z^{-1}L_{i-1}/L_{i-1}\rightarrow z^{-1}L_{i-1}/L_{i}\rightarrow 0, & \displaystyle \nonumber\\ \displaystyle & 0\rightarrow z^{-1}L_{i-1}/L_{i}\rightarrow z^{-1}L_{i}/L_{i}\rightarrow z^{-1}L_{i}/z^{-1}L_{i-1}\rightarrow 0 & \displaystyle \nonumber\end{eqnarray}$$
$$\begin{eqnarray}\displaystyle & 0\rightarrow L_{i}/L_{i-1}\rightarrow z^{-1}L_{i-1}/L_{i-1}\rightarrow z^{-1}L_{i-1}/L_{i}\rightarrow 0, & \displaystyle \nonumber\\ \displaystyle & 0\rightarrow z^{-1}L_{i-1}/L_{i}\rightarrow z^{-1}L_{i}/L_{i}\rightarrow z^{-1}L_{i}/z^{-1}L_{i-1}\rightarrow 0 & \displaystyle \nonumber\end{eqnarray}$$
we get that
 $$\begin{eqnarray}[V_{i}]=x_{i}+[V_{i+1}]-[(z^{-1}L_{i}/z^{-1}L_{i-1})^{\vee }].\end{eqnarray}$$
$$\begin{eqnarray}[V_{i}]=x_{i}+[V_{i+1}]-[(z^{-1}L_{i}/z^{-1}L_{i-1})^{\vee }].\end{eqnarray}$$
On the other hand, we have the isomorphism
 $$\begin{eqnarray}z^{-1}L_{i}/z^{-1}L_{i-1}\xrightarrow[{}]{{\sim}}L_{i}/L_{i-1}\{2\}\end{eqnarray}$$
$$\begin{eqnarray}z^{-1}L_{i}/z^{-1}L_{i-1}\xrightarrow[{}]{{\sim}}L_{i}/L_{i-1}\{2\}\end{eqnarray}$$
induced by multiplication by
![]() $z$
(the
$z$
(the
![]() $\{2\}$
shift is for the same reason as in (24)). This implies that
$\{2\}$
shift is for the same reason as in (24)). This implies that
 $[(z^{-1}L_{i}/z^{-1}L_{i-1})^{\vee }]=q^{2}x_{i}$
and so we get
$[(z^{-1}L_{i}/z^{-1}L_{i-1})^{\vee }]=q^{2}x_{i}$
and so we get
 $$\begin{eqnarray}[V_{i+1}]+x_{i}=[V_{i}]+q^{2}x_{i}.\end{eqnarray}$$
$$\begin{eqnarray}[V_{i+1}]+x_{i}=[V_{i}]+q^{2}x_{i}.\end{eqnarray}$$
Applying
![]() $\bigwedge ^{j}$
we get
$\bigwedge ^{j}$
we get
 $$\begin{eqnarray}\biggl[\bigwedge ^{j}V_{i+1}\biggr]+x_{i}\biggl[\bigwedge ^{j-1}V_{i+1}\biggr]=\biggl[\bigwedge ^{j}V_{i}\biggr]+q^{2}x_{i}\biggl[\bigwedge ^{j-1}V_{i}\biggr]\end{eqnarray}$$
$$\begin{eqnarray}\biggl[\bigwedge ^{j}V_{i+1}\biggr]+x_{i}\biggl[\bigwedge ^{j-1}V_{i+1}\biggr]=\biggl[\bigwedge ^{j}V_{i}\biggr]+q^{2}x_{i}\biggl[\bigwedge ^{j-1}V_{i}\biggr]\end{eqnarray}$$
which is relation (33).
Now, we can rewrite (32) as
 $$\begin{eqnarray}e_{j}^{(i+1)}=e_{j}^{(i)}+(q^{2}-1)x_{i}e_{j-1}^{(i)}-x_{i}(q^{2}-1)(x_{i}e_{j-2}^{(i)}-x_{i}^{2}e_{j-3}^{(i-1)}+\cdots \,).\end{eqnarray}$$
$$\begin{eqnarray}e_{j}^{(i+1)}=e_{j}^{(i)}+(q^{2}-1)x_{i}e_{j-1}^{(i)}-x_{i}(q^{2}-1)(x_{i}e_{j-2}^{(i)}-x_{i}^{2}e_{j-3}^{(i-1)}+\cdots \,).\end{eqnarray}$$
Assuming (32) is true for
![]() $j-1$
then we know
$j-1$
then we know
 $$\begin{eqnarray}(q^{2}-1)(x_{i}e_{j-2}^{(i)}-x_{i}^{2}e_{j-3}^{(i-1)}+\cdots \,)=e_{j-1}^{(i+1)}-e_{j-1}^{(i)}.\end{eqnarray}$$
$$\begin{eqnarray}(q^{2}-1)(x_{i}e_{j-2}^{(i)}-x_{i}^{2}e_{j-3}^{(i-1)}+\cdots \,)=e_{j-1}^{(i+1)}-e_{j-1}^{(i)}.\end{eqnarray}$$
So it remains to show that
 $$\begin{eqnarray}e_{j}^{(i+1)}=e_{j}^{(i)}+(q^{2}-1)x_{i}e_{j-1}^{(i)}-x_{i}(e_{j-1}^{(i+1)}-e_{j-1}^{(i)}).\end{eqnarray}$$
$$\begin{eqnarray}e_{j}^{(i+1)}=e_{j}^{(i)}+(q^{2}-1)x_{i}e_{j-1}^{(i)}-x_{i}(e_{j-1}^{(i+1)}-e_{j-1}^{(i)}).\end{eqnarray}$$
This easily simplifies to (33), which we proved above. ◻
Recall the definition of the
![]() $E[q^{\pm }]$
-algebra
$E[q^{\pm }]$
-algebra
![]() $R_{n,[q^{\pm }]}^{m}$
from § 7.3.
$R_{n,[q^{\pm }]}^{m}$
from § 7.3.
Lemma 8.14. We have
 $K^{\operatorname{SL}_{n}\times \mathbb{C}^{\times }}(Y(1^{m}))\cong R_{n,[q^{\pm }]}^{m}$
as
$K^{\operatorname{SL}_{n}\times \mathbb{C}^{\times }}(Y(1^{m}))\cong R_{n,[q^{\pm }]}^{m}$
as
![]() $E[q^{\pm }]$
-modules.
$E[q^{\pm }]$
-modules.
Proof. Inside
 $K^{\operatorname{SL}_{n}\times \mathbb{C}^{\times }}(Y(1^{m}))$
we have the standard exact sequence
$K^{\operatorname{SL}_{n}\times \mathbb{C}^{\times }}(Y(1^{m}))$
we have the standard exact sequence
 $$\begin{eqnarray}0\rightarrow L_{i}/L_{i-1}\rightarrow z^{-1}L_{i-1}/L_{i-1}\rightarrow z^{-1}L_{i-1}/L_{i}\rightarrow 0\end{eqnarray}$$
$$\begin{eqnarray}0\rightarrow L_{i}/L_{i-1}\rightarrow z^{-1}L_{i-1}/L_{i-1}\rightarrow z^{-1}L_{i-1}/L_{i}\rightarrow 0\end{eqnarray}$$
which implies that
 $\bigwedge ^{n}[(z^{-1}L_{i-1}/L_{i-1})^{\vee }-(L_{i}/L_{i-1})^{\vee }]=0$
. The defining relation of
$\bigwedge ^{n}[(z^{-1}L_{i-1}/L_{i-1})^{\vee }-(L_{i}/L_{i-1})^{\vee }]=0$
. The defining relation of
![]() $R_{n,[q^{\pm }]}^{m}$
now follows using that
$R_{n,[q^{\pm }]}^{m}$
now follows using that
 $e_{j}^{(i)}=[\bigwedge ^{j}(z^{-1}L_{i-1}/L_{i-1})^{\vee }]$
,
$e_{j}^{(i)}=[\bigwedge ^{j}(z^{-1}L_{i-1}/L_{i-1})^{\vee }]$
,
 $x_{i}=[\det (L_{i}/L_{i-1})^{\vee }]$
and the general identity
$x_{i}=[\det (L_{i}/L_{i-1})^{\vee }]$
and the general identity
 $$\begin{eqnarray}\bigwedge ^{r}(A-B)=\bigwedge ^{r}(A)-\bigwedge ^{r-1}(A)\cdot B+\bigwedge ^{r-2}(A)\cdot \operatorname{Sym}^{2}(B)-\bigwedge ^{r-3}(A)\cdot \operatorname{Sym}^{3}(B)+\cdots\end{eqnarray}$$
$$\begin{eqnarray}\bigwedge ^{r}(A-B)=\bigwedge ^{r}(A)-\bigwedge ^{r-1}(A)\cdot B+\bigwedge ^{r-2}(A)\cdot \operatorname{Sym}^{2}(B)-\bigwedge ^{r-3}(A)\cdot \operatorname{Sym}^{3}(B)+\cdots\end{eqnarray}$$
in K-theory. There are no further relations since
![]() $Y(1^{m})$
is an iterated
$Y(1^{m})$
is an iterated
![]() $\mathbb{P}^{n-1}$
-bundle and
$\mathbb{P}^{n-1}$
-bundle and
 $$\begin{eqnarray}K^{\operatorname{SL}_{n}\times \mathbb{C}^{\times }}(Y(1))=K^{\operatorname{SL}_{n}\times \mathbb{C}^{\times }}(\mathbb{P}^{n-1})\cong E[q^{\pm }][x]/(x^{n}-e_{1}x^{n-1}+e_{2}x^{n-2}-\cdots +(-1)^{n})\end{eqnarray}$$
$$\begin{eqnarray}K^{\operatorname{SL}_{n}\times \mathbb{C}^{\times }}(Y(1))=K^{\operatorname{SL}_{n}\times \mathbb{C}^{\times }}(\mathbb{P}^{n-1})\cong E[q^{\pm }][x]/(x^{n}-e_{1}x^{n-1}+e_{2}x^{n-2}-\cdots +(-1)^{n})\end{eqnarray}$$
where
 $x={\mathcal{O}}_{\mathbb{P}^{n-1}}(1)$
.◻
$x={\mathcal{O}}_{\mathbb{P}^{n-1}}(1)$
.◻
Recall the
![]() $E[q^{\pm }]$
-algebra
$E[q^{\pm }]$
-algebra
![]() $\operatorname{Sym}(\text{}\underline{x})$
consisting of symmetric functions in the
$\operatorname{Sym}(\text{}\underline{x})$
consisting of symmetric functions in the
![]() $x_{i}$
which acts on
$x_{i}$
which acts on
![]() $R_{n,[q^{\pm }]}^{m}$
as discussed in § 7.3.
$R_{n,[q^{\pm }]}^{m}$
as discussed in § 7.3.
Corollary 8.15. The natural inclusion
 $i:Z(1^{m},1^{m})\rightarrow Y(1^{m})\times Y(1^{m})$
induces an injective map
$i:Z(1^{m},1^{m})\rightarrow Y(1^{m})\times Y(1^{m})$
induces an injective map
 $$\begin{eqnarray}S:K^{\operatorname{SL}_{n}\times \mathbb{C}^{\times }}(Z(1^{m},1^{m}))\rightarrow \operatorname{End}_{\operatorname{ Sym}(\text{}\underline{x})}(R_{n,[q^{\pm }]}^{m}).\end{eqnarray}$$
$$\begin{eqnarray}S:K^{\operatorname{SL}_{n}\times \mathbb{C}^{\times }}(Z(1^{m},1^{m}))\rightarrow \operatorname{End}_{\operatorname{ Sym}(\text{}\underline{x})}(R_{n,[q^{\pm }]}^{m}).\end{eqnarray}$$
Proof. Since
 $Y(1^{m})\times Y(1^{m})$
is an iterated projective bundle, it has property
$Y(1^{m})\times Y(1^{m})$
is an iterated projective bundle, it has property
![]() $T_{A}$
where
$T_{A}$
where
 $A=\operatorname{SL}_{n}\times \mathbb{C}^{\times }$
. It follows that
$A=\operatorname{SL}_{n}\times \mathbb{C}^{\times }$
. It follows that
 $$\begin{eqnarray}\displaystyle K^{\operatorname{SL}_{n}\times \mathbb{C}^{\times }}(Y(1^{m})\times Y(1^{m})) & \cong & \displaystyle K_{0,\text{top}}^{\operatorname{SL}_{n}\times \mathbb{C}^{\times }}(Y(1^{m})\times Y(1^{m}))\nonumber\\ \displaystyle & \cong & \displaystyle \operatorname{End}_{K_{0,\text{top}}^{\operatorname{SL}_{n}\times \mathbb{C}^{\times }}(pt)}(K_{0,\text{top}}^{\operatorname{SL}_{n}\times \mathbb{C}^{\times }}(Y(1^{m})))\nonumber\\ \displaystyle & \cong & \displaystyle \operatorname{End}_{K^{\operatorname{SL}_{n}\times \mathbb{C}^{\times }}(pt)}(K^{\operatorname{SL}_{n}\times \mathbb{C}^{\times }}(Y(1^{m}))).\nonumber\end{eqnarray}$$
$$\begin{eqnarray}\displaystyle K^{\operatorname{SL}_{n}\times \mathbb{C}^{\times }}(Y(1^{m})\times Y(1^{m})) & \cong & \displaystyle K_{0,\text{top}}^{\operatorname{SL}_{n}\times \mathbb{C}^{\times }}(Y(1^{m})\times Y(1^{m}))\nonumber\\ \displaystyle & \cong & \displaystyle \operatorname{End}_{K_{0,\text{top}}^{\operatorname{SL}_{n}\times \mathbb{C}^{\times }}(pt)}(K_{0,\text{top}}^{\operatorname{SL}_{n}\times \mathbb{C}^{\times }}(Y(1^{m})))\nonumber\\ \displaystyle & \cong & \displaystyle \operatorname{End}_{K^{\operatorname{SL}_{n}\times \mathbb{C}^{\times }}(pt)}(K^{\operatorname{SL}_{n}\times \mathbb{C}^{\times }}(Y(1^{m}))).\nonumber\end{eqnarray}$$
Subsequently, by Lemma 8.12, we have an inclusion
 $$\begin{eqnarray}K^{\operatorname{SL}_{n}\times \mathbb{C}^{\times }}(Z(1^{m},1^{m}))\rightarrow \operatorname{End}(K^{\operatorname{SL}_{n}\times \mathbb{C}^{\times }}(Y(1^{m})))\end{eqnarray}$$
$$\begin{eqnarray}K^{\operatorname{SL}_{n}\times \mathbb{C}^{\times }}(Z(1^{m},1^{m}))\rightarrow \operatorname{End}(K^{\operatorname{SL}_{n}\times \mathbb{C}^{\times }}(Y(1^{m})))\end{eqnarray}$$
while, by the previous lemma,
 $K^{\operatorname{SL}_{n}\times \mathbb{C}^{\times }}(Y(1^{m}))\cong R_{n,[q^{\pm }]}^{m}$
.
$K^{\operatorname{SL}_{n}\times \mathbb{C}^{\times }}(Y(1^{m}))\cong R_{n,[q^{\pm }]}^{m}$
.
On the other hand, since
 $x_{i}=[\det (L_{i}/L_{i-1})^{\vee }]$
, we see that the symmetric functions in the
$x_{i}=[\det (L_{i}/L_{i-1})^{\vee }]$
, we see that the symmetric functions in the
![]() $x_{i}$
are generated by
$x_{i}$
are generated by
 $\wedge ^{j}(L_{m}/L_{0})^{\vee }$
. These clearly commute with any kernel supported on
$\wedge ^{j}(L_{m}/L_{0})^{\vee }$
. These clearly commute with any kernel supported on
 $Z(1^{m},1^{m})$
since
$Z(1^{m},1^{m})$
since
 $Z(1^{m},1^{m})$
is defined by the condition
$Z(1^{m},1^{m})$
is defined by the condition
 $L_{m}=L_{m}^{\prime }$
. The result follows.◻
$L_{m}=L_{m}^{\prime }$
. The result follows.◻
9 Isomorphism for
 $1^{m}$
$1^{m}$
We are now in a position to prove the isomorphism for
![]() $1^{m}$
.
$1^{m}$
.
Theorem 9.1. The functor
![]() $\unicode[STIX]{x1D6F7}$
gives an isomorphism
$\unicode[STIX]{x1D6F7}$
gives an isomorphism
 $$\begin{eqnarray}\operatorname{End}_{{\mathcal{A}}{\mathcal{S}}p_{n}}(1^{m})\xrightarrow[{}]{{\sim}}K^{\operatorname{SL}_{n}}(Z(1^{m},1^{m}))\end{eqnarray}$$
$$\begin{eqnarray}\operatorname{End}_{{\mathcal{A}}{\mathcal{S}}p_{n}}(1^{m})\xrightarrow[{}]{{\sim}}K^{\operatorname{SL}_{n}}(Z(1^{m},1^{m}))\end{eqnarray}$$
making the following diagram of isomorphisms commute

where
![]() $\unicode[STIX]{x1D6FE}$
comes from setting
$\unicode[STIX]{x1D6FE}$
comes from setting
![]() $e_{n}=1$
in Theorem 7.2.
$e_{n}=1$
in Theorem 7.2.
Theorem 9.2. The functor
![]() $\unicode[STIX]{x1D6F7}$
also gives an isomophism
$\unicode[STIX]{x1D6F7}$
also gives an isomophism
 $$\begin{eqnarray}\operatorname{End}_{{\mathcal{A}}{\mathcal{S}}p_{n}(q)}(1^{m})\xrightarrow[{}]{{\sim}}K^{\operatorname{SL}_{n}\times \mathbb{C}^{\times }}(Z(1^{m},1^{m}))\otimes _{\mathbb{ C}[q^{\pm }]}\mathbb{C}(q).\end{eqnarray}$$
$$\begin{eqnarray}\operatorname{End}_{{\mathcal{A}}{\mathcal{S}}p_{n}(q)}(1^{m})\xrightarrow[{}]{{\sim}}K^{\operatorname{SL}_{n}\times \mathbb{C}^{\times }}(Z(1^{m},1^{m}))\otimes _{\mathbb{ C}[q^{\pm }]}\mathbb{C}(q).\end{eqnarray}$$
9.1 The big diagram
The proof relies on the following diagram of
![]() $E[q^{\pm }]$
-algebras
$E[q^{\pm }]$
-algebras

where
![]() $\unicode[STIX]{x1D712}$
is obtained (by setting
$\unicode[STIX]{x1D712}$
is obtained (by setting
![]() $e_{n}=1$
) from
$e_{n}=1$
) from
![]() $\overline{\unicode[STIX]{x1D712}}$
which was defined in § 7.3.
$\overline{\unicode[STIX]{x1D712}}$
which was defined in § 7.3.
Lemma 9.3. This diagram commutes.
Proof. It suffices to check this on the generators
![]() $X_{i},T_{i}$
of
$X_{i},T_{i}$
of
![]() $AB_{m}$
.
$AB_{m}$
.
By definition
 $\unicode[STIX]{x1D6F7}(\unicode[STIX]{x1D6FD}(X_{i}))=[\unicode[STIX]{x1D6E5}_{\ast }\det (L_{i}/L_{i-1})^{\vee }]$
and, following the isomorphism from Lemma 8.14,
$\unicode[STIX]{x1D6F7}(\unicode[STIX]{x1D6FD}(X_{i}))=[\unicode[STIX]{x1D6E5}_{\ast }\det (L_{i}/L_{i-1})^{\vee }]$
and, following the isomorphism from Lemma 8.14,
 $S(\unicode[STIX]{x1D6E5}_{\ast }\det (L_{i}/L_{i-1})^{\vee })$
acts on
$S(\unicode[STIX]{x1D6E5}_{\ast }\det (L_{i}/L_{i-1})^{\vee })$
acts on
![]() $R_{n,[q^{\pm }]}^{m}$
as multiplication by
$R_{n,[q^{\pm }]}^{m}$
as multiplication by
![]() $x_{i}$
. On the other hand,
$x_{i}$
. On the other hand,
![]() $\unicode[STIX]{x1D712}(X_{i})$
is by definition multiplication by
$\unicode[STIX]{x1D712}(X_{i})$
is by definition multiplication by
![]() $x_{i}$
.
$x_{i}$
.
Now consider the correspondence
 $$\begin{eqnarray}Y(1^{i-1},2,1^{m-i-1})\xleftarrow[{}]{\unicode[STIX]{x1D70B}}W=\{L_{0}\subset \cdots \subset L_{m}:zL_{i+1}\subset L_{i-1}\}\xrightarrow[{}]{i}Y(1^{m}),\end{eqnarray}$$
$$\begin{eqnarray}Y(1^{i-1},2,1^{m-i-1})\xleftarrow[{}]{\unicode[STIX]{x1D70B}}W=\{L_{0}\subset \cdots \subset L_{m}:zL_{i+1}\subset L_{i-1}\}\xrightarrow[{}]{i}Y(1^{m}),\end{eqnarray}$$
where
![]() $\unicode[STIX]{x1D70B}$
is the projection which forgets
$\unicode[STIX]{x1D70B}$
is the projection which forgets
![]() $L_{i}$
and
$L_{i}$
and
![]() $i$
is an inclusion. Recall that
$i$
is an inclusion. Recall that
 $(\unicode[STIX]{x1D6F7}\circ \unicode[STIX]{x1D6FD})(T_{i})=q\cdot \operatorname{id}-E_{i}F_{i}$
(cf. Remark 5.3) where
$(\unicode[STIX]{x1D6F7}\circ \unicode[STIX]{x1D6FD})(T_{i})=q\cdot \operatorname{id}-E_{i}F_{i}$
(cf. Remark 5.3) where
![]() $E_{i}$
and
$E_{i}$
and
![]() $F_{i}$
act on
$F_{i}$
act on
 $K^{\operatorname{SL}_{n}\times \mathbb{C}^{\times }}(Y(1^{m}))\cong R_{n,[q^{\pm }]}^{m}$
as follows:
$K^{\operatorname{SL}_{n}\times \mathbb{C}^{\times }}(Y(1^{m}))\cong R_{n,[q^{\pm }]}^{m}$
as follows:
 $$\begin{eqnarray}\displaystyle E_{i}(\cdot ) & = & \displaystyle -q^{-1}[i_{\ast }\unicode[STIX]{x1D70B}^{\ast }(\cdot )\otimes \det (L_{i}/L_{i-1})],\nonumber\\ \displaystyle F_{i}(\cdot ) & = & \displaystyle \unicode[STIX]{x1D70B}_{\ast }i^{\ast }((\cdot )\otimes \det (L_{i+1}/L_{i})^{-1}).\nonumber\end{eqnarray}$$
$$\begin{eqnarray}\displaystyle E_{i}(\cdot ) & = & \displaystyle -q^{-1}[i_{\ast }\unicode[STIX]{x1D70B}^{\ast }(\cdot )\otimes \det (L_{i}/L_{i-1})],\nonumber\\ \displaystyle F_{i}(\cdot ) & = & \displaystyle \unicode[STIX]{x1D70B}_{\ast }i^{\ast }((\cdot )\otimes \det (L_{i+1}/L_{i})^{-1}).\nonumber\end{eqnarray}$$
From this description it is clear that for any
 $y\in R_{n,[q^{\pm }]}^{m}$
we have
$y\in R_{n,[q^{\pm }]}^{m}$
we have
 $$\begin{eqnarray}\displaystyle (\unicode[STIX]{x1D6F7}\circ \unicode[STIX]{x1D6FD})(T_{i})(yx_{j}) & = & \displaystyle x_{j}(\unicode[STIX]{x1D6F7}\circ \unicode[STIX]{x1D6FD})(T_{i})(y)\quad \text{if }j\neq i,i+1,\nonumber\\ \displaystyle (\unicode[STIX]{x1D6F7}\circ \unicode[STIX]{x1D6FD})(T_{i})((x_{i}+x_{i+1})y) & = & \displaystyle (x_{i}+x_{i+1})(\unicode[STIX]{x1D6F7}\circ \unicode[STIX]{x1D6FD})(T_{i})(y),\nonumber\\ \displaystyle (\unicode[STIX]{x1D6F7}\circ \unicode[STIX]{x1D6FD})(T_{i})(x_{i}x_{i+1}y) & = & \displaystyle x_{i}x_{i+1}(\unicode[STIX]{x1D6F7}\circ \unicode[STIX]{x1D6FD})(T_{i})(y).\nonumber\end{eqnarray}$$
$$\begin{eqnarray}\displaystyle (\unicode[STIX]{x1D6F7}\circ \unicode[STIX]{x1D6FD})(T_{i})(yx_{j}) & = & \displaystyle x_{j}(\unicode[STIX]{x1D6F7}\circ \unicode[STIX]{x1D6FD})(T_{i})(y)\quad \text{if }j\neq i,i+1,\nonumber\\ \displaystyle (\unicode[STIX]{x1D6F7}\circ \unicode[STIX]{x1D6FD})(T_{i})((x_{i}+x_{i+1})y) & = & \displaystyle (x_{i}+x_{i+1})(\unicode[STIX]{x1D6F7}\circ \unicode[STIX]{x1D6FD})(T_{i})(y),\nonumber\\ \displaystyle (\unicode[STIX]{x1D6F7}\circ \unicode[STIX]{x1D6FD})(T_{i})(x_{i}x_{i+1}y) & = & \displaystyle x_{i}x_{i+1}(\unicode[STIX]{x1D6F7}\circ \unicode[STIX]{x1D6FD})(T_{i})(y).\nonumber\end{eqnarray}$$
Since the same is true for
![]() $\unicode[STIX]{x1D712}$
in place of
$\unicode[STIX]{x1D712}$
in place of
![]() $(\unicode[STIX]{x1D6F7}\circ \unicode[STIX]{x1D6FD})$
, it suffices to show that the actions of
$(\unicode[STIX]{x1D6F7}\circ \unicode[STIX]{x1D6FD})$
, it suffices to show that the actions of
 $(\unicode[STIX]{x1D6F7}\circ \unicode[STIX]{x1D6FD})(T_{i})$
and
$(\unicode[STIX]{x1D6F7}\circ \unicode[STIX]{x1D6FD})(T_{i})$
and
![]() $\unicode[STIX]{x1D712}(T_{i})$
agree on
$\unicode[STIX]{x1D712}(T_{i})$
agree on
![]() $1$
and
$1$
and
![]() $x_{i}$
.
$x_{i}$
.
Now
 $F_{i}(1)=0$
which means that
$F_{i}(1)=0$
which means that
 $(\unicode[STIX]{x1D6F7}\circ \unicode[STIX]{x1D6FD})(T_{i})(1)=q=\unicode[STIX]{x1D712}(T_{i})(1)$
.
$(\unicode[STIX]{x1D6F7}\circ \unicode[STIX]{x1D6FD})(T_{i})(1)=q=\unicode[STIX]{x1D712}(T_{i})(1)$
.
On the other hand,
 $E_{i}F_{i}(x_{i})=-q^{-1}x_{i+1}[{\mathcal{O}}_{W}]$
so we need to determine the class of
$E_{i}F_{i}(x_{i})=-q^{-1}x_{i+1}[{\mathcal{O}}_{W}]$
so we need to determine the class of
![]() ${\mathcal{O}}_{W}$
inside
${\mathcal{O}}_{W}$
inside
 $K^{\operatorname{SL}_{n}\times \mathbb{C}^{\times }}(Y(1^{m}))$
. To do this consider the map of bundles on
$K^{\operatorname{SL}_{n}\times \mathbb{C}^{\times }}(Y(1^{m}))$
. To do this consider the map of bundles on
![]() $Y(1^{m})$
$Y(1^{m})$
 $$\begin{eqnarray}z:L_{i+1}/L_{i}\rightarrow L_{i}/L_{i-1}\{2\},\end{eqnarray}$$
$$\begin{eqnarray}z:L_{i+1}/L_{i}\rightarrow L_{i}/L_{i-1}\{2\},\end{eqnarray}$$
where the shift by
![]() $\{2\}$
is because of the
$\{2\}$
is because of the
![]() $\mathbb{C}^{\times }$
action on
$\mathbb{C}^{\times }$
action on
![]() $z$
(cf. the map in (24)). This map vanishes exactly along
$z$
(cf. the map in (24)). This map vanishes exactly along
![]() $W$
and hence
$W$
and hence
 $[{\mathcal{O}}_{W}]=1-q^{2}x_{i}x_{i+1}^{-1}$
. Putting this together we find that
$[{\mathcal{O}}_{W}]=1-q^{2}x_{i}x_{i+1}^{-1}$
. Putting this together we find that
 $$\begin{eqnarray}\displaystyle (\unicode[STIX]{x1D6F7}\circ \unicode[STIX]{x1D6FD})(T_{i})(x_{i}) & = & \displaystyle qx_{i}-E_{i}F_{i}(x_{i})\nonumber\\ \displaystyle & = & \displaystyle qx_{i}+q^{-1}x_{i+1}(1-q^{2}x_{i}x_{i+1}^{-1})\nonumber\\ \displaystyle & = & \displaystyle q^{-1}x_{i+1}=\unicode[STIX]{x1D712}(T_{i})(x_{i}).\nonumber\end{eqnarray}$$
$$\begin{eqnarray}\displaystyle (\unicode[STIX]{x1D6F7}\circ \unicode[STIX]{x1D6FD})(T_{i})(x_{i}) & = & \displaystyle qx_{i}-E_{i}F_{i}(x_{i})\nonumber\\ \displaystyle & = & \displaystyle qx_{i}+q^{-1}x_{i+1}(1-q^{2}x_{i}x_{i+1}^{-1})\nonumber\\ \displaystyle & = & \displaystyle q^{-1}x_{i+1}=\unicode[STIX]{x1D712}(T_{i})(x_{i}).\nonumber\end{eqnarray}$$
This concludes the proof. ◻
9.2 The proofs
Proof of Theorem 9.1.
We take the diagram (36) and tensor over
![]() $\mathbb{C}[q^{\pm }]$
with
$\mathbb{C}[q^{\pm }]$
with
![]() $\mathbb{C}$
(at
$\mathbb{C}$
(at
![]() $q=1$
) to obtain the following.
$q=1$
) to obtain the following.

Now by Theorems 7.2 and 4.5, we obtain isomorphisms
 $$\begin{eqnarray}\operatorname{End}_{ASp_{n}}(1^{m})\xrightarrow[{}]{A\unicode[STIX]{x1D6E4}}\operatorname{End}_{{\mathcal{O}}({\textstyle \frac{\operatorname{SL}_{n}}{\operatorname{SL}_{n}}})\operatorname{-mod}}({\mathcal{O}}(\operatorname{SL}_{n})\otimes (\mathbb{C}^{n})^{\otimes m})\xrightarrow[{}]{{\sim}}\operatorname{End}_{\operatorname{ Sym}(\text{}\underline{x})}(R_{n}^{m})\end{eqnarray}$$
$$\begin{eqnarray}\operatorname{End}_{ASp_{n}}(1^{m})\xrightarrow[{}]{A\unicode[STIX]{x1D6E4}}\operatorname{End}_{{\mathcal{O}}({\textstyle \frac{\operatorname{SL}_{n}}{\operatorname{SL}_{n}}})\operatorname{-mod}}({\mathcal{O}}(\operatorname{SL}_{n})\otimes (\mathbb{C}^{n})^{\otimes m})\xrightarrow[{}]{{\sim}}\operatorname{End}_{\operatorname{ Sym}(\text{}\underline{x})}(R_{n}^{m})\end{eqnarray}$$
so that our diagram becomes the following.

Now the top left triangle commutes by Remark 7.5. Then the commutativity of the bottom right triangle follows from the commutativity of the whole square and the surjectivity of
![]() $\unicode[STIX]{x1D6FD}$
. Note that the bottom right triangle is rewritten as a square in the statement of the theorem.
$\unicode[STIX]{x1D6FD}$
. Note that the bottom right triangle is rewritten as a square in the statement of the theorem.
Since
![]() $A\unicode[STIX]{x1D6E4}$
is an isomorphism and
$A\unicode[STIX]{x1D6E4}$
is an isomorphism and
![]() $S$
is injective, we see that
$S$
is injective, we see that
![]() $\unicode[STIX]{x1D6F7}$
is an isomorphism.◻
$\unicode[STIX]{x1D6F7}$
is an isomorphism.◻
Proof of Theorem 9.2.
We take the diagram (36) and tensor over
![]() $\mathbb{C}[q^{\pm }]$
with
$\mathbb{C}[q^{\pm }]$
with
![]() $\mathbb{C}(q)$
to obtain the following.
$\mathbb{C}(q)$
to obtain the following.

From Proposition 7.7 we see that
![]() $\unicode[STIX]{x1D712}$
is surjective. On the other hand, from Corollary 8.15 we see that
$\unicode[STIX]{x1D712}$
is surjective. On the other hand, from Corollary 8.15 we see that
![]() $S$
is injective. Thus
$S$
is injective. Thus
![]() $\unicode[STIX]{x1D6F7}$
is surjective.
$\unicode[STIX]{x1D6F7}$
is surjective.
Now we will prove that
![]() $\unicode[STIX]{x1D6F7}$
is injective. Let
$\unicode[STIX]{x1D6F7}$
is injective. Let
![]() $\text{}\underline{l},\text{}\underline{l}^{\prime }$
be two sequences of length
$\text{}\underline{l},\text{}\underline{l}^{\prime }$
be two sequences of length
![]() $m^{\prime }$
which are each obtained from
$m^{\prime }$
which are each obtained from
![]() $1^{m}$
by adding some
$1^{m}$
by adding some
![]() $0$
s and
$0$
s and
![]() $n$
s. Consider the map
$n$
s. Consider the map
 $$\begin{eqnarray}\unicode[STIX]{x1D6F7}_{m^{\prime }}:\operatorname{Hom}_{(\dot{U}_{[q^{\pm }]}L\mathfrak{g}\mathfrak{l}_{m^{\prime }})^{n}}(\text{}\underline{l},\text{}\underline{l}^{\prime })\rightarrow K^{\operatorname{SL}_{n}\times \mathbb{C}^{\times }}(Z(1^{m},1^{m}))\end{eqnarray}$$
$$\begin{eqnarray}\unicode[STIX]{x1D6F7}_{m^{\prime }}:\operatorname{Hom}_{(\dot{U}_{[q^{\pm }]}L\mathfrak{g}\mathfrak{l}_{m^{\prime }})^{n}}(\text{}\underline{l},\text{}\underline{l}^{\prime })\rightarrow K^{\operatorname{SL}_{n}\times \mathbb{C}^{\times }}(Z(1^{m},1^{m}))\end{eqnarray}$$
and recall that this map factors as
 $$\begin{eqnarray}\operatorname{Hom}_{(\dot{U}_{[q^{\pm }]}L\mathfrak{g}\mathfrak{l}_{m^{\prime }})^{n}}(\text{}\underline{l},\text{}\underline{l}^{\prime })\xrightarrow[{}]{\unicode[STIX]{x1D6F9}_{m^{\prime }}}\operatorname{End}_{{\mathcal{A}}{\mathcal{S}}p_{n}[q^{\pm }]}(1^{m})\xrightarrow[{}]{\unicode[STIX]{x1D6F7}}K^{\operatorname{SL}_{n}\times \mathbb{C}^{\times }}(Z(1^{m},1^{m})),\end{eqnarray}$$
$$\begin{eqnarray}\operatorname{Hom}_{(\dot{U}_{[q^{\pm }]}L\mathfrak{g}\mathfrak{l}_{m^{\prime }})^{n}}(\text{}\underline{l},\text{}\underline{l}^{\prime })\xrightarrow[{}]{\unicode[STIX]{x1D6F9}_{m^{\prime }}}\operatorname{End}_{{\mathcal{A}}{\mathcal{S}}p_{n}[q^{\pm }]}(1^{m})\xrightarrow[{}]{\unicode[STIX]{x1D6F7}}K^{\operatorname{SL}_{n}\times \mathbb{C}^{\times }}(Z(1^{m},1^{m})),\end{eqnarray}$$
where the first map is injective by Theorem 5.8.
Now
![]() $\unicode[STIX]{x1D6F7}$
is injective at
$\unicode[STIX]{x1D6F7}$
is injective at
![]() $q=1$
by Theorem 9.1 and hence
$q=1$
by Theorem 9.1 and hence
![]() $\unicode[STIX]{x1D6F7}_{m^{\prime }}$
is injective at
$\unicode[STIX]{x1D6F7}_{m^{\prime }}$
is injective at
![]() $q=1$
. Since both sides of (38) are free
$q=1$
. Since both sides of (38) are free
![]() $\mathbb{C}[q^{\pm }]$
-modules (the left-hand side by Lemma 5.2 and the right-hand side by Corollary 8.11), Lemma 9.4 implies that
$\mathbb{C}[q^{\pm }]$
-modules (the left-hand side by Lemma 5.2 and the right-hand side by Corollary 8.11), Lemma 9.4 implies that
![]() $\unicode[STIX]{x1D6F7}_{m^{\prime }}$
is injective.
$\unicode[STIX]{x1D6F7}_{m^{\prime }}$
is injective.
Since, by Theorem 5.8, every element of
 $\operatorname{End}_{{\mathcal{A}}{\mathcal{S}}p_{n}[q^{\pm }]}(1^{m})$
is in the image of
$\operatorname{End}_{{\mathcal{A}}{\mathcal{S}}p_{n}[q^{\pm }]}(1^{m})$
is in the image of
![]() $\unicode[STIX]{x1D6F9}_{m^{\prime }}$
for some
$\unicode[STIX]{x1D6F9}_{m^{\prime }}$
for some
![]() $m^{\prime },\text{}\underline{l},\text{}\underline{l}^{\prime }$
, this implies that
$m^{\prime },\text{}\underline{l},\text{}\underline{l}^{\prime }$
, this implies that
![]() $\unicode[STIX]{x1D6F7}$
is injective.◻
$\unicode[STIX]{x1D6F7}$
is injective.◻
Lemma 9.4. Let
 $f:M\rightarrow N$
be a map between free
$f:M\rightarrow N$
be a map between free
![]() $\mathbb{C}[q^{\pm }]$
-modules such that
$\mathbb{C}[q^{\pm }]$
-modules such that
![]() $f|_{q=1}$
is injective. Then
$f|_{q=1}$
is injective. Then
![]() $f$
is injective.
$f$
is injective.
Proof. Since the submodule of a free
![]() $\mathbb{C}[q^{\pm }]$
-module is free, we can assume that
$\mathbb{C}[q^{\pm }]$
-module is free, we can assume that
![]() $f$
is surjective (by replacing
$f$
is surjective (by replacing
![]() $N$
with the image of
$N$
with the image of
![]() $f$
). Thus we have a short exact sequence
$f$
). Thus we have a short exact sequence
 $$\begin{eqnarray}0\rightarrow K\rightarrow M\xrightarrow[{}]{f}N\rightarrow 0,\end{eqnarray}$$
$$\begin{eqnarray}0\rightarrow K\rightarrow M\xrightarrow[{}]{f}N\rightarrow 0,\end{eqnarray}$$
where
![]() $K$
is the kernel of
$K$
is the kernel of
![]() $f$
. Applying
$f$
. Applying
 $\otimes _{\mathbb{C}[q^{\pm }]}\mathbb{C}_{1}$
, we obtain the long exact sequence
$\otimes _{\mathbb{C}[q^{\pm }]}\mathbb{C}_{1}$
, we obtain the long exact sequence
 $$\begin{eqnarray}\operatorname{Tor}_{1}^{\mathbb{C}[q^{\pm }]}(N,\mathbb{C}_{1})\rightarrow K\otimes _{\mathbb{C}[q^{\pm }]}\mathbb{C}_{1}\rightarrow M\otimes _{\mathbb{C}[q^{\pm }]}\mathbb{C}_{1}\xrightarrow[{}]{f|_{q=1}}N\otimes _{\mathbb{C}[q^{\pm }]}\rightarrow 0.\end{eqnarray}$$
$$\begin{eqnarray}\operatorname{Tor}_{1}^{\mathbb{C}[q^{\pm }]}(N,\mathbb{C}_{1})\rightarrow K\otimes _{\mathbb{C}[q^{\pm }]}\mathbb{C}_{1}\rightarrow M\otimes _{\mathbb{C}[q^{\pm }]}\mathbb{C}_{1}\xrightarrow[{}]{f|_{q=1}}N\otimes _{\mathbb{C}[q^{\pm }]}\rightarrow 0.\end{eqnarray}$$
Since
![]() $N$
is free,
$N$
is free,
 $\operatorname{Tor}_{1}^{\mathbb{C}[q^{\pm }]}(N,\mathbb{C}_{1})=0$
.
$\operatorname{Tor}_{1}^{\mathbb{C}[q^{\pm }]}(N,\mathbb{C}_{1})=0$
.
On the other hand, since
![]() $f|_{q=1}$
is injective, the map
$f|_{q=1}$
is injective, the map
 $\operatorname{Tor}_{1}^{\mathbb{C}[q^{\pm }]}(N,\mathbb{C}_{1})\rightarrow K\otimes _{\mathbb{C}[q^{\pm }]}\mathbb{C}_{1}$
is surjective. Thus
$\operatorname{Tor}_{1}^{\mathbb{C}[q^{\pm }]}(N,\mathbb{C}_{1})\rightarrow K\otimes _{\mathbb{C}[q^{\pm }]}\mathbb{C}_{1}$
is surjective. Thus
 $K\otimes _{\mathbb{C}[q^{\pm }]}\mathbb{C}_{1}=0$
. Since
$K\otimes _{\mathbb{C}[q^{\pm }]}\mathbb{C}_{1}=0$
. Since
![]() $K$
is a submodule of a free module, it is free, and thus
$K$
is a submodule of a free module, it is free, and thus
![]() $K=0$
.◻
$K=0$
.◻
10 The structure of
 $\operatorname{End}_{{\mathcal{A}}{\mathcal{S}}p_{n}[q^{\pm }]}(1^{m})$
and cyclotomic Hecke algebras
$\operatorname{End}_{{\mathcal{A}}{\mathcal{S}}p_{n}[q^{\pm }]}(1^{m})$
and cyclotomic Hecke algebras
This section stands somewhat separate from the main results in the paper but may be of independent interest. As we noted earlier, the weight
![]() $1^{m}$
plays an important role in the categories we have studied. We will now discuss in a little more detail the structure of the
$1^{m}$
plays an important role in the categories we have studied. We will now discuss in a little more detail the structure of the
![]() $E[q^{\pm }]$
-algebra
$E[q^{\pm }]$
-algebra
 $\operatorname{End}_{{\mathcal{A}}{\mathcal{S}}p_{n}[q^{\pm }]}(1^{m})$
.
$\operatorname{End}_{{\mathcal{A}}{\mathcal{S}}p_{n}[q^{\pm }]}(1^{m})$
.
10.1 Affine Hecke algebras
The annular braid group
![]() $AB_{m}$
has a natural quotient which is the affine Hecke algebra. We will consider a slight variant, denoted by
$AB_{m}$
has a natural quotient which is the affine Hecke algebra. We will consider a slight variant, denoted by
![]() $\widehat{{\mathcal{H}}}_{m}[q^{\pm }]$
, which is the quotient of
$\widehat{{\mathcal{H}}}_{m}[q^{\pm }]$
, which is the quotient of
 $E[q^{\pm }][AB_{m}]$
by the relation
$E[q^{\pm }][AB_{m}]$
by the relation
 $$\begin{eqnarray}T_{i}^{2}=(q-q^{-1})T_{i}+1\quad \text{for }i=1,\ldots ,m-1.\end{eqnarray}$$
$$\begin{eqnarray}T_{i}^{2}=(q-q^{-1})T_{i}+1\quad \text{for }i=1,\ldots ,m-1.\end{eqnarray}$$
As usual, we denote by
![]() $\widehat{{\mathcal{H}}}_{m}(q)$
the same algebra over
$\widehat{{\mathcal{H}}}_{m}(q)$
the same algebra over
![]() $\mathbb{C}(q)$
and by
$\mathbb{C}(q)$
and by
![]() $\widehat{{\mathcal{H}}}_{m}$
the specialization to
$\widehat{{\mathcal{H}}}_{m}$
the specialization to
![]() $q=1$
. Note that
$q=1$
. Note that
 $\widehat{{\mathcal{H}}}_{m}\cong E[AS_{m}]$
where
$\widehat{{\mathcal{H}}}_{m}\cong E[AS_{m}]$
where
![]() $AS_{m}$
is the affine symmetric group.
$AS_{m}$
is the affine symmetric group.
Remark 10.1. The usual generators of the affine Hecke algebra use
![]() $qT_{i}$
instead of
$qT_{i}$
instead of
![]() $T_{i}$
which means that the Hecke relation becomes the more familiar
$T_{i}$
which means that the Hecke relation becomes the more familiar
 $T_{i}^{2}=(q^{2}-1)T_{i}+q^{2}$
while the relation
$T_{i}^{2}=(q^{2}-1)T_{i}+q^{2}$
while the relation
 $T_{i}X_{i}T_{i}=X_{i+1}$
becomes
$T_{i}X_{i}T_{i}=X_{i+1}$
becomes
 $T_{i}X_{i}T_{i}=q^{2}X_{i+1}$
.
$T_{i}X_{i}T_{i}=q^{2}X_{i+1}$
.
Now consider the composition
 $$\begin{eqnarray}\widehat{{\mathcal{H}}}_{m}[q^{\pm }]\rightarrow \operatorname{End}_{{\mathcal{A}}{\mathcal{S}}p_{n}[q^{\pm }]}(1^{m})\rightarrow \operatorname{End}_{\operatorname{ Sym}(\text{}\underline{x})}(R_{n,[q^{\pm }]}^{m}).\end{eqnarray}$$
$$\begin{eqnarray}\widehat{{\mathcal{H}}}_{m}[q^{\pm }]\rightarrow \operatorname{End}_{{\mathcal{A}}{\mathcal{S}}p_{n}[q^{\pm }]}(1^{m})\rightarrow \operatorname{End}_{\operatorname{ Sym}(\text{}\underline{x})}(R_{n,[q^{\pm }]}^{m}).\end{eqnarray}$$
By Proposition 7.7 this composition, denoted by
![]() $\unicode[STIX]{x1D712}$
, is surjective if we tensor over
$\unicode[STIX]{x1D712}$
, is surjective if we tensor over
![]() $\mathbb{C}(q)$
. Moreover, the second map is an isomorphism over
$\mathbb{C}(q)$
. Moreover, the second map is an isomorphism over
![]() $\mathbb{C}(q)$
. We conjecture that both these results also hold over
$\mathbb{C}(q)$
. We conjecture that both these results also hold over
![]() $\mathbb{C}[q^{\pm }]$
. So to understand
$\mathbb{C}[q^{\pm }]$
. So to understand
 $\operatorname{End}_{{\mathcal{A}}{\mathcal{S}}p_{n}[q^{\pm }]}(1^{m})$
we need some description of the kernel of
$\operatorname{End}_{{\mathcal{A}}{\mathcal{S}}p_{n}[q^{\pm }]}(1^{m})$
we need some description of the kernel of
![]() $\unicode[STIX]{x1D712}$
.
$\unicode[STIX]{x1D712}$
.
10.2 When
 $q=1$
$q=1$
Conjecture 10.2. The kernel of
 $\unicode[STIX]{x1D712}:E[AS_{m}]\rightarrow \operatorname{End}_{\operatorname{Sym}(\text{}\underline{x})}(R_{n}^{m})$
is generated by
$\unicode[STIX]{x1D712}:E[AS_{m}]\rightarrow \operatorname{End}_{\operatorname{Sym}(\text{}\underline{x})}(R_{n}^{m})$
is generated by
 $$\begin{eqnarray}e_{\operatorname{sgn}}(T_{1},\ldots ,T_{k})(h_{n-k}-e_{1}h_{n-k-1}+e_{2}h_{n-k-2}-\cdots +(-1)^{n-k}e_{n-k})\end{eqnarray}$$
$$\begin{eqnarray}e_{\operatorname{sgn}}(T_{1},\ldots ,T_{k})(h_{n-k}-e_{1}h_{n-k-1}+e_{2}h_{n-k-2}-\cdots +(-1)^{n-k}e_{n-k})\end{eqnarray}$$
for
 $k=0,\ldots ,\min (n,m-1)$
. Here
$k=0,\ldots ,\min (n,m-1)$
. Here
 $e_{\operatorname{sgn}}(T_{1},\ldots ,T_{k})\in \mathbb{C}[S_{k}]\subset \mathbb{C}[S_{m}]$
is the sign idempotent and
$e_{\operatorname{sgn}}(T_{1},\ldots ,T_{k})\in \mathbb{C}[S_{k}]\subset \mathbb{C}[S_{m}]$
is the sign idempotent and
 $h_{j}=h_{j}(X_{1},\ldots ,X_{k+1})$
denotes the homogeneous symmetric function of degree
$h_{j}=h_{j}(X_{1},\ldots ,X_{k+1})$
denotes the homogeneous symmetric function of degree
![]() $j$
.
$j$
.
This conjecture interpolates between the Cayley–Hamilton theorem and Schur–Weyl duality. This is because when
![]() $k=0$
the relation in (39) becomes
$k=0$
the relation in (39) becomes
 $$\begin{eqnarray}X_{1}^{n}-e_{1}X_{1}^{n-1}+\cdots \pm e_{n-1}X_{1}\mp 1=0.\end{eqnarray}$$
$$\begin{eqnarray}X_{1}^{n}-e_{1}X_{1}^{n-1}+\cdots \pm e_{n-1}X_{1}\mp 1=0.\end{eqnarray}$$
However, under the isomorphism
 $$\begin{eqnarray}R_{n}^{m}\cong \operatorname{Maps}_{\operatorname{ SL}_{n}}(\operatorname{SL}_{n},\operatorname{End}((\mathbb{C}^{n})^{\otimes m}))\end{eqnarray}$$
$$\begin{eqnarray}R_{n}^{m}\cong \operatorname{Maps}_{\operatorname{ SL}_{n}}(\operatorname{SL}_{n},\operatorname{End}((\mathbb{C}^{n})^{\otimes m}))\end{eqnarray}$$
the image of
 $\unicode[STIX]{x1D712}(X_{1}^{n}-e_{1}X_{1}^{n-1}+\cdots \pm e_{n-1}X_{1}\mp 1)$
is the map
$\unicode[STIX]{x1D712}(X_{1}^{n}-e_{1}X_{1}^{n-1}+\cdots \pm e_{n-1}X_{1}\mp 1)$
is the map
 $g\mapsto p(g)\otimes I\otimes \cdots \otimes I$
, where
$g\mapsto p(g)\otimes I\otimes \cdots \otimes I$
, where
![]() $p(y)$
is the characteristic polynomial of
$p(y)$
is the characteristic polynomial of
![]() $g$
. Thus, this relation holds by the Cayley–Hamilton theorem.
$g$
. Thus, this relation holds by the Cayley–Hamilton theorem.
On the other hand, when
![]() $k=n$
(assuming
$k=n$
(assuming
![]() $m>n$
), then the relation in (39) becomes just
$m>n$
), then the relation in (39) becomes just
 $e_{\operatorname{sgn}}(T_{1},\ldots ,T_{n})$
which, by Schur–Weyl duality, generates the kernel of
$e_{\operatorname{sgn}}(T_{1},\ldots ,T_{n})$
which, by Schur–Weyl duality, generates the kernel of
 $\mathbb{C}[S_{m}]\rightarrow \operatorname{End}((\mathbb{C}^{n})^{\otimes m})$
and thus also holds in
$\mathbb{C}[S_{m}]\rightarrow \operatorname{End}((\mathbb{C}^{n})^{\otimes m})$
and thus also holds in
 $\operatorname{Maps}_{\operatorname{SL}_{n}}(\operatorname{SL}_{n},\operatorname{End}((\mathbb{C}^{n})^{\otimes m}))$
.
$\operatorname{Maps}_{\operatorname{SL}_{n}}(\operatorname{SL}_{n},\operatorname{End}((\mathbb{C}^{n})^{\otimes m}))$
.
10.3 Over
 $\mathbb{C}(q)$
$\mathbb{C}(q)$
Define
 $e_{j}^{(i)}\in \widehat{{\mathcal{H}}}_{m}[q^{\pm }]$
recursively using
$e_{j}^{(i)}\in \widehat{{\mathcal{H}}}_{m}[q^{\pm }]$
recursively using
 $$\begin{eqnarray}e_{j}^{(i)}:=e_{j}^{(i-1)}+(q^{2}-1)[X_{i-1}e_{j-1}^{(i-1)}-X_{i-1}^{2}e_{j-2}^{(i-1)}+X_{i-1}^{3}e_{j-3}^{(i-1)}-\cdots \,].\end{eqnarray}$$
$$\begin{eqnarray}e_{j}^{(i)}:=e_{j}^{(i-1)}+(q^{2}-1)[X_{i-1}e_{j-1}^{(i-1)}-X_{i-1}^{2}e_{j-2}^{(i-1)}+X_{i-1}^{3}e_{j-3}^{(i-1)}-\cdots \,].\end{eqnarray}$$
This follows the definition of
 $e_{j}^{(i)}\in R_{n,[q^{\pm }]}^{m}$
from § 7.3.
$e_{j}^{(i)}\in R_{n,[q^{\pm }]}^{m}$
from § 7.3.
Conjecture 10.3. The kernel of
 $\unicode[STIX]{x1D712}:\widehat{{\mathcal{H}}}_{m}(q)\rightarrow \operatorname{End}_{\operatorname{Sym}(\text{}\underline{x})}(R_{n,(q)}^{m})$
is generated by
$\unicode[STIX]{x1D712}:\widehat{{\mathcal{H}}}_{m}(q)\rightarrow \operatorname{End}_{\operatorname{Sym}(\text{}\underline{x})}(R_{n,(q)}^{m})$
is generated by
 $$\begin{eqnarray}X_{i}^{n}-e_{1}^{(i)}X_{i}^{n-1}+e_{2}^{(i)}X_{i}^{n-2}-\cdots +(-1)^{n}e_{n}^{(i)}=0\end{eqnarray}$$
$$\begin{eqnarray}X_{i}^{n}-e_{1}^{(i)}X_{i}^{n-1}+e_{2}^{(i)}X_{i}^{n-2}-\cdots +(-1)^{n}e_{n}^{(i)}=0\end{eqnarray}$$
for
 $i=1,\ldots ,m$
.
$i=1,\ldots ,m$
.
Some remarks are in order. If one conjugates, for instance, the relation in (41) when
![]() $i=1$
by
$i=1$
by
![]() $T_{1}$
then one obtains the relation in (41) when
$T_{1}$
then one obtains the relation in (41) when
![]() $i=2$
plus an extra term. This extra term contains a factor of
$i=2$
plus an extra term. This extra term contains a factor of
![]() $q-1$
but after dividing by
$q-1$
but after dividing by
![]() $q-1$
gives us another relation. One can repeat this argument to get new relations, such as the ones in (39), but it seems only as long as
$q-1$
gives us another relation. One can repeat this argument to get new relations, such as the ones in (39), but it seems only as long as
![]() $q$
is not a root of unity.
$q$
is not a root of unity.
Thus, Conjecture 10.3 is not true over
![]() $\mathbb{C}[q^{\pm }]$
and, in particular, when
$\mathbb{C}[q^{\pm }]$
and, in particular, when
![]() $q=1$
. Moreover, although it might be tempting to only impose relation (41) when
$q=1$
. Moreover, although it might be tempting to only impose relation (41) when
![]() $i=1$
(like for the usual cyclotomic affine Hecke algebras), this is also incorrect.
$i=1$
(like for the usual cyclotomic affine Hecke algebras), this is also incorrect.
10.4 Over
 $\mathbb{C}[q^{\pm }]$
$\mathbb{C}[q^{\pm }]$
Conjecture 10.4. The kernel of
 $\unicode[STIX]{x1D712}:\widehat{{\mathcal{H}}}_{m}[q^{\pm }]\rightarrow \operatorname{End}_{\operatorname{Sym}(\text{}\underline{x})}(R_{n,[q^{\pm }]}^{m})$
is generated by
$\unicode[STIX]{x1D712}:\widehat{{\mathcal{H}}}_{m}[q^{\pm }]\rightarrow \operatorname{End}_{\operatorname{Sym}(\text{}\underline{x})}(R_{n,[q^{\pm }]}^{m})$
is generated by
 $$\begin{eqnarray}[k+1]!\cdot e_{\operatorname{sgn}}(T_{i},\ldots ,T_{i+k-1})(h_{n-k}-e_{1}^{(i)}h_{n-k-1}+\cdots +(-1)^{n-k}e_{n-k}^{(i)})\end{eqnarray}$$
$$\begin{eqnarray}[k+1]!\cdot e_{\operatorname{sgn}}(T_{i},\ldots ,T_{i+k-1})(h_{n-k}-e_{1}^{(i)}h_{n-k-1}+\cdots +(-1)^{n-k}e_{n-k}^{(i)})\end{eqnarray}$$
for
 $k=0,\ldots ,\min (n,m-1)$
and
$k=0,\ldots ,\min (n,m-1)$
and
 $i=1,\ldots ,m-k$
.
$i=1,\ldots ,m-k$
.
Remark 10.5. Here
 $[k+1]!\cdot e_{\operatorname{sgn}}(T_{i},\ldots ,T_{i+k-1})\in {\mathcal{H}}_{m}[q^{\pm }]$
is the sign quasi-idempotent inside the finite Hecke algebra where the sign representation corresponds to
$[k+1]!\cdot e_{\operatorname{sgn}}(T_{i},\ldots ,T_{i+k-1})\in {\mathcal{H}}_{m}[q^{\pm }]$
is the sign quasi-idempotent inside the finite Hecke algebra where the sign representation corresponds to
![]() $T_{i}$
acting by
$T_{i}$
acting by
![]() $-q^{-1}$
. Moreover,
$-q^{-1}$
. Moreover,
 $h_{j}=h_{j}(X_{i},\ldots ,X_{i+k})$
is the homogeneous symmetric function of degree
$h_{j}=h_{j}(X_{i},\ldots ,X_{i+k})$
is the homogeneous symmetric function of degree
![]() $j$
.
$j$
.
Let us explain why the term in (42) belongs to the kernel of
 $$\begin{eqnarray}\unicode[STIX]{x1D712}:\widehat{{\mathcal{H}}}_{m}[q^{\pm }]\rightarrow \operatorname{End}_{\operatorname{ Sym}(\text{}\underline{x})}(R_{n,[q^{\pm }]}^{m}).\end{eqnarray}$$
$$\begin{eqnarray}\unicode[STIX]{x1D712}:\widehat{{\mathcal{H}}}_{m}[q^{\pm }]\rightarrow \operatorname{End}_{\operatorname{ Sym}(\text{}\underline{x})}(R_{n,[q^{\pm }]}^{m}).\end{eqnarray}$$
The map
![]() $\unicode[STIX]{x1D712}$
can be factored as
$\unicode[STIX]{x1D712}$
can be factored as
 $$\begin{eqnarray}\widehat{{\mathcal{H}}}_{m}[q^{\pm }]\xrightarrow[{}]{\unicode[STIX]{x1D6FF}}K^{\operatorname{SL}_{n}\times \mathbb{C}^{\times }}(Z(1^{m},1^{m}))\xrightarrow[{}]{S}\operatorname{End}_{\operatorname{ Sym}(\text{}\underline{x})}(R_{n,[q^{\pm }]}^{m}).\end{eqnarray}$$
$$\begin{eqnarray}\widehat{{\mathcal{H}}}_{m}[q^{\pm }]\xrightarrow[{}]{\unicode[STIX]{x1D6FF}}K^{\operatorname{SL}_{n}\times \mathbb{C}^{\times }}(Z(1^{m},1^{m}))\xrightarrow[{}]{S}\operatorname{End}_{\operatorname{ Sym}(\text{}\underline{x})}(R_{n,[q^{\pm }]}^{m}).\end{eqnarray}$$
Thus it is enough to show that the image of (42) under
![]() $\unicode[STIX]{x1D6FF}$
is zero.
$\unicode[STIX]{x1D6FF}$
is zero.
In [Reference Cautis, Kamnitzer and LicataCKL10, Reference CautisCau05] we constructed a categorical
![]() $\mathfrak{s}\mathfrak{l}_{m}$
action on
$\mathfrak{s}\mathfrak{l}_{m}$
action on
 $\bigoplus _{\text{}\underline{k}}Y(\text{}\underline{k})$
where
$\bigoplus _{\text{}\underline{k}}Y(\text{}\underline{k})$
where
 $\text{}\underline{k}=(k_{1},\ldots ,k_{m})$
with
$\text{}\underline{k}=(k_{1},\ldots ,k_{m})$
with
 $\sum _{i}k_{i}=m$
. Consider the composition
$\sum _{i}k_{i}=m$
. Consider the composition
 $$\begin{eqnarray}E_{i+k-1}^{(k)}\ldots E_{i+1}^{(2)}E_{i}:K^{\operatorname{SL}_{n}\times \mathbb{C}^{\times }}(Y(1^{m}))\rightarrow K^{\operatorname{SL}_{n}\times \mathbb{C}^{\times }}(Y(1^{i-1},k+1,1^{m-k})).\end{eqnarray}$$
$$\begin{eqnarray}E_{i+k-1}^{(k)}\ldots E_{i+1}^{(2)}E_{i}:K^{\operatorname{SL}_{n}\times \mathbb{C}^{\times }}(Y(1^{m}))\rightarrow K^{\operatorname{SL}_{n}\times \mathbb{C}^{\times }}(Y(1^{i-1},k+1,1^{m-k})).\end{eqnarray}$$
On the one hand, it is fairly straightforward to compute this composition. More precisely, consider the subvariety
 $X_{i}^{k}(1^{m})\subset Y(1^{m})$
given by the locus where
$X_{i}^{k}(1^{m})\subset Y(1^{m})$
given by the locus where
 $zL_{i+k}\subset L_{i-1}$
and the associated diagram.
$zL_{i+k}\subset L_{i-1}$
and the associated diagram.

Here
![]() $i$
is inclusion and
$i$
is inclusion and
![]() $q$
the projection which forgets
$q$
the projection which forgets
 $L_{i},L_{i+1},\ldots ,L_{i+k-1}$
. Thus we can consider
$L_{i},L_{i+1},\ldots ,L_{i+k-1}$
. Thus we can consider
 $X_{i}^{k}(1^{m})\subset Y(1^{m})\times Y(1^{i-1},k+1,1^{m-k})$
via the embedding
$X_{i}^{k}(1^{m})\subset Y(1^{m})\times Y(1^{i-1},k+1,1^{m-k})$
via the embedding
![]() $i\times q$
. Then the functor in (43) is induced by the kernel
$i\times q$
. Then the functor in (43) is induced by the kernel
 $$\begin{eqnarray}[{\mathcal{P}}]:=[{\mathcal{O}}_{X_{i}^{k}(1^{m})}\otimes {\mathcal{L}}]\in K^{\operatorname{SL}_{n}\times \mathbb{C}^{\times }}(Y(1^{m})\times Y(1^{i-1},k+1,1^{m-k})),\end{eqnarray}$$
$$\begin{eqnarray}[{\mathcal{P}}]:=[{\mathcal{O}}_{X_{i}^{k}(1^{m})}\otimes {\mathcal{L}}]\in K^{\operatorname{SL}_{n}\times \mathbb{C}^{\times }}(Y(1^{m})\times Y(1^{i-1},k+1,1^{m-k})),\end{eqnarray}$$
where
![]() ${\mathcal{L}}$
is some line bundle (this line bundle can be explicitly identified but we do not need to know it precisely).
${\mathcal{L}}$
is some line bundle (this line bundle can be explicitly identified but we do not need to know it precisely).
On the other hand, we have
 $$\begin{eqnarray}\displaystyle K^{\operatorname{SL}_{n}\times \mathbb{C}^{\times }}(Y(1^{m})) & \cong & \displaystyle (\mathbb{C}^{n})^{\otimes (i-1)}\otimes (\mathbb{C}^{n})^{\otimes k}\otimes (\mathbb{C}^{n})^{\otimes (m-k)},\nonumber\\ \displaystyle K^{\operatorname{SL}_{n}\times \mathbb{C}^{\times }}(Y(1^{i-1},k+1,1^{m-k})) & \cong & \displaystyle (\mathbb{C}^{n})^{\otimes (i-1)}\otimes \bigwedge ^{k}(\mathbb{C}^{n})\otimes (\mathbb{C}^{n})^{\otimes (m-k)},\nonumber\end{eqnarray}$$
$$\begin{eqnarray}\displaystyle K^{\operatorname{SL}_{n}\times \mathbb{C}^{\times }}(Y(1^{m})) & \cong & \displaystyle (\mathbb{C}^{n})^{\otimes (i-1)}\otimes (\mathbb{C}^{n})^{\otimes k}\otimes (\mathbb{C}^{n})^{\otimes (m-k)},\nonumber\\ \displaystyle K^{\operatorname{SL}_{n}\times \mathbb{C}^{\times }}(Y(1^{i-1},k+1,1^{m-k})) & \cong & \displaystyle (\mathbb{C}^{n})^{\otimes (i-1)}\otimes \bigwedge ^{k}(\mathbb{C}^{n})\otimes (\mathbb{C}^{n})^{\otimes (m-k)},\nonumber\end{eqnarray}$$
and the main result of [Reference Cautis, Kamnitzer and MorrisonCKM14] implies that the composition in (43) is induced by the (quasi-)projection
 $(\mathbb{C}^{n})^{\otimes k}\rightarrow \bigwedge ^{k}(\mathbb{C}^{n})$
corresponding to the sign representation. It then follows that (up to a power of
$(\mathbb{C}^{n})^{\otimes k}\rightarrow \bigwedge ^{k}(\mathbb{C}^{n})$
corresponding to the sign representation. It then follows that (up to a power of
![]() $q$
)
$q$
)
 $$\begin{eqnarray}[{\mathcal{P}}^{L}]\ast [{\mathcal{P}}]\cong \unicode[STIX]{x1D6FF}([k+1]!\cdot e_{\operatorname{ sgn}}(T_{i},\ldots ,T_{i+k-1}))\in K^{\operatorname{SL}_{n}\times \mathbb{C}^{\times }}(Y(1^{m})\times Y(1^{m}))\end{eqnarray}$$
$$\begin{eqnarray}[{\mathcal{P}}^{L}]\ast [{\mathcal{P}}]\cong \unicode[STIX]{x1D6FF}([k+1]!\cdot e_{\operatorname{ sgn}}(T_{i},\ldots ,T_{i+k-1}))\in K^{\operatorname{SL}_{n}\times \mathbb{C}^{\times }}(Y(1^{m})\times Y(1^{m}))\end{eqnarray}$$
where
![]() ${\mathcal{P}}^{L}$
denotes the left adjoint of
${\mathcal{P}}^{L}$
denotes the left adjoint of
![]() ${\mathcal{P}}$
.
${\mathcal{P}}$
.
This gives a geometric interpretation of
 $\unicode[STIX]{x1D6FF}([k+1]!\cdot e_{\operatorname{sgn}})$
. Thus relation (42) follows if we can show that
$\unicode[STIX]{x1D6FF}([k+1]!\cdot e_{\operatorname{sgn}})$
. Thus relation (42) follows if we can show that
 $$\begin{eqnarray}i^{\ast }\unicode[STIX]{x1D6FF}(h_{n-k}-e_{1}^{(i)}h_{n-k-1}+\cdots +(-1)^{n-k}e_{n-k}^{(i)})=0\end{eqnarray}$$
$$\begin{eqnarray}i^{\ast }\unicode[STIX]{x1D6FF}(h_{n-k}-e_{1}^{(i)}h_{n-k-1}+\cdots +(-1)^{n-k}e_{n-k}^{(i)})=0\end{eqnarray}$$
inside
 $K^{\operatorname{SL}_{n}\times \mathbb{C}^{\times }}(X_{i}^{k}(1^{m}))$
. Using the exact sequence
$K^{\operatorname{SL}_{n}\times \mathbb{C}^{\times }}(X_{i}^{k}(1^{m}))$
. Using the exact sequence
 $$\begin{eqnarray}0\rightarrow L_{i+k}/L_{i-1}\rightarrow z^{-1}L_{i-1}/L_{i-1}\rightarrow z^{-1}L_{i-1}/L_{i+k}\rightarrow 0\end{eqnarray}$$
$$\begin{eqnarray}0\rightarrow L_{i+k}/L_{i-1}\rightarrow z^{-1}L_{i-1}/L_{i-1}\rightarrow z^{-1}L_{i-1}/L_{i+k}\rightarrow 0\end{eqnarray}$$
we see that
 $[(z^{-1}L_{i-1}/L_{i+k})^{\vee }]=e_{1}^{(i)}-[(L_{i+k}/L_{i-1})^{\vee }]$
. On the other hand,
$[(z^{-1}L_{i-1}/L_{i+k})^{\vee }]=e_{1}^{(i)}-[(L_{i+k}/L_{i-1})^{\vee }]$
. On the other hand,
 $$\begin{eqnarray}\bigwedge ^{n-k}(z^{-1}L_{i-1}/L_{i+k})^{\vee }=0,\end{eqnarray}$$
$$\begin{eqnarray}\bigwedge ^{n-k}(z^{-1}L_{i-1}/L_{i+k})^{\vee }=0,\end{eqnarray}$$
since
 $\dim (z^{-1}L_{i-1}/L_{i+k})=n-k-1$
. Moreover,
$\dim (z^{-1}L_{i-1}/L_{i+k})=n-k-1$
. Moreover,
 $[(L_{i+k}/L_{i-1})^{\vee }]=X_{i}+\cdots +X_{i+k}$
. Then (45) follows from the general fact that
$[(L_{i+k}/L_{i-1})^{\vee }]=X_{i}+\cdots +X_{i+k}$
. Then (45) follows from the general fact that
 $$\begin{eqnarray}\bigwedge ^{r}(A-B)=\bigwedge ^{r}(A)-\bigwedge ^{r-1}(A)\cdot B+\bigwedge ^{r-2}(A)\cdot \operatorname{Sym}^{2}(B)-\bigwedge ^{r-3}(A)\cdot \operatorname{Sym}^{3}(B)+\cdots\end{eqnarray}$$
$$\begin{eqnarray}\bigwedge ^{r}(A-B)=\bigwedge ^{r}(A)-\bigwedge ^{r-1}(A)\cdot B+\bigwedge ^{r-2}(A)\cdot \operatorname{Sym}^{2}(B)-\bigwedge ^{r-3}(A)\cdot \operatorname{Sym}^{3}(B)+\cdots\end{eqnarray}$$
and that
 $\operatorname{Sym}^{j}(X_{i}+\cdots +X_{i+k})=h_{j}$
.
$\operatorname{Sym}^{j}(X_{i}+\cdots +X_{i+k})=h_{j}$
.
11 Comparison with the Steinberg variety
Denote by
![]() ${\mathcal{B}}$
the full flag variety of
${\mathcal{B}}$
the full flag variety of
![]() $\operatorname{SL}_{n}$
and
$\operatorname{SL}_{n}$
and
![]() $Z$
the associated Steinberg variety. Since the Steinberg variety is the fibre product of
$Z$
the associated Steinberg variety. Since the Steinberg variety is the fibre product of
![]() $T^{\ast }{\mathcal{B}}$
with itself over its affinization, its equivariant K-theory
$T^{\ast }{\mathcal{B}}$
with itself over its affinization, its equivariant K-theory
 $K^{\operatorname{SL}_{n}\times \mathbb{C}^{\times }}(Z)$
is equipped with a convolution product. The following result is due to Ginzburg [Reference Chriss and GinzburgCG97, Theorem 7.2.5] and Kazhdan and Lusztig [Reference Kazhdan and LusztigKL87].
$K^{\operatorname{SL}_{n}\times \mathbb{C}^{\times }}(Z)$
is equipped with a convolution product. The following result is due to Ginzburg [Reference Chriss and GinzburgCG97, Theorem 7.2.5] and Kazhdan and Lusztig [Reference Kazhdan and LusztigKL87].
Proposition 11.1. There exists an isomorphism of algebras between
 $K^{\operatorname{SL}_{n}\times \mathbb{C}^{\times }}(Z)$
and the affine Hecke algebra
$K^{\operatorname{SL}_{n}\times \mathbb{C}^{\times }}(Z)$
and the affine Hecke algebra
![]() $\widehat{\mathbb{H}}_{n}[q^{\pm }]$
.
$\widehat{\mathbb{H}}_{n}[q^{\pm }]$
.
In the result above,
![]() $\widehat{\mathbb{H}}_{n}[q^{\pm }]$
denotes the affine Hecke algebra generated over
$\widehat{\mathbb{H}}_{n}[q^{\pm }]$
denotes the affine Hecke algebra generated over
![]() $\mathbb{C}[q^{\pm }]$
by the
$\mathbb{C}[q^{\pm }]$
by the
![]() $T_{i}$
generators and
$T_{i}$
generators and
![]() $X_{i}$
generators with the usual relations but without the
$X_{i}$
generators with the usual relations but without the
![]() $e_{i}$
generators. In other words,
$e_{i}$
generators. In other words,
 $\widehat{\mathbb{H}}_{n}[q^{\pm }]=\widehat{{\mathcal{H}}}_{n}[q^{\pm }]\otimes _{E}\mathbb{C}$
. We would like to explain now the relation between Proposition 11.1 and our results.
$\widehat{\mathbb{H}}_{n}[q^{\pm }]=\widehat{{\mathcal{H}}}_{n}[q^{\pm }]\otimes _{E}\mathbb{C}$
. We would like to explain now the relation between Proposition 11.1 and our results.
We will need to consider only the special case
![]() $m=n$
. In this case we have varieties
$m=n$
. In this case we have varieties
![]() $Y(1^{n})$
and
$Y(1^{n})$
and
 $Z(1^{n},1^{n})$
.
$Z(1^{n},1^{n})$
.
Lemma 11.2. We have natural
 $\operatorname{SL}_{n}\times \mathbb{C}^{\times }$
-equivariant open embeddings
$\operatorname{SL}_{n}\times \mathbb{C}^{\times }$
-equivariant open embeddings
 $i:T^{\ast }{\mathcal{B}}\rightarrow Y(1^{n})$
and
$i:T^{\ast }{\mathcal{B}}\rightarrow Y(1^{n})$
and
 $j:Z\rightarrow Z(1^{n},1^{n})$
.
$j:Z\rightarrow Z(1^{n},1^{n})$
.
Proof. Let
 $\mathbb{C}^{n}=z^{-1}L_{0}/L_{0}$
and consider the space
$\mathbb{C}^{n}=z^{-1}L_{0}/L_{0}$
and consider the space
 $\mathbb{C}^{n^{2}}=\mathbb{C}^{n}\otimes \text{span}\{z^{-1},\ldots ,z^{-n}\}$
. Then
$\mathbb{C}^{n^{2}}=\mathbb{C}^{n}\otimes \text{span}\{z^{-1},\ldots ,z^{-n}\}$
. Then
 $$\begin{eqnarray}Y(1^{n})=\{L_{0}\subset \cdots \subset L_{n}\subset \mathbb{C}^{n^{2}}:\dim (L_{i}/L_{i-1})=1,zL_{i}\subset L_{i-1}\}.\end{eqnarray}$$
$$\begin{eqnarray}Y(1^{n})=\{L_{0}\subset \cdots \subset L_{n}\subset \mathbb{C}^{n^{2}}:\dim (L_{i}/L_{i-1})=1,zL_{i}\subset L_{i-1}\}.\end{eqnarray}$$
Now denote by
 $P:\mathbb{C}^{n^{2}}\rightarrow \mathbb{C}^{n}$
the projection which takes
$P:\mathbb{C}^{n^{2}}\rightarrow \mathbb{C}^{n}$
the projection which takes
 $\mathbb{C}^{n}\otimes z^{-i}$
to zero if
$\mathbb{C}^{n}\otimes z^{-i}$
to zero if
![]() $i>1$
and onto
$i>1$
and onto
![]() $\mathbb{C}^{n}$
if
$\mathbb{C}^{n}$
if
![]() $i=1$
. Consider inside
$i=1$
. Consider inside
![]() $Y(1^{n})$
the open locus
$Y(1^{n})$
the open locus
![]() $U$
consisting of
$U$
consisting of
![]() $L_{\bullet }$
such that
$L_{\bullet }$
such that
 $P(L_{n})=\mathbb{C}^{n}$
.
$P(L_{n})=\mathbb{C}^{n}$
.
On
![]() $U$
we have an isomorphism
$U$
we have an isomorphism
 $P:L_{n}\xrightarrow[{}]{{\sim}}\mathbb{C}^{n}$
. Using this isomorphism we can transfer the map
$P:L_{n}\xrightarrow[{}]{{\sim}}\mathbb{C}^{n}$
. Using this isomorphism we can transfer the map
![]() $z$
to a nilpotent endomorphism of
$z$
to a nilpotent endomorphism of
![]() $\mathbb{C}^{n}$
and we can transfer
$\mathbb{C}^{n}$
and we can transfer
 $L_{1},\ldots ,L_{n-1}$
to a flag in
$L_{1},\ldots ,L_{n-1}$
to a flag in
![]() $\mathbb{C}^{n}$
. Thus we get a map
$\mathbb{C}^{n}$
. Thus we get a map
 $U\rightarrow T^{\ast }{\mathcal{B}}$
. One can check that this map is actually an isomorphism. This idea is originally due to Ngo [Reference NgoNgo99] and it is also a special case of [Reference Mirković and VybornovMV03, Theorem 3.2].
$U\rightarrow T^{\ast }{\mathcal{B}}$
. One can check that this map is actually an isomorphism. This idea is originally due to Ngo [Reference NgoNgo99] and it is also a special case of [Reference Mirković and VybornovMV03, Theorem 3.2].
Under this isomorphism the map
 $Y(1^{m})\rightarrow Gr$
which takes
$Y(1^{m})\rightarrow Gr$
which takes
![]() $L_{\bullet }$
to
$L_{\bullet }$
to
![]() $L_{n}$
corresponds to the affinization map of
$L_{n}$
corresponds to the affinization map of
 $T^{\ast }{\mathcal{B}}\rightarrow {\mathcal{N}}$
to the nilpotent cone. It follows that
$T^{\ast }{\mathcal{B}}\rightarrow {\mathcal{N}}$
to the nilpotent cone. It follows that
 $Z=T^{\ast }{\mathcal{B}}\times _{{\mathcal{N}}}T^{\ast }{\mathcal{B}}$
naturally embeds into
$Z=T^{\ast }{\mathcal{B}}\times _{{\mathcal{N}}}T^{\ast }{\mathcal{B}}$
naturally embeds into
 $Z(1^{n},1^{n})=Y(1^{n})\times _{Gr}Y(1^{n})$
.◻
$Z(1^{n},1^{n})=Y(1^{n})\times _{Gr}Y(1^{n})$
.◻
Thus we have the following maps:
 $$\begin{eqnarray}\widehat{{\mathcal{H}}}_{n}[q^{\pm }]\rightarrow K^{\operatorname{SL}_{n}\times \mathbb{C}^{\times }}(Z(1^{n},1^{n}))=\operatorname{End}_{{\mathcal{A}}{\mathcal{S}}p_{n}[q^{\pm }]}(1^{n})\xrightarrow[{}]{j^{\ast }}K^{\operatorname{SL}_{n}\times \mathbb{C}^{\times }}(Z)\cong \widehat{\mathbb{H}}_{n}[q^{\pm }],\end{eqnarray}$$
$$\begin{eqnarray}\widehat{{\mathcal{H}}}_{n}[q^{\pm }]\rightarrow K^{\operatorname{SL}_{n}\times \mathbb{C}^{\times }}(Z(1^{n},1^{n}))=\operatorname{End}_{{\mathcal{A}}{\mathcal{S}}p_{n}[q^{\pm }]}(1^{n})\xrightarrow[{}]{j^{\ast }}K^{\operatorname{SL}_{n}\times \mathbb{C}^{\times }}(Z)\cong \widehat{\mathbb{H}}_{n}[q^{\pm }],\end{eqnarray}$$
where
![]() $j^{\ast }$
denotes the restriction on K-theory using
$j^{\ast }$
denotes the restriction on K-theory using
![]() $j$
.
$j$
.
Proposition 11.3. The composition map
 $\widehat{{\mathcal{H}}}_{n}[q^{\pm }]\rightarrow \widehat{\mathbb{H}}_{n}[q^{\pm }]$
sends
$\widehat{{\mathcal{H}}}_{n}[q^{\pm }]\rightarrow \widehat{\mathbb{H}}_{n}[q^{\pm }]$
sends
 $T_{i}\mapsto T_{i},X_{i}\mapsto X_{i}$
and
$T_{i}\mapsto T_{i},X_{i}\mapsto X_{i}$
and
 $$\begin{eqnarray}e_{i}^{(j)}\mapsto e_{i}(q^{2}X_{1},q^{2}X_{2},\ldots ,q^{2}X_{j-1},X_{j},\ldots ,X_{n})\end{eqnarray}$$
$$\begin{eqnarray}e_{i}^{(j)}\mapsto e_{i}(q^{2}X_{1},q^{2}X_{2},\ldots ,q^{2}X_{j-1},X_{j},\ldots ,X_{n})\end{eqnarray}$$
where the latter are elementary symmetric functions in the variables indicated.
Proof. Suppose
 ${\mathcal{B}}=\{0=V_{0}\subset V_{1}\subset \cdots \subset V_{n}=\mathbb{C}^{n}\}$
. Then it is clear
${\mathcal{B}}=\{0=V_{0}\subset V_{1}\subset \cdots \subset V_{n}=\mathbb{C}^{n}\}$
. Then it is clear
 $L_{i}/L_{i-1}$
is mapped to the natural bundle
$L_{i}/L_{i-1}$
is mapped to the natural bundle
![]() $V_{i}/V_{i-1}$
on
$V_{i}/V_{i-1}$
on
![]() $T^{\ast }{\mathcal{B}}$
which explains why
$T^{\ast }{\mathcal{B}}$
which explains why
 $X_{i}\mapsto X_{i}$
.
$X_{i}\mapsto X_{i}$
.
Next, notice that
![]() $T_{i}$
can be identified on the one hand with the structure sheaf of the fibre product
$T_{i}$
can be identified on the one hand with the structure sheaf of the fibre product
 $T^{\ast }{\mathcal{B}}\times _{(T^{\ast }{\mathcal{B}})_{i}}T^{\ast }{\mathcal{B}}$
where
$T^{\ast }{\mathcal{B}}\times _{(T^{\ast }{\mathcal{B}})_{i}}T^{\ast }{\mathcal{B}}$
where
![]() $(T^{\ast }{\mathcal{B}})_{i}$
is obtained from
$(T^{\ast }{\mathcal{B}})_{i}$
is obtained from
![]() $T^{\ast }{\mathcal{B}}$
by forgetting
$T^{\ast }{\mathcal{B}}$
by forgetting
![]() $V_{i}$
. On the other hand the image of
$V_{i}$
. On the other hand the image of
![]() $T_{i}$
in
$T_{i}$
in
 $K(Z(1^{n},1^{n}))$
is identified with the structure sheaf of
$K(Z(1^{n},1^{n}))$
is identified with the structure sheaf of
 $Y(1^{n})\times _{Y(1^{n})_{i}}Y(1^{n})$
where
$Y(1^{n})\times _{Y(1^{n})_{i}}Y(1^{n})$
where
![]() $Y(1^{n})_{i}$
is obtained from
$Y(1^{n})_{i}$
is obtained from
![]() $Y(1^{n})$
by forgetting
$Y(1^{n})$
by forgetting
![]() $L_{i}$
. It is then easy to check that
$L_{i}$
. It is then easy to check that
 $$\begin{eqnarray}j^{-1}((1^{n})\times _{Y(1^{n})_{i}}Y(1^{n}))=T^{\ast }{\mathcal{B}}\times _{(T^{\ast }{\mathcal{B}})_{i}}T^{\ast }{\mathcal{B}}.\end{eqnarray}$$
$$\begin{eqnarray}j^{-1}((1^{n})\times _{Y(1^{n})_{i}}Y(1^{n}))=T^{\ast }{\mathcal{B}}\times _{(T^{\ast }{\mathcal{B}})_{i}}T^{\ast }{\mathcal{B}}.\end{eqnarray}$$
This explains why
 $T_{i}\mapsto T_{i}$
.
$T_{i}\mapsto T_{i}$
.
Finally, on
![]() $T^{\ast }{\mathcal{B}}$
we have
$T^{\ast }{\mathcal{B}}$
we have
 $\sum _{i}X_{i}=[\mathbb{C}^{n}]^{\vee }$
and more generally
$\sum _{i}X_{i}=[\mathbb{C}^{n}]^{\vee }$
and more generally
 $e_{i}(X_{1},\ldots ,X_{n})=[\bigwedge ^{i}(\mathbb{C}^{n})^{\vee }]$
. This shows that
$e_{i}(X_{1},\ldots ,X_{n})=[\bigwedge ^{i}(\mathbb{C}^{n})^{\vee }]$
. This shows that
 $e_{i}\mapsto e_{i}(X_{1},\ldots ,X_{n})$
. The general expression for the image of
$e_{i}\mapsto e_{i}(X_{1},\ldots ,X_{n})$
. The general expression for the image of
![]() $e_{i}^{(j)}$
is then a non-trivial but elementary calculation using the recursive relations
$e_{i}^{(j)}$
is then a non-trivial but elementary calculation using the recursive relations
 $$\begin{eqnarray}e_{j}^{(i+1)}+X_{i}e_{j-1}^{(i+1)}=e_{j}^{(i)}+q^{2}X_{i}e_{j-1}^{(i)}\end{eqnarray}$$
$$\begin{eqnarray}e_{j}^{(i+1)}+X_{i}e_{j-1}^{(i+1)}=e_{j}^{(i)}+q^{2}X_{i}e_{j-1}^{(i)}\end{eqnarray}$$
It is worth noting what happens to all the conjectured relations (42). They are all mapped to zero since
 $$\begin{eqnarray}h_{n-k}-e_{1}^{(i)}h_{n-k-1}+e_{2}^{(i)}h_{n-k-2}-\cdots +(-1)^{n-k}e_{n-k}^{(i)}=0\end{eqnarray}$$
$$\begin{eqnarray}h_{n-k}-e_{1}^{(i)}h_{n-k-1}+e_{2}^{(i)}h_{n-k-2}-\cdots +(-1)^{n-k}e_{n-k}^{(i)}=0\end{eqnarray}$$
by the standard relations between homogeneous and elementary symmetric functions. Thus Conjecture 10.4 recovers Proposition 11.1.
Remark 11.4. Note that in relation (46) the
![]() $e_{i}$
are functions of
$e_{i}$
are functions of
 $X_{1},\ldots ,X_{n}$
while the
$X_{1},\ldots ,X_{n}$
while the
![]() $h_{i}$
are homogeneous symmetric functions in
$h_{i}$
are homogeneous symmetric functions in
 $X_{i},\ldots ,X_{k+i}$
.
$X_{i},\ldots ,X_{k+i}$
.
Acknowledgements
We would like to thank Pierre Baumann, David Ben-Zvi, Alexander Braverman, Adrien Brochier, Roman Bezrukavnikov, Chris Dodd, Ben Elias, Pavel Etingof, Michael Finkelberg, Dennis Gaitsgory, David Jordan, Chia-Cheng Liu, Peter McNamara, Scott Morrison, Hoel Queffelec, David Rose, Peter Samuelson, Xinwen Zhu for helpful discussions. We particularly thank Michael Finkelberg for helping us to formulate the main conjecture. We also thank the anonymous referee for many helpful suggestions. The first author was supported by NSERC and thanks MSRI for their support and hospitality. The second author was supported by NSERC, Sloan Foundation, Simons Foundation, and SwissMAP, and he thanks the geometry group at EPFL for their hospitality.