1. Introduction
A liquid wetting the surface of a solid is a common observation in daily experiences. A classical example is that of raindrops hitting a glass window and falling along its surface, leaving trails of water. The physics underlying this supposedly simple situation is in fact quite rich as the properties of all the involved media matter, including those of the surrounding atmosphere. Moreover, length scales from the molecular up to the millimetre range must be considered, leading to a high level of theoretical complexity. A drop of simple fluid spreading onto a solid substrate is subjected to three competing physical mechanisms, namely gravity, capillarity and viscosity (see e.g. Bonn et al. Reference Bonn, Eggers, Indekeu, Meunier and Rolley2009). The shape and dynamics of the droplet depend on the length scale at which they are analysed with respect to the capillary length ![]() $\ell _c=(\gamma /\rho g)^{1/2}$, with
$\ell _c=(\gamma /\rho g)^{1/2}$, with ![]() $\gamma$ the surface tension of the solid,
$\gamma$ the surface tension of the solid, ![]() $\rho$ its density, and
$\rho$ its density, and ![]() $g$ the acceleration due to gravity. If we consider droplets with radius
$g$ the acceleration due to gravity. If we consider droplets with radius ![]() $R\gg \ell _c$, then the balance between gravity and capillarity controls the shape and dynamics at length scales comparable to
$R\gg \ell _c$, then the balance between gravity and capillarity controls the shape and dynamics at length scales comparable to ![]() $R$. At microscopic scales near the triple-phase contact line, the balance involves instead viscosity and capillarity. As the height diminishes at the approach of the contact line, viscous stresses diverge when using the classical no-slip boundary condition on the substrate. A variety of models have been proposed to regularise this non-integrable singularity. A common way to circumvent this divergence issue has been to replace the no-slip boundary condition by a Navier slip condition, i.e. to introduce a microscopic cut-off length scale
$R$. At microscopic scales near the triple-phase contact line, the balance involves instead viscosity and capillarity. As the height diminishes at the approach of the contact line, viscous stresses diverge when using the classical no-slip boundary condition on the substrate. A variety of models have been proposed to regularise this non-integrable singularity. A common way to circumvent this divergence issue has been to replace the no-slip boundary condition by a Navier slip condition, i.e. to introduce a microscopic cut-off length scale ![]() $\lambda$ in the continuum modelling (Huh & Scriven Reference Huh and Scriven1971; Dussan V. & Davis Reference Dussan V. and Davis1974). For the intermediate scales, gravity and viscosity as well as capillarity participate into the dynamics of the drop.
$\lambda$ in the continuum modelling (Huh & Scriven Reference Huh and Scriven1971; Dussan V. & Davis Reference Dussan V. and Davis1974). For the intermediate scales, gravity and viscosity as well as capillarity participate into the dynamics of the drop.
The above picture becomes more involved when the spreading fluid is complex, such as a polymer solution (Lee & Müller-Plathe Reference Lee and Müller-Plathe2022), a polymeric melt (Seemann et al. Reference Seemann, Herminghaus, Neto, Schlagowski, Podzimek, Konrad, Mantz and Jacobs2005) or a viscoplastic material (Spaid & Homsy Reference Spaid and Homsy1996). Such fluids can have intrinsic time scales (e.g. relaxation, agitation) or characteristic length scales (e.g. particle size, persistence length) that need to be accounted for in the spreading dynamics. The present work focuses on the spreading of dense granular suspensions of large spherical particles that do not experience Brownian motion. These particulate systems are characterised by an additional length scale, the particle size, that must be addressed in the multiscale description of an advancing contact line. The interplay of the vanishing height of the flow and the finite size of the particles should control the distance at which the particles can approach the contact line. This view has been confirmed in our previous study of the motion of the triple-phase contact line surrounding a droplet of monomodal granular suspension (Zhao et al. Reference Zhao, Oléron, Pelosse, Limat, Guazzelli and Roché2020). Interestingly, the relation between the dynamic contact angle – i.e. the angle between the liquid–gas interface and the solid–liquid interface measured in the droplet – and the speed of the contact line happens to be similar to that found for a simple liquid, known as the Cox–Voinov law (Voinov Reference Voinov1976; Cox Reference Cox1986). In dimensionless form, this speed was reported in terms of the capillary number ![]() $Ca=\eta U/\gamma$, measuring the relative effect of viscous to surface tension forces, where
$Ca=\eta U/\gamma$, measuring the relative effect of viscous to surface tension forces, where ![]() $\eta$ is the viscosity of the liquid, and
$\eta$ is the viscosity of the liquid, and ![]() $U$ is the velocity of the contact line. We found that the viscosity involved in this capillary number differed from the widely studied bulk viscosity of suspensions as it depended on particle diameter
$U$ is the velocity of the contact line. We found that the viscosity involved in this capillary number differed from the widely studied bulk viscosity of suspensions as it depended on particle diameter ![]() $d$ in addition to particle volume fraction
$d$ in addition to particle volume fraction ![]() $\phi$. This observation resulted from the aforementioned ability of the particles to approach the contact line closely enough to affect dissipation. In particular, we showed that the apparent viscosity reduced to the viscosity of the suspending fluid when the particle size became larger than approximately
$\phi$. This observation resulted from the aforementioned ability of the particles to approach the contact line closely enough to affect dissipation. In particular, we showed that the apparent viscosity reduced to the viscosity of the suspending fluid when the particle size became larger than approximately ![]() $100\,\mathrm {\mu }$m. This study suggests that a granular suspension may be an interesting system for the study of wetting as the discrete nature of this complex fluid can be used to probe the size of the domain in which the Cox–Voinov relation is a valid description of the relation between the dynamic contact angle and the velocity of the contact line.
$100\,\mathrm {\mu }$m. This study suggests that a granular suspension may be an interesting system for the study of wetting as the discrete nature of this complex fluid can be used to probe the size of the domain in which the Cox–Voinov relation is a valid description of the relation between the dynamic contact angle and the velocity of the contact line.
Another feature specific to the spreading of a granular suspension is that there is a self-organisation of the advancing front rows of particles near the rim of the drop (Zhao et al. Reference Zhao, Oléron, Pelosse, Limat, Guazzelli and Roché2020). To give a full picture, the close vicinity of the contact line is a region devoid of particles. Behind this particle-depleted region, a few layers of crystallised beads are observed. As the height increases further, the particles switch from a crystal-like to a disordered structure. This ordering is seen particularly for dense suspensions, e.g. for packing fractions ![]() $\phi$ of 40 % or above. Confinement by the free interface seems to be responsible for this observed organisation. However, the role of this ordered particle phase in energy dissipation and its effects on the dynamics of spreading are still open problems that require scrutiny. A simple model that matches the shape of the droplet in the depleted region to that of a particle-rich region with no constraint on the ordering of particles fails to describe the relation between contact angle and velocity (Zhao et al. Reference Zhao, Oléron, Pelosse, Limat, Guazzelli and Roché2020).
$\phi$ of 40 % or above. Confinement by the free interface seems to be responsible for this observed organisation. However, the role of this ordered particle phase in energy dissipation and its effects on the dynamics of spreading are still open problems that require scrutiny. A simple model that matches the shape of the droplet in the depleted region to that of a particle-rich region with no constraint on the ordering of particles fails to describe the relation between contact angle and velocity (Zhao et al. Reference Zhao, Oléron, Pelosse, Limat, Guazzelli and Roché2020).
Particles near a receding contact line have been studied experimentally when a plate is withdrawn from a bath of non-Brownian suspension. In this configuration, named dip-coating, the key result is that the plate can be coated by particles when the entrained film is thicker than the particle diameter. More precisely, increasing the withdrawal speed leads to different regimes of coating, going from a film devoid of particles to a heterogeneous monolayer of particles, and finally to a thick film of suspension entrained by the plate (Gans et al. Reference Gans, Dressaire, Colnet, Saingier, Bazant and Sauret2019; Palma & Lhuissier Reference Palma and Lhuissier2019). When the suspension contains two sizes of particles, the small particles are first entrained on the plate to form a heterogeneous monolayer, and the large particles begin to be entrained only with a further increase in withdrawal speed (Jeong et al. Reference Jeong, Lee, Thiévenaz, Bazant and Sauret2022). In the heterogeneous regime, confined particles gather in clusters without clear ordering, in contrast to the highly structured phase observed near the advancing contact line during the spreading of suspension drops on a solid substrate (Zhao et al. Reference Zhao, Oléron, Pelosse, Limat, Guazzelli and Roché2020).
In this work, we examine the advancing contact line of a dense granular suspension, with the aim of clarifying the origin of the difference between bulk viscosity and its counterpart extracted from wetting experiments. In § 2, we discuss the range of interface heights for which we should expect the viscous–capillary balance at play in the Cox–Voinov relation to be valid. The materials and methods used in the experiments are described in § 3. In § 4, we test experimentally the predictions of § 2 with simple fluids. Then we resort to the discrete nature of the particles in a suspension to probe dissipation in the vicinity of the contact line. These experiments are another test of the outcomes of § 2. Results obtained for monodisperse and bidisperse suspensions consisting of different particle combinations are presented in § 5. While bidisperse suspensions seem to be a more complicated system, they offer the possibility to use two different sizes for scrutinising dissipation. We discuss our findings and provide concluding remarks in § 6.
2. Elements of the wetting theory
2.1. General framework
The classical situation of a fluid droplet of radius ![]() $R$ and central height
$R$ and central height ![]() $h_{0}$ that spreads onto the surface of a rigid substrate is depicted in figure 1. The fluid has dynamic viscosity
$h_{0}$ that spreads onto the surface of a rigid substrate is depicted in figure 1. The fluid has dynamic viscosity ![]() $\eta$, density
$\eta$, density ![]() $\rho$, and surface tension
$\rho$, and surface tension ![]() $\gamma$. In most situations, inertia is negligible, i.e. the Reynolds number is small,
$\gamma$. In most situations, inertia is negligible, i.e. the Reynolds number is small, ![]() $Re=\rho Uh_0/\eta \ll 1$, where
$Re=\rho Uh_0/\eta \ll 1$, where ![]() $U$ is the characteristic spreading velocity. Since
$U$ is the characteristic spreading velocity. Since ![]() $h_0\ll R$, the lubrication approximation can be applied. As the flow is axisymmetric, we use cylindrical coordinates with the
$h_0\ll R$, the lubrication approximation can be applied. As the flow is axisymmetric, we use cylindrical coordinates with the ![]() $z$-axis being the axis of symmetry. Under these assumptions, the height of the air–liquid interface,
$z$-axis being the axis of symmetry. Under these assumptions, the height of the air–liquid interface, ![]() $h(r)$, is a solution of the free-surface thin-film equation
$h(r)$, is a solution of the free-surface thin-film equation
where ![]() $g$ is the gravitational acceleration (Hocking Reference Hocking1981, Reference Hocking1983; Savva & Kalliadasis Reference Savva and Kalliadasis2012). A particular feature of (2.1) is that a characteristic length scale,
$g$ is the gravitational acceleration (Hocking Reference Hocking1981, Reference Hocking1983; Savva & Kalliadasis Reference Savva and Kalliadasis2012). A particular feature of (2.1) is that a characteristic length scale, ![]() $\lambda$, has been introduced to relax the no-slip boundary condition at the line of contact between the droplet, the substrate and the surrounding gas (Huh & Scriven Reference Huh and Scriven1971; Dussan V. & Davis Reference Dussan V. and Davis1974). In the context of the present work, we grant
$\lambda$, has been introduced to relax the no-slip boundary condition at the line of contact between the droplet, the substrate and the surrounding gas (Huh & Scriven Reference Huh and Scriven1971; Dussan V. & Davis Reference Dussan V. and Davis1974). In the context of the present work, we grant ![]() $\lambda$ its usual role of a slip length, and we take it to be of the order of the size of a few nanometres, comparable to that of a molecule of the liquid.
$\lambda$ its usual role of a slip length, and we take it to be of the order of the size of a few nanometres, comparable to that of a molecule of the liquid.
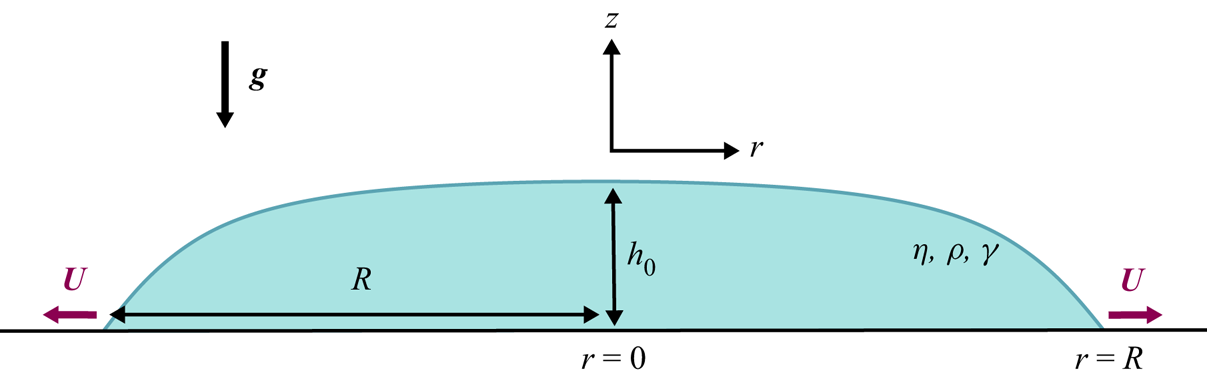
Figure 1. Sketch of a fluid droplet spreading on a rigid substrate.
The resolution of (2.1) requires appropriate boundary conditions to be specified as
where ![]() $V_0$ is the volume of the droplet, and
$V_0$ is the volume of the droplet, and ![]() $\theta _m$ is the microscopic contact angle.
$\theta _m$ is the microscopic contact angle.
Rather than providing detailed derivations of the solutions of (2.1) with these boundary conditions (2.2a–c) (see e.g. Hocking Reference Hocking1983; Cox Reference Cox1986; Savva & Kalliadasis Reference Savva and Kalliadasis2009; Sibley, Nold & Kalliadasis Reference Sibley, Nold and Kalliadasis2015), we give some insight into the different length scales involved in the problem described by (2.1) with (2.2a–c). Besides the slip length ![]() $\lambda$, we also identify the capillary length
$\lambda$, we also identify the capillary length ![]() $\ell _{c}=(\gamma /\rho g)^{1/2}$, for which gravitational forces balance capillary forces, and the radius of a sphere having the same volume
$\ell _{c}=(\gamma /\rho g)^{1/2}$, for which gravitational forces balance capillary forces, and the radius of a sphere having the same volume ![]() ${V}_0$ as that of the droplet,
${V}_0$ as that of the droplet, ![]() $R_0=(3{V}_0/4{\rm \pi} )^{1/3}$. In experiments, it usually happens that
$R_0=(3{V}_0/4{\rm \pi} )^{1/3}$. In experiments, it usually happens that ![]() $\ell _{c}\gg \lambda$ and
$\ell _{c}\gg \lambda$ and ![]() $R_0\gg \lambda$ by several orders of magnitude. There is thus a region in the close vicinity of the contact line in which the force balance involves only viscous and capillary forces, with slip being dominant, and gravity negligible. This viscous–capillary region will be introduced in § 2.2. On the opposite range, the large scales are governed by the balance between gravity and capillarity. This capillary–gravity region will be presented in § 2.3. In between, the three contributions of the competing viscous, capillary and gravity forces must be retained as developed in § 2.4.
$R_0\gg \lambda$ by several orders of magnitude. There is thus a region in the close vicinity of the contact line in which the force balance involves only viscous and capillary forces, with slip being dominant, and gravity negligible. This viscous–capillary region will be introduced in § 2.2. On the opposite range, the large scales are governed by the balance between gravity and capillarity. This capillary–gravity region will be presented in § 2.3. In between, the three contributions of the competing viscous, capillary and gravity forces must be retained as developed in § 2.4.
2.2. Viscous–capillary region
This region corresponds to the very close vicinity of the contact line, i.e. at length scales much smaller than ![]() $\ell _c$. As mentioned earlier, in § 2.1, the introduction of a Navier slip is an important ingredient as viscous dissipation would diverge as
$\ell _c$. As mentioned earlier, in § 2.1, the introduction of a Navier slip is an important ingredient as viscous dissipation would diverge as ![]() $h\rightarrow 0$ otherwise. Resolution of the reduced equation (2.1) where the gravity term has been dropped, with the additional assumption that spreading is quasi-steady, leads to a relation often referred to as the Cox–Voinov law (Voinov Reference Voinov1976; Cox Reference Cox1986; Snoeijer Reference Snoeijer2006; Bonn et al. Reference Bonn, Eggers, Indekeu, Meunier and Rolley2009) between the velocity
$h\rightarrow 0$ otherwise. Resolution of the reduced equation (2.1) where the gravity term has been dropped, with the additional assumption that spreading is quasi-steady, leads to a relation often referred to as the Cox–Voinov law (Voinov Reference Voinov1976; Cox Reference Cox1986; Snoeijer Reference Snoeijer2006; Bonn et al. Reference Bonn, Eggers, Indekeu, Meunier and Rolley2009) between the velocity ![]() $U$ of the contact line and the dynamic contact angle
$U$ of the contact line and the dynamic contact angle ![]() $\theta _{app}(x)$, measured at distance
$\theta _{app}(x)$, measured at distance ![]() $x=R-r$ from the moving rim of the droplet:
$x=R-r$ from the moving rim of the droplet:
where ![]() $Ca=\eta U/\gamma$ is the capillary number. In the case of viscous liquids, the microscopic contact angle
$Ca=\eta U/\gamma$ is the capillary number. In the case of viscous liquids, the microscopic contact angle ![]() $\theta _m$ is close to the static value (Bonn et al. Reference Bonn, Eggers, Indekeu, Meunier and Rolley2009). For (nearly) perfectly wetting liquids, it is found that
$\theta _m$ is close to the static value (Bonn et al. Reference Bonn, Eggers, Indekeu, Meunier and Rolley2009). For (nearly) perfectly wetting liquids, it is found that ![]() $\theta _m\ll 1$ is therefore negligible in (2.3). Equation (2.3) indicates that
$\theta _m\ll 1$ is therefore negligible in (2.3). Equation (2.3) indicates that ![]() $\theta _{app}(x)$ is an increasing function of the distance
$\theta _{app}(x)$ is an increasing function of the distance ![]() $x$ to the contact line at a given capillary number
$x$ to the contact line at a given capillary number ![]() ${Ca}$. The interface in this viscous–capillary region must then have a positive curvature when measured in the frame defined in figure 1.
${Ca}$. The interface in this viscous–capillary region must then have a positive curvature when measured in the frame defined in figure 1.
2.3. Capillary–gravity region
The opposite limit corresponds to the region where ![]() $r\rightarrow 0$, i.e.
$r\rightarrow 0$, i.e. ![]() $x\sim R\sim R_0$. Moreover, we are interested in the limit where
$x\sim R\sim R_0$. Moreover, we are interested in the limit where ![]() $R_0\gg \ell _c$. At these scales, viscous forces are insignificant and the time-derivative term in (2.1) can be dropped. In addition, in this macroscopic region,
$R_0\gg \ell _c$. At these scales, viscous forces are insignificant and the time-derivative term in (2.1) can be dropped. In addition, in this macroscopic region, ![]() $\lambda$ can be neglected in front of
$\lambda$ can be neglected in front of ![]() $h$, which is of the order of
$h$, which is of the order of ![]() $h_0$. Hence we are left with a capillary–gravity balance, and (2.1) reduces to
$h_0$. Hence we are left with a capillary–gravity balance, and (2.1) reduces to
This equation can be integrated once. Using the boundary condition ![]() $h(r=R)=0$, the integration constant is seen to be zero. At that stage of the calculation, it is convenient to normalise the
$h(r=R)=0$, the integration constant is seen to be zero. At that stage of the calculation, it is convenient to normalise the ![]() $r$ and
$r$ and ![]() $h$ scales as
$h$ scales as ![]() $r=R_0\tilde {r}$ and
$r=R_0\tilde {r}$ and ![]() $h=h_{0}\tilde {h}$, where
$h=h_{0}\tilde {h}$, where ![]() $R_0$ and
$R_0$ and ![]() $h_0$ are the radius of the spherical drop and the characteristic interface height in this region, respectively. Performing another integration leads to
$h_0$ are the radius of the spherical drop and the characteristic interface height in this region, respectively. Performing another integration leads to
where ![]() $C$ is a constant, and
$C$ is a constant, and ![]() $Bo=\rho g R_0^2/\gamma =(R_0/\ell _c)^2$ is the Bond number of the droplet. The exact solution of (2.5) with the boundary conditions (2.2a–c) is
$Bo=\rho g R_0^2/\gamma =(R_0/\ell _c)^2$ is the Bond number of the droplet. The exact solution of (2.5) with the boundary conditions (2.2a–c) is
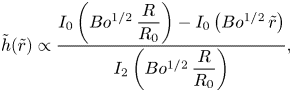 \begin{equation} \tilde{h}(\tilde{r})\propto\frac{I_0\left(Bo^{1/2}\, \dfrac{R}{R_0}\right)-I_0\left(Bo^{1/2}\,\tilde{r}\right)}{I_2\left(Bo^{1/2}\,\dfrac{R}{R_0}\right)}, \end{equation}
\begin{equation} \tilde{h}(\tilde{r})\propto\frac{I_0\left(Bo^{1/2}\, \dfrac{R}{R_0}\right)-I_0\left(Bo^{1/2}\,\tilde{r}\right)}{I_2\left(Bo^{1/2}\,\dfrac{R}{R_0}\right)}, \end{equation}
where ![]() $I_n(x)$ is the
$I_n(x)$ is the ![]() $n$th modified Bessel function of the first kind (Hocking Reference Hocking1983). With dimensional coordinates, the solution (2.6) reads
$n$th modified Bessel function of the first kind (Hocking Reference Hocking1983). With dimensional coordinates, the solution (2.6) reads
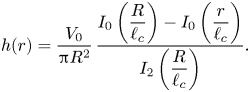 \begin{equation} h(r)=\frac{{V}_0}{{\rm \pi} R^2}\,\frac{I_0\left(\dfrac{R}{\ell_c}\right)-I_0 \left(\dfrac{r}{\ell_c}\right)}{I_2\left(\dfrac{R}{\ell_c}\right)}. \end{equation}
\begin{equation} h(r)=\frac{{V}_0}{{\rm \pi} R^2}\,\frac{I_0\left(\dfrac{R}{\ell_c}\right)-I_0 \left(\dfrac{r}{\ell_c}\right)}{I_2\left(\dfrac{R}{\ell_c}\right)}. \end{equation}
Droplets are spherical caps when ![]() $Bo\ll 1$, whereas their top surface flattens and they look like puddles in the limit
$Bo\ll 1$, whereas their top surface flattens and they look like puddles in the limit ![]() ${Bo}\gg 1$. In the frame of reference defined in figure 1, the shape of the interface in the macroscopic region has a negative curvature.
${Bo}\gg 1$. In the frame of reference defined in figure 1, the shape of the interface in the macroscopic region has a negative curvature.
2.4. Viscous–capillary–gravity region
We finally turn to the examination of the region for which all the contributions of the viscous, capillary and gravity forces must be kept in (2.1). In this viscous–capillary–gravity region, the length scale is comparable to neither ![]() $\lambda$ nor
$\lambda$ nor ![]() $R_{0}$, and the sole remaining length scale is the capillary length. Since
$R_{0}$, and the sole remaining length scale is the capillary length. Since ![]() $x, h\gg \lambda$, the reduced equation reads
$x, h\gg \lambda$, the reduced equation reads
where we consider quasi-static spreading and use ![]() $\partial _{t}h=U\,\partial _{r}h$. This assumption means that at any time, the velocity of the contact line sets the drop shape with no transient involved. This constraint is enforced by the hypothesis that
$\partial _{t}h=U\,\partial _{r}h$. This assumption means that at any time, the velocity of the contact line sets the drop shape with no transient involved. This constraint is enforced by the hypothesis that ![]() $Re\ll 1$ (Gratton et al. Reference Gratton, Diez, Thomas, Marino and Betelú1996). The capillary number
$Re\ll 1$ (Gratton et al. Reference Gratton, Diez, Thomas, Marino and Betelú1996). The capillary number ![]() $Ca=\eta U/\gamma$ then appears as a natural way to build a dimensionless velocity.
$Ca=\eta U/\gamma$ then appears as a natural way to build a dimensionless velocity.
As mentioned above, the capillary length ![]() $\ell _c$ is the only length available. It is the scale for the variation along the horizontal direction,
$\ell _c$ is the only length available. It is the scale for the variation along the horizontal direction, ![]() $r=\ell _{c}\hat {r}$. However, no obvious length scale emerges in the vertical direction. We thus define
$r=\ell _{c}\hat {r}$. However, no obvious length scale emerges in the vertical direction. We thus define ![]() $h=h^\star \hat {h}$, where
$h=h^\star \hat {h}$, where ![]() $h^\star$ is the (still unknown) relevant scale for the drop height. Using these renormalisations in (2.8) yields
$h^\star$ is the (still unknown) relevant scale for the drop height. Using these renormalisations in (2.8) yields
For the two terms to be of the same order in (2.9), one must take the height scale to be
This scale represents the typical height separating the viscous–capillary region governed by the Cox–Voinov law from the viscous–capillary–gravity region where gravity comes into play in the force balance. In other words, this transition scale corresponds to the upper bound of the region of the drop where the Cox–Voinov relation (2.3) is still valid. Another interesting interpretation of ![]() $h^\star$ is that it may delineate the change in surface curvature and thus can be understood as the inflection point of the drop interface.
$h^\star$ is that it may delineate the change in surface curvature and thus can be understood as the inflection point of the drop interface.
Some orders of magnitude can be provided for the present experimental conditions. The range of ![]() $h^\star$ is
$h^\star$ is ![]() $20\leq h^\star \leq 800\,\mathrm {\mu }$m for typically
$20\leq h^\star \leq 800\,\mathrm {\mu }$m for typically ![]() $\ell _c\simeq 2$ mm and
$\ell _c\simeq 2$ mm and ![]() $10^{-6}\leq Ca\leq 10^{-2}$. As a consequence, liquids with sub-millimetre characteristic length scales, such as suspensions of non-Brownian particles, may show non-trivial
$10^{-6}\leq Ca\leq 10^{-2}$. As a consequence, liquids with sub-millimetre characteristic length scales, such as suspensions of non-Brownian particles, may show non-trivial ![]() $\theta _{app}\unicode{x2013}Ca$ relations. Indeed, adding density-matched particles should not modify the drop behaviour in the gravity-driven region, while it should enhance dissipation provided that the particles can access the region where viscosity matters, namely the dissipation region for
$\theta _{app}\unicode{x2013}Ca$ relations. Indeed, adding density-matched particles should not modify the drop behaviour in the gravity-driven region, while it should enhance dissipation provided that the particles can access the region where viscosity matters, namely the dissipation region for ![]() $h\lesssim h^\star$.
$h\lesssim h^\star$.
3. Experimental methods
3.1. Particles and fluid
The suspending fluid is a Newtonian PEG copolymer, poly(ethylene glycol-ran-propylene glycol) monobutyl ether (average ![]() $M_n\simeq 3900$, Sigma-Aldrich reference 438189), with a density close to that of polystyrene,
$M_n\simeq 3900$, Sigma-Aldrich reference 438189), with a density close to that of polystyrene, ![]() $\rho =1056$ kg m
$\rho =1056$ kg m![]() $^{-3}$, at temperature
$^{-3}$, at temperature ![]() $25\,^{\circ }$C. Its dynamic viscosity
$25\,^{\circ }$C. Its dynamic viscosity ![]() $\eta _f=2.4\pm 0.1$ Pa s is constant over a large range of shear rate (0.01–10 s
$\eta _f=2.4\pm 0.1$ Pa s is constant over a large range of shear rate (0.01–10 s![]() $^{-1}$) at
$^{-1}$) at ![]() $25\,^{\circ }$C. Particles are spherical polystyrene beads (Dynoseeds TS, Microbeads, Norway) that are sieved when necessary to remove small dust particles or to narrow the size distribution below a tenth of particle diameter. The mean particle diameters
$25\,^{\circ }$C. Particles are spherical polystyrene beads (Dynoseeds TS, Microbeads, Norway) that are sieved when necessary to remove small dust particles or to narrow the size distribution below a tenth of particle diameter. The mean particle diameters ![]() $d$ used in the experiment are 10, 20, 40, 80, 140 and
$d$ used in the experiment are 10, 20, 40, 80, 140 and ![]() $250\,\mathrm {\mu }$m. Density-matching between the liquid and the particles is sufficient to prevent buoyancy effects over hours at temperature
$250\,\mathrm {\mu }$m. Density-matching between the liquid and the particles is sufficient to prevent buoyancy effects over hours at temperature ![]() $25\,^{\circ }$C in the air-conditioned room. To prepare the suspension mixture, the suspending fluid is weighted and poured into a test tube. A desired mass of particles is then added to reach the target volume fraction
$25\,^{\circ }$C in the air-conditioned room. To prepare the suspension mixture, the suspending fluid is weighted and poured into a test tube. A desired mass of particles is then added to reach the target volume fraction ![]() $\phi$. Good mixing while avoiding entrapping of air is achieved by hand mixing followed by slow mixing on a rolling device overnight. In the following experiments, the solid volume fraction is
$\phi$. Good mixing while avoiding entrapping of air is achieved by hand mixing followed by slow mixing on a rolling device overnight. In the following experiments, the solid volume fraction is ![]() $\phi =0.4$ as we aim to study the strongest effects expected at large volume fractions (Zhao et al. Reference Zhao, Oléron, Pelosse, Limat, Guazzelli and Roché2020). The particle surface is completely wet by the suspending fluid, i.e. particles remain suspended in the fluids and do not aggregate. We measured the surface tension of the suspension using pendant drop experiments. We find that the suspension surface tension is equal to the surface tension of the suspending fluid,
$\phi =0.4$ as we aim to study the strongest effects expected at large volume fractions (Zhao et al. Reference Zhao, Oléron, Pelosse, Limat, Guazzelli and Roché2020). The particle surface is completely wet by the suspending fluid, i.e. particles remain suspended in the fluids and do not aggregate. We measured the surface tension of the suspension using pendant drop experiments. We find that the suspension surface tension is equal to the surface tension of the suspending fluid, ![]() $\gamma =\gamma _f\simeq 35\,{\rm mN}\,{\rm m}^{-1}$, a similar result to that reported in Couturier et al. (Reference Couturier, Boyer, Pouliquen and Guazzelli2011).
$\gamma =\gamma _f\simeq 35\,{\rm mN}\,{\rm m}^{-1}$, a similar result to that reported in Couturier et al. (Reference Couturier, Boyer, Pouliquen and Guazzelli2011).
3.2. Bulk suspension rheology
A thorough discussion of our results requires a comparison of the bulk viscosity of the granular suspensions with their apparent viscosity extracted from drop spreading experiments; see § 5. Rheological measurements have been performed using an ARES G2 rheometer (TA Instruments) with a 25 mm-wide plate–plate geometry for solid blends of moderate-size particles with diameters 10, 20, 40 and ![]() $80\,\mathrm {\mu }$m. The thickness of the gap between the plates is typically
$80\,\mathrm {\mu }$m. The thickness of the gap between the plates is typically ![]() $1.5$ mm, i.e. at least 20 particle diameters, to prevent confinement effects (Peyla & Verdier Reference Peyla and Verdier2011). As wall-slip effects depend on the gap thickness, the fact that no viscosity variation is measured while changing the gap thickness from 1 to 2 mm indicates that sliding is negligible for these small particles (Yoshimura & Prud'homme Reference Yoshimura and Prud'homme1988; Jana, Kapoor & Acrivos Reference Jana, Kapoor and Acrivos1995).
$1.5$ mm, i.e. at least 20 particle diameters, to prevent confinement effects (Peyla & Verdier Reference Peyla and Verdier2011). As wall-slip effects depend on the gap thickness, the fact that no viscosity variation is measured while changing the gap thickness from 1 to 2 mm indicates that sliding is negligible for these small particles (Yoshimura & Prud'homme Reference Yoshimura and Prud'homme1988; Jana, Kapoor & Acrivos Reference Jana, Kapoor and Acrivos1995).
Confinement and slip become important when performing rheological measurements with suspensions of particles with diameters of 140 or ![]() $250\,\mathrm {\mu }$m. Slip is avoided using a 25 mm-wide plate–plate cross-hatched geometry with typical roughness 1 mm. Confinement is a trickier issue since increasing the gap thickness leads to a larger meniscus and thus to a significant error in viscosity measurements (Cardinaels, Reddy & Clasen Reference Cardinaels, Reddy and Clasen2019). We circumvent this issue by using a wide reservoir (a 5 cm-wide cup) mounted on the lower plate and filled with a 5 mm-thick layer of suspension (
$250\,\mathrm {\mu }$m. Slip is avoided using a 25 mm-wide plate–plate cross-hatched geometry with typical roughness 1 mm. Confinement is a trickier issue since increasing the gap thickness leads to a larger meniscus and thus to a significant error in viscosity measurements (Cardinaels, Reddy & Clasen Reference Cardinaels, Reddy and Clasen2019). We circumvent this issue by using a wide reservoir (a 5 cm-wide cup) mounted on the lower plate and filled with a 5 mm-thick layer of suspension (![]() ${\gtrsim }20d_p$) on which the upper tool is lowered to touch the free interface (Château et al. Reference Château, Guazzelli and Lhuissier2018; Château & Lhuissier Reference Château and Lhuissier2019). The additional torque exerted by the exceeding fluid in the reservoir can be computed analytically if the reservoir width and the suspension thickness are known (Vrentas, Venerus & Vrentas Reference Vrentas, Venerus and Vrentas1991). We have implemented this correction numerically, and we have been able to reproduce both published data and experimental results with and without the reservoir for Newtonian fluids and dense suspensions of 80
${\gtrsim }20d_p$) on which the upper tool is lowered to touch the free interface (Château et al. Reference Château, Guazzelli and Lhuissier2018; Château & Lhuissier Reference Château and Lhuissier2019). The additional torque exerted by the exceeding fluid in the reservoir can be computed analytically if the reservoir width and the suspension thickness are known (Vrentas, Venerus & Vrentas Reference Vrentas, Venerus and Vrentas1991). We have implemented this correction numerically, and we have been able to reproduce both published data and experimental results with and without the reservoir for Newtonian fluids and dense suspensions of 80 ![]() $\mathrm {\mu }$m particles.
$\mathrm {\mu }$m particles.
The relative bulk viscosity of monomodal granular suspensions, ![]() $\eta _s$, is defined as the viscosity of the whole suspension relative to that of the viscosity of the suspending fluid. It is independent of the particle size and shear rate, and is solely an increasing function of the particle volume fraction
$\eta _s$, is defined as the viscosity of the whole suspension relative to that of the viscosity of the suspending fluid. It is independent of the particle size and shear rate, and is solely an increasing function of the particle volume fraction ![]() $\phi$ that diverges at a maximum value
$\phi$ that diverges at a maximum value ![]() $\phi _c$ for which the suspension ceases to flow as shown in figure 2(a). Note that the value
$\phi _c$ for which the suspension ceases to flow as shown in figure 2(a). Note that the value ![]() $\phi _c\simeq 0.53$ inferred from curve fitting is provided for the plot, but a more exhaustive study of the viscosity in the dense regime would be required to confirm this value. The value of
$\phi _c\simeq 0.53$ inferred from curve fitting is provided for the plot, but a more exhaustive study of the viscosity in the dense regime would be required to confirm this value. The value of ![]() $\phi _c$ depends on the frictional contacts between particles (see e.g. Tapia, Pouliquen & Guazzelli Reference Tapia, Pouliquen and Guazzelli2019). It is important to note for the following discussion that
$\phi _c$ depends on the frictional contacts between particles (see e.g. Tapia, Pouliquen & Guazzelli Reference Tapia, Pouliquen and Guazzelli2019). It is important to note for the following discussion that ![]() $\phi _c$ also depends on the particle-size distribution for polydisperse suspensions.
$\phi _c$ also depends on the particle-size distribution for polydisperse suspensions.
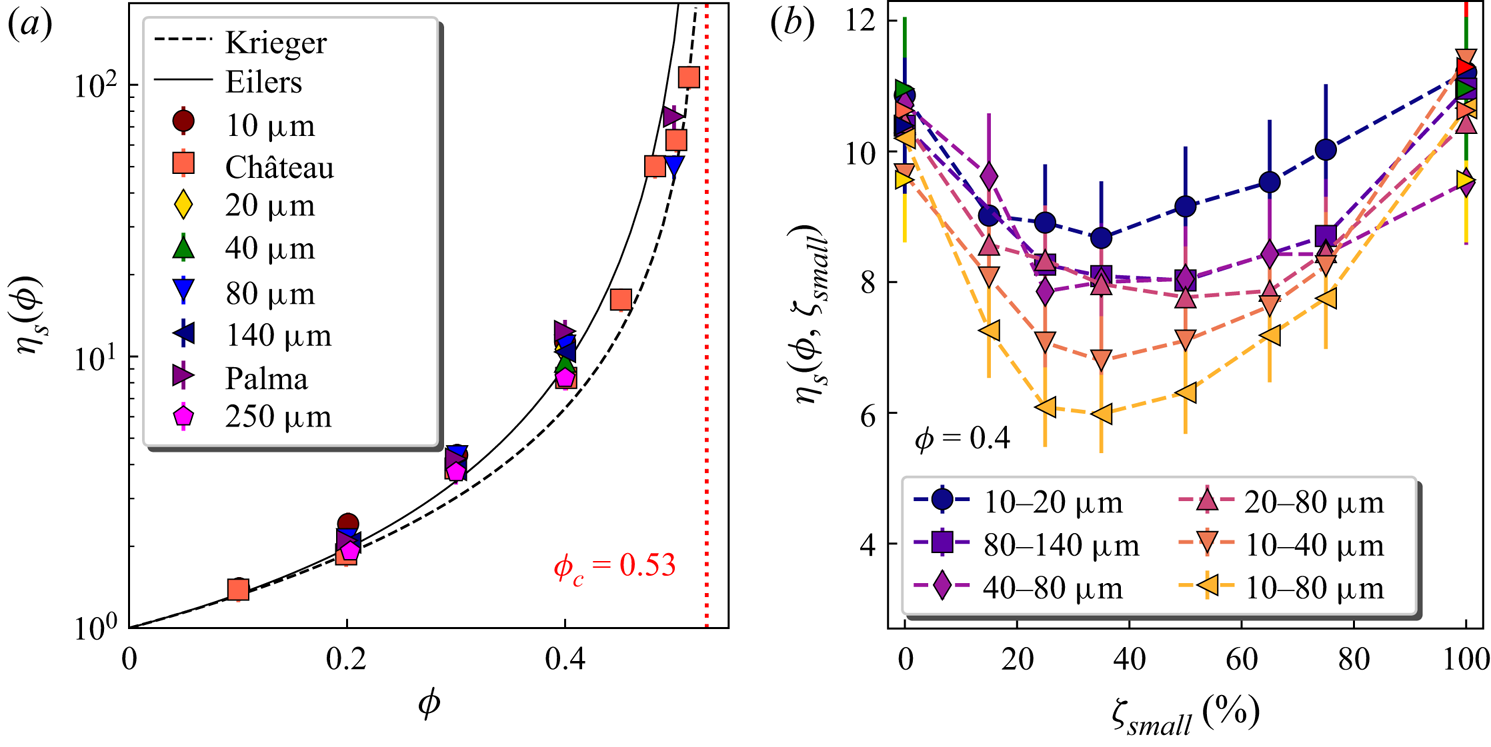
Figure 2. Relative viscosity (i.e. shear viscosity of the suspension relative to that of the suspending fluid) ![]() $\eta _s$ of (a) monomodal and (b) bimodal suspensions averaged for shear rates between 0.1 and 1 s
$\eta _s$ of (a) monomodal and (b) bimodal suspensions averaged for shear rates between 0.1 and 1 s![]() $^{-1}$ corresponding to the range of shear rates of the spreading experiments. (a) Relative viscosity of monomodal suspensions as a function of particle volume fraction
$^{-1}$ corresponding to the range of shear rates of the spreading experiments. (a) Relative viscosity of monomodal suspensions as a function of particle volume fraction ![]() $\phi$ for particles with diameters 10, 20, 40, 80, 140,
$\phi$ for particles with diameters 10, 20, 40, 80, 140, ![]() $250\,\mathrm {\mu }$m and comparison with experimental data for particles with diameters
$250\,\mathrm {\mu }$m and comparison with experimental data for particles with diameters ![]() $10$ and
$10$ and ![]() $140\,\mathrm {\mu }$m from the experiments of Château, Guazzelli & Lhuissier (Reference Château, Guazzelli and Lhuissier2018) and Palma & Lhuissier (Reference Palma and Lhuissier2019), respectively. The vertical dotted line is an estimate of the maximum volume fraction
$140\,\mathrm {\mu }$m from the experiments of Château, Guazzelli & Lhuissier (Reference Château, Guazzelli and Lhuissier2018) and Palma & Lhuissier (Reference Palma and Lhuissier2019), respectively. The vertical dotted line is an estimate of the maximum volume fraction ![]() $\phi _c\simeq 0.53$ used to compare data with the empirical correlations of Krieger & Dougherty (Reference Krieger and Dougherty1959),
$\phi _c\simeq 0.53$ used to compare data with the empirical correlations of Krieger & Dougherty (Reference Krieger and Dougherty1959), ![]() $\eta _s=(1-\phi /\phi _c)^{-[\eta ]\phi _c}$, and Eilers (Reference Eilers1941),
$\eta _s=(1-\phi /\phi _c)^{-[\eta ]\phi _c}$, and Eilers (Reference Eilers1941), ![]() $\eta _s=(1+[\eta ]/2\phi /(1-\phi /\phi _c))^2$ (where
$\eta _s=(1+[\eta ]/2\phi /(1-\phi /\phi _c))^2$ (where ![]() $[\eta ]=2.5$ is the intrinsic viscosity of the suspension). (b) Relative viscosity of bimodal suspensions at a fixed total solid volume fraction
$[\eta ]=2.5$ is the intrinsic viscosity of the suspension). (b) Relative viscosity of bimodal suspensions at a fixed total solid volume fraction ![]() $\phi =0.4$ as a function of the fraction of the small particles in the solid phase,
$\phi =0.4$ as a function of the fraction of the small particles in the solid phase, ![]() $\zeta _{small}$, for two-size blends (see legend).
$\zeta _{small}$, for two-size blends (see legend).
For bimodal suspensions, the viscosity depends not only on ![]() $\phi$ but also on the particle sizes
$\phi$ but also on the particle sizes ![]() $d_1$ and
$d_1$ and ![]() $d_2$ (
$d_2$ (![]() $d_1< d_2$) of the two species, and on the fraction of small particles in the solid phase,
$d_1< d_2$) of the two species, and on the fraction of small particles in the solid phase, ![]() $\zeta _{small}$; see figure 2(b). Experimental studies of dense bimodal systems in the literature indicate that their viscosity is also controlled by the value of the maximum packing fraction
$\zeta _{small}$; see figure 2(b). Experimental studies of dense bimodal systems in the literature indicate that their viscosity is also controlled by the value of the maximum packing fraction ![]() $\phi _c$, which is found to be higher than that of monomodal suspensions (Chong, Christiansen & Baer Reference Chong, Christiansen and Baer1971; Chang & Powell Reference Chang and Powell1994). This increase in
$\phi _c$, which is found to be higher than that of monomodal suspensions (Chong, Christiansen & Baer Reference Chong, Christiansen and Baer1971; Chang & Powell Reference Chang and Powell1994). This increase in ![]() $\phi _c$ results from the ability of small particles to fill the holes between the large ones (Macosko Reference Macosko1994). For bimodal suspensions with a given size ratio
$\phi _c$ results from the ability of small particles to fill the holes between the large ones (Macosko Reference Macosko1994). For bimodal suspensions with a given size ratio ![]() $d_2/d_1$, the relative bulk viscosity
$d_2/d_1$, the relative bulk viscosity ![]() $\eta _s$ is equal to that obtained in the sole presence of the large particles, when
$\eta _s$ is equal to that obtained in the sole presence of the large particles, when ![]() $\zeta _{small}=0\,\%$. Increasing
$\zeta _{small}=0\,\%$. Increasing ![]() $\zeta _{small}$ leads to a decrease of
$\zeta _{small}$ leads to a decrease of ![]() $\eta _s$, down to a minimum located between
$\eta _s$, down to a minimum located between ![]() $\zeta _{small}=25\,\%$ and
$\zeta _{small}=25\,\%$ and ![]() $\zeta _{small}=50\,\%$, and then to an increase up to the value obtained for a suspension of small particles,
$\zeta _{small}=50\,\%$, and then to an increase up to the value obtained for a suspension of small particles, ![]() $\zeta _{small}=100\,\%$. The minimum in viscosity is more pronounced with increasing
$\zeta _{small}=100\,\%$. The minimum in viscosity is more pronounced with increasing ![]() $d_2/d_1$; see figure 2(b).
$d_2/d_1$; see figure 2(b).
3.3. Experimental apparatus
We create droplets of suspension having volume ![]() $V_0= 300\,\mathrm {\mu }$l (spherical radius
$V_0= 300\,\mathrm {\mu }$l (spherical radius ![]() ${R_0=4.15}$ mm) with a syringe pump (flow rate 10 ml min
${R_0=4.15}$ mm) with a syringe pump (flow rate 10 ml min![]() $^{-1}$), as shown in figure 3. The droplets spread over a silicon wafer (Si-Mat) cleaned with ethanol and distilled water, and dried with clean-room wipes (plasma cleaning did not change the results or the quality of the data and was therefore considered an unnecessary precaution). Acquisition is made from side and top views with two synchronised monochrome cameras (Basler acA2440-35um,
$^{-1}$), as shown in figure 3. The droplets spread over a silicon wafer (Si-Mat) cleaned with ethanol and distilled water, and dried with clean-room wipes (plasma cleaning did not change the results or the quality of the data and was therefore considered an unnecessary precaution). Acquisition is made from side and top views with two synchronised monochrome cameras (Basler acA2440-35um, ![]() $2000\times 2448$ pixels) on which 1 : 1 macro objectives are mounted (I2S visions, MC series). High spatial resolution is required to capture the dynamics of the contact line. These optics give resolution
$2000\times 2448$ pixels) on which 1 : 1 macro objectives are mounted (I2S visions, MC series). High spatial resolution is required to capture the dynamics of the contact line. These optics give resolution ![]() $3.45\,\mathrm {\mu }$m px
$3.45\,\mathrm {\mu }$m px![]() $^{-1}$. Frame rates from 5 to 10 f.p.s. are required for the side view, especially at the beginning as the drop spreads quickly. Frame rates of 0.5 f.p.s. are sufficient for the top view as most of the interesting data are extracted at long times when spreading is slow and the slope of the drop interface is not too steep. A typical set of experiments for a single suspension batch is made of 10 different runs of spreading drops. These runs are acquired after 10 unused runs (corresponding to a total amount
$^{-1}$. Frame rates from 5 to 10 f.p.s. are required for the side view, especially at the beginning as the drop spreads quickly. Frame rates of 0.5 f.p.s. are sufficient for the top view as most of the interesting data are extracted at long times when spreading is slow and the slope of the drop interface is not too steep. A typical set of experiments for a single suspension batch is made of 10 different runs of spreading drops. These runs are acquired after 10 unused runs (corresponding to a total amount ![]() $\sim$3 ml) to avoid effects coming from the front of the advancing suspension in the tubing and in the needle. After performing these blank runs, the experiments are seen to be very reproducible at the desired volume fraction
$\sim$3 ml) to avoid effects coming from the front of the advancing suspension in the tubing and in the needle. After performing these blank runs, the experiments are seen to be very reproducible at the desired volume fraction ![]() $\phi =0.4$. Care is also taken to account for temperature and humidity variations. These two factors impact mainly the suspending fluid viscosity
$\phi =0.4$. Care is also taken to account for temperature and humidity variations. These two factors impact mainly the suspending fluid viscosity ![]() $\eta _f$. To this end, systematic viscosity measurements are performed during the experiments using a capillary viscometer.
$\eta _f$. To this end, systematic viscosity measurements are performed during the experiments using a capillary viscometer.
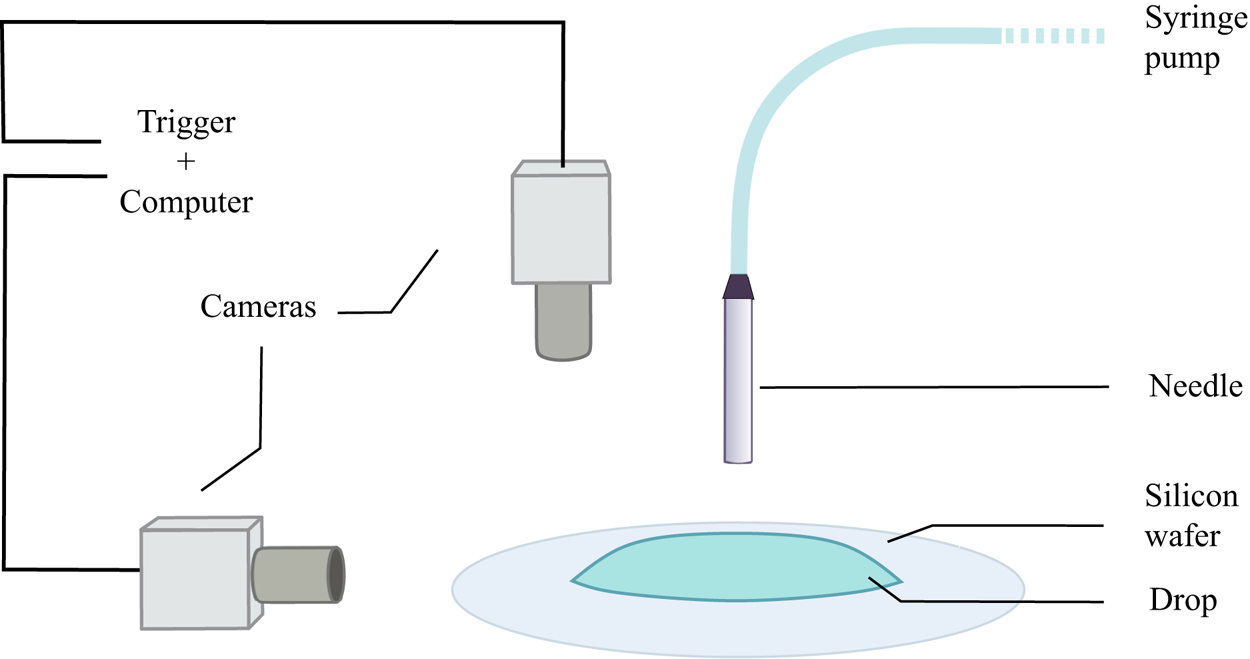
Figure 3. Sketch of the experimental apparatus.
3.4. Side-view analysis
We characterise the dynamics of spreading by measuring the dynamic contact angle ![]() $\theta _{app}$ as a function of the dimensionless contact line velocity
$\theta _{app}$ as a function of the dimensionless contact line velocity ![]() $U$. Angle measurement from the side views has been improved from the previous work of Zhao et al. (Reference Zhao, Oléron, Pelosse, Limat, Guazzelli and Roché2020) owing to better optical resolution and the possibility of performing an automated local angle measurement. We tailor the background lighting of our system with masks so that the drops captured by the side camera appear bright on a dark background, as seen on the top part of figure 4(a). Drop-shape detection is performed with the Sobel filter of the scikit-image package in Python, shown in figure 4(b), and further thresholded to extract the contact line coordinates and the drop profile
$U$. Angle measurement from the side views has been improved from the previous work of Zhao et al. (Reference Zhao, Oléron, Pelosse, Limat, Guazzelli and Roché2020) owing to better optical resolution and the possibility of performing an automated local angle measurement. We tailor the background lighting of our system with masks so that the drops captured by the side camera appear bright on a dark background, as seen on the top part of figure 4(a). Drop-shape detection is performed with the Sobel filter of the scikit-image package in Python, shown in figure 4(b), and further thresholded to extract the contact line coordinates and the drop profile ![]() $h(x)$, with
$h(x)$, with ![]() $x=0$ being the position of the contact line; see figure 4(c). The position of the contact line is defined as the leftmost bright pixel after image processing, as presented in figures 4(b,c). The drop profile is then smoothed with a cubic spline, as shown in figures 4(c,d). The contact line velocity
$x=0$ being the position of the contact line; see figure 4(c). The position of the contact line is defined as the leftmost bright pixel after image processing, as presented in figures 4(b,c). The drop profile is then smoothed with a cubic spline, as shown in figures 4(c,d). The contact line velocity ![]() $U$ is obtained by locating the triple contact line, while the apparent dynamic contact angle
$U$ is obtained by locating the triple contact line, while the apparent dynamic contact angle ![]() $\theta _{app}$ is inferred from the derivation of this spline. A spline is a piecewise polynomial function defined by the number of points, or knots, that it passes through. Spline functions are regular at zero, first and second order of derivation, as demonstrated in figure 4(d). To optimise spline adjustment to the data at all slopes, a small knot-to-knot distance is chosen at early times and then increased as the drop flattens. This process prevents meaningless oscillations at small slopes (large distance between knots). For all pictures, improper fits due to loss of focus or dust are discarded. The results are found to be similar to those obtained by adjusting manually a straight line to the air/liquid interface near the contact line in the range
$\theta _{app}$ is inferred from the derivation of this spline. A spline is a piecewise polynomial function defined by the number of points, or knots, that it passes through. Spline functions are regular at zero, first and second order of derivation, as demonstrated in figure 4(d). To optimise spline adjustment to the data at all slopes, a small knot-to-knot distance is chosen at early times and then increased as the drop flattens. This process prevents meaningless oscillations at small slopes (large distance between knots). For all pictures, improper fits due to loss of focus or dust are discarded. The results are found to be similar to those obtained by adjusting manually a straight line to the air/liquid interface near the contact line in the range ![]() $30^{\circ } \lesssim \theta _{app}\lesssim 85^{\circ }$. The fitted profile can then be derived once or twice at any point of the interface. The possibility of changing the measurement height
$30^{\circ } \lesssim \theta _{app}\lesssim 85^{\circ }$. The fitted profile can then be derived once or twice at any point of the interface. The possibility of changing the measurement height ![]() $h$ of the contact angle is one of the major benefits of this automated numerical procedure compared to previous manual measurements; see figure 4(d).
$h$ of the contact angle is one of the major benefits of this automated numerical procedure compared to previous manual measurements; see figure 4(d).
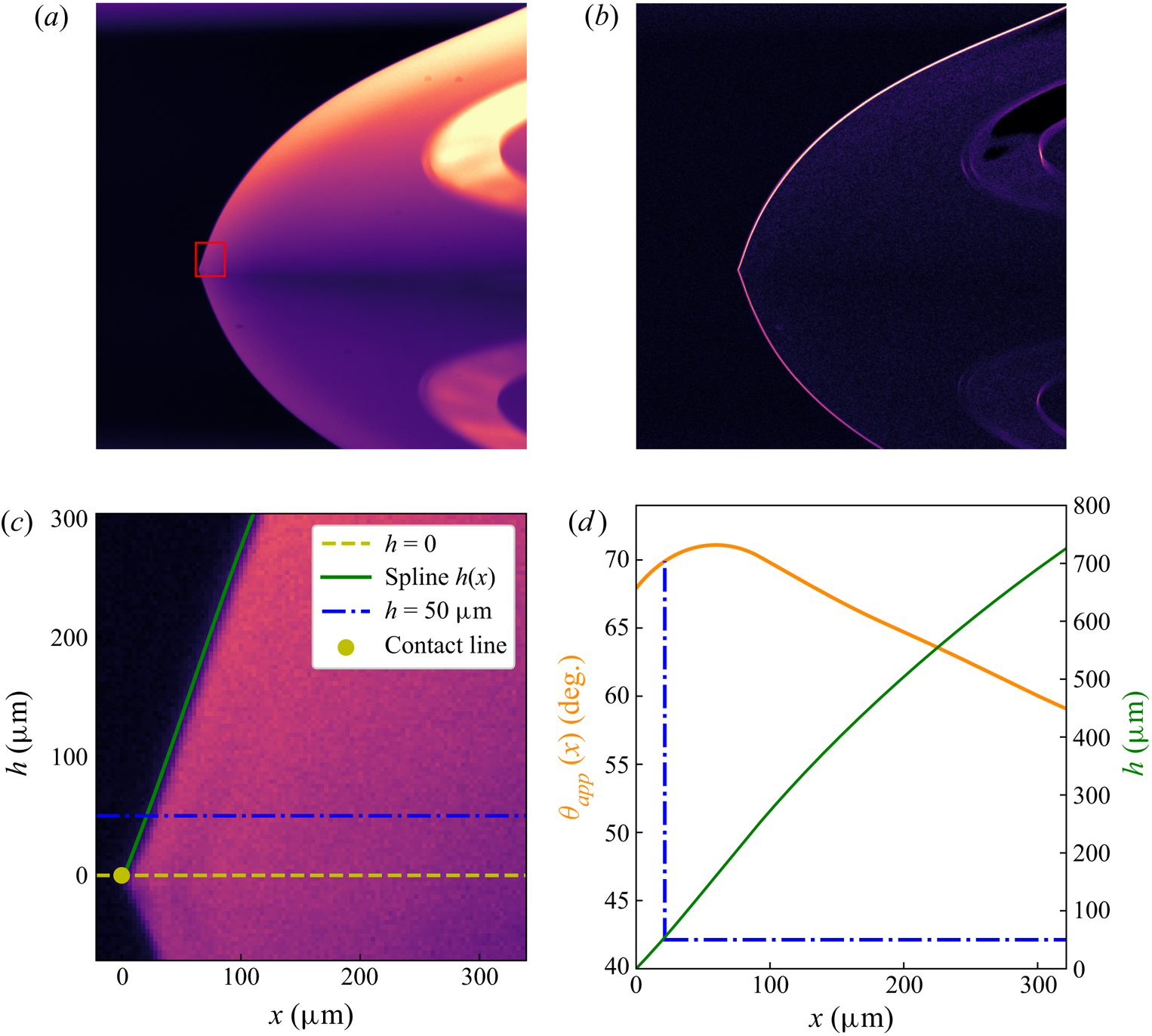
Figure 4. Data extraction from a picture of a spreading drop. Reflection on the wafer helps to detect the advancing contact line: (a) raw picture, and (b) Sobel filtering. The red rectangle in (a) corresponds to the blown-up region in (c), showing the fitted spline of the drop profile (green curve), the position of the contact line (yellow dot), and the drop height ![]() $h=50\,\mathrm {\mu }$m (dash-dotted blue line). (d) Results extracted from the fit: drop height
$h=50\,\mathrm {\mu }$m (dash-dotted blue line). (d) Results extracted from the fit: drop height ![]() $h$ as a function of the distance to the contact line
$h$ as a function of the distance to the contact line ![]() $x$ (green), and contact angle computed from the spline derivation according to
$x$ (green), and contact angle computed from the spline derivation according to ![]() $\theta _{app}(x)=\tan ^{-1}({{\rm d}h}/{{\rm d}\kern0.7pt x})$ (orange).
$\theta _{app}(x)=\tan ^{-1}({{\rm d}h}/{{\rm d}\kern0.7pt x})$ (orange).
3.5. Top-view analysis
Top views are used to visualise the structure of the particle network near the contact line, and also to measure the distance between the particles and the contact line ![]() $L$. Measurements using the ImageJ FiJi software package (Schindelin et al. Reference Schindelin2012) are performed over roughly 30 particles at the front. The precision of these measurements is set by the resolution of the pictures (
$L$. Measurements using the ImageJ FiJi software package (Schindelin et al. Reference Schindelin2012) are performed over roughly 30 particles at the front. The precision of these measurements is set by the resolution of the pictures (![]() $3.45\,\mathrm {\mu }$m px
$3.45\,\mathrm {\mu }$m px![]() $^{-1}$).
$^{-1}$).
4. Identifying the region of validity of the Cox–Voinov law
4.1. Simple fluids
In § 2.4, we have identified the length scale ![]() $h^\star$ that characterises the height of the interface at the transition between the viscous–capillary regime governed by the Cox–Voinov relation (2.3) and the viscous–capillary–gravity regime where gravity starts to prevail and where an inflection point should exist. We start our experimental characterisation of
$h^\star$ that characterises the height of the interface at the transition between the viscous–capillary regime governed by the Cox–Voinov relation (2.3) and the viscous–capillary–gravity regime where gravity starts to prevail and where an inflection point should exist. We start our experimental characterisation of ![]() $h^\star$ by investigating the shape of the interface in the case of simple fluids.
$h^\star$ by investigating the shape of the interface in the case of simple fluids.
Inspired by the form of the Cox–Voinov law (2.3), we measure, for capillary numbers in the range ![]() $0.0025\leq Ca\leq 0.0125$, how the cube of the angle between the interface and the horizontal,
$0.0025\leq Ca\leq 0.0125$, how the cube of the angle between the interface and the horizontal, ![]() $\theta _{app}^3$, depends on the interface height
$\theta _{app}^3$, depends on the interface height ![]() $h$ and on the horizontal distance to the contact line
$h$ and on the horizontal distance to the contact line ![]() $x$; see figures 5(a,b), respectively. The data come from the average over 7 experimental runs. We identify two regions. Starting from the contact line, for any capillary number,
$x$; see figures 5(a,b), respectively. The data come from the average over 7 experimental runs. We identify two regions. Starting from the contact line, for any capillary number, ![]() $\theta _{app}^3$ is first independent of the height at which it is measured; see figure 5(a). A plateau can thus be defined for
$\theta _{app}^3$ is first independent of the height at which it is measured; see figure 5(a). A plateau can thus be defined for ![]() $h$ ranging from 10 to almost
$h$ ranging from 10 to almost ![]() $100\,\mathrm {\mu }$m. Note that this plateau is better seen in semi-log scale in figure 5(a). Discussion of these results in the light of the Cox–Voinov law would lead us to expect that
$100\,\mathrm {\mu }$m. Note that this plateau is better seen in semi-log scale in figure 5(a). Discussion of these results in the light of the Cox–Voinov law would lead us to expect that ![]() $\theta _{app}^3$ is an increasing function of
$\theta _{app}^3$ is an increasing function of ![]() $h$. However, two experimental facts may prevent us from seeing this increase. First, an inflection point can be seen for some experiments (see, for instance, figure 4d), but the process of averaging over several runs likely smears out the change of curvature. Second, the length scales that we can probe are at least three orders of magnitude larger than the nanometric cut-off scale
$h$. However, two experimental facts may prevent us from seeing this increase. First, an inflection point can be seen for some experiments (see, for instance, figure 4d), but the process of averaging over several runs likely smears out the change of curvature. Second, the length scales that we can probe are at least three orders of magnitude larger than the nanometric cut-off scale ![]() $\lambda$. We thus expect the logarithmic term to increase slowly with distance, leading to difficulties in distinguishing the shape of the interface from a straight line. Similar conclusions regarding the local slope near the contact line have been reached by Rio (Reference Rio2005). It is worth mentioning that the plateau value increases with the capillary number as expected from the Cox–Voinov law (2.3). Away from the contact line, the angle decreases, suggesting a growing contribution of gravity to the force balance. In figure 5(b), the experimental contact angle is plotted, and the theoretical prediction obtained from the balance between gravity and capillarity is superimposed at largest distances from the contact line. We find that the agreement of the static solution (2.7) with the data is satisfactory and improves with decreasing
$\lambda$. We thus expect the logarithmic term to increase slowly with distance, leading to difficulties in distinguishing the shape of the interface from a straight line. Similar conclusions regarding the local slope near the contact line have been reached by Rio (Reference Rio2005). It is worth mentioning that the plateau value increases with the capillary number as expected from the Cox–Voinov law (2.3). Away from the contact line, the angle decreases, suggesting a growing contribution of gravity to the force balance. In figure 5(b), the experimental contact angle is plotted, and the theoretical prediction obtained from the balance between gravity and capillarity is superimposed at largest distances from the contact line. We find that the agreement of the static solution (2.7) with the data is satisfactory and improves with decreasing ![]() $Ca$, provided that we leave the radius of the droplet as a fitting parameter since it cannot be inferred in our experiments. Indeed, the imaging field does not cover the whole drop as the focus is on the contact line region, which requires a significant magnification.
$Ca$, provided that we leave the radius of the droplet as a fitting parameter since it cannot be inferred in our experiments. Indeed, the imaging field does not cover the whole drop as the focus is on the contact line region, which requires a significant magnification.
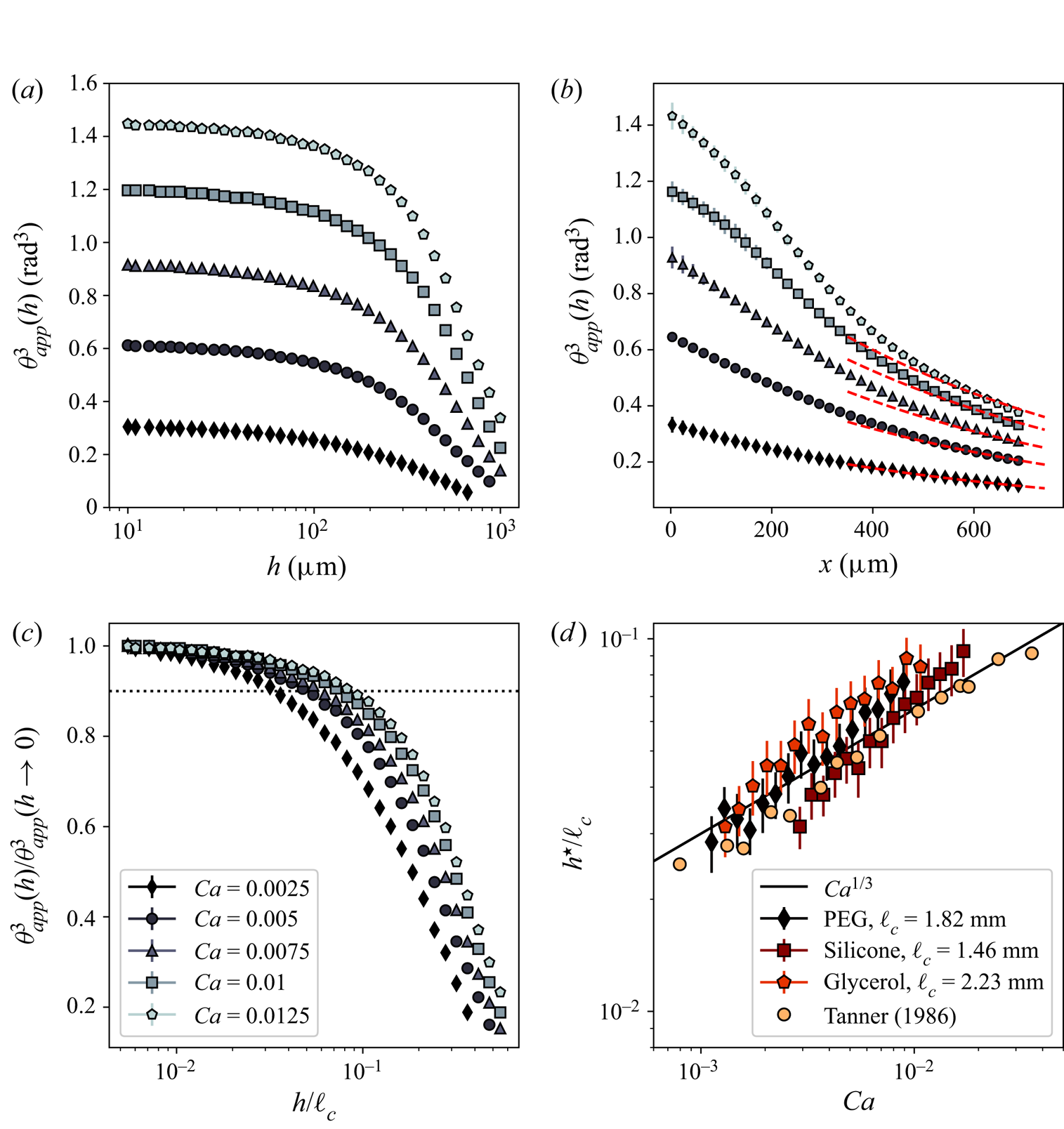
Figure 5. Cube of the contact angle ![]() $\theta _{app}^3$ versus (a) the measurement height
$\theta _{app}^3$ versus (a) the measurement height ![]() $h$, and (b) the horizontal distance to the contact line
$h$, and (b) the horizontal distance to the contact line ![]() $x$, averaged over 7 experimental runs for 5 capillary numbers
$x$, averaged over 7 experimental runs for 5 capillary numbers ![]() $Ca$, namely 0.0025 (
$Ca$, namely 0.0025 (![]() $\lozenge$), 0.005 (
$\lozenge$), 0.005 (![]() $\circ$), 0.0075 (
$\circ$), 0.0075 (![]() $\triangle$), 0.01 (
$\triangle$), 0.01 (![]() $\square$), 0.0125 (
$\square$), 0.0125 (![]() ), using a Newtonian fluid (PEG copolymer). Red dashed lines indicate static shape (2.7) for
), using a Newtonian fluid (PEG copolymer). Red dashed lines indicate static shape (2.7) for ![]() $R=8.5,8.7,8.9,9.3, 10$ mm (estimated so as to provide the best fit with the experimental data) and
$R=8.5,8.7,8.9,9.3, 10$ mm (estimated so as to provide the best fit with the experimental data) and ![]() $\ell _c=1.82$ mm. (c) Normalised cube of the contact angle
$\ell _c=1.82$ mm. (c) Normalised cube of the contact angle ![]() $\theta _{app}^3/\theta _{app}^3(h\rightarrow 0)$ versus normalised height
$\theta _{app}^3/\theta _{app}^3(h\rightarrow 0)$ versus normalised height ![]() $h/\ell _c$. Black dotted line indicates the threshold for the plateau length at
$h/\ell _c$. Black dotted line indicates the threshold for the plateau length at ![]() $\theta ^3(h^\star )/\theta ^3(h\rightarrow 0)=0.9$. (d) Normalised transition height
$\theta ^3(h^\star )/\theta ^3(h\rightarrow 0)=0.9$. (d) Normalised transition height ![]() $h^\star /\ell _c$ versus
$h^\star /\ell _c$ versus ![]() $Ca$ for three different Newtonian fluids: PEG (black
$Ca$ for three different Newtonian fluids: PEG (black ![]() $\lozenge$), silicone oil V1000 (maroon
$\lozenge$), silicone oil V1000 (maroon ![]() $\square$;
$\square$; ![]() $\rho =970$ kg m
$\rho =970$ kg m![]() $^{-3}$,
$^{-3}$, ![]() $\gamma =21$ mN m
$\gamma =21$ mN m![]() $^{-1}$,
$^{-1}$, ![]() $\eta =1.0$ Pa s,
$\eta =1.0$ Pa s, ![]() $\ell _c=1.46$ mm), and glycerol (red
$\ell _c=1.46$ mm), and glycerol (red ![]() ;
; ![]() $\rho =1260$ kg m
$\rho =1260$ kg m![]() $^{-3}$,
$^{-3}$, ![]() $\gamma =63$ mN m
$\gamma =63$ mN m![]() $^{-1}$,
$^{-1}$, ![]() $\eta =1.3$ Pa s,
$\eta =1.3$ Pa s, ![]() $\ell _c=2.23$ mm), as well as the inflection-point measurements (gold
$\ell _c=2.23$ mm), as well as the inflection-point measurements (gold ![]() $\circ$) of Tanner (Reference Tanner1986) with highly viscous silicone oil. Black solid line indicates
$\circ$) of Tanner (Reference Tanner1986) with highly viscous silicone oil. Black solid line indicates ![]() $h^\star /\ell _c=0.3\,Ca^{1/3}$.
$h^\star /\ell _c=0.3\,Ca^{1/3}$.
Comparison of the datasets is made easier if we normalise ![]() $\theta _{app}^3(h)$ by its asymptotic value
$\theta _{app}^3(h)$ by its asymptotic value ![]() $\theta _{app}^3(h\rightarrow 0)$, and
$\theta _{app}^3(h\rightarrow 0)$, and ![]() $h$ by the capillary length
$h$ by the capillary length ![]() $\ell _c$; see figure 5(c). From these plots, we define the experimental transition height
$\ell _c$; see figure 5(c). From these plots, we define the experimental transition height ![]() $h^\star$ as the height at which
$h^\star$ as the height at which ![]() $\theta _{app}^3(h)$ departs from
$\theta _{app}^3(h)$ departs from ![]() $\theta _{app}^3(h\rightarrow 0)$ by 10 %. Figure 5(d) shows the inferred
$\theta _{app}^3(h\rightarrow 0)$ by 10 %. Figure 5(d) shows the inferred ![]() $h^\star$ as a function of
$h^\star$ as a function of ![]() $Ca$ for different simple fluids. The normalised transition height
$Ca$ for different simple fluids. The normalised transition height ![]() $h^\star /\ell _c$ increases as
$h^\star /\ell _c$ increases as ![]() $Ca^{1/3}$ in agreement with the prediction (2.10) of the dimensional analysis in § 2.4. We also report in this graph the measurements of the inflection point of the interface obtained by Tanner (Reference Tanner1986), although the present interpretation as an upper limit of dissipation was not mentioned in this work. These data agree well with the present estimates of
$Ca^{1/3}$ in agreement with the prediction (2.10) of the dimensional analysis in § 2.4. We also report in this graph the measurements of the inflection point of the interface obtained by Tanner (Reference Tanner1986), although the present interpretation as an upper limit of dissipation was not mentioned in this work. These data agree well with the present estimates of ![]() $h^\star$ as well as with the
$h^\star$ as well as with the ![]() $Ca^{1/3}$ scaling. Note that this scaling still holds when varying the threshold between 1 % and 15 %. The threshold of 10 % provides the best match with the measurements of Tanner (Reference Tanner1986). If we grant
$Ca^{1/3}$ scaling. Note that this scaling still holds when varying the threshold between 1 % and 15 %. The threshold of 10 % provides the best match with the measurements of Tanner (Reference Tanner1986). If we grant ![]() $h^\star$ the interpretation of a viscous–capillary cut-off length and refer to figure 5(d), then we can conclude that measuring contact angles at heights well below
$h^\star$ the interpretation of a viscous–capillary cut-off length and refer to figure 5(d), then we can conclude that measuring contact angles at heights well below ![]() $100\,\mathrm {\mu }$m warrants probing the region of the droplet where the apparent dynamic contact angle is set by a balance between viscous dissipation and capillarity only.
$100\,\mathrm {\mu }$m warrants probing the region of the droplet where the apparent dynamic contact angle is set by a balance between viscous dissipation and capillarity only.
4.2. Granular suspensions
We now test the relevance of ![]() $h^\star$ to the spreading of drops of granular suspensions. Because they are density-matched to the suspending fluid and do not modify surface tension, the particles are expected to modify only viscous dissipation and to leave gravitational and capillary effects unchanged.
$h^\star$ to the spreading of drops of granular suspensions. Because they are density-matched to the suspending fluid and do not modify surface tension, the particles are expected to modify only viscous dissipation and to leave gravitational and capillary effects unchanged.
Figure 6(a) presents the variation of ![]() $\theta _{app}^3$ with the measurement height
$\theta _{app}^3$ with the measurement height ![]() $h$ for monomodal granular suspensions of 10
$h$ for monomodal granular suspensions of 10 ![]() $\mathrm {\mu }$m particles and bimodal suspensions of 10–80
$\mathrm {\mu }$m particles and bimodal suspensions of 10–80 ![]() $\mathrm {\mu }$m particles with
$\mathrm {\mu }$m particles with ![]() $\zeta _{10}=50\,\%$, at a constant capillary number
$\zeta _{10}=50\,\%$, at a constant capillary number ![]() $Ca_0=\eta _f U/\gamma _f$, where subscript
$Ca_0=\eta _f U/\gamma _f$, where subscript ![]() $0$ on the capillary number emphasises that it is computed using properties of the suspending fluid. Reference data for the pure suspending fluid at
$0$ on the capillary number emphasises that it is computed using properties of the suspending fluid. Reference data for the pure suspending fluid at ![]() $Ca_0$ are also provided for comparison in figure 6(a). The behaviour of
$Ca_0$ are also provided for comparison in figure 6(a). The behaviour of ![]() $\theta _{app}^3(h)$ for the suspensions is similar to that seen for the reference fluid; see also figures 5(a,c). A plateau region is again observed close to the contact line, for
$\theta _{app}^3(h)$ for the suspensions is similar to that seen for the reference fluid; see also figures 5(a,c). A plateau region is again observed close to the contact line, for ![]() $10\lesssim h\lesssim 100\,\mathrm {\mu }$m, while there is a decay at larger distances. The addition of the particles leads to an increase in the plateau value of
$10\lesssim h\lesssim 100\,\mathrm {\mu }$m, while there is a decay at larger distances. The addition of the particles leads to an increase in the plateau value of ![]() $\theta _{app}^3$, which depends on the particle mixture components. Provided that measurements are undertaken within the plateau region at constant height across all experiments, we can obtain an unequivocal apparent contact angle, at a given capillary number. The dependence between these two quantities is then a priori interpretable in terms of the Cox–Voinov relation. In the following, the measurement height is set at
$\theta _{app}^3$, which depends on the particle mixture components. Provided that measurements are undertaken within the plateau region at constant height across all experiments, we can obtain an unequivocal apparent contact angle, at a given capillary number. The dependence between these two quantities is then a priori interpretable in terms of the Cox–Voinov relation. In the following, the measurement height is set at ![]() $h=50\,\mathrm {\mu }$m. This chosen height seems a good compromise between smaller heights having large measurement noise and larger heights that might fall outside of the region where viscosity matters. Note that taking
$h=50\,\mathrm {\mu }$m. This chosen height seems a good compromise between smaller heights having large measurement noise and larger heights that might fall outside of the region where viscosity matters. Note that taking ![]() $h$ in the range 20 to
$h$ in the range 20 to ![]() $100\,\mathrm {\mu }$m yields similar results for the apparent wetting viscosity that will be introduced below.
$100\,\mathrm {\mu }$m yields similar results for the apparent wetting viscosity that will be introduced below.
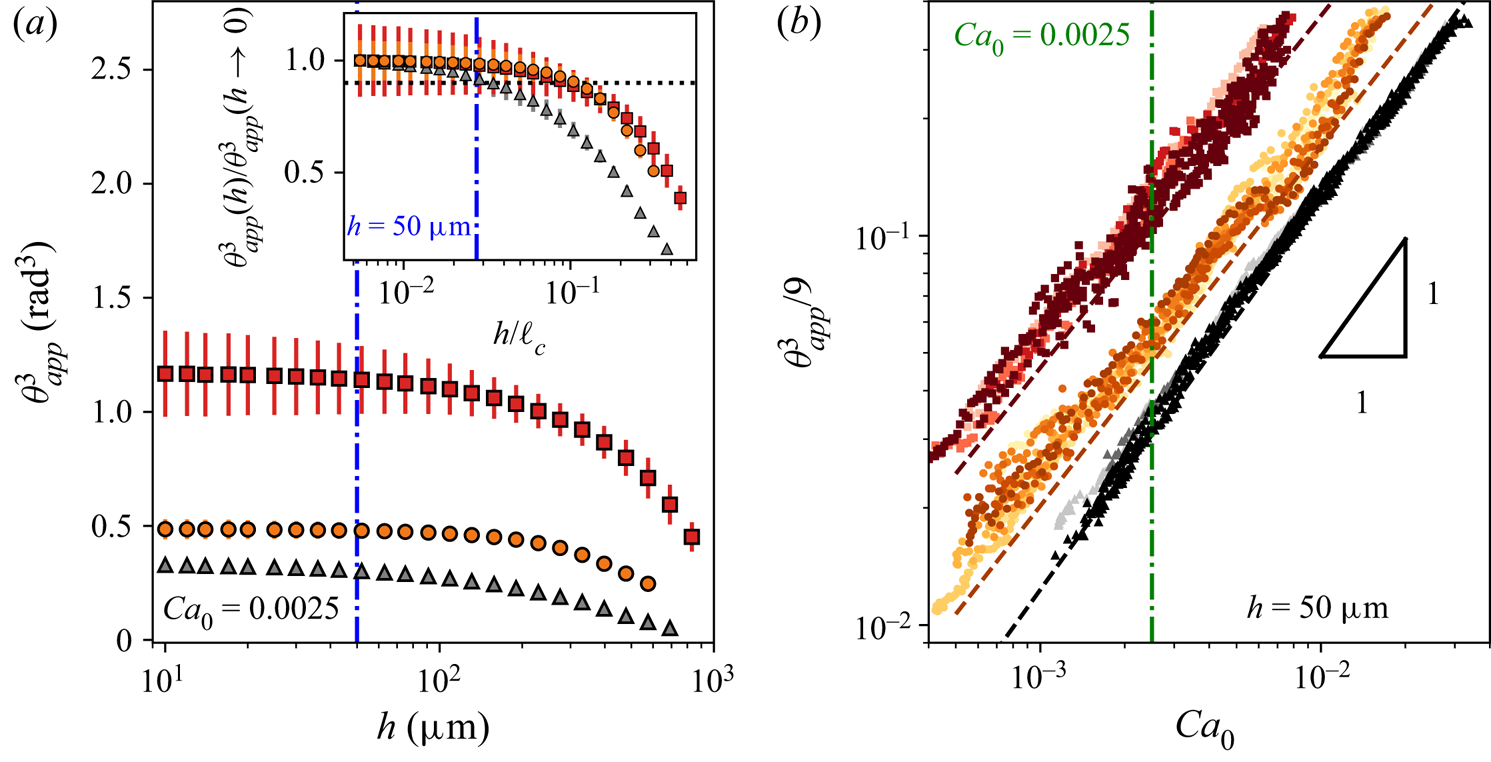
Figure 6. (a) Cube of the contact angle ![]() $\theta _{app}^3$ versus the measurement height
$\theta _{app}^3$ versus the measurement height ![]() $h$ for different fluids: pure suspending fluid (grey
$h$ for different fluids: pure suspending fluid (grey ![]() $\triangle$), 10
$\triangle$), 10 ![]() $\mathrm {\mu }$m monomodal suspension (red
$\mathrm {\mu }$m monomodal suspension (red ![]() $\square$), and 10–80
$\square$), and 10–80 ![]() $\mathrm {\mu }$m bimodal suspension at
$\mathrm {\mu }$m bimodal suspension at ![]() $\zeta _{10}=50\,\%$ (orange
$\zeta _{10}=50\,\%$ (orange ![]() $\circ$), resulting from the analysis of 7, 8 and 10 drop-spreading runs, respectively, and at the same fluid capillary number
$\circ$), resulting from the analysis of 7, 8 and 10 drop-spreading runs, respectively, and at the same fluid capillary number ![]() $Ca_0=\eta _f U/\gamma _f=0.0025$. Inset: normalised cube of the contact angle
$Ca_0=\eta _f U/\gamma _f=0.0025$. Inset: normalised cube of the contact angle ![]() $\theta _{app}^3/\theta _{app}^3(h\rightarrow 0)$ versus normalised height
$\theta _{app}^3/\theta _{app}^3(h\rightarrow 0)$ versus normalised height ![]() $h/\ell _c$. Blue dash-dotted line indicates selected measurement height
$h/\ell _c$. Blue dash-dotted line indicates selected measurement height ![]() $h=50\,\mathrm {\mu }$m. (b) Variation of
$h=50\,\mathrm {\mu }$m. (b) Variation of ![]() $\theta _{app}^3/9$ as a function of
$\theta _{app}^3/9$ as a function of ![]() $Ca_0$ performed at height
$Ca_0$ performed at height ![]() $h=50\,\mathrm {\mu }$m for the different runs for spreading drops made of pure suspending fluid (grey dots), 10
$h=50\,\mathrm {\mu }$m for the different runs for spreading drops made of pure suspending fluid (grey dots), 10 ![]() $\mathrm {\mu }$m monomodal suspension (red dots), and 10–80
$\mathrm {\mu }$m monomodal suspension (red dots), and 10–80 ![]() $\mathrm {\mu }$m bimodal suspensions at
$\mathrm {\mu }$m bimodal suspensions at ![]() $\zeta _{10}=50\,\%$ (orange dots). The different colour shades represent different experiments. The dashed lines correspond to the average of the linear fits of data coming from each run and are used to infer the relative apparent viscosity
$\zeta _{10}=50\,\%$ (orange dots). The different colour shades represent different experiments. The dashed lines correspond to the average of the linear fits of data coming from each run and are used to infer the relative apparent viscosity ![]() $\eta _w$.
$\eta _w$.
Figure 6(b) displays typical variations of ![]() $\theta _{app}^3/9$ as a function of the capillary number of the suspending fluid,
$\theta _{app}^3/9$ as a function of the capillary number of the suspending fluid, ![]() $Ca_0$. Data from different experimental runs are plotted for the same fluids as those used in figure 6(a). For a given fluid (suspensions or reference fluid), the tight collapse of the different
$Ca_0$. Data from different experimental runs are plotted for the same fluids as those used in figure 6(a). For a given fluid (suspensions or reference fluid), the tight collapse of the different ![]() $\theta _{app}^3(Ca_0)$ curves coming from the different runs bears witness to the good reproducibility of the experiments. All the datasets collapse on straight lines with unity slopes in log-log representation, i.e.
$\theta _{app}^3(Ca_0)$ curves coming from the different runs bears witness to the good reproducibility of the experiments. All the datasets collapse on straight lines with unity slopes in log-log representation, i.e. ![]() $\theta _{app}^3/9\propto Ca_0$. For each run, a linear fit is performed and the average (dashed) line for a given fluid is the average of the corresponding linear fits. Typically, the measured angles lie between 30
$\theta _{app}^3/9\propto Ca_0$. For each run, a linear fit is performed and the average (dashed) line for a given fluid is the average of the corresponding linear fits. Typically, the measured angles lie between 30![]() $^{\circ }$ and 90
$^{\circ }$ and 90![]() $^{\circ }$, the upper limit being set by the algorithm. Tracking is interrupted below 30
$^{\circ }$, the upper limit being set by the algorithm. Tracking is interrupted below 30![]() $^{\circ }$ due to the failure of the Cox–Voinov law. Protrusions of the particles from the free surface are observed at small contact angles and might be responsible for this discrepancy.
$^{\circ }$ due to the failure of the Cox–Voinov law. Protrusions of the particles from the free surface are observed at small contact angles and might be responsible for this discrepancy.
As expected, the data from the suspending fluid are in excellent agreement with the Cox–Voinov law (2.3). The logarithm factor in (2.3) is found to be ![]() ${\simeq }11.9$, in good agreement with values in the literature (Voinov Reference Voinov1976). It is important to note that the measurements are undertaken at a constant height
${\simeq }11.9$, in good agreement with values in the literature (Voinov Reference Voinov1976). It is important to note that the measurements are undertaken at a constant height ![]() $h$ within the plateau region, and not at a constant
$h$ within the plateau region, and not at a constant ![]() $x$. However, since
$x$. However, since ![]() $x$ and
$x$ and ![]() $h$ are of the same order of magnitude and sufficiently large compared to
$h$ are of the same order of magnitude and sufficiently large compared to ![]() $\lambda$, the logarithm factor is not varying significantly and can be considered constant.
$\lambda$, the logarithm factor is not varying significantly and can be considered constant.
For suspensions, data for ![]() $\theta _{app}^3(Ca_0)$ in figure 6(b) equally collapse on a straight line with a slope of unity in the log-log representation (red and orange dashed lines): the spreading of these materials still seems to follow a Cox–Voinov relation (2.3). However, since the values of
$\theta _{app}^3(Ca_0)$ in figure 6(b) equally collapse on a straight line with a slope of unity in the log-log representation (red and orange dashed lines): the spreading of these materials still seems to follow a Cox–Voinov relation (2.3). However, since the values of ![]() $\theta _{app}^3$ in the plateau are changed by the addition of particles as shown in figure 6(a), the different
$\theta _{app}^3$ in the plateau are changed by the addition of particles as shown in figure 6(a), the different ![]() $\theta _{app}^3(Ca_0)$ lines are shifted with respect to each other in figure 6(b), in agreement with previous experiments (Zhao et al. Reference Zhao, Oléron, Pelosse, Limat, Guazzelli and Roché2020). Assuming that the logarithmic factor has the same order of magnitude for the pure suspending fluid and for suspensions (as we do not expect the particles to modify the mechanics at the nanometric scale), we can superimpose all curves and recover the Cox–Voinov law (2.3) for all liquids if we adjust the viscosity used in the capillary number
$\theta _{app}^3(Ca_0)$ lines are shifted with respect to each other in figure 6(b), in agreement with previous experiments (Zhao et al. Reference Zhao, Oléron, Pelosse, Limat, Guazzelli and Roché2020). Assuming that the logarithmic factor has the same order of magnitude for the pure suspending fluid and for suspensions (as we do not expect the particles to modify the mechanics at the nanometric scale), we can superimpose all curves and recover the Cox–Voinov law (2.3) for all liquids if we adjust the viscosity used in the capillary number ![]() $Ca=\eta U/\gamma$, with
$Ca=\eta U/\gamma$, with ![]() $\eta =\eta _f\eta _w$ where
$\eta =\eta _f\eta _w$ where ![]() $\eta _w$ is the relative apparent wetting viscosity of the suspensions. Again, the shift and consequently the apparent wetting viscosity strongly depend on the particle mixture components. Here, we see that the suspension of 10
$\eta _w$ is the relative apparent wetting viscosity of the suspensions. Again, the shift and consequently the apparent wetting viscosity strongly depend on the particle mixture components. Here, we see that the suspension of 10 ![]() $\mathrm {\mu }$m particles has a larger apparent wetting viscosity than the 10–80
$\mathrm {\mu }$m particles has a larger apparent wetting viscosity than the 10–80 ![]() $\mathrm {\mu }$m bimodal suspension. The behaviour of the apparent viscosity
$\mathrm {\mu }$m bimodal suspension. The behaviour of the apparent viscosity ![]() $\eta _w$ is examined in detail in § 5 for suspensions consisting of different particle combinations.
$\eta _w$ is examined in detail in § 5 for suspensions consisting of different particle combinations.
5. Probing dissipation with particles
5.1. Suspensions with particles having a large difference in size
We focus first on suspensions consisting of particles having a large difference in diameter, ![]() $d_1=10\,\mathrm {\mu }$m and
$d_1=10\,\mathrm {\mu }$m and ![]() $d_2=80\,\mathrm {\mu }$m (
$d_2=80\,\mathrm {\mu }$m (![]() $d_2/d_1=8$). Figure 7(a) shows that the relative wetting viscosity of these suspensions,
$d_2/d_1=8$). Figure 7(a) shows that the relative wetting viscosity of these suspensions, ![]() $\eta _w$, increases with increasing fraction of the small particles,
$\eta _w$, increases with increasing fraction of the small particles, ![]() $\zeta _{10}$, with a steeper growth beyond
$\zeta _{10}$, with a steeper growth beyond ![]() $\zeta _{10} \simeq 50\,\%$. This behaviour is in stark contrast with the
$\zeta _{10} \simeq 50\,\%$. This behaviour is in stark contrast with the ![]() $\zeta _{10}$ dependence of the relative bulk viscosity of the same mixtures shown in figure 2(b) and plotted again in the inset in figure 7(a). The relative bulk viscosity of the blends presents a minimum at
$\zeta _{10}$ dependence of the relative bulk viscosity of the same mixtures shown in figure 2(b) and plotted again in the inset in figure 7(a). The relative bulk viscosity of the blends presents a minimum at ![]() $\zeta _{10}=35\,\%$, i.e. a mixture containing roughly a third of small particles. This minimum viscosity is 40 % smaller than the values obtained in the monomodal cases at
$\zeta _{10}=35\,\%$, i.e. a mixture containing roughly a third of small particles. This minimum viscosity is 40 % smaller than the values obtained in the monomodal cases at ![]() $\zeta _{10}=0\,\%$ and 100 % (consisting of monomodal suspensions of 80 and
$\zeta _{10}=0\,\%$ and 100 % (consisting of monomodal suspensions of 80 and ![]() $10\,\mathrm {\mu }$m, respectively). It is worth noting that even in the monomodal case with the small particles,
$10\,\mathrm {\mu }$m, respectively). It is worth noting that even in the monomodal case with the small particles, ![]() $\eta _w$ is smaller (by a factor of order 2) than the corresponding value of its bulk viscosity,
$\eta _w$ is smaller (by a factor of order 2) than the corresponding value of its bulk viscosity, ![]() $\eta _s$. This inability to reach the bulk value is always observed even for the smallest particles as there is always a small region devoid of particles at the tip followed by an ordered region, as discussed in the following and in § 6.
$\eta _s$. This inability to reach the bulk value is always observed even for the smallest particles as there is always a small region devoid of particles at the tip followed by an ordered region, as discussed in the following and in § 6.
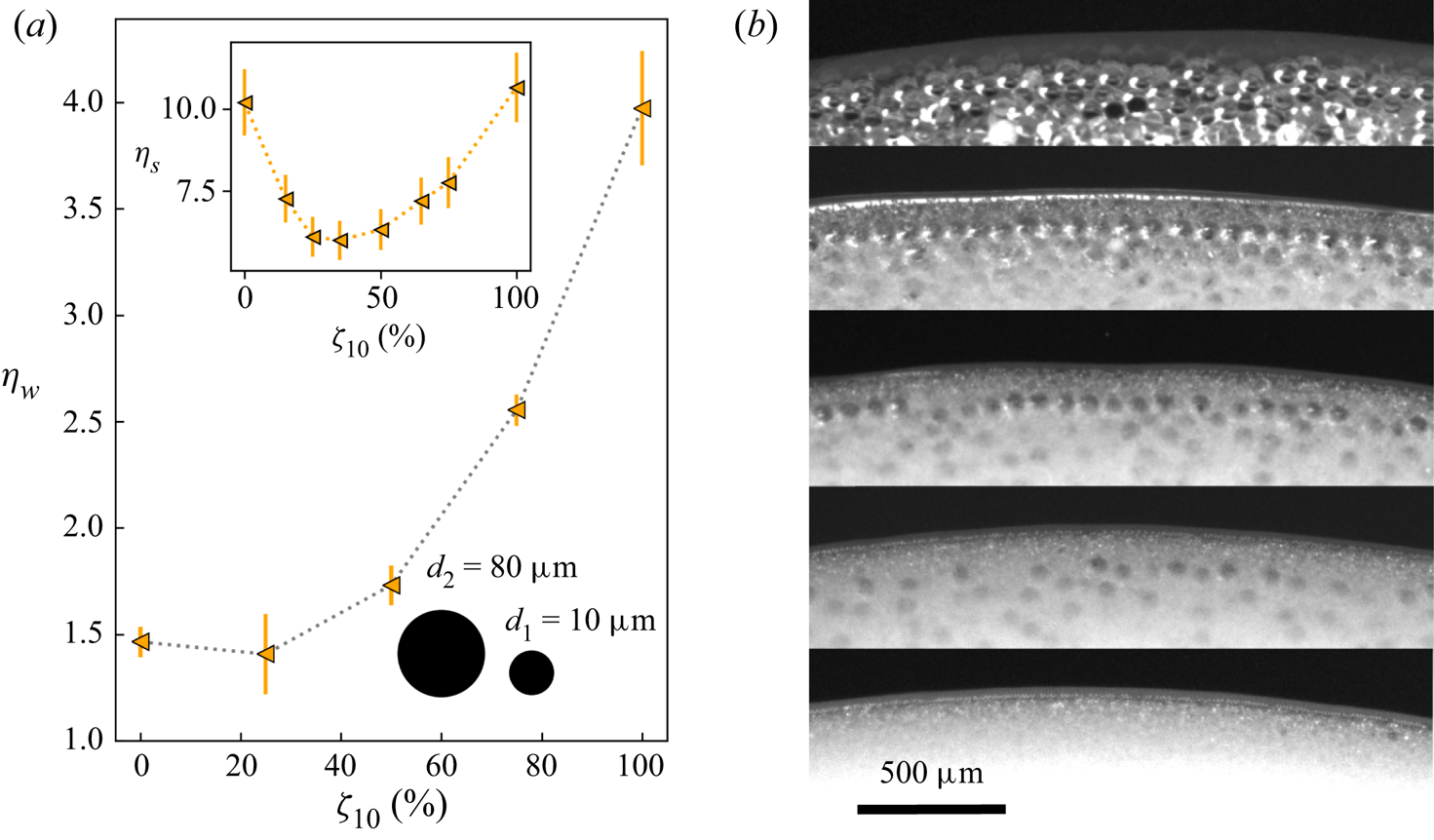
Figure 7. Experimental results for suspension blends with fixed ![]() $d_1=10\,\mathrm {\mu }$m and
$d_1=10\,\mathrm {\mu }$m and ![]() $d_2=80\,\mathrm {\mu }$m, and varying
$d_2=80\,\mathrm {\mu }$m, and varying ![]() $\zeta _{10}$ at
$\zeta _{10}$ at ![]() $\phi =0.4$. (a) Relative wetting viscosity
$\phi =0.4$. (a) Relative wetting viscosity ![]() $\eta _w$ as a function of the fraction of the small particles in the solid phase,
$\eta _w$ as a function of the fraction of the small particles in the solid phase, ![]() $\zeta _{10}$. Inset: bulk viscosity
$\zeta _{10}$. Inset: bulk viscosity ![]() $\eta _s$ of the corresponding suspensions versus
$\eta _s$ of the corresponding suspensions versus ![]() $\zeta _{10}$. The dotted lines are guides for the eyes. (b) Top-view pictures taken when
$\zeta _{10}$. The dotted lines are guides for the eyes. (b) Top-view pictures taken when ![]() $\theta _{app}=35^{\circ }$ at
$\theta _{app}=35^{\circ }$ at ![]() $h=50\,\mathrm {\mu }$m for
$h=50\,\mathrm {\mu }$m for ![]() $\zeta _{10}=0\,\%,25\,\%,50\,\%,75\,\%,100\,\%$ from top to bottom, respectively.
$\zeta _{10}=0\,\%,25\,\%,50\,\%,75\,\%,100\,\%$ from top to bottom, respectively.
Top-view pictures of the suspension near the moving contact line provide information about the origin of the discrepancy between the apparent viscosity extracted from bulk rheology and its counterpart extracted from the dynamics of spreading; see figure 7(b). As shown previously in the monomodal case (Zhao et al. Reference Zhao, Oléron, Pelosse, Limat, Guazzelli and Roché2020), there is a pure-fluid region devoid of particles near the contact line. We observe a similar region in the monomodal and bimodal cases depicted in figure 7(b). The extent of this region is larger in the case of the 80 ![]() $\mathrm {\mu }$m particles,
$\mathrm {\mu }$m particles, ![]() $\zeta _{10}=0\,\%$ (top picture), than in the 10
$\zeta _{10}=0\,\%$ (top picture), than in the 10 ![]() $\mathrm {\mu }$m case,
$\mathrm {\mu }$m case, ![]() $\zeta _{10}=100\,\%$ (bottom picture). For intermediate values of
$\zeta _{10}=100\,\%$ (bottom picture). For intermediate values of ![]() $\zeta _{10}$, the 10
$\zeta _{10}$, the 10 ![]() $\mathrm {\mu }$m particles are able to move in between the 80
$\mathrm {\mu }$m particles are able to move in between the 80 ![]() $\mathrm {\mu }$m particles. The particles closest to the contact line arrange in an orderly, crystalline structure. This ordering is particularly marked for the 80
$\mathrm {\mu }$m particles. The particles closest to the contact line arrange in an orderly, crystalline structure. This ordering is particularly marked for the 80 ![]() $\mathrm {\mu }$m particles, seen in the top pictures of figure 7(b). The large 80
$\mathrm {\mu }$m particles, seen in the top pictures of figure 7(b). The large 80 ![]() $\mathrm {\mu }$m particles seem to be maintained at the same distance from the contact line as small 10
$\mathrm {\mu }$m particles seem to be maintained at the same distance from the contact line as small 10 ![]() $\mathrm {\mu }$m particles are added, i.e. as
$\mathrm {\mu }$m particles are added, i.e. as ![]() $\zeta _{10}$ is increased, but their linear density decreases.
$\zeta _{10}$ is increased, but their linear density decreases.
The images displayed in figure 7(b) are obtained for the same dynamic contact angle ![]() $\theta _{app}=35^{\circ }$. The real capillary number of all these experiments (using the effective viscosity of the suspension,
$\theta _{app}=35^{\circ }$. The real capillary number of all these experiments (using the effective viscosity of the suspension, ![]() $Ca = \eta _w\,Ca_0$) is thus constant, and equal here to approximately
$Ca = \eta _w\,Ca_0$) is thus constant, and equal here to approximately ![]() $2\times 10^{-3}$, leading to
$2\times 10^{-3}$, leading to ![]() $h^\star \sim 100\,\mathrm {\mu }$m according to (2.10) and using the prefactor inferred from figure 5(d), i.e.
$h^\star \sim 100\,\mathrm {\mu }$m according to (2.10) and using the prefactor inferred from figure 5(d), i.e. ![]() $h^\star \simeq 0.3 \ell _c\,Ca^{1/3}$. The discrepancy between the viscosity measured in the bulk and that estimated from spreading experiments is now clear. The 80
$h^\star \simeq 0.3 \ell _c\,Ca^{1/3}$. The discrepancy between the viscosity measured in the bulk and that estimated from spreading experiments is now clear. The 80 ![]() $\mathrm {\mu }$m particles experience strong confinement in the viscous–capillary region since
$\mathrm {\mu }$m particles experience strong confinement in the viscous–capillary region since ![]() $h^\star \sim d_{2}$, and only a few of them can penetrate this region. In contrast,
$h^\star \sim d_{2}$, and only a few of them can penetrate this region. In contrast, ![]() $h^\star$ is 10 times larger than the diameter of the 10
$h^\star$ is 10 times larger than the diameter of the 10 ![]() $\mathrm {\mu }$m particles. Even if these small particles experience confinement close to the contact line, a significant part of the viscous–capillary region is filled with a dense phase of small particles akin to a suspension bulk. Thus the contribution of the 10
$\mathrm {\mu }$m particles. Even if these small particles experience confinement close to the contact line, a significant part of the viscous–capillary region is filled with a dense phase of small particles akin to a suspension bulk. Thus the contribution of the 10 ![]() $\mathrm {\mu }$m particles to dissipation in the Cox–Voinov region is expected to be larger than that of the 80
$\mathrm {\mu }$m particles to dissipation in the Cox–Voinov region is expected to be larger than that of the 80 ![]() $\mathrm {\mu }$m particles, as reported in experiments with monomodal suspensions. In the case of the bimodal suspensions studied in this section, increasing the small particle fraction
$\mathrm {\mu }$m particles, as reported in experiments with monomodal suspensions. In the case of the bimodal suspensions studied in this section, increasing the small particle fraction ![]() $\zeta _{10}$ is expected to lead to a continuous increase in
$\zeta _{10}$ is expected to lead to a continuous increase in ![]() $\eta _w$, as observed in figure 7(a).
$\eta _w$, as observed in figure 7(a).
5.2. Varying the size of the large particles
We now turn to bimodal suspensions consisting of 10 ![]() $\mathrm {\mu }$m particles but with large particles of variable diameter (i.e.
$\mathrm {\mu }$m particles but with large particles of variable diameter (i.e. ![]() $d_2= 20, 40, 80\,\mathrm {\mu }$m) at
$d_2= 20, 40, 80\,\mathrm {\mu }$m) at ![]() $\zeta _{small}=25\,\%$. Bimodal suspensions formulated this way should have a bulk viscosity close to the minimum observed on the curves of figure 2(b). Figure 8(a) shows that the apparent wetting viscosity of these suspensions is maximum in the monomodal case, and decreases for bimodal suspensions as the large particle size increases, i.e. with increasing
$\zeta _{small}=25\,\%$. Bimodal suspensions formulated this way should have a bulk viscosity close to the minimum observed on the curves of figure 2(b). Figure 8(a) shows that the apparent wetting viscosity of these suspensions is maximum in the monomodal case, and decreases for bimodal suspensions as the large particle size increases, i.e. with increasing ![]() $d_2/d_1$. This result again confirms that particles with a diameter much smaller than
$d_2/d_1$. This result again confirms that particles with a diameter much smaller than ![]() $h^\star$ increase the dissipation in the Cox–Voinov region. This trend is similar to that of the bulk viscosity
$h^\star$ increase the dissipation in the Cox–Voinov region. This trend is similar to that of the bulk viscosity ![]() $\eta _s$, with increasing
$\eta _s$, with increasing ![]() $d_2/d_1$ for
$d_2/d_1$ for ![]() $\zeta _{small}=25\,\%$; see the inset of figure 8(a). However, the magnitude of the size-ratio effect comes from two distinct physical origins. For example, the value of the apparent wetting viscosity
$\zeta _{small}=25\,\%$; see the inset of figure 8(a). However, the magnitude of the size-ratio effect comes from two distinct physical origins. For example, the value of the apparent wetting viscosity ![]() $\eta _w$ for
$\eta _w$ for ![]() $d_2/d_1=8$ is close to that of the suspending fluid, whereas the value of the bulk viscosity
$d_2/d_1=8$ is close to that of the suspending fluid, whereas the value of the bulk viscosity ![]() $\eta _s$ is much larger. The decrease of the bulk viscosity comes from the size ratio affecting the maximum packing fraction
$\eta _s$ is much larger. The decrease of the bulk viscosity comes from the size ratio affecting the maximum packing fraction ![]() $\phi _c$ (larger for large
$\phi _c$ (larger for large ![]() $d_2/d_1$), while the wetting viscosity reduction comes from confinement effects near the contact line as the dissipation is greater for particles that can efficiently reach the dissipation region near the contact line (
$d_2/d_1$), while the wetting viscosity reduction comes from confinement effects near the contact line as the dissipation is greater for particles that can efficiently reach the dissipation region near the contact line (![]() $d\ll h^\star$). In the case of figure 8, the small particles are participating less in the dissipation as
$d\ll h^\star$). In the case of figure 8, the small particles are participating less in the dissipation as ![]() $\zeta _{10}$ is small and the overall dissipation is set mostly by the large particles.
$\zeta _{10}$ is small and the overall dissipation is set mostly by the large particles.
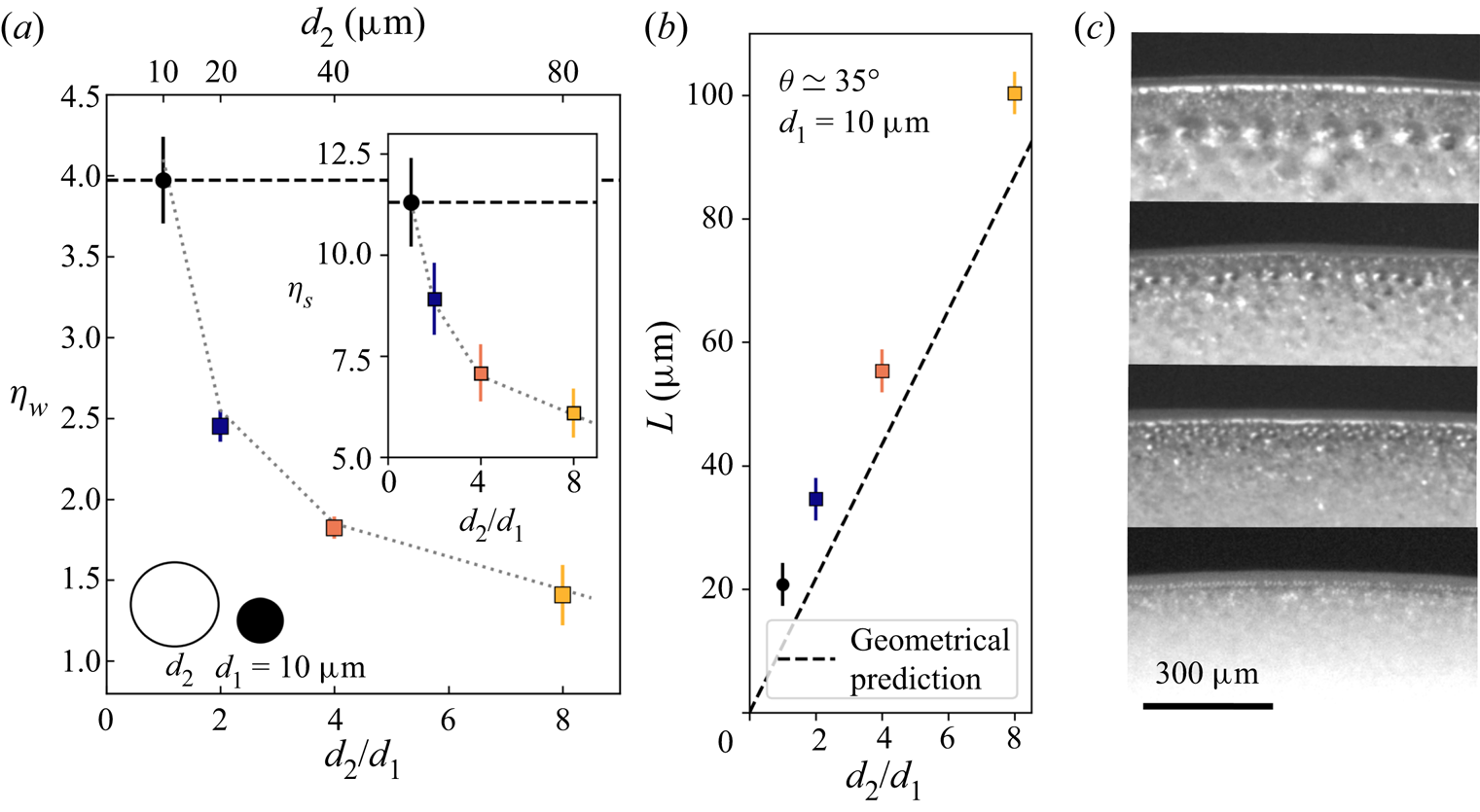
Figure 8. Experimental results for ![]() $10\,\mathrm {\mu }$m monomodal suspension (
$10\,\mathrm {\mu }$m monomodal suspension (![]() $\bullet$ symbols) and bimodal blends with
$\bullet$ symbols) and bimodal blends with ![]() ${d_1=10\,\mathrm {\mu }}$m and varying
${d_1=10\,\mathrm {\mu }}$m and varying ![]() $d_2$ (
$d_2$ (![]() $= 20$, 40, 80
$= 20$, 40, 80 ![]() $\mathrm {\mu }$m) at fixed
$\mathrm {\mu }$m) at fixed ![]() $\zeta _{10}=25\,\%$ and
$\zeta _{10}=25\,\%$ and ![]() $\phi =0.4$ (
$\phi =0.4$ (![]() $\square$ symbols). (a) Relative wetting viscosity
$\square$ symbols). (a) Relative wetting viscosity ![]() $\eta _w$ as a function of the size ratio
$\eta _w$ as a function of the size ratio ![]() $d_2/d_1$. The horizontal dashed line indicates the viscosity value for the monomodal suspension consisting of the sole small particles of size
$d_2/d_1$. The horizontal dashed line indicates the viscosity value for the monomodal suspension consisting of the sole small particles of size ![]() $10\,\mathrm {\mu }$m. Inset: bulk viscosity
$10\,\mathrm {\mu }$m. Inset: bulk viscosity ![]() $\eta _s$ of the corresponding suspensions versus
$\eta _s$ of the corresponding suspensions versus ![]() $d_2/d_1$. The grey dotted lines are guides for the eyes. (b) Distance of approach of the large particles for the bimodal suspensions with
$d_2/d_1$. The grey dotted lines are guides for the eyes. (b) Distance of approach of the large particles for the bimodal suspensions with ![]() $d_1=10\,\mathrm {\mu }$m and
$d_1=10\,\mathrm {\mu }$m and ![]() $\zeta _{10}=25\,\%$ (
$\zeta _{10}=25\,\%$ (![]() $\square$ symbols) and the
$\square$ symbols) and the ![]() $10\,\mathrm {\mu }$m monomodal suspension (
$10\,\mathrm {\mu }$m monomodal suspension (![]() $\bullet$ symbol). The dashed line corresponds to the geometrical prediction (5.1). (c) Top-view pictures taken when
$\bullet$ symbol). The dashed line corresponds to the geometrical prediction (5.1). (c) Top-view pictures taken when ![]() $\theta _{app}=35^{\circ }$ at
$\theta _{app}=35^{\circ }$ at ![]() $h=50\,\mathrm {\mu }$m for monomodal suspension of size
$h=50\,\mathrm {\mu }$m for monomodal suspension of size ![]() $10\,\mathrm {\mu }$m and bimodal suspensions with
$10\,\mathrm {\mu }$m and bimodal suspensions with ![]() $(d_1,\zeta _{10})=(10\,\mathrm {\mu }{\rm m}, 25\,\%)$ and
$(d_1,\zeta _{10})=(10\,\mathrm {\mu }{\rm m}, 25\,\%)$ and ![]() $d_2 = 20, 40, 80\,\mathrm {\mu }$m (from bottom to top, respectively).
$d_2 = 20, 40, 80\,\mathrm {\mu }$m (from bottom to top, respectively).
Figure 8(b) shows that the distance of approach of the large particles, ![]() $L$, increases with their diameter. This measured length follows the prediction of a geometrical model describing the minimal distance of approach of a particle in a wedge,
$L$, increases with their diameter. This measured length follows the prediction of a geometrical model describing the minimal distance of approach of a particle in a wedge,
where ![]() $\theta _{app}$ is the apparent contact angle near the contact line. We find that this distance is not affected sensibly by the presence of the small particles. The relation (5.1) holds for both monomodal and bimodal cases using the diameter of the corresponding particles. In the monomodal case, it determines the size of the depleted region (Zhao et al. Reference Zhao, Oléron, Pelosse, Limat, Guazzelli and Roché2020).
$\theta _{app}$ is the apparent contact angle near the contact line. We find that this distance is not affected sensibly by the presence of the small particles. The relation (5.1) holds for both monomodal and bimodal cases using the diameter of the corresponding particles. In the monomodal case, it determines the size of the depleted region (Zhao et al. Reference Zhao, Oléron, Pelosse, Limat, Guazzelli and Roché2020).
The top-view pictures in figure 8(c) confirm the existence of size segregation at the contact line as already mentioned in § 5.1. The large particles form ordered rows behind the small particle region as already noted in § 5.1. However, we observe that the 10 ![]() $\mathrm {\mu }$m particles do not go through the network formed by the 20
$\mathrm {\mu }$m particles do not go through the network formed by the 20 ![]() $\mathrm {\mu }$m particles; see the bottom image of figure 8(c). We move to this aspect of suspension spreading in the following subsection, with clearer visualisations with larger particles.
$\mathrm {\mu }$m particles; see the bottom image of figure 8(c). We move to this aspect of suspension spreading in the following subsection, with clearer visualisations with larger particles.
5.3. Varying the size of the small particles
Figure 9(a) gathers the wetting viscosity ![]() $\eta _w$ of the monomodal 80
$\eta _w$ of the monomodal 80 ![]() $\mathrm {\mu }$m suspension and bimodal blends having a fixed
$\mathrm {\mu }$m suspension and bimodal blends having a fixed ![]() $d_2=80\,\mathrm {\mu }$m and varying
$d_2=80\,\mathrm {\mu }$m and varying ![]() $d_1$, and
$d_1$, and ![]() $\zeta _{small}$. When the solid phase consists mainly of small particles (
$\zeta _{small}$. When the solid phase consists mainly of small particles (![]() $\zeta _{small}=75\,\%$),
$\zeta _{small}=75\,\%$), ![]() $\eta _w$ decreases with increasing
$\eta _w$ decreases with increasing ![]() $d_1$, as seen in figure 9(a). This observation confirms again that the wetting viscosity is set by the possibility of particles having diameter much smaller than
$d_1$, as seen in figure 9(a). This observation confirms again that the wetting viscosity is set by the possibility of particles having diameter much smaller than ![]() $h^\star$ approaching close to the contact line. However, a continuous decrease of
$h^\star$ approaching close to the contact line. However, a continuous decrease of ![]() $\eta _w$ with
$\eta _w$ with ![]() $d_1$ is absent when
$d_1$ is absent when ![]() $\zeta _{small}=25\,\%$ or
$\zeta _{small}=25\,\%$ or ![]() $\zeta _{small}=50\,\%$, i.e. when large particles constitute a significant portion of the solid blend. The relative wetting viscosity
$\zeta _{small}=50\,\%$, i.e. when large particles constitute a significant portion of the solid blend. The relative wetting viscosity ![]() $\eta _w$ reaches a maximum around
$\eta _w$ reaches a maximum around ![]() $d_1/d_2=0.25$, but it otherwise shows low values, even lower than those obtained for the monomodal suspensions of 80
$d_1/d_2=0.25$, but it otherwise shows low values, even lower than those obtained for the monomodal suspensions of 80 ![]() $\mathrm {\mu }$m particles for
$\mathrm {\mu }$m particles for ![]() $d_1/d_2 = 0.5$. In other words, for
$d_1/d_2 = 0.5$. In other words, for ![]() $\zeta _{small}=25\,\%\unicode{x2013}50\,\%$, the apparent wetting viscosity of the 10–80 and 40–80
$\zeta _{small}=25\,\%\unicode{x2013}50\,\%$, the apparent wetting viscosity of the 10–80 and 40–80 ![]() $\mathrm {\mu }$m blends are particularly low compared to that of the 20–80
$\mathrm {\mu }$m blends are particularly low compared to that of the 20–80 ![]() $\mathrm {\mu }$m and even to that of the monomodal 80
$\mathrm {\mu }$m and even to that of the monomodal 80 ![]() $\mathrm {\mu }$m suspension.
$\mathrm {\mu }$m suspension.
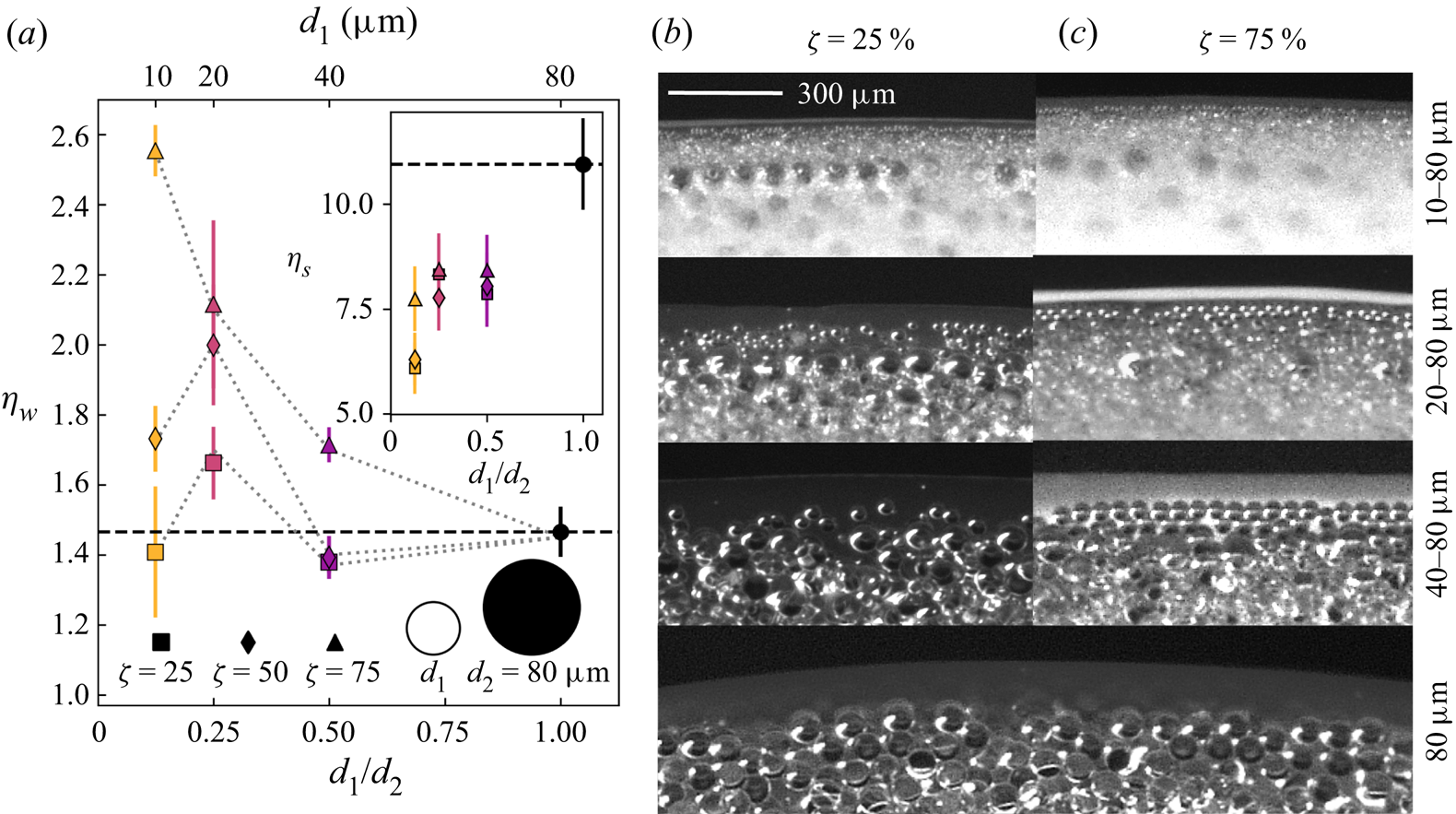
Figure 9. Experimental results for suspension blends with ![]() $d_2=80\,\mathrm {\mu }$m and varying
$d_2=80\,\mathrm {\mu }$m and varying ![]() $d_1$ (
$d_1$ (![]() $= 10, 20, 40\,\mathrm {\mu }$m) at
$= 10, 20, 40\,\mathrm {\mu }$m) at ![]() $\zeta _{small}=25\,\%$ (
$\zeta _{small}=25\,\%$ (![]() $\square$ symbols),
$\square$ symbols), ![]() $\zeta _{small}=50\,\%$ (
$\zeta _{small}=50\,\%$ (![]() $\lozenge$ symbols), and
$\lozenge$ symbols), and ![]() $\zeta _{small}=75\,\%$ (
$\zeta _{small}=75\,\%$ (![]() $\triangle$ symbols). (a) Relative wetting viscosity
$\triangle$ symbols). (a) Relative wetting viscosity ![]() $\eta _w$ as a function of
$\eta _w$ as a function of ![]() $d_1/d_2$. The dashed line indicates the viscosity value for the monomodal suspension consisting of the sole large particles of size
$d_1/d_2$. The dashed line indicates the viscosity value for the monomodal suspension consisting of the sole large particles of size ![]() $80\,\mathrm {\mu }$m. Inset: bulk viscosity of the corresponding suspensions. (b,c) Top-view pictures taken when
$80\,\mathrm {\mu }$m. Inset: bulk viscosity of the corresponding suspensions. (b,c) Top-view pictures taken when ![]() $\theta _{app}=35^{\circ }$ at
$\theta _{app}=35^{\circ }$ at ![]() $h=50\,\mathrm {\mu }$m for bimodal suspensions, with
$h=50\,\mathrm {\mu }$m for bimodal suspensions, with ![]() $d_2=80\,\mathrm {\mu }$m,
$d_2=80\,\mathrm {\mu }$m, ![]() $\zeta _{small}=25\,\%$ (b), and
$\zeta _{small}=25\,\%$ (b), and ![]() $\zeta _{small}=75\,\%$ (c). Small particle size is increasing from top to bottom (
$\zeta _{small}=75\,\%$ (c). Small particle size is increasing from top to bottom (![]() $d_1=10, 20, 40\,\mathrm {\mu }$m, and monomodal suspension of size
$d_1=10, 20, 40\,\mathrm {\mu }$m, and monomodal suspension of size ![]() $80\,\mathrm {\mu }$m).
$80\,\mathrm {\mu }$m).
The top views shown in figure 9(b) provide some clues about the variation of the apparent wetting viscosity. At ![]() $\zeta _{small}=25\,\%$, for small values of
$\zeta _{small}=25\,\%$, for small values of ![]() $d_1/d_2$ (top two pictures), small particles flow through the large particle network and get close to the contact line. In contrast, for
$d_1/d_2$ (top two pictures), small particles flow through the large particle network and get close to the contact line. In contrast, for ![]() $d_1/d_2=0.5$ (third picture from the top), the presence of 40
$d_1/d_2=0.5$ (third picture from the top), the presence of 40 ![]() $\mathrm {\mu }$m particles disrupts the ordering of the 80
$\mathrm {\mu }$m particles disrupts the ordering of the 80 ![]() $\mathrm {\mu }$m particles, compared to the other cases. A similar trend is observed for
$\mathrm {\mu }$m particles, compared to the other cases. A similar trend is observed for ![]() $\zeta _{small}=50\,\%$. In contrast, for
$\zeta _{small}=50\,\%$. In contrast, for ![]() $\zeta _{small}=75\,\%$, there is a large amount of ordered small particles near the contact line in front of the large spheres, as seen in figure 9(c).
$\zeta _{small}=75\,\%$, there is a large amount of ordered small particles near the contact line in front of the large spheres, as seen in figure 9(c).
Geometrical considerations can explain the effect observed for ![]() $d_1/d_2=0.5$. Two large particles with radius
$d_1/d_2=0.5$. Two large particles with radius ![]() $R_2=d_2/2$ sitting on the surface of a solid come to contact if the distance
$R_2=d_2/2$ sitting on the surface of a solid come to contact if the distance ![]() $l$ between them goes to zero; see figure 10. A small particle of radius
$l$ between them goes to zero; see figure 10. A small particle of radius ![]() $R_1$ can pass through the hole between the two particles and the solid surface if its radius is at most
$R_1$ can pass through the hole between the two particles and the solid surface if its radius is at most ![]() $R_1=R_2/4$. Consequently, while the 10 and 20
$R_1=R_2/4$. Consequently, while the 10 and 20 ![]() $\mathrm {\mu }$m particles can flow through the interstices created by the large 80
$\mathrm {\mu }$m particles can flow through the interstices created by the large 80 ![]() $\mathrm {\mu }$m particles, the 40
$\mathrm {\mu }$m particles, the 40 ![]() $\mathrm {\mu }$m particles cannot. Instead, these particles induce defects in the 80
$\mathrm {\mu }$m particles cannot. Instead, these particles induce defects in the 80 ![]() $\mathrm {\mu }$m particle network, leading to the distortion of the large-particle matrix when the portion of small particles is not too large (
$\mathrm {\mu }$m particle network, leading to the distortion of the large-particle matrix when the portion of small particles is not too large (![]() $\zeta _{small} \lesssim 50\,\%$). This loss of organisation seems detrimental to the local dissipation. These geometrical considerations coupled with the wetting viscosity measurements suggest that the structure and therefore the local solid volume fraction near the contact line is a key element to explain the value of the wetting viscosity of granular suspensions.
$\zeta _{small} \lesssim 50\,\%$). This loss of organisation seems detrimental to the local dissipation. These geometrical considerations coupled with the wetting viscosity measurements suggest that the structure and therefore the local solid volume fraction near the contact line is a key element to explain the value of the wetting viscosity of granular suspensions.
Figure 10. Sketch of two large particles separated by a small one on a solid plane.
However, the above geometrical arguments cannot explain the lower values of ![]() $\eta _w$ for the 10–80
$\eta _w$ for the 10–80 ![]() $\mathrm {\mu }$m blends compared to those of the 20–80
$\mathrm {\mu }$m blends compared to those of the 20–80 ![]() $\mathrm {\mu }$m blends for
$\mathrm {\mu }$m blends for ![]() $\zeta _{small}=25\unicode{x2013}50\,\%$ in figure 9(a). Instead, this lessening effect may be attributed to bulk effects impacting on the variation of the wetting viscosity. The inset of figure 9(a) indicates that the bulk viscosity is significantly smaller for the 10–80
$\zeta _{small}=25\unicode{x2013}50\,\%$ in figure 9(a). Instead, this lessening effect may be attributed to bulk effects impacting on the variation of the wetting viscosity. The inset of figure 9(a) indicates that the bulk viscosity is significantly smaller for the 10–80 ![]() $\mathrm {\mu }$m blends than for the 20–80
$\mathrm {\mu }$m blends than for the 20–80 ![]() $\mathrm {\mu }$m blends for a given value of
$\mathrm {\mu }$m blends for a given value of ![]() $\zeta _{small}$. Moreover, the bulk viscosity for
$\zeta _{small}$. Moreover, the bulk viscosity for ![]() $\zeta _{small}=25\unicode{x2013}50\,\%$ is lower than for
$\zeta _{small}=25\unicode{x2013}50\,\%$ is lower than for ![]() $\zeta _{small}=75\,\%$ as it corresponds to the minimum bulk viscosity for bimodal blends, as seen in figure 2(b). Bulk effects are therefore evidenced in this specific example and impact the value of
$\zeta _{small}=75\,\%$ as it corresponds to the minimum bulk viscosity for bimodal blends, as seen in figure 2(b). Bulk effects are therefore evidenced in this specific example and impact the value of ![]() $\eta _w$ as they happen to overcome size effects.
$\eta _w$ as they happen to overcome size effects.
It is worth noting that in the monomodal case, variation of the wetting viscosity can come only from the confinement effect near the contact line, as the bulk viscosity does not vary with particle size, as shown in figure 2(a). The case of fixed ![]() $d_2$ and increasing
$d_2$ and increasing ![]() $d_1$ evidences two competing effects: confinement effect governing the particle ability to approach the contact line, and the variation of the bulk viscosity with
$d_1$ evidences two competing effects: confinement effect governing the particle ability to approach the contact line, and the variation of the bulk viscosity with ![]() $\zeta _{small}$ and
$\zeta _{small}$ and ![]() $d_1/d_2$. In conclusion, for bimodal suspensions, a high wetting viscosity results from a complex compromise between a high fraction of small particles
$d_1/d_2$. In conclusion, for bimodal suspensions, a high wetting viscosity results from a complex compromise between a high fraction of small particles ![]() $\zeta _{small}$, a large size ratio
$\zeta _{small}$, a large size ratio ![]() $d_2/d_1$, and a high bulk viscosity
$d_2/d_1$, and a high bulk viscosity ![]() $\eta _s$, in addition to size effects already demonstrated.
$\eta _s$, in addition to size effects already demonstrated.
6. Concluding remarks
The spreading of large drops onto a solid substrate is a rich and complex phenomenon by itself. Adding particles affects the spreading dynamics in a non-trivial way as there exists a high degree of inhomogeneity in the particulate drop going from a random solid bulk phase far from the contact line (![]() $h\gg d$), to ordered dense monolayers when particles undergo confinement (
$h\gg d$), to ordered dense monolayers when particles undergo confinement (![]() $h\gtrsim d$), and finally to a particle-depleted region in the very close vicinity of the contact line (
$h\gtrsim d$), and finally to a particle-depleted region in the very close vicinity of the contact line (![]() $h< d$). Using granular suspensions nonetheless offers an interesting way to investigate dynamical wetting as one can take advantage of this complex particulate organisation to modify locally the dissipation near the contact line.
$h< d$). Using granular suspensions nonetheless offers an interesting way to investigate dynamical wetting as one can take advantage of this complex particulate organisation to modify locally the dissipation near the contact line.
Dimensional analysis of the equation governing the spreading of large drops (![]() $Bo\gtrsim 1$) shows that the profile of the liquid/gas interface between the droplet and the atmosphere is set by a viscous–capillary balance as long as its height is smaller than a length scale
$Bo\gtrsim 1$) shows that the profile of the liquid/gas interface between the droplet and the atmosphere is set by a viscous–capillary balance as long as its height is smaller than a length scale ![]() $h^\star \sim \ell _c\,Ca^{1/3}$ beyond which the drop profile becomes also sensitive to gravity. This scaling has been validated in the present work for both simple fluids and suspensions, and care was taken to perform measurements below this length scale (typically
$h^\star \sim \ell _c\,Ca^{1/3}$ beyond which the drop profile becomes also sensitive to gravity. This scaling has been validated in the present work for both simple fluids and suspensions, and care was taken to perform measurements below this length scale (typically ![]() $50\,\mathrm {\mu }$m) to ensure that gravity is negligible across the range of capillary numbers that we can probe. Drops of granular suspensions were then seen to follow the Cox–Voinov law relating the contact angle to the capillary number in a way similar to that found for regular Newtonian fluids. However, the relative apparent viscosity
$50\,\mathrm {\mu }$m) to ensure that gravity is negligible across the range of capillary numbers that we can probe. Drops of granular suspensions were then seen to follow the Cox–Voinov law relating the contact angle to the capillary number in a way similar to that found for regular Newtonian fluids. However, the relative apparent viscosity ![]() $\eta _w$ involved in the capillary number was found to differ from that of the bulk suspension,
$\eta _w$ involved in the capillary number was found to differ from that of the bulk suspension, ![]() $\eta _s$.
$\eta _s$.
In the present experiments, the typical magnitude of ![]() $h^\star \sim 100\,\mathrm {\mu }$m lies in the size range of the non-Brownian particles used. Therefore, dissipation is affected by particles during the spreading when
$h^\star \sim 100\,\mathrm {\mu }$m lies in the size range of the non-Brownian particles used. Therefore, dissipation is affected by particles during the spreading when ![]() $d\lesssim h^\star$, while the spreading dynamics is close to that of the pure fluid when
$d\lesssim h^\star$, while the spreading dynamics is close to that of the pure fluid when ![]() $d\gtrsim h^\star$, i.e. when particles cannot reach the viscous–capillary region. These geometrical considerations help to rationalise that the relative wetting viscosity
$d\gtrsim h^\star$, i.e. when particles cannot reach the viscous–capillary region. These geometrical considerations help to rationalise that the relative wetting viscosity ![]() $\eta _w$ depends on the particle size
$\eta _w$ depends on the particle size ![]() $d$, unlike the relative bulk viscosity
$d$, unlike the relative bulk viscosity ![]() $\eta _s$, which depends only on the particle volume fraction
$\eta _s$, which depends only on the particle volume fraction ![]() $\phi$. The relative wetting viscosity
$\phi$. The relative wetting viscosity ![]() $\eta _w$ is found to be maximum for the smallest particles, and decreases to values close to the suspending fluid viscosity for
$\eta _w$ is found to be maximum for the smallest particles, and decreases to values close to the suspending fluid viscosity for ![]() $d\gtrsim 100\,\mathrm {\mu }$m even though
$d\gtrsim 100\,\mathrm {\mu }$m even though ![]() $\eta _s$ is much larger than
$\eta _s$ is much larger than ![]() $\eta _w\simeq \eta _f$ for these dense suspensions (
$\eta _w\simeq \eta _f$ for these dense suspensions (![]() $\phi =0.4$); see figure 4 of Zhao et al. (Reference Zhao, Oléron, Pelosse, Limat, Guazzelli and Roché2020). This size cut-off of the wetting viscosity is thus roughly of the order of
$\phi =0.4$); see figure 4 of Zhao et al. (Reference Zhao, Oléron, Pelosse, Limat, Guazzelli and Roché2020). This size cut-off of the wetting viscosity is thus roughly of the order of ![]() $h^\star$. This confirms that particles affect the wetting dynamics only if their size is small enough for them to reach the region dominated by viscosity.
$h^\star$. This confirms that particles affect the wetting dynamics only if their size is small enough for them to reach the region dominated by viscosity.
It may seem surprising that the Cox–Voinov law applies to such a complex system. Indeed, the possibility for the particles to occupy the viscous–capillary region in the case of a spreading droplet evolves with time as ![]() $h^\star \propto Ca^{1/3}\propto U^{1/3}$ decreases with increasing time. However, in the present experiments, the variation of
$h^\star \propto Ca^{1/3}\propto U^{1/3}$ decreases with increasing time. However, in the present experiments, the variation of ![]() $Ca$ over only one decade prevents a strong change in
$Ca$ over only one decade prevents a strong change in ![]() $h^\star$. Performing measurements in a much lower
$h^\star$. Performing measurements in a much lower ![]() $Ca$ range, while rather challenging, may reveal intriguing effects.
$Ca$ range, while rather challenging, may reveal intriguing effects.
Predicting the value of the apparent wetting viscosity when ![]() $d\lesssim h^\star$ remains a difficult task. The value of the bulk viscosity
$d\lesssim h^\star$ remains a difficult task. The value of the bulk viscosity ![]() $\eta _s$ certainly affects the wetting viscosity
$\eta _s$ certainly affects the wetting viscosity ![]() $\eta _w$. However, knowing whether this observation comes from long-range effects of the bulk phase far from the contact line is not easy. One must also keep in mind that
$\eta _w$. However, knowing whether this observation comes from long-range effects of the bulk phase far from the contact line is not easy. One must also keep in mind that ![]() $\eta _s$ varies with
$\eta _s$ varies with ![]() $\phi _c-\phi$, and strongly diverges as
$\phi _c-\phi$, and strongly diverges as ![]() $\phi \rightarrow \phi _c$. For bimodal suspensions, a lower
$\phi \rightarrow \phi _c$. For bimodal suspensions, a lower ![]() $\eta _s$ is the signature of a higher
$\eta _s$ is the signature of a higher ![]() $\phi _c$ for the corresponding solid phase and therefore produces a lower
$\phi _c$ for the corresponding solid phase and therefore produces a lower ![]() $\eta _w$, as seen in the present experiments.
$\eta _w$, as seen in the present experiments.
Another fundamental ingredient to consider in predicting ![]() $\eta _w$ is the possibility for the particles to crystallise in the viscous region. For monomodal suspensions, a monolayer of several rows of ordered particles is always observed in the vicinity of the contact line. In the bimodal case, crystallisation of the two population sizes can be hindered when the small particles cannot flow through large-particle holes, leading to a significant diminution of the apparent wetting viscosity. The structure of the particulate network near the contact line therefore impacts directly the drop-spreading dynamics captured in
$\eta _w$ is the possibility for the particles to crystallise in the viscous region. For monomodal suspensions, a monolayer of several rows of ordered particles is always observed in the vicinity of the contact line. In the bimodal case, crystallisation of the two population sizes can be hindered when the small particles cannot flow through large-particle holes, leading to a significant diminution of the apparent wetting viscosity. The structure of the particulate network near the contact line therefore impacts directly the drop-spreading dynamics captured in ![]() $\eta _w$. It also explains that even for the smallest particles for which
$\eta _w$. It also explains that even for the smallest particles for which ![]() $d< h^\star$, the wetting viscosity
$d< h^\star$, the wetting viscosity ![]() $\eta _w$ cannot reach the bulk value
$\eta _w$ cannot reach the bulk value ![]() $\eta _s$, because of this ordered region that possesses a lower viscosity.
$\eta _s$, because of this ordered region that possesses a lower viscosity.
This ordering very likely comes from the confinement of the particles near the contact line combined with the pressure of the dense particulate phase farther out. Rheological measurements combined with direct visualisation of dense colloidal suspensions (![]() $\phi =0.52$) have established clearly the relation between a significant viscosity drop and moderate confinement, owing to the ordering of the particulate phase in sliding layers (Ramaswamy et al. Reference Ramaswamy, Lin, Leahy, Ness, Fiore, Swan and Cohen2017). Conversely, for many dilute granular suspensions (
$\phi =0.52$) have established clearly the relation between a significant viscosity drop and moderate confinement, owing to the ordering of the particulate phase in sliding layers (Ramaswamy et al. Reference Ramaswamy, Lin, Leahy, Ness, Fiore, Swan and Cohen2017). Conversely, for many dilute granular suspensions (![]() $\phi \leq 0.2$), rheological measurements have exhibited a monotonous increase in dissipation for gap sizes of ten diameters and less (Peyla & Verdier Reference Peyla and Verdier2011). This apparent disagreement could be explained by the nature of the solid phase (colloidal/granular) or the dissipation mechanisms (friction/hydrodynamics) that depends on the solid volume fraction (Gallier et al. Reference Gallier, Lemaire, Peters and Lobry2014). Indeed, at low volume fraction, dissipation is due mainly to hydrodynamic interactions, while frictional contacts dominate for dense suspensions and may depend crucially on the local solid structure (Guazzelli & Pouliquen Reference Guazzelli and Pouliquen2018).
$\phi \leq 0.2$), rheological measurements have exhibited a monotonous increase in dissipation for gap sizes of ten diameters and less (Peyla & Verdier Reference Peyla and Verdier2011). This apparent disagreement could be explained by the nature of the solid phase (colloidal/granular) or the dissipation mechanisms (friction/hydrodynamics) that depends on the solid volume fraction (Gallier et al. Reference Gallier, Lemaire, Peters and Lobry2014). Indeed, at low volume fraction, dissipation is due mainly to hydrodynamic interactions, while frictional contacts dominate for dense suspensions and may depend crucially on the local solid structure (Guazzelli & Pouliquen Reference Guazzelli and Pouliquen2018).
With confinement strengthening, complex behaviours become even more apparent, e.g. viscosity minima when the gap thickness is commensurate with the particle diameters (Ramaswamy et al. Reference Ramaswamy, Lin, Leahy, Ness, Fiore, Swan and Cohen2017). Such oscillatory values of the viscosity as a function of the gap have been reported under high confinement and high shear in numerical simulations of dense granular suspensions (Fornari et al. Reference Fornari, Brandt, Chaudhuri, Lopez, Mitra and Picano2016). In the present experiments, confinement effects may, however, be less easy to quantify for the following reasons. Confinement is changing over time as the drop spreads and the local fluid thickness varies with the radial position. Moreover, it is set by a solid surface and a free interface that can deform to relax high stress, contrary to solid boundaries in a rheometer and most of the simulations.
Finally, the present work may help us to understand the spreading of suspensions that are closer to those used in industrial processes and have a wide range of particle sizes (e.g. from sub-micron to hundreds of microns in cement paste; see Bentz et al. Reference Bentz, Garboczi, Haecker and Jensen1999; Celik Reference Celik2009). Bimodal suspensions can be seen as a first step towards polydisperse solid blends as a smart choice in particle size, and fraction in a bidisperse system can partially mimic an equivalent polydisperse suspension (Pednekar, Chun & Morris Reference Pednekar, Chun and Morris2018).
Declaration of interests
The authors report no conflict of interest.








































































































































