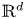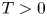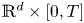1. Introduction
In the domain of telecommunication network performance evaluation, one of the oldest models used for the dynamics of moving nodes is the random direction mobility model (for reference, see [Reference Royer, Melliar-Smith and Moser15] or [Reference Camp, Boleng and Davies5]). Nowadays, it is available within standard evaluation frameworks surveyed in [Reference Dede, Förster, Hernández-Orallo, Herrera-Tapia, Kuladinithi, Kuppusamy, Manzoni, bin Muslim, Udugama and Vatandas6]. The random direction model belongs to the group of standard, basic models used in nearly every performance evaluation to understand the elementary properties in well-known standard scenarios before considering more sophisticated and more realistic ones. Within a performance analysis, it is common to analyze a series of states of the model indexed by time. However, for networks that are delay tolerant, such as opportunistic networks, longer periods of time are more interesting. Opportunistic networks follow the store-carry-forward paradigm, where the movement of the devices is used to carry the messages to their destinations. In this domain, it is particularly interesting to answer certain questions for a longer period of time such as:
(1) Will a message reach a node (at all)?
(2) Does a node stay isolated?
Since it is clear that mobility changes the properties of a network, there are first results to consider the dynamics of mobile communication networks, see [Reference Díaz, Mitsche and Pérez-Giménez7] for example, starting with discrete snapshots of the random direction model on the torus. In [Reference Döring, Faraud and König8], the nodes of the telecommunication network move according to the random waypoint model and the connection time of two random nodes is studied. The very recent work [Reference Hirsch, Jahnel and Cali12] also deals with a dynamic Boolean model, where Hirsch, Jahnel, and Cali consider two different kinds of movement, small movements with a low speed and a few large movements with a high speed. They derive asymptotic formulas for the percolation time and the ![]() $k$-hop connection time.
$k$-hop connection time.
In this paper, we propose the time bounded cylinder (TBC) model which enables an analysis over a complete timeframe by modeling the movement in ![]() $\mathbb{R} ^d$ and the resulting communication capabilities via cylinders in
$\mathbb{R} ^d$ and the resulting communication capabilities via cylinders in ![]() $\mathbb{R} ^d \times [0,T]$. Our first step will be to establish the theory for a rigid movement model where nodes pick a direction and speed at random and keep these for the complete timeframe. In a second step, we will propose a method to introduce changes in direction and speed.
$\mathbb{R} ^d \times [0,T]$. Our first step will be to establish the theory for a rigid movement model where nodes pick a direction and speed at random and keep these for the complete timeframe. In a second step, we will propose a method to introduce changes in direction and speed.
The following is a slightly simplified construction, which will be made more precise in Section 2. We take a set of points in ![]() $\mathbb{R} ^d \times \{0\}$ sampled from a homogeneous Poisson point process with intensity
$\mathbb{R} ^d \times \{0\}$ sampled from a homogeneous Poisson point process with intensity ![]() $0 < \gamma < \infty$. For each of these points
$0 < \gamma < \infty$. For each of these points ![]() $\mathbf {p}_{\mathbf {0}}$, we randomly choose a vector
$\mathbf {p}_{\mathbf {0}}$, we randomly choose a vector ![]() $\mathbf {v}$ from the upper half of the
$\mathbf {v}$ from the upper half of the ![]() $d+1$-dimensional unit sphere. Then, we fix some
$d+1$-dimensional unit sphere. Then, we fix some ![]() $T\geq 0$ and look at
$T\geq 0$ and look at ![]() $\mathbf {p}_{\mathbf {0}}+\mathbf {v} \in \mathbb{R} ^{d+1}$. We scale this vector to a length so that its tip
$\mathbf {p}_{\mathbf {0}}+\mathbf {v} \in \mathbb{R} ^{d+1}$. We scale this vector to a length so that its tip ![]() $\mathbf {p_T}$ lies in the affine space
$\mathbf {p_T}$ lies in the affine space ![]() $\mathbb{R} ^d \times \{T\}$. We fix some radius
$\mathbb{R} ^d \times \{T\}$. We fix some radius ![]() $r>0$ and for every point
$r>0$ and for every point ![]() $\mathbf {x}$ on this line consider the ball
$\mathbf {x}$ on this line consider the ball ![]() $\mathbb {B}_{d}(\mathbf {x},r)$. The union of these balls defines the TBC on
$\mathbb {B}_{d}(\mathbf {x},r)$. The union of these balls defines the TBC on ![]() $\mathbf {p}_{\mathbf {0}}$ with velocity
$\mathbf {p}_{\mathbf {0}}$ with velocity ![]() $\mathbf {v}$. Labeling
$\mathbf {v}$. Labeling ![]() $\mathbf {v}$ the velocity of the cylinder is a slight abuse of notation, which we will explain further down in this section. Let
$\mathbf {v}$ the velocity of the cylinder is a slight abuse of notation, which we will explain further down in this section. Let ![]() $Z$ denote the union of all cylinders created this way for some Poisson process and let
$Z$ denote the union of all cylinders created this way for some Poisson process and let ![]() $W_s = [-{s}/{2}, {s}/{2}]^d \times [0,T]$. Our first main result is this:
$W_s = [-{s}/{2}, {s}/{2}]^d \times [0,T]$. Our first main result is this:
Theorem 1.1. As ![]() $s \to \infty$, the standardized covered volume of the TBC model satisfies
$s \to \infty$, the standardized covered volume of the TBC model satisfies
We prove this by applying results derived from the Malliavin–Stein method and see that the rate of convergence in the Wasserstein distance is of order ![]() $1/\sqrt {\lambda _{d+1}(W_s)}$, see Theorem 5.1. Theorem 6.6 gives an analogous result in the setting allowing for changes in velocity. The covered volume is an interesting quantity in network simulation, as it gives some insight into the connectedness of the model. Less volume means more overlap of the communication zones. Therefore, since the TBC model considers the complete timeframe, its covered volume actually gives some insight into the achievable throughput of the network.
$1/\sqrt {\lambda _{d+1}(W_s)}$, see Theorem 5.1. Theorem 6.6 gives an analogous result in the setting allowing for changes in velocity. The covered volume is an interesting quantity in network simulation, as it gives some insight into the connectedness of the model. Less volume means more overlap of the communication zones. Therefore, since the TBC model considers the complete timeframe, its covered volume actually gives some insight into the achievable throughput of the network.
The next property considered is the number of isolated nodes, which means cylinders that do not intersect with the rest of the model within the timeframe.
Theorem 1.2. Let ![]() $\mathrm {Iso}_{\mathrm {Z}}(s)$ denote the number of cylinders with basepoint in
$\mathrm {Iso}_{\mathrm {Z}}(s)$ denote the number of cylinders with basepoint in ![]() $[-{s}/{2}, {s}/{2}]^{d}$ that do not intersect with any cylinder in the TBC model. Then,
$[-{s}/{2}, {s}/{2}]^{d}$ that do not intersect with any cylinder in the TBC model. Then,
as ![]() $s \to \infty$.
$s \to \infty$.
As before, we additionally offer a rate of convergence (see Theorem 5.2) and a version for changeable velocities (see Theorem 6.7). These nodes are of particular interest in opportunistic networks, as one can not communicate with them. Let us assume a sensor node (e.g. deployed for wildlife monitoring [Reference Anthony, Bennett, Vuran, Dwyer, Elbaum, Lacy, Engels and Wehtje1]) that can store the sensor data for some time, but has to transmit the data before it runs out of memory. If this node stays isolated for too long, it results in loss of data (e.g. inaccuracies in the wildlife tracking trace). Lastly, we come to a quantity of more theoretical significance and present a limit theorem for the Euler characteristic of the model, a precise definition of which is given in Section 5.
Theorem 1.3. For ![]() $s \to \infty$, the Euler characteristic
$s \to \infty$, the Euler characteristic ![]() $\chi$ of the TBC model
$\chi$ of the TBC model ![]() $Z$ restricted to a window
$Z$ restricted to a window ![]() $W_s=[-{s}/{2}, {s}/{2}]^{d}$ satisfies a central limit theorem, namely
$W_s=[-{s}/{2}, {s}/{2}]^{d}$ satisfies a central limit theorem, namely
Since the Euler characteristic can be defined as the alternating sum of Betti numbers, we see this result as an incentive for further mathematical studies of the Betti numbers of the TBC model. These would give great insight into the topological structure of the model, such as the number of connected components or the number of holes. From a computer science perspective, both of these would be of special interest.
2. Construction of the cylinders
We consider a stationary Poisson process ![]() $\eta$ in
$\eta$ in ![]() $\mathbb{R} ^d$ with intensity
$\mathbb{R} ^d$ with intensity ![]() $\gamma \in (0, \infty )$. We will refer to its points as the basepoints of the cylinders we are about to construct. In terms of random networks, think of these points as the positions of our nodes at time
$\gamma \in (0, \infty )$. We will refer to its points as the basepoints of the cylinders we are about to construct. In terms of random networks, think of these points as the positions of our nodes at time ![]() $0$. Next, let
$0$. Next, let ![]() $h \in (0,1)$ denote a real constant and define (Figure 1)
$h \in (0,1)$ denote a real constant and define (Figure 1)
and let ![]() $\mathbb{Q}$ denote some probability measure on
$\mathbb{Q}$ denote some probability measure on ![]() $\mathbb{M}_h^d$. We shall refer to vectors chosen according to this measure as the velocities of our cylinders.
$\mathbb{M}_h^d$. We shall refer to vectors chosen according to this measure as the velocities of our cylinders. ![]() $\mathbb{Q}$ may be discrete or continuous, we do not impose any restrictions on it other than not being allowed to depend on the position of the basepoints. As long as the velocity is chosen independently and identically for all basepoints, the arguments made in this paper will hold.
$\mathbb{Q}$ may be discrete or continuous, we do not impose any restrictions on it other than not being allowed to depend on the position of the basepoints. As long as the velocity is chosen independently and identically for all basepoints, the arguments made in this paper will hold.

Figure 1. The blue shaded area is the set of possible velocities when ![]() $d=2$.
$d=2$.
To construct a cylinder, fix some ![]() $T \in [0,\infty )$. We call this parameter the time horizon of the model. For
$T \in [0,\infty )$. We call this parameter the time horizon of the model. For ![]() $(x_1,\ldots,x_d) \in \mathbb{R} ^d$ and
$(x_1,\ldots,x_d) \in \mathbb{R} ^d$ and ![]() $u \in \mathbb{R}$, we set
$u \in \mathbb{R}$, we set ![]() $\mathbf {\hat {x}_u} = (x_1,\ldots,x_d,u) \in \mathbb{R} ^{d+1}$. Given a basepoint
$\mathbf {\hat {x}_u} = (x_1,\ldots,x_d,u) \in \mathbb{R} ^{d+1}$. Given a basepoint ![]() $\mathbf {p} \in \mathbb{R} ^d$ and a velocity
$\mathbf {p} \in \mathbb{R} ^d$ and a velocity ![]() $\mathbf {v} \in \mathbb{M}_h^d$, we define a TBC as a union of Minkowski sums.
$\mathbf {v} \in \mathbb{M}_h^d$, we define a TBC as a union of Minkowski sums. ![]() $\mathcal {C}^{d}$ shall denote the system of compact subsets of
$\mathcal {C}^{d}$ shall denote the system of compact subsets of ![]() $\mathbb{R} ^{d}$.
$\mathbb{R} ^{d}$.
Definition 2.1. Given a radius ![]() $r \geq 0$ and a time horizon
$r \geq 0$ and a time horizon ![]() $T$, the value of the function
$T$, the value of the function
 \begin{align*} & \mathrm{Cyl}_{r,T}:\ \mathbb{R}^d \times \mathbb{M}_h^d \to \mathcal{C}^{d+1}\\ & (\mathbf{p},\mathbf{v}) \mapsto \bigcup_{t \in [0,1]} \left(\left(\frac{tT}{v_{d+1}} \cdot \mathbf{v} + \mathbf{\hat{p}_0}\right) + \mathbb{B}_d(r)\right) \end{align*}
\begin{align*} & \mathrm{Cyl}_{r,T}:\ \mathbb{R}^d \times \mathbb{M}_h^d \to \mathcal{C}^{d+1}\\ & (\mathbf{p},\mathbf{v}) \mapsto \bigcup_{t \in [0,1]} \left(\left(\frac{tT}{v_{d+1}} \cdot \mathbf{v} + \mathbf{\hat{p}_0}\right) + \mathbb{B}_d(r)\right) \end{align*}
is called a time bounded cylinder.
The first ![]() $d$ entries of a vector
$d$ entries of a vector ![]() $\mathbf {v} \in \mathbb{M}_h^d$ thus encode the direction, in which a node is moving in. The entry with index
$\mathbf {v} \in \mathbb{M}_h^d$ thus encode the direction, in which a node is moving in. The entry with index ![]() $d+1$ encodes the speed at which that node is traveling in. Thus, the velocity of the node is given by
$d+1$ encodes the speed at which that node is traveling in. Thus, the velocity of the node is given by ![]() $({1}/{v_{d+1}})(v_1,\ldots,v_d)$ and we slightly abuse notation by labeling the vector
$({1}/{v_{d+1}})(v_1,\ldots,v_d)$ and we slightly abuse notation by labeling the vector ![]() $\mathbf {v} \in \mathbb{M}_h^d$ as such. We can now see that
$\mathbf {v} \in \mathbb{M}_h^d$ as such. We can now see that ![]() $v_{d+1}=1$ means a node remains in place, while smaller values for
$v_{d+1}=1$ means a node remains in place, while smaller values for ![]() $v_{d+1}$ imply faster movement.
$v_{d+1}$ imply faster movement. ![]() $v_{d+1}=0$ would imply infinite speed which, in turn, would imply cylinders of infinite length. Thus, we need the restriction
$v_{d+1}=0$ would imply infinite speed which, in turn, would imply cylinders of infinite length. Thus, we need the restriction ![]() $v_{d+1} > h$ to limit the movement speed of nodes.
$v_{d+1} > h$ to limit the movement speed of nodes.
Since ![]() $r$ and
$r$ and ![]() $T$ are constant in our model, we define
$T$ are constant in our model, we define ![]() $\mathrm {Cyl}(\mathbf {p},\mathbf {v}) := \mathrm {Cyl}_{r,T}(\mathbf {p},\mathbf {v})$ for ease of notation. It will prove fruitful to think of the cylinders themselves as elements of a Poisson point process. To that end, we take the points of
$\mathrm {Cyl}(\mathbf {p},\mathbf {v}) := \mathrm {Cyl}_{r,T}(\mathbf {p},\mathbf {v})$ for ease of notation. It will prove fruitful to think of the cylinders themselves as elements of a Poisson point process. To that end, we take the points of ![]() $\eta$ and attach the velocities as markings, cf. [Reference Last and Penrose13, Definition 5.3].
$\eta$ and attach the velocities as markings, cf. [Reference Last and Penrose13, Definition 5.3].
Definition 2.2. Let ![]() $\eta$ and
$\eta$ and ![]() $\mathbb{Q}$ be defined as above. Mark every point in the support of
$\mathbb{Q}$ be defined as above. Mark every point in the support of ![]() $\eta$ with a velocity from
$\eta$ with a velocity from ![]() $\mathbb{M}_h^d$, randomly chosen i.i.d. according to
$\mathbb{M}_h^d$, randomly chosen i.i.d. according to ![]() $\mathbb{Q}$. The resulting marked point process
$\mathbb{Q}$. The resulting marked point process ![]() $\mathbf {\xi }$, defined on
$\mathbf {\xi }$, defined on ![]() $\mathbb{R} ^d \times \mathbb{M}_h^d$, is called the process of time bounded cylinders.
$\mathbb{R} ^d \times \mathbb{M}_h^d$, is called the process of time bounded cylinders.
Lemma 2.3. ![]() $\xi$ is a Poisson point process with intensity measure
$\xi$ is a Poisson point process with intensity measure ![]() $\Lambda = \gamma \lambda _d \otimes \mathbb{Q}$.
$\Lambda = \gamma \lambda _d \otimes \mathbb{Q}$.
Proof. By Definition [Reference Last and Penrose13, Definition 5.3], ![]() $\xi$ is an independent
$\xi$ is an independent ![]() $\mathbb{Q}$-marking. The asserted statement now follows directly from the Marking Theorem [Reference Last and Penrose13, Theorem 5.6].
$\mathbb{Q}$-marking. The asserted statement now follows directly from the Marking Theorem [Reference Last and Penrose13, Theorem 5.6].
We are now in a position to define our model (Figure 2):
Definition 2.4. With the point process ![]() $\xi$ given as above, the TBC model is the random closed set
$\xi$ given as above, the TBC model is the random closed set
In this notation, we identify the random measure ![]() $\xi$ with its support.
$\xi$ with its support.

Figure 2. In the left picture, we see a cylinder with basepoint ![]() $\mathbf {p}$ and velocity
$\mathbf {p}$ and velocity ![]() $\mathbf {v}$. The arrow marks the displaced vector
$\mathbf {v}$. The arrow marks the displaced vector ![]() $\mathbf {\hat {p}_0}+\mathbf {v}$. To the right, we have an excerpt of a TBC model
$\mathbf {\hat {p}_0}+\mathbf {v}$. To the right, we have an excerpt of a TBC model ![]() $Z$ constructed on
$Z$ constructed on ![]() $\mathbb{R} ^2$.
$\mathbb{R} ^2$.
This model is a modification of the Poisson cylinder model (see e.g. [Reference Weil17]), where a cylinder in ![]() $\mathbb{R} ^d$ is constructed by choosing a
$\mathbb{R} ^d$ is constructed by choosing a ![]() $q$-dimensional,
$q$-dimensional, ![]() $0 \leq q \leq d-1$, linear subspace of
$0 \leq q \leq d-1$, linear subspace of ![]() $\mathbb{R} ^d$ and taking the Minkowksi sum of this subspace and a set taken from its orthogonal complement. A Poisson cylinder process is then simply a Poisson process on the space of these cylinders. The union
$\mathbb{R} ^d$ and taking the Minkowksi sum of this subspace and a set taken from its orthogonal complement. A Poisson cylinder process is then simply a Poisson process on the space of these cylinders. The union ![]() $Z$ of the cylinders created by such a process in the stationary case has been subject to recent study. In [Reference Heinrich and Spiess10], Heinrich and Spiess derive a central limit theorem for the
$Z$ of the cylinders created by such a process in the stationary case has been subject to recent study. In [Reference Heinrich and Spiess10], Heinrich and Spiess derive a central limit theorem for the ![]() $d$-dimensional volume of
$d$-dimensional volume of ![]() $Z$ restricted to a growing window of observation by taking into account the long-range dependencies and applying the method of cumulants. In [Reference Heinrich and Spiess11], the authors modified that limit theorem using weakened assumptions on the cylinder bases and proved a new central limit theorem for the surface content of the model. In [Reference Baci, Betken, Gusakova and Thäle2], Baci et al. were able to derive concentration inequalities for the volume and the intrinsic volumes of the model, again restricted to a compact window of observation. Assumptions of convexity on the cylinder bases and isotropy of
$Z$ restricted to a growing window of observation by taking into account the long-range dependencies and applying the method of cumulants. In [Reference Heinrich and Spiess11], the authors modified that limit theorem using weakened assumptions on the cylinder bases and proved a new central limit theorem for the surface content of the model. In [Reference Baci, Betken, Gusakova and Thäle2], Baci et al. were able to derive concentration inequalities for the volume and the intrinsic volumes of the model, again restricted to a compact window of observation. Assumptions of convexity on the cylinder bases and isotropy of ![]() $Z$ were made. In the very recent preprint [Reference Betken, Schulte and Thäle3], Betken et al. show central limit theorems for geometric funtionals for Poisson cylinder processes. The special case of
$Z$ were made. In the very recent preprint [Reference Betken, Schulte and Thäle3], Betken et al. show central limit theorems for geometric funtionals for Poisson cylinder processes. The special case of ![]() $q=1$ and spherical cylinder bases is studied in [Reference Broman and Tykesson4], where Broman and Tykesson focus on connectivity properties. In the preprint [Reference Flimmel and Heinrich9], Flimmel and Heinrich also followed the idea of cylinders constructed by marked point processes, but they restrict the underlying point process to lie on the real line. They determine the asymptotic limit for the variance of the covered area for stripes of random thickness and prove a law of large numbers.
$q=1$ and spherical cylinder bases is studied in [Reference Broman and Tykesson4], where Broman and Tykesson focus on connectivity properties. In the preprint [Reference Flimmel and Heinrich9], Flimmel and Heinrich also followed the idea of cylinders constructed by marked point processes, but they restrict the underlying point process to lie on the real line. They determine the asymptotic limit for the variance of the covered area for stripes of random thickness and prove a law of large numbers.
The classical Poisson cylinder model has two properties that do not fit to the telecommunication network: the cylinders at a fixed time step would imply ellipses as a communication zone depending on individual speed and direction—smaller angles (representing high speed) imply higher eccentricity. In a telecommunication network however, the spherical communication area is preserved at any time step independently of the movement. Secondly, almost horizontally running cylinders as in the classical Poisson cylinder model would mean that one travels with almost infinite speed. The TBC model takes up these two aspects. Since for fast movements the communication zone resembles flat tubes rather than cylinders, which has direct influence on the covered volume of their intersection. On the other hand, the cylinders which cross almost horizontally in the classical Poisson cylinder model have an impact on the connection of the cylinders because they connect many other cylinders at once. This is why we consider it interesting to study the asymptotics of the modified TBC model.
3. Preliminaries
A helpful tool in the study of random closed sets in general and in particular when proving the main results presented in this chapter are capacity functionals. These can be seen as analogues to the distribution functions of real-valued random variables for random closed sets, see [Reference Schneider and Weil16] for reference.
Definition 3.1. The capacity functional of a random closed set ![]() $Z \subset \mathbb{R} ^d$ is a mapping defined by the probability
$Z \subset \mathbb{R} ^d$ is a mapping defined by the probability
with argument ![]() $C \in \mathcal {C}^d$.
$C \in \mathcal {C}^d$.
To derive the capacity functional of our model, we will need the following definition.
Definition 3.2. Given a set ![]() $C \in \mathbb{R} ^d \times [0,T]$ and a velocity
$C \in \mathbb{R} ^d \times [0,T]$ and a velocity ![]() $\mathbf {v} \in \mathbb{M}_h^d$ we denote by
$\mathbf {v} \in \mathbb{M}_h^d$ we denote by ![]() $\bar {C}_\mathbf {v}$ the
$\bar {C}_\mathbf {v}$ the ![]() $\mathbf {v}$-shadow of
$\mathbf {v}$-shadow of ![]() $C$ onto
$C$ onto ![]() $\mathbb{R} ^d$, that is the set
$\mathbb{R} ^d$, that is the set
Intuitively speaking, the ![]() $\mathbf {v}$-shadow of a point
$\mathbf {v}$-shadow of a point ![]() $\mathbf {x} \in \mathbb{R} ^{d+1}$ is the point of intersection of the line
$\mathbf {x} \in \mathbb{R} ^{d+1}$ is the point of intersection of the line ![]() $\{\mathbf {x}+s\cdot \mathbf {v} \,|\, s \in \mathbb{R} \}$ and
$\{\mathbf {x}+s\cdot \mathbf {v} \,|\, s \in \mathbb{R} \}$ and ![]() $\mathbb{R} ^d \times \{0\}$. That is the projection of
$\mathbb{R} ^d \times \{0\}$. That is the projection of ![]() $\mathbf {x}$ on
$\mathbf {x}$ on ![]() $\mathbb{R} ^d \times \{0\}$ along
$\mathbb{R} ^d \times \{0\}$ along ![]() $\mathbf {v}$. With this, we can formulate our next lemma which gives a concise form of the capacity functional for the TBC model.
$\mathbf {v}$. With this, we can formulate our next lemma which gives a concise form of the capacity functional for the TBC model.
Lemma 3.3. For ![]() $Z(\xi )$ as in Definition 2.4 and a compact
$Z(\xi )$ as in Definition 2.4 and a compact ![]() $C \subset \mathbb{R} ^d \times [0,T]$, we have
$C \subset \mathbb{R} ^d \times [0,T]$, we have
 $$\mathbb{P}(Z(\xi) \cap C \neq \emptyset) = 1 - \exp\left(-\gamma \cdot \int_{\mathbb{M}_h^d} \lambda_d(\bar{C}_\mathbf{v} + \mathbb{B}_d(r)) \mathbb{Q}(\mathrm{d}\mathbf{v})\right).$$
$$\mathbb{P}(Z(\xi) \cap C \neq \emptyset) = 1 - \exp\left(-\gamma \cdot \int_{\mathbb{M}_h^d} \lambda_d(\bar{C}_\mathbf{v} + \mathbb{B}_d(r)) \mathbb{Q}(\mathrm{d}\mathbf{v})\right).$$
Proof. Define the set
By Lemma 2.3, ![]() $\xi$ is a Poisson point process. Thus, we have that
$\xi$ is a Poisson point process. Thus, we have that
Note that for any fixed ![]() $\mathbf {v} \in \mathbb{M}_h^d$ and
$\mathbf {v} \in \mathbb{M}_h^d$ and ![]() $\mathbf {x} \in \mathbb{R} ^d \times [0,T]$, there exists a ball of radius
$\mathbf {x} \in \mathbb{R} ^d \times [0,T]$, there exists a ball of radius ![]() $r$ in
$r$ in ![]() $\mathbb{R} ^d$ such that a cylinder with velocity
$\mathbb{R} ^d$ such that a cylinder with velocity ![]() $\mathbf {v}$ will include
$\mathbf {v}$ will include ![]() $\mathbf {x}$ if and only if its basepoint is included in that ball. The union of these balls for all points
$\mathbf {x}$ if and only if its basepoint is included in that ball. The union of these balls for all points ![]() $\mathbf {x} \in C$ coincides with the set
$\mathbf {x} \in C$ coincides with the set ![]() $\bar {C}_\mathbf {v} + \mathbb {B}_d(r)$. We get
$\bar {C}_\mathbf {v} + \mathbb {B}_d(r)$. We get
 \begin{align*} \Lambda(A_C) & = \gamma \int_{\mathbb{M}_h^d} \int_{\mathbb{R}^d} \mathbb{1}(\rm{Cyl}(\mathbf{p},\mathbf{v}) \cap C \neq \emptyset) \lambda_d (\rm{d}\mathbf{p}) \mathbb{Q}(\rm{d}\mathbf{v}) \\ & = \gamma\int_{\mathbb{M}_h^d} \int_{\bar{C}_\mathbf{v} + \mathbb{B}_d(r)} 1 \lambda_d(\rm{d}\mathbf{p}) \mathbb{Q}(\rm{d}\mathbf{v}) = \gamma \int_{\mathbb{M}_h^d} \lambda_d (\bar{C}_\mathbf{v} + \mathbb{B}_d(r)) \mathbb{Q}(\rm{d}\mathbf{v}). \end{align*}
\begin{align*} \Lambda(A_C) & = \gamma \int_{\mathbb{M}_h^d} \int_{\mathbb{R}^d} \mathbb{1}(\rm{Cyl}(\mathbf{p},\mathbf{v}) \cap C \neq \emptyset) \lambda_d (\rm{d}\mathbf{p}) \mathbb{Q}(\rm{d}\mathbf{v}) \\ & = \gamma\int_{\mathbb{M}_h^d} \int_{\bar{C}_\mathbf{v} + \mathbb{B}_d(r)} 1 \lambda_d(\rm{d}\mathbf{p}) \mathbb{Q}(\rm{d}\mathbf{v}) = \gamma \int_{\mathbb{M}_h^d} \lambda_d (\bar{C}_\mathbf{v} + \mathbb{B}_d(r)) \mathbb{Q}(\rm{d}\mathbf{v}). \end{align*}
If one wants to express the probability that a particular point ![]() $\mathbf {x} \in \mathbb{R} ^d \times [0,T]$ gets hit by the set of cylinders, then Lemma 3.3 with
$\mathbf {x} \in \mathbb{R} ^d \times [0,T]$ gets hit by the set of cylinders, then Lemma 3.3 with ![]() $C := \{\mathbf {x}\}$ yields
$C := \{\mathbf {x}\}$ yields
where ![]() $\kappa _d$ denotes the volume of the
$\kappa _d$ denotes the volume of the ![]() $d$-dimensional unit ball. To give bounds on the capacity functional, we sometimes need the following definition.
$d$-dimensional unit ball. To give bounds on the capacity functional, we sometimes need the following definition.
Definition 3.4. Given a pair ![]() $(\mathbf {p},\mathbf {v}) \in \mathbb{R} ^d \times \mathbb{M}_h^d$, we call the distance between a basepoint
$(\mathbf {p},\mathbf {v}) \in \mathbb{R} ^d \times \mathbb{M}_h^d$, we call the distance between a basepoint ![]() $(p_1,\ldots,p_d,0)$ and the projection of the endpoint
$(p_1,\ldots,p_d,0)$ and the projection of the endpoint ![]() $({T}/{v_{d+1}})(v_1,\ldots,v_{d+1}) + (p_1,\ldots,p_d,0)$ onto
$({T}/{v_{d+1}})(v_1,\ldots,v_{d+1}) + (p_1,\ldots,p_d,0)$ onto ![]() $\mathbb{R} ^d$,
$\mathbb{R} ^d$,
 $$R_{\mathbf{v}} := \left\|\frac{T}{v_{d+1}}(v_1,\ldots,v_d, 0)\right\| = T\cdot \sqrt{\frac{1}{v_{d+1}^2}-1}$$
$$R_{\mathbf{v}} := \left\|\frac{T}{v_{d+1}}(v_1,\ldots,v_d, 0)\right\| = T\cdot \sqrt{\frac{1}{v_{d+1}^2}-1}$$
the scope of the corresponding cylinder ![]() $\mathrm {Cyl}(\mathbf {p},\mathbf {v})$. We denote the maximum scope of cylinders in our model by
$\mathrm {Cyl}(\mathbf {p},\mathbf {v})$. We denote the maximum scope of cylinders in our model by ![]() $R_h := T\cdot \sqrt {{1}/{h^2}-1}$.
$R_h := T\cdot \sqrt {{1}/{h^2}-1}$.
Think of the scope of a cylinder as the radius of its ![]() $d$-dimensional area of influence. For
$d$-dimensional area of influence. For ![]() $(\mathbf {p},\mathbf {v}),(\mathbf {q},\mathbf {w}) \in \mathbb{R} ^d \times \mathbb{M}_h^d$ the cylinders
$(\mathbf {p},\mathbf {v}),(\mathbf {q},\mathbf {w}) \in \mathbb{R} ^d \times \mathbb{M}_h^d$ the cylinders ![]() $\mathrm {Cyl}(\mathbf {p},\mathbf {v})$ and
$\mathrm {Cyl}(\mathbf {p},\mathbf {v})$ and ![]() $\mathrm {Cyl}(\mathbf {q},\mathbf {w})$ can intersect only if
$\mathrm {Cyl}(\mathbf {q},\mathbf {w})$ can intersect only if ![]() $\|\mathbf {p}-\mathbf {q}\| \leq R_\mathbf {v} + R_\mathbf {w} + 2r \leq 2(R_h+r)$. Now we want to estimate
$\|\mathbf {p}-\mathbf {q}\| \leq R_\mathbf {v} + R_\mathbf {w} + 2r \leq 2(R_h+r)$. Now we want to estimate ![]() $\mathbb{P} (\mathrm {Cyl}(\mathbf {p},\mathbf {v}) \cap Z(\xi ) \neq \emptyset )$. Notice that
$\mathbb{P} (\mathrm {Cyl}(\mathbf {p},\mathbf {v}) \cap Z(\xi ) \neq \emptyset )$. Notice that ![]() $\lambda _d(\overline {\mathrm {Cyl}(\mathbf {p},\mathbf {v})_\mathbf {w}} + \mathbb {B}_d(r))$ takes its minimum in the case
$\lambda _d(\overline {\mathrm {Cyl}(\mathbf {p},\mathbf {v})_\mathbf {w}} + \mathbb {B}_d(r))$ takes its minimum in the case ![]() $\mathbf {w} = \mathbf {v}$. Then, we have that
$\mathbf {w} = \mathbf {v}$. Then, we have that ![]() $\overline {\mathrm {Cyl}(\mathbf {p},\mathbf {v})}_{\mathbf {v}} = \mathbb {B}_d(\mathbf {p},r)$. The maximum is reached when
$\overline {\mathrm {Cyl}(\mathbf {p},\mathbf {v})}_{\mathbf {v}} = \mathbb {B}_d(\mathbf {p},r)$. The maximum is reached when ![]() $(v_1,\ldots,v_d)$ and
$(v_1,\ldots,v_d)$ and ![]() $(w_1,\ldots,w_d)$ have opposite velocities while
$(w_1,\ldots,w_d)$ have opposite velocities while ![]() $v_{d+1}=w_{d+1} = h$. Then, it follows that
$v_{d+1}=w_{d+1} = h$. Then, it follows that
for all ![]() $\mathbf {v} \in \mathbb{M}_h^d$. We get
$\mathbf {v} \in \mathbb{M}_h^d$. We get
and thus by Lemma 3.3
 \begin{align} 1 - \exp(-\gamma (2r)^d \kappa_d) & \leq \mathbb{P}(\mathrm{Cyl}(\mathbf{p},\mathbf{v}) \cap Z(\xi) \neq \emptyset) \nonumber\\ & \leq 1 - \exp(-\gamma 2^d r^{d-1}(r\kappa_d + (R_h +r)\kappa_{d-1})). \end{align}
\begin{align} 1 - \exp(-\gamma (2r)^d \kappa_d) & \leq \mathbb{P}(\mathrm{Cyl}(\mathbf{p},\mathbf{v}) \cap Z(\xi) \neq \emptyset) \nonumber\\ & \leq 1 - \exp(-\gamma 2^d r^{d-1}(r\kappa_d + (R_h +r)\kappa_{d-1})). \end{align}
4. Applying the Malliavin–Stein bound
We follow the general definition in [Reference Last and Penrose13, Chapter 18] and consider a measurable space ![]() $(\mathbb {X}, \mathcal {X})$ and denote by
$(\mathbb {X}, \mathcal {X})$ and denote by ![]() $\mathbf {N}$ the space of all locally finite counting measures on
$\mathbf {N}$ the space of all locally finite counting measures on ![]() $\mathbb {X}$. Let
$\mathbb {X}$. Let ![]() $\eta$ denote a Poisson process on
$\eta$ denote a Poisson process on ![]() $\mathbb {X}$ with
$\mathbb {X}$ with ![]() $\sigma$-finite intensity measure
$\sigma$-finite intensity measure ![]() $\Lambda$.
$\Lambda$.
Definition 4.1. A random variable ![]() $F$, such that
$F$, such that ![]() $F = f(\eta )$
$F = f(\eta )$ ![]() $\mathbb{P}$-a.s. for some measurable function
$\mathbb{P}$-a.s. for some measurable function ![]() $f: \mathbf {N} \to \mathbb{R}$, is called a Poisson functional. In this notion,
$f: \mathbf {N} \to \mathbb{R}$, is called a Poisson functional. In this notion, ![]() $f$ is called a representative of
$f$ is called a representative of ![]() $F$.
$F$.
Our aim in this paper is to derive asymptotic distributions of Poisson functionals based on ![]() $\xi$. This involves the following operator which can be seen as a discrete analogue to classical derivatives.
$\xi$. This involves the following operator which can be seen as a discrete analogue to classical derivatives.
Definition 4.2. For ![]() $\mathbf {x} \in \mathbb {X}$, we define a map
$\mathbf {x} \in \mathbb {X}$, we define a map ![]() $\mathrm {D}_\mathbf {x}f: \mathbf {N} \to \mathbb{R}$ by
$\mathrm {D}_\mathbf {x}f: \mathbf {N} \to \mathbb{R}$ by
This map is called the difference (or add-one-cost) operator of ![]() $f(\mu )$. We can extend this definition inductively for
$f(\mu )$. We can extend this definition inductively for ![]() $n \geq 2$ and
$n \geq 2$ and ![]() $(\mathbf {x_1},\ldots, \mathbf {x_n}) \in \mathbb {X}^n$ by setting
$(\mathbf {x_1},\ldots, \mathbf {x_n}) \in \mathbb {X}^n$ by setting ![]() $\mathrm {D}^1 := \mathrm {D}$ and defining
$\mathrm {D}^1 := \mathrm {D}$ and defining ![]() $\mathrm {D}_{\mathbf {x_1},\ldots, \mathbf {x_n}}^nf : \mathbf {N} \to \mathbb{R}$ by
$\mathrm {D}_{\mathbf {x_1},\ldots, \mathbf {x_n}}^nf : \mathbf {N} \to \mathbb{R}$ by
We then call ![]() $\mathrm {D}_{\mathbf {x_1},\ldots,\mathbf {x_n}}^nf$ the
$\mathrm {D}_{\mathbf {x_1},\ldots,\mathbf {x_n}}^nf$ the ![]() $\mathbf {n}$th order difference operator.
$\mathbf {n}$th order difference operator.
Let us denote the Wasserstein distance of two random variables ![]() $X$ and
$X$ and ![]() $Y$ by
$Y$ by ![]() ${\mathrm {d_W}}(X,Y):=\sup _{f\in \rm {Lip}(1)} |\mathbb{E} [f(X)]-\mathbb{E} [f(Y)]|$, where
${\mathrm {d_W}}(X,Y):=\sup _{f\in \rm {Lip}(1)} |\mathbb{E} [f(X)]-\mathbb{E} [f(Y)]|$, where ![]() $\mathrm {Lip}(1)$ is the space of all Lipschitz functions
$\mathrm {Lip}(1)$ is the space of all Lipschitz functions ![]() $f:\mathbb{R} \to \mathbb{R}$ with Lipschitz constant less than or equal to one. The following well-known theorem is derived from the Malliavian–Stein method and uses difference operators to give a bound on the Wasserstein distance
$f:\mathbb{R} \to \mathbb{R}$ with Lipschitz constant less than or equal to one. The following well-known theorem is derived from the Malliavian–Stein method and uses difference operators to give a bound on the Wasserstein distance ![]() $\mathrm{d_W}$ of the law of a Poisson functional and the standard normal distribution.
$\mathrm{d_W}$ of the law of a Poisson functional and the standard normal distribution.
Theorem 4.3. [Reference Last and Penrose13, Theorem 21.3]
Let ![]() $\eta$ denote a Poisson process with intensity measure
$\eta$ denote a Poisson process with intensity measure ![]() $\Lambda$. Consider a Poisson functional
$\Lambda$. Consider a Poisson functional ![]() $F$ on
$F$ on ![]() $\eta$ with
$\eta$ with ![]() $\mathbb{E} [F] = 0$ and
$\mathbb{E} [F] = 0$ and ![]() $\mathbb{V} [F]=1$.
$\mathbb{V} [F]=1$. ![]() $N$ shall denote a standard normal random variable. If
$N$ shall denote a standard normal random variable. If ![]() $\mathbb{E} \left [\int (\mathrm {D}_\mathbf {x}F)^2 \Lambda (\mathrm {d}\mathbf {x}) \right ] < \infty$, then there are constants
$\mathbb{E} \left [\int (\mathrm {D}_\mathbf {x}F)^2 \Lambda (\mathrm {d}\mathbf {x}) \right ] < \infty$, then there are constants
 \begin{align*} \alpha_1(F) & = \int \sqrt{\mathbb{E}[(\mathrm{D}_\mathbf{x}F)^2 (\mathrm{D}_\mathbf{y}F)^2]} \cdot \sqrt{\mathbb{E}[(D_{\mathbf{x},\mathbf{z}}^2F)^2 (D_{\mathbf{y},\mathbf{z}}^2F)^2]} \Lambda^3(\mathrm{d}(\mathbf{x},\mathbf{y},\mathbf{z})),\\ \alpha_2(F) & = \int\mathbb{E}[(\mathrm{D}_{\mathbf{x},\mathbf{z}}^2F)^2(\mathrm{D}_{\mathbf{y},\mathbf{z}}F)^2] \Lambda^3(\mathrm{d}(\mathbf{x},\mathbf{y},\mathbf{z})),\\ \alpha_3(F) & = \int \mathbb{E}[|\mathrm{D}_\mathbf{x}F|^3] \Lambda(\mathrm{d}\mathbf{x}), \end{align*}
\begin{align*} \alpha_1(F) & = \int \sqrt{\mathbb{E}[(\mathrm{D}_\mathbf{x}F)^2 (\mathrm{D}_\mathbf{y}F)^2]} \cdot \sqrt{\mathbb{E}[(D_{\mathbf{x},\mathbf{z}}^2F)^2 (D_{\mathbf{y},\mathbf{z}}^2F)^2]} \Lambda^3(\mathrm{d}(\mathbf{x},\mathbf{y},\mathbf{z})),\\ \alpha_2(F) & = \int\mathbb{E}[(\mathrm{D}_{\mathbf{x},\mathbf{z}}^2F)^2(\mathrm{D}_{\mathbf{y},\mathbf{z}}F)^2] \Lambda^3(\mathrm{d}(\mathbf{x},\mathbf{y},\mathbf{z})),\\ \alpha_3(F) & = \int \mathbb{E}[|\mathrm{D}_\mathbf{x}F|^3] \Lambda(\mathrm{d}\mathbf{x}), \end{align*}
such that
We will now apply this theorem to our setting.
Lemma 4.4. Let ![]() $f: \mathcal {C}^{d+1} \to \mathbb{R}$,
$f: \mathcal {C}^{d+1} \to \mathbb{R}$, ![]() $s\geq 1$ and
$s\geq 1$ and ![]() $W_s = [-{s}/{2}, {s}/{2}]^{d} \times [0,T]$. Assume that
$W_s = [-{s}/{2}, {s}/{2}]^{d} \times [0,T]$. Assume that ![]() $|f(A)|<\infty$ for all
$|f(A)|<\infty$ for all ![]() $A \in \mathcal {C}^{d+1}$ and that there exist constants
$A \in \mathcal {C}^{d+1}$ and that there exist constants ![]() $c_1$,
$c_1$, ![]() $c_2$,
$c_2$, ![]() $c_3$ and
$c_3$ and ![]() $R \in \mathbb{R}$ such that the following conditions are met for all
$R \in \mathbb{R}$ such that the following conditions are met for all ![]() $\mathbf {x} = (\mathbf {p},\mathbf {v}), \mathbf {y}= (\mathbf {q},\mathbf {w}) \in \mathbb{R} ^d \times \mathbb{M}_h^d$:
$\mathbf {x} = (\mathbf {p},\mathbf {v}), \mathbf {y}= (\mathbf {q},\mathbf {w}) \in \mathbb{R} ^d \times \mathbb{M}_h^d$:
(A)
 $\mathrm {D}_\mathbf {x}F(Z(\xi ) \cap W_s) = 0\quad \mathbb{P} \text {-a.s.}$ for
$\mathrm {D}_\mathbf {x}F(Z(\xi ) \cap W_s) = 0\quad \mathbb{P} \text {-a.s.}$ for  $\|\mathbf {p}\| > R+s$,
$\|\mathbf {p}\| > R+s$,(B)
 $\mathbb{V} [f(Z(\xi ) \cap W_s)] \geq c_1 \cdot \lambda _{d+1}(W_s)$,
$\mathbb{V} [f(Z(\xi ) \cap W_s)] \geq c_1 \cdot \lambda _{d+1}(W_s)$,(C)
 $\max \{\mathbb{E} [\mathrm {D}_{\mathbf {x}}f(Z(\xi ) \cap W_s)^4]$,
$\max \{\mathbb{E} [\mathrm {D}_{\mathbf {x}}f(Z(\xi ) \cap W_s)^4]$,  $\mathbb{E} [\mathrm {D}_{\mathbf {x}}f(Z(\xi +\delta _y) \cap W_s)^4t]\} \leq c_2$,
$\mathbb{E} [\mathrm {D}_{\mathbf {x}}f(Z(\xi +\delta _y) \cap W_s)^4t]\} \leq c_2$,(D)
 $\|\mathbf {p} - \mathbf {q}\|>R \Rightarrow \mathbb{E} [(\mathrm {D}_{\mathbf {x},\mathbf {y}}^2 f(Z(\xi ) \cap W_s))^4] \leq {c_3}/{\lambda _{d+1}(W_s)^4}$.
$\|\mathbf {p} - \mathbf {q}\|>R \Rightarrow \mathbb{E} [(\mathrm {D}_{\mathbf {x},\mathbf {y}}^2 f(Z(\xi ) \cap W_s))^4] \leq {c_3}/{\lambda _{d+1}(W_s)^4}$.
Then, there is a constant ![]() $c \in \mathbb{R}$ such that, for a standard normal random variable
$c \in \mathbb{R}$ such that, for a standard normal random variable ![]() $N$,
$N$,
 $$\mathrm{d_W}\left(\frac{f(Z(\xi) \cap W_s)-\mathbb{E}[f(Z(\xi) \cap W_s)]}{\sqrt{\mathbb{V}[f(Z(\xi) \cap W_s)]}}, N\right) \leq \frac{c}{\sqrt{\lambda_{d+1}(W_s)}}.$$
$$\mathrm{d_W}\left(\frac{f(Z(\xi) \cap W_s)-\mathbb{E}[f(Z(\xi) \cap W_s)]}{\sqrt{\mathbb{V}[f(Z(\xi) \cap W_s)]}}, N\right) \leq \frac{c}{\sqrt{\lambda_{d+1}(W_s)}}.$$
The proof of this lemma gives insight into the composition of ![]() $c$, which is rather complex. When proving our main results however, we will always set
$c$, which is rather complex. When proving our main results however, we will always set ![]() $c_3=0$. In that case, the constant is reduced to the following:
$c_3=0$. In that case, the constant is reduced to the following:
Remark 4.5. Let ![]() $c_3=0$. In that case, the constant
$c_3=0$. In that case, the constant ![]() $c$ in Lemma 4.4 is given by
$c$ in Lemma 4.4 is given by
where ![]() $c_{d,R,T} = {[2^{2d-1}(R^d+{1}/{2^d})]}/{T}$. Note however, that
$c_{d,R,T} = {[2^{2d-1}(R^d+{1}/{2^d})]}/{T}$. Note however, that ![]() $R$ will depend on
$R$ will depend on ![]() $T$.
$T$.
An interesting fact is that the assumptions in the lemma imply an upper bound on the variance, which is of the same order as the lower bound.
Remark 4.6. Since (C) implies ![]() $\mathbb{E} [\mathrm {D}_{\mathbf {x}}f(Z(\xi ) \cap W_s)^2] \leq 1+c_2$, the Poincaré inequality gives us the upper bound
$\mathbb{E} [\mathrm {D}_{\mathbf {x}}f(Z(\xi ) \cap W_s)^2] \leq 1+c_2$, the Poincaré inequality gives us the upper bound
Proof of Lemma 4.4. We start by defining
and aim to use Theorem 4.3 on the Poisson functional ![]() $G$ with representative
$G$ with representative ![]() $g$. First let us check if the prerequisites are met. From the finiteness of
$g$. First let us check if the prerequisites are met. From the finiteness of ![]() $f$ and condition (B), it follows that
$f$ and condition (B), it follows that ![]() $\mathbb{E} [|G|^2] < \infty$. As we have seen before, as a function of
$\mathbb{E} [|G|^2] < \infty$. As we have seen before, as a function of ![]() $f$ the difference operator is linear. This
$f$ the difference operator is linear. This ![]() $\mathbb{P} \text {-a.s.}$ leads to
$\mathbb{P} \text {-a.s.}$ leads to
It follows now from conditions (A) and (B) that ![]() $\mathbb{E} [\int (\mathrm {D}_\mathbf {x} G)^2 \Lambda (\mathrm {d}\mathbf {x}) ] < \infty$. Thus, we can apply the theorem and must now derive bounds for
$\mathbb{E} [\int (\mathrm {D}_\mathbf {x} G)^2 \Lambda (\mathrm {d}\mathbf {x}) ] < \infty$. Thus, we can apply the theorem and must now derive bounds for ![]() $\alpha _1(G)$,
$\alpha _1(G)$, ![]() $\alpha _2(G)$, and
$\alpha _2(G)$, and ![]() $\alpha _3(G)$. So let
$\alpha _3(G)$. So let ![]() $\mathbf {x},\mathbf {y} \in \mathbb{R} ^d \times \mathbb{M}_h^d$. By the Cauchy–Schwarz inequality, (4.1) and stationarity of the Poisson process we have
$\mathbf {x},\mathbf {y} \in \mathbb{R} ^d \times \mathbb{M}_h^d$. By the Cauchy–Schwarz inequality, (4.1) and stationarity of the Poisson process we have
 \begin{align} \mathbb{E}[(\mathrm{D}_{\mathbf{x}}G)^2 (\mathrm{D}_{\mathbf{y}}G)^2] & \leq \sqrt{\mathbb{E}[(\mathrm{D}_{\mathbf{x}}G)^4]} \sqrt{\mathbb{E}[(\mathrm{D}_{\mathbf{y}}G)^4]} \ \cr & =\frac{\mathbb{E}[(\mathrm{D}_{\mathbf{x}}f(Z(\xi) \cap W_s))^4]}{\sqrt{\mathbb{V}[f(Z(\xi) \cap W_s)]}^4} \ \cr & \leq \frac{c_2}{c_1^2 \cdot \lambda_{d+1}(W_s)^2}, \end{align}
\begin{align} \mathbb{E}[(\mathrm{D}_{\mathbf{x}}G)^2 (\mathrm{D}_{\mathbf{y}}G)^2] & \leq \sqrt{\mathbb{E}[(\mathrm{D}_{\mathbf{x}}G)^4]} \sqrt{\mathbb{E}[(\mathrm{D}_{\mathbf{y}}G)^4]} \ \cr & =\frac{\mathbb{E}[(\mathrm{D}_{\mathbf{x}}f(Z(\xi) \cap W_s))^4]}{\sqrt{\mathbb{V}[f(Z(\xi) \cap W_s)]}^4} \ \cr & \leq \frac{c_2}{c_1^2 \cdot \lambda_{d+1}(W_s)^2}, \end{align}
where the last inequality follows from conditions (B) and (C). To get a bound on the second order operators, we use the well-known fact that for ![]() $a,b \in \mathbb{R}$ and
$a,b \in \mathbb{R}$ and ![]() $q\geq 1$, the inequality
$q\geq 1$, the inequality ![]() $|a+b|^q \leq 2^{q-1}(|a|^q+|b|^q)$ holds. Additionally, we use the linearity of the difference operator and then (B) and (C) again.
$|a+b|^q \leq 2^{q-1}(|a|^q+|b|^q)$ holds. Additionally, we use the linearity of the difference operator and then (B) and (C) again.
 \begin{align} \mathbb{E}[|\mathrm{D}^2_{\mathbf{x},\mathbf{y}}G|^4] & = \frac{\mathbb{E}[|\mathrm{D}_{\mathbf{x},\mathbf{y}}^2f(Z(\xi) \cap W_s)|^4]}{\mathbb{V}[f(Z(\xi) \cap W_s)]^2} \ \cr & \leq \frac{2^3 \cdot(\mathbb{E}[|\mathrm{D}_{\mathbf{x}}f(Z(\xi + \delta_y) \cap W_s))|^4]+\mathbb{E}[|\mathrm{D}_{\mathbf{x}}f(Z(\xi) \cap W_s)|^4])}{c_1^2 \cdot \lambda_{d+1}(W_s)^2} \ \cr & \leq \frac{2^4 \cdot c_2}{c_1^2 \cdot \lambda_{d+1}(W_s)^2}. \end{align}
\begin{align} \mathbb{E}[|\mathrm{D}^2_{\mathbf{x},\mathbf{y}}G|^4] & = \frac{\mathbb{E}[|\mathrm{D}_{\mathbf{x},\mathbf{y}}^2f(Z(\xi) \cap W_s)|^4]}{\mathbb{V}[f(Z(\xi) \cap W_s)]^2} \ \cr & \leq \frac{2^3 \cdot(\mathbb{E}[|\mathrm{D}_{\mathbf{x}}f(Z(\xi + \delta_y) \cap W_s))|^4]+\mathbb{E}[|\mathrm{D}_{\mathbf{x}}f(Z(\xi) \cap W_s)|^4])}{c_1^2 \cdot \lambda_{d+1}(W_s)^2} \ \cr & \leq \frac{2^4 \cdot c_2}{c_1^2 \cdot \lambda_{d+1}(W_s)^2}. \end{align}
Condition (D) sharpens this estimate to
Now let ![]() $\bar {W}_{R,s} = [-{s}/{2},{s}/{2}]^d + \mathbb {B}_d(R)$. It follows from condition (A), (4.2) and Cauchy–Schwarz that
$\bar {W}_{R,s} = [-{s}/{2},{s}/{2}]^d + \mathbb {B}_d(R)$. It follows from condition (A), (4.2) and Cauchy–Schwarz that
 \begin{align*} \alpha_1(G) & = \int_{(\mathbb{R}^d \times \mathbb{M}_h^d)^3} \sqrt{\mathbb{E}[(\mathrm{D}_{\mathbf{x}}G)^2 (\mathrm{D}_{\mathbf{y}}G)^2]}\sqrt{\mathbb{E}[(\mathrm{D}_{\mathbf{x},\mathbf{z}}^2G)^2 (\mathrm{D}_{\mathbf{y},\mathbf{z}}^2G)^2]} \Lambda^3 (\mathrm{d}(\mathbf{x},\mathbf{y},\mathbf{z}))\ \cr & = \int_{(\bar{W}_{R,s} \times \mathbb{M}_h^d)^3} \sqrt{\mathbb{E}[(\mathrm{D}_{\mathbf{x}}G)^2 (\mathrm{D}_{\mathbf{y}}G)^2]}\sqrt{\mathbb{E}[(\mathrm{D}_{\mathbf{x},\mathbf{z}}^2G)^2 (\mathrm{D}_{\mathbf{y},\mathbf{z}}^2G)^2]} \Lambda^3 (\mathrm{d}(\mathbf{x},\mathbf{y},\mathbf{z}))\ \cr & \leq \int_{(\bar{W}_{R,s} \times \mathbb{M}_h^d)^3} \frac{\sqrt{c_2}}{c_1 \cdot \lambda_{d+1}(W_s)} \cdot \sqrt{\mathbb{E}[(\mathrm{D}_{\mathbf{x},\mathbf{z}}^2G)^2 (\mathrm{D}_{\mathbf{y},\mathbf{z}}^2G)^2]}\Lambda^3 (\mathrm{d}(\mathbf{x},\mathbf{y},\mathbf{z})) \ \cr & \leq \int_{(\bar{W}_{R,s} \times \mathbb{M}_h^d)^3} \frac{\sqrt{c_2}}{c_1 \cdot \lambda_{d+1}(W_s)} \cdot \sqrt[4]{\mathbb{E}[(\mathrm{D}_{\mathbf{x},\mathbf{z}}^2G)^4]}\sqrt[4]{\mathbb{E}[(\mathrm{D}_{\mathbf{y},\mathbf{z}}^2G)^4]} \Lambda^3 (\mathrm{d}(\mathbf{x},\mathbf{y},\mathbf{z})). \end{align*}
\begin{align*} \alpha_1(G) & = \int_{(\mathbb{R}^d \times \mathbb{M}_h^d)^3} \sqrt{\mathbb{E}[(\mathrm{D}_{\mathbf{x}}G)^2 (\mathrm{D}_{\mathbf{y}}G)^2]}\sqrt{\mathbb{E}[(\mathrm{D}_{\mathbf{x},\mathbf{z}}^2G)^2 (\mathrm{D}_{\mathbf{y},\mathbf{z}}^2G)^2]} \Lambda^3 (\mathrm{d}(\mathbf{x},\mathbf{y},\mathbf{z}))\ \cr & = \int_{(\bar{W}_{R,s} \times \mathbb{M}_h^d)^3} \sqrt{\mathbb{E}[(\mathrm{D}_{\mathbf{x}}G)^2 (\mathrm{D}_{\mathbf{y}}G)^2]}\sqrt{\mathbb{E}[(\mathrm{D}_{\mathbf{x},\mathbf{z}}^2G)^2 (\mathrm{D}_{\mathbf{y},\mathbf{z}}^2G)^2]} \Lambda^3 (\mathrm{d}(\mathbf{x},\mathbf{y},\mathbf{z}))\ \cr & \leq \int_{(\bar{W}_{R,s} \times \mathbb{M}_h^d)^3} \frac{\sqrt{c_2}}{c_1 \cdot \lambda_{d+1}(W_s)} \cdot \sqrt{\mathbb{E}[(\mathrm{D}_{\mathbf{x},\mathbf{z}}^2G)^2 (\mathrm{D}_{\mathbf{y},\mathbf{z}}^2G)^2]}\Lambda^3 (\mathrm{d}(\mathbf{x},\mathbf{y},\mathbf{z})) \ \cr & \leq \int_{(\bar{W}_{R,s} \times \mathbb{M}_h^d)^3} \frac{\sqrt{c_2}}{c_1 \cdot \lambda_{d+1}(W_s)} \cdot \sqrt[4]{\mathbb{E}[(\mathrm{D}_{\mathbf{x},\mathbf{z}}^2G)^4]}\sqrt[4]{\mathbb{E}[(\mathrm{D}_{\mathbf{y},\mathbf{z}}^2G)^4]} \Lambda^3 (\mathrm{d}(\mathbf{x},\mathbf{y},\mathbf{z})). \end{align*}
We will now disassemble the domain of integration in order to properly apply our conditions. To that end, set ![]() $A_\mathbf {x} = \mathbb {B}_d(\mathbf {x},R)\times \mathbb{M}_h^d$ and
$A_\mathbf {x} = \mathbb {B}_d(\mathbf {x},R)\times \mathbb{M}_h^d$ and ![]() $A_\mathbf {x}^C = \bar {W}_{R,s}\backslash \mathbb {B}_d(\mathbf {x},R) \times \mathbb{M}_h^d$. This gives us the decomposition
$A_\mathbf {x}^C = \bar {W}_{R,s}\backslash \mathbb {B}_d(\mathbf {x},R) \times \mathbb{M}_h^d$. This gives us the decomposition
 \begin{align} & \int_{(\bar{W}_{R,s} \times \mathbb{M}_h^d)^3} \sqrt[4]{\mathbb{E}[(\mathrm{D}_{\mathbf{x},\mathbf{z}}^2G)^4]}\sqrt[4]{\mathbb{E}[(\mathrm{D}_{\mathbf{y},\mathbf{z}}^2G)^4]} \Lambda^3 (\mathrm{d}(\mathbf{x},\mathbf{y},\mathbf{z}))\ \cr & \quad= \int_{\bar{W}_{R,s} \times \mathbb{M}_h^d}\int_{A_\mathbf{z}} \int_{A_\mathbf{z}} \sqrt[4]{\mathbb{E}[(\mathrm{D}_{\mathbf{x},\mathbf{z}}^2G)^4]}\sqrt[4]{\mathbb{E}[(\mathrm{D}_{\mathbf{y},\mathbf{z}}^2G)^4]} \Lambda (\mathrm{d}\mathbf{x})\Lambda (\mathrm{d}\mathbf{y}) \Lambda (\mathrm{d}\mathbf{z})\ \cr & \qquad+ \int_{\bar{W}_{R,s} \times \mathbb{M}_h^d} \int_{A_\mathbf{z}} \int_{A_\mathbf{z}^C} \sqrt[4]{\mathbb{E}[(\mathrm{D}_{\mathbf{x},\mathbf{z}}^2G)^4]}\sqrt[4]{\mathbb{E}[(\mathrm{D}_{\mathbf{y},\mathbf{z}}^2G)^4]} \Lambda (\mathrm{d}\mathbf{x})\Lambda (\mathrm{d}\mathbf{y}) ~\Lambda (\mathrm{d}\mathbf{z}) \ \cr & \qquad+ \int_{\bar{W}_{R,s} \times \mathbb{M}_h^d}\int_{A_\mathbf{z}^C} \int_{A_\mathbf{z}} \sqrt[4]{\mathbb{E}[(\mathrm{D}_{\mathbf{x},\mathbf{z}}^2G)^4]}\sqrt[4]{\mathbb{E}[(\mathrm{D}_{\mathbf{y},\mathbf{z}}^2G)^4]} \Lambda (\mathrm{d}\mathbf{x})\Lambda (\mathrm{d}\mathbf{y}) \Lambda (\mathrm{d}\mathbf{z})\ \cr & \qquad+ \int_{\bar{W}_{R,s} \times \mathbb{M}_h^d}\int_{A_\mathbf{z}^C} \int_{A_\mathbf{z}^C} \sqrt[4]{\mathbb{E}[(\mathrm{D}_{\mathbf{x},\mathbf{z}}^2G)^4]}\sqrt[4]{\mathbb{E}[(\mathrm{D}_{\mathbf{y},\mathbf{z}}^2G)^4]} \Lambda (\mathrm{d}\mathbf{x})\Lambda (\mathrm{d}\mathbf{y}) \Lambda (\mathrm{d}\mathbf{z}). \end{align}
\begin{align} & \int_{(\bar{W}_{R,s} \times \mathbb{M}_h^d)^3} \sqrt[4]{\mathbb{E}[(\mathrm{D}_{\mathbf{x},\mathbf{z}}^2G)^4]}\sqrt[4]{\mathbb{E}[(\mathrm{D}_{\mathbf{y},\mathbf{z}}^2G)^4]} \Lambda^3 (\mathrm{d}(\mathbf{x},\mathbf{y},\mathbf{z}))\ \cr & \quad= \int_{\bar{W}_{R,s} \times \mathbb{M}_h^d}\int_{A_\mathbf{z}} \int_{A_\mathbf{z}} \sqrt[4]{\mathbb{E}[(\mathrm{D}_{\mathbf{x},\mathbf{z}}^2G)^4]}\sqrt[4]{\mathbb{E}[(\mathrm{D}_{\mathbf{y},\mathbf{z}}^2G)^4]} \Lambda (\mathrm{d}\mathbf{x})\Lambda (\mathrm{d}\mathbf{y}) \Lambda (\mathrm{d}\mathbf{z})\ \cr & \qquad+ \int_{\bar{W}_{R,s} \times \mathbb{M}_h^d} \int_{A_\mathbf{z}} \int_{A_\mathbf{z}^C} \sqrt[4]{\mathbb{E}[(\mathrm{D}_{\mathbf{x},\mathbf{z}}^2G)^4]}\sqrt[4]{\mathbb{E}[(\mathrm{D}_{\mathbf{y},\mathbf{z}}^2G)^4]} \Lambda (\mathrm{d}\mathbf{x})\Lambda (\mathrm{d}\mathbf{y}) ~\Lambda (\mathrm{d}\mathbf{z}) \ \cr & \qquad+ \int_{\bar{W}_{R,s} \times \mathbb{M}_h^d}\int_{A_\mathbf{z}^C} \int_{A_\mathbf{z}} \sqrt[4]{\mathbb{E}[(\mathrm{D}_{\mathbf{x},\mathbf{z}}^2G)^4]}\sqrt[4]{\mathbb{E}[(\mathrm{D}_{\mathbf{y},\mathbf{z}}^2G)^4]} \Lambda (\mathrm{d}\mathbf{x})\Lambda (\mathrm{d}\mathbf{y}) \Lambda (\mathrm{d}\mathbf{z})\ \cr & \qquad+ \int_{\bar{W}_{R,s} \times \mathbb{M}_h^d}\int_{A_\mathbf{z}^C} \int_{A_\mathbf{z}^C} \sqrt[4]{\mathbb{E}[(\mathrm{D}_{\mathbf{x},\mathbf{z}}^2G)^4]}\sqrt[4]{\mathbb{E}[(\mathrm{D}_{\mathbf{y},\mathbf{z}}^2G)^4]} \Lambda (\mathrm{d}\mathbf{x})\Lambda (\mathrm{d}\mathbf{y}) \Lambda (\mathrm{d}\mathbf{z}). \end{align}
The first summand on the right-hand side of (4.5) can now be bounded using (4.3). This yields
 \begin{align*} & \int_{\bar{W}_{R,s} \times \mathbb{M}_h^d} \int_{A_\mathbf{z}} \int_{A_\mathbf{z}} \sqrt[4]{\mathbb{E}[(\mathrm{D}_{\mathbf{x},\mathbf{z}}^2G)^4]}\sqrt[4]{\mathbb{E}[(\mathrm{D}_{\mathbf{y},\mathbf{z}}^2G)^4]} \Lambda (\mathrm{d}\mathbf{x})\Lambda (\mathrm{d}\mathbf{y}) \Lambda (\mathrm{d}\mathbf{z})\ \cr & \quad\leq \lambda_{d}(\bar{W}_{R,s}) \lambda_{d}(\mathbb{B}_d(R))^2 \frac{4\gamma^3 \sqrt{c_2}}{c_1 \cdot \lambda_{d+1}(W_s)}. \end{align*}
\begin{align*} & \int_{\bar{W}_{R,s} \times \mathbb{M}_h^d} \int_{A_\mathbf{z}} \int_{A_\mathbf{z}} \sqrt[4]{\mathbb{E}[(\mathrm{D}_{\mathbf{x},\mathbf{z}}^2G)^4]}\sqrt[4]{\mathbb{E}[(\mathrm{D}_{\mathbf{y},\mathbf{z}}^2G)^4]} \Lambda (\mathrm{d}\mathbf{x})\Lambda (\mathrm{d}\mathbf{y}) \Lambda (\mathrm{d}\mathbf{z})\ \cr & \quad\leq \lambda_{d}(\bar{W}_{R,s}) \lambda_{d}(\mathbb{B}_d(R))^2 \frac{4\gamma^3 \sqrt{c_2}}{c_1 \cdot \lambda_{d+1}(W_s)}. \end{align*}
By Fubini's Theorem, the second and third summand are the same. Note that the implication in condition ![]() $(D)$ applies to all pairs
$(D)$ applies to all pairs ![]() $(\mathbf {x},\mathbf {w})$ with
$(\mathbf {x},\mathbf {w})$ with ![]() $\mathbf {w} \in A_\mathbf {x}^C$, since the required distance is met. Thus, we can bound these summands by using (4.3) and (4.4) which gives us
$\mathbf {w} \in A_\mathbf {x}^C$, since the required distance is met. Thus, we can bound these summands by using (4.3) and (4.4) which gives us
 \begin{align*} & 2\cdot\int_{\bar{W}_{R,s} \times \mathbb{M}_h^d} \int_{A_\mathbf{z}} \int_{A_\mathbf{z}^C} \sqrt[4]{\mathbb{E}[(\mathrm{D}_{\mathbf{x},\mathbf{z}}^2G)^4]}\sqrt[4]{\mathbb{E}[(\mathrm{D}_{\mathbf{y},\mathbf{z}}^2G)^4]} \Lambda (\mathrm{d}\mathbf{x}) \Lambda (\mathrm{d}\mathbf{y}) \Lambda (\mathrm{d}\mathbf{z})\\ & \quad \leq 2\gamma^3 \cdot\lambda_{d}(\mathbb{B}_d(R))\lambda_{d}(\bar{W}_{R,s})^2 \frac{2\sqrt[4]{c_2}}{\sqrt{c_1} \cdot \sqrt{\lambda_{d+1}(W_s)}}\frac{\sqrt[4]{c_3}}{\sqrt{c_1} \cdot \lambda_{d+1}(W_s)^{{3}/{2}}}. \end{align*}
\begin{align*} & 2\cdot\int_{\bar{W}_{R,s} \times \mathbb{M}_h^d} \int_{A_\mathbf{z}} \int_{A_\mathbf{z}^C} \sqrt[4]{\mathbb{E}[(\mathrm{D}_{\mathbf{x},\mathbf{z}}^2G)^4]}\sqrt[4]{\mathbb{E}[(\mathrm{D}_{\mathbf{y},\mathbf{z}}^2G)^4]} \Lambda (\mathrm{d}\mathbf{x}) \Lambda (\mathrm{d}\mathbf{y}) \Lambda (\mathrm{d}\mathbf{z})\\ & \quad \leq 2\gamma^3 \cdot\lambda_{d}(\mathbb{B}_d(R))\lambda_{d}(\bar{W}_{R,s})^2 \frac{2\sqrt[4]{c_2}}{\sqrt{c_1} \cdot \sqrt{\lambda_{d+1}(W_s)}}\frac{\sqrt[4]{c_3}}{\sqrt{c_1} \cdot \lambda_{d+1}(W_s)^{{3}/{2}}}. \end{align*}
Another application of (4.4) gives us a bound on the last summand
 \begin{align*} & \int_{\bar{W}_{R,s} \times \mathbb{M}_h^d} \int_{A_\mathbf{z}^C} \int_{A_\mathbf{z}^C} \sqrt[4]{\mathbb{E}[(\mathrm{D}_{\mathbf{x},\mathbf{z}}^2G)^4]}\sqrt[4]{\mathbb{E}[(\mathrm{D}_{\mathbf{y},\mathbf{z}}^2G)^4]} \Lambda (\mathrm{d}\mathbf{x}) \Lambda (\mathrm{d}\mathbf{y}) \Lambda (\mathrm{d}\mathbf{z}) \ \cr & \quad \leq \lambda_{d}(\bar{W}_{R,s})^3 \frac{\gamma^3\sqrt{c_3}}{c_1 \cdot \lambda_{d+1}(W_s)^3}. \end{align*}
\begin{align*} & \int_{\bar{W}_{R,s} \times \mathbb{M}_h^d} \int_{A_\mathbf{z}^C} \int_{A_\mathbf{z}^C} \sqrt[4]{\mathbb{E}[(\mathrm{D}_{\mathbf{x},\mathbf{z}}^2G)^4]}\sqrt[4]{\mathbb{E}[(\mathrm{D}_{\mathbf{y},\mathbf{z}}^2G)^4]} \Lambda (\mathrm{d}\mathbf{x}) \Lambda (\mathrm{d}\mathbf{y}) \Lambda (\mathrm{d}\mathbf{z}) \ \cr & \quad \leq \lambda_{d}(\bar{W}_{R,s})^3 \frac{\gamma^3\sqrt{c_3}}{c_1 \cdot \lambda_{d+1}(W_s)^3}. \end{align*}
Next, we note that for the volume of ![]() $\bar {W}_{R,s}$, we have
$\bar {W}_{R,s}$, we have
 \begin{align*} \lambda_{d}(\bar{W}_{R,s}) & \leq (2R+s)^d \leq 2^{d-1}(2^dR^d+s^d) \leq 2^{d-1}(2^dR^d+1)s^d\nonumber\\ & =\frac{2^{2d-1}(R^d+\frac{1}{2^d})}{T}\lambda_{d+1}(W_s) =: c_{d,R,T}\cdot\lambda_{d+1}(W_s). \end{align*}
\begin{align*} \lambda_{d}(\bar{W}_{R,s}) & \leq (2R+s)^d \leq 2^{d-1}(2^dR^d+s^d) \leq 2^{d-1}(2^dR^d+1)s^d\nonumber\\ & =\frac{2^{2d-1}(R^d+\frac{1}{2^d})}{T}\lambda_{d+1}(W_s) =: c_{d,R,T}\cdot\lambda_{d+1}(W_s). \end{align*}
Using these results, we can now further estimate ![]() $\alpha _1(G)$ by
$\alpha _1(G)$ by
 \begin{align*} \alpha_1(G) & \leq \frac{\sqrt{c_2}}{c_1 \cdot \lambda_{d+1}(W_s)} \cdot \int_{(\bar{W}_{R,s} \times \mathbb{M}_h^d)^3} \sqrt[4]{\mathbb{E}[(\mathrm{D}_{\mathbf{x},\mathbf{z}}^2G)^4]}\sqrt[4]{\mathbb{E}[(\mathrm{D}_{\mathbf{y},\mathbf{z}}^2G)^4]} \Lambda^3 (\mathrm{d}(\mathbf{x},\mathbf{y},\mathbf{z}))\ \cr & \leq \lambda_{d}(\bar{W}_{R,s}) \lambda_{d}(\mathbb{B}_d(R))^2 \frac{4\gamma^3c_2}{c_1^2 \cdot \lambda_{d+1}(W_s)^2}\ \cr & \quad + 2\cdot\lambda_{d}(\mathbb{B}_d(R))\lambda_{d}(\bar{W}_{R,s})^2 \frac{2\gamma^3c_2^\frac{3}{4}\sqrt[4]{c_3}}{c_1^2 \cdot \lambda_{d+1}(W_s)^3}\ \cr & \quad +\lambda_{d}(\bar{W}_{R,s})^3 \frac{\gamma^3\sqrt{c_2}\sqrt{c_3}}{c_1^2 \cdot \lambda_{d+1}(W_s)^4}\ \cr & = \frac{\gamma^3 c_{d,R,T}\sqrt{c_2}}{c_1^2 \cdot \lambda_{d+1}(W_s)}(4\sqrt{c_2}\lambda_{d}(\mathbb{B}_d(R))^2 + 4\sqrt[4]{c_2 c_3}c_{d,R,T}\lambda_{d}(\mathbb{B}_d(R)) + \sqrt{c_3}c_{d,R,T}^2). \end{align*}
\begin{align*} \alpha_1(G) & \leq \frac{\sqrt{c_2}}{c_1 \cdot \lambda_{d+1}(W_s)} \cdot \int_{(\bar{W}_{R,s} \times \mathbb{M}_h^d)^3} \sqrt[4]{\mathbb{E}[(\mathrm{D}_{\mathbf{x},\mathbf{z}}^2G)^4]}\sqrt[4]{\mathbb{E}[(\mathrm{D}_{\mathbf{y},\mathbf{z}}^2G)^4]} \Lambda^3 (\mathrm{d}(\mathbf{x},\mathbf{y},\mathbf{z}))\ \cr & \leq \lambda_{d}(\bar{W}_{R,s}) \lambda_{d}(\mathbb{B}_d(R))^2 \frac{4\gamma^3c_2}{c_1^2 \cdot \lambda_{d+1}(W_s)^2}\ \cr & \quad + 2\cdot\lambda_{d}(\mathbb{B}_d(R))\lambda_{d}(\bar{W}_{R,s})^2 \frac{2\gamma^3c_2^\frac{3}{4}\sqrt[4]{c_3}}{c_1^2 \cdot \lambda_{d+1}(W_s)^3}\ \cr & \quad +\lambda_{d}(\bar{W}_{R,s})^3 \frac{\gamma^3\sqrt{c_2}\sqrt{c_3}}{c_1^2 \cdot \lambda_{d+1}(W_s)^4}\ \cr & = \frac{\gamma^3 c_{d,R,T}\sqrt{c_2}}{c_1^2 \cdot \lambda_{d+1}(W_s)}(4\sqrt{c_2}\lambda_{d}(\mathbb{B}_d(R))^2 + 4\sqrt[4]{c_2 c_3}c_{d,R,T}\lambda_{d}(\mathbb{B}_d(R)) + \sqrt{c_3}c_{d,R,T}^2). \end{align*}
Next, we take care of ![]() $\alpha _2(G)$. We use the Cauchy–Schwarz inequality to get
$\alpha _2(G)$. We use the Cauchy–Schwarz inequality to get
 \begin{align*} \alpha_2(G) & = \int_{(\mathbb{R}^d \times \mathbb{M}_h^d)^3} \mathbb{E}[(\mathrm{D}_{\mathbf{x},\mathbf{z}}^2G)^2 (\mathrm{D}_{\mathbf{y},\mathbf{z}}^2G)^2] \Lambda^3 (\mathrm{d}(\mathbf{x},\mathbf{y},\mathbf{z}))\ \cr & \leq \int_{(\bar{W}_{R,s} \times\mathbb{M}_h^d)^3} \sqrt{\mathbb{E}[(\mathrm{D}_{\mathbf{x},\mathbf{z}}^2G)^4]}\sqrt{\mathbb{E}[(\mathrm{D}_{\mathbf{y},\mathbf{z}}^2G)^4]} \Lambda^3 (\mathrm{d}(\mathbf{x},\mathbf{y},\mathbf{z})) \end{align*}
\begin{align*} \alpha_2(G) & = \int_{(\mathbb{R}^d \times \mathbb{M}_h^d)^3} \mathbb{E}[(\mathrm{D}_{\mathbf{x},\mathbf{z}}^2G)^2 (\mathrm{D}_{\mathbf{y},\mathbf{z}}^2G)^2] \Lambda^3 (\mathrm{d}(\mathbf{x},\mathbf{y},\mathbf{z}))\ \cr & \leq \int_{(\bar{W}_{R,s} \times\mathbb{M}_h^d)^3} \sqrt{\mathbb{E}[(\mathrm{D}_{\mathbf{x},\mathbf{z}}^2G)^4]}\sqrt{\mathbb{E}[(\mathrm{D}_{\mathbf{y},\mathbf{z}}^2G)^4]} \Lambda^3 (\mathrm{d}(\mathbf{x},\mathbf{y},\mathbf{z})) \end{align*}
and apply the same decomposition argument as in the treatment of ![]() $\alpha _1(G)$.
$\alpha _1(G)$.
 \begin{align*} \alpha_2(G) & \leq \lambda_{d}(\bar{W}_{R,s}) \lambda_{d}(\mathbb{B}_d(R))^2 \frac{2^4 \gamma^3 \cdot c_2}{c_1^2 \cdot \lambda_{d+1}(W_s)^2}\ \cr & \quad +2\cdot\lambda_{d}(\mathbb{B}_d(R))\lambda_{d}(\bar{W}_{R,s})^2 \frac{4\gamma^3\sqrt{c_2}}{c_1 \cdot \lambda_{d+1}(W_s)}\frac{\sqrt{c_3}}{c_1 \cdot \lambda_{d+1}(W_s)^3}\ \cr & \quad +\lambda_{d}(\bar{W}_{R,s})^3 \frac{\gamma^3c_3}{c_1^2 \cdot \lambda_{d+1}(W_s)^6}\ \cr & \leq \frac{\gamma^3c_{d,R,T}}{c_1^2 \cdot \lambda_{d+1}(W_s)}(16c_2\lambda_{d}(\mathbb{B}_d(R))^2 + 8\sqrt{c_2c_3}c_{d,R,T}\lambda_{d}(\mathbb{B}_d(R)) + c_3c_{d,R,T}^2 ). \end{align*}
\begin{align*} \alpha_2(G) & \leq \lambda_{d}(\bar{W}_{R,s}) \lambda_{d}(\mathbb{B}_d(R))^2 \frac{2^4 \gamma^3 \cdot c_2}{c_1^2 \cdot \lambda_{d+1}(W_s)^2}\ \cr & \quad +2\cdot\lambda_{d}(\mathbb{B}_d(R))\lambda_{d}(\bar{W}_{R,s})^2 \frac{4\gamma^3\sqrt{c_2}}{c_1 \cdot \lambda_{d+1}(W_s)}\frac{\sqrt{c_3}}{c_1 \cdot \lambda_{d+1}(W_s)^3}\ \cr & \quad +\lambda_{d}(\bar{W}_{R,s})^3 \frac{\gamma^3c_3}{c_1^2 \cdot \lambda_{d+1}(W_s)^6}\ \cr & \leq \frac{\gamma^3c_{d,R,T}}{c_1^2 \cdot \lambda_{d+1}(W_s)}(16c_2\lambda_{d}(\mathbb{B}_d(R))^2 + 8\sqrt{c_2c_3}c_{d,R,T}\lambda_{d}(\mathbb{B}_d(R)) + c_3c_{d,R,T}^2 ). \end{align*}
Finally, we use (4.1), (B) and then note that (C) implies ![]() $\mathbb{E} [|\mathrm {D}_{\mathbf {x}}f(Z(\xi \cap W_s))|^3] \leq 1 + c_2$ to get
$\mathbb{E} [|\mathrm {D}_{\mathbf {x}}f(Z(\xi \cap W_s))|^3] \leq 1 + c_2$ to get
 \begin{align*} \alpha_3(G) & \leq \int_{\bar{W}_{R,s} \times \mathbb{M}_h^d} \mathbb{E}[|\mathrm{D}_{\mathbf{x}}G|^3] \Lambda(\mathrm{d}\mathbf{x})\ \cr & = \int_{\bar{W}_{R,s} \times \mathbb{M}_h^d}\mathbb{E}\left[\frac{|\mathrm{D}_{\mathbf{x}}f(Z(\xi \cap W_s))|^3}{\sqrt{\mathbb{V}[f(Z(\xi \cap W_s))]}^3}\right] \Lambda(\mathrm{d}\mathbf{x})\ \cr & \leq \int_{\bar{W}_{R,s} \times \mathbb{M}_h^d} \frac{1}{c_1^{{3}/{2}} \lambda_{d+1}(W_s)^{{3}/{2}}} \cdot \mathbb{E}[|\mathrm{D}_{\mathbf{x}}f(Z(\xi \cap W_s))|^3] \Lambda(\mathrm{d}\mathbf{x})\ \cr & \leq \frac{\gamma(1+c_2)\cdot c_{d,R,T}}{c_1^{{3}/{2}} \sqrt{\lambda_{d+1}(W_s)}}. \end{align*}
\begin{align*} \alpha_3(G) & \leq \int_{\bar{W}_{R,s} \times \mathbb{M}_h^d} \mathbb{E}[|\mathrm{D}_{\mathbf{x}}G|^3] \Lambda(\mathrm{d}\mathbf{x})\ \cr & = \int_{\bar{W}_{R,s} \times \mathbb{M}_h^d}\mathbb{E}\left[\frac{|\mathrm{D}_{\mathbf{x}}f(Z(\xi \cap W_s))|^3}{\sqrt{\mathbb{V}[f(Z(\xi \cap W_s))]}^3}\right] \Lambda(\mathrm{d}\mathbf{x})\ \cr & \leq \int_{\bar{W}_{R,s} \times \mathbb{M}_h^d} \frac{1}{c_1^{{3}/{2}} \lambda_{d+1}(W_s)^{{3}/{2}}} \cdot \mathbb{E}[|\mathrm{D}_{\mathbf{x}}f(Z(\xi \cap W_s))|^3] \Lambda(\mathrm{d}\mathbf{x})\ \cr & \leq \frac{\gamma(1+c_2)\cdot c_{d,R,T}}{c_1^{{3}/{2}} \sqrt{\lambda_{d+1}(W_s)}}. \end{align*}
Using these bounds, Theorem 4.3 now gives us the asserted statement.
5. Central limit theorems
We will now present our limit theorems on the asymptotic behavior of ![]() $Z(\xi )$. We start with the volume of the union of TBCs restricted to a compact window of observation. To be more precise, we are interested in the asymptotic distribution of the random variable
$Z(\xi )$. We start with the volume of the union of TBCs restricted to a compact window of observation. To be more precise, we are interested in the asymptotic distribution of the random variable
where, as before, ![]() $W_s := [-{s}/{2}, {s}/{2}]^{d} \times [0,T]$. Additionally to Theorem 1.1, we will provide a rate of convergence and in fact prove the following:
$W_s := [-{s}/{2}, {s}/{2}]^{d} \times [0,T]$. Additionally to Theorem 1.1, we will provide a rate of convergence and in fact prove the following:
Theorem 5.1. Let ![]() $N$ denote a standard normal random variable and
$N$ denote a standard normal random variable and ![]() $Z(\xi )$ as in Definition 2.4. Assume
$Z(\xi )$ as in Definition 2.4. Assume ![]() $r< s$. Then, there exists a constant
$r< s$. Then, there exists a constant ![]() $c \in \mathbb{R} _+$ such that
$c \in \mathbb{R} _+$ such that
 $$\mathrm{{d}_W}\left(\frac{\lambda_{d+1}(Z(\xi) \cap W_s) - \mathbb{E}[\lambda_{d+1}(Z(\xi) \cap W_s)]}{\sqrt{\mathbb{V}[\lambda_{d+1}(Z(\xi) \cap W_s)]}}, N\right) \leq \frac{c}{\sqrt{\lambda_{d+1}(W_s)}}.$$
$$\mathrm{{d}_W}\left(\frac{\lambda_{d+1}(Z(\xi) \cap W_s) - \mathbb{E}[\lambda_{d+1}(Z(\xi) \cap W_s)]}{\sqrt{\mathbb{V}[\lambda_{d+1}(Z(\xi) \cap W_s)]}}, N\right) \leq \frac{c}{\sqrt{\lambda_{d+1}(W_s)}}.$$
We will remark that the capacity functional of the model admits a beautiful formula for the expected volume. An application of Fubini's theorem and (3.1) immediately yield
 \begin{align*} \mathbb{E}[\lambda_{d+1}(Z(\xi) \cap W_s)] & = \mathbb{E}\left[\int_{W_s} \mathbb{1}(\mathbf{x} \in Z(\xi)) \lambda_{d+1}(\mathrm{d}\mathbf{x})\right] \ \cr & = (1 - \exp(-\gamma \cdot r^d \kappa_d)) \cdot \lambda_{d+1}(W_s). \end{align*}
\begin{align*} \mathbb{E}[\lambda_{d+1}(Z(\xi) \cap W_s)] & = \mathbb{E}\left[\int_{W_s} \mathbb{1}(\mathbf{x} \in Z(\xi)) \lambda_{d+1}(\mathrm{d}\mathbf{x})\right] \ \cr & = (1 - \exp(-\gamma \cdot r^d \kappa_d)) \cdot \lambda_{d+1}(W_s). \end{align*}
Our second main result concerns itself with isolated cylinders. These represent nodes that have no contact to other nodes for the time frame at all. As before, we prove Theorem 1.2 by proving a stronger result offering rates of convergence. We start by considering the point process of isolated cylinders ![]() $\xi _{\text {Iso}}$ where
$\xi _{\text {Iso}}$ where
counts the isolated cylinders with basepoint in ![]() $A \subset \mathbb{R} ^d$. Let us make a few remarks about its expectation. By the Mecke equation and Lemma 3.3, we have
$A \subset \mathbb{R} ^d$. Let us make a few remarks about its expectation. By the Mecke equation and Lemma 3.3, we have
 \begin{align*} \mathbb{E}[\xi_{\text{Iso}}(A)] & = \int_{A \times \mathbb{M}_h^d} \mathbb{P}[\mathrm{Cyl}(\mathbf{x}) \cap Z(\xi) = \emptyset] \Lambda(\mathrm{d}\mathbf{x}) \ \cr & = \int_{A \times \mathbb{M}_h^d} 1-\exp\left(-\gamma \cdot \int_{\mathbb{M}_h^d} \lambda_d(\overline{\mathrm{Cyl}(\mathbf{x})}_\mathbf{w} + \mathbb{B}_d(r)) \mathbb{Q}(\mathrm{d}\mathbf{w})\right) \Lambda(\mathrm{d}\mathbf{x}) \ \cr & = \gamma \cdot \int_{\mathbb{M}_h^d} 1 - \exp\left(-\gamma \cdot \int_{\mathbb{M}_h^d} \lambda_d(\overline{\mathrm{Cyl}(0,\mathbf{v})}_\mathbf{w} + \mathbb{B}_d(r)) \mathbb{Q}(\mathrm{d}\mathbf{w})\right) \mathbb{Q}(\mathrm{d}\mathbf{v}) \cdot \lambda_d(A) \end{align*}
\begin{align*} \mathbb{E}[\xi_{\text{Iso}}(A)] & = \int_{A \times \mathbb{M}_h^d} \mathbb{P}[\mathrm{Cyl}(\mathbf{x}) \cap Z(\xi) = \emptyset] \Lambda(\mathrm{d}\mathbf{x}) \ \cr & = \int_{A \times \mathbb{M}_h^d} 1-\exp\left(-\gamma \cdot \int_{\mathbb{M}_h^d} \lambda_d(\overline{\mathrm{Cyl}(\mathbf{x})}_\mathbf{w} + \mathbb{B}_d(r)) \mathbb{Q}(\mathrm{d}\mathbf{w})\right) \Lambda(\mathrm{d}\mathbf{x}) \ \cr & = \gamma \cdot \int_{\mathbb{M}_h^d} 1 - \exp\left(-\gamma \cdot \int_{\mathbb{M}_h^d} \lambda_d(\overline{\mathrm{Cyl}(0,\mathbf{v})}_\mathbf{w} + \mathbb{B}_d(r)) \mathbb{Q}(\mathrm{d}\mathbf{w})\right) \mathbb{Q}(\mathrm{d}\mathbf{v}) \cdot \lambda_d(A) \end{align*}
for the intensity of the point process ![]() $\xi _{\text {Iso}}$. Taking (3.2) into account yields
$\xi _{\text {Iso}}$. Taking (3.2) into account yields
 \begin{align*} \gamma \lambda_d(A) \cdot \exp(-\gamma 2^d r^{d-1}(r\kappa_d + (R_h + r)\kappa_{d-1})) & \leq \mathbb{E}[\xi_{\text{Iso}}(A)] \ \cr & \leq \gamma \lambda_d(A) \cdot \exp(-\gamma (2r)^d \kappa_d). \end{align*}
\begin{align*} \gamma \lambda_d(A) \cdot \exp(-\gamma 2^d r^{d-1}(r\kappa_d + (R_h + r)\kappa_{d-1})) & \leq \mathbb{E}[\xi_{\text{Iso}}(A)] \ \cr & \leq \gamma \lambda_d(A) \cdot \exp(-\gamma (2r)^d \kappa_d). \end{align*}
As before, let ![]() $s>0$ and
$s>0$ and ![]() $W_s = [-{s}/{2},{s}/{2}]^d \times [0,T]$. By
$W_s = [-{s}/{2},{s}/{2}]^d \times [0,T]$. By
we define the random variable counting the number of isolated cylinders with basepoint in ![]() $W_s$. We present the following limit theorem.
$W_s$. We present the following limit theorem.
Theorem 5.2. Assume ![]() $s \geq 6(R_h+r)$ and let
$s \geq 6(R_h+r)$ and let ![]() $N$ denote a standard normal random variable. There exists a constant
$N$ denote a standard normal random variable. There exists a constant ![]() $c \in \mathbb{R} _+$ such that
$c \in \mathbb{R} _+$ such that
 $$\mathrm{{d}_W}\left(\frac{\mathrm{Iso}_{Z(\xi)}(W_s) - \mathbb{E}[\mathrm{Iso}_{Z(\xi)}(W_s)]}{\sqrt{\mathbb{V}[\mathrm{Iso}_{Z(\xi)}(W_s)]}}, N\right) \leq \frac{c}{\sqrt{\lambda_{d+1}(W_s)}}.$$
$$\mathrm{{d}_W}\left(\frac{\mathrm{Iso}_{Z(\xi)}(W_s) - \mathbb{E}[\mathrm{Iso}_{Z(\xi)}(W_s)]}{\sqrt{\mathbb{V}[\mathrm{Iso}_{Z(\xi)}(W_s)]}}, N\right) \leq \frac{c}{\sqrt{\lambda_{d+1}(W_s)}}.$$
The last main result takes a first step in analyzing the topological structure of the TBC model and gives insight into its Euler characteristic. By ![]() $\mathcal {R}^{d}$ let us denote the convex ring over
$\mathcal {R}^{d}$ let us denote the convex ring over ![]() $\mathbb{R} ^{d}$ that is the system containing all unions of finitely many compact, convex subsets of
$\mathbb{R} ^{d}$ that is the system containing all unions of finitely many compact, convex subsets of ![]() $\mathbb{R} ^{d}$ (cf. [Reference Schneider and Weil16, p. 601]).
$\mathbb{R} ^{d}$ (cf. [Reference Schneider and Weil16, p. 601]).
Definition 5.3. In the context of convex geometry, the Euler characteristic is a function
with the properties
•
 $\chi (K)=1$ if
$\chi (K)=1$ if  $K \subset \mathbb{R} ^d$ convex,
$K \subset \mathbb{R} ^d$ convex,•
 $\chi (\emptyset )=0$ and
$\chi (\emptyset )=0$ and•
 $\chi (A \cup B) = \chi (A) + \chi (B) - \chi (A \cap B)$ for all
$\chi (A \cup B) = \chi (A) + \chi (B) - \chi (A \cap B)$ for all  $A,B \subset \mathbb{R} ^d$.
$A,B \subset \mathbb{R} ^d$.
For reference, see [Reference Schneider and Weil16, p. 625]. Since our cylinders clearly are convex sets in ![]() ${\mathcal {R}}^{d+1}$ and
${\mathcal {R}}^{d+1}$ and ![]() $\eta$ is a Poisson process with finite intensity,
$\eta$ is a Poisson process with finite intensity, ![]() $\chi (Z(\xi ) \cap W_s)$ is well defined for
$\chi (Z(\xi ) \cap W_s)$ is well defined for ![]() $W_s$ as given above. Theorem 1.3 follows from:
$W_s$ as given above. Theorem 1.3 follows from:
Theorem 5.4. Assume ![]() $s \geq 6(R_h+r)$ and let
$s \geq 6(R_h+r)$ and let ![]() $N$ denote a standard normal random variable. There exists a constant
$N$ denote a standard normal random variable. There exists a constant ![]() $c \in \mathbb{R} _+$ such that
$c \in \mathbb{R} _+$ such that
 $$\mathrm{{d}_W}\left(\frac{\chi(Z(\xi) \cap W_s) - \mathbb{E}[\chi(Z(\xi) \cap W_s)]}{\sqrt{\mathbb{V}[\chi(Z(\xi) \cap W_s)]}}, N\right) \leq \frac{c}{\sqrt{\lambda_{d+1}(W_s)}}.$$
$$\mathrm{{d}_W}\left(\frac{\chi(Z(\xi) \cap W_s) - \mathbb{E}[\chi(Z(\xi) \cap W_s)]}{\sqrt{\mathbb{V}[\chi(Z(\xi) \cap W_s)]}}, N\right) \leq \frac{c}{\sqrt{\lambda_{d+1}(W_s)}}.$$
5.1. Proof for the covered volume
We start with the proof of the limit theorem concerning the covered volume of ![]() $Z(\xi )$ in
$Z(\xi )$ in ![]() $W_s$.
$W_s$.
Proof of Theorem 5.1. We aim to use Lemma 4.4 with
Clearly ![]() $\lambda _{d+1}(A)<\infty$ for all
$\lambda _{d+1}(A)<\infty$ for all ![]() $A \in \mathcal {C}^{d+1}$. Next, note that for
$A \in \mathcal {C}^{d+1}$. Next, note that for ![]() $\mathbf {x} = (\mathbf {p},\mathbf {v}) \in \mathbb{R} ^d \times \mathbb{M}_h^d$, we
$\mathbf {x} = (\mathbf {p},\mathbf {v}) \in \mathbb{R} ^d \times \mathbb{M}_h^d$, we ![]() $\mathbb{P} \text {-a.s.}$ have
$\mathbb{P} \text {-a.s.}$ have ![]() $\mathrm {D}_\mathbf {x}\lambda _{d+1}(Z(\xi ) \cap W_s) = 0$ for
$\mathrm {D}_\mathbf {x}\lambda _{d+1}(Z(\xi ) \cap W_s) = 0$ for ![]() $\|\mathbf {p}\| > R_h + s$ since in this case
$\|\mathbf {p}\| > R_h + s$ since in this case ![]() $\mathrm {Cyl}(\mathbf {x}) \cap W_s = \emptyset$. If we set further
$\mathrm {Cyl}(\mathbf {x}) \cap W_s = \emptyset$. If we set further ![]() $\mathbf {y} = (\mathbf {q},\mathbf {w}) \in \mathbb{R} ^d \times \mathbb{M}_h^d$, we have
$\mathbf {y} = (\mathbf {q},\mathbf {w}) \in \mathbb{R} ^d \times \mathbb{M}_h^d$, we have ![]() $\mathrm {D}_{\mathbf {x},\mathbf {y}}^2\lambda _{d+1}(Z(\xi ) \cap W_s) = 0$ for
$\mathrm {D}_{\mathbf {x},\mathbf {y}}^2\lambda _{d+1}(Z(\xi ) \cap W_s) = 0$ for ![]() $\|\mathbf {p} - \mathbf {q}\| > 2(R_h+r)$
$\|\mathbf {p} - \mathbf {q}\| > 2(R_h+r)$ ![]() $\mathbb{P} \text {-a.s.}$ since
$\mathbb{P} \text {-a.s.}$ since ![]() $\mathrm {Cyl}(\mathbf {x}) \cap \mathrm {Cyl}(\mathbf {y}) = \emptyset$:
$\mathrm {Cyl}(\mathbf {x}) \cap \mathrm {Cyl}(\mathbf {y}) = \emptyset$:
 \begin{align*} \mathrm{D}_{\mathbf{x},\mathbf{y}}^2\lambda_{d+1}(Z(\xi) \cap W_s) & = \mathrm{D}_\mathbf{x} \mathrm{D}_\mathbf{y} \lambda_{d+1}(Z(\xi)\cap W_s)\\ & = \mathrm{D}_\mathbf{x} (\lambda_{d+1}(Z(\xi+\delta_\mathbf{y})\cap W_s) - \lambda_{d+1}(Z(\xi)\cap W_s))\\ & =\mathrm{D}_\mathbf{x} \lambda_{d+1}(Z(\xi+\delta_\mathbf{y})\cap W_s) - \mathrm{D}_\mathbf{x} \lambda_{d+1}(Z(\xi)\cap W_s) = 0 \end{align*}
\begin{align*} \mathrm{D}_{\mathbf{x},\mathbf{y}}^2\lambda_{d+1}(Z(\xi) \cap W_s) & = \mathrm{D}_\mathbf{x} \mathrm{D}_\mathbf{y} \lambda_{d+1}(Z(\xi)\cap W_s)\\ & = \mathrm{D}_\mathbf{x} (\lambda_{d+1}(Z(\xi+\delta_\mathbf{y})\cap W_s) - \lambda_{d+1}(Z(\xi)\cap W_s))\\ & =\mathrm{D}_\mathbf{x} \lambda_{d+1}(Z(\xi+\delta_\mathbf{y})\cap W_s) - \mathrm{D}_\mathbf{x} \lambda_{d+1}(Z(\xi)\cap W_s) = 0 \end{align*}
![]() $\mathbb{P} \text {-a.s.}$. Thus, conditions (A) and (D) are fulfilled and we have
$\mathbb{P} \text {-a.s.}$. Thus, conditions (A) and (D) are fulfilled and we have ![]() $c_3 = 0$. Condition (C) is next. Note that all cylinders in our model are of the same volume. An application of Fubini's Theorem shows that
$c_3 = 0$. Condition (C) is next. Note that all cylinders in our model are of the same volume. An application of Fubini's Theorem shows that
for all ![]() $(\mathbf {p},\mathbf {v}) \in \mathbb{R} ^d \times \mathbb{M}_h^d$. When we add a cylinder to the model, in the extreme case it becomes a subset of
$(\mathbf {p},\mathbf {v}) \in \mathbb{R} ^d \times \mathbb{M}_h^d$. When we add a cylinder to the model, in the extreme case it becomes a subset of ![]() $W_s$ and intersects with none of the preexisting cylinders. In that case, it adds the entirety of its volume to
$W_s$ and intersects with none of the preexisting cylinders. In that case, it adds the entirety of its volume to ![]() $\lambda _{d+1}(Z(\xi ) \cap W_s)$. We can conclude
$\lambda _{d+1}(Z(\xi ) \cap W_s)$. We can conclude
and thus from (5.1) that
and thus get condition (C). It remains to prove the lower bound on the variance. An application of Fubini's theorem yields
 \begin{align*} & \mathbb{V}[\lambda_{d+1}(Z(\xi) \cap W_s)] \ \cr & \quad= \mathbb{E}\left[\int_{W_s^2} \mathbb{1}(\mathbf{x} \in Z(\xi), \mathbf{y} \in Z(\xi))\lambda_{d+1}^2(\mathrm{d}(\mathbf{x},\mathbf{y})) \right] - \mathbb{E}\left[ \int_{W_s} \mathbb{1}(\mathbf{x} \in Z(\xi)) \lambda_{d+1}(\mathrm{d}\mathbf{x})\right]^2 \ \cr & \quad= \int_{W_s^2} \mathbb{P}(\mathbf{x} \in Z(\xi), \mathbf{y} \in Z(\xi)) - \mathbb{P}(\mathbf{x} \in Z(\xi))\mathbb{P}(\mathbf{y} \in Z(\xi)) \lambda_{d+1}^2(\mathrm{d}(\mathbf{x},\mathbf{y})) \ \cr & \quad= \int_{W_s^2} \mathbb{P}(\mathbf{x} \notin Z(\xi), \mathbf{y} \notin Z(\xi)) - \mathbb{P}(\mathbf{x} \notin Z(\xi))\mathbb{P}(\mathbf{y} \notin Z(\xi)) \lambda_{d+1}^2(\mathrm{d}(\mathbf{x},\mathbf{y})), \end{align*}
\begin{align*} & \mathbb{V}[\lambda_{d+1}(Z(\xi) \cap W_s)] \ \cr & \quad= \mathbb{E}\left[\int_{W_s^2} \mathbb{1}(\mathbf{x} \in Z(\xi), \mathbf{y} \in Z(\xi))\lambda_{d+1}^2(\mathrm{d}(\mathbf{x},\mathbf{y})) \right] - \mathbb{E}\left[ \int_{W_s} \mathbb{1}(\mathbf{x} \in Z(\xi)) \lambda_{d+1}(\mathrm{d}\mathbf{x})\right]^2 \ \cr & \quad= \int_{W_s^2} \mathbb{P}(\mathbf{x} \in Z(\xi), \mathbf{y} \in Z(\xi)) - \mathbb{P}(\mathbf{x} \in Z(\xi))\mathbb{P}(\mathbf{y} \in Z(\xi)) \lambda_{d+1}^2(\mathrm{d}(\mathbf{x},\mathbf{y})) \ \cr & \quad= \int_{W_s^2} \mathbb{P}(\mathbf{x} \notin Z(\xi), \mathbf{y} \notin Z(\xi)) - \mathbb{P}(\mathbf{x} \notin Z(\xi))\mathbb{P}(\mathbf{y} \notin Z(\xi)) \lambda_{d+1}^2(\mathrm{d}(\mathbf{x},\mathbf{y})), \end{align*}
where the last equality follows from an application of DeMorgan's laws. Lemma 3.3 now yields
 \begin{align*} \mathbb{P}(\mathbf{x} \notin Z(\xi), \mathbf{y}\notin Z(\xi)) & = \mathbb{P}(\{\mathbf{x},\mathbf{y}\} \cap Z(\xi) = \emptyset)\ \cr & = \exp\left(-\gamma \cdot \int_{\mathbb{M}_h^d} \lambda_d(\overline{\{\mathbf{x},\mathbf{y}\}_\mathbf{v}} + \mathbb{B}_d(r)) \mathbb{Q}(\mathrm{d}\mathbf{v})\right). \end{align*}
\begin{align*} \mathbb{P}(\mathbf{x} \notin Z(\xi), \mathbf{y}\notin Z(\xi)) & = \mathbb{P}(\{\mathbf{x},\mathbf{y}\} \cap Z(\xi) = \emptyset)\ \cr & = \exp\left(-\gamma \cdot \int_{\mathbb{M}_h^d} \lambda_d(\overline{\{\mathbf{x},\mathbf{y}\}_\mathbf{v}} + \mathbb{B}_d(r)) \mathbb{Q}(\mathrm{d}\mathbf{v})\right). \end{align*}
To estimate this probability, consider some ![]() $\mathbf {x},\mathbf {y} \in W_s$ and assume
$\mathbf {x},\mathbf {y} \in W_s$ and assume ![]() $\|\mathbf {x}-\mathbf {y}\| \leq r$. Then, the distance of their respective
$\|\mathbf {x}-\mathbf {y}\| \leq r$. Then, the distance of their respective ![]() $v$-shadows satisfies the same, that is,
$v$-shadows satisfies the same, that is, ![]() $\|\bar {\mathbf {x}}_{\mathbf {v}} - \bar {\mathbf {y}}_{\mathbf {v}}\| \leq r$ for
$\|\bar {\mathbf {x}}_{\mathbf {v}} - \bar {\mathbf {y}}_{\mathbf {v}}\| \leq r$ for ![]() $\bar {\mathbf {x}}_{\mathbf {v}} := \overline {\{\mathbf {x}\}}_\mathbf {v}$ and
$\bar {\mathbf {x}}_{\mathbf {v}} := \overline {\{\mathbf {x}\}}_\mathbf {v}$ and ![]() $\bar {\mathbf {y}}_{\mathbf {v}} := \overline {\{\mathbf {y}\}}_\mathbf {v}$. Also denote by
$\bar {\mathbf {y}}_{\mathbf {v}} := \overline {\{\mathbf {y}\}}_\mathbf {v}$. Also denote by ![]() $H_{w}^d(z)$ the cap of a
$H_{w}^d(z)$ the cap of a ![]() $d$-dimensional hypersphere with radius
$d$-dimensional hypersphere with radius ![]() $z$ and height
$z$ and height ![]() $w$. Then,
$w$. Then,
Since ![]() $e^x>1$ for all
$e^x>1$ for all ![]() $x>0$, we get
$x>0$, we get
 \begin{align*} & \mathbb{P}(\mathbf{x} \notin Z(\xi), \mathbf{y} \notin Z(\xi)) - \mathbb{P}(\mathbf{x} \notin Z(\xi))\mathbb{P}(\mathbf{y} \notin Z(\xi))\ \cr & \quad \geq \exp({-}2\gamma \lambda_d(\mathbb{B}_d(r))+2\gamma\cdot \lambda_d(H_{{r}/{2}}^d(r))) - \exp({-}2 \gamma \lambda_d(\mathbb{B}_d(r))) =: \tau > 0 \end{align*}
\begin{align*} & \mathbb{P}(\mathbf{x} \notin Z(\xi), \mathbf{y} \notin Z(\xi)) - \mathbb{P}(\mathbf{x} \notin Z(\xi))\mathbb{P}(\mathbf{y} \notin Z(\xi))\ \cr & \quad \geq \exp({-}2\gamma \lambda_d(\mathbb{B}_d(r))+2\gamma\cdot \lambda_d(H_{{r}/{2}}^d(r))) - \exp({-}2 \gamma \lambda_d(\mathbb{B}_d(r))) =: \tau > 0 \end{align*}
for all ![]() $\mathbf {x} \in \mathbb {B}_{d+1}(\mathbf {y},r)$ and
$\mathbf {x} \in \mathbb {B}_{d+1}(\mathbf {y},r)$ and ![]() $\mathbf {y} \in W_s$. Then,
$\mathbf {y} \in W_s$. Then,
 \begin{align*} \mathbb{V}[\lambda_{d+1}(Z(\xi) \cap W_s)] & \geq \int_{W_s} \int_{\mathbb{B}_{d+1}(\mathbf{y},r) \cap W_s} \mathbb{P}(\mathbf{x} \notin Z(\xi), \mathbf{y} \notin Z(\xi))\ \cr & \quad - \mathbb{P}(\mathbf{x} \notin Z(\xi))\mathbb{P}(\mathbf{y} \notin Z(\xi)) \lambda_{d+1}(\mathrm{d}\mathbf{x}) \lambda_{d+1}(\mathrm{d}\mathbf{y}) \ \cr & \geq\int_{W_s} \int_{\mathbb{B}_{d+1}(\mathbf{y},r) \cap W_s} \tau \lambda_{d+1}(\mathrm{d}\mathbf{x})~\lambda_{d+1}(\mathrm{d}\mathbf{y})\ \cr & = \tau \int_{W_s}\lambda_{d+1}(\mathbb{B}_{d+1}(\mathbf{y},r) \cap W_s) \lambda_{d+1}(\mathrm{d}\mathbf{y}). \end{align*}
\begin{align*} \mathbb{V}[\lambda_{d+1}(Z(\xi) \cap W_s)] & \geq \int_{W_s} \int_{\mathbb{B}_{d+1}(\mathbf{y},r) \cap W_s} \mathbb{P}(\mathbf{x} \notin Z(\xi), \mathbf{y} \notin Z(\xi))\ \cr & \quad - \mathbb{P}(\mathbf{x} \notin Z(\xi))\mathbb{P}(\mathbf{y} \notin Z(\xi)) \lambda_{d+1}(\mathrm{d}\mathbf{x}) \lambda_{d+1}(\mathrm{d}\mathbf{y}) \ \cr & \geq\int_{W_s} \int_{\mathbb{B}_{d+1}(\mathbf{y},r) \cap W_s} \tau \lambda_{d+1}(\mathrm{d}\mathbf{x})~\lambda_{d+1}(\mathrm{d}\mathbf{y})\ \cr & = \tau \int_{W_s}\lambda_{d+1}(\mathbb{B}_{d+1}(\mathbf{y},r) \cap W_s) \lambda_{d+1}(\mathrm{d}\mathbf{y}). \end{align*}
For ![]() $\mathbf {y} \in W_s$, we also have that
$\mathbf {y} \in W_s$, we also have that
 \begin{align*} \lambda_{d+1}(\mathbb{B}_{d+1}(\mathbf{y},r) \cap W_s) & \geq \frac{1}{2^{d+1}} \cdot \lambda_{d+1}(\mathbb{B}_{d+1}(\min\{r, T\})) \\ & =\frac{\kappa_{d+1} \cdot \min\{r, T\}^{d+1}}{2^{d+1}}, \end{align*}
\begin{align*} \lambda_{d+1}(\mathbb{B}_{d+1}(\mathbf{y},r) \cap W_s) & \geq \frac{1}{2^{d+1}} \cdot \lambda_{d+1}(\mathbb{B}_{d+1}(\min\{r, T\})) \\ & =\frac{\kappa_{d+1} \cdot \min\{r, T\}^{d+1}}{2^{d+1}}, \end{align*}
where we have equality if ![]() $y$ sits just in a corner of the observation window
$y$ sits just in a corner of the observation window ![]() $W_s$. For instance in the case
$W_s$. For instance in the case ![]() $d=1$,
$d=1$, ![]() $r< T$, and
$r< T$, and ![]() $\mathbf {y}=(-{s}/{2},T)$, one quarter of
$\mathbf {y}=(-{s}/{2},T)$, one quarter of ![]() $\mathbb {B}_{2}(\mathbf {y},r)$ intersects with
$\mathbb {B}_{2}(\mathbf {y},r)$ intersects with ![]() $W_s$. Now, we can derive the bound
$W_s$. Now, we can derive the bound
 \begin{align*} & \mathbb{V}[\lambda_{d+1}(Z(\xi) \cap W_s)] \geq \tau \int_{W_s} \frac{\kappa_{d+1} \cdot \min\{r, T\}^{d+1}}{2^{d+1}} ~\lambda_{d+1}(\mathrm{d}y)\nonumber\\ & \quad = \frac{\tau \cdot \kappa_{d+1} \cdot \min\{r, T\}^{d+1}}{2^{d+1}} \cdot \lambda_{d+1}(W_s) =: c_1 \cdot \lambda_{d+1}(W_s). \end{align*}
\begin{align*} & \mathbb{V}[\lambda_{d+1}(Z(\xi) \cap W_s)] \geq \tau \int_{W_s} \frac{\kappa_{d+1} \cdot \min\{r, T\}^{d+1}}{2^{d+1}} ~\lambda_{d+1}(\mathrm{d}y)\nonumber\\ & \quad = \frac{\tau \cdot \kappa_{d+1} \cdot \min\{r, T\}^{d+1}}{2^{d+1}} \cdot \lambda_{d+1}(W_s) =: c_1 \cdot \lambda_{d+1}(W_s). \end{align*}
This shows condition ![]() $\mathrm {(B)}$ of Lemma 4.4 and concludes the proof.
$\mathrm {(B)}$ of Lemma 4.4 and concludes the proof.
Taking up Remark 4.6, we note that both lower and upper bound on the variance are of the same order.
5.2. Proof for the isolated nodes
Next, we deal with the limit theorem for the isolated cylinders.
Proof of Theorem 5.2. As we did for the covered volume, we aim to apply Lemma 4.4 to the function
counting the number of isolated cylinders created by ![]() $\xi$. Since the Poisson process of basepoints
$\xi$. Since the Poisson process of basepoints ![]() $\eta$ has finite intensity, it holds that
$\eta$ has finite intensity, it holds that ![]() $\mathrm {Iso}_{Z(\xi )}(A)< \infty$
$\mathrm {Iso}_{Z(\xi )}(A)< \infty$ ![]() $\mathbb{P}$-a.s. for all
$\mathbb{P}$-a.s. for all ![]() $A \in \mathcal {C}^{d+1}$. Next, we verify condition (A) and (D). Set
$A \in \mathcal {C}^{d+1}$. Next, we verify condition (A) and (D). Set ![]() $R = 2(R_h + r)$ and
$R = 2(R_h + r)$ and ![]() $c_3 =0$. Since two cylinders can only intersect if the distance between their basepoints is smaller than
$c_3 =0$. Since two cylinders can only intersect if the distance between their basepoints is smaller than ![]() $R$, both conditions are satisfied. This argument follows analogously to our reasoning in the proof of Theorem 5.1. For the same reason, we can bound the first-order difference operator by
$R$, both conditions are satisfied. This argument follows analogously to our reasoning in the proof of Theorem 5.1. For the same reason, we can bound the first-order difference operator by
Set ![]() $a := \mathbb{E} [\eta (\mathbb {B}_d(R))] = \gamma \cdot \lambda _d(\mathbb {B}_ d(0,R))$ and
$a := \mathbb{E} [\eta (\mathbb {B}_d(R))] = \gamma \cdot \lambda _d(\mathbb {B}_ d(0,R))$ and ![]() $x\in \mathbb{R} ^d \times \mathbb{M}_h^d$. The number of isolated cylinders that can be connected by adding
$x\in \mathbb{R} ^d \times \mathbb{M}_h^d$. The number of isolated cylinders that can be connected by adding ![]() $\mathrm {Cyl}(x)$ to the model is limited by the total number of cylinders within maximum range. By using the fourth moment of the Poisson distributed random variable
$\mathrm {Cyl}(x)$ to the model is limited by the total number of cylinders within maximum range. By using the fourth moment of the Poisson distributed random variable ![]() ${\eta (\mathbb {B}_d(R))}$, we get
${\eta (\mathbb {B}_d(R))}$, we get
Thus, condition (C) is satisfied with ![]() $c_2 := a^4 + 6a^3 + 7a^2 + a + 1$. To verify (B), we use a strategy applied in [Reference Reitzner14] and disassemble
$c_2 := a^4 + 6a^3 + 7a^2 + a + 1$. To verify (B), we use a strategy applied in [Reference Reitzner14] and disassemble ![]() $[-{s}/{2}, {s}/{2}]^d$ into boxes of side length
$[-{s}/{2}, {s}/{2}]^d$ into boxes of side length ![]() $6(R_h+r)$. Without loss of generality, we can assume
$6(R_h+r)$. Without loss of generality, we can assume ![]() $s = n \cdot 6(R_h+r)$ for some
$s = n \cdot 6(R_h+r)$ for some ![]() $n \in \mathbb{N}$, as the area outside these boxes is of no consequence to what follows. We index these sets by indices collected in the set
$n \in \mathbb{N}$, as the area outside these boxes is of no consequence to what follows. We index these sets by indices collected in the set ![]() $I$. For each
$I$. For each ![]() $i \in I$ consider
$i \in I$ consider ![]() $C_i$, a box of side length
$C_i$, a box of side length ![]() $2(R_h + r)$ in the center of the corresponding greater box
$2(R_h + r)$ in the center of the corresponding greater box ![]() $S_i$ of side length
$S_i$ of side length ![]() $6(R_h + r)$. We define the event
$6(R_h + r)$. We define the event
Let the ![]() $\sigma$-algebra
$\sigma$-algebra ![]() $\mathcal {F}$ contain information on basepoints and velocities of all cylinders of
$\mathcal {F}$ contain information on basepoints and velocities of all cylinders of ![]() $Z(\xi )$, except those with basepoint in a square
$Z(\xi )$, except those with basepoint in a square ![]() $S_i$ with
$S_i$ with ![]() $\mathbb{1}(A_i) = 1$. Now we decompose the variance
$\mathbb{1}(A_i) = 1$. Now we decompose the variance
 \begin{align} \mathbb{V}[\mathrm{Iso}_{Z(\xi)}(W_s)] & = \mathbb{E}[\mathbb{V}[\mathrm{Iso}_{Z(\xi)}(W_s) \,|\, \mathcal{F}]] + \mathbb{V}[\mathbb{E}[\mathrm{Iso}_{Z(\xi)}(W_s) \,|\, \mathcal{F}]]\ \cr & \geq\mathbb{E}[\mathbb{V}[\mathrm{Iso}_{Z(\xi)}(W_s) \,|\, \mathcal{F}]]\ \cr & = \mathbb{E}\left[\sum_{\mathbb{1}(A_i)=1} \mathbb{V}_{X_{i,1},X_{i,2}}[\mathrm{Iso}_{Z(\xi)}(W_s)] \right], \end{align}
\begin{align} \mathbb{V}[\mathrm{Iso}_{Z(\xi)}(W_s)] & = \mathbb{E}[\mathbb{V}[\mathrm{Iso}_{Z(\xi)}(W_s) \,|\, \mathcal{F}]] + \mathbb{V}[\mathbb{E}[\mathrm{Iso}_{Z(\xi)}(W_s) \,|\, \mathcal{F}]]\ \cr & \geq\mathbb{E}[\mathbb{V}[\mathrm{Iso}_{Z(\xi)}(W_s) \,|\, \mathcal{F}]]\ \cr & = \mathbb{E}\left[\sum_{\mathbb{1}(A_i)=1} \mathbb{V}_{X_{i,1},X_{i,2}}[\mathrm{Iso}_{Z(\xi)}(W_s)] \right], \end{align}
where the right-hand side variance is taken with respect only to the two random elements ![]() $X_{i,1},X_{i,2} \in \mathbb{R} ^d \times \mathbb{M}_h^d$, created by the event
$X_{i,1},X_{i,2} \in \mathbb{R} ^d \times \mathbb{M}_h^d$, created by the event ![]() $A_i$. Since these two cylinders can not intersect with any other cylinders of the model, the number of isolated nodes outside
$A_i$. Since these two cylinders can not intersect with any other cylinders of the model, the number of isolated nodes outside ![]() $A_i$ is independent of that contributed by
$A_i$ is independent of that contributed by ![]() $X_{i,1}$ and
$X_{i,1}$ and ![]() $X_{i,2}$. Let
$X_{i,2}$. Let ![]() $\Delta _{X_{i,1},X_{i,2}}\mathrm {Iso}_{Z(\xi )}(W_s)$ denote that contribution. Note that
$\Delta _{X_{i,1},X_{i,2}}\mathrm {Iso}_{Z(\xi )}(W_s)$ denote that contribution. Note that
This yields
 \begin{align*} & \mathbb{V}_{X_{i,1},X_{i,2}}[\mathrm{Iso}_{Z(\xi)}(W_s)]\\ & \quad =\mathbb{V}_{X_{i,1},X_{i,2}}[\mathrm{Iso}_{Z(\xi - \delta_{X_{i,1}} - \delta_{X_{i,2}})}(W_s) + \Delta_{X_{i,1},X_{i,2}}\mathrm{Iso}_{Z(\xi)}(W_s)] \\ & \quad =\mathbb{V}_{X_{i,1},X_{i,2}}[\Delta_{X_{i,1},X_{i,2}}\mathrm{Iso}_{Z(\xi)}(W_s)]\\ & \quad = 4 \cdot \mathbb{P}[\mathrm{Cyl}(X_{i,1}) \cap \mathrm{Cyl}(X_{i,2}) = \emptyset] \cdot \mathbb{P}[\mathrm{Cyl}(X_{i,1}) \cap \mathrm{Cyl}(X_{i,2}) \neq \emptyset] =: c_4, \end{align*}
\begin{align*} & \mathbb{V}_{X_{i,1},X_{i,2}}[\mathrm{Iso}_{Z(\xi)}(W_s)]\\ & \quad =\mathbb{V}_{X_{i,1},X_{i,2}}[\mathrm{Iso}_{Z(\xi - \delta_{X_{i,1}} - \delta_{X_{i,2}})}(W_s) + \Delta_{X_{i,1},X_{i,2}}\mathrm{Iso}_{Z(\xi)}(W_s)] \\ & \quad =\mathbb{V}_{X_{i,1},X_{i,2}}[\Delta_{X_{i,1},X_{i,2}}\mathrm{Iso}_{Z(\xi)}(W_s)]\\ & \quad = 4 \cdot \mathbb{P}[\mathrm{Cyl}(X_{i,1}) \cap \mathrm{Cyl}(X_{i,2}) = \emptyset] \cdot \mathbb{P}[\mathrm{Cyl}(X_{i,1}) \cap \mathrm{Cyl}(X_{i,2}) \neq \emptyset] =: c_4, \end{align*}
since both probabilities clearly are strictly positive. Using this in (5.2) together with the stationarity and independence properties of ![]() $\eta$ as well as
$\eta$ as well as ![]() $|I| = ({s}/{6(R_h+r)})^d$, we have
$|I| = ({s}/{6(R_h+r)})^d$, we have
 \begin{align*} \mathbb{V}[\mathrm{Iso}_{Z(\xi)}(W_s)] & \geq c_4 \cdot \sum_{i \in I} \mathbb{P}[A_i] \\ & \geq c_4 \cdot \sum_{i \in I} \mathbb{P}[\eta(C_i)=2] \cdot \mathbb{P}[\eta(S_i \backslash C_i)=0]\\ & \geq c_4 \cdot \sum_{i \in I} c_5= c_6 \cdot \left(\frac{s}{6(R_h+r)}\right)^d \\ & = \frac{c_6}{6^d T(R_h+r)^d} \lambda_{d+1}(W_s) \end{align*}
\begin{align*} \mathbb{V}[\mathrm{Iso}_{Z(\xi)}(W_s)] & \geq c_4 \cdot \sum_{i \in I} \mathbb{P}[A_i] \\ & \geq c_4 \cdot \sum_{i \in I} \mathbb{P}[\eta(C_i)=2] \cdot \mathbb{P}[\eta(S_i \backslash C_i)=0]\\ & \geq c_4 \cdot \sum_{i \in I} c_5= c_6 \cdot \left(\frac{s}{6(R_h+r)}\right)^d \\ & = \frac{c_6}{6^d T(R_h+r)^d} \lambda_{d+1}(W_s) \end{align*}
and thus condition (B). In the last equality, we have used that ![]() $\lambda _{d+1}(W_s) = s^d \cdot T$.
$\lambda _{d+1}(W_s) = s^d \cdot T$.
Again, the lower bound matches the order of the upper bound as given in Remark 4.6.
5.3. Proof for the Euler characteristic
It remains to prove the limit theorem for the Euler characteristic.
Proof of Theorem 5.4. We aim to use Lemma 4.4 on ![]() $f_{(\cdot )}$ for
$f_{(\cdot )}$ for ![]() $f_{\xi }: \mathcal {C}^{d+1} \to \mathbb{Z}$ with
$f_{\xi }: \mathcal {C}^{d+1} \to \mathbb{Z}$ with
Since ![]() $\eta$ has finite intensity, the properties of
$\eta$ has finite intensity, the properties of ![]() $\chi$ imply that
$\chi$ imply that ![]() $f(A) < \infty$ for all
$f(A) < \infty$ for all ![]() $A \in \mathcal {C}^{d+1}$
$A \in \mathcal {C}^{d+1}$ ![]() $\mathbb{P}$-a.s. Once again we start by checking conditions (A) and (D). Again, set
$\mathbb{P}$-a.s. Once again we start by checking conditions (A) and (D). Again, set ![]() $R = 2(R_h+r)$ and
$R = 2(R_h+r)$ and ![]() $c_3 = 0$. As
$c_3 = 0$. As ![]() $\mathrm {Cyl}(\mathbf {p},\mathbf {v})\cap W_s = \emptyset$ for any
$\mathrm {Cyl}(\mathbf {p},\mathbf {v})\cap W_s = \emptyset$ for any ![]() $(\mathbf {p},\mathbf {v}) \in \mathbb{R} ^d \times \mathbb{M}_h^d$ with
$(\mathbf {p},\mathbf {v}) \in \mathbb{R} ^d \times \mathbb{M}_h^d$ with ![]() $\|\mathbf {p}\| \geq R+s$, condition (A) is satisfied.
$\|\mathbf {p}\| \geq R+s$, condition (A) is satisfied.
Also, for ![]() $(\mathbf {q},\mathbf {w})\in \mathbb{R} ^d \times \mathbb{M}_h^d$,
$(\mathbf {q},\mathbf {w})\in \mathbb{R} ^d \times \mathbb{M}_h^d$, ![]() $\|\mathbf {p}-\mathbf {q}\| \geq R$ implies
$\|\mathbf {p}-\mathbf {q}\| \geq R$ implies ![]() $\mathrm{Cyl} (\mathbf {p},\mathbf {v})\cap \mathrm{Cyl} (\mathbf {q},\mathbf {w}) = \emptyset$ and thus
$\mathrm{Cyl} (\mathbf {p},\mathbf {v})\cap \mathrm{Cyl} (\mathbf {q},\mathbf {w}) = \emptyset$ and thus ![]() $\mathrm {D}_{(\mathbf {p},\mathbf {v})}(\chi (Z(\xi +\delta _{(\mathbf {q},\mathbf {w})})\cap W_s)) - \mathrm {D}_{(\mathbf {p},\mathbf {v})}(\chi (Z(\xi )\cap W_s)) =0$
$\mathrm {D}_{(\mathbf {p},\mathbf {v})}(\chi (Z(\xi +\delta _{(\mathbf {q},\mathbf {w})})\cap W_s)) - \mathrm {D}_{(\mathbf {p},\mathbf {v})}(\chi (Z(\xi )\cap W_s)) =0$ ![]() $\mathbb{P} \text {-a.s.}$ To verify (C), we note that for
$\mathbb{P} \text {-a.s.}$ To verify (C), we note that for ![]() $\mathbf {x} \in \mathbb{R} ^d \times \mathbb{M}_h^d$, the definition of
$\mathbf {x} \in \mathbb{R} ^d \times \mathbb{M}_h^d$, the definition of ![]() $\chi$ gives us
$\chi$ gives us
 \begin{align*} \mathrm{D}_{\mathbf{x}} \chi(Z(\xi) \cap W_s) & = \chi(Z(\xi+\delta_\mathbf{x}) \cap W_s) - \chi(Z(\xi) \cap W_s)\\ & = \chi((Z(\xi) \cup \mathrm{Cyl}(\mathbf{x})) \cap W_s) - \chi(Z(\xi) \cap W_s)\nonumber\\ & = \chi((Z(\xi) \cap W_s) \cup (\mathrm{Cyl}(\mathbf{x})\cap W_s)) - \chi(Z(\xi) \cap W_s)\nonumber\\ & = \chi(\mathrm{Cyl}(\mathbf{x}) \cap W_s) - \chi(Z(\xi) \cap \mathrm{Cyl}(\mathbf{x}) \cap W_s ) \quad \mathbb{P} \text{-a.s.} \end{align*}
\begin{align*} \mathrm{D}_{\mathbf{x}} \chi(Z(\xi) \cap W_s) & = \chi(Z(\xi+\delta_\mathbf{x}) \cap W_s) - \chi(Z(\xi) \cap W_s)\\ & = \chi((Z(\xi) \cup \mathrm{Cyl}(\mathbf{x})) \cap W_s) - \chi(Z(\xi) \cap W_s)\nonumber\\ & = \chi((Z(\xi) \cap W_s) \cup (\mathrm{Cyl}(\mathbf{x})\cap W_s)) - \chi(Z(\xi) \cap W_s)\nonumber\\ & = \chi(\mathrm{Cyl}(\mathbf{x}) \cap W_s) - \chi(Z(\xi) \cap \mathrm{Cyl}(\mathbf{x}) \cap W_s ) \quad \mathbb{P} \text{-a.s.} \end{align*}
Furthermore, it holds true that ![]() $\chi (\mathrm {Cyl}(\mathbf {x}) \cap W_s) = \mathbb{1}(\mathrm {Cyl}(\mathbf {x}) \cap W_s \neq \emptyset )$ and since
$\chi (\mathrm {Cyl}(\mathbf {x}) \cap W_s) = \mathbb{1}(\mathrm {Cyl}(\mathbf {x}) \cap W_s \neq \emptyset )$ and since ![]() $\chi (Z(\xi ) \cap \mathrm {Cyl}(\mathbf {x}) \cap W_s)$ counts the number of disjoint intersections of
$\chi (Z(\xi ) \cap \mathrm {Cyl}(\mathbf {x}) \cap W_s)$ counts the number of disjoint intersections of ![]() $\mathrm {Cyl}(\mathbf {x}) \cap W_s$ with cylinders of
$\mathrm {Cyl}(\mathbf {x}) \cap W_s$ with cylinders of ![]() $Z(\xi )$, we also have
$Z(\xi )$, we also have
Thus, the triangle inequality gives
![]() $\mathbb{P}$-a.s. for all
$\mathbb{P}$-a.s. for all ![]() $\mathbf {x} \in \mathbb{R} ^d \times \mathbb{M}_h^d$ and
$\mathbf {x} \in \mathbb{R} ^d \times \mathbb{M}_h^d$ and ![]() $\mathbf {y} \in \mathbb{R} ^d$. Therefore, we conclude that (C) is fulfilled with
$\mathbf {y} \in \mathbb{R} ^d$. Therefore, we conclude that (C) is fulfilled with
To verify (B), we use the same strategy as in the proof of Theorem 5.2 and now have to consider ![]() $\mathbb{V} _{X_{i,1},X_{i,2}}[\chi (Z(\xi ) \cap W_s)]$. Again, since the cylinders created by
$\mathbb{V} _{X_{i,1},X_{i,2}}[\chi (Z(\xi ) \cap W_s)]$. Again, since the cylinders created by ![]() $X_{i,1}$ and
$X_{i,1}$ and ![]() $X_{i,2}$ can not intersect with any other cylinder outside the box
$X_{i,2}$ can not intersect with any other cylinder outside the box ![]() $C_i$, we can denote this contribution as before by
$C_i$, we can denote this contribution as before by ![]() $\Delta _{X_{i,1},X_{i,2}}\chi (Z(\xi ) \cap W_s)$ and use the additivity of the Euler characteristic to get
$\Delta _{X_{i,1},X_{i,2}}\chi (Z(\xi ) \cap W_s)$ and use the additivity of the Euler characteristic to get
 \begin{align*} & \mathbb{V}_{X_{i,1},X_{i,2}}[\chi(Z(\xi) \cap W_s)]\\ & \quad= \mathbb{V}_{X_{i,1},X_{i,2}}[\chi(Z(\xi - \delta_{X_{i,1}} - \delta_{X_{i,2}}) \cap W_s) + \Delta_{X_{i,1},X_{i,2}}\chi(Z(\xi) \cap W_s)]\\ & \quad= \mathbb{V}_{X_{i,1},X_{i,2}}[\Delta_{X_{i,1},X_{i,2}}\chi(Z(\xi) \cap W_s)]. \end{align*}
\begin{align*} & \mathbb{V}_{X_{i,1},X_{i,2}}[\chi(Z(\xi) \cap W_s)]\\ & \quad= \mathbb{V}_{X_{i,1},X_{i,2}}[\chi(Z(\xi - \delta_{X_{i,1}} - \delta_{X_{i,2}}) \cap W_s) + \Delta_{X_{i,1},X_{i,2}}\chi(Z(\xi) \cap W_s)]\\ & \quad= \mathbb{V}_{X_{i,1},X_{i,2}}[\Delta_{X_{i,1},X_{i,2}}\chi(Z(\xi) \cap W_s)]. \end{align*}
Since ![]() $\Delta _{X_{i,1},X_{i,2}}\chi (Z(\xi ) \cap W_s) \in \{1,2\}$, we get
$\Delta _{X_{i,1},X_{i,2}}\chi (Z(\xi ) \cap W_s) \in \{1,2\}$, we get
Thus, condition (B) follows as it did for Theorem 5.2.
Note that, again, the order of the lower bound on the variance coincides with that of the upper bound found in Remark 4.6.
6. Stacked time bounded cylinders
Up to this point, our model supports movements in one direction only. To allow for the nodes to change direction and speed, we iterate the marking process, giving a node a new velocity vector at fixed points in time. These times can be given deterministically or randomly, but independent of all other random variables. In view of application, one could think of a deterministic setting like a daily routine or an exponentially distributed random variable for the time distances.
6.1. Construction of the cylinderstacks
Set ![]() $t_0 := 0$,
$t_0 := 0$, ![]() $t_{K+1} :=T$, and let
$t_{K+1} :=T$, and let ![]() $\mathbf {T_{K}} = (t_0,t_1,t_2,\ldots,t_{K+1})$, for some
$\mathbf {T_{K}} = (t_0,t_1,t_2,\ldots,t_{K+1})$, for some ![]() $K\in \mathbb{N}$, be a strictly monotone sequence of times in
$K\in \mathbb{N}$, be a strictly monotone sequence of times in ![]() $[0,T]$. So we supplement our TBC model by
$[0,T]$. So we supplement our TBC model by ![]() $K$ time steps at which the walkers are allowed to change their velocities. Now recall the definition of a cylinder as given in Definition 2.1. We will now modify it to reflect the expanded setting. To a point
$K$ time steps at which the walkers are allowed to change their velocities. Now recall the definition of a cylinder as given in Definition 2.1. We will now modify it to reflect the expanded setting. To a point ![]() $\mathbf {p} \in \eta$ let
$\mathbf {p} \in \eta$ let ![]() $\mathbf {V} = (\mathbf {v_{0}},\ldots,\mathbf {v_{K}})$ be the vector of velocities chosen, that is
$\mathbf {V} = (\mathbf {v_{0}},\ldots,\mathbf {v_{K}})$ be the vector of velocities chosen, that is ![]() $\mathbf {v_{i}} \in \mathbb{M}_h^d$ for
$\mathbf {v_{i}} \in \mathbb{M}_h^d$ for ![]() $i \in \{0,\ldots,K\}$. Consider the projection
$i \in \{0,\ldots,K\}$. Consider the projection ![]() $\pi : \mathbb{M}_h^d \to [0,1]$ onto the time, that is
$\pi : \mathbb{M}_h^d \to [0,1]$ onto the time, that is ![]() $\pi (\mathbf {v}) = v_{d+1}$ for
$\pi (\mathbf {v}) = v_{d+1}$ for ![]() $\mathbf {v}\in \mathbb{M}_h^d$, and recall that
$\mathbf {v}\in \mathbb{M}_h^d$, and recall that ![]() $\mathbf {\hat {p}_{0}} \in \mathbb{R} ^{d+1}$ is the vector
$\mathbf {\hat {p}_{0}} \in \mathbb{R} ^{d+1}$ is the vector ![]() $\mathbf {p}$ but with an additional coordinate with value zero. Then,
$\mathbf {p}$ but with an additional coordinate with value zero. Then,
 $$\mathbf{\hat{p}_{k}} := \mathbf{\hat{p}_{0}} + \sum_{j=0}^{k-1} \frac{|t_{j+1} - t_j|}{\pi(\mathbf{v_{j}})} \mathbf{v_{j}}.$$
$$\mathbf{\hat{p}_{k}} := \mathbf{\hat{p}_{0}} + \sum_{j=0}^{k-1} \frac{|t_{j+1} - t_j|}{\pi(\mathbf{v_{j}})} \mathbf{v_{j}}.$$
In the context of random networks, think of this vector as the coordinates (in space and time) of a node at time ![]() $t_k$ which started its journey in
$t_k$ which started its journey in ![]() $\mathbf {p}\in \mathbb{R} ^d$ at time zero and moved with velocities
$\mathbf {p}\in \mathbb{R} ^d$ at time zero and moved with velocities ![]() $\mathbf {v_j}$ for the time segment
$\mathbf {v_j}$ for the time segment ![]() $[t_j,t_{j+1}]$ for
$[t_j,t_{j+1}]$ for ![]() $j=0,\ldots,k-1$. We are now in a position to modify Definition 2.1 for this expanded setting (Figure 3).
$j=0,\ldots,k-1$. We are now in a position to modify Definition 2.1 for this expanded setting (Figure 3).
Definition 6.1. Given a radius ![]() $r \geq 0$ and
$r \geq 0$ and ![]() $\mathbf {T_K}$ as above, the values of the function
$\mathbf {T_K}$ as above, the values of the function
 \begin{align*} & \mathrm{Cyl}_{r,\mathbf{T_K}}:\ \mathbb{R}^{d} \times (\mathbb{M}_h^d)^{K+1} \to \mathcal{C}^{d+1}\\ & (\mathbf{p},\mathbf{v}) \mapsto \bigcup_{k=0}^K \bigcup_{u \in [0,1]} \left( \left(\mathbf{\hat{p}_k} + \frac{u |t_{k+1}-t_{k}|}{\pi(\mathbf{v_{k}})} \cdot \mathbf{v_{k}}\right) + \mathbb{B}_d(r)\right) \end{align*}
\begin{align*} & \mathrm{Cyl}_{r,\mathbf{T_K}}:\ \mathbb{R}^{d} \times (\mathbb{M}_h^d)^{K+1} \to \mathcal{C}^{d+1}\\ & (\mathbf{p},\mathbf{v}) \mapsto \bigcup_{k=0}^K \bigcup_{u \in [0,1]} \left( \left(\mathbf{\hat{p}_k} + \frac{u |t_{k+1}-t_{k}|}{\pi(\mathbf{v_{k}})} \cdot \mathbf{v_{k}}\right) + \mathbb{B}_d(r)\right) \end{align*}
are the time bounded cylinderstacks.

Figure 3. An excerpt of the TBC model in the expanded setting.
Our idea is that at every time ![]() $t \in \mathbf {T_K}$, a cylinder has the opportunity to change velocity and will do so with probability
$t \in \mathbf {T_K}$, a cylinder has the opportunity to change velocity and will do so with probability ![]() $q \in [0,1]$. A new velocity is always drawn with respect to the probability measure
$q \in [0,1]$. A new velocity is always drawn with respect to the probability measure ![]() $\mathbb{Q}$ introduced in Section 2. Thus, the aforementioned vector
$\mathbb{Q}$ introduced in Section 2. Thus, the aforementioned vector ![]() $\mathbf {V} = (\mathbf {v_{0}},\ldots,\mathbf {v_{K}})\in (\mathbb{M}_h^d )^{K+1}$ is drawn with respect to the probability measure
$\mathbf {V} = (\mathbf {v_{0}},\ldots,\mathbf {v_{K}})\in (\mathbb{M}_h^d )^{K+1}$ is drawn with respect to the probability measure
We can now give analogues to Definition 2.2 and Lemma 2.3.
Definition 6.2. Let ![]() $\eta$ be defined as in Section 2 and
$\eta$ be defined as in Section 2 and ![]() $\mathbb{Q} _K$ as above. Mark every point in the support of
$\mathbb{Q} _K$ as above. Mark every point in the support of ![]() $\eta$ with a direction from
$\eta$ with a direction from ![]() $(\mathbb{M}_h^d )^{K+1}$, randomly with respect to
$(\mathbb{M}_h^d )^{K+1}$, randomly with respect to ![]() $\mathbb{Q} _K$. The resulting marked point process
$\mathbb{Q} _K$. The resulting marked point process ![]() $\mathbf {\xi }_K$ defined on
$\mathbf {\xi }_K$ defined on ![]() $\mathbb{R} ^d \times (\mathbb{M}_h^d )^{K+1}$ is called the process of time bounded cylinderstacks.
$\mathbb{R} ^d \times (\mathbb{M}_h^d )^{K+1}$ is called the process of time bounded cylinderstacks.
Lemma 6.3. ![]() $\xi _K$ is a Poisson point process with intensity measure
$\xi _K$ is a Poisson point process with intensity measure ![]() $\Lambda _{K} = \gamma \lambda _d \otimes \mathbb{Q} _K$.
$\Lambda _{K} = \gamma \lambda _d \otimes \mathbb{Q} _K$.
Proof. Since ![]() $\mathbb{Q} _K$ is independent of the Poisson process
$\mathbb{Q} _K$ is independent of the Poisson process ![]() $\eta$, we have an independent marking again and thus the statement follows as it did for Lemma 2.3.
$\eta$, we have an independent marking again and thus the statement follows as it did for Lemma 2.3.
That the process of time bounded cylinderstacks preserves the Poisson properties of the original point process seems remarkable, but can be intuitively explained by using thinnings. Since for ![]() $t_1\geq T$, the model remains unchanged let us consider
$t_1\geq T$, the model remains unchanged let us consider ![]() $t_1< T$. We start with the point process
$t_1< T$. We start with the point process ![]() $\xi$ as introduced in Definition 2.2. From Lemma 2.3, we know that
$\xi$ as introduced in Definition 2.2. From Lemma 2.3, we know that ![]() $\xi$ is a Poisson point process. Now we take a
$\xi$ is a Poisson point process. Now we take a ![]() $q$-thinning of
$q$-thinning of ![]() $\xi$, namely a Bernoulli experiment with parameter
$\xi$, namely a Bernoulli experiment with parameter ![]() $q$ which decides for each point of the Poisson process if it belongs to
$q$ which decides for each point of the Poisson process if it belongs to ![]() $\xi (q)$ or
$\xi (q)$ or ![]() $\xi -\xi (q)$. The Thinning Theorem [Reference Last and Penrose13, Corollary 5.9] implies that both
$\xi -\xi (q)$. The Thinning Theorem [Reference Last and Penrose13, Corollary 5.9] implies that both ![]() $\xi (q)$ and
$\xi (q)$ and ![]() $\xi -\xi (q)$ are Poisson processes.
$\xi -\xi (q)$ are Poisson processes.
For the points in ![]() $\xi (q)$, we now choose a new velocity and by adding this into another component of the marking, we get a new marked point process which we call
$\xi (q)$, we now choose a new velocity and by adding this into another component of the marking, we get a new marked point process which we call ![]() $\xi (q)^M$. Analogously to the single velocity case the Marking Theorem implies that this process is Poisson. For points in
$\xi (q)^M$. Analogously to the single velocity case the Marking Theorem implies that this process is Poisson. For points in ![]() $\xi -\xi (q)$, the velocity stays the same, nevertheless, as for
$\xi -\xi (q)$, the velocity stays the same, nevertheless, as for ![]() $\xi (q)$ we add the previous velocity as a new marking and again obtain a marked point process
$\xi (q)$ we add the previous velocity as a new marking and again obtain a marked point process ![]() $\xi (1-q)^M$. As a superposition of two Poisson processes,
$\xi (1-q)^M$. As a superposition of two Poisson processes, ![]() $\xi _1:=\xi (q)^M \oplus \xi (1-q)^M$ is also Poisson. We proceed in thinning, marking, and gluing together for each time step
$\xi _1:=\xi (q)^M \oplus \xi (1-q)^M$ is also Poisson. We proceed in thinning, marking, and gluing together for each time step ![]() $t_i< T$ and obtain the Poisson process of cylinderstacks. We can now conveniently define the expanded model as follows.
$t_i< T$ and obtain the Poisson process of cylinderstacks. We can now conveniently define the expanded model as follows.
Definition 6.4. With the point process ![]() $\xi _K$ given as above, the stacked time bounded cylinder (sTBC) model is the random closed set
$\xi _K$ given as above, the stacked time bounded cylinder (sTBC) model is the random closed set
In this notation, we identify the random measure ![]() $\xi _K$ with its support.
$\xi _K$ with its support.
With these definitions, we can now rephrase Lemma 4.4 to work with our modifications.
Lemma 6.5. Let ![]() $f: \mathcal {C}^{d+1} \to \mathbb{R}$,
$f: \mathcal {C}^{d+1} \to \mathbb{R}$, ![]() $s\geq 1$ and
$s\geq 1$ and ![]() $W_s = [-{s}/{2}, {s}/{2}]^{d} \times [0,T]$. Assume that
$W_s = [-{s}/{2}, {s}/{2}]^{d} \times [0,T]$. Assume that ![]() $|f(A)|<\infty$ for all
$|f(A)|<\infty$ for all ![]() $A \in \mathcal {C}^{d+1}$ and that there exist constants
$A \in \mathcal {C}^{d+1}$ and that there exist constants ![]() $c_1$,
$c_1$, ![]() $c_2$,
$c_2$, ![]() $c_3$ and
$c_3$ and ![]() $R \in \mathbb{R}$ such that the following conditions are met for all
$R \in \mathbb{R}$ such that the following conditions are met for all ![]() $\mathbf {x} = (\mathbf {p},\mathbf {v}), \mathbf {y} = (\mathbf {q},\mathbf {w}) \in \mathbb{R} ^d \times (\mathbb{M}_h^d )^{K+1}$:
$\mathbf {x} = (\mathbf {p},\mathbf {v}), \mathbf {y} = (\mathbf {q},\mathbf {w}) \in \mathbb{R} ^d \times (\mathbb{M}_h^d )^{K+1}$:
(A)
 $\mathrm {D}_\mathbf {x}F(Z(\xi _K) \cap W_s) = 0 \quad \mathbb{P} \text {-a.s.}$ for
$\mathrm {D}_\mathbf {x}F(Z(\xi _K) \cap W_s) = 0 \quad \mathbb{P} \text {-a.s.}$ for  $\|\mathbf {p}\| > R+s$,
$\|\mathbf {p}\| > R+s$,(B)
 $\mathbb{V} [f(Z(\xi _K) \cap W_s)] \geq c_1 \cdot \lambda _{d+1}(W_s)$,
$\mathbb{V} [f(Z(\xi _K) \cap W_s)] \geq c_1 \cdot \lambda _{d+1}(W_s)$,(C)
 $\max \{\mathbb{E} [\mathrm {D}_{\mathbf {x}}f(Z(\xi _K) \cap W_s)^4]$,
$\max \{\mathbb{E} [\mathrm {D}_{\mathbf {x}}f(Z(\xi _K) \cap W_s)^4]$,  $\mathbb{E} [\mathrm {D}_{\mathbf {x}}f(Z(\xi _K+\delta _\mathbf {y}) \cap W_s)^4]\} \leq c_2$,
$\mathbb{E} [\mathrm {D}_{\mathbf {x}}f(Z(\xi _K+\delta _\mathbf {y}) \cap W_s)^4]\} \leq c_2$,(D)
 $\|\mathbf {p} - \mathbf {q}\|>R \Rightarrow \mathbb{E} [(\mathrm {D}_{\mathbf {x},\mathbf {y}}^2 f(Z(\xi _K) \cap W_s))^4] \leq \frac {c_3}{\lambda _{d+1}(W_s)^4}$.
$\|\mathbf {p} - \mathbf {q}\|>R \Rightarrow \mathbb{E} [(\mathrm {D}_{\mathbf {x},\mathbf {y}}^2 f(Z(\xi _K) \cap W_s))^4] \leq \frac {c_3}{\lambda _{d+1}(W_s)^4}$.
Then, there is a constant ![]() $c \in \mathbb{R}$ such that, for a standard normal random variable
$c \in \mathbb{R}$ such that, for a standard normal random variable ![]() $N$,
$N$,
 $$\mathrm{d_W}\left(\frac{f(Z(\xi_K) \cap W_s)-\mathbb{E}[f(Z(\xi_K) \cap W_s)]}{\sqrt{\mathbb{V}[f(Z(\xi_K) \cap W_s)]}}, N\right) \leq \frac{c}{\sqrt{\lambda_{d+1}(W_s)}}.$$
$$\mathrm{d_W}\left(\frac{f(Z(\xi_K) \cap W_s)-\mathbb{E}[f(Z(\xi_K) \cap W_s)]}{\sqrt{\mathbb{V}[f(Z(\xi_K) \cap W_s)]}}, N\right) \leq \frac{c}{\sqrt{\lambda_{d+1}(W_s)}}.$$
As the proof in Section 4 relies only on the assumed bounds and not on how the model is constructed, we can use the same techniques and estimates we used there and prove this lemma analogously.
6.2. Covered volume
As usual, let ![]() $W_s := [-{s}/{2}, {s}/{2}]^{d} \times [0,T]$. We will now study the covered volume of the sTBC model that is the random variable
$W_s := [-{s}/{2}, {s}/{2}]^{d} \times [0,T]$. We will now study the covered volume of the sTBC model that is the random variable
As this is an additive function, our strategy for working with this quantity will be to split the sTBC model into TBC models and evaluate the volume for each of them. To that end let ![]() $Z_t(\xi )$ denote the TBC model with time horizon
$Z_t(\xi )$ denote the TBC model with time horizon ![]() $t \geq 0$. We will first apply our strategy when computing the expectation of the volume. Using (3.1) and Fubini, we have
$t \geq 0$. We will first apply our strategy when computing the expectation of the volume. Using (3.1) and Fubini, we have
 \begin{align*} \mathbb{E}[\lambda_{d+1}(Z(\xi_K) \cap W_s)] & = \mathbb{E}\left[\int_{W_s} \mathbb{1}(\mathbf{x} \in Z(\xi_K)) \,\mathrm{d}\mathbf{x}\right]\\ & = \mathbb{E}\left[\sum_{k=0}^{K} \int_{[-{s}/{2},{s}/{2}]^d \times [t_k, t_{k+1}]} \mathbb{1}(\mathbf{x} \in Z_{|t_{k+1}-t_k|}(\xi))\,\mathrm{d}\mathbf{x}\right]\\ & =\mathbb{E}\left[\sum_{k=0}^{K} \mathbb{E}\left[\int_{[-{s}/{2},{s}/{2}]^d \times [t_k, t_{k+1}]} \mathbb{1}(\mathbf{x} \in Z_{|t_{k+1}-t_k|}(\xi))~\mathrm{d}\mathbf{x} \,|\, \mathbf{T_K}\right]\right]\\ & = (1 - \exp(-\gamma \cdot r^d \kappa_d)) \cdot \mathbb{E}\left[\sum_{k=0}^{K} \lambda_{d+1}\left(\left[-\frac{s}{2},\frac{s}{2}\right]^d \times [t_k, t_{k+1}]\right)\right]\\ & = (1 - \exp(-\gamma \cdot r^d \kappa_d)) \cdot \lambda_{d+1}(W_s). \end{align*}
\begin{align*} \mathbb{E}[\lambda_{d+1}(Z(\xi_K) \cap W_s)] & = \mathbb{E}\left[\int_{W_s} \mathbb{1}(\mathbf{x} \in Z(\xi_K)) \,\mathrm{d}\mathbf{x}\right]\\ & = \mathbb{E}\left[\sum_{k=0}^{K} \int_{[-{s}/{2},{s}/{2}]^d \times [t_k, t_{k+1}]} \mathbb{1}(\mathbf{x} \in Z_{|t_{k+1}-t_k|}(\xi))\,\mathrm{d}\mathbf{x}\right]\\ & =\mathbb{E}\left[\sum_{k=0}^{K} \mathbb{E}\left[\int_{[-{s}/{2},{s}/{2}]^d \times [t_k, t_{k+1}]} \mathbb{1}(\mathbf{x} \in Z_{|t_{k+1}-t_k|}(\xi))~\mathrm{d}\mathbf{x} \,|\, \mathbf{T_K}\right]\right]\\ & = (1 - \exp(-\gamma \cdot r^d \kappa_d)) \cdot \mathbb{E}\left[\sum_{k=0}^{K} \lambda_{d+1}\left(\left[-\frac{s}{2},\frac{s}{2}\right]^d \times [t_k, t_{k+1}]\right)\right]\\ & = (1 - \exp(-\gamma \cdot r^d \kappa_d)) \cdot \lambda_{d+1}(W_s). \end{align*}
We see that the expected volume remains unchanged, which is unsurprising given the homogeneous nature of our model.
Theorem 6.6. Let ![]() $N$ denote a standard normal random variable and assume
$N$ denote a standard normal random variable and assume ![]() $r< s$. There exists a constant
$r< s$. There exists a constant ![]() $c \in \mathbb{R} _+$ such that
$c \in \mathbb{R} _+$ such that
 $$\mathrm{{d}_W}\left(\frac{\lambda_{d+1}(Z(\xi_K) \cap W_s) - \mathbb{E}[\lambda_{d+1}(Z(\xi_K) \cap W_s)]}{\sqrt{\mathbb{V}[\lambda_{d+1}(Z(\xi_K) \cap W_s)]}}, N\right) \leq \frac{c}{\sqrt{\lambda_{d+1}(W_s)}}.$$
$$\mathrm{{d}_W}\left(\frac{\lambda_{d+1}(Z(\xi_K) \cap W_s) - \mathbb{E}[\lambda_{d+1}(Z(\xi_K) \cap W_s)]}{\sqrt{\mathbb{V}[\lambda_{d+1}(Z(\xi_K) \cap W_s)]}}, N\right) \leq \frac{c}{\sqrt{\lambda_{d+1}(W_s)}}.$$
Proof. We use Lemma 6.5 on the function ![]() $f=\lambda _{d+1}$. Since the maximum scope of a cylinderstack is the same as in the single velocity model, we can verify conditions (A) and (D) by the same observation we made in the proof of Theorem 5.1, again using
$f=\lambda _{d+1}$. Since the maximum scope of a cylinderstack is the same as in the single velocity model, we can verify conditions (A) and (D) by the same observation we made in the proof of Theorem 5.1, again using ![]() $R = 2(R_{h} + r)$ and
$R = 2(R_{h} + r)$ and ![]() $c_3=0$. The same is true for condition (C) which once more is satisfied with
$c_3=0$. The same is true for condition (C) which once more is satisfied with ![]() $c_2 := (T\kappa _d r^d)^4$. To verify (B), we apply the first term of the Wiener-Itô chaos expansion and bound
$c_2 := (T\kappa _d r^d)^4$. To verify (B), we apply the first term of the Wiener-Itô chaos expansion and bound
 \begin{align*} \mathbb{V}[\lambda_{d+1}(Z(\xi_K) \cap W_s)] & \geq \int_{\mathbb{R}^d \times (\mathbb{M}_h^d )^{K+1} } \mathbb{E}[D_{\mathbf{x}}(\lambda_{d+1}(Z(\xi_K) \cap W_s)]^2 \Lambda_K(\mathrm{d}\mathbf{x})\\ & \geq \int_{[-{s}/{2},{s}/{2}]^d \times (\mathbb{M}_h^d)^{K+1} } \mathbb{E}[D_{\mathbf{x}}(\lambda_{d+1}(Z(\xi_K) \cap W_s)]^2 \Lambda_K(\mathrm{d}\mathbf{x}), \end{align*}
\begin{align*} \mathbb{V}[\lambda_{d+1}(Z(\xi_K) \cap W_s)] & \geq \int_{\mathbb{R}^d \times (\mathbb{M}_h^d )^{K+1} } \mathbb{E}[D_{\mathbf{x}}(\lambda_{d+1}(Z(\xi_K) \cap W_s)]^2 \Lambda_K(\mathrm{d}\mathbf{x})\\ & \geq \int_{[-{s}/{2},{s}/{2}]^d \times (\mathbb{M}_h^d)^{K+1} } \mathbb{E}[D_{\mathbf{x}}(\lambda_{d+1}(Z(\xi_K) \cap W_s)]^2 \Lambda_K(\mathrm{d}\mathbf{x}), \end{align*}
see for example [Reference Last and Penrose13, Ex. 18.8]. As ![]() $D_{\mathbf {x}}(\lambda _{d+1}(Z(\xi _K) \cap W_s)\geq 0$
$D_{\mathbf {x}}(\lambda _{d+1}(Z(\xi _K) \cap W_s)\geq 0$ ![]() $\mathbb{P}$-a.s., the expectation is, for all
$\mathbb{P}$-a.s., the expectation is, for all ![]() $\mathbf {x}\in [-{s}/{2},{s}/{2}]^d \times (\mathbb{M}_h^d )^{K+1}$, lower bounded by
$\mathbf {x}\in [-{s}/{2},{s}/{2}]^d \times (\mathbb{M}_h^d )^{K+1}$, lower bounded by
Since all cylinders have a finite scope, the cylinders that are further away than two times this scope can not meet regardless of any kinetics. This implies that
The minimal volume ![]() $\lambda _{d+1}(\mathrm {Cyl}(\mathbf {x})\cap W_s)$ is attained for a cylinder
$\lambda _{d+1}(\mathrm {Cyl}(\mathbf {x})\cap W_s)$ is attained for a cylinder ![]() $L$ starting at a corner of
$L$ starting at a corner of ![]() $[-{s}/{2},{s}/{2}]^d$ and leaving the window with the fastest velocity. For
$[-{s}/{2},{s}/{2}]^d$ and leaving the window with the fastest velocity. For ![]() $d=2$ and
$d=2$ and ![]() $r>1$, for example, consider the volume of the enclosed tetrahedron with edge length
$r>1$, for example, consider the volume of the enclosed tetrahedron with edge length ![]() $r$ in both directions and an edge of length
$r$ in both directions and an edge of length ![]() ${r}/{(r-1)}\cdot h$ along the time axis which implies
${r}/{(r-1)}\cdot h$ along the time axis which implies ![]() $\lambda _3(L)\geq \frac {1}{3} \cdot {r^2}/{2} \cdot {r}/{(r-1)} \cdot h$. In higher dimensions, one can consider the enclosed simplices accordingly. In any case,
$\lambda _3(L)\geq \frac {1}{3} \cdot {r^2}/{2} \cdot {r}/{(r-1)} \cdot h$. In higher dimensions, one can consider the enclosed simplices accordingly. In any case, ![]() $\lambda _{d+1}(L)$ is strictly positive and depending on
$\lambda _{d+1}(L)$ is strictly positive and depending on ![]() $r,d$, and
$r,d$, and ![]() $h$ only. This yields the needed lower bound on the variance
$h$ only. This yields the needed lower bound on the variance
 \begin{align*} \mathbb{V}[\lambda_{d+1}(Z(\xi_K) \cap W_s)] & \geq \int_{[-{s}/{2},{s}/{2}]^d \times (\mathbb{M}_h^d )^{K+1} } \mathbb{E}[D_{\mathbf{x}}(\lambda_{d+1}(Z(\xi_K) \cap W_s)]^2 \Lambda_K(\mathrm{d}\mathbf{x}) \\ & \geq c_1 \cdot \lambda_{d+1}(W_s) \end{align*}
\begin{align*} \mathbb{V}[\lambda_{d+1}(Z(\xi_K) \cap W_s)] & \geq \int_{[-{s}/{2},{s}/{2}]^d \times (\mathbb{M}_h^d )^{K+1} } \mathbb{E}[D_{\mathbf{x}}(\lambda_{d+1}(Z(\xi_K) \cap W_s)]^2 \Lambda_K(\mathrm{d}\mathbf{x}) \\ & \geq c_1 \cdot \lambda_{d+1}(W_s) \end{align*}
for ![]() $c_1 = \lambda _{d+1}(L)^2\cdot {1}/{T} \cdot e^{-2 \gamma \lambda _d(B_d(2(R_h+r))}$. Note that this method of estimating the variance is made possible by the finite scope of our cylinders. Although it would also be applicable in the single direction case, it leads to a worse bound than the method presented in Theorem 5.1 in the nonstacked TBC.
$c_1 = \lambda _{d+1}(L)^2\cdot {1}/{T} \cdot e^{-2 \gamma \lambda _d(B_d(2(R_h+r))}$. Note that this method of estimating the variance is made possible by the finite scope of our cylinders. Although it would also be applicable in the single direction case, it leads to a worse bound than the method presented in Theorem 5.1 in the nonstacked TBC.
6.3. Isolated cylinders
We are now interested in the isolated stacks in the sTBC model. The point process of isolated cylinder stacks with basepoint in ![]() $A \subset \mathbb{R} ^d$ is given by
$A \subset \mathbb{R} ^d$ is given by
The next theorem shows asymptotic normality of ![]() $\mathrm {Iso}_{Z(\xi _K)}(W_s) = \mu (W_s)$.
$\mathrm {Iso}_{Z(\xi _K)}(W_s) = \mu (W_s)$.
Theorem 6.7. Let ![]() $N$ denote a standard normal random variable and assume
$N$ denote a standard normal random variable and assume ![]() $s \geq 6(R_h+r)$. There exists a constant
$s \geq 6(R_h+r)$. There exists a constant ![]() $c \in \mathbb{R} _+$ such that
$c \in \mathbb{R} _+$ such that
 $$\mathrm{{d}_W}\left(\frac{\mathrm{Iso}_{Z(\xi_K)}(W_s) - \mathbb{E}[\mathrm{Iso}_{Z(\xi_K)}(W_s)]}{\sqrt{\mathbb{V}[\mathrm{Iso}_{Z(\xi_K)}(W_s)]}}, N\right) \leq \frac{c}{\sqrt{\lambda_{d+1}(W_s)}}.$$
$$\mathrm{{d}_W}\left(\frac{\mathrm{Iso}_{Z(\xi_K)}(W_s) - \mathbb{E}[\mathrm{Iso}_{Z(\xi_K)}(W_s)]}{\sqrt{\mathbb{V}[\mathrm{Iso}_{Z(\xi_K)}(W_s)]}}, N\right) \leq \frac{c}{\sqrt{\lambda_{d+1}(W_s)}}.$$
Proof. Note that the maximum scope of a cylinder remains unchanged in the multi-directional setting. Thus, conditions (A), (C), and (D) are derived in the same way as in the proof of Theorem 5.2, using the same choices for ![]() $R$,
$R$, ![]() $c_2$, and
$c_2$, and ![]() $c_3$. To verify (B), we use the same strategy as before and get to
$c_3$. To verify (B), we use the same strategy as before and get to
Even in this modified setting, it is clear that these probabilities are not zero, as they can be estimated using ![]() $r$ and
$r$ and ![]() $R$. It follows that (B) holds true, which concludes the proof.
$R$. It follows that (B) holds true, which concludes the proof.
Competing interests
The authors declare none.