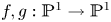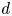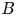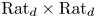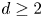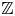1. Introduction
Fix an integer ![]() $d \geq 2$. Let
$d \geq 2$. Let ![]() ${\mathbb {P}}^1$ denote the complex projective line, and let
${\mathbb {P}}^1$ denote the complex projective line, and let ![]() $\mathrm {Rat}_d$ denote the space of all holomorphic maps
$\mathrm {Rat}_d$ denote the space of all holomorphic maps ![]() $f: {\mathbb {P}}^1 \to {\mathbb {P}}^1$ of degree
$f: {\mathbb {P}}^1 \to {\mathbb {P}}^1$ of degree ![]() $d$. Parameterizing these maps by their coefficients, throughout this article, we identify
$d$. Parameterizing these maps by their coefficients, throughout this article, we identify ![]() $\mathrm {Rat}_d$ with a Zariski-open subset of the complex projective space
$\mathrm {Rat}_d$ with a Zariski-open subset of the complex projective space ![]() ${\mathbb {P}}^{2d+1}$. For
${\mathbb {P}}^{2d+1}$. For ![]() $f \in \mathrm {Rat}_d({\mathbb {C}})$, let
$f \in \mathrm {Rat}_d({\mathbb {C}})$, let ![]() $\mathrm {Preper}(f)$ denote its set of preperiodic points in
$\mathrm {Preper}(f)$ denote its set of preperiodic points in ![]() ${\mathbb {P}}^1({\mathbb {C}})$.
${\mathbb {P}}^1({\mathbb {C}})$.
Given any pair ![]() $f, g: {\mathbb {P}}^1 \to {\mathbb {P}}^1$ of degrees
$f, g: {\mathbb {P}}^1 \to {\mathbb {P}}^1$ of degrees ![]() $>1$, it is known that either
$>1$, it is known that either ![]() $\mathrm {Preper}(f)\cap \mathrm {Preper}(g)$ is a finite set or
$\mathrm {Preper}(f)\cap \mathrm {Preper}(g)$ is a finite set or ![]() $\mathrm {Preper}(f) = \mathrm {Preper}(g)$ and the two maps have the same measure of maximal entropy [Reference Baker and DeMarcoBDeM11, Reference Yuan and ZhangYZ13]. Moreover, if we assume that
$\mathrm {Preper}(f) = \mathrm {Preper}(g)$ and the two maps have the same measure of maximal entropy [Reference Baker and DeMarcoBDeM11, Reference Yuan and ZhangYZ13]. Moreover, if we assume that ![]() $f$ and
$f$ and ![]() $g$ are non-exceptional, then equality of their preperiodic points holds if and only if the maps satisfy a strong compositional relation [Reference Levin and PrzytyckiLP97]. Further background is provided in § 2.
$g$ are non-exceptional, then equality of their preperiodic points holds if and only if the maps satisfy a strong compositional relation [Reference Levin and PrzytyckiLP97]. Further background is provided in § 2.
In this article, we show there exists a uniform bound on the size of ![]() $\mathrm {Preper}(f)\cap \mathrm {Preper}(g)$ for general pairs
$\mathrm {Preper}(f)\cap \mathrm {Preper}(g)$ for general pairs ![]() $(f,g)$ of any given degree
$(f,g)$ of any given degree ![]() $d\geq 2$, addressing a conjecture of [Reference DeMarco, Krieger and YeDeMKY22]. The conjecture of [Reference DeMarco, Krieger and YeDeMKY22] was in part motivated by a conjecture of Bogomolov, Fu, and Tschinkel in the setting of Lattès maps, that is, the maps arising as quotients of endomorphisms on elliptic curves [Reference Bogomolov, Fu and TschinkelBFT18]. We prove a generalization of their conjecture where
$d\geq 2$, addressing a conjecture of [Reference DeMarco, Krieger and YeDeMKY22]. The conjecture of [Reference DeMarco, Krieger and YeDeMKY22] was in part motivated by a conjecture of Bogomolov, Fu, and Tschinkel in the setting of Lattès maps, that is, the maps arising as quotients of endomorphisms on elliptic curves [Reference Bogomolov, Fu and TschinkelBFT18]. We prove a generalization of their conjecture where ![]() $f$ is a Lattès map and
$f$ is a Lattès map and ![]() $g$ is arbitrary.
$g$ is arbitrary.
The proofs involve a combination of techniques from arithmetic geometry and complex dynamics. As much as possible, we mimic the arguments for 1-parameter families of pairs ![]() $(f,g)$ acting on
$(f,g)$ acting on ![]() ${\mathbb {P}}^1\times {\mathbb {P}}^1$ of [Reference Mavraki and SchmidtMS22]. The new ingredients here involve the passage from one-parameter families to higher-dimensional parameter spaces: we rely on the recent equidistribution results of Yuan and Zhang [Reference Yuan and ZhangYZ21], and we take inspiration from the analysis of bifurcation currents in [Reference Bassanelli and BertelootBB07, Reference Buff and EpsteinBE09, Reference Berteloot, Bianchi and DupontBBD18], and especially the recent work of Gauthier and Vigny [Reference Gauthier and VignyGV19].
${\mathbb {P}}^1\times {\mathbb {P}}^1$ of [Reference Mavraki and SchmidtMS22]. The new ingredients here involve the passage from one-parameter families to higher-dimensional parameter spaces: we rely on the recent equidistribution results of Yuan and Zhang [Reference Yuan and ZhangYZ21], and we take inspiration from the analysis of bifurcation currents in [Reference Bassanelli and BertelootBB07, Reference Buff and EpsteinBE09, Reference Berteloot, Bianchi and DupontBBD18], and especially the recent work of Gauthier and Vigny [Reference Gauthier and VignyGV19].
1.1 Summary of main results
The first main goal of this article is to prove the existence of a uniform bound on the size of the intersection ![]() $\mathrm {Preper}(f)\cap \mathrm {Preper}(g)$, for a general pair
$\mathrm {Preper}(f)\cap \mathrm {Preper}(g)$, for a general pair ![]() $f, g: {\mathbb {P}}^1 \to {\mathbb {P}}^1$ in each degree.
$f, g: {\mathbb {P}}^1 \to {\mathbb {P}}^1$ in each degree.
Theorem 1.1 For each degree ![]() $d \geq 2$, there is a proper closed algebraic subvariety
$d \geq 2$, there is a proper closed algebraic subvariety ![]() $V_d$ of
$V_d$ of ![]() $\,\mathrm {Rat}_d\times \mathrm {Rat}_d$ defined over
$\,\mathrm {Rat}_d\times \mathrm {Rat}_d$ defined over ![]() $\overline {\mathbb {Q}}$ and a constant
$\overline {\mathbb {Q}}$ and a constant ![]() $B_d$ so that
$B_d$ so that
for all pairs ![]() $(f,g) \in (\mathrm {Rat}_d\times \mathrm {Rat}_d \setminus V_d)({\mathbb {C}})$.
$(f,g) \in (\mathrm {Rat}_d\times \mathrm {Rat}_d \setminus V_d)({\mathbb {C}})$.
The same result holds in the space of polynomial pairs.
Theorem 1.2 For each degree ![]() $d \geq 2$, there is a proper closed algebraic subvariety
$d \geq 2$, there is a proper closed algebraic subvariety ![]() $W_d$ of
$W_d$ of ![]() $\mathrm {Poly}_d\times \mathrm {Poly}_d$ defined over
$\mathrm {Poly}_d\times \mathrm {Poly}_d$ defined over ![]() $\overline {\mathbb {Q}}$ and a constant
$\overline {\mathbb {Q}}$ and a constant ![]() $B'_d$ so that
$B'_d$ so that
for all pairs ![]() $(f,g) \in (\mathrm {Poly}_d\times \mathrm {Poly}_d \setminus W_d)({\mathbb {C}})$, where
$(f,g) \in (\mathrm {Poly}_d\times \mathrm {Poly}_d \setminus W_d)({\mathbb {C}})$, where ![]() $\mathrm {Poly}_d$ is the
$\mathrm {Poly}_d$ is the ![]() $(d+1)$-dimensional space of all complex polynomials of degree
$(d+1)$-dimensional space of all complex polynomials of degree ![]() $d$.
$d$.
Conjecture 1.4 of [Reference DeMarco, Krieger and YeDeMKY22] posited that, for each degree ![]() $d \geq 2$, there should exist a constant
$d \geq 2$, there should exist a constant ![]() $B_d$ so that every pair
$B_d$ so that every pair ![]() $f, g \in \mathrm {Rat}_d$ has either
$f, g \in \mathrm {Rat}_d$ has either ![]() $\mathrm {Preper}(f) = \mathrm {Preper}(g)$ or
$\mathrm {Preper}(f) = \mathrm {Preper}(g)$ or ![]() $|\mathrm {Preper}(f) \cap \mathrm {Preper}(g)| \leq B_d$. The proof of Theorem 1.1 does not provide an explicit description of the subvariety
$|\mathrm {Preper}(f) \cap \mathrm {Preper}(g)| \leq B_d$. The proof of Theorem 1.1 does not provide an explicit description of the subvariety ![]() $V_d$, and so it fails to provide a complete proof of this conjecture in any degree
$V_d$, and so it fails to provide a complete proof of this conjecture in any degree ![]() $d$, though it allows us to deduce Theorem 1.2.
$d$, though it allows us to deduce Theorem 1.2.
In some settings, our approach to Theorem 1.1 allows us to characterize the excluded subvarieties, and we obtain new proofs of the main results of [Reference DeMarco, Krieger and YeDeMKY22] and [Reference DeMarco, Krieger and YeDeMKY20], stated as Theorems 1.12 and 1.13 here. We also prove the following generalization of the Bogomolov–Fu-Tschinkel conjecture [Reference Bogomolov, Fu and TschinkelBFT18].
Theorem 1.3 For each ![]() $d\geq 2$, there exists a uniform bound
$d\geq 2$, there exists a uniform bound ![]() $M_{d}$ so that for each elliptic curve
$M_{d}$ so that for each elliptic curve ![]() $E$ over
$E$ over ![]() ${\mathbb {C}}$ and each
${\mathbb {C}}$ and each ![]() $f\in \mathrm {Rat}_d({\mathbb {C}})$ we have that either
$f\in \mathrm {Rat}_d({\mathbb {C}})$ we have that either
where ![]() $x(E_{\mathrm {tors}})$ denotes the
$x(E_{\mathrm {tors}})$ denotes the ![]() $x$-coordinates of the torsion points of a Weierstrass model of
$x$-coordinates of the torsion points of a Weierstrass model of ![]() $E$.
$E$.
The latter case, where ![]() $\mathrm {Preper}(f) = x(E_{\mathrm {tors}})$, will only hold if
$\mathrm {Preper}(f) = x(E_{\mathrm {tors}})$, will only hold if ![]() $f$ is a Lattès map arising as the quotient of a map on the same elliptic curve
$f$ is a Lattès map arising as the quotient of a map on the same elliptic curve ![]() $E$; see § 2.3 for background on the preperiodic points of Lattès maps. The conjecture of Bogomolov, Fu, and Tschinkel is the case of Theorem 1.3 where
$E$; see § 2.3 for background on the preperiodic points of Lattès maps. The conjecture of Bogomolov, Fu, and Tschinkel is the case of Theorem 1.3 where ![]() $f$ is assumed to be a Lattès map, and it is stated here as Corollary 8.2; the conjecture has recently been established by Poineau [Reference PoineauPoi22] and also follows by Kühne's work [Reference KühneKüh23] and a result of Gao, Ge, and Kühne [Reference Gao, Ge and KühneGGK21]. We also include a proof here to illustrate the differences in approach.
$f$ is assumed to be a Lattès map, and it is stated here as Corollary 8.2; the conjecture has recently been established by Poineau [Reference PoineauPoi22] and also follows by Kühne's work [Reference KühneKüh23] and a result of Gao, Ge, and Kühne [Reference Gao, Ge and KühneGGK21]. We also include a proof here to illustrate the differences in approach.
Easy examples (or an interpolation argument) show that there are maps ![]() $f$ and
$f$ and ![]() $g$ in every degree
$g$ in every degree ![]() $d\geq 2$ so that
$d\geq 2$ so that
The question remains of how large this intersection can be (when finite), if we bound the degree. Doyle and Hyde have shown there exist pairs ![]() $(f,g)$ of degree
$(f,g)$ of degree ![]() $d$ with
$d$ with
for every ![]() $d\geq 2$ (see [Reference Doyle and HydeDH22]). Corollary 1.7, stated in the following, shows that the general bound
$d\geq 2$ (see [Reference Doyle and HydeDH22]). Corollary 1.7, stated in the following, shows that the general bound ![]() $B_d$ of Theorem 1.1 must be at least
$B_d$ of Theorem 1.1 must be at least ![]() $4d-1$. In fact, we believe the following may hold.
$4d-1$. In fact, we believe the following may hold.
Conjecture 1.4 We can take ![]() $B_d=4d-1$ in Theorem 1.1.
$B_d=4d-1$ in Theorem 1.1.
A key ingredient in the proof of Theorem 1.1 is the following result that we consider interesting in its own right.
Theorem 1.5 For each degree ![]() $d\geq 2$, the pairwise-bifurcation measure
$d\geq 2$, the pairwise-bifurcation measure ![]() $\mu _\Delta$ is nonzero on the moduli space
$\mu _\Delta$ is nonzero on the moduli space
of all pairs ![]() $(f,g)$ of degree
$(f,g)$ of degree ![]() $d$.
$d$.
Here, ![]() $\operatorname {Aut}{\mathbb {P}}^1 \simeq \mathrm {PSL}_2{\mathbb {C}}$ acts on the space
$\operatorname {Aut}{\mathbb {P}}^1 \simeq \mathrm {PSL}_2{\mathbb {C}}$ acts on the space ![]() $\mathrm {Rat}_d\times \mathrm {Rat}_d$ by simultaneous conjugation,
$\mathrm {Rat}_d\times \mathrm {Rat}_d$ by simultaneous conjugation,
and the moduli space is well defined as a complex orbifold of dimension ![]() $4d-1$. The pairwise-bifurcation current is a closed, positive
$4d-1$. The pairwise-bifurcation current is a closed, positive ![]() $(1,1)$-current on
$(1,1)$-current on ![]() $\mathrm {Rat}_d \times \mathrm {Rat}_d$ defined by
$\mathrm {Rat}_d \times \mathrm {Rat}_d$ defined by
where ![]() $\pi : (\mathrm {Rat}_d \times \mathrm {Rat}_d)\times {\mathbb {P}}^1 \to \mathrm {Rat}_d \times \mathrm {Rat}_d$ is the projection;
$\pi : (\mathrm {Rat}_d \times \mathrm {Rat}_d)\times {\mathbb {P}}^1 \to \mathrm {Rat}_d \times \mathrm {Rat}_d$ is the projection; ![]() $\hat {T}$ is the dynamical Green current on
$\hat {T}$ is the dynamical Green current on ![]() $\mathrm {Rat}_d \times {\mathbb {P}}^1$ associated to the universal family; and
$\mathrm {Rat}_d \times {\mathbb {P}}^1$ associated to the universal family; and ![]() $p_i$ is the projection
$p_i$ is the projection ![]() $(\mathrm {Rat}_d \times \mathrm {Rat}_d)\times {\mathbb {P}}^1 \to \mathrm {Rat}_d\times {\mathbb {P}}^1$ given by
$(\mathrm {Rat}_d \times \mathrm {Rat}_d)\times {\mathbb {P}}^1 \to \mathrm {Rat}_d\times {\mathbb {P}}^1$ given by ![]() $p_i(f_1, f_2, z) = (f_i, z)$ for
$p_i(f_1, f_2, z) = (f_i, z)$ for ![]() $i = 1, 2$. (See § 2.5 for the definition of
$i = 1, 2$. (See § 2.5 for the definition of ![]() $\hat {T}$ and § 4.1 for more information about
$\hat {T}$ and § 4.1 for more information about ![]() $\hat {T}_\Delta$.) The associated pairwise-bifurcation measure is defined by
$\hat {T}_\Delta$.) The associated pairwise-bifurcation measure is defined by
on ![]() $\mathrm {Rat}_d\times \mathrm {Rat}_d$, which projects to a measure on the moduli space of pairs
$\mathrm {Rat}_d\times \mathrm {Rat}_d$, which projects to a measure on the moduli space of pairs ![]() $(f,g)$. The current
$(f,g)$. The current ![]() $\hat {T}_\Delta$ is a special case of the bifurcation currents introduced in [Reference Gauthier and VignyGV19], extending the notions of bifurcation current and measure that characterize stability for holomorphic families of maps on
$\hat {T}_\Delta$ is a special case of the bifurcation currents introduced in [Reference Gauthier and VignyGV19], extending the notions of bifurcation current and measure that characterize stability for holomorphic families of maps on ![]() ${\mathbb {P}}^1$ (see [Reference DeMarcoDeM01, Reference DeMarcoDeM03, Reference Bassanelli and BertelootBB07, Reference Dujardin and FavreDF08]). With this perspective the statement of Theorem 1.5 may be compared with [Reference Bassanelli and BertelootBB07, Proposition 6.3] that the (standard) bifurcation measure does not vanish identically on the moduli space
${\mathbb {P}}^1$ (see [Reference DeMarcoDeM01, Reference DeMarcoDeM03, Reference Bassanelli and BertelootBB07, Reference Dujardin and FavreDF08]). With this perspective the statement of Theorem 1.5 may be compared with [Reference Bassanelli and BertelootBB07, Proposition 6.3] that the (standard) bifurcation measure does not vanish identically on the moduli space ![]() $\mathrm {M}_d = \mathrm {Rat}_d/\operatorname {Aut}{\mathbb {P}}^1$. More details are given in § 4.
$\mathrm {M}_d = \mathrm {Rat}_d/\operatorname {Aut}{\mathbb {P}}^1$. More details are given in § 4.
In working towards Theorems 1.1 and 1.3, we actually prove two contrasting results in a more general setting. Let ![]() $S$ be a smooth and irreducible quasiprojective variety over
$S$ be a smooth and irreducible quasiprojective variety over ![]() ${\mathbb {C}}$, and let
${\mathbb {C}}$, and let ![]() $k = {\mathbb {C}}(S)$ be its function field. An algebraic family of pairs
$k = {\mathbb {C}}(S)$ be its function field. An algebraic family of pairs ![]() $(f,g)$ of degree
$(f,g)$ of degree ![]() $d\geq 2$ over
$d\geq 2$ over ![]() $S$ is a pair of rational functions
$S$ is a pair of rational functions ![]() $f, g \in k(z)$ of degree
$f, g \in k(z)$ of degree ![]() $d$ for which
$d$ for which ![]() $f$ and
$f$ and ![]() $g$ each induce holomorphic maps
$g$ each induce holomorphic maps ![]() $S \times {\mathbb {P}}^1 \to {\mathbb {P}}^1$ via specialization
$S \times {\mathbb {P}}^1 \to {\mathbb {P}}^1$ via specialization ![]() $(t, z) \mapsto f_t(z)$. We say that the family
$(t, z) \mapsto f_t(z)$. We say that the family ![]() $(f,g)$ is isotrivial if the induced map
$(f,g)$ is isotrivial if the induced map ![]() $S \to (\mathrm {Rat}_d \times \mathrm {Rat}_d)/\operatorname {Aut}{\mathbb {P}}^1$ is constant; the family
$S \to (\mathrm {Rat}_d \times \mathrm {Rat}_d)/\operatorname {Aut}{\mathbb {P}}^1$ is constant; the family ![]() $(f,g)$ is maximally non-isotrivial if the induced map
$(f,g)$ is maximally non-isotrivial if the induced map ![]() $S \to (\mathrm {Rat}_d\times \mathrm {Rat}_d)/\operatorname {Aut}{\mathbb {P}}^1$ is finite-to-one.
$S \to (\mathrm {Rat}_d\times \mathrm {Rat}_d)/\operatorname {Aut}{\mathbb {P}}^1$ is finite-to-one.
Theorem 1.6 Let ![]() $S$ be a smooth and irreducible quasiprojective variety over
$S$ be a smooth and irreducible quasiprojective variety over ![]() ${\mathbb {C}}$. Suppose that
${\mathbb {C}}$. Suppose that ![]() $(f,g)$ is a maximally non-isotrivial algebraic family of pairs over
$(f,g)$ is a maximally non-isotrivial algebraic family of pairs over ![]() $S$ of degree
$S$ of degree ![]() $d\geq 2$. Let
$d\geq 2$. Let ![]() $m = \dim _{\mathbb {C}} S$. Then the set of points
$m = \dim _{\mathbb {C}} S$. Then the set of points
is Zariski dense in ![]() $S \times ({\mathbb {P}}^1)^\ell$ for each
$S \times ({\mathbb {P}}^1)^\ell$ for each ![]() $1 \leq \ell \leq m$.
$1 \leq \ell \leq m$.
Corollary 1.7 In every degree ![]() $d \geq 2$, the set of pairs
$d \geq 2$, the set of pairs ![]() $(f,g)$ sharing at least
$(f,g)$ sharing at least ![]() $4d-1$ distinct preperiodic points is Zariski dense in
$4d-1$ distinct preperiodic points is Zariski dense in ![]() $\mathrm {Rat}_d \times \mathrm {Rat}_d$.
$\mathrm {Rat}_d \times \mathrm {Rat}_d$.
Let ![]() $(f,g)$ be an algebraic family of pairs parameterized by
$(f,g)$ be an algebraic family of pairs parameterized by ![]() $S$, with
$S$, with ![]() $m = \dim _{\mathbb {C}} S$. An
$m = \dim _{\mathbb {C}} S$. An ![]() $m$-tuple
$m$-tuple ![]() ${\bf x} = (x_1, \ldots, x_m) \in ({\mathbb {P}}^1)^m$ is a rigid
${\bf x} = (x_1, \ldots, x_m) \in ({\mathbb {P}}^1)^m$ is a rigid ![]() $m$-repeller at
$m$-repeller at ![]() $s_0 \in S$ if (1) each
$s_0 \in S$ if (1) each ![]() $x_i$ is preperiodic to a repelling cycle for
$x_i$ is preperiodic to a repelling cycle for ![]() $f_{s_0}$ and for
$f_{s_0}$ and for ![]() $g_{s_0}$, and (2) there is no non-constant holomorphic disk
$g_{s_0}$, and (2) there is no non-constant holomorphic disk ![]() $\varphi : {\mathbb {D}} \to S \times ({\mathbb {P}}^1)^m$ parametrizing a family of
$\varphi : {\mathbb {D}} \to S \times ({\mathbb {P}}^1)^m$ parametrizing a family of ![]() $m$ common preperiodic points for
$m$ common preperiodic points for ![]() $(f_{\pi (\varphi (t))}, g_{\pi (\varphi (t))})$ with
$(f_{\pi (\varphi (t))}, g_{\pi (\varphi (t))})$ with ![]() $\varphi (0) = (s_0, {\bf x})$, where
$\varphi (0) = (s_0, {\bf x})$, where ![]() $\pi$ is the projection to
$\pi$ is the projection to ![]() $S$.
$S$.
The following non-density result should be contrasted with the density result of Theorem 1.6.
Theorem 1.8 Fix degree ![]() $d \geq 2$, and suppose that
$d \geq 2$, and suppose that ![]() $S$ is a smooth, irreducible quasiprojective variety, parameterizing an algebraic family of pairs
$S$ is a smooth, irreducible quasiprojective variety, parameterizing an algebraic family of pairs ![]() $(f,g)$ of degree
$(f,g)$ of degree ![]() $d$, defined over
$d$, defined over ![]() $\overline {\mathbb {Q}}$. Let
$\overline {\mathbb {Q}}$. Let ![]() $m = \dim _{\mathbb {C}} S$. Suppose there exists a rigid
$m = \dim _{\mathbb {C}} S$. Suppose there exists a rigid ![]() $m$-repeller at some
$m$-repeller at some ![]() $s_0 \in S({\mathbb {C}})$, and assume that
$s_0 \in S({\mathbb {C}})$, and assume that ![]() $f$ and
$f$ and ![]() $g$ are not both conjugate to
$g$ are not both conjugate to ![]() $z^{\pm d}$ over the algebraic closure of
$z^{\pm d}$ over the algebraic closure of ![]() $k = \overline {\mathbb {Q}}(S)$. Then the set of points
$k = \overline {\mathbb {Q}}(S)$. Then the set of points
is not Zariski dense in ![]() $S \times ({\mathbb {P}}^1)^{m+1}$.
$S \times ({\mathbb {P}}^1)^{m+1}$.
Under the hypotheses of Theorem 1.8, Theorem 1.6 implies that there is a Zariski-dense collection of pairs ![]() $(f_s, g_s)$ in
$(f_s, g_s)$ in ![]() $S({\mathbb {C}})$ which have at least
$S({\mathbb {C}})$ which have at least ![]() $m$ common preperiodic points. However, we will deduce from Theorem 1.8 that if just one of them forms a rigid
$m$ common preperiodic points. However, we will deduce from Theorem 1.8 that if just one of them forms a rigid ![]() $m$-repeller at
$m$-repeller at ![]() $s_0 \in S({\mathbb {C}})$, there will be a uniform bound on the number of common preperiodic points for a general pair
$s_0 \in S({\mathbb {C}})$, there will be a uniform bound on the number of common preperiodic points for a general pair ![]() $(f_s, g_s)$ for complex parameters
$(f_s, g_s)$ for complex parameters ![]() $s \in S({\mathbb {C}})$. See Theorem 5.2 and Corollary 4.9.
$s \in S({\mathbb {C}})$. See Theorem 5.2 and Corollary 4.9.
Remark 1.9 The family defined by ![]() $f_s(z) = z^d$ and
$f_s(z) = z^d$ and ![]() $g_s(z) = s^{d-1} \, z^d$ for
$g_s(z) = s^{d-1} \, z^d$ for ![]() $s\in {\mathbb {C}}^*$ does not satisfy the conclusion of Theorem 1.8, though it satisfies all the other hypotheses of the theorem. For example, near
$s\in {\mathbb {C}}^*$ does not satisfy the conclusion of Theorem 1.8, though it satisfies all the other hypotheses of the theorem. For example, near ![]() $s_0=1$, the common fixed point at
$s_0=1$, the common fixed point at ![]() $z=1$ splits into distinct fixed points at
$z=1$ splits into distinct fixed points at ![]() $z=1$ for
$z=1$ for ![]() $f_s$ and
$f_s$ and ![]() $z=1/s$ for
$z=1/s$ for ![]() $g_s$ near
$g_s$ near ![]() $s_0$, so it forms a rigid
$s_0$, so it forms a rigid ![]() $1$-repeller at
$1$-repeller at ![]() $s_0$. However, we have
$s_0$. However, we have ![]() $\mathrm {Preper}(f_s) = \mathrm {Preper}(g_s)$ for all roots of unity
$\mathrm {Preper}(f_s) = \mathrm {Preper}(g_s)$ for all roots of unity ![]() $s$. In the terminology of [Reference Mavraki and SchmidtMS22], the diagonal in
$s$. In the terminology of [Reference Mavraki and SchmidtMS22], the diagonal in ![]() ${\mathbb {P}}^1\times {\mathbb {P}}^1$ is weakly
${\mathbb {P}}^1\times {\mathbb {P}}^1$ is weakly ![]() $(f,g)$-special for this example, over the function field
$(f,g)$-special for this example, over the function field ![]() ${\mathbb {C}}(s)$.
${\mathbb {C}}(s)$.
A proof of Theorem 1.1 is obtained from Theorem 1.8 by showing that the pair
for ![]() $\zeta = e^{2\pi i/(d+1)}$ has a rigid
$\zeta = e^{2\pi i/(d+1)}$ has a rigid ![]() $(4d-1)$-repeller, which also implies Theorem 1.5. The rigidity for this pair
$(4d-1)$-repeller, which also implies Theorem 1.5. The rigidity for this pair ![]() $(f_0, g_0)$ is deduced from the following.
$(f_0, g_0)$ is deduced from the following.
Theorem 1.10 Fix degree ![]() $d\geq 2$. Let
$d\geq 2$. Let ![]() $f_0(z) = z^d$ and
$f_0(z) = z^d$ and ![]() $g_0(z) = \zeta z^d$ for
$g_0(z) = \zeta z^d$ for ![]() $\zeta = e^{2\pi i/(d+1)}$, and let
$\zeta = e^{2\pi i/(d+1)}$, and let ![]() $\psi = (f,g): {\mathbb {D}} \to \mathrm {Rat}_d\times \mathrm {Rat}_d$ be a holomorphic map from the unit disk
$\psi = (f,g): {\mathbb {D}} \to \mathrm {Rat}_d\times \mathrm {Rat}_d$ be a holomorphic map from the unit disk ![]() ${\mathbb {D}}\subset {\mathbb {C}}$ with
${\mathbb {D}}\subset {\mathbb {C}}$ with ![]() $\psi (0) = (f_0, g_0)$. If
$\psi (0) = (f_0, g_0)$. If
for all ![]() $t \in {\mathbb {D}}$, where
$t \in {\mathbb {D}}$, where ![]() $J$ denotes the Julia set, then this family of pairs is isotrivial.
$J$ denotes the Julia set, then this family of pairs is isotrivial.
Remark 1.11 The conclusion of Theorem 1.10 is false if we allow ![]() $\zeta$ to be a root of unity of any order
$\zeta$ to be a root of unity of any order ![]() $\leq d$. See § 7.4. The proof of Theorem 1.10, and thus of Theorem 1.5, does not involve any arithmetic ingredients. This is in contrast to the proofs of related statements in [Reference Mavraki and SchmidtMS22].
$\leq d$. See § 7.4. The proof of Theorem 1.10, and thus of Theorem 1.5, does not involve any arithmetic ingredients. This is in contrast to the proofs of related statements in [Reference Mavraki and SchmidtMS22].
1.2 Background and proof ideas
Recently, there has been a series of breakthroughs in arithmetic geometry and dynamics, leading to powerful height estimates and equidistribution results, and ultimately to uniform bounds in related settings, especially for families of abelian varieties. Dimitrov, Gao, and Habegger [Reference Dimitrov, Gao and HabeggerDGH21b] and Kühne [Reference KühneKüh21] established uniformity in the Mordell–Lang conjecture following the blueprint they laid out in [Reference Dimitrov, Gao and HabeggerDGH21a, Reference Gao and HabeggerGH19, Reference HabeggerHab13]. Kühne [Reference KühneKüh21] established an arithmetic equidistribution theorem in families of abelian varieties and combined it with Gao's results [Reference GaoGao20a, Reference GaoGao20b] to prove uniformity in the Manin–Mumford and Bogomolov conjectures for curves in their Jacobians, a result that Yuan also obtained later with a different approach [Reference YuanYua21]. Kühne's approach has been extended to higher dimensional subvarieties of abelian varieties by Gao, Ge, and Kühne [Reference Gao, Ge and KühneGGK21]; see Gao's survey article and the references therein for more about these developments [Reference GaoGao21]. In a study of more general dynamical systems, the recent complex-analytic results of Gauthier and Vigny [Reference Gauthier and VignyGV19] and the arithmetic equidistribution theorems of Yuan and Zhang [Reference Yuan and ZhangYZ21] and Gauthier [Reference GauthierGau21] provide a whole host of new tools. These equidistribution results played an important role in recent work by the second author and Schmidt, who obtained for example a version of Theorem 1.1 for families of pairs ![]() $(f,g)$ on
$(f,g)$ on ![]() ${\mathbb {P}}^1$ parameterized by curves (see Theorem 1.14) [Reference Mavraki and SchmidtMS22]. This article grew out of an effort to synthesize these ideas and to extend the results of the first author with Krieger and Ye in [Reference DeMarco, Krieger and YeDeMKY20, Reference DeMarco, Krieger and YeDeMKY22].
${\mathbb {P}}^1$ parameterized by curves (see Theorem 1.14) [Reference Mavraki and SchmidtMS22]. This article grew out of an effort to synthesize these ideas and to extend the results of the first author with Krieger and Ye in [Reference DeMarco, Krieger and YeDeMKY20, Reference DeMarco, Krieger and YeDeMKY22].
For maps ![]() $f, g: {\mathbb {P}}^1\to {\mathbb {P}}^1$ defined over
$f, g: {\mathbb {P}}^1\to {\mathbb {P}}^1$ defined over ![]() ${\mathbb {C}}$, uniform bounds on the intersections
${\mathbb {C}}$, uniform bounds on the intersections ![]() $\mathrm {Preper}(f)\cap \mathrm {Preper}(g)$ were obtained by DeMarco, Krieger, and Ye for two families of maps, with proofs that also involved both arithmetic and complex-dynamical techniques, but which relied on computations specific to the families studied.
$\mathrm {Preper}(f)\cap \mathrm {Preper}(g)$ were obtained by DeMarco, Krieger, and Ye for two families of maps, with proofs that also involved both arithmetic and complex-dynamical techniques, but which relied on computations specific to the families studied.
Theorem 1.12 [Reference DeMarco, Krieger and YeDeMKY22]
Suppose that ![]() $f_t$ is the family of quadratic polynomials,
$f_t$ is the family of quadratic polynomials, ![]() $f_t(z) = z^2 +t$ for
$f_t(z) = z^2 +t$ for ![]() $t \in {\mathbb {C}}$. There is a uniform
$t \in {\mathbb {C}}$. There is a uniform ![]() $B$ so that
$B$ so that
for all ![]() $t_1 \not = t_2$.
$t_1 \not = t_2$.
Theorem 1.13 [Reference DeMarco, Krieger and YeDeMKY20]
Suppose that ![]() $f_t$ is the family of flexible Lattès maps
$f_t$ is the family of flexible Lattès maps ![]() $f_t(z) = (z^2-t)^2/(4z(z-1)(z-t))$ for
$f_t(z) = (z^2-t)^2/(4z(z-1)(z-t))$ for ![]() $t \in {\mathbb {C}}\setminus \{0,1\}$. There is a uniform
$t \in {\mathbb {C}}\setminus \{0,1\}$. There is a uniform ![]() $B$ so that
$B$ so that
for all ![]() $t_1 \not = t_2$.
$t_1 \not = t_2$.
Theorem 1.13 addressed a conjecture of Bogomolov, Fu, and Tschinkel [Reference Bogomolov, Fu and TschinkelBFT18] about torsion points on pairs of elliptic curves. Indeed, the preperiodic points of the Lattès map ![]() $f_t$ are the images of the torsion points on the Legendre curve
$f_t$ are the images of the torsion points on the Legendre curve ![]() $\{y^2 = x(x-1)(x-t)\}$ under the projection to the
$\{y^2 = x(x-1)(x-t)\}$ under the projection to the ![]() $x$-coordinate. The full conjecture from [Reference Bogomolov, Fu and TschinkelBFT18] is now a theorem: there exists a uniform bound
$x$-coordinate. The full conjecture from [Reference Bogomolov, Fu and TschinkelBFT18] is now a theorem: there exists a uniform bound ![]() $B$ so that every pair
$B$ so that every pair ![]() $(f,g)$ of (flexible) Lattès maps (in any choice of coordinates on
$(f,g)$ of (flexible) Lattès maps (in any choice of coordinates on ![]() ${\mathbb {P}}^1$) will either share all of their preperiodic points or have at most
${\mathbb {P}}^1$) will either share all of their preperiodic points or have at most ![]() $B$ in common. A proof was recently obtained by Poineau in [Reference PoineauPoi22], and it can also be deduced from the ‘relative Bogomolov’ theorem proved by Kühne [Reference KühneKüh23] or the main theorem of [Reference Gao, Ge and KühneGGK21]. We present an alternate proof as a corollary to Theorem 1.3.
$B$ in common. A proof was recently obtained by Poineau in [Reference PoineauPoi22], and it can also be deduced from the ‘relative Bogomolov’ theorem proved by Kühne [Reference KühneKüh23] or the main theorem of [Reference Gao, Ge and KühneGGK21]. We present an alternate proof as a corollary to Theorem 1.3.
Note that Theorems 1.12 and 1.13 each covered a two-parameter family of pairs ![]() $(t_1, t_2)$, but, as mentioned above, the proofs were specific to these particular families. For one-parameter families of pairs, Mavraki and Schmidt recently obtained uniform bounds that did not rely on particular dynamical features of the maps.
$(t_1, t_2)$, but, as mentioned above, the proofs were specific to these particular families. For one-parameter families of pairs, Mavraki and Schmidt recently obtained uniform bounds that did not rely on particular dynamical features of the maps.
Theorem 1.14 [Reference Mavraki and SchmidtMS22]
Let ![]() $C$ be any algebraic curve in
$C$ be any algebraic curve in ![]() $\mathrm {Rat}_d \times \mathrm {Rat}_d$ defined over
$\mathrm {Rat}_d \times \mathrm {Rat}_d$ defined over ![]() $\overline {\mathbb {Q}}$, parameterizing a pair of maps
$\overline {\mathbb {Q}}$, parameterizing a pair of maps ![]() $(f_t, g_t)$ for
$(f_t, g_t)$ for ![]() $t \in C({\mathbb {C}})$. Then there exists a constant
$t \in C({\mathbb {C}})$. Then there exists a constant ![]() $B = B(C)$ so that, for each
$B = B(C)$ so that, for each ![]() $t \in C({\mathbb {C}})$, either
$t \in C({\mathbb {C}})$, either
In this article, we follow the strategy of [Reference Mavraki and SchmidtMS22] to treat more general families. Their approach uses an arithmetic equidistribution theorem of Yuan and Zhang [Reference Yuan and ZhangYZ21] amongst other ingredients, allowing them to reduce the problem to a result of Levin and Przytycki on maps sharing a measure of maximal entropy [Reference Levin and PrzytyckiLP97]. But in order to apply Yuan and Zhang's equidistribution theorem, the challenge is to prove that a non-degeneracy hypothesis is satisfied. This non-degeneracy is defined in terms of a volume of a certain adelically metrized line bundle, and its positivity can be deduced from showing that a certain measure is nonzero [Reference Yuan and ZhangYZ21, Lemma 5.4.4]. In [Reference Mavraki and SchmidtMS22] the authors relied on arithmetic ingredients to provide a characterization of this positivity for ![]() $1$-parameter families of products
$1$-parameter families of products ![]() $(f,g)$ acting on
$(f,g)$ acting on ![]() ${\mathbb {P}}^1 \times {\mathbb {P}}^1$ (see [Reference Mavraki and SchmidtMS22, Theorems 4.1 and 4.3]). In contrast, to prove that this positivity condition is satisfied over the full space of pairs
${\mathbb {P}}^1 \times {\mathbb {P}}^1$ (see [Reference Mavraki and SchmidtMS22, Theorems 4.1 and 4.3]). In contrast, to prove that this positivity condition is satisfied over the full space of pairs ![]() $\mathrm {Rat}_d\times \mathrm {Rat}_d$, we interpret it here as a notion of dynamical stability, inspired by the recent work of Gauthier and Vigny [Reference Gauthier and VignyGV19]. The non-degeneracy condition is then reduced to showing the positivity of the bifurcation measure
$\mathrm {Rat}_d\times \mathrm {Rat}_d$, we interpret it here as a notion of dynamical stability, inspired by the recent work of Gauthier and Vigny [Reference Gauthier and VignyGV19]. The non-degeneracy condition is then reduced to showing the positivity of the bifurcation measure ![]() $\mu _\Delta$ defined above in (1.2). We exhibit this positivity by mimicking the proofs that Misiurewicz maps lie in support of the (usual) bifurcation measure in the moduli space of maps of degree
$\mu _\Delta$ defined above in (1.2). We exhibit this positivity by mimicking the proofs that Misiurewicz maps lie in support of the (usual) bifurcation measure in the moduli space of maps of degree ![]() $d$ on
$d$ on ![]() ${\mathbb {P}}^1$ (see [Reference Buff and EpsteinBE09]), and the proofs of [Reference Berteloot, Bianchi and DupontBBD18, Proposition 3.7] and [Reference Gauthier and VignyGV19, Lemma 4.8]. Finally, the rigidity we rely upon to prove Theorem 1.1 (stated as Theorem 1.10), follows from a general treatment of monomial maps and symmetries of maps on
${\mathbb {P}}^1$ (see [Reference Buff and EpsteinBE09]), and the proofs of [Reference Berteloot, Bianchi and DupontBBD18, Proposition 3.7] and [Reference Gauthier and VignyGV19, Lemma 4.8]. Finally, the rigidity we rely upon to prove Theorem 1.1 (stated as Theorem 1.10), follows from a general treatment of monomial maps and symmetries of maps on ![]() ${\mathbb {P}}^1$. The analogous rigidity result we rely upon for Theorem 1.3 follows by repeated applications of the main theorem in [Reference DeMarcoDeM16] on the stability of a family of maps
${\mathbb {P}}^1$. The analogous rigidity result we rely upon for Theorem 1.3 follows by repeated applications of the main theorem in [Reference DeMarcoDeM16] on the stability of a family of maps ![]() $f$ on
$f$ on ![]() ${\mathbb {P}}^1$ equipped with a marked point.
${\mathbb {P}}^1$ equipped with a marked point.
1.3 Outline
In § 2, we provide some background on the dynamics of maps on ![]() ${\mathbb {P}}^1$, recalling the notion of exceptional map and the relation between the measures of maximal entropy and the preperiodic points of the map. In § 3 we prove Theorem 1.6 and deduce Corollary 1.7. These results are presented as a consequence of the main theorem in [Reference DeMarcoDeM16]. For a proof of Theorem 1.8, we follow the strategy of Mavraki and Schmidt in [Reference Mavraki and SchmidtMS22]. To prove that the non-degeneracy assumption required to use the equidistribution result in [Reference Yuan and ZhangYZ21] is satisfied, we use the complex-analytic tools (of bifurcation currents and measures) developed by Gauthier and Vigny in [Reference Gauthier and VignyGV19]. More precisely, in § 4 we recall the definitions from [Reference Gauthier and VignyGV19] of a generalized bifurcation current associated to an arbitrary family of polarized dynamical systems and subvarieties. In Proposition 4.8 we show that certain rigid pre-repelling parameters are in the support of our (generalized) bifurcation measure, giving a criterion for non-degeneracy. We complete the proof of Theorem 1.8 in § 5 and deduce its consequence towards uniform bounds in the number of common preperiodic points therein; see Theorem 5.2. In § 6, we include an explanation of how this method gives an alternative proof of Theorem 1.12, using the special quadratic polynomial examples of [Reference Doyle and HydeDH22] and the results of Mavraki and Schmidt [Reference Mavraki and SchmidtMS22]. In § 7, we prove Theorem 1.10, and we construct a rigid repeller, completing the proof of Theorems 1.1, 1.2, and 1.5. In § 8, we study pairs
${\mathbb {P}}^1$, recalling the notion of exceptional map and the relation between the measures of maximal entropy and the preperiodic points of the map. In § 3 we prove Theorem 1.6 and deduce Corollary 1.7. These results are presented as a consequence of the main theorem in [Reference DeMarcoDeM16]. For a proof of Theorem 1.8, we follow the strategy of Mavraki and Schmidt in [Reference Mavraki and SchmidtMS22]. To prove that the non-degeneracy assumption required to use the equidistribution result in [Reference Yuan and ZhangYZ21] is satisfied, we use the complex-analytic tools (of bifurcation currents and measures) developed by Gauthier and Vigny in [Reference Gauthier and VignyGV19]. More precisely, in § 4 we recall the definitions from [Reference Gauthier and VignyGV19] of a generalized bifurcation current associated to an arbitrary family of polarized dynamical systems and subvarieties. In Proposition 4.8 we show that certain rigid pre-repelling parameters are in the support of our (generalized) bifurcation measure, giving a criterion for non-degeneracy. We complete the proof of Theorem 1.8 in § 5 and deduce its consequence towards uniform bounds in the number of common preperiodic points therein; see Theorem 5.2. In § 6, we include an explanation of how this method gives an alternative proof of Theorem 1.12, using the special quadratic polynomial examples of [Reference Doyle and HydeDH22] and the results of Mavraki and Schmidt [Reference Mavraki and SchmidtMS22]. In § 7, we prove Theorem 1.10, and we construct a rigid repeller, completing the proof of Theorems 1.1, 1.2, and 1.5. In § 8, we study pairs ![]() $(f,g)$ where
$(f,g)$ where ![]() $f$ is a Lattès map and prove Theorem 1.3.
$f$ is a Lattès map and prove Theorem 1.3.
2. Background on 1-dimensional dynamics
In this section, we provide some important background information on the dynamics of maps ![]() $f: {\mathbb {P}}^1 \to {\mathbb {P}}^1$ defined over
$f: {\mathbb {P}}^1 \to {\mathbb {P}}^1$ defined over ![]() ${\mathbb {C}}$.
${\mathbb {C}}$.
2.1 The measure of maximal entropy
For each rational map ![]() $f: {\mathbb {P}}^1\to {\mathbb {P}}^1$ of degree
$f: {\mathbb {P}}^1\to {\mathbb {P}}^1$ of degree ![]() $d \geq 2$, there is a unique probability measure
$d \geq 2$, there is a unique probability measure ![]() $\mu _f$ of maximal entropy. Its support is equal to the Julia set of
$\mu _f$ of maximal entropy. Its support is equal to the Julia set of ![]() $f$, and it is characterized by the properties that it has no atoms, so
$f$, and it is characterized by the properties that it has no atoms, so ![]() $\mu _f(\{z\}) = 0$ for all
$\mu _f(\{z\}) = 0$ for all ![]() $z \in {\mathbb {P}}^1({\mathbb {C}})$, and
$z \in {\mathbb {P}}^1({\mathbb {C}})$, and ![]() $\frac {1}{d}f^* \mu _f = \mu _f$, meaning that
$\frac {1}{d}f^* \mu _f = \mu _f$, meaning that
 \[ \frac{1}{d} \int_{{\mathbb{P}}^1} \bigg(\sum_{f(x)=y} \varphi(x) \bigg) \mu_f(y) = \int_{{\mathbb{P}}^1} \varphi(x) \mu_f(x) \]
\[ \frac{1}{d} \int_{{\mathbb{P}}^1} \bigg(\sum_{f(x)=y} \varphi(x) \bigg) \mu_f(y) = \int_{{\mathbb{P}}^1} \varphi(x) \mu_f(x) \]
for all continuous functions ![]() $\varphi$ on
$\varphi$ on ![]() ${\mathbb {P}}^1$ (see [Reference MañéMañ83, Reference Freire, Lopes and MañéFLM83, Reference LyubichLyu83a]).
${\mathbb {P}}^1$ (see [Reference MañéMañ83, Reference Freire, Lopes and MañéFLM83, Reference LyubichLyu83a]).
2.2 Exceptional maps
We say that a map ![]() $f : {\mathbb {P}}^1\to {\mathbb {P}}^1$ of degree
$f : {\mathbb {P}}^1\to {\mathbb {P}}^1$ of degree ![]() $d\geq 2$ is exceptional if it is the quotient of an affine transformation of
$d\geq 2$ is exceptional if it is the quotient of an affine transformation of ![]() ${\mathbb {C}}$; see [Reference MilnorMil06] for details. Every exceptional
${\mathbb {C}}$; see [Reference MilnorMil06] for details. Every exceptional ![]() $f$ is conjugate by an element of
$f$ is conjugate by an element of ![]() $\operatorname {Aut} {\mathbb {P}}^1 \simeq \mathrm {PSL}_2{\mathbb {C}}$ to a power map
$\operatorname {Aut} {\mathbb {P}}^1 \simeq \mathrm {PSL}_2{\mathbb {C}}$ to a power map ![]() $z^{\pm d}$, a Tchebyshev polynomial
$z^{\pm d}$, a Tchebyshev polynomial ![]() $\pm T_d$, or it is a Lattès map, meaning that it is the quotient of a map on an elliptic curve. The exceptional maps are distinguished by properties of their measures
$\pm T_d$, or it is a Lattès map, meaning that it is the quotient of a map on an elliptic curve. The exceptional maps are distinguished by properties of their measures ![]() $\mu _f$. In each case, the Julia set
$\mu _f$. In each case, the Julia set ![]() $J(f)$ is a real submanifold of
$J(f)$ is a real submanifold of ![]() ${\mathbb {P}}^1({\mathbb {C}})$ (with boundary, in the case of the Tchebyshev polynomials), and the measure
${\mathbb {P}}^1({\mathbb {C}})$ (with boundary, in the case of the Tchebyshev polynomials), and the measure ![]() $\mu _f$ is absolutely continuous with respect to the Hausdorff measure on
$\mu _f$ is absolutely continuous with respect to the Hausdorff measure on ![]() $J(f)$. Zdunik proved the converse: the exceptional maps are the only maps for which this absolute continuity can hold [Reference ZdunikZdu90].
$J(f)$. Zdunik proved the converse: the exceptional maps are the only maps for which this absolute continuity can hold [Reference ZdunikZdu90].
2.3 Preperiodic points and the maximal measure
It is well known that the preperiodic points of ![]() $f$ are uniformly distributed with respect to the measure
$f$ are uniformly distributed with respect to the measure ![]() $\mu _f$. That is, defining discrete measures
$\mu _f$. That is, defining discrete measures
 \[ \mu_{n,m} = \frac{1}{d^n} \sum_{f^n(z)=f^m(z)} \delta_z \]
\[ \mu_{n,m} = \frac{1}{d^n} \sum_{f^n(z)=f^m(z)} \delta_z \]
in ![]() ${\mathbb {P}}^1$ for every pair of integers
${\mathbb {P}}^1$ for every pair of integers ![]() $n > m\geq 0$, then for any sequence
$n > m\geq 0$, then for any sequence ![]() $(n_k,m_k)$ of integers
$(n_k,m_k)$ of integers ![]() $n_k > m_k\geq 0$ with
$n_k > m_k\geq 0$ with ![]() $\max \{n_k,m_k\} \to \infty$ as
$\max \{n_k,m_k\} \to \infty$ as ![]() $k\to \infty$, the measures
$k\to \infty$, the measures ![]() $\mu _{n_k, m_k}$ converge weakly to the measure
$\mu _{n_k, m_k}$ converge weakly to the measure ![]() $\mu _f$ (see [Reference MañéMañ83, Reference Freire, Lopes and MañéFLM83, Reference LyubichLyu83a]).
$\mu _f$ (see [Reference MañéMañ83, Reference Freire, Lopes and MañéFLM83, Reference LyubichLyu83a]).
But the preperiodic points determine the measure ![]() $\mu _f$ in a stronger sense, without ordering them by period or orbit length.
$\mu _f$ in a stronger sense, without ordering them by period or orbit length.
Theorem 2.1 [Reference Levin and PrzytyckiLP97, Reference Baker and DeMarcoBDeM11, Reference Yuan and ZhangYZ13]
For any maps ![]() $f, g: {\mathbb {P}}^1\to {\mathbb {P}}^1$ of degrees
$f, g: {\mathbb {P}}^1\to {\mathbb {P}}^1$ of degrees ![]() $>1$ defined over
$>1$ defined over ![]() ${\mathbb {C}}$, the following are equivalent:
${\mathbb {C}}$, the following are equivalent:
(1)
 $|\mathrm {Preper}(f) \cap \mathrm {Preper}(g)| = \infty$; and
$|\mathrm {Preper}(f) \cap \mathrm {Preper}(g)| = \infty$; and(2)
 $\mathrm {Preper}(f) = \mathrm {Preper}(g)$;
$\mathrm {Preper}(f) = \mathrm {Preper}(g)$;
and these conditions imply that
(3)
 $\mu _f = \mu _g$.
$\mu _f = \mu _g$.
Moreover, if at least one of ![]() $f$ or
$f$ or ![]() $g$ is not conjugate to a power map, then condition (3) is equivalent to conditions (1) and (2).
$g$ is not conjugate to a power map, then condition (3) is equivalent to conditions (1) and (2).
Remark 2.2 The main theorem of [Reference Levin and PrzytyckiLP97] states that if ![]() $\mu _f = \mu _g$, and if
$\mu _f = \mu _g$, and if ![]() $f$ and
$f$ and ![]() $g$ are non-exceptional, then there exist iterates
$g$ are non-exceptional, then there exist iterates ![]() $f^n$ and
$f^n$ and ![]() $g^m$ and positive integers
$g^m$ and positive integers ![]() $\ell$ and
$\ell$ and ![]() $k$ so that
$k$ so that
for some (possibly multi-valued) branches of the inverse ![]() $g^{-m}$ and
$g^{-m}$ and ![]() $f^{-n}$. It follows that
$f^{-n}$. It follows that ![]() $\mathrm {Preper}(f) = \mathrm {Preper}(g)$; see [Reference Levin and PrzytyckiLP97, Theorem A and Remark 2].
$\mathrm {Preper}(f) = \mathrm {Preper}(g)$; see [Reference Levin and PrzytyckiLP97, Theorem A and Remark 2].
As the equivalences of Theorem 2.1 are not stated this way in the literature, we outline the proof ingredients.
Sketch proof of Theorem 2.1 The implication that condition (2) ![]() $\implies$ condition (1) is immediate, because all maps of degree
$\implies$ condition (1) is immediate, because all maps of degree ![]() $>1$ have infinitely many distinct preperiodic points. The implications condition (1)
$>1$ have infinitely many distinct preperiodic points. The implications condition (1) ![]() $\implies$ condition (2)
$\implies$ condition (2) ![]() $\implies$ condition (3) are proved in [Reference Baker and DeMarcoBDeM11, Theorem 1.2] and [Reference Yuan and ZhangYZ13, Theorems 1.3 and 1.4]. The key input is the equidistribution of points of small canonical height for a map
$\implies$ condition (3) are proved in [Reference Baker and DeMarcoBDeM11, Theorem 1.2] and [Reference Yuan and ZhangYZ13, Theorems 1.3 and 1.4]. The key input is the equidistribution of points of small canonical height for a map ![]() $f: {\mathbb {P}}^1\to {\mathbb {P}}^1$, working over number fields or, more generally, fields that are finitely generated over
$f: {\mathbb {P}}^1\to {\mathbb {P}}^1$, working over number fields or, more generally, fields that are finitely generated over ![]() ${\mathbb {Q}}$.
${\mathbb {Q}}$.
If ![]() $f$ and
$f$ and ![]() $g$ are non-exceptional, then the implication condition (3)
$g$ are non-exceptional, then the implication condition (3) ![]() $\implies$ condition (2) is proved in [Reference Levin and PrzytyckiLP97, Theorem A and Remark 2]. See Remark 2.2.
$\implies$ condition (2) is proved in [Reference Levin and PrzytyckiLP97, Theorem A and Remark 2]. See Remark 2.2.
It remains to carry out a case-by-case analysis of the measures for exceptional maps, appealing to Zdunik's characterization of exceptional maps by their measures in [Reference ZdunikZdu90].
If ![]() $f$ is a Tchebyshev polynomial
$f$ is a Tchebyshev polynomial ![]() $\pm T_d$, its measure
$\pm T_d$, its measure ![]() $\mu _f$ is supported on a closed interval. If
$\mu _f$ is supported on a closed interval. If ![]() $\mu _g = \mu _f$, then
$\mu _g = \mu _f$, then ![]() $g$ must be equal to
$g$ must be equal to ![]() $\pm T_e$, where
$\pm T_e$, where ![]() $e = \deg g$; indeed, we know that
$e = \deg g$; indeed, we know that ![]() $g$ must be conjugate to
$g$ must be conjugate to ![]() $\pm T_e$, but the only
$\pm T_e$, but the only ![]() $A \in \operatorname {Aut} {\mathbb {P}}^1$ for which
$A \in \operatorname {Aut} {\mathbb {P}}^1$ for which ![]() $A_*\mu _g = \mu _g$ are
$A_*\mu _g = \mu _g$ are ![]() $A(z) = \pm z$. All of these maps have the same sets of preperiodic points.
$A(z) = \pm z$. All of these maps have the same sets of preperiodic points.
If ![]() $f(z) = z^{\pm d}$, then
$f(z) = z^{\pm d}$, then ![]() $\mu _f$ is the uniform distribution on the unit circle, and
$\mu _f$ is the uniform distribution on the unit circle, and ![]() $\mu _f = \mu _g$ implies that
$\mu _f = \mu _g$ implies that ![]() $g$ must also be a power map. In this case, either
$g$ must also be a power map. In this case, either ![]() $\mathrm {Preper}(f) = \mathrm {Preper}(g)$ or
$\mathrm {Preper}(f) = \mathrm {Preper}(g)$ or ![]() $\mathrm {Preper}(f) \cap \mathrm {Preper}(g) = \emptyset$; writing
$\mathrm {Preper}(f) \cap \mathrm {Preper}(g) = \emptyset$; writing ![]() $g(z) = \alpha z^{\pm e}$ with
$g(z) = \alpha z^{\pm e}$ with ![]() $|\alpha |=1$ and depending on whether or not
$|\alpha |=1$ and depending on whether or not ![]() $\alpha$ is a root of unity.
$\alpha$ is a root of unity.
Finally, suppose ![]() $f$ is a Lattès map. Then the measure
$f$ is a Lattès map. Then the measure ![]() $\mu _f$ is the projection of the Haar measure from the associated elliptic curve. In particular, the measure knows the branch points of this quotient map and the ramification degree at each point. In other words, the measure
$\mu _f$ is the projection of the Haar measure from the associated elliptic curve. In particular, the measure knows the branch points of this quotient map and the ramification degree at each point. In other words, the measure ![]() $\mu _f$ uniquely determines the orbifold structure on the quotient Riemann sphere. As such, it uniquely determines the isomorphism class of the elliptic curve over
$\mu _f$ uniquely determines the orbifold structure on the quotient Riemann sphere. As such, it uniquely determines the isomorphism class of the elliptic curve over ![]() ${\mathbb {C}}$ and thus the set of preperiodic points of
${\mathbb {C}}$ and thus the set of preperiodic points of ![]() $f$, which is equal to the projection of the torsion points of the elliptic curve. It follows that if
$f$, which is equal to the projection of the torsion points of the elliptic curve. It follows that if ![]() $\mu _f = \mu _g$ for some
$\mu _f = \mu _g$ for some ![]() $g$, then
$g$, then ![]() $g$ is a Lattès map from the same elliptic curve with the same set of preperiodic points. See [Reference MilnorMil06] for more information on these Lattès maps.
$g$ is a Lattès map from the same elliptic curve with the same set of preperiodic points. See [Reference MilnorMil06] for more information on these Lattès maps.
Remark 2.3 In [Reference PakovichPak21], Pakovich proved that each ![]() $f \in \mathrm {Rat}_d$ of degree
$f \in \mathrm {Rat}_d$ of degree ![]() $d \geq 4$ with
$d \geq 4$ with ![]() $2d-2$ distinct critical values satisfies
$2d-2$ distinct critical values satisfies
As these form a Zariski-dense and -open subset of ![]() $\mathrm {Rat}_d$, this implies, when combined with Theorem 2.1 for degrees
$\mathrm {Rat}_d$, this implies, when combined with Theorem 2.1 for degrees ![]() $d \geq 4$, the set of pairs
$d \geq 4$, the set of pairs ![]() $(f,g)$ with
$(f,g)$ with ![]() $|\mathrm {Preper}(f) \cap \mathrm {Preper}(g)| = \infty$ is not Zariski dense in the space
$|\mathrm {Preper}(f) \cap \mathrm {Preper}(g)| = \infty$ is not Zariski dense in the space ![]() $\mathrm {Rat}_d\times \mathrm {Rat}_d$ of all pairs with
$\mathrm {Rat}_d\times \mathrm {Rat}_d$ of all pairs with ![]() $d\geq 4$.
$d\geq 4$.
2.4 Why not periodic points?
It is reasonable to ask why we work with all preperiodic points and not the subset ![]() $\mathrm {Per}(f)$ of periodic points of
$\mathrm {Per}(f)$ of periodic points of ![]() $f$, which are also uniformly distributed with respect to
$f$, which are also uniformly distributed with respect to ![]() $\mu _f$. Of course, the uniform bound on
$\mu _f$. Of course, the uniform bound on ![]() $|\mathrm {Preper}(f)\cap \mathrm {Preper}(g)|$ in Theorem 1.1 is stronger than a bound on
$|\mathrm {Preper}(f)\cap \mathrm {Preper}(g)|$ in Theorem 1.1 is stronger than a bound on ![]() $|\mathrm {Per}(f)\cap \mathrm {Per}(g)|$, but there are two underlying reasons for our focus on preperiodic points. First, if we were to replace
$|\mathrm {Per}(f)\cap \mathrm {Per}(g)|$, but there are two underlying reasons for our focus on preperiodic points. First, if we were to replace ![]() $\mathrm {Preper}(f)$ with
$\mathrm {Preper}(f)$ with ![]() $\mathrm {Per}(f)$, then the equivalences of Theorem 2.1 would break down. For example, if
$\mathrm {Per}(f)$, then the equivalences of Theorem 2.1 would break down. For example, if ![]() $f$ and
$f$ and ![]() $g$ are Lattès maps induced from
$g$ are Lattès maps induced from ![]() $P\mapsto 2P$ and
$P\mapsto 2P$ and ![]() $P \mapsto 3P$ on the same elliptic curve via the same projection to
$P \mapsto 3P$ on the same elliptic curve via the same projection to ![]() ${\mathbb {P}}^1$, then
${\mathbb {P}}^1$, then ![]() $\mu _f = \mu _g$ with
$\mu _f = \mu _g$ with ![]() $|\mathrm {Per}(f) \cap \mathrm {Per}(g)| = \infty$ but
$|\mathrm {Per}(f) \cap \mathrm {Per}(g)| = \infty$ but ![]() $\mathrm {Per}(f) \not = \mathrm {Per}(f)$. In addition, there are many non-exceptional examples with
$\mathrm {Per}(f) \not = \mathrm {Per}(f)$. In addition, there are many non-exceptional examples with ![]() $\mu _f = \mu _g$ but
$\mu _f = \mu _g$ but ![]() $|\mathrm {Per}(f) \cap \mathrm {Per}(g)| < \infty$, such as
$|\mathrm {Per}(f) \cap \mathrm {Per}(g)| < \infty$, such as ![]() $f(z) = z^2 + c$ and
$f(z) = z^2 + c$ and ![]() $g(z) = -(z^2+c)$ for
$g(z) = -(z^2+c)$ for ![]() $c \in {\mathbb {C}}$. On the other hand, it follows from the proof of [Reference Levin and PrzytyckiLP97, Theorem A] that if
$c \in {\mathbb {C}}$. On the other hand, it follows from the proof of [Reference Levin and PrzytyckiLP97, Theorem A] that if ![]() $\mu _f = \mu _g$ for non-exceptional
$\mu _f = \mu _g$ for non-exceptional ![]() $f$ and
$f$ and ![]() $g$, and if there exists just one common repelling periodic point
$g$, and if there exists just one common repelling periodic point ![]() $x \in \mathrm {Per}(f) \cap \mathrm {Per}(g)$, then
$x \in \mathrm {Per}(f) \cap \mathrm {Per}(g)$, then ![]() $\mathrm {Per}(f) = \mathrm {Per}(g)$; see [Reference YeYe15, Theorem 1.5]. A second reason is our method of proof and original motivation for this project. For maps
$\mathrm {Per}(f) = \mathrm {Per}(g)$; see [Reference YeYe15, Theorem 1.5]. A second reason is our method of proof and original motivation for this project. For maps ![]() $f: {\mathbb {P}}^1\to {\mathbb {P}}^1$ defined over
$f: {\mathbb {P}}^1\to {\mathbb {P}}^1$ defined over ![]() $\overline {\mathbb {Q}}$, the preperiodic points for
$\overline {\mathbb {Q}}$, the preperiodic points for ![]() $f$ are precisely the points in
$f$ are precisely the points in ![]() ${\mathbb {P}}^1(\overline {\mathbb {Q}})$ for which the canonical height
${\mathbb {P}}^1(\overline {\mathbb {Q}})$ for which the canonical height ![]() $\hat {h}_f$ vanishes [Reference Call and SilvermanCS93]. Though somewhat hidden in this article, much of our analysis is, fundamentally, about properties of these height functions.
$\hat {h}_f$ vanishes [Reference Call and SilvermanCS93]. Though somewhat hidden in this article, much of our analysis is, fundamentally, about properties of these height functions.
2.5 Stability and the bifurcation current
Let ![]() $\Lambda$ be a connected complex manifold and
$\Lambda$ be a connected complex manifold and ![]() $f: \Lambda \times {\mathbb {P}}^1 \to \Lambda \times {\mathbb {P}}^1$ a holomorphic map defined by
$f: \Lambda \times {\mathbb {P}}^1 \to \Lambda \times {\mathbb {P}}^1$ a holomorphic map defined by ![]() $(\lambda, z)\mapsto (\lambda, f_\lambda (z))$ where each
$(\lambda, z)\mapsto (\lambda, f_\lambda (z))$ where each ![]() $f_\lambda$ has degree
$f_\lambda$ has degree ![]() $d \geq 2$. The measures
$d \geq 2$. The measures ![]() $\mu _{f_\lambda }$ can be packaged together into a positive
$\mu _{f_\lambda }$ can be packaged together into a positive ![]() $(1,1)$-current on the total space
$(1,1)$-current on the total space ![]() $\Lambda \times {\mathbb {P}}^1$ as follows. Let
$\Lambda \times {\mathbb {P}}^1$ as follows. Let ![]() $\omega$ be a smooth and positive
$\omega$ be a smooth and positive ![]() $(1,1)$-form on
$(1,1)$-form on ![]() ${\mathbb {P}}^1$ with
${\mathbb {P}}^1$ with ![]() $\int _{{\mathbb {P}}^1} \omega = 1$, and consider
$\int _{{\mathbb {P}}^1} \omega = 1$, and consider ![]() $p^*\omega$ on
$p^*\omega$ on ![]() $\Lambda \times {\mathbb {P}}^1$, where
$\Lambda \times {\mathbb {P}}^1$, where ![]() $p: \Lambda \times {\mathbb {P}}^1 \to {\mathbb {P}}^1$ is the projection. The dynamical Green current for
$p: \Lambda \times {\mathbb {P}}^1 \to {\mathbb {P}}^1$ is the projection. The dynamical Green current for ![]() $f$ on
$f$ on ![]() $\Lambda \times {\mathbb {P}}^1$ is
$\Lambda \times {\mathbb {P}}^1$ is
Then ![]() $\hat {T}_f$ is a closed, positive
$\hat {T}_f$ is a closed, positive ![]() $(1,1)$-current on
$(1,1)$-current on ![]() $\Lambda \times {\mathbb {P}}^1$ with continuous potentials, and the slice current
$\Lambda \times {\mathbb {P}}^1$ with continuous potentials, and the slice current ![]() $\hat {T}_f|_{\{\lambda \}\times {\mathbb {P}}^1}$ coincides with the measure
$\hat {T}_f|_{\{\lambda \}\times {\mathbb {P}}^1}$ coincides with the measure ![]() $\mu _{f_\lambda }$. See, for example, [Reference Dujardin and FavreDF08, § 3]. If
$\mu _{f_\lambda }$. See, for example, [Reference Dujardin and FavreDF08, § 3]. If ![]() $\Lambda = \mathrm {Rat}_d$ is the space of all maps of degree
$\Lambda = \mathrm {Rat}_d$ is the space of all maps of degree ![]() $d$, then we simply denote this current by
$d$, then we simply denote this current by ![]() $\hat {T}$, as in the introduction.
$\hat {T}$, as in the introduction.
We say the family ![]() $f_\lambda$, for
$f_\lambda$, for ![]() $\lambda \in \Lambda$, is stable if the Julia sets of
$\lambda \in \Lambda$, is stable if the Julia sets of ![]() $f_\lambda$ are moving holomorphically with
$f_\lambda$ are moving holomorphically with ![]() $\lambda$; see [Reference Mañé, Sad and SullivanMSS83, Reference LyubichLyu83b, Reference McMullenMcM94] for background. Following [Reference DeMarcoDeM01, Reference Dujardin and FavreDF08], the bifurcation current for
$\lambda$; see [Reference Mañé, Sad and SullivanMSS83, Reference LyubichLyu83b, Reference McMullenMcM94] for background. Following [Reference DeMarcoDeM01, Reference Dujardin and FavreDF08], the bifurcation current for ![]() $f$ is defined by
$f$ is defined by
where ![]() $\pi _\Lambda : \Lambda \times {\mathbb {P}}^1 \to \Lambda$ is the projection and
$\pi _\Lambda : \Lambda \times {\mathbb {P}}^1 \to \Lambda$ is the projection and ![]() $[C]$ is the current of integration along the critical locus of
$[C]$ is the current of integration along the critical locus of ![]() $f$; it is a closed and positive
$f$; it is a closed and positive ![]() $(1,1)$-current on
$(1,1)$-current on ![]() $\Lambda$ with continuous potentials. In [Reference DeMarcoDeM01], it is proved that
$\Lambda$ with continuous potentials. In [Reference DeMarcoDeM01], it is proved that ![]() $T_{f, \mathrm {bif}} = 0$ if and only if the family is stable.
$T_{f, \mathrm {bif}} = 0$ if and only if the family is stable.
For algebraic families, namely where ![]() $\Lambda$ is a smooth quasiprojective complex algebraic variety, and
$\Lambda$ is a smooth quasiprojective complex algebraic variety, and ![]() $f$ is a morphism, McMullen proved in [Reference McMullenMcM87] that the family
$f$ is a morphism, McMullen proved in [Reference McMullenMcM87] that the family ![]() $\{f_\lambda : \lambda \in \Lambda \}$ is stable if and only if either
$\{f_\lambda : \lambda \in \Lambda \}$ is stable if and only if either ![]() $f$ is isotrivial or
$f$ is isotrivial or ![]() $f$ is a family of flexible Lattès maps. (The family
$f$ is a family of flexible Lattès maps. (The family ![]() $f$ is isotrivial if all
$f$ is isotrivial if all ![]() $f_\lambda$ are conjugate by elements of
$f_\lambda$ are conjugate by elements of ![]() $\operatorname {Aut}{\mathbb {P}}^1$.) Specifically, McMullen proved that if
$\operatorname {Aut}{\mathbb {P}}^1$.) Specifically, McMullen proved that if ![]() $f$ is stable but not isotrivial, then each critical point of
$f$ is stable but not isotrivial, then each critical point of ![]() $f_\lambda$ is preperiodic for all
$f_\lambda$ is preperiodic for all ![]() $\lambda \in \Lambda$. In [Reference Dujardin and FavreDF08], Dujardin and Favre extended this result by studying the iterates of each critical point independently. Namely, if
$\lambda \in \Lambda$. In [Reference Dujardin and FavreDF08], Dujardin and Favre extended this result by studying the iterates of each critical point independently. Namely, if ![]() $c: \Lambda \to {\mathbb {P}}^1$ parameterizes a critical point for
$c: \Lambda \to {\mathbb {P}}^1$ parameterizes a critical point for ![]() $f_\lambda$, they introduced the current
$f_\lambda$, they introduced the current
on ![]() $\Lambda$, where
$\Lambda$, where ![]() $\Gamma _c \subset \Lambda \times {\mathbb {P}}^1$ is the graph of
$\Gamma _c \subset \Lambda \times {\mathbb {P}}^1$ is the graph of ![]() $c$, and they proved that
$c$, and they proved that ![]() $\hat {T}_{f,c} = 0$ if and only if
$\hat {T}_{f,c} = 0$ if and only if ![]() $f$ is isotrivial or
$f$ is isotrivial or ![]() $c$ is persistently preperiodic for
$c$ is persistently preperiodic for ![]() $f_\lambda$ (see [Reference Dujardin and FavreDF08, Theorems 2.5 and 3.2]).
$f_\lambda$ (see [Reference Dujardin and FavreDF08, Theorems 2.5 and 3.2]).
2.6 Stability of a marked point
Assume that ![]() $\Lambda$ is a smooth quasiprojective complex algebraic variety. Suppose that
$\Lambda$ is a smooth quasiprojective complex algebraic variety. Suppose that ![]() $a \in {\mathbb {P}}^1(k)$ is any point defined over the function field
$a \in {\mathbb {P}}^1(k)$ is any point defined over the function field ![]() $k = {\mathbb {C}}(\Lambda )$ defining a holomorphic map
$k = {\mathbb {C}}(\Lambda )$ defining a holomorphic map ![]() $a: \Lambda \to {\mathbb {P}}^1$. The pair
$a: \Lambda \to {\mathbb {P}}^1$. The pair ![]() $(f,a)$ is isotrivial if both
$(f,a)$ is isotrivial if both ![]() $f$ and
$f$ and ![]() $a$, after changing coordinates by Möbius transformation defined over a finite extension of
$a$, after changing coordinates by Möbius transformation defined over a finite extension of ![]() $k = {\mathbb {C}}(\Lambda )$, become independent of the parameter
$k = {\mathbb {C}}(\Lambda )$, become independent of the parameter ![]() $\lambda$. In other words, working over
$\lambda$. In other words, working over ![]() ${\mathbb {C}}$, the group
${\mathbb {C}}$, the group ![]() $\operatorname {Aut} {\mathbb {P}}^1$ acts on pairs
$\operatorname {Aut} {\mathbb {P}}^1$ acts on pairs ![]() $(f,a) \in \mathrm {Rat}_d \times {\mathbb {P}}^1$ by
$(f,a) \in \mathrm {Rat}_d \times {\mathbb {P}}^1$ by ![]() $A\cdot (f,a) = (A\circ f \circ A^{-1}, A\circ a)$, and a pair
$A\cdot (f,a) = (A\circ f \circ A^{-1}, A\circ a)$, and a pair ![]() $(f,a)$ defined over
$(f,a)$ defined over ![]() $k$ is isotrivial if the associated map
$k$ is isotrivial if the associated map ![]() $\Lambda \to (\mathrm {Rat}_d\times {\mathbb {P}}^1)/\operatorname {Aut}{\mathbb {P}}^1$ is constant.
$\Lambda \to (\mathrm {Rat}_d\times {\mathbb {P}}^1)/\operatorname {Aut}{\mathbb {P}}^1$ is constant.
Similarly to (2.3), we can define ![]() $\hat {T}_{f,a} := (\pi _\Lambda )_* (\hat {T}_f \wedge [\Gamma _a])$ by intersecting the graph
$\hat {T}_{f,a} := (\pi _\Lambda )_* (\hat {T}_f \wedge [\Gamma _a])$ by intersecting the graph ![]() $\Gamma _a$ with
$\Gamma _a$ with ![]() $\hat {T}_f$ in
$\hat {T}_f$ in ![]() $\Lambda \times {\mathbb {P}}^1$. Then
$\Lambda \times {\mathbb {P}}^1$. Then ![]() $\hat {T}_{f,a} = 0$ if and only if the pair
$\hat {T}_{f,a} = 0$ if and only if the pair ![]() $(f,a)$ is either isotrivial or persistently preperiodic [Reference DeMarcoDeM16, Theorem 1.4]. (Strictly speaking, the theorem there is only proved for
$(f,a)$ is either isotrivial or persistently preperiodic [Reference DeMarcoDeM16, Theorem 1.4]. (Strictly speaking, the theorem there is only proved for ![]() $\Lambda$ of dimension 1, but it holds more generally, and it is not formulated in terms of the current
$\Lambda$ of dimension 1, but it holds more generally, and it is not formulated in terms of the current ![]() $\hat {T}_{f,a}$. The equivalence between the stability condition there and the vanishing of
$\hat {T}_{f,a}$. The equivalence between the stability condition there and the vanishing of ![]() $\hat {T}_{f,a}$ is proved in [Reference DeMarcoDeM03, Theorem 9.1].) This characterization of stability was reproved and extended to a more general setting by Gauthier and Vigny in [Reference Gauthier and VignyGV19]. We need the following consequence.
$\hat {T}_{f,a}$ is proved in [Reference DeMarcoDeM03, Theorem 9.1].) This characterization of stability was reproved and extended to a more general setting by Gauthier and Vigny in [Reference Gauthier and VignyGV19]. We need the following consequence.
Theorem 2.4 [Reference DeMarcoDeM16]
Suppose ![]() $\Lambda$ is a smooth, irreducible complex quasiprojective algebraic variety, and let
$\Lambda$ is a smooth, irreducible complex quasiprojective algebraic variety, and let ![]() $k = {\mathbb {C}}(\Lambda )$ be its function field. Suppose that
$k = {\mathbb {C}}(\Lambda )$ be its function field. Suppose that ![]() $f \in k(z)$ defines a holomorphic family of maps
$f \in k(z)$ defines a holomorphic family of maps ![]() $f_\lambda : {\mathbb {P}}^1\to {\mathbb {P}}^1$ of degree
$f_\lambda : {\mathbb {P}}^1\to {\mathbb {P}}^1$ of degree ![]() $d\geq 2$ for
$d\geq 2$ for ![]() $\lambda \in \Lambda$; fix
$\lambda \in \Lambda$; fix ![]() $a \in {\mathbb {P}}^1(k)$ defining a holomorphic map
$a \in {\mathbb {P}}^1(k)$ defining a holomorphic map ![]() $a: \Lambda \to {\mathbb {P}}^1$. If the pair
$a: \Lambda \to {\mathbb {P}}^1$. If the pair ![]() $(f,a)$ is neither isotrivial nor persistently preperiodic, then there exists
$(f,a)$ is neither isotrivial nor persistently preperiodic, then there exists ![]() $\lambda _0 \in \Lambda$ for which
$\lambda _0 \in \Lambda$ for which ![]() $a(\lambda _0)$ is preperiodic to a repelling cycle for
$a(\lambda _0)$ is preperiodic to a repelling cycle for ![]() $f_{\lambda _0}$.
$f_{\lambda _0}$.
Proof. The hypothesis that ![]() $(f,a)$ is neither isotrivial nor persistently preperiodic on
$(f,a)$ is neither isotrivial nor persistently preperiodic on ![]() $\Lambda$ implies we can find an algebraic curve
$\Lambda$ implies we can find an algebraic curve ![]() $C$ in
$C$ in ![]() $\Lambda$ along which
$\Lambda$ along which ![]() $(f,a)$ is neither isotrivial nor persistently preperiodic. Indeed, if
$(f,a)$ is neither isotrivial nor persistently preperiodic. Indeed, if ![]() $(f,a)$ is not isotrivial, then the associated map
$(f,a)$ is not isotrivial, then the associated map ![]() $\Lambda \to (\mathrm {Rat}_d \times {\mathbb {P}}^1)/\operatorname {Aut}{\mathbb {P}}^1$ is non-constant; by the irreducibility of
$\Lambda \to (\mathrm {Rat}_d \times {\mathbb {P}}^1)/\operatorname {Aut}{\mathbb {P}}^1$ is non-constant; by the irreducibility of ![]() $\Lambda$, every
$\Lambda$, every ![]() $\lambda \in \Lambda$ is contained in some algebraic curve along which
$\lambda \in \Lambda$ is contained in some algebraic curve along which ![]() $(f,a)$ is not isotrivial. But if the pair is persistently preperiodic along all such curves, then the pair would be preperiodic on all of
$(f,a)$ is not isotrivial. But if the pair is persistently preperiodic along all such curves, then the pair would be preperiodic on all of ![]() $\Lambda$. Note, moreover, that if
$\Lambda$. Note, moreover, that if ![]() $(f,a)$ is neither isotrivial nor persistently preperiodic on a curve
$(f,a)$ is neither isotrivial nor persistently preperiodic on a curve ![]() $C$, then it is also the case on the complement of any finite set of points in
$C$, then it is also the case on the complement of any finite set of points in ![]() $C$. Thus, it suffices to prove the result for a smooth and quasiprojective curve
$C$. Thus, it suffices to prove the result for a smooth and quasiprojective curve ![]() $\Lambda$.
$\Lambda$.
Now assume that ![]() $\Lambda$ is a smooth, quasiprojective algebraic curve defined over
$\Lambda$ is a smooth, quasiprojective algebraic curve defined over ![]() ${\mathbb {C}}$. From [Reference DeMarcoDeM16, Theorem 1.4], the hypothesis that
${\mathbb {C}}$. From [Reference DeMarcoDeM16, Theorem 1.4], the hypothesis that ![]() $(f,a)$ is neither isotrivial nor persistently preperiodic implies that the sequence of holomorphic functions
$(f,a)$ is neither isotrivial nor persistently preperiodic implies that the sequence of holomorphic functions ![]() $\{\lambda \mapsto f_\lambda ^n(a(\lambda ))\}_{n\geq 0}$ fails to be normal on
$\{\lambda \mapsto f_\lambda ^n(a(\lambda ))\}_{n\geq 0}$ fails to be normal on ![]() $\Lambda$. Thus, as a consequence of Montel's theorem, there must be a parameter
$\Lambda$. Thus, as a consequence of Montel's theorem, there must be a parameter ![]() $\lambda _0 \in U$ and positive integer
$\lambda _0 \in U$ and positive integer ![]() $n_0$ so that
$n_0$ so that ![]() $f_{\lambda _0}^{n_0}(a(\lambda _0))$ is a repelling periodic point for
$f_{\lambda _0}^{n_0}(a(\lambda _0))$ is a repelling periodic point for ![]() $f_{\lambda _0}$; see [Reference DeMarcoDeM16, Proposition 5.1].
$f_{\lambda _0}$; see [Reference DeMarcoDeM16, Proposition 5.1].
3. Zariski density of preperiodic points
In this section we prove Theorem 1.6, restated here as Theorem 3.1.
Throughout, we assume that ![]() $S$ is a smooth and irreducible quasiprojective variety over
$S$ is a smooth and irreducible quasiprojective variety over ![]() ${\mathbb {C}}$. Let
${\mathbb {C}}$. Let ![]() $k = {\mathbb {C}}(S)$ be its function field. An algebraic family of pairs
$k = {\mathbb {C}}(S)$ be its function field. An algebraic family of pairs ![]() $(f,g)$ over
$(f,g)$ over ![]() $S$ is a pair of rational functions
$S$ is a pair of rational functions ![]() $f, g \in k(z)$ for which
$f, g \in k(z)$ for which ![]() $f$ and
$f$ and ![]() $g$ each induce holomorphic maps
$g$ each induce holomorphic maps ![]() $S \times {\mathbb {P}}^1 \to {\mathbb {P}}^1$ via specialization
$S \times {\mathbb {P}}^1 \to {\mathbb {P}}^1$ via specialization ![]() $(s, z) \mapsto f_s(z)$. The pair
$(s, z) \mapsto f_s(z)$. The pair ![]() $(f,g)$ induces a holomorphic map we denote by
$(f,g)$ induces a holomorphic map we denote by
given by ![]() $(s, x,y) \mapsto (s, f_s(x), g_s(y))$. We say that
$(s, x,y) \mapsto (s, f_s(x), g_s(y))$. We say that ![]() $\Phi = (f,g)$ has degree
$\Phi = (f,g)$ has degree ![]() $d \geq 2$ if
$d \geq 2$ if ![]() $f_s$ and
$f_s$ and ![]() $g_s$ are both of degree
$g_s$ are both of degree ![]() $d$ for each
$d$ for each ![]() $t\in S$.
$t\in S$.
Recall that ![]() $f \in k(z)$ is isotrivial if the induced map
$f \in k(z)$ is isotrivial if the induced map ![]() $S \to \mathrm {Rat}_d$ given by
$S \to \mathrm {Rat}_d$ given by ![]() $s \mapsto f_s$ has constant image in the quotient space
$s \mapsto f_s$ has constant image in the quotient space ![]() $\mathrm {M}_d = \mathrm {Rat}_d/\operatorname {Aut}{\mathbb {P}}^1$. Equivalently, there exists a finite extension
$\mathrm {M}_d = \mathrm {Rat}_d/\operatorname {Aut}{\mathbb {P}}^1$. Equivalently, there exists a finite extension ![]() $k'$ of
$k'$ of ![]() $k$ and a linear fractional transformation
$k$ and a linear fractional transformation ![]() $B$ defined over
$B$ defined over ![]() $k'$ so that
$k'$ so that ![]() $B \circ f \circ B^{-1}$ is in
$B \circ f \circ B^{-1}$ is in ![]() ${\mathbb {C}}(z)$. An algebraic family of pairs
${\mathbb {C}}(z)$. An algebraic family of pairs ![]() $(f,g)$ is isotrivial if the induced map
$(f,g)$ is isotrivial if the induced map ![]() $S \to \mathrm {Rat}_d \times \mathrm {Rat}_d$ is constant when passing to the quotient space
$S \to \mathrm {Rat}_d \times \mathrm {Rat}_d$ is constant when passing to the quotient space ![]() $(\mathrm {Rat}_d\times \mathrm {Rat}_d)/\operatorname {Aut} {\mathbb {P}}^1$. Here,
$(\mathrm {Rat}_d\times \mathrm {Rat}_d)/\operatorname {Aut} {\mathbb {P}}^1$. Here, ![]() $\operatorname {Aut}{\mathbb {P}}^1 \simeq \mathrm {PSL}_2{\mathbb {C}}$ is acting diagonally by conjugation, so that
$\operatorname {Aut}{\mathbb {P}}^1 \simeq \mathrm {PSL}_2{\mathbb {C}}$ is acting diagonally by conjugation, so that ![]() $A\cdot (f,g) = (A\circ f\circ A^{-1}, A\circ g\circ A^{-1})$ and
$A\cdot (f,g) = (A\circ f\circ A^{-1}, A\circ g\circ A^{-1})$ and ![]() $\dim (\mathrm {Rat}_d\times \mathrm {Rat}_d)/\operatorname {Aut}{\mathbb {P}}^1 = 4d-1$. We say that an algebraic family of pairs
$\dim (\mathrm {Rat}_d\times \mathrm {Rat}_d)/\operatorname {Aut}{\mathbb {P}}^1 = 4d-1$. We say that an algebraic family of pairs ![]() $\Phi = (f,g)$ over
$\Phi = (f,g)$ over ![]() $S$ is maximally non-isotrivial if the family determines a finite map from
$S$ is maximally non-isotrivial if the family determines a finite map from ![]() $S$ to
$S$ to ![]() $(\mathrm {Rat}_d\times \mathrm {Rat}_d)/\operatorname {Aut}{\mathbb {P}}^1$.
$(\mathrm {Rat}_d\times \mathrm {Rat}_d)/\operatorname {Aut}{\mathbb {P}}^1$.
For each integer ![]() $\ell \geq 1$, we let
$\ell \geq 1$, we let ![]() $\Phi ^{(\ell )}$ denote the map on
$\Phi ^{(\ell )}$ denote the map on ![]() $S \times ({\mathbb {P}}^1\times {\mathbb {P}}^1)^\ell$ given by the product action of
$S \times ({\mathbb {P}}^1\times {\mathbb {P}}^1)^\ell$ given by the product action of ![]() $\Phi$ on the fiber power.
$\Phi$ on the fiber power.
Theorem 3.1 Suppose ![]() $\Phi$ is a maximally non-isotrivial algebraic family of pairs over
$\Phi$ is a maximally non-isotrivial algebraic family of pairs over ![]() $S$, of degree
$S$, of degree ![]() $d \geq 2$, and let
$d \geq 2$, and let ![]() $\Delta \subset {\mathbb {P}}^1\times {\mathbb {P}}^1$ be the diagonal. The preperiodic points of
$\Delta \subset {\mathbb {P}}^1\times {\mathbb {P}}^1$ be the diagonal. The preperiodic points of ![]() $\Phi ^{(\ell )}$ in
$\Phi ^{(\ell )}$ in ![]() $S\times \Delta ^{\ell }$ form a Zariski dense subset of
$S\times \Delta ^{\ell }$ form a Zariski dense subset of ![]() $S \times \Delta ^\ell$, for every
$S \times \Delta ^\ell$, for every ![]() $1 \leq \ell \leq \dim S$.
$1 \leq \ell \leq \dim S$.
The key ingredient in the proof is the characterization of stability of marked points ![]() $(f,a)$, for an algebraic family of maps
$(f,a)$, for an algebraic family of maps ![]() $f$ on
$f$ on ![]() ${\mathbb {P}}^1$ and holomorphic
${\mathbb {P}}^1$ and holomorphic ![]() $a: S\to {\mathbb {P}}^1$, from [Reference DeMarcoDeM16]; see Theorem 2.4.
$a: S\to {\mathbb {P}}^1$, from [Reference DeMarcoDeM16]; see Theorem 2.4.
3.1 Proof of Theorem 3.1 when dimension of  $S$ is 1
$S$ is 1
For simplicity, we first present the proof when ![]() $S$ is a curve. Let
$S$ is a curve. Let ![]() $\Omega$ be any Zariski-open subset of
$\Omega$ be any Zariski-open subset of ![]() $S \times {\mathbb {P}}^1$. It suffices to show there exists a single point
$S \times {\mathbb {P}}^1$. It suffices to show there exists a single point ![]() $(s_0, z_0) \in \Omega$ for which
$(s_0, z_0) \in \Omega$ for which ![]() $z_0 \in \mathrm {Preper}(f_{s_0}) \cap \mathrm {Preper}(g_{s_0})$. Choose any irreducible, algebraic curve
$z_0 \in \mathrm {Preper}(f_{s_0}) \cap \mathrm {Preper}(g_{s_0})$. Choose any irreducible, algebraic curve ![]() $P \subset S\times {\mathbb {P}}^1$ parameterizing a periodic point of
$P \subset S\times {\mathbb {P}}^1$ parameterizing a periodic point of ![]() $f$ that intersects
$f$ that intersects ![]() $\Omega$. Note that there are infinitely many choices of such curves, because
$\Omega$. Note that there are infinitely many choices of such curves, because ![]() $f_s$ has infinitely many periodic points for every
$f_s$ has infinitely many periodic points for every ![]() $s \in S$. In fact, there exists a choice of
$s \in S$. In fact, there exists a choice of ![]() $s$ so that all periodic points of sufficiently large period for
$s$ so that all periodic points of sufficiently large period for ![]() $f_s$ will lie in
$f_s$ will lie in ![]() $\Omega$ (a fact that will be relevant to our argument). We may view the curve
$\Omega$ (a fact that will be relevant to our argument). We may view the curve ![]() $P$ as the graph of a point in
$P$ as the graph of a point in ![]() ${\mathbb {P}}^1(k')$ for some finite extension
${\mathbb {P}}^1(k')$ for some finite extension ![]() $k'$ of
$k'$ of ![]() $k = {\mathbb {C}}(S)$. Let
$k = {\mathbb {C}}(S)$. Let ![]() $S'\to S$ denote a finite branched covering map so that
$S'\to S$ denote a finite branched covering map so that ![]() $k' = {\mathbb {C}}(S')$. By construction, the pair
$k' = {\mathbb {C}}(S')$. By construction, the pair ![]() $(f,P)$ is persistently preperiodic over
$(f,P)$ is persistently preperiodic over ![]() $S'$.
$S'$.
Now assume that the pair ![]() $(g, P)$ is not isotrivial. If the pair
$(g, P)$ is not isotrivial. If the pair ![]() $(g,P)$ is also persistently preperiodic for
$(g,P)$ is also persistently preperiodic for ![]() $g$, then we are done. Otherwise, by Theorem 2.4, there exists
$g$, then we are done. Otherwise, by Theorem 2.4, there exists ![]() $s_0\in S'$ at which
$s_0\in S'$ at which ![]() $P_{s_0}$ is preperiodic for
$P_{s_0}$ is preperiodic for ![]() $g_{s_0}$. This completes the proof under this assumption of non-isotriviality of
$g_{s_0}$. This completes the proof under this assumption of non-isotriviality of ![]() $(g,P)$.
$(g,P)$.
If ![]() $(g,P)$ is isotrivial, it is convenient to pass to a further finite branched cover
$(g,P)$ is isotrivial, it is convenient to pass to a further finite branched cover ![]() $S' \to S$, if necessary, and change coordinates so that the family
$S' \to S$, if necessary, and change coordinates so that the family ![]() $g_s$ is independent of
$g_s$ is independent of ![]() $s \in S'$ and the point
$s \in S'$ and the point ![]() $P_s$ is constant. In these new coordinates, if the pair
$P_s$ is constant. In these new coordinates, if the pair ![]() $(g,P)$ is persistently preperiodic, the proof is complete. If the pair
$(g,P)$ is persistently preperiodic, the proof is complete. If the pair ![]() $(g,P)$ is isotrivial but with infinite orbit, we then repeat the argument with a different choice of curve
$(g,P)$ is isotrivial but with infinite orbit, we then repeat the argument with a different choice of curve ![]() $P$. If the pair
$P$. If the pair ![]() $(g,P)$ is isotrivial for all curves
$(g,P)$ is isotrivial for all curves ![]() $P$ parameterizing points of a given large period for
$P$ parameterizing points of a given large period for ![]() $f$, then each of these periodic points for
$f$, then each of these periodic points for ![]() $f$ is constant in these coordinates over
$f$ is constant in these coordinates over ![]() $S'$. In particular, by an interpolation argument,
$S'$. In particular, by an interpolation argument, ![]() $f$ itself must be a constant family. More precisely, choosing any period
$f$ itself must be a constant family. More precisely, choosing any period ![]() $N > 2d+1$, we would be able to find a set of distinct points
$N > 2d+1$, we would be able to find a set of distinct points ![]() $z_1, z_2, \ldots, z_N \in {\mathbb {P}}^1({\mathbb {C}})$ so that
$z_1, z_2, \ldots, z_N \in {\mathbb {P}}^1({\mathbb {C}})$ so that ![]() $f_s(z_i) = z_{i+1}$ for all
$f_s(z_i) = z_{i+1}$ for all ![]() $s \in S'$ and all
$s \in S'$ and all ![]() $i = 1, \ldots, N-1$, and this would imply that the maps
$i = 1, \ldots, N-1$, and this would imply that the maps ![]() $f_s$ are constant in
$f_s$ are constant in ![]() $s$ (see [Reference DeMarcoDeM16, Lemma 2.5]). In other words, the pair
$s$ (see [Reference DeMarcoDeM16, Lemma 2.5]). In other words, the pair ![]() $(f,g)$ is isotrivial, violating the hypothesis. This completes the proof.
$(f,g)$ is isotrivial, violating the hypothesis. This completes the proof.
3.2 Proof of Theorem 3.1 for any base  $S$
$S$
Let ![]() $m = \dim _{\mathbb {C}} S$. Let
$m = \dim _{\mathbb {C}} S$. Let ![]() $\Omega$ be any Zariski-open subset of
$\Omega$ be any Zariski-open subset of ![]() $S \times ({\mathbb {P}}^1)^m$. It suffices to show that there exists a single point
$S \times ({\mathbb {P}}^1)^m$. It suffices to show that there exists a single point ![]() $(s_0, z_1, z_2, \ldots, z_m) \in \Omega$ for which
$(s_0, z_1, z_2, \ldots, z_m) \in \Omega$ for which
for all ![]() $i = 1, \ldots, m$. Indeed, this shows Zariski density of the preperiodic points of
$i = 1, \ldots, m$. Indeed, this shows Zariski density of the preperiodic points of ![]() $\Phi ^{(m)}$ in
$\Phi ^{(m)}$ in ![]() $S \times \Delta ^m$. For
$S \times \Delta ^m$. For ![]() $S \times \Delta ^\ell$ with
$S \times \Delta ^\ell$ with ![]() $\ell < m$, we observe that the projection, forgetting some factors of
$\ell < m$, we observe that the projection, forgetting some factors of ![]() $\Delta$, will still be Zariski dense, which will complete the proof.
$\Delta$, will still be Zariski dense, which will complete the proof.
The proof proceeds by induction on the dimension of ![]() $S$.
$S$.
First let ![]() $P_1$ denote an irreducible subvariety in
$P_1$ denote an irreducible subvariety in ![]() $S \times ({\mathbb {P}}^1)^m$ of codimension 1 having nontrivial intersection with
$S \times ({\mathbb {P}}^1)^m$ of codimension 1 having nontrivial intersection with ![]() $\Omega$, and for which
$\Omega$, and for which ![]() $z_1$ is periodic for
$z_1$ is periodic for ![]() $f_s$ for all
$f_s$ for all ![]() $(s, z_1, \ldots, z_m) \in P_1$. As the periodic points of
$(s, z_1, \ldots, z_m) \in P_1$. As the periodic points of ![]() $f$ are Zariski dense in
$f$ are Zariski dense in ![]() $S \times {\mathbb {P}}^1$, we can always find such a
$S \times {\mathbb {P}}^1$, we can always find such a ![]() $P_1$. Projecting
$P_1$. Projecting ![]() $P_1$ to the
$P_1$ to the ![]() $z_1$ coordinate, we may view this
$z_1$ coordinate, we may view this ![]() $P_1$ as single marked point defined on a finite (branched) cover
$P_1$ as single marked point defined on a finite (branched) cover ![]() $S'$ of
$S'$ of ![]() $S$. Now consider the pair
$S$. Now consider the pair ![]() $(g,P_1)$ over
$(g,P_1)$ over ![]() $S'$, abusing the notation slightly to identify
$S'$, abusing the notation slightly to identify ![]() $P_1$ with its projection. If this pair is isotrivial over
$P_1$ with its projection. If this pair is isotrivial over ![]() $S'$, then there is a change of coordinates (passing to a further finite branched cover of
$S'$, then there is a change of coordinates (passing to a further finite branched cover of ![]() $S'$ if necessary) so that the pair is constant. In this case, we select a different periodic point
$S'$ if necessary) so that the pair is constant. In this case, we select a different periodic point ![]() $P_1$ for
$P_1$ for ![]() $f$. If all periodic points of large period for
$f$. If all periodic points of large period for ![]() $f$ lead to isotrivial pairs for
$f$ lead to isotrivial pairs for ![]() $g$, then we carry out an interpolation argument as in § 3.1 to deduce that
$g$, then we carry out an interpolation argument as in § 3.1 to deduce that ![]() $f$ must also be constant in the new coordinates over
$f$ must also be constant in the new coordinates over ![]() $S'$. In other words, the pair
$S'$. In other words, the pair ![]() $(f,g)$ is isotrivial, a contradiction.
$(f,g)$ is isotrivial, a contradiction.
Thus, we may assume that there exists a periodic point ![]() $P_1$ for
$P_1$ for ![]() $f$ so that
$f$ so that ![]() $P_1 \cap \Omega \not = \emptyset$ and the pair
$P_1 \cap \Omega \not = \emptyset$ and the pair ![]() $(g, P_1)$ is not isotrivial over
$(g, P_1)$ is not isotrivial over ![]() $S$. It follows from Theorem 2.4 that the pair
$S$. It follows from Theorem 2.4 that the pair ![]() $(g,P_1)$ is either persistently preperiodic, in which case we let
$(g,P_1)$ is either persistently preperiodic, in which case we let ![]() $x_1$ be any element of
$x_1$ be any element of ![]() $P_1\cap \Omega$, or there exists a point
$P_1\cap \Omega$, or there exists a point ![]() $x_1 = (s_1, z_1, \ldots, z_m) \in P_1 \cap \Omega$ so that
$x_1 = (s_1, z_1, \ldots, z_m) \in P_1 \cap \Omega$ so that ![]() $z_1$ is preperiodic to a repelling cycle of
$z_1$ is preperiodic to a repelling cycle of ![]() $g_{s_1}$. We then consider an irreducible subvariety
$g_{s_1}$. We then consider an irreducible subvariety ![]() $P_1' \subset P_1$ containing
$P_1' \subset P_1$ containing ![]() $x_1$ along which
$x_1$ along which ![]() $z_1$ is persistently preperiodic for
$z_1$ is persistently preperiodic for ![]() $g$. Note that the codimension of
$g$. Note that the codimension of ![]() $P_1'$ is at most 1 and its projection to
$P_1'$ is at most 1 and its projection to ![]() $S$ will have codimension at most 1. If the codimension is 1, we let
$S$ will have codimension at most 1. If the codimension is 1, we let ![]() $S_1$ be its projection to the base. If this codimension is 0, we replace
$S_1$ be its projection to the base. If this codimension is 0, we replace ![]() $P_1'$ with its intersection with
$P_1'$ with its intersection with ![]() $\pi ^{-1}(S_1)$ for an arbitrarily chosen irreducible subvariety
$\pi ^{-1}(S_1)$ for an arbitrarily chosen irreducible subvariety ![]() $S_1$ of codimension 1 in
$S_1$ of codimension 1 in ![]() $S$ passing through
$S$ passing through ![]() $s_1$. Therefore,
$s_1$. Therefore, ![]() $P_1'$ has nonempty intersection with
$P_1'$ has nonempty intersection with ![]() $\Omega$, the projection of
$\Omega$, the projection of ![]() $P_1'$ to the base
$P_1'$ to the base ![]() $S$ has dimension
$S$ has dimension ![]() $m-1$, and the
$m-1$, and the ![]() $z_1$-coordinate of
$z_1$-coordinate of ![]() $P_1'$ is persistently preperiodic for both
$P_1'$ is persistently preperiodic for both ![]() $f$ and
$f$ and ![]() $g$. If
$g$. If ![]() $S_1$ is singular, we replace it with the regular part, so that it will be a smooth and irreducible quasiprojective variety of dimension
$S_1$ is singular, we replace it with the regular part, so that it will be a smooth and irreducible quasiprojective variety of dimension ![]() $m-1$.
$m-1$.
We now repeat the process, beginning with a subvariety ![]() $P_2$ of codimension 1 in
$P_2$ of codimension 1 in ![]() $P_1'$, having nonempty intersection with
$P_1'$, having nonempty intersection with ![]() $\Omega$, and for which the second coordinate
$\Omega$, and for which the second coordinate ![]() $z_2$ is periodic for
$z_2$ is periodic for ![]() $f$ over all of
$f$ over all of ![]() $S_1$, with
$S_1$, with ![]() $z_2$ not identically equal to
$z_2$ not identically equal to ![]() $z_1$ throughout
$z_1$ throughout ![]() $P_2$. Projecting to the
$P_2$. Projecting to the ![]() $z_2$-coordinate, we consider the associated pair
$z_2$-coordinate, we consider the associated pair ![]() $(g,P_2)$, passing to a further finite branched cover
$(g,P_2)$, passing to a further finite branched cover ![]() $S' \to S$ if needed. If this pair is isotrivial, we replace
$S' \to S$ if needed. If this pair is isotrivial, we replace ![]() $P_2$ with another choice of periodic point for
$P_2$ with another choice of periodic point for ![]() $f$; as above, if all periodic points of sufficiently large period for
$f$; as above, if all periodic points of sufficiently large period for ![]() $f$ lead to isotrivial pairs
$f$ lead to isotrivial pairs ![]() $(g,P_2)$, then the pair
$(g,P_2)$, then the pair ![]() $(f,g)$ would be isotrivial along
$(f,g)$ would be isotrivial along ![]() $S_1$. Here we use the assumption that
$S_1$. Here we use the assumption that ![]() $(f,g)$ is maximally non-isotrivial, not just non-isotrivial. So we can find a
$(f,g)$ is maximally non-isotrivial, not just non-isotrivial. So we can find a ![]() $P_2$ that has nonempty intersection with
$P_2$ that has nonempty intersection with ![]() $\Omega$ and so that, when projecting to the
$\Omega$ and so that, when projecting to the ![]() $z_2$-coordinate, the pair
$z_2$-coordinate, the pair ![]() $(f,P_2)$ is persistently periodic and the pair
$(f,P_2)$ is persistently periodic and the pair ![]() $(g,P_2)$ is not isotrivial.
$(g,P_2)$ is not isotrivial.
In this way, we inductively reduce the problem to the argument of § 3.1. This completes the proof of Theorem 3.1.
4. Non-degeneracy and the bifurcation measure
In this section, we work in the more general setting of families of polarized dynamical systems over a complex quasiprojective variety ![]() $S$. We review some important notions introduced in [Reference Gauthier and VignyGV19] and [Reference Yuan and ZhangYZ21] and remind the reader of their relations to the non-degeneracy conditions introduced by Habegger [Reference HabeggerHab13] and studied by Gao [Reference GaoGao20a] for subvarieties in families of abelian varieties. Finally, in § 4.3, we establish a criterion for non-degeneracy for certain families of polarized dynamical systems and subvarieties.
$S$. We review some important notions introduced in [Reference Gauthier and VignyGV19] and [Reference Yuan and ZhangYZ21] and remind the reader of their relations to the non-degeneracy conditions introduced by Habegger [Reference HabeggerHab13] and studied by Gao [Reference GaoGao20a] for subvarieties in families of abelian varieties. Finally, in § 4.3, we establish a criterion for non-degeneracy for certain families of polarized dynamical systems and subvarieties.
4.1 The bifurcation current and measure for families of endomorphisms
Suppose that ![]() $S$ is a smooth and irreducible quasiprojective variety defined over
$S$ is a smooth and irreducible quasiprojective variety defined over ![]() ${\mathbb {C}}$. A family of (
${\mathbb {C}}$. A family of ( ![]() $k$-dimensional) polarized dynamical systems
$k$-dimensional) polarized dynamical systems ![]() $(X\to S, \Phi, \mathcal {L})$ is given by a family of complex projective varieties
$(X\to S, \Phi, \mathcal {L})$ is given by a family of complex projective varieties ![]() $X\to S$, flat over
$X\to S$, flat over ![]() $S$ with smooth fibers
$S$ with smooth fibers ![]() $X_s$ of dimension
$X_s$ of dimension ![]() $k$ over each
$k$ over each ![]() $s\in S$, a regular map
$s\in S$, a regular map ![]() $\Phi : X\to X$ that preserves the fibers
$\Phi : X\to X$ that preserves the fibers ![]() $X_s$, and a relatively ample line bundle
$X_s$, and a relatively ample line bundle ![]() $\mathcal {L}$ on
$\mathcal {L}$ on ![]() $X$ such that for each
$X$ such that for each ![]() $s\in S$, we have
$s\in S$, we have ![]() $(\Phi |_{X_s})^{*}(\mathcal {L}|_{X_s})\simeq (\mathcal {L}|_{X_s})^{\otimes d}$ for some
$(\Phi |_{X_s})^{*}(\mathcal {L}|_{X_s})\simeq (\mathcal {L}|_{X_s})^{\otimes d}$ for some ![]() $d>0$.
$d>0$.
Example 4.1 Let ![]() $\Phi = (f,g)$ be an algebraic family of pairs over
$\Phi = (f,g)$ be an algebraic family of pairs over ![]() $S$, of degree
$S$, of degree ![]() $d\geq 1$, as considered in the previous section. Then
$d\geq 1$, as considered in the previous section. Then ![]() $\Phi$ defines a family of 2-dimensional polarized dynamical systems. The degree
$\Phi$ defines a family of 2-dimensional polarized dynamical systems. The degree ![]() $d$ is the degree of a polarization of
$d$ is the degree of a polarization of ![]() $\Phi$, taking line bundle
$\Phi$, taking line bundle ![]() $L = p_1^*O(1)\otimes p_2^*O(1)$ on
$L = p_1^*O(1)\otimes p_2^*O(1)$ on ![]() $S \times {\mathbb {P}}^1\times {\mathbb {P}}^1$, where
$S \times {\mathbb {P}}^1\times {\mathbb {P}}^1$, where ![]() $p_i: S\times {\mathbb {P}}^1\times {\mathbb {P}}^1 \to {\mathbb {P}}^1$ is the projection to the
$p_i: S\times {\mathbb {P}}^1\times {\mathbb {P}}^1 \to {\mathbb {P}}^1$ is the projection to the ![]() $i$th factor of
$i$th factor of ![]() ${\mathbb {P}}^1$,
${\mathbb {P}}^1$, ![]() $i = 1,2$.
$i = 1,2$.
As explained, for instance, in [Reference Gauthier and VignyGV19, § 2.3], to such a family we can associate a dynamical Green current, denoted by ![]() $\hat {T}_{\Phi }$, as follows. We let
$\hat {T}_{\Phi }$, as follows. We let ![]() $\hat {\omega }$ be a smooth positive
$\hat {\omega }$ be a smooth positive ![]() $(1,1)$-form on
$(1,1)$-form on ![]() $X$ cohomologous to a multiple of
$X$ cohomologous to a multiple of ![]() $\mathcal {L}$ such that
$\mathcal {L}$ such that ![]() $\omega _s :=\hat {\omega }|_{X_{s}}$ is Kähler for all
$\omega _s :=\hat {\omega }|_{X_{s}}$ is Kähler for all ![]() $s\in S$ and
$s\in S$ and
for each ![]() $s\in S$, where
$s\in S$, where ![]() $k = \dim X_s$. The sequence
$k = \dim X_s$. The sequence ![]() $d^{-n}(\Phi ^n)^{*}(\hat {\omega })$ converges weakly to a closed positive
$d^{-n}(\Phi ^n)^{*}(\hat {\omega })$ converges weakly to a closed positive ![]() $(1,1)$-current
$(1,1)$-current ![]() $\hat {T}_{\Phi }$ with continuous potentials.
$\hat {T}_{\Phi }$ with continuous potentials.
Example 4.2 For ![]() $X = S \times {\mathbb {P}}^1$ and family of maps
$X = S \times {\mathbb {P}}^1$ and family of maps ![]() $f$, the dynamical Green current of
$f$, the dynamical Green current of ![]() $f$ coincides with the current defined in (2.1), taking
$f$ coincides with the current defined in (2.1), taking ![]() $\hat \omega$ to be
$\hat \omega$ to be ![]() $p^*\omega$ for the projection
$p^*\omega$ for the projection ![]() $p: S\times {\mathbb {P}}^1\to {\mathbb {P}}^1$. If
$p: S\times {\mathbb {P}}^1\to {\mathbb {P}}^1$. If ![]() $\Phi = (f,g)$ is an algebraic family of pairs over
$\Phi = (f,g)$ is an algebraic family of pairs over ![]() $S$, polarized as in Example 4.1, then
$S$, polarized as in Example 4.1, then ![]() $\hat {T}_\Phi = ({1}/{\sqrt {2}}) (p_1^*\hat {T}_f + p_2^*\hat {T}_g)$, taking
$\hat {T}_\Phi = ({1}/{\sqrt {2}}) (p_1^*\hat {T}_f + p_2^*\hat {T}_g)$, taking ![]() $\hat {\omega } = ({1}/{\sqrt {2}}) ( p_1^* \hat \omega + p_2^*\hat \omega )$ with
$\hat {\omega } = ({1}/{\sqrt {2}}) ( p_1^* \hat \omega + p_2^*\hat \omega )$ with ![]() $p_i: S\times {\mathbb {P}}^1\times {\mathbb {P}}^1 \to S \times {\mathbb {P}}^1$ the projection to the product of
$p_i: S\times {\mathbb {P}}^1\times {\mathbb {P}}^1 \to S \times {\mathbb {P}}^1$ the projection to the product of ![]() $S$ with the
$S$ with the ![]() $i$th factor of
$i$th factor of ![]() ${\mathbb {P}}^1$,
${\mathbb {P}}^1$, ![]() $i = 1,2$. Note that the constant
$i = 1,2$. Note that the constant ![]() $1/\sqrt {2}$ comes from the normalization (4.1).
$1/\sqrt {2}$ comes from the normalization (4.1).
Suppose ![]() $(X \to S, \Phi, \mathcal {L})$ is a family of
$(X \to S, \Phi, \mathcal {L})$ is a family of ![]() $k$-dimensional polarized dynamical systems. Suppose that
$k$-dimensional polarized dynamical systems. Suppose that ![]() $Y$ is closed subvariety of
$Y$ is closed subvariety of ![]() $X$ of codimension equal to
$X$ of codimension equal to ![]() $r$, defining a flat family over
$r$, defining a flat family over ![]() $S$. As defined in [Reference Gauthier and VignyGV19], the bifurcation current for the triple
$S$. As defined in [Reference Gauthier and VignyGV19], the bifurcation current for the triple ![]() $(X, Y, \Phi )$ is defined by
$(X, Y, \Phi )$ is defined by
where ![]() $\pi :X \to S$ is the projection. The bifurcation measure is given by
$\pi :X \to S$ is the projection. The bifurcation measure is given by
on ![]() $S$. The wedge powers are well defined because the current has continuous potentials. Also as a consequence of having a continuous potential, the bifurcation measure
$S$. The wedge powers are well defined because the current has continuous potentials. Also as a consequence of having a continuous potential, the bifurcation measure ![]() $\mu _{\Phi, Y}$ does not charge pluripolar sets in
$\mu _{\Phi, Y}$ does not charge pluripolar sets in ![]() $S$ (see [Reference KlimekKli91, Proposition 4.6.4]).
$S$ (see [Reference KlimekKli91, Proposition 4.6.4]).
Example 4.3 Suppose that ![]() $f$ is an algebraic family of maps on
$f$ is an algebraic family of maps on ![]() ${\mathbb {P}}^1$ of degree
${\mathbb {P}}^1$ of degree ![]() $d > 1$, parameterized by a smooth and irreducible
$d > 1$, parameterized by a smooth and irreducible ![]() $S$. Let
$S$. Let ![]() $Y$ be the critical locus of
$Y$ be the critical locus of ![]() $f$ in
$f$ in ![]() $S \times {\mathbb {P}}^1$. Then the bifurcation current
$S \times {\mathbb {P}}^1$. Then the bifurcation current ![]() $\hat {T}_{f, Y}$ coincides with the bifurcation current
$\hat {T}_{f, Y}$ coincides with the bifurcation current ![]() $\hat {T}_{f, \mathrm {bif}}$ defined above in (2.2), introduced in [Reference DeMarcoDeM01, Reference Dujardin and FavreDF08], and the bifurcation measure coincides with that of [Reference Bassanelli and BertelootBB07].
$\hat {T}_{f, \mathrm {bif}}$ defined above in (2.2), introduced in [Reference DeMarcoDeM01, Reference Dujardin and FavreDF08], and the bifurcation measure coincides with that of [Reference Bassanelli and BertelootBB07].
Example 4.4 For any algebraic family of pairs ![]() $\Phi = (f,g)$ over a smooth and irreducible complex quasiprojective variety
$\Phi = (f,g)$ over a smooth and irreducible complex quasiprojective variety ![]() $S$, with projection
$S$, with projection ![]() $\pi : S\times ({\mathbb {P}}^1)^2 \to S$, we let
$\pi : S\times ({\mathbb {P}}^1)^2 \to S$, we let ![]() $X = S \times ({\mathbb {P}}^1\times {\mathbb {P}}^1)$ and set
$X = S \times ({\mathbb {P}}^1\times {\mathbb {P}}^1)$ and set ![]() $Y = S \times \Delta$, where
$Y = S \times \Delta$, where ![]() $\Delta \subset {\mathbb {P}}^1 \times {\mathbb {P}}^1$ is the diagonal. Then we refer to
$\Delta \subset {\mathbb {P}}^1 \times {\mathbb {P}}^1$ is the diagonal. Then we refer to ![]() $\hat {T}_{\Phi, Y}$ as the pairwise-bifurcation current associated to
$\hat {T}_{\Phi, Y}$ as the pairwise-bifurcation current associated to ![]() $\Phi$ and denote it by
$\Phi$ and denote it by ![]() $\hat {T}_{\Phi,\Delta }$. In the notation of Example 4.2, we have
$\hat {T}_{\Phi,\Delta }$. In the notation of Example 4.2, we have
 \begin{align*} \hat{T}_{\Phi, \Delta} &= \pi_* (\hat{T}_{\Phi}^{\wedge 2} \wedge [S \times \Delta]) \\ &= \pi_* ( p_1^*\hat{T}_f \wedge p_2^* \hat{T}_g \wedge [S \times \Delta] ) \\ &= \pi_*' ( \hat{T}_f \wedge \hat{T}_g ), \end{align*}
\begin{align*} \hat{T}_{\Phi, \Delta} &= \pi_* (\hat{T}_{\Phi}^{\wedge 2} \wedge [S \times \Delta]) \\ &= \pi_* ( p_1^*\hat{T}_f \wedge p_2^* \hat{T}_g \wedge [S \times \Delta] ) \\ &= \pi_*' ( \hat{T}_f \wedge \hat{T}_g ), \end{align*}
where ![]() $\pi '$ denotes the projection from
$\pi '$ denotes the projection from ![]() $S \times {\mathbb {P}}^1$ to
$S \times {\mathbb {P}}^1$ to ![]() $S$. In particular, when
$S$. In particular, when ![]() $S$ is the total space
$S$ is the total space ![]() $\mathrm {Rat}_d\times \mathrm {Rat}_d$, this agrees with the pairwise-bifurcation current
$\mathrm {Rat}_d\times \mathrm {Rat}_d$, this agrees with the pairwise-bifurcation current ![]() $\hat {T}_{\Delta }$ defined in (1.1). The pairwise-bifurcation measure is defined as
$\hat {T}_{\Delta }$ defined in (1.1). The pairwise-bifurcation measure is defined as
4.2 Non-degeneracy and equidistribution
Suppose ![]() $(X \to S, \Phi, {\mathcal {L}})$ is a family of
$(X \to S, \Phi, {\mathcal {L}})$ is a family of ![]() $k$-dimensional polarized dynamical systems. Suppose that
$k$-dimensional polarized dynamical systems. Suppose that ![]() $Y$ is a closed subvariety of
$Y$ is a closed subvariety of ![]() $X$ of codimension equal to
$X$ of codimension equal to ![]() $r$, defining a flat family of subvarieties in
$r$, defining a flat family of subvarieties in ![]() $X$. We say that the triple
$X$. We say that the triple ![]() $(X, Y, \Phi )$ is non-degenerate if the current
$(X, Y, \Phi )$ is non-degenerate if the current
is nonzero on ![]() $X$. This is an exact analog of the notion of non-degeneracy introduced by Habegger in [Reference HabeggerHab13] and studied in general by Gao [Reference GaoGao20a] for subvarieties in families of abelian varieties, where the Betti form is replaced by
$X$. This is an exact analog of the notion of non-degeneracy introduced by Habegger in [Reference HabeggerHab13] and studied in general by Gao [Reference GaoGao20a] for subvarieties in families of abelian varieties, where the Betti form is replaced by ![]() $\hat {T}_{\Phi }$ on the total space
$\hat {T}_{\Phi }$ on the total space ![]() $X$. This notion of non-degeneracy agrees with the one introduced by Yuan and Zhang [Reference Yuan and ZhangYZ21, § 6.2.2] as they demonstrate in [Reference Yuan and ZhangYZ21, Lemma 5.4.4].
$X$. This notion of non-degeneracy agrees with the one introduced by Yuan and Zhang [Reference Yuan and ZhangYZ21, § 6.2.2] as they demonstrate in [Reference Yuan and ZhangYZ21, Lemma 5.4.4].
For a family of hypersurfaces ![]() $Y$, Gauthier, Taflin, and Vigny recently observed a relation between the bifurcation measure and non-degeneracy on a fiber power of
$Y$, Gauthier, Taflin, and Vigny recently observed a relation between the bifurcation measure and non-degeneracy on a fiber power of ![]() $X$ (see [Reference Gauthier, Taflin and VignyGTV23]; compare [Reference YuanYua21, Lemma 4.1]). For any integer
$X$ (see [Reference Gauthier, Taflin and VignyGTV23]; compare [Reference YuanYua21, Lemma 4.1]). For any integer ![]() $m\geq 1$, let
$m\geq 1$, let
be the fiber power of ![]() $\Phi$ acting on the
$\Phi$ acting on the ![]() $m$th fiber power of
$m$th fiber power of ![]() $X$ over
$X$ over ![]() $S$. It is polarized by the line bundle
$S$. It is polarized by the line bundle ![]() $p_1^* {\mathcal {L}}\otimes \cdots \otimes p_m^* {\mathcal {L}}$, where
$p_1^* {\mathcal {L}}\otimes \cdots \otimes p_m^* {\mathcal {L}}$, where ![]() $p_i: X^{(m)} \to X$ is the projection to the
$p_i: X^{(m)} \to X$ is the projection to the ![]() $i$th factor. Let
$i$th factor. Let ![]() $Y^{(m)}$ be the corresponding fiber power of
$Y^{(m)}$ be the corresponding fiber power of ![]() $Y$ over
$Y$ over ![]() $S$. We continue to denote the projection to
$S$. We continue to denote the projection to ![]() $S$ by
$S$ by ![]() $\pi$.
$\pi$.
Proposition 4.5 [Reference Gauthier, Taflin and VignyGTV23, Proposition 1.4]
Suppose ![]() $(X \to S, \Phi, {\mathcal {L}})$ is a family of
$(X \to S, \Phi, {\mathcal {L}})$ is a family of ![]() $k$-dimensional polarized dynamical systems, and let
$k$-dimensional polarized dynamical systems, and let ![]() $m = \dim S$. Assume that
$m = \dim S$. Assume that ![]() $Y$ is a closed hypersurface in
$Y$ is a closed hypersurface in ![]() $X$, defining a flat family of hypersurfaces over
$X$, defining a flat family of hypersurfaces over ![]() $S$. Then the bifurcation measure
$S$. Then the bifurcation measure ![]() $\mu _{\Phi, Y}$ on
$\mu _{\Phi, Y}$ on ![]() $S$ satisfies
$S$ satisfies
In particular, the triple ![]() $(X^{(m)}, Y^{(m)}, \Phi ^{(m)})$ is non-degenerate if and only if the bifurcation measure
$(X^{(m)}, Y^{(m)}, \Phi ^{(m)})$ is non-degenerate if and only if the bifurcation measure ![]() $\mu _{\Phi, Y}$ is nonzero.
$\mu _{\Phi, Y}$ is nonzero.
Proof. The first equality is simply the definition of ![]() $\mu _{\Phi,Y}$, and we need to prove the second. Since the dimension of each fiber of
$\mu _{\Phi,Y}$, and we need to prove the second. Since the dimension of each fiber of ![]() $X \to S$ is
$X \to S$ is ![]() $k$, it follows that
$k$, it follows that ![]() $\hat {T}_\Phi ^{\wedge (k+1)} = 0$ on
$\hat {T}_\Phi ^{\wedge (k+1)} = 0$ on ![]() $X$. Let
$X$. Let ![]() $m = \dim S$, and note that the fibers of
$m = \dim S$, and note that the fibers of ![]() $X^{(m)}\to S$ have dimension
$X^{(m)}\to S$ have dimension ![]() $mk$ and
$mk$ and ![]() $Y^{(m)}$ has codimension
$Y^{(m)}$ has codimension ![]() $m$. Let
$m$. Let ![]() $p_j: X^{(m)} \to X$ be the projection to the
$p_j: X^{(m)} \to X$ be the projection to the ![]() $j$th factor. Then there is a constant
$j$th factor. Then there is a constant ![]() $C>0$ so that
$C>0$ so that
 \begin{align*} \hat{T}_{\Phi^{(m)}}^{\wedge (mk)} &= C (p_1^* \hat{T}_\Phi + \cdots + p_m^* \hat{T}_\Phi)^{\wedge (mk)} \\ &= C \frac{(mk)!}{(k!)^m} \bigwedge_{j=1}^m p_j^* \hat{T}_\Phi^{\wedge k}. \end{align*}
\begin{align*} \hat{T}_{\Phi^{(m)}}^{\wedge (mk)} &= C (p_1^* \hat{T}_\Phi + \cdots + p_m^* \hat{T}_\Phi)^{\wedge (mk)} \\ &= C \frac{(mk)!}{(k!)^m} \bigwedge_{j=1}^m p_j^* \hat{T}_\Phi^{\wedge k}. \end{align*}
Because of the normalization that ![]() $\hat {T}_{\Phi ^{(m)}}^{\wedge (mk)}$ be a probability measure on each slice over
$\hat {T}_{\Phi ^{(m)}}^{\wedge (mk)}$ be a probability measure on each slice over ![]() $t \in S$, we must take
$t \in S$, we must take ![]() $C = {(k!)^m}/{(mk)!}$. On the other hand, we have
$C = {(k!)^m}/{(mk)!}$. On the other hand, we have
 \[ [Y^{(m)}] = \bigwedge_{j=1}^m p_j^*[Y], \]
\[ [Y^{(m)}] = \bigwedge_{j=1}^m p_j^*[Y], \]
so that
 \[ \hat{T}_{\Phi^{(m)}}^{\wedge (mk)} \wedge [Y^{(m)}] = \bigwedge_{j=1}^m \, p_j^* (\hat{T}_\Phi^{\wedge k} \wedge [Y] ) \]
\[ \hat{T}_{\Phi^{(m)}}^{\wedge (mk)} \wedge [Y^{(m)}] = \bigwedge_{j=1}^m \, p_j^* (\hat{T}_\Phi^{\wedge k} \wedge [Y] ) \]
and the conclusion follows.
Now assume that the triple ![]() $(X, Y, \Phi )$ is defined over a number field and is non-degenerate. Yuan and Zhang recently proved an equidistribution theorem in [Reference Yuan and ZhangYZ21] for points of small fiber-wise canonical height in
$(X, Y, \Phi )$ is defined over a number field and is non-degenerate. Yuan and Zhang recently proved an equidistribution theorem in [Reference Yuan and ZhangYZ21] for points of small fiber-wise canonical height in ![]() $Y$, extending a result of Kühne [Reference KühneKüh21]. A closely related result has also recently been obtained by Gauthier [Reference GauthierGau21]. A sequence of points
$Y$, extending a result of Kühne [Reference KühneKüh21]. A closely related result has also recently been obtained by Gauthier [Reference GauthierGau21]. A sequence of points ![]() $y_n \in Y(\overline {\mathbb {Q}})$ is said to be generic if no subsequence lies in a proper, Zariski-closed subset of
$y_n \in Y(\overline {\mathbb {Q}})$ is said to be generic if no subsequence lies in a proper, Zariski-closed subset of ![]() $Y$.
$Y$.
Theorem 4.6 [Reference Yuan and ZhangYZ21, Theorem 6.2.3]
Suppose ![]() $(X \to S, \Phi, {\mathcal {L}})$ is a family of
$(X \to S, \Phi, {\mathcal {L}})$ is a family of ![]() $k$-dimensional polarized dynamical systems over smooth, irreducible, quasiprojective
$k$-dimensional polarized dynamical systems over smooth, irreducible, quasiprojective ![]() $S$, defined over a number field
$S$, defined over a number field ![]() $K$. Suppose that the triple
$K$. Suppose that the triple ![]() $(X, Y, \Phi )$ is non-degenerate, where
$(X, Y, \Phi )$ is non-degenerate, where ![]() $Y\!$ is a closed subvariety of
$Y\!$ is a closed subvariety of ![]() $X$ of codimension
$X$ of codimension ![]() $r$, defining a flat family over
$r$, defining a flat family over ![]() $S$, and also defined over
$S$, and also defined over ![]() $K$. Then for any generic sequence of preperiodic points of
$K$. Then for any generic sequence of preperiodic points of ![]() $\Phi$ in
$\Phi$ in ![]() $Y(\overline {K})$, their
$Y(\overline {K})$, their ![]() $\operatorname {Gal}(\overline {K}/K)$-orbits are uniformly distributed with respect to the measure
$\operatorname {Gal}(\overline {K}/K)$-orbits are uniformly distributed with respect to the measure ![]() $\hat {T}_{\Phi }^{\wedge (k-r+\dim S)} \wedge [Y]$ on
$\hat {T}_{\Phi }^{\wedge (k-r+\dim S)} \wedge [Y]$ on ![]() $X({\mathbb {C}})$. More precisely, given any continuous function
$X({\mathbb {C}})$. More precisely, given any continuous function ![]() $\varphi$ with compact support in
$\varphi$ with compact support in ![]() $X$, and given any generic sequence
$X$, and given any generic sequence ![]() $\{y_n\}$ of points in
$\{y_n\}$ of points in ![]() $Y(\overline {K})$ that are preperiodic for
$Y(\overline {K})$ that are preperiodic for ![]() $\Phi$, we have
$\Phi$, we have
 \[ \frac{1}{\# \operatorname{Gal}(\overline{K}/K)\cdot y_n} \sum_{y \in \operatorname{Gal}(\overline{K}/K)\cdot y_n} \varphi(y) \longrightarrow \frac{1}{\operatorname{vol}(Y)} \int_{X({\mathbb{C}})} \varphi (\hat{T}_{\Phi}^{\wedge (k-r+\dim S)} \wedge [Y]), \]
\[ \frac{1}{\# \operatorname{Gal}(\overline{K}/K)\cdot y_n} \sum_{y \in \operatorname{Gal}(\overline{K}/K)\cdot y_n} \varphi(y) \longrightarrow \frac{1}{\operatorname{vol}(Y)} \int_{X({\mathbb{C}})} \varphi (\hat{T}_{\Phi}^{\wedge (k-r+\dim S)} \wedge [Y]), \]
as ![]() $n\to \infty$ where
$n\to \infty$ where ![]() $\operatorname {vol}(Y) = \int _{X({\mathbb {C}})} \hat {T}_{\Phi }^{\wedge (k-r+\dim S)} \wedge [Y]$.
$\operatorname {vol}(Y) = \int _{X({\mathbb {C}})} \hat {T}_{\Phi }^{\wedge (k-r+\dim S)} \wedge [Y]$.
4.3 A repelling-cycle criterion to show non-degeneracy
Suppose ![]() $(\pi : X \to S, \Phi, {\mathcal {L}})$ is a family of
$(\pi : X \to S, \Phi, {\mathcal {L}})$ is a family of ![]() $k$-dimensional polarized dynamical systems. Now suppose that
$k$-dimensional polarized dynamical systems. Now suppose that ![]() $Y$ is a closed subvariety of
$Y$ is a closed subvariety of ![]() $X$ of codimension
$X$ of codimension ![]() $m = \dim S$ in
$m = \dim S$ in ![]() $X$, defining a flat family of subvarieties with codimension
$X$, defining a flat family of subvarieties with codimension ![]() $m$. We say that a point
$m$. We say that a point ![]() $y_0 \in Y({\mathbb {C}})$ is a rigid repeller for
$y_0 \in Y({\mathbb {C}})$ is a rigid repeller for ![]() $(X, Y, \Phi )$ if:
$(X, Y, \Phi )$ if:
(1) some iterate
 $x_0 = \Phi ^{n_0}(y_0)$ is a repelling periodic point for
$x_0 = \Phi ^{n_0}(y_0)$ is a repelling periodic point for  $\Phi _{s_0}$, where
$\Phi _{s_0}$, where  $s_0 = \pi (y_0)$;
$s_0 = \pi (y_0)$;(2) the point
 $y_0$ lies in the support of the equilibrium measure
$y_0$ lies in the support of the equilibrium measure  $\mu _{s_0} := \big (\hat {T}_\Phi |_{X_{s_0}}\big )^k$ in the fiber
$\mu _{s_0} := \big (\hat {T}_\Phi |_{X_{s_0}}\big )^k$ in the fiber  $X_{s_0}$; and
$X_{s_0}$; and(3) there is a holomorphic section
 $\eta$ over a neighborhood of
$\eta$ over a neighborhood of  $s_0$ in
$s_0$ in  $S$ parameterizing a repelling periodic point of
$S$ parameterizing a repelling periodic point of  $\Phi _s$, with
$\Phi _s$, with  $\eta (s_0) = x_0$, so that
$\eta (s_0) = x_0$, so that  $x_0$ is an isolated point of the intersection of
$x_0$ is an isolated point of the intersection of  $\Phi ^{n_0}(Y)$ with the image of
$\Phi ^{n_0}(Y)$ with the image of  $\eta$.
$\eta$.
Remark 4.7 If ![]() $\Phi = (f,g)$ is an algebraic family of pairs over
$\Phi = (f,g)$ is an algebraic family of pairs over ![]() $S$, as defined in § 3 and Example 4.1, with
$S$, as defined in § 3 and Example 4.1, with ![]() $m = \dim S$, a rigid repeller for the fiber product
$m = \dim S$, a rigid repeller for the fiber product ![]() $\Phi ^{(m)}: X^{(m)} \to X^{(m)}$ in
$\Phi ^{(m)}: X^{(m)} \to X^{(m)}$ in ![]() $Y = S \times \Delta ^m \subset X^{(m)}$, where
$Y = S \times \Delta ^m \subset X^{(m)}$, where ![]() $X=S\times {\mathbb {P}}^1\times {\mathbb {P}}^1$, coincides with the notion of the rigid
$X=S\times {\mathbb {P}}^1\times {\mathbb {P}}^1$, coincides with the notion of the rigid ![]() $m$-repeller for
$m$-repeller for ![]() $\Phi$ from the Introduction. In this setting, the repelling periodic points and their preimages are always in the support of the equilibrium measure.
$\Phi$ from the Introduction. In this setting, the repelling periodic points and their preimages are always in the support of the equilibrium measure.
The next proposition is a minor modification of [Reference Gauthier and VignyGV19, Lemma 4.8], and the proof is very similar to that of [Reference Berteloot, Bianchi and DupontBBD18, Proposition 3.7].
Proposition 4.8 Suppose ![]() $(X \to S, \Phi, {\mathcal {L}})$ is a family of
$(X \to S, \Phi, {\mathcal {L}})$ is a family of ![]() $k$-dimensional polarized dynamical systems over quasiprojective
$k$-dimensional polarized dynamical systems over quasiprojective ![]() $S$. Suppose that
$S$. Suppose that ![]() $Y$ is a closed subvariety of
$Y$ is a closed subvariety of ![]() $X$ of codimension equal to
$X$ of codimension equal to ![]() $\dim S$, defining a flat family over
$\dim S$, defining a flat family over ![]() $S$. Suppose there exists a rigid repeller for
$S$. Suppose there exists a rigid repeller for ![]() $(X, Y, \Phi )$ at
$(X, Y, \Phi )$ at ![]() $y_0 \in Y({\mathbb {C}})$. Then
$y_0 \in Y({\mathbb {C}})$. Then ![]() $y_0$ lies in the support of the (nonzero) measure
$y_0$ lies in the support of the (nonzero) measure
on ![]() $X({\mathbb {C}})$. In particular, the triple
$X({\mathbb {C}})$. In particular, the triple ![]() $(X, Y, \Phi )$ is non-degenerate.
$(X, Y, \Phi )$ is non-degenerate.
Proof. Let ![]() $d \geq 2$ be the polarization degree of
$d \geq 2$ be the polarization degree of ![]() $\Phi$. Let
$\Phi$. Let ![]() $x_0 = \Phi ^{n_0}(y_0) \in \Phi ^{n_0}(Y)$ be a repelling periodic point in the orbit of
$x_0 = \Phi ^{n_0}(y_0) \in \Phi ^{n_0}(Y)$ be a repelling periodic point in the orbit of ![]() $y_0$. Let
$y_0$. Let ![]() $s_0 = \pi (x_0) \in S$. Since
$s_0 = \pi (x_0) \in S$. Since ![]() $y_0$ is in the support of the equilibrium measure
$y_0$ is in the support of the equilibrium measure ![]() $\mu _{s_0} = (\hat {T}_\Phi |_{X_{s_0}})^k$, it follows that
$\mu _{s_0} = (\hat {T}_\Phi |_{X_{s_0}})^k$, it follows that ![]() $x_0$ is also in this support. Let
$x_0$ is also in this support. Let ![]() $p$ be the period of
$p$ be the period of ![]() $x_0$. Let
$x_0$. Let ![]() $\eta$ denote the parameterization of the nearby repelling periodic points over a neighborhood
$\eta$ denote the parameterization of the nearby repelling periodic points over a neighborhood ![]() $U$ of
$U$ of ![]() $s_0$, and let
$s_0$, and let ![]() $\Gamma _\eta$ denote its image in
$\Gamma _\eta$ denote its image in ![]() $X$. By hypothesis,
$X$. By hypothesis, ![]() $x_0$ is an isolated point of the intersection of
$x_0$ is an isolated point of the intersection of ![]() $\Gamma _\eta$ with
$\Gamma _\eta$ with ![]() $\Phi ^{n}(Y_0)$.
$\Phi ^{n}(Y_0)$.
Shrinking ![]() $U$ if necessary, there exists a tubular neighborhood
$U$ if necessary, there exists a tubular neighborhood ![]() $N$ of
$N$ of ![]() $\Gamma _\eta$ in
$\Gamma _\eta$ in ![]() $\pi ^{-1}(U)$ and a constant
$\pi ^{-1}(U)$ and a constant ![]() $K>1$ so that
$K>1$ so that
for all ![]() $x \in N \cap X_s$ and all
$x \in N \cap X_s$ and all ![]() $s \in U$ and for any reasonable choice of distance function
$s \in U$ and for any reasonable choice of distance function ![]() $d_{X_s}$ on the fibers. In particular, there exists a nested sequence of tubular neighborhoods
$d_{X_s}$ on the fibers. In particular, there exists a nested sequence of tubular neighborhoods ![]() $N_n \subset N$ around
$N_n \subset N$ around ![]() $\Gamma _\eta \cap \pi ^{-1}(U)$, for
$\Gamma _\eta \cap \pi ^{-1}(U)$, for ![]() $n\geq 1$, so that
$n\geq 1$, so that ![]() $\Phi ^{np}: N_n \to N$ is proper and one-to-one. Then for all integers
$\Phi ^{np}: N_n \to N$ is proper and one-to-one. Then for all integers ![]() $n\geq 0$,
$n\geq 0$,
 \begin{align*} d^{npk} \int_{N_n} \hat{T}_\Phi^{\wedge k} \wedge [\Phi^{n_0}(Y)] &= \int_{N_n} (\Phi^{np})^* \hat{T}_\Phi^{\wedge k} \wedge [\Phi^{n_0}(Y)] \\ &= \int_N \hat{T}_\Phi^{\wedge k} \wedge (\Phi^{np})_* [\Phi^{n_0}(Y)] \\ &= \int_N \hat{T}_\Phi^{\wedge k} \wedge [\Phi^{n_0+np}(Y)]. \end{align*}
\begin{align*} d^{npk} \int_{N_n} \hat{T}_\Phi^{\wedge k} \wedge [\Phi^{n_0}(Y)] &= \int_{N_n} (\Phi^{np})^* \hat{T}_\Phi^{\wedge k} \wedge [\Phi^{n_0}(Y)] \\ &= \int_N \hat{T}_\Phi^{\wedge k} \wedge (\Phi^{np})_* [\Phi^{n_0}(Y)] \\ &= \int_N \hat{T}_\Phi^{\wedge k} \wedge [\Phi^{n_0+np}(Y)]. \end{align*}
On the other hand, we have
for some ![]() $\alpha >0$, in the weak sense of currents, where
$\alpha >0$, in the weak sense of currents, where ![]() $\chi _N$ is the indicator function. Indeed, since
$\chi _N$ is the indicator function. Indeed, since ![]() $N\cap \Phi ^{n_0}(Y) \cap \Gamma _\eta = \{x_0\}$, the vertical expansion of
$N\cap \Phi ^{n_0}(Y) \cap \Gamma _\eta = \{x_0\}$, the vertical expansion of ![]() $\Phi ^p$ shows that the limit must be supported in the fiber
$\Phi ^p$ shows that the limit must be supported in the fiber ![]() $X_{s_0}$. As the limit current is closed and positive and nonzero, it must be (a scalar multiple of) the current of integration along
$X_{s_0}$. As the limit current is closed and positive and nonzero, it must be (a scalar multiple of) the current of integration along ![]() $X_{s_0}\cap N$. Finally, since
$X_{s_0}\cap N$. Finally, since ![]() $x_0$ is in the support of the measure
$x_0$ is in the support of the measure ![]() $\mu _{s_0} = \hat {T}_\Phi ^{\wedge k}|_{X_{s_0}}$, we have
$\mu _{s_0} = \hat {T}_\Phi ^{\wedge k}|_{X_{s_0}}$, we have
so that
for all sufficiently large ![]() $n$.
$n$.
Now choose an open set ![]() $V$ around
$V$ around ![]() $y_0$ so that
$y_0$ so that ![]() $\Phi ^{n_0}: V \to N$ is proper. Then
$\Phi ^{n_0}: V \to N$ is proper. Then
 \begin{align*} d^{n_0k} \int_V \hat{T}_\Phi^{\wedge k} \wedge [Y] &= \int_V (\Phi^n)^* \hat{T}_\Phi^{\wedge k} \wedge [Y] \\ &= \int_{N} \hat{T}_\Phi^{\wedge k} \wedge (\Phi^{n_0})_* [Y] \\ &\geq \int_{N} \hat{T}_\Phi^{\wedge k} \wedge [\Phi^{n_0}(Y)] \\ &\geq \int_{N_n} \hat{T}_\Phi^{\wedge k} \wedge [\Phi^{n_0}(Y)] \end{align*}
\begin{align*} d^{n_0k} \int_V \hat{T}_\Phi^{\wedge k} \wedge [Y] &= \int_V (\Phi^n)^* \hat{T}_\Phi^{\wedge k} \wedge [Y] \\ &= \int_{N} \hat{T}_\Phi^{\wedge k} \wedge (\Phi^{n_0})_* [Y] \\ &\geq \int_{N} \hat{T}_\Phi^{\wedge k} \wedge [\Phi^{n_0}(Y)] \\ &\geq \int_{N_n} \hat{T}_\Phi^{\wedge k} \wedge [\Phi^{n_0}(Y)] \end{align*}
for all ![]() $n\geq 1$. Therefore,
$n\geq 1$. Therefore,
Now let ![]() $S$ be a smooth and irreducible complex quasiprojective variety. Recall that an algebraic family of pairs
$S$ be a smooth and irreducible complex quasiprojective variety. Recall that an algebraic family of pairs ![]() $\Phi = (f,g)$ was defined in § 3, and the pairwise-bifurcation current was defined in Example 4.4.
$\Phi = (f,g)$ was defined in § 3, and the pairwise-bifurcation current was defined in Example 4.4.
Corollary 4.9 Let ![]() $S$ be a smooth and irreducible complex quasiprojective variety of dimension
$S$ be a smooth and irreducible complex quasiprojective variety of dimension ![]() $m$. Suppose that
$m$. Suppose that ![]() $\Phi = (f,g)$ is an algebraic family of pairs over
$\Phi = (f,g)$ is an algebraic family of pairs over ![]() $S$. If there exists a rigid
$S$. If there exists a rigid ![]() $m$-repeller at some parameter
$m$-repeller at some parameter ![]() $s_0 \in S({\mathbb {C}})$, then the pairwise-bifurcation measure
$s_0 \in S({\mathbb {C}})$, then the pairwise-bifurcation measure ![]() $\mu _{\Phi, \Delta }$ is nonzero on
$\mu _{\Phi, \Delta }$ is nonzero on ![]() $S({\mathbb {C}})$.
$S({\mathbb {C}})$.
Proof. As observed above, a rigid ![]() $m$-repeller for
$m$-repeller for ![]() $\Phi$ implies there is a rigid repeller for the
$\Phi$ implies there is a rigid repeller for the ![]() $m$th fiber power
$m$th fiber power ![]() $\Phi ^{(m)}$ in
$\Phi ^{(m)}$ in ![]() $S \times \Delta ^m \subset S \times ({\mathbb {P}}^1\times {\mathbb {P}}^1)^m$. Proposition 4.8 implies that
$S \times \Delta ^m \subset S \times ({\mathbb {P}}^1\times {\mathbb {P}}^1)^m$. Proposition 4.8 implies that ![]() $(\hat {T}_{\Phi ^{(m)}})^{\wedge 2m} \wedge [S \times \Delta ^m]$ is nonzero. Proposition 4.5 then implies that the measure
$(\hat {T}_{\Phi ^{(m)}})^{\wedge 2m} \wedge [S \times \Delta ^m]$ is nonzero. Proposition 4.5 then implies that the measure ![]() $\mu _{\Phi, \Delta }$ is nonzero on
$\mu _{\Phi, \Delta }$ is nonzero on ![]() $S$.
$S$.
5. Proof of Theorem 1.8
We will deduce Theorem 1.8 from the following result, combined with the material of the previous section. Recall that the pairwise-bifurcation measure ![]() $\mu _{\Phi, \Delta }$ was defined in Example 4.4.
$\mu _{\Phi, \Delta }$ was defined in Example 4.4.
Theorem 5.1 Fix degree ![]() $d \geq 2$, and suppose that
$d \geq 2$, and suppose that ![]() $S$ is a smooth, irreducible quasiprojective variety of dimension
$S$ is a smooth, irreducible quasiprojective variety of dimension ![]() $m$ parameterizing an algebraic family of pairs
$m$ parameterizing an algebraic family of pairs ![]() $\Phi = (f,g)$ of degree
$\Phi = (f,g)$ of degree ![]() $d\ge 2$ over
$d\ge 2$ over ![]() $S$, all defined over
$S$, all defined over ![]() $\overline {\mathbb {Q}}$. Assume that
$\overline {\mathbb {Q}}$. Assume that ![]() $f$ and
$f$ and ![]() $g$ are not both conjugate to
$g$ are not both conjugate to ![]() $z^{\pm d}$ over the algebraic closure of
$z^{\pm d}$ over the algebraic closure of ![]() $k = \overline {\mathbb {Q}}(S)$. If the pairwise-bifurcation measure
$k = \overline {\mathbb {Q}}(S)$. If the pairwise-bifurcation measure ![]() $\mu _{\Phi, \Delta }$ is nonzero on
$\mu _{\Phi, \Delta }$ is nonzero on ![]() $S({\mathbb {C}})$, then the set of points
$S({\mathbb {C}})$, then the set of points
is not Zariski dense in ![]() $S \times ({\mathbb {P}}^1)^{m+1}$.
$S \times ({\mathbb {P}}^1)^{m+1}$.
To prove Theorem 5.1, we follow the proof strategy from [Reference Mavraki and SchmidtMS22], which exploits the product structure of ![]() $(f,g)$ acting on
$(f,g)$ acting on ![]() ${\mathbb {P}}^1\times {\mathbb {P}}^1$ and relies on the general equidistribution result of Yuan and Zhang [Reference Yuan and ZhangYZ21], stated above as Theorem 4.6. As a consequence, we infer the following result.
${\mathbb {P}}^1\times {\mathbb {P}}^1$ and relies on the general equidistribution result of Yuan and Zhang [Reference Yuan and ZhangYZ21], stated above as Theorem 4.6. As a consequence, we infer the following result.
Theorem 5.2 Fix degree ![]() $d \geq 2$, and suppose that
$d \geq 2$, and suppose that ![]() $S$ is a smooth, irreducible quasiprojective variety parameterizing an algebraic family of pairs
$S$ is a smooth, irreducible quasiprojective variety parameterizing an algebraic family of pairs ![]() $\Phi = (f,g)$ of degree
$\Phi = (f,g)$ of degree ![]() $d\ge 2$ over
$d\ge 2$ over ![]() $S$, all defined over
$S$, all defined over ![]() $\overline {\mathbb {Q}}$. Assume that
$\overline {\mathbb {Q}}$. Assume that ![]() $f$ and
$f$ and ![]() $g$ are not both conjugate to
$g$ are not both conjugate to ![]() $z^{\pm d}$ over the algebraic closure of
$z^{\pm d}$ over the algebraic closure of ![]() $k = \overline {\mathbb {Q}}(S)$. If the pairwise-bifurcation measure
$k = \overline {\mathbb {Q}}(S)$. If the pairwise-bifurcation measure ![]() $\mu _{\Phi, \Delta }$ is nonzero on
$\mu _{\Phi, \Delta }$ is nonzero on ![]() $S({\mathbb {C}})$, then there exist a Zariski-closed proper subvariety
$S({\mathbb {C}})$, then there exist a Zariski-closed proper subvariety ![]() $V\subset S$ defined over
$V\subset S$ defined over ![]() $\overline {\mathbb {Q}}$ and
$\overline {\mathbb {Q}}$ and ![]() $M >0$ such that
$M >0$ such that
for all ![]() $s\in (S\setminus V)({\mathbb {C}})$.
$s\in (S\setminus V)({\mathbb {C}})$.
5.1 Product structure
Let ![]() $\Phi = (f,g)$ act on
$\Phi = (f,g)$ act on ![]() ${\mathbb {P}}^1\times {\mathbb {P}}^1$, defined over the field
${\mathbb {P}}^1\times {\mathbb {P}}^1$, defined over the field ![]() $k = \overline {\mathbb {Q}}(S)$. Let
$k = \overline {\mathbb {Q}}(S)$. Let ![]() $\Delta \subset {\mathbb {P}}^1\times {\mathbb {P}}^1$ be the diagonal. For
$\Delta \subset {\mathbb {P}}^1\times {\mathbb {P}}^1$ be the diagonal. For ![]() $m = \dim S$, we let
$m = \dim S$, we let ![]() $\Phi ^{(m)}$ denote the product map acting on
$\Phi ^{(m)}$ denote the product map acting on ![]() $({\mathbb {P}}^1 \times {\mathbb {P}}^1)^m$ over
$({\mathbb {P}}^1 \times {\mathbb {P}}^1)^m$ over ![]() $k$. Following [Reference Mavraki and SchmidtMS22], we consider the product of
$k$. Following [Reference Mavraki and SchmidtMS22], we consider the product of ![]() $({\mathbb {P}}^1\times {\mathbb {P}}^1)^{m}$ with another copy of
$({\mathbb {P}}^1\times {\mathbb {P}}^1)^{m}$ with another copy of ![]() ${\mathbb {P}}^1$, acted on by
${\mathbb {P}}^1$, acted on by ![]() $f$ or by
$f$ or by ![]() $g$. This defines maps over
$g$. This defines maps over ![]() ${\mathbb {C}}$ as
${\mathbb {C}}$ as
 \begin{gather*} (\Phi^{(m)},f): S \times ({\mathbb{P}}^1)^{2m + 1} \to S \times ({\mathbb{P}}^1)^{2m + 1}\\ (s, z_1, \ldots, z_{2m + 1}) \mapsto (s, f_s(z_1), g_s(z_2), f_s(z_3), \ldots, g_s(z_{2 m}), f_s(z_{2m + 1})) \end{gather*}
\begin{gather*} (\Phi^{(m)},f): S \times ({\mathbb{P}}^1)^{2m + 1} \to S \times ({\mathbb{P}}^1)^{2m + 1}\\ (s, z_1, \ldots, z_{2m + 1}) \mapsto (s, f_s(z_1), g_s(z_2), f_s(z_3), \ldots, g_s(z_{2 m}), f_s(z_{2m + 1})) \end{gather*}
and
 \begin{gather*} (\Phi^{(m)},g): S \times ({\mathbb{P}}^1)^{2m + 1} \to S \times ({\mathbb{P}}^1)^{2m +1}\\ (s, z_1, \ldots, z_{2m + 1}) \mapsto (s, f_s(z_1), g_s(z_2), f_s(z_3), \ldots, g_s(z_{2 \dim S}), g_s(z_{2m + 1})). \end{gather*}
\begin{gather*} (\Phi^{(m)},g): S \times ({\mathbb{P}}^1)^{2m + 1} \to S \times ({\mathbb{P}}^1)^{2m +1}\\ (s, z_1, \ldots, z_{2m + 1}) \mapsto (s, f_s(z_1), g_s(z_2), f_s(z_3), \ldots, g_s(z_{2 \dim S}), g_s(z_{2m + 1})). \end{gather*}
Let
be the projection forgetting the final factor of ![]() ${\mathbb {P}}^1$. Let
${\mathbb {P}}^1$. Let
denote the projection forgetting the intermediate factor.
Proposition 5.3 Let ![]() $S$ be an irreducible quasiprojective complex algebraic variety of dimension
$S$ be an irreducible quasiprojective complex algebraic variety of dimension ![]() $m$, and suppose
$m$, and suppose ![]() $\Phi = (f,g)$ is an algebraic family of pairs of degree
$\Phi = (f,g)$ is an algebraic family of pairs of degree ![]() $d>1$ over
$d>1$ over ![]() $S$. We have
$S$. We have
where
Similarly for ![]() $g$ and
$g$ and
Consequently, if the bifurcation measure ![]() $\mu _{\Phi, \Delta }$ is nonzero for a family of pairs
$\mu _{\Phi, \Delta }$ is nonzero for a family of pairs ![]() $\Phi = (f,g)$ parameterized by
$\Phi = (f,g)$ parameterized by ![]() $S$, then
$S$, then ![]() $M_f$ and
$M_f$ and ![]() $M_g$ are nonzero.
$M_g$ are nonzero.
Proof. Suppose that ![]() $f$ is an algebraic family of maps on
$f$ is an algebraic family of maps on ![]() ${\mathbb {P}}^1$ over
${\mathbb {P}}^1$ over ![]() $S$. Then
$S$. Then ![]() $\hat {T}_f$ on
$\hat {T}_f$ on ![]() $S \times {\mathbb {P}}^1$ satisfies
$S \times {\mathbb {P}}^1$ satisfies ![]() $\hat {T}_f^{\wedge 2} = 0$. It follows that, for any fiber product of such maps,
$\hat {T}_f^{\wedge 2} = 0$. It follows that, for any fiber product of such maps, ![]() $(f_1, \ldots, f_\ell )$ on
$(f_1, \ldots, f_\ell )$ on ![]() $({\mathbb {P}}^1)^\ell$ over
$({\mathbb {P}}^1)^\ell$ over ![]() $S$, we have
$S$, we have
for the projections ![]() $q_i: S\times ({\mathbb {P}}^1)^\ell \to S\times {\mathbb {P}}^1$. In the setting of the proposition, it follows that
$q_i: S\times ({\mathbb {P}}^1)^\ell \to S\times {\mathbb {P}}^1$. In the setting of the proposition, it follows that
and
The first statements of the proposition follow. Finally, since ![]() $\Delta \subset {\mathbb {P}}^1\times {\mathbb {P}}^1$ is a hypersurface, we know from Proposition 4.5 that
$\Delta \subset {\mathbb {P}}^1\times {\mathbb {P}}^1$ is a hypersurface, we know from Proposition 4.5 that ![]() $\mu _{\Phi, \Delta }$ is nonzero if and only if
$\mu _{\Phi, \Delta }$ is nonzero if and only if
In this case, we see immediately that ![]() $M_f$ and
$M_f$ and ![]() $M_g$ are also nonzero.
$M_g$ are also nonzero.
5.2 Proof of Theorem 5.1
Recall that a sequence of points ![]() $z_n$ in a variety
$z_n$ in a variety ![]() $Z$ is said to be generic if no subsequence lies in a proper, Zariski-closed subset of
$Z$ is said to be generic if no subsequence lies in a proper, Zariski-closed subset of ![]() $Z$.
$Z$.
Let ![]() $m=\dim _{\mathbb {C}} S$. Note that the set
$m=\dim _{\mathbb {C}} S$. Note that the set
in the statement of Theorem 5.1 is naturally identified with the set
for the ![]() $(m+1)$th fiber power of
$(m+1)$th fiber power of ![]() $\Phi$ over
$\Phi$ over ![]() $S$.
$S$.
Let ![]() $K$ be a number field over which
$K$ be a number field over which ![]() $\Phi$ and
$\Phi$ and ![]() $S$ are defined. Suppose, towards a contradiction, that
$S$ are defined. Suppose, towards a contradiction, that ![]() $\mathrm {Preper}(\Phi ^{(m+1)})$ is Zariski dense in
$\mathrm {Preper}(\Phi ^{(m+1)})$ is Zariski dense in ![]() $S(\overline {K})\times \Delta ^{m+1}$. Via the projection of
$S(\overline {K})\times \Delta ^{m+1}$. Via the projection of ![]() $\Delta \subset {\mathbb {P}}^1\times {\mathbb {P}}^1$ to the component
$\Delta \subset {\mathbb {P}}^1\times {\mathbb {P}}^1$ to the component ![]() ${\mathbb {P}}^1$'s, these preperiodic points of
${\mathbb {P}}^1$'s, these preperiodic points of ![]() $\Phi ^{(m+1)}$ in
$\Phi ^{(m+1)}$ in ![]() $S\times \Delta ^{m+1}$ project to define a generic sequence of points in
$S\times \Delta ^{m+1}$ project to define a generic sequence of points in ![]() $(S\times \Delta ^{m}\times {\mathbb {P}}^1)(\overline {K})$ that are preperiodic for both the maps
$(S\times \Delta ^{m}\times {\mathbb {P}}^1)(\overline {K})$ that are preperiodic for both the maps ![]() $(\Phi ^{(\dim S)}, f)$ and
$(\Phi ^{(\dim S)}, f)$ and ![]() $(\Phi ^{(\dim S)}, g)$. Since the pairwise-bifurcation measure
$(\Phi ^{(\dim S)}, g)$. Since the pairwise-bifurcation measure ![]() $\mu _{\Phi, \Delta }$ is nonzero on
$\mu _{\Phi, \Delta }$ is nonzero on ![]() $S({\mathbb {C}})$, we know from Proposition 5.3 that the measures
$S({\mathbb {C}})$, we know from Proposition 5.3 that the measures ![]() $M_g$ and
$M_g$ and ![]() $M_f$ are nonzero on
$M_f$ are nonzero on ![]() $( S\times ({\mathbb {P}}^1\times {\mathbb {P}}^1)^m\times {\mathbb {P}}^1)({\mathbb {C}})$. In other words, setting
$( S\times ({\mathbb {P}}^1\times {\mathbb {P}}^1)^m\times {\mathbb {P}}^1)({\mathbb {C}})$. In other words, setting
the triples ![]() $(X, Y, (\Phi ^{(m)},f))$ and
$(X, Y, (\Phi ^{(m)},f))$ and ![]() $(X, Y, (\Phi ^{(m)},g))$ are non-degenerate. By Theorem 4.6, it follows that the
$(X, Y, (\Phi ^{(m)},g))$ are non-degenerate. By Theorem 4.6, it follows that the ![]() $\operatorname {Gal}(\overline {K}/K)$-orbits of these preperiodic points must be uniformly distributed with respect to the measures
$\operatorname {Gal}(\overline {K}/K)$-orbits of these preperiodic points must be uniformly distributed with respect to the measures ![]() $M_f$ and
$M_f$ and ![]() $M_g$. Consequently, we have
$M_g$. Consequently, we have ![]() $M_f = M_g$ in
$M_f = M_g$ in ![]() $X({\mathbb {C}})$.
$X({\mathbb {C}})$.
Now let ![]() $p_1: S \times ({\mathbb {P}}^1\times {\mathbb {P}}^1)^{m}\times {\mathbb {P}}^1 \to S \times ({\mathbb {P}}^1\times {\mathbb {P}}^1)^{m}$ be the projection forgetting the final factor of
$p_1: S \times ({\mathbb {P}}^1\times {\mathbb {P}}^1)^{m}\times {\mathbb {P}}^1 \to S \times ({\mathbb {P}}^1\times {\mathbb {P}}^1)^{m}$ be the projection forgetting the final factor of ![]() ${\mathbb {P}}^1$, as in Proposition 5.3. By slicing
${\mathbb {P}}^1$, as in Proposition 5.3. By slicing ![]() $M_f$ and
$M_f$ and ![]() $M_g$, we conclude that
$M_g$, we conclude that
for every continuous and compactly supported function ![]() $\varphi$ on
$\varphi$ on ![]() $S\times ({\mathbb {P}}^1)^{2m+1}$ and the
$S\times ({\mathbb {P}}^1)^{2m+1}$ and the ![]() $R$ of Proposition 5.3. Here,
$R$ of Proposition 5.3. Here, ![]() $\pi : S\times ({\mathbb {P}}^1)^m \to S$ denotes the projection to the base, and
$\pi : S\times ({\mathbb {P}}^1)^m \to S$ denotes the projection to the base, and ![]() $\mu _{f_{\pi (t)}}$ and
$\mu _{f_{\pi (t)}}$ and ![]() $\mu _{g_{\pi (t)}}$ are the measures of maximal entropy introduced in § 2.1. But since
$\mu _{g_{\pi (t)}}$ are the measures of maximal entropy introduced in § 2.1. But since ![]() $\pi _*R = \mu _{\Phi, \Delta }$, we infer that
$\pi _*R = \mu _{\Phi, \Delta }$, we infer that
on ![]() ${\mathbb {P}}^1$ for
${\mathbb {P}}^1$ for ![]() $\mu _{\Phi, \Delta }$-almost every parameter
$\mu _{\Phi, \Delta }$-almost every parameter ![]() $s \in S({\mathbb {C}})$. Indeed, suppose there exists
$s \in S({\mathbb {C}})$. Indeed, suppose there exists ![]() $b \in S({\mathbb {C}})$ with
$b \in S({\mathbb {C}})$ with ![]() $\mu _{f_b} \not = \mu _{g_b}$ and so that
$\mu _{f_b} \not = \mu _{g_b}$ and so that ![]() $\mu _{\Phi,\Delta }(U) >0$ for every open neighborhood
$\mu _{\Phi,\Delta }(U) >0$ for every open neighborhood ![]() $U$ of
$U$ of ![]() $b$. Then we can find a continuous function
$b$. Then we can find a continuous function ![]() $\psi$ on
$\psi$ on ![]() ${\mathbb {P}}^1({\mathbb {C}})$ such that
${\mathbb {P}}^1({\mathbb {C}})$ such that ![]() $\int \psi \mu _{f_b} \neq \int \psi \mu _{g_b}$. By continuity of the measures we find that
$\int \psi \mu _{f_b} \neq \int \psi \mu _{g_b}$. By continuity of the measures we find that ![]() $\int \psi \mu _{f_t} \neq \int \psi \mu _{g_t}$ for all
$\int \psi \mu _{f_t} \neq \int \psi \mu _{g_t}$ for all ![]() $t$ in a neighborhood
$t$ in a neighborhood ![]() $U$ of
$U$ of ![]() $b$. Therefore, setting
$b$. Therefore, setting ![]() $\varphi (t, x_1, \ldots, x_{2m}, x_{2m+1}) = h_b(t) \psi (x_{2m+1})$ on
$\varphi (t, x_1, \ldots, x_{2m}, x_{2m+1}) = h_b(t) \psi (x_{2m+1})$ on ![]() $S \times ({\mathbb {P}}^1)^{2m+1}$ for a bump function
$S \times ({\mathbb {P}}^1)^{2m+1}$ for a bump function ![]() $h_b$ supported in
$h_b$ supported in ![]() $U$, the equality (5.1) will fail.
$U$, the equality (5.1) will fail.
Now we use the hypothesis that ![]() $f$ and
$f$ and ![]() $g$ are not both conjugate to a power map
$g$ are not both conjugate to a power map ![]() $z^{\pm d}$ over all of
$z^{\pm d}$ over all of ![]() $S$. Let
$S$. Let ![]() $V \subset S$ be the (possibly empty) proper subvariety over which the maps
$V \subset S$ be the (possibly empty) proper subvariety over which the maps ![]() $f$ and
$f$ and ![]() $g$ are both conjugate to
$g$ are both conjugate to ![]() $\pm z^d$. It follows from Theorem 2.1 that
$\pm z^d$. It follows from Theorem 2.1 that ![]() $\mathrm {Preper}(f_s) = \mathrm {Preper}(g_s)$ for all
$\mathrm {Preper}(f_s) = \mathrm {Preper}(g_s)$ for all ![]() $s\in (\operatorname {supp} \mu _{\Phi, \Delta } \setminus V)({\mathbb {C}})$. As
$s\in (\operatorname {supp} \mu _{\Phi, \Delta } \setminus V)({\mathbb {C}})$. As ![]() $\mu _{\Phi,\Delta }$ does not charge pluripolar sets, we conclude that
$\mu _{\Phi,\Delta }$ does not charge pluripolar sets, we conclude that ![]() $\mathrm {Preper}(f_s) = \mathrm {Preper}(g_s)$ for all
$\mathrm {Preper}(f_s) = \mathrm {Preper}(g_s)$ for all ![]() $s \in (S \setminus V)({\mathbb {C}})$. Indeed, the preperiodic points of
$s \in (S \setminus V)({\mathbb {C}})$. Indeed, the preperiodic points of ![]() $f$ or
$f$ or ![]() $g$ each form a countable union of hypersurfaces in
$g$ each form a countable union of hypersurfaces in ![]() $(S\setminus V) \times {\mathbb {P}}^1$. For each irreducible hypersurface
$(S\setminus V) \times {\mathbb {P}}^1$. For each irreducible hypersurface ![]() $P \subset S\times {\mathbb {P}}^1$ which is preperiodic for
$P \subset S\times {\mathbb {P}}^1$ which is preperiodic for ![]() $f$, its intersection with
$f$, its intersection with ![]() $\mathrm {Preper}(g)$ contains all of
$\mathrm {Preper}(g)$ contains all of ![]() $P \cap \pi ^{-1}(\operatorname {supp} \mu _{\Phi, \Delta } \setminus V)$ and so cannot lie in a countable union of hypersurfaces of
$P \cap \pi ^{-1}(\operatorname {supp} \mu _{\Phi, \Delta } \setminus V)$ and so cannot lie in a countable union of hypersurfaces of ![]() $P$. Therefore
$P$. Therefore ![]() $P$ must be persistently preperiodic for
$P$ must be persistently preperiodic for ![]() $g$. This shows that
$g$. This shows that ![]() $\mathrm {Preper}(f_s) \subset \mathrm {Preper}(g_s)$ for all
$\mathrm {Preper}(f_s) \subset \mathrm {Preper}(g_s)$ for all ![]() $s \in (S\setminus V)({\mathbb {C}})$; equality follows from the same argument in reverse.
$s \in (S\setminus V)({\mathbb {C}})$; equality follows from the same argument in reverse.
Again using Theorem 2.1, it follows that ![]() $\mu _{f_s} = \mu _{g_s}$ for all
$\mu _{f_s} = \mu _{g_s}$ for all ![]() $s \in (S\setminus V)({\mathbb {C}})$. By continuity of the equilibrium measures, we conclude that
$s \in (S\setminus V)({\mathbb {C}})$. By continuity of the equilibrium measures, we conclude that ![]() $\mu _{f_s} = \mu _{g_s}$ for all
$\mu _{f_s} = \mu _{g_s}$ for all ![]() $s\in S({\mathbb {C}})$. Now fix a small open
$s\in S({\mathbb {C}})$. Now fix a small open ![]() $D$ in the base
$D$ in the base ![]() $S$, and let
$S$, and let ![]() $U$ be a continuous potential for
$U$ be a continuous potential for ![]() $\hat {T}_f - \hat {T}_g$ for
$\hat {T}_f - \hat {T}_g$ for ![]() $(s,z) \in D \times {\mathbb {P}}^1$. As
$(s,z) \in D \times {\mathbb {P}}^1$. As ![]() $\hat {T}_f$ and
$\hat {T}_f$ and ![]() $\hat {T}_g$ have the same slice measures for every
$\hat {T}_g$ have the same slice measures for every ![]() $s$, we see that
$s$, we see that ![]() $U$ depends only on the variable
$U$ depends only on the variable ![]() $s \in D$. As
$s \in D$. As ![]() $\hat {T}_f^{\wedge 2} = \hat {T}_g^{\wedge 2} = 0$, we compute
$\hat {T}_f^{\wedge 2} = \hat {T}_g^{\wedge 2} = 0$, we compute
for the projection ![]() $\pi ': S \times {\mathbb {P}}^1 \to S$ (as in Example 4.4). The current
$\pi ': S \times {\mathbb {P}}^1 \to S$ (as in Example 4.4). The current ![]() $\hat {T}_{\Phi, \Delta }$ vanishes on all open
$\hat {T}_{\Phi, \Delta }$ vanishes on all open ![]() $D \subset S$, so we may conclude that
$D \subset S$, so we may conclude that ![]() $\mu _{\Phi, \Delta } = 0$ on all of
$\mu _{\Phi, \Delta } = 0$ on all of ![]() $S({\mathbb {C}})$, contradicting our hypothesis.
$S({\mathbb {C}})$, contradicting our hypothesis.
5.3 Proof of Theorem 1.8
We assume there exists a rigid ![]() $m$-repeller for the family
$m$-repeller for the family ![]() $(f,g)$ over
$(f,g)$ over ![]() $S$, where
$S$, where ![]() $m = \dim S$. Corollary 4.9 implies that the bifurcation measure
$m = \dim S$. Corollary 4.9 implies that the bifurcation measure ![]() $\mu _{\Phi, \Delta }$ is nonzero on the space
$\mu _{\Phi, \Delta }$ is nonzero on the space ![]() $S$. Finally, Theorem 5.1 gives us the result we desire.
$S$. Finally, Theorem 5.1 gives us the result we desire.
5.4 Proof of Theorem 5.2
Recall that a sequence of points ![]() $s_n \in S$ is said to be generic if no subsequence lies in a proper, Zariski-closed subset of
$s_n \in S$ is said to be generic if no subsequence lies in a proper, Zariski-closed subset of ![]() $S$. We start with the following lemma.
$S$. We start with the following lemma.
Lemma 5.4 Let ![]() $\Phi = (f,g)$ be an algebraic family of pairs parameterized by a smooth and irreducible
$\Phi = (f,g)$ be an algebraic family of pairs parameterized by a smooth and irreducible ![]() $S$, defined over
$S$, defined over ![]() ${\mathbb {C}}$. If there is a generic sequence of points
${\mathbb {C}}$. If there is a generic sequence of points ![]() $s_n \in S({\mathbb {C}})$,
$s_n \in S({\mathbb {C}})$, ![]() $n\geq 1$, over which the number of common preperiodic points for
$n\geq 1$, over which the number of common preperiodic points for ![]() $f_{s_n}$ and
$f_{s_n}$ and ![]() $g_{s_n}$ is either infinite or increasing to
$g_{s_n}$ is either infinite or increasing to ![]() $\infty$, then the preperiodic points of
$\infty$, then the preperiodic points of ![]() $\Phi ^{(m)}$ are Zariski dense in
$\Phi ^{(m)}$ are Zariski dense in ![]() $S \times \Delta ^m$ for every
$S \times \Delta ^m$ for every ![]() $m \geq 1$.
$m \geq 1$.
Proof. Fix ![]() $m \geq 1$. For each
$m \geq 1$. For each ![]() $n$, let
$n$, let
so be chosen so that ![]() $M(n) \to \infty$ as
$M(n) \to \infty$ as ![]() $n\to \infty$. The points of
$n\to \infty$. The points of ![]() $\mathrm {Preper}(f_{s_n}) \cap \mathrm {Preper}(g_{s_n})$ determine a configuration of
$\mathrm {Preper}(f_{s_n}) \cap \mathrm {Preper}(g_{s_n})$ determine a configuration of ![]() $M(n)^m$ points in
$M(n)^m$ points in ![]() $\Delta ^m$ that are preperiodic for
$\Delta ^m$ that are preperiodic for ![]() $\Phi _{s_n}^{(m)}$. Note that this collection of points is symmetric under permutation of the coordinates on
$\Phi _{s_n}^{(m)}$. Note that this collection of points is symmetric under permutation of the coordinates on ![]() $\Delta ^m$.
$\Delta ^m$.
Let ![]() $Z$ be the Zariski closure of these points in
$Z$ be the Zariski closure of these points in ![]() $S \times \Delta ^m$. The symmetry of the preperiodic points in
$S \times \Delta ^m$. The symmetry of the preperiodic points in ![]() $\Delta ^m$ implies that
$\Delta ^m$ implies that ![]() $Z$ is also symmetric under permuting the
$Z$ is also symmetric under permuting the ![]() $m$ coordinates of
$m$ coordinates of ![]() $\Delta ^m$. Moreover, because the sequence
$\Delta ^m$. Moreover, because the sequence ![]() $\{s_n\}$ is Zariski dense in
$\{s_n\}$ is Zariski dense in ![]() $S$, we see that
$S$, we see that ![]() $\pi (Z) = S$ for the projection
$\pi (Z) = S$ for the projection ![]() $\pi : S\times \Delta ^m \to S$.
$\pi : S\times \Delta ^m \to S$.
Now suppose that ![]() $Z$ is not all of
$Z$ is not all of ![]() $S\times \Delta ^m$. Then, over a Zariski-open subset
$S\times \Delta ^m$. Then, over a Zariski-open subset ![]() $U\subset S$,
$U\subset S$, ![]() $Z$ is contained in a family of hypersurfaces in
$Z$ is contained in a family of hypersurfaces in ![]() $\Delta ^m \simeq ({\mathbb {P}}^1)^m$ over
$\Delta ^m \simeq ({\mathbb {P}}^1)^m$ over ![]() $U$ that are symmetric under permuting the
$U$ that are symmetric under permuting the ![]() $m$ coordinates. Shrinking
$m$ coordinates. Shrinking ![]() $U$ if necessary, these hypersurfaces will have a well-defined degree
$U$ if necessary, these hypersurfaces will have a well-defined degree ![]() $(r, \ldots, r)$ for some
$(r, \ldots, r)$ for some ![]() $r \geq 1$; that is, each projection that forgets one component
$r \geq 1$; that is, each projection that forgets one component ![]() $\Delta$ will be of degree
$\Delta$ will be of degree ![]() $r$. But since the sequence
$r$. But since the sequence ![]() $\{s_n\}$ is generic, this implies that
$\{s_n\}$ is generic, this implies that ![]() $M(n) \leq r$ for all sufficiently large
$M(n) \leq r$ for all sufficiently large ![]() $n$. This is a contradiction.
$n$. This is a contradiction.
Now to prove Theorem 5.2, let ![]() $S$ be a smooth, irreducible quasiprojective variety parameterizing an algebraic family of pairs
$S$ be a smooth, irreducible quasiprojective variety parameterizing an algebraic family of pairs ![]() $(f,g)$, all defined over
$(f,g)$, all defined over ![]() $\overline {\mathbb {Q}}$ as in its statement. By Theorem 5.1 and in view of Lemma 5.4 we infer that there exists a strict Zariski closed
$\overline {\mathbb {Q}}$ as in its statement. By Theorem 5.1 and in view of Lemma 5.4 we infer that there exists a strict Zariski closed ![]() $V\subset S$ defined over
$V\subset S$ defined over ![]() $\overline {\mathbb {Q}}$ and
$\overline {\mathbb {Q}}$ and ![]() $M\in {\mathbb {R}}$ such that
$M\in {\mathbb {R}}$ such that
for all ![]() $s\in (S\setminus V)(\overline {\mathbb {Q}})$. Write
$s\in (S\setminus V)(\overline {\mathbb {Q}})$. Write ![]() $U:=S\setminus V$. We want to show that
$U:=S\setminus V$. We want to show that ![]() $M$ can be chosen so that (5.2) holds for all
$M$ can be chosen so that (5.2) holds for all ![]() $s\in U({\mathbb {C}})$. Fix
$s\in U({\mathbb {C}})$. Fix ![]() $s_0\in U({\mathbb {C}})\setminus U(\overline {\mathbb {Q}})$ and let
$s_0\in U({\mathbb {C}})\setminus U(\overline {\mathbb {Q}})$ and let ![]() $P_{s_0}:= \mathrm {Preper}(f_{s_0})\cap \mathrm {Preper}(g_{s_0})$. Let
$P_{s_0}:= \mathrm {Preper}(f_{s_0})\cap \mathrm {Preper}(g_{s_0})$. Let ![]() $L$ be a finitely generated subfield of
$L$ be a finitely generated subfield of ![]() ${\mathbb {C}}$ (with transcendence degree at least
${\mathbb {C}}$ (with transcendence degree at least ![]() $1$) such that
$1$) such that ![]() $\Phi _{s_0}$ is defined over
$\Phi _{s_0}$ is defined over ![]() $L$. Thus, there is a quasiprojective variety
$L$. Thus, there is a quasiprojective variety ![]() $X$ over
$X$ over ![]() $\overline {\mathbb {Q}}$ of finite type with function field
$\overline {\mathbb {Q}}$ of finite type with function field ![]() $L$ over which we can extend
$L$ over which we can extend ![]() $\Phi _{s_0}$ (viewing
$\Phi _{s_0}$ (viewing ![]() $s_0$ as an element of
$s_0$ as an element of ![]() $L$) to an endomorphism
$L$) to an endomorphism ![]() $\Phi _X: X\times {\mathbb {P}}^1\times {\mathbb {P}}^1\to X\times {\mathbb {P}}^1\times {\mathbb {P}}^1$ defined over
$\Phi _X: X\times {\mathbb {P}}^1\times {\mathbb {P}}^1\to X\times {\mathbb {P}}^1\times {\mathbb {P}}^1$ defined over ![]() $\overline {\mathbb {Q}}$. We also extend
$\overline {\mathbb {Q}}$. We also extend ![]() $P_{s_0}$ to
$P_{s_0}$ to ![]() $P_X\subset X\times {\mathbb {P}}^1\times {\mathbb {P}}^1$. Note that each specialization
$P_X\subset X\times {\mathbb {P}}^1\times {\mathbb {P}}^1$. Note that each specialization ![]() $(\Phi _X)_t = (f_t, g_t)$ for
$(\Phi _X)_t = (f_t, g_t)$ for ![]() $t\in X(\overline {\mathbb {Q}})$ is naturally identified with some
$t\in X(\overline {\mathbb {Q}})$ is naturally identified with some ![]() $\Phi _s$ for
$\Phi _s$ for ![]() $s \in U(\overline {\mathbb {Q}})$. Thus, for each
$s \in U(\overline {\mathbb {Q}})$. Thus, for each ![]() $t\in X(\overline {\mathbb {Q}})$ we have a uniform bound on
$t\in X(\overline {\mathbb {Q}})$ we have a uniform bound on ![]() $\# \mathrm {Preper}(f_t)\cap \mathrm {Preper}(g_t)$. But clearly the specializations of the distinct points in
$\# \mathrm {Preper}(f_t)\cap \mathrm {Preper}(g_t)$. But clearly the specializations of the distinct points in ![]() $P_X$ remain distinct at some
$P_X$ remain distinct at some ![]() $t\in X(\overline {\mathbb {Q}})$. The proof is complete.
$t\in X(\overline {\mathbb {Q}})$. The proof is complete.
6. Quadratic polynomials
Before proceeding to the proof of Theorem 1.1, we present in this section a new proof of Theorem 1.12. The strategy of proof is the same as for Theorem 1.1, but the argument for proving that the pairwise-bifurcation measure is nonzero is considerably simpler for these pairs of quadratic polynomials. In addition, because the parameter space is two dimensional, we can use Theorem 1.14 to complete the proof of Theorem 1.12, allowing us to provide a complete description of the subset of pairs of quadratic polynomials for which the uniform bound cannot exist.
Theorem 6.1 Let ![]() $f_c(z) = z^2+c$ for
$f_c(z) = z^2+c$ for ![]() $c\in {\mathbb {C}}$, and consider the algebraic family of pairs
$c\in {\mathbb {C}}$, and consider the algebraic family of pairs ![]() $\Phi _{(c_1, c_2)} = (f_{c_1}, f_{c_2})$ parameterized by
$\Phi _{(c_1, c_2)} = (f_{c_1}, f_{c_2})$ parameterized by ![]() $(c_1, c_2)\in {\mathbb {C}}^2$. The pairwise-bifurcation measure
$(c_1, c_2)\in {\mathbb {C}}^2$. The pairwise-bifurcation measure ![]() $\mu _{\Phi, \Delta }$ is nonzero on
$\mu _{\Phi, \Delta }$ is nonzero on ![]() ${\mathbb {C}}^2$.
${\mathbb {C}}^2$.
Proof. We appeal to Corollary 4.9 and study the pair
These two polynomials have at least 26 common preperiodic points in ![]() ${\mathbb {C}}$; see [Reference Doyle and HydeDH22] for a construction of these quadratic polynomials and similar examples in higher degrees. We will show that two of the common preperiodic points define a rigid
${\mathbb {C}}$; see [Reference Doyle and HydeDH22] for a construction of these quadratic polynomials and similar examples in higher degrees. We will show that two of the common preperiodic points define a rigid ![]() $2$-repeller over
$2$-repeller over ![]() $S = {\mathbb {C}}^2$.
$S = {\mathbb {C}}^2$.
The procedure is as follows. Let ![]() $(a_0, b_0) = (-21/16, -29/16) \in S$. Suppose
$(a_0, b_0) = (-21/16, -29/16) \in S$. Suppose ![]() $p_0, q_0\in {\mathbb {C}}$ are common preperiodic points, each iterating to a repelling cycle for both
$p_0, q_0\in {\mathbb {C}}$ are common preperiodic points, each iterating to a repelling cycle for both ![]() $f_{a_0}$ and
$f_{a_0}$ and ![]() $f_{b_0}$, and suppose that we are given a holomorphic map
$f_{b_0}$, and suppose that we are given a holomorphic map ![]() $R: U \to {\mathbb {C}}^4$ from a small neighborhood
$R: U \to {\mathbb {C}}^4$ from a small neighborhood ![]() $U$ of
$U$ of ![]() $(a_0, b_0) \in S$, with coordinate functions defined by
$(a_0, b_0) \in S$, with coordinate functions defined by
so that ![]() $R(a_0, b_0) = (p_0, p_0, q_0, q_0) \in \Delta ^2$ and
$R(a_0, b_0) = (p_0, p_0, q_0, q_0) \in \Delta ^2$ and ![]() $R(c_1, c_2)$ is persistently preperiodic for the fiber power
$R(c_1, c_2)$ is persistently preperiodic for the fiber power ![]() $\Phi ^{(2)}$ over
$\Phi ^{(2)}$ over ![]() $S$. Then the pair
$S$. Then the pair ![]() $(p_0, q_0)$ will form a rigid 2-repeller in
$(p_0, q_0)$ will form a rigid 2-repeller in ![]() $({\mathbb {P}}^1 \times {\mathbb {P}}^1)^2$ at
$({\mathbb {P}}^1 \times {\mathbb {P}}^1)^2$ at ![]() $(a_0,b_0)$ if
$(a_0,b_0)$ if
 \[ \det \left( \begin{array}{cccccc} 1 & 0 & 0 & 0 & 1 & 0 \\ 0 & 1 & 0 & 0 & 0 & 1 \\ 0 & 0 & 1 & 0 & p_1'(a_0) & 0 \\ 0 & 0 & 1 & 0 & 0 & p_2'(b_0) \\ 0 & 0 & 0 & 1 & q_1'(a_0) & 0 \\ 0 & 0 & 0 & 1 & 0 & q_2'(b_0) \end{array} \right) \not= 0 \]
\[ \det \left( \begin{array}{cccccc} 1 & 0 & 0 & 0 & 1 & 0 \\ 0 & 1 & 0 & 0 & 0 & 1 \\ 0 & 0 & 1 & 0 & p_1'(a_0) & 0 \\ 0 & 0 & 1 & 0 & 0 & p_2'(b_0) \\ 0 & 0 & 0 & 1 & q_1'(a_0) & 0 \\ 0 & 0 & 0 & 1 & 0 & q_2'(b_0) \end{array} \right) \not= 0 \]
for any such ![]() $R$. The first four columns are a basis for the tangent space to
$R$. The first four columns are a basis for the tangent space to ![]() $S \times \Delta ^2$ in
$S \times \Delta ^2$ in ![]() $S \times ({\mathbb {P}}^1 \times {\mathbb {P}}^1)^2$, while the second two columns span the tangent space to the graph of
$S \times ({\mathbb {P}}^1 \times {\mathbb {P}}^1)^2$, while the second two columns span the tangent space to the graph of ![]() $R$ over a neighborhood of
$R$ over a neighborhood of ![]() $(a_0,b_0) \in S$. In fact, showing this determinant is nonzero is stronger than being a rigid repeller, since this will show the graph of
$(a_0,b_0) \in S$. In fact, showing this determinant is nonzero is stronger than being a rigid repeller, since this will show the graph of ![]() $R$ intersects
$R$ intersects ![]() $\Delta ^2$ transversely over
$\Delta ^2$ transversely over ![]() $(a_0, b_0)$.
$(a_0, b_0)$.
A simple computation shows that the above determinant is equal to
Now let us take ![]() $p_0 = 5/4$ and
$p_0 = 5/4$ and ![]() $q_0 = -7/4$. The orbits of
$q_0 = -7/4$. The orbits of ![]() $p_0$ and
$p_0$ and ![]() $q_0$ for
$q_0$ for ![]() $f_{a_0}$ are
$f_{a_0}$ are
 \begin{gather*} \tfrac54 \mapsto \tfrac14 \mapsto -\tfrac54 \mapsto \tfrac14,\\ -\tfrac74 \mapsto \tfrac74 \mapsto \tfrac74 \end{gather*}
\begin{gather*} \tfrac54 \mapsto \tfrac14 \mapsto -\tfrac54 \mapsto \tfrac14,\\ -\tfrac74 \mapsto \tfrac74 \mapsto \tfrac74 \end{gather*}
with each landing on a repelling cycle. The orbits of ![]() $p_0$ and
$p_0$ and ![]() $q_0$ for
$q_0$ for ![]() $f_{b_0}$ are
$f_{b_0}$ are
with each in a repelling cycle of period 3. To compute the values of ![]() $p_1'(a_0)$,
$p_1'(a_0)$, ![]() $p_2'(b_0)$,
$p_2'(b_0)$, ![]() $q_1'(a_0)$, and
$q_1'(a_0)$, and ![]() $q_2'(b_0)$, we determine the equations for these cycles as a function of the parameter
$q_2'(b_0)$, we determine the equations for these cycles as a function of the parameter ![]() $c$, and use implicit differentiation.
$c$, and use implicit differentiation.
The equation for a (strictly) preperiodic point ![]() $z$ so that
$z$ so that ![]() $f_c(z)$ is in a cycle of period 2 is
$f_c(z)$ is in a cycle of period 2 is
so that
The prefixed points for ![]() $f_c$ satisfy
$f_c$ satisfy
so
The period-three cycles for ![]() $f_c$ satisfy
$f_c$ satisfy
This gives
 \begin{gather*} p_2'(b_0) = -\frac{\partial P_2}{\partial c}\bigg/\frac{\partial P_2}{\partial z} \bigg|_{c = b_0, z = p_0} = 2/9,\\ q_2'(b_0) = -\frac{\partial P_2}{\partial c}\bigg/\frac{\partial P_2}{\partial z} \bigg|_{c = b_0, z = q_0} = 2/9. \end{gather*}
\begin{gather*} p_2'(b_0) = -\frac{\partial P_2}{\partial c}\bigg/\frac{\partial P_2}{\partial z} \bigg|_{c = b_0, z = p_0} = 2/9,\\ q_2'(b_0) = -\frac{\partial P_2}{\partial c}\bigg/\frac{\partial P_2}{\partial z} \bigg|_{c = b_0, z = q_0} = 2/9. \end{gather*}
We conclude that
With Corollary 4.9, this completes the proof of Theorem 6.1.
Proof of Theorem 1.12 Let ![]() $S = {\mathbb {C}}^2$. In view of Theorem 6.1, Theorem 5.2 implies that there is a finite collection of irreducible, algebraic curves
$S = {\mathbb {C}}^2$. In view of Theorem 6.1, Theorem 5.2 implies that there is a finite collection of irreducible, algebraic curves ![]() $C_1,\ldots, C_m\subset S$ all defined over
$C_1,\ldots, C_m\subset S$ all defined over ![]() $\overline {{\mathbb {Q}}}$ and a constant
$\overline {{\mathbb {Q}}}$ and a constant ![]() $B$ so that
$B$ so that
for all ![]() $(t_1,t_2)\in {\mathbb {C}}^2 \setminus (\bigcup _i C_i)$. Applying Theorem 1.14 to each
$(t_1,t_2)\in {\mathbb {C}}^2 \setminus (\bigcup _i C_i)$. Applying Theorem 1.14 to each ![]() $C_i$ we see that (enlarging
$C_i$ we see that (enlarging ![]() $B$ if necessary) the bound in (6.1) holds for each
$B$ if necessary) the bound in (6.1) holds for each ![]() $(t_1,t_2)\in {\mathbb {C}}^2$ unless
$(t_1,t_2)\in {\mathbb {C}}^2$ unless ![]() $\mathrm {Preper}(f_{t_1})=\mathrm {Preper}(f_{t_2})$. The latter happens only if the Julia sets of
$\mathrm {Preper}(f_{t_1})=\mathrm {Preper}(f_{t_2})$. The latter happens only if the Julia sets of ![]() $f_{t_1}$ and
$f_{t_1}$ and ![]() $f_{t_2}$ coincide, and so by [Reference Baker and ErëmenkoBE87], only if
$f_{t_2}$ coincide, and so by [Reference Baker and ErëmenkoBE87], only if ![]() $t_1=t_2$, which completes our proof.
$t_1=t_2$, which completes our proof.
7. Monomials
In this section, we complete the proof of Theorem 1.1. To achieve this, we will prove the following result.
Theorem 7.1 For each degree ![]() $d\geq 2$, the pair
$d\geq 2$, the pair ![]() $(z^d, \zeta \, z^d)$ for primitive root of unity
$(z^d, \zeta \, z^d)$ for primitive root of unity ![]() $\zeta ^{d+1}=1$ has a rigid
$\zeta ^{d+1}=1$ has a rigid ![]() $(4d-1)$-repeller.
$(4d-1)$-repeller.
Recall that the bifurcation measure ![]() $\mu _\Delta$ on the
$\mu _\Delta$ on the ![]() $(4d-1)$-dimensional moduli space of pairs
$(4d-1)$-dimensional moduli space of pairs ![]() $(\mathrm {Rat}_d \times \mathrm {Rat}_d)/\operatorname {Aut} {\mathbb {P}}^1$ was defined in (1.2). Via Corollary 4.9, Theorem 7.1 will imply that
$(\mathrm {Rat}_d \times \mathrm {Rat}_d)/\operatorname {Aut} {\mathbb {P}}^1$ was defined in (1.2). Via Corollary 4.9, Theorem 7.1 will imply that ![]() $\mu _\Delta$ is nonzero. But we must be careful: the moduli space is likely to be singular at pairs
$\mu _\Delta$ is nonzero. But we must be careful: the moduli space is likely to be singular at pairs ![]() $(f,g)$ with automorphisms, and this pair
$(f,g)$ with automorphisms, and this pair ![]() $(z^d, \zeta \, z^d)$ has automorphisms of the form
$(z^d, \zeta \, z^d)$ has automorphisms of the form ![]() $A(z) = \omega z$ for
$A(z) = \omega z$ for ![]() $\omega ^{d-1} = 1$. Throughout this section, we work with the subspace
$\omega ^{d-1} = 1$. Throughout this section, we work with the subspace
consisting of pairs ![]() $(f,g)$ where
$(f,g)$ where
 \[ f(z) = \frac{z^d + a_{d-1} z + \cdots + a_1 z}{b_{d-1}z^{d-1} + \cdots + b_1 z + \Big(1 + \sum_{i = 1}^{d-1} a_i -\sum_{j=1}^{d-1} b_j\Big)} \]
\[ f(z) = \frac{z^d + a_{d-1} z + \cdots + a_1 z}{b_{d-1}z^{d-1} + \cdots + b_1 z + \Big(1 + \sum_{i = 1}^{d-1} a_i -\sum_{j=1}^{d-1} b_j\Big)} \]
with ![]() $a_i, b_j \in {\mathbb {C}}$ and
$a_i, b_j \in {\mathbb {C}}$ and ![]() $g$ is arbitrary. Note that
$g$ is arbitrary. Note that ![]() $S_d$ is a smooth and irreducible quasiprojective complex algebraic variety. This normalization for
$S_d$ is a smooth and irreducible quasiprojective complex algebraic variety. This normalization for ![]() $f$ fixes the three elements of
$f$ fixes the three elements of ![]() $\{0,1,\infty \}$ in
$\{0,1,\infty \}$ in ![]() ${\mathbb {P}}^1$, and the projection from
${\mathbb {P}}^1$, and the projection from ![]() $S_d$ to the moduli space
$S_d$ to the moduli space ![]() $(\mathrm {Rat}_d \times \mathrm {Rat}_d)/\operatorname {Aut} {\mathbb {P}}^1$ is finite-to-one. In other words, this
$(\mathrm {Rat}_d \times \mathrm {Rat}_d)/\operatorname {Aut} {\mathbb {P}}^1$ is finite-to-one. In other words, this ![]() $S_d$ defines a maximally non-isotrivial algebraic family of pairs of degree
$S_d$ defines a maximally non-isotrivial algebraic family of pairs of degree ![]() $d$, with
$d$, with ![]() $\dim S_d = 4d-1$. It is not surjective to the moduli space of pairs, but it covers a Zariski-open subset. The pair
$\dim S_d = 4d-1$. It is not surjective to the moduli space of pairs, but it covers a Zariski-open subset. The pair ![]() $(z^d, \zeta z^d)$ is an element of
$(z^d, \zeta z^d)$ is an element of ![]() $S_d$ for any choice of primitive
$S_d$ for any choice of primitive ![]() $(d+1)$th root of unity
$(d+1)$th root of unity ![]() $\zeta$.
$\zeta$.
7.1 Proof of Theorem 1.1, assuming Theorem 7.1
Let ![]() $\mu _{\Phi, \Delta }$ denote the pairwise-bifurcation measure on
$\mu _{\Phi, \Delta }$ denote the pairwise-bifurcation measure on ![]() $S_d({\mathbb {C}})$ for the family of all pairs
$S_d({\mathbb {C}})$ for the family of all pairs ![]() $\Phi = (f,g)$ parameterized by
$\Phi = (f,g)$ parameterized by ![]() $S_d$, as defined in (4.3) and Example 4.4. With Theorem 7.1, we may apply Corollary 4.9 to deduce that the pairwise-bifurcation measure
$S_d$, as defined in (4.3) and Example 4.4. With Theorem 7.1, we may apply Corollary 4.9 to deduce that the pairwise-bifurcation measure ![]() $\mu _{\Phi, \Delta }$ is nonzero on
$\mu _{\Phi, \Delta }$ is nonzero on ![]() $S_d({\mathbb {C}})$. We then apply Theorem 5.2 to conclude that there is a Zariski-open subset
$S_d({\mathbb {C}})$. We then apply Theorem 5.2 to conclude that there is a Zariski-open subset ![]() $U$ of
$U$ of ![]() $S_d$, defined over
$S_d$, defined over ![]() $\overline {\mathbb {Q}}$, for which there is a uniform bound on the number of common preperiodic points of
$\overline {\mathbb {Q}}$, for which there is a uniform bound on the number of common preperiodic points of ![]() $f_s$ and
$f_s$ and ![]() $g_s$ for all
$g_s$ for all ![]() $s \in U({\mathbb {C}})$. Taking the union of all (
$s \in U({\mathbb {C}})$. Taking the union of all (![]() $\operatorname {Aut} {\mathbb {P}}^1$)-orbits of
$\operatorname {Aut} {\mathbb {P}}^1$)-orbits of ![]() $U$ in
$U$ in ![]() $\mathrm {Rat}_d \times \mathrm {Rat}_d$ completes the proof.
$\mathrm {Rat}_d \times \mathrm {Rat}_d$ completes the proof.
7.2 Proof of Theorem 1.5, assuming Theorem 7.1
From § 7.1, we know that the measure ![]() $\mu _{\Phi, \Delta }$ is nonzero on the space
$\mu _{\Phi, \Delta }$ is nonzero on the space ![]() $S_d$. By construction, the natural map from
$S_d$. By construction, the natural map from ![]() $S_d$ to the moduli space of pairs
$S_d$ to the moduli space of pairs ![]() $(\mathrm {Rat}_d \times \mathrm {Rat}_d)/\operatorname {Aut} {\mathbb {P}}^1$ is dominant and finite-to-one to its image. Recall that the pairwise-bifurcation measure
$(\mathrm {Rat}_d \times \mathrm {Rat}_d)/\operatorname {Aut} {\mathbb {P}}^1$ is dominant and finite-to-one to its image. Recall that the pairwise-bifurcation measure ![]() $\mu _\Delta$ was defined in (1.2). It is (a nonzero multiple of) the push-forward of
$\mu _\Delta$ was defined in (1.2). It is (a nonzero multiple of) the push-forward of ![]() $\mu _{\Phi,\Delta }$ under the natural map from
$\mu _{\Phi,\Delta }$ under the natural map from ![]() $S_d$. Therefore
$S_d$. Therefore ![]() $\mu _\Delta$ is nonzero.
$\mu _\Delta$ is nonzero.
7.3 Proof of Theorem 1.2, assuming Theorem 7.1
Fix degree ![]() $d\geq 2$. Let
$d\geq 2$. Let ![]() $\mathcal {P}_d$ be the space of polynomial pairs of the form
$\mathcal {P}_d$ be the space of polynomial pairs of the form
with ![]() $a_i, b_j \in {\mathbb {C}}$ and
$a_i, b_j \in {\mathbb {C}}$ and ![]() $b_0\not = 0$, parameterized by their coefficients. This space
$b_0\not = 0$, parameterized by their coefficients. This space ![]() $\mathcal {P}_d$ has dimension
$\mathcal {P}_d$ has dimension ![]() $2d$ and maps surjectively and finite-to-one to the moduli space of polynomial pairs
$2d$ and maps surjectively and finite-to-one to the moduli space of polynomial pairs ![]() $(\mathrm {Poly}_d \times \mathrm {Poly}_d)/\operatorname {Aut} {\mathbb {C}}$. Theorem 7.1 implies that the pair
$(\mathrm {Poly}_d \times \mathrm {Poly}_d)/\operatorname {Aut} {\mathbb {C}}$. Theorem 7.1 implies that the pair ![]() $(z^d, \zeta \, z^d)$ for primitive root of unity
$(z^d, \zeta \, z^d)$ for primitive root of unity ![]() $\zeta ^{d+1}=1$ has a rigid
$\zeta ^{d+1}=1$ has a rigid ![]() $(2d)$-repeller over the parameter space
$(2d)$-repeller over the parameter space ![]() $\mathcal {P}_d$. As in § 7.1, we deduce the uniform bound on the number of common preperiodic points for all pairs of polynomials in a Zariski open subset of
$\mathcal {P}_d$. As in § 7.1, we deduce the uniform bound on the number of common preperiodic points for all pairs of polynomials in a Zariski open subset of ![]() $\mathcal {P}_d$.
$\mathcal {P}_d$.
7.4 Rigidity of the monomial pair
We now aim to prove Theorem 1.10. Fix degree ![]() $d\geq 2$. Let
$d\geq 2$. Let ![]() $f_0(z) = z^d$ and
$f_0(z) = z^d$ and ![]() $g_0(z) = \zeta z^d$ for
$g_0(z) = \zeta z^d$ for ![]() $\zeta = e^{2\pi i/(d+1)}$. By conjugating the image of
$\zeta = e^{2\pi i/(d+1)}$. By conjugating the image of ![]() $\psi$ and shrinking the domain disk if necessary, we may assume that its image lies in the subvariety
$\psi$ and shrinking the domain disk if necessary, we may assume that its image lies in the subvariety ![]() $S_d \subset \mathrm {Rat}_d\times \mathrm {Rat}_d$. Thus, let
$S_d \subset \mathrm {Rat}_d\times \mathrm {Rat}_d$. Thus, let ![]() ${\mathbb {D}}\subset {\mathbb {C}}$ denote the unit disk, and suppose that
${\mathbb {D}}\subset {\mathbb {C}}$ denote the unit disk, and suppose that ![]() $\psi = (\psi _1, \psi _2): {\mathbb {D}}\to S_d$ is a holomorphic map with
$\psi = (\psi _1, \psi _2): {\mathbb {D}}\to S_d$ is a holomorphic map with ![]() $\psi (0) = (f_0, g_0)$ so that
$\psi (0) = (f_0, g_0)$ so that
for all ![]() $t \in {\mathbb {D}}$. We need to show that
$t \in {\mathbb {D}}$. We need to show that ![]() $\psi$ is constant.
$\psi$ is constant.
Remark 7.2 The conclusion of Theorem 1.10 is false if we allow ![]() $\zeta$ to be a root of unity of any order
$\zeta$ to be a root of unity of any order ![]() $\leq d$. For each
$\leq d$. For each ![]() $m \leq d$ and
$m \leq d$ and ![]() $\zeta$ with
$\zeta$ with ![]() $\zeta ^m = 1$, let
$\zeta ^m = 1$, let
for ![]() $c\in {\mathbb {C}}$. Then
$c\in {\mathbb {C}}$. Then ![]() $\zeta$ is a symmetry of the Julia set of
$\zeta$ is a symmetry of the Julia set of ![]() $f_c$, and
$f_c$, and ![]() $f_c(\zeta z) = \zeta ^{d-m} f_c(z) = \zeta ^d f_c(z)$. Note that
$f_c(\zeta z) = \zeta ^{d-m} f_c(z) = \zeta ^d f_c(z)$. Note that ![]() $g_c^n(z) = \zeta ^{1 + \cdots + d^{n-1}} f^n_c(z)$ for all
$g_c^n(z) = \zeta ^{1 + \cdots + d^{n-1}} f^n_c(z)$ for all ![]() $n$ and all
$n$ and all ![]() $c$. If a point
$c$. If a point ![]() $x$ is preperiodic for
$x$ is preperiodic for ![]() $f_c$, then the iterates
$f_c$, then the iterates ![]() $g_c^n(x)$ must eventually cycle, and vice versa. That is,
$g_c^n(x)$ must eventually cycle, and vice versa. That is, ![]() $\mathrm {Preper}(f_c) = \mathrm {Preper}(g_c)$ for all
$\mathrm {Preper}(f_c) = \mathrm {Preper}(g_c)$ for all ![]() $c\in {\mathbb {C}}$ and
$c\in {\mathbb {C}}$ and ![]() $J(f_c) = J(g_c)$ for all
$J(f_c) = J(g_c)$ for all ![]() $c \in {\mathbb {C}}$. See, for example, [Reference Baker and ErëmenkoBE87] for more information on symmetries.
$c \in {\mathbb {C}}$. See, for example, [Reference Baker and ErëmenkoBE87] for more information on symmetries.
Returning to our setting, where ![]() $\zeta = e^{2\pi i/(d+1)}$, note that the second iterates of
$\zeta = e^{2\pi i/(d+1)}$, note that the second iterates of ![]() $f_0$ and
$f_0$ and ![]() $g_0$ coincide. We first observe that the same relation must hold throughout
$g_0$ coincide. We first observe that the same relation must hold throughout ![]() ${\mathbb {D}}$; that is, we have
${\mathbb {D}}$; that is, we have
for all ![]() $t\in {\mathbb {D}}$. Indeed, both
$t\in {\mathbb {D}}$. Indeed, both ![]() $f_0$ and
$f_0$ and ![]() $g_0$ are
$g_0$ are ![]() $J$-stable in
$J$-stable in ![]() $\mathrm {Rat}_d$, and so there is a holomorphic motion of the Julia sets, inducing conjugacies between
$\mathrm {Rat}_d$, and so there is a holomorphic motion of the Julia sets, inducing conjugacies between ![]() $\psi _i(0)$ and
$\psi _i(0)$ and ![]() $\psi _i(t)$ on their Julia sets for
$\psi _i(t)$ on their Julia sets for ![]() $t$ small,
$t$ small, ![]() $i = 1,2$. In particular, because all preperiodic points of
$i = 1,2$. In particular, because all preperiodic points of ![]() $\psi _i(t)$,
$\psi _i(t)$, ![]() $i=1,2$, in the Julia set must coincide for all
$i=1,2$, in the Julia set must coincide for all ![]() $t$, the motions
$t$, the motions ![]() $z_t$ of these preperiodic points
$z_t$ of these preperiodic points ![]() $z \in J(\psi _1(0)) = J(\psi _2(0))$ must coincide for
$z \in J(\psi _1(0)) = J(\psi _2(0))$ must coincide for ![]() $\psi _1(t)$ and for
$\psi _1(t)$ and for ![]() $\psi _2(t)$, for all
$\psi _2(t)$, for all ![]() $t$ small. The induced conjugacy forces a relation on the second iterates,
$t$ small. The induced conjugacy forces a relation on the second iterates, ![]() $\psi _1(t)^2(z_t) = \psi _2(t)^2(z_t)$, holding for all preperiodic points
$\psi _1(t)^2(z_t) = \psi _2(t)^2(z_t)$, holding for all preperiodic points ![]() $z \in J(\psi _1(0)) = J(\psi _2(0))$ for all
$z \in J(\psi _1(0)) = J(\psi _2(0))$ for all ![]() $t$ small. As there are infinitely many preperiodic points in the Julia set, we have equality of iterates
$t$ small. As there are infinitely many preperiodic points in the Julia set, we have equality of iterates ![]() $\psi _1(t)^2 = \psi _2(t)^2$ for all
$\psi _1(t)^2 = \psi _2(t)^2$ for all ![]() $t$ small. Finally, by holomorphic continuation, the equality persists for all
$t$ small. Finally, by holomorphic continuation, the equality persists for all ![]() $t \in {\mathbb {D}}$.
$t \in {\mathbb {D}}$.
Now consider the map ![]() $F = f^2-g^2$ from the space
$F = f^2-g^2$ from the space ![]() $\mathrm {Rat}_d\times \mathrm {Rat}_d$ to the set of all rational functions
$\mathrm {Rat}_d\times \mathrm {Rat}_d$ to the set of all rational functions ![]() $R_{2d^2} \subset {\mathbb {C}}(z)$ of degree at most
$R_{2d^2} \subset {\mathbb {C}}(z)$ of degree at most ![]() $2d^2$. Recall that the image of
$2d^2$. Recall that the image of ![]() $\psi$ lies in the subspace
$\psi$ lies in the subspace ![]() $S_d$, which maps finite-to-one to
$S_d$, which maps finite-to-one to ![]() $(\mathrm {Rat}_d\times \mathrm {Rat}_d)/\operatorname {Aut}{\mathbb {P}}^1$, and we have shown that
$(\mathrm {Rat}_d\times \mathrm {Rat}_d)/\operatorname {Aut}{\mathbb {P}}^1$, and we have shown that ![]() $F(\psi (t)) = 0$ for all
$F(\psi (t)) = 0$ for all ![]() $t \in {\mathbb {D}}$. We aim to conclude that
$t \in {\mathbb {D}}$. We aim to conclude that ![]() $\psi$ is constant. Choosing coefficients for coordinates on
$\psi$ is constant. Choosing coefficients for coordinates on ![]() $\mathrm {Rat}_d\times \mathrm {Rat}_d$ near the point
$\mathrm {Rat}_d\times \mathrm {Rat}_d$ near the point ![]() $(f_0, g_0)$ and on the target space
$(f_0, g_0)$ and on the target space ![]() $R_{2d^2}$, it is enough to show that the derivative matrix
$R_{2d^2}$, it is enough to show that the derivative matrix ![]() $DF_{(f_0, g_0)}$ has the maximal possible rank of
$DF_{(f_0, g_0)}$ has the maximal possible rank of ![]() $4d-1$. Indeed, since
$4d-1$. Indeed, since ![]() $F$ vanishes on the fiber of the quotient
$F$ vanishes on the fiber of the quotient ![]() $\mathrm {Rat}_d\times \mathrm {Rat}_d \to (\mathrm {Rat}_d\times \mathrm {Rat}_d)/\operatorname {Aut}{\mathbb {P}}^1$ through
$\mathrm {Rat}_d\times \mathrm {Rat}_d \to (\mathrm {Rat}_d\times \mathrm {Rat}_d)/\operatorname {Aut}{\mathbb {P}}^1$ through ![]() $(f_0, g_0)$, this will imply, by the chain rule, that some (possibly higher-order) derivative of
$(f_0, g_0)$, this will imply, by the chain rule, that some (possibly higher-order) derivative of ![]() $t \mapsto F(\psi (t))(z)$ will be nonzero at
$t \mapsto F(\psi (t))(z)$ will be nonzero at ![]() $t=0$, whenever
$t=0$, whenever ![]() $\psi$ is non-constant.
$\psi$ is non-constant.
We have thus reduced the proof of Theorem 1.10 to the following lemma.
Lemma 7.3 For ![]() $d\ge 2$, let
$d\ge 2$, let
Let ![]() $F=f^2-g^2$. Let
$F=f^2-g^2$. Let ![]() $\vec {a}=(1,0,\ldots,0)$ corresponding to
$\vec {a}=(1,0,\ldots,0)$ corresponding to ![]() $z^d$ and
$z^d$ and ![]() $\vec {A}=(\zeta,0,\ldots,0)$ corresponding to
$\vec {A}=(\zeta,0,\ldots,0)$ corresponding to ![]() $\zeta z^d$ for
$\zeta z^d$ for ![]() $\zeta ^{d+1}=1$ a primitive
$\zeta ^{d+1}=1$ a primitive ![]() $(d+1)$th root of unity. Then the vectors
$(d+1)$th root of unity. Then the vectors ![]() $\partial _{a_i}F(\vec {a}), \partial _{b_j}F(\vec {a}), \partial _{A_k}F(\vec {A}), \partial _{B_{\ell }}F(\vec {A})$, for all
$\partial _{a_i}F(\vec {a}), \partial _{b_j}F(\vec {a}), \partial _{A_k}F(\vec {A}), \partial _{B_{\ell }}F(\vec {A})$, for all ![]() $i,k\in \{0,\ldots,d\}$ and
$i,k\in \{0,\ldots,d\}$ and ![]() $j,\ell \in \{1,\ldots, d\}$ generate a subspace of
$j,\ell \in \{1,\ldots, d\}$ generate a subspace of ![]() ${\mathbb {C}}[z]$ of dimension
${\mathbb {C}}[z]$ of dimension ![]() $4d-1$.
$4d-1$.
Proof. First we compute the derivatives
 \begin{equation} \begin{aligned} \partial_{A_k}F(\vec{A}) & =-\frac{1}{\zeta}d z^{d^2-d+k}-\zeta^{k}z^{dk},\\ \partial_{B_{\ell}}F(\vec{A}) & =\zeta^{\ell}z^{d^2+\ell d}+dz^{d^2+\ell},\\ \partial_{a_i}F(\vec{a}) & =dz^{d^2-d+i}+z^{id},\\ \partial_{b_j}F(\vec{a}) & =-z^{d^2+jd}-dz^{d^2+j}. \end{aligned} \end{equation}
\begin{equation} \begin{aligned} \partial_{A_k}F(\vec{A}) & =-\frac{1}{\zeta}d z^{d^2-d+k}-\zeta^{k}z^{dk},\\ \partial_{B_{\ell}}F(\vec{A}) & =\zeta^{\ell}z^{d^2+\ell d}+dz^{d^2+\ell},\\ \partial_{a_i}F(\vec{a}) & =dz^{d^2-d+i}+z^{id},\\ \partial_{b_j}F(\vec{a}) & =-z^{d^2+jd}-dz^{d^2+j}. \end{aligned} \end{equation}
Let ![]() $M$ be the matrix with
$M$ be the matrix with ![]() $s$th column consisting of the coefficients of
$s$th column consisting of the coefficients of ![]() $z^{s-1}$ as they occur in order
$z^{s-1}$ as they occur in order ![]() $\partial _{A_0}F(\vec {A}),\ldots,\partial _{A_d}F(\vec {A})$,
$\partial _{A_0}F(\vec {A}),\ldots,\partial _{A_d}F(\vec {A})$, ![]() $\partial _{B_1}F(\vec {A}), \ldots, \partial _{B_d}F(\vec {A})$,
$\partial _{B_1}F(\vec {A}), \ldots, \partial _{B_d}F(\vec {A})$, ![]() $\partial _{a_0}F(\vec {a}), \ldots, \partial _{a_d}F(\vec {a})$,
$\partial _{a_0}F(\vec {a}), \ldots, \partial _{a_d}F(\vec {a})$, ![]() $\partial _{b_1}F(\vec {a}),\ldots,\partial _{b_d}F(\vec {a})$. Each is a polynomial in
$\partial _{b_1}F(\vec {a}),\ldots,\partial _{b_d}F(\vec {a})$. Each is a polynomial in ![]() $z$ with degree at most
$z$ with degree at most ![]() $2d^2$, so this a
$2d^2$, so this a ![]() $(4d+2)\times (2d^2+1)$ matrix.
$(4d+2)\times (2d^2+1)$ matrix.
Set ![]() $\{e_i\}$ to be the standard basis vectors for
$\{e_i\}$ to be the standard basis vectors for ![]() ${\mathbb {C}}^{4d+2}$. Note that all powers of
${\mathbb {C}}^{4d+2}$. Note that all powers of ![]() $z$ that appear, appear twice with the exception of
$z$ that appear, appear twice with the exception of ![]() $z^{d(d-1)}=z^{d^2-d}$ and
$z^{d(d-1)}=z^{d^2-d}$ and ![]() $z^{d^2+d}$ which appear
$z^{d^2+d}$ which appear ![]() $4$ times. The
$4$ times. The ![]() $2d-1+1+2d-1=4d-1$ nonzero columns of
$2d-1+1+2d-1=4d-1$ nonzero columns of ![]() $M$ are as follows:
$M$ are as follows:
 \begin{equation} \begin{aligned} m_{kd+1} & =-\zeta^ke_{k+1}+e_{2d+k+2}, \quad k=0,\ldots,d-2,\\ m_{(d-1)d+1} & =-\frac{d}{\zeta}e_1-\zeta^{d-1}e_d+de_{2d+2}+e_{3d+1},\\ m_{(d-1)d+1+i} & =-\frac{d}{\zeta}e_{i+1}+de_{2d+2+i}, \quad i=1,\ldots,d-1. \end{aligned} \end{equation}
\begin{equation} \begin{aligned} m_{kd+1} & =-\zeta^ke_{k+1}+e_{2d+k+2}, \quad k=0,\ldots,d-2,\\ m_{(d-1)d+1} & =-\frac{d}{\zeta}e_1-\zeta^{d-1}e_d+de_{2d+2}+e_{3d+1},\\ m_{(d-1)d+1+i} & =-\frac{d}{\zeta}e_{i+1}+de_{2d+2+i}, \quad i=1,\ldots,d-1. \end{aligned} \end{equation}
This covers the first ![]() $d(d-1)+d$ columns of the matrix. The central column of
$d(d-1)+d$ columns of the matrix. The central column of ![]() $M$ is
$M$ is
The following nonzero columns are
 \begin{equation} \begin{aligned}m_{d^2+1+j} & =de_{d+1+j}-de_{3d+2+j}, \quad j=1,\ldots,d-1,\\ m_{d(d+1)+1} & = \zeta e_{d+2}+d e_{2d+1}-e_{3d+3}-de_{4d+2},\\ m_{d(d+1)+1+sd} & =\zeta^{s+1} e_{d+s+2}- e_{3d+3+s}, \quad s=1,\ldots, d-1. \end{aligned} \end{equation}
\begin{equation} \begin{aligned}m_{d^2+1+j} & =de_{d+1+j}-de_{3d+2+j}, \quad j=1,\ldots,d-1,\\ m_{d(d+1)+1} & = \zeta e_{d+2}+d e_{2d+1}-e_{3d+3}-de_{4d+2},\\ m_{d(d+1)+1+sd} & =\zeta^{s+1} e_{d+s+2}- e_{3d+3+s}, \quad s=1,\ldots, d-1. \end{aligned} \end{equation}
and the space generated by the above column vectors ![]() $V$ has dimension
$V$ has dimension ![]() $2d-4+2d-4$. Note that we have not yet considered the column vectors
$2d-4+2d-4$. Note that we have not yet considered the column vectors
 \begin{equation} \begin{aligned} m_1 & =-e_1+e_{2d+2},\\ m_{d^2} & =-\frac{d}{\zeta}e_{d}+de_{3d+1} ,\\ m_{d^2+2} & =de_{d+2}-de_{3d+3},\\ m_{2d^2+1} & =\frac{1}{\zeta}e_{2d+1}-e_{4d+2},\\ m_{d^2+1} & =-\frac{1}{\zeta}(d+1)e_{d+1}+(d+1)e_{3d+2}, \end{aligned} \end{equation}
\begin{equation} \begin{aligned} m_1 & =-e_1+e_{2d+2},\\ m_{d^2} & =-\frac{d}{\zeta}e_{d}+de_{3d+1} ,\\ m_{d^2+2} & =de_{d+2}-de_{3d+3},\\ m_{2d^2+1} & =\frac{1}{\zeta}e_{2d+1}-e_{4d+2},\\ m_{d^2+1} & =-\frac{1}{\zeta}(d+1)e_{d+1}+(d+1)e_{3d+2}, \end{aligned} \end{equation}
which are mutually orthogonal and so generate a ![]() $5$-dimensional space
$5$-dimensional space ![]() $W$. Further
$W$. Further ![]() $W$ is contained in the orthogonal complement of
$W$ is contained in the orthogonal complement of ![]() $V$ so that
$V$ so that ![]() $\dim V+W = 4d-3$. Finally, look at the vectors
$\dim V+W = 4d-3$. Finally, look at the vectors
 \begin{equation} \begin{aligned} m_{(d-1)d+1} & =-\frac{d}{\zeta}e_1-\zeta^{d-1}e_d+de_{2d+2}+e_{3d+1},\\ m_{d(d+1)+1} & = \zeta e_{d+2}+d e_{2d+1}-e_{3d+3}-de_{4d+2}. \end{aligned} \end{equation}
\begin{equation} \begin{aligned} m_{(d-1)d+1} & =-\frac{d}{\zeta}e_1-\zeta^{d-1}e_d+de_{2d+2}+e_{3d+1},\\ m_{d(d+1)+1} & = \zeta e_{d+2}+d e_{2d+1}-e_{3d+3}-de_{4d+2}. \end{aligned} \end{equation}
They are clearly linearly independent so generate a ![]() $2$-dimensional
$2$-dimensional ![]() $U$. We can easily see that they do not belong in
$U$. We can easily see that they do not belong in ![]() $V+W$. Indeed, the only vector in
$V+W$. Indeed, the only vector in ![]() $V+W$ involving
$V+W$ involving ![]() $e_1$ is
$e_1$ is ![]() $m_1$, but note that it also involves
$m_1$, but note that it also involves ![]() $e_{2d+2}$ and the coefficients do not match that of
$e_{2d+2}$ and the coefficients do not match that of ![]() $m_{(d-1)d+1}$. Similarly, the only vector involving
$m_{(d-1)d+1}$. Similarly, the only vector involving ![]() $e_{d+2}$ in
$e_{d+2}$ in ![]() $V+W$ is
$V+W$ is ![]() $m_{d^2+2}$, which also involves
$m_{d^2+2}$, which also involves ![]() $e_{3d+3}$ in a way that does not match
$e_{3d+3}$ in a way that does not match ![]() $m_{d(d+1)+1}$.
$m_{d(d+1)+1}$.
Thus the rank of our matrix is at least ![]() $\dim V+W+U = 4d-1$ and the lemma follows.
$\dim V+W+U = 4d-1$ and the lemma follows.
Remark 7.4 It is necessary to take a root of unity with order at least ![]() $(d+1)$ for the dimension in Lemma 7.3 to be
$(d+1)$ for the dimension in Lemma 7.3 to be ![]() $4d-1$. Clearly, the dimension is smaller for
$4d-1$. Clearly, the dimension is smaller for ![]() $\zeta =1$. If, on the other hand, we chose
$\zeta =1$. If, on the other hand, we chose ![]() $\zeta$ with
$\zeta$ with ![]() $\zeta ^d=\zeta ^k$ for some
$\zeta ^d=\zeta ^k$ for some ![]() $k\in \{0,\ldots, d-2\}$, then (at least) two nonzero columns of the matrix
$k\in \{0,\ldots, d-2\}$, then (at least) two nonzero columns of the matrix ![]() $M$ in the proof of Lemma 7.3 are related. For instance, we have
$M$ in the proof of Lemma 7.3 are related. For instance, we have
7.5 Proof of Theorem 7.1
With Theorem 1.10 in hand, we can now complete the proof of Theorem 7.1.
Enumerate the roots of unity as ![]() $\{\xi _i\}_{i\geq 1}$, in any order. For pairs
$\{\xi _i\}_{i\geq 1}$, in any order. For pairs ![]() $(f,g) \in S_d$ near
$(f,g) \in S_d$ near ![]() $(f_0, g_0)$, let
$(f_0, g_0)$, let ![]() $P_i$ (respectively,
$P_i$ (respectively, ![]() $Q_i$) denote a parameterization of the preperiodic point of
$Q_i$) denote a parameterization of the preperiodic point of ![]() $f$ (respectively,
$f$ (respectively, ![]() $g$) that agrees with
$g$) that agrees with ![]() $\xi _i$ at
$\xi _i$ at ![]() $(f_0, g_0)$. By stability, each of these
$(f_0, g_0)$. By stability, each of these ![]() $P_i$ and
$P_i$ and ![]() $Q_i$ is well defined and smooth at
$Q_i$ is well defined and smooth at ![]() $(f_0, g_0)$. Note also that the subvariety of
$(f_0, g_0)$. Note also that the subvariety of ![]() $S_d$ defined by
$S_d$ defined by ![]() $V_1 = \{P_1 = Q_1\}$ cannot be all of
$V_1 = \{P_1 = Q_1\}$ cannot be all of ![]() $S_d$, because there exist pairs
$S_d$, because there exist pairs ![]() $(f,g)$ with all of their preperiodic points disjoint. Thus, the codimension of
$(f,g)$ with all of their preperiodic points disjoint. Thus, the codimension of ![]() $V_1$ is 1. Now consider the subvarieties
$V_1$ is 1. Now consider the subvarieties ![]() $V_i = \{P_i = Q_i\}$ and their intersections with
$V_i = \{P_i = Q_i\}$ and their intersections with ![]() $V_1$, for all
$V_1$, for all ![]() $i$. If all of them coincide with
$i$. If all of them coincide with ![]() $V_1$ near
$V_1$ near ![]() $(f_0, g_0)$, then we would have
$(f_0, g_0)$, then we would have ![]() $\mathrm {Preper}(f) \cap J(f) = \mathrm {Preper}(g) \cap J(g)$ persistently along
$\mathrm {Preper}(f) \cap J(f) = \mathrm {Preper}(g) \cap J(g)$ persistently along ![]() $V_1$ near
$V_1$ near ![]() $(f_0, g_0)$. This contradicts Theorem 1.10. Therefore, there exists an index
$(f_0, g_0)$. This contradicts Theorem 1.10. Therefore, there exists an index ![]() $i$ so that
$i$ so that ![]() $V_1 \cap V_i$ has codimension 2 near
$V_1 \cap V_i$ has codimension 2 near ![]() $(f_0, g_0)$. Continuing inductively in this way, we find a
$(f_0, g_0)$. Continuing inductively in this way, we find a ![]() $(4d-1)$-tuple of roots of unity that form a rigid
$(4d-1)$-tuple of roots of unity that form a rigid ![]() $(4d-1)$-repeller at
$(4d-1)$-repeller at ![]() $(f_0, g_0)$.
$(f_0, g_0)$.
This completes the proof of Theorem 7.1.
8. Lattès maps
In this final section, we prove Theorem 1.3, restated here as Theorem 8.1.
Let ![]() ${\mathcal {L}}$ denote the Legendre family of flexible Lattès maps in degree 4, defined by
${\mathcal {L}}$ denote the Legendre family of flexible Lattès maps in degree 4, defined by
for ![]() $t \in {\mathbb {C}}\setminus \{0,1\}$. This
$t \in {\mathbb {C}}\setminus \{0,1\}$. This ![]() $f_t$ is the quotient of the multiplication-by-2 endomorphism of the Legendre elliptic curve
$f_t$ is the quotient of the multiplication-by-2 endomorphism of the Legendre elliptic curve
via the projection ![]() $(x,y)\mapsto x$. The preperiodic points of
$(x,y)\mapsto x$. The preperiodic points of ![]() $f_t$ coincide with the projection of the torsion points of
$f_t$ coincide with the projection of the torsion points of ![]() $E_t$.
$E_t$.
Theorem 8.1 For each degree ![]() $d\geq 2$, there exists a uniform bound
$d\geq 2$, there exists a uniform bound ![]() $M_d$ so that either
$M_d$ so that either
for all pairs ![]() $(f,g)$ with
$(f,g)$ with ![]() $f \in {\mathcal {L}}$ and
$f \in {\mathcal {L}}$ and ![]() $g \in \mathrm {Rat}_d$.
$g \in \mathrm {Rat}_d$.
Corollary 8.2 There exists a constant ![]() $M>0$ such that for every pair of elliptic curves
$M>0$ such that for every pair of elliptic curves ![]() $E_1$ and
$E_1$ and ![]() $E_2$ over
$E_2$ over ![]() ${\mathbb {C}}$, equipped with degree-two projections
${\mathbb {C}}$, equipped with degree-two projections ![]() $\pi _i: E_i \to {\mathbb {P}}^1$ ramified at the 2-torsion points
$\pi _i: E_i \to {\mathbb {P}}^1$ ramified at the 2-torsion points ![]() $E_i[2]$, we have
$E_i[2]$, we have
if and only if ![]() $\pi _1(E_1[2]) \not = \pi _2(E_2[2])$.
$\pi _1(E_1[2]) \not = \pi _2(E_2[2])$.
Corollary 8.3 Let ![]() $\mu _{\infty }\subset {\mathbb {C}}$ denote the set of roots of unity. There exists a constant
$\mu _{\infty }\subset {\mathbb {C}}$ denote the set of roots of unity. There exists a constant ![]() $B>0$ such that
$B>0$ such that
for every elliptic curve ![]() $E$ defined over
$E$ defined over ![]() ${\mathbb {C}}$ and any degree-2 projection
${\mathbb {C}}$ and any degree-2 projection ![]() $\pi :E\to {\mathbb {P}}^1$ ramified at the 2-torsion points of
$\pi :E\to {\mathbb {P}}^1$ ramified at the 2-torsion points of ![]() $E$.
$E$.
8.1 Non-isotriviality
Fix a degree ![]() $d \geq 2$. Let
$d \geq 2$. Let ![]() ${\mathcal {L}}(d) := {\mathcal {L}} \times \mathrm {Rat}_d$. Consider the map
${\mathcal {L}}(d) := {\mathcal {L}} \times \mathrm {Rat}_d$. Consider the map ![]() ${\mathcal {L}}(d) \to \mathrm {Rat}_{d^2} \times \mathrm {Rat}_{d^2}$ which sends a pair
${\mathcal {L}}(d) \to \mathrm {Rat}_{d^2} \times \mathrm {Rat}_{d^2}$ which sends a pair ![]() $(f_t, g)$ to the pair
$(f_t, g)$ to the pair ![]() $(f_{d,t}, g^2)$, where
$(f_{d,t}, g^2)$, where ![]() $f_{d,t}$ is the quotient of the multiplication-by-
$f_{d,t}$ is the quotient of the multiplication-by-![]() $d$ endomorphism on the elliptic curve
$d$ endomorphism on the elliptic curve ![]() $E_t$ and
$E_t$ and ![]() $g^2$ is the second iterate of
$g^2$ is the second iterate of ![]() $g$. Note that
$g$. Note that ![]() $\mathrm {Preper}(f_t) = \mathrm {Preper}(f_{d,t})$ for all
$\mathrm {Preper}(f_t) = \mathrm {Preper}(f_{d,t})$ for all ![]() $t\in {\mathbb {C}}\setminus \{0,1\}$ and
$t\in {\mathbb {C}}\setminus \{0,1\}$ and ![]() $\mathrm {Preper}(g) = \mathrm {Preper}(g^2)$.
$\mathrm {Preper}(g) = \mathrm {Preper}(g^2)$.
Proposition 8.4 The induced map ![]() ${\mathcal {L}}(d) \to (\mathrm {Rat}_{d^2} \times \mathrm {Rat}_{d^2})/\operatorname {Aut}{\mathbb {P}}^1$ to the moduli space of pairs is finite-to-one, so
${\mathcal {L}}(d) \to (\mathrm {Rat}_{d^2} \times \mathrm {Rat}_{d^2})/\operatorname {Aut}{\mathbb {P}}^1$ to the moduli space of pairs is finite-to-one, so ![]() $S = {\mathcal {L}}(d)$ parametrizes a maximally non-isotrivial family of pairs of maps of degree
$S = {\mathcal {L}}(d)$ parametrizes a maximally non-isotrivial family of pairs of maps of degree ![]() $d^2$.
$d^2$.
Proof. Two maps ![]() $f_{d, t_1}$ and
$f_{d, t_1}$ and ![]() $f_{d,t_2}$ are conjugate if and only if the elliptic curves
$f_{d,t_2}$ are conjugate if and only if the elliptic curves ![]() $E_{t_1}$ and
$E_{t_1}$ and ![]() $E_{t_2}$ are isomorphic. Moreover, the map
$E_{t_2}$ are isomorphic. Moreover, the map ![]() $\mathrm {Rat}_d \to \mathrm {Rat}_{d^2}$ defined by iteration is finite, because it is proper between affine varieties; see, e.g., [Reference DeMarcoDeM05, Corollary 0.3].
$\mathrm {Rat}_d \to \mathrm {Rat}_{d^2}$ defined by iteration is finite, because it is proper between affine varieties; see, e.g., [Reference DeMarcoDeM05, Corollary 0.3].
8.2 Non-degeneracy
Fix a degree ![]() $d \geq 2$. Let
$d \geq 2$. Let ![]() ${\mathcal {L}}(d) := {\mathcal {L}} \times \mathrm {Rat}_d$ parameterize the family of pairs of degree
${\mathcal {L}}(d) := {\mathcal {L}} \times \mathrm {Rat}_d$ parameterize the family of pairs of degree ![]() $d^2$ as in § 8.1.
$d^2$ as in § 8.1.
Proposition 8.5 Let ![]() $S \to {\mathcal {L}}(d)$ be a finite map from a smooth, irreducible quasiprojective algebraic variety
$S \to {\mathcal {L}}(d)$ be a finite map from a smooth, irreducible quasiprojective algebraic variety ![]() $S$ of dimension
$S$ of dimension ![]() $m \geq 1$, defined over
$m \geq 1$, defined over ![]() ${\mathbb {C}}$, and let
${\mathbb {C}}$, and let ![]() $\Phi = (f,g)$ be the associated algebraic family of pairs of degree
$\Phi = (f,g)$ be the associated algebraic family of pairs of degree ![]() $d^2$ over
$d^2$ over ![]() $S$. Then either there exists a rigid
$S$. Then either there exists a rigid ![]() $m$-repeller at some point
$m$-repeller at some point ![]() $s_0 \in S({\mathbb {C}})$ or
$s_0 \in S({\mathbb {C}})$ or ![]() $\mathrm {Preper}(f_s) = \mathrm {Preper}(g_s)$ for all
$\mathrm {Preper}(f_s) = \mathrm {Preper}(g_s)$ for all ![]() $s \in S({\mathbb {C}})$.
$s \in S({\mathbb {C}})$.
Proof. First note that ![]() $\Phi = (f,g)$ is maximally non-isotrivial, because the map to
$\Phi = (f,g)$ is maximally non-isotrivial, because the map to ![]() ${\mathcal {L}}(d)$ is finite. Let
${\mathcal {L}}(d)$ is finite. Let ![]() $m = \dim S$. Assume that we do not have
$m = \dim S$. Assume that we do not have ![]() $\mathrm {Preper}(f_s) = \mathrm {Preper}(g_s)$ for all
$\mathrm {Preper}(f_s) = \mathrm {Preper}(g_s)$ for all ![]() $s \in S({\mathbb {C}})$. To show the existence of a rigid
$s \in S({\mathbb {C}})$. To show the existence of a rigid ![]() $m$-repeller at a parameter
$m$-repeller at a parameter ![]() $s_0 \in S({\mathbb {C}})$, we repeat the arguments in the proof of Theorem 1.6 to build common preperiodic points. While Theorem 1.6 shows there are at least
$s_0 \in S({\mathbb {C}})$, we repeat the arguments in the proof of Theorem 1.6 to build common preperiodic points. While Theorem 1.6 shows there are at least ![]() $m$ common preperiodic points for a Zariski-dense set of pairs
$m$ common preperiodic points for a Zariski-dense set of pairs ![]() $(f_s, g_s)$ in
$(f_s, g_s)$ in ![]() $S({\mathbb {C}})$, it does not give control over whether they are repellers nor whether they will be rigid. We use the fact that
$S({\mathbb {C}})$, it does not give control over whether they are repellers nor whether they will be rigid. We use the fact that ![]() $f$ is Lattès to provide this.
$f$ is Lattès to provide this.
For simplicity, we first give the proof assuming that both ![]() $f$ and
$f$ and ![]() $g$ are Lattès maps throughout
$g$ are Lattès maps throughout ![]() $S$. In particular, the periodic points of
$S$. In particular, the periodic points of ![]() $f_s$ and
$f_s$ and ![]() $g_s$ are all repelling, for all
$g_s$ are all repelling, for all ![]() $s \in S({\mathbb {C}})$. Moreover, the subset of pairs
$s \in S({\mathbb {C}})$. Moreover, the subset of pairs ![]() $(f_s, g_s) \in S$ for which
$(f_s, g_s) \in S$ for which ![]() $\mathrm {Preper}(f_s) = \mathrm {Preper}(g_s)$ is a Zariski-closed algebraic subvariety
$\mathrm {Preper}(f_s) = \mathrm {Preper}(g_s)$ is a Zariski-closed algebraic subvariety ![]() $Z$. Indeed, we know from Theorem 2.1 and its proof that this set coincides with the set of pairs for which
$Z$. Indeed, we know from Theorem 2.1 and its proof that this set coincides with the set of pairs for which ![]() $\mu _{f_s} = \mu _{g_s}$, and so the pairs for which the corresponding elliptic curves are isomorphic and equipped with the same degree-2 projections to
$\mu _{f_s} = \mu _{g_s}$, and so the pairs for which the corresponding elliptic curves are isomorphic and equipped with the same degree-2 projections to ![]() ${\mathbb {P}}^1$. By replacing
${\mathbb {P}}^1$. By replacing ![]() $S$ with the Zariski open subset
$S$ with the Zariski open subset ![]() $S\setminus Z$, we may assume that
$S\setminus Z$, we may assume that ![]() $\mathrm {Preper}(f_s) \not = \mathrm {Preper}(g_s)$ for all
$\mathrm {Preper}(f_s) \not = \mathrm {Preper}(g_s)$ for all ![]() $s \in S$.
$s \in S$.
Let ![]() $P_1$ denote a hypersurface in
$P_1$ denote a hypersurface in ![]() $S \times {\mathbb {P}}^1$ parameterizing a periodic point for
$S \times {\mathbb {P}}^1$ parameterizing a periodic point for ![]() $f_s$, chosen so that it is not persistently preperiodic for
$f_s$, chosen so that it is not persistently preperiodic for ![]() $g$. If no such hypersurface exists, then we deduce that
$g$. If no such hypersurface exists, then we deduce that ![]() $\mathrm {Preper}(f) = \mathrm {Preper}(g)$ throughout
$\mathrm {Preper}(f) = \mathrm {Preper}(g)$ throughout ![]() $S$ (as a consequence of Theorem 2.1), which is a contradiction. Thus, we assume that we have such a
$S$ (as a consequence of Theorem 2.1), which is a contradiction. Thus, we assume that we have such a ![]() $P_1$. As in the proof of Theorem 1.6, we will apply Theorem 2.4 to the pair
$P_1$. As in the proof of Theorem 1.6, we will apply Theorem 2.4 to the pair ![]() $(g, P_1)$ over a branched cover
$(g, P_1)$ over a branched cover ![]() $S_1 \to S$ where
$S_1 \to S$ where ![]() $P_1$ may be viewed as the graph of a point in
$P_1$ may be viewed as the graph of a point in ![]() $S_1\times {\mathbb {P}}^1$. If the pair
$S_1\times {\mathbb {P}}^1$. If the pair ![]() $(g,P_1)$ is isotrivial over
$(g,P_1)$ is isotrivial over ![]() $S_1$, then we replace
$S_1$, then we replace ![]() $P_1$ with another periodic point for
$P_1$ with another periodic point for ![]() $f$. If the pair
$f$. If the pair ![]() $(g,P_1)$ is isotrivial for all periodic points
$(g,P_1)$ is isotrivial for all periodic points ![]() $P_1$ of a given large period
$P_1$ of a given large period ![]() $>2d^2$, then interpolation (as in the proof of Theorem 1.6) implies that the pair
$>2d^2$, then interpolation (as in the proof of Theorem 1.6) implies that the pair ![]() $(f,g)$ must be isotrivial, contradicting our assumption. We conclude from Theorem 2.4 that there exists a parameter
$(f,g)$ must be isotrivial, contradicting our assumption. We conclude from Theorem 2.4 that there exists a parameter ![]() $s_1 \in S_1({\mathbb {C}})$ at which
$s_1 \in S_1({\mathbb {C}})$ at which ![]() $P_1$ is preperiodic to a repelling point for
$P_1$ is preperiodic to a repelling point for ![]() $g_{s_1}$. We then let
$g_{s_1}$. We then let ![]() $P_1' \subset P_1$ be the subvariety of codimension 1 containing
$P_1' \subset P_1$ be the subvariety of codimension 1 containing ![]() $(s_1, P_1(s_1))$ along which both
$(s_1, P_1(s_1))$ along which both ![]() $f$ and
$f$ and ![]() $g$ are persistently preperiodic. Then
$g$ are persistently preperiodic. Then ![]() $P_1'$ projects to a subvariety
$P_1'$ projects to a subvariety ![]() $S_1' \subset S_1$ of codimension 1. We now repeat the argument with another periodic point
$S_1' \subset S_1$ of codimension 1. We now repeat the argument with another periodic point ![]() $P_2$ for
$P_2$ for ![]() $f$ over
$f$ over ![]() $S_1'$, distinct from
$S_1'$, distinct from ![]() $P_1'$. We continue inductively, using the fact that
$P_1'$. We continue inductively, using the fact that ![]() $(f,g)$ is maximally non-isotrivial, to find
$(f,g)$ is maximally non-isotrivial, to find ![]() $m$ distinct common preperiodic points at some parameter
$m$ distinct common preperiodic points at some parameter ![]() $s_0\in S({\mathbb {C}})$ that form a rigid
$s_0\in S({\mathbb {C}})$ that form a rigid ![]() $m$-repeller.
$m$-repeller.
Now we assume that ![]() $g$ is not everywhere Lattès. As the Lattès pairs
$g$ is not everywhere Lattès. As the Lattès pairs ![]() $(f,g)$ form a proper subvariety of
$(f,g)$ form a proper subvariety of ![]() $S$, we replace
$S$, we replace ![]() $S$ with a Zariski-open subset so that
$S$ with a Zariski-open subset so that ![]() $g$ is not a Lattès map for any
$g$ is not a Lattès map for any ![]() $s \in S({\mathbb {C}})$.
$s \in S({\mathbb {C}})$.
Again let ![]() $m = \dim S$. Let
$m = \dim S$. Let ![]() $P_1$ denote a hypersurface in
$P_1$ denote a hypersurface in ![]() $S \times {\mathbb {P}}^1$ parameterizing a periodic point for
$S \times {\mathbb {P}}^1$ parameterizing a periodic point for ![]() $f$, chosen so that it is not persistently preperiodic for
$f$, chosen so that it is not persistently preperiodic for ![]() $g$. If no such curve exists, then, as above, we have
$g$. If no such curve exists, then, as above, we have ![]() $\mathrm {Preper}(f) = \mathrm {Preper}(g)$ and we are done. Thus, we may assume that
$\mathrm {Preper}(f) = \mathrm {Preper}(g)$ and we are done. Thus, we may assume that ![]() $P_1$ exists. Again as in the proof of Theorem 1.6, we pass to a branched cover
$P_1$ exists. Again as in the proof of Theorem 1.6, we pass to a branched cover ![]() $S_1\to S$ so that
$S_1\to S$ so that ![]() $P_1$ may be viewed as the graph of a point in
$P_1$ may be viewed as the graph of a point in ![]() $S_1\times {\mathbb {P}}^1$. If the pair
$S_1\times {\mathbb {P}}^1$. If the pair ![]() $(g, P_1)$ is isotrivial, and if this holds for all choices of
$(g, P_1)$ is isotrivial, and if this holds for all choices of ![]() $P_1$, then the pair
$P_1$, then the pair ![]() $(f,g)$ is isotrivial by an interpolation argument, and we have a contradiction. So from Theorem 2.4, there exists a parameter
$(f,g)$ is isotrivial by an interpolation argument, and we have a contradiction. So from Theorem 2.4, there exists a parameter ![]() $s_1\in S_1({\mathbb {C}})$ where the point
$s_1\in S_1({\mathbb {C}})$ where the point ![]() $P_1$ is preperiodic to a repelling cycle for
$P_1$ is preperiodic to a repelling cycle for ![]() $g$, but not persistently so. As above, we let
$g$, but not persistently so. As above, we let ![]() $P_1' \subset P_1$ be the subvariety of codimension 1 containing
$P_1' \subset P_1$ be the subvariety of codimension 1 containing ![]() $(s_1, P_1(s_1))$ along which both
$(s_1, P_1(s_1))$ along which both ![]() $f$ and
$f$ and ![]() $g$ are persistently preperiodic. Then
$g$ are persistently preperiodic. Then ![]() $P_1'$ projects to a subvariety
$P_1'$ projects to a subvariety ![]() $S_1' \subset S_1$ of codimension 1.
$S_1' \subset S_1$ of codimension 1.
Since ![]() $P_1'$ is preperiodic to a repelling cycle for
$P_1'$ is preperiodic to a repelling cycle for ![]() $g_{s_1}$, there is an open neighborhood
$g_{s_1}$, there is an open neighborhood ![]() $U_1$ of
$U_1$ of ![]() $s_1$ in
$s_1$ in ![]() $S_1'$ on which that cycle remains repelling for
$S_1'$ on which that cycle remains repelling for ![]() $g_s$. The density of stability implies that we can find an open
$g_s$. The density of stability implies that we can find an open ![]() $V_1 \subset U_1$ on which the family
$V_1 \subset U_1$ on which the family ![]() $g_s$ is stable for
$g_s$ is stable for ![]() $s \in V_1$, so its Julia set (and, in particular, including all repelling periodic points) is moving holomorphically. As the family
$s \in V_1$, so its Julia set (and, in particular, including all repelling periodic points) is moving holomorphically. As the family ![]() $f$ is stable over all of
$f$ is stable over all of ![]() $S$, we also have a holomorphic motion of its preperiodic points, and these are dense in
$S$, we also have a holomorphic motion of its preperiodic points, and these are dense in ![]() ${\mathbb {P}}^1$ over every
${\mathbb {P}}^1$ over every ![]() $s\in S$. Thus there are only two possibilities: either there is a codimension-1 intersection of one of the pre-repelling points of
$s\in S$. Thus there are only two possibilities: either there is a codimension-1 intersection of one of the pre-repelling points of ![]() $g$ with a preperiodic point
$g$ with a preperiodic point ![]() $\not = P_1'$ of
$\not = P_1'$ of ![]() $f$ at some parameter in
$f$ at some parameter in ![]() $V_1$, or each of the preperiodic points of
$V_1$, or each of the preperiodic points of ![]() $g$ in its Julia set becomes a leaf of the holomorphic motion of the Julia set of
$g$ in its Julia set becomes a leaf of the holomorphic motion of the Julia set of ![]() $f$. In the latter case, by analytic continuation, this shared holomorphic motion must persist over all of
$f$. In the latter case, by analytic continuation, this shared holomorphic motion must persist over all of ![]() $S_1'$. But then the algebraic family of maps
$S_1'$. But then the algebraic family of maps ![]() $g$ must itself be stable on all of
$g$ must itself be stable on all of ![]() $S_1'$, as there would be no collisions between the distinct periodic points; see § 2.5. It follows from McMullen's theorem [Reference McMullenMcM87] that
$S_1'$, as there would be no collisions between the distinct periodic points; see § 2.5. It follows from McMullen's theorem [Reference McMullenMcM87] that ![]() $g$ is also a family of Lattès maps, which is a contradiction. Thus, we can find a parameter
$g$ is also a family of Lattès maps, which is a contradiction. Thus, we can find a parameter ![]() $s_2 \in V_1$ so that preperiodic points of
$s_2 \in V_1$ so that preperiodic points of ![]() $f$ and
$f$ and ![]() $g$ in their Julia sets intersect in a subvariety of codimension 1 in
$g$ in their Julia sets intersect in a subvariety of codimension 1 in ![]() $V_1 \times {\mathbb {P}}^1$.
$V_1 \times {\mathbb {P}}^1$.
The proof is completed by induction on dimension.
8.3 Proof of Theorem 8.1 and its corollaries
Proof of Theorem 8.1 Fix a degree ![]() $d \geq 2$. As in § 8.1, we let
$d \geq 2$. As in § 8.1, we let ![]() ${\mathcal {L}}(d) = {\mathcal {L}} \times \mathrm {Rat}_d$ and let
${\mathcal {L}}(d) = {\mathcal {L}} \times \mathrm {Rat}_d$ and let ![]() $\Phi = (f,g)$ denote the algebraic family of maps of degree
$\Phi = (f,g)$ denote the algebraic family of maps of degree ![]() $d^2$ parameterized by
$d^2$ parameterized by ![]() ${\mathcal {L}}(d)$. This
${\mathcal {L}}(d)$. This ![]() $\Phi$ is maximally non-isotrivial, by Proposition 8.4. Note that
$\Phi$ is maximally non-isotrivial, by Proposition 8.4. Note that ![]() $\dim {\mathcal {L}}(d) = 2d+2$.
$\dim {\mathcal {L}}(d) = 2d+2$.
Since there exist ![]() $g \in \mathrm {Rat}_d$ with Julia sets
$g \in \mathrm {Rat}_d$ with Julia sets ![]() $J(g) \not = {\mathbb {P}}^1$, we do not have
$J(g) \not = {\mathbb {P}}^1$, we do not have ![]() $\mathrm {Preper}(f_s) = \mathrm {Preper}(g_s)$ for all
$\mathrm {Preper}(f_s) = \mathrm {Preper}(g_s)$ for all ![]() $s \in {\mathcal {L}}(d)$. Thus, from Proposition 8.5, there exists a rigid
$s \in {\mathcal {L}}(d)$. Thus, from Proposition 8.5, there exists a rigid ![]() $(2d+2)$-repeller at some parameter
$(2d+2)$-repeller at some parameter ![]() $s_0 \in {\mathcal {L}}(d)$. It follows from Corollary 4.9 that the pairwise-bifurcation measure
$s_0 \in {\mathcal {L}}(d)$. It follows from Corollary 4.9 that the pairwise-bifurcation measure ![]() $\mu _{\Phi, \Delta }$ is nonzero on
$\mu _{\Phi, \Delta }$ is nonzero on ![]() ${\mathcal {L}}(d)$. Then from Theorem 5.2, there exists a Zariski-closed subvariety
${\mathcal {L}}(d)$. Then from Theorem 5.2, there exists a Zariski-closed subvariety ![]() $V_1 \subset {\mathcal {L}}(d)$ of codimension 1, defined over
$V_1 \subset {\mathcal {L}}(d)$ of codimension 1, defined over ![]() $\overline {\mathbb {Q}}$, and a constant
$\overline {\mathbb {Q}}$, and a constant ![]() $M_1$ so that
$M_1$ so that
for all ![]() $s \in ({\mathcal {L}}(d) \setminus V_1)({\mathbb {C}})$.
$s \in ({\mathcal {L}}(d) \setminus V_1)({\mathbb {C}})$.
We then repeat these arguments on each irreducible component ![]() $V_1'$ of
$V_1'$ of ![]() $V_1$. Either
$V_1$. Either ![]() $\mathrm {Preper}(f_s) = \mathrm {Preper}(g_s)$ for all
$\mathrm {Preper}(f_s) = \mathrm {Preper}(g_s)$ for all ![]() $s \in V_1'({\mathbb {C}})$ or there is a subvariety
$s \in V_1'({\mathbb {C}})$ or there is a subvariety ![]() $V_2' \subset V_1'$ of codimension 1, defined over
$V_2' \subset V_1'$ of codimension 1, defined over ![]() $\overline {\mathbb {Q}}$, and a constant
$\overline {\mathbb {Q}}$, and a constant ![]() $M_2$ so that
$M_2$ so that ![]() $\# \mathrm {Preper}(f_s) \cap \mathrm {Preper}(g_s) \leq M_2$ for all
$\# \mathrm {Preper}(f_s) \cap \mathrm {Preper}(g_s) \leq M_2$ for all ![]() $s \in V_1' \setminus V_2')({\mathbb {C}})$. We let
$s \in V_1' \setminus V_2')({\mathbb {C}})$. We let ![]() $V_2$ be the union over all of the
$V_2$ be the union over all of the ![]() $V_2'$. It has codimension 2 in
$V_2'$. It has codimension 2 in ![]() ${\mathcal {L}}(d)$. Induction on dimension completes the proof.
${\mathcal {L}}(d)$. Induction on dimension completes the proof.
Proof of Corollary 8.2 We apply Theorem 8.1 to the algebraic family of pairs ![]() $\Phi = (f,g)$ for
$\Phi = (f,g)$ for ![]() $f \in {\mathcal {L}}$ and
$f \in {\mathcal {L}}$ and ![]() $g$ the family of all conjugates of maps in
$g$ the family of all conjugates of maps in ![]() ${\mathcal {L}}$. More precisely, we consider the subvariety
${\mathcal {L}}$. More precisely, we consider the subvariety ![]() $V \subset \mathrm {Rat}_4$ of all maps that are conjugate to elements of
$V \subset \mathrm {Rat}_4$ of all maps that are conjugate to elements of ![]() ${\mathcal {L}}$ by Möbius transformations, and let
${\mathcal {L}}$ by Möbius transformations, and let ![]() $S = {\mathcal {L}} \times V$. Theorem 8.1 then implies that there is a constant
$S = {\mathcal {L}} \times V$. Theorem 8.1 then implies that there is a constant ![]() $M$ so that either
$M$ so that either
for all ![]() $s \in S({\mathbb {C}})$. For any pair of elliptic curves
$s \in S({\mathbb {C}})$. For any pair of elliptic curves ![]() $E_1$ and
$E_1$ and ![]() $E_2$ over
$E_2$ over ![]() ${\mathbb {C}}$, equipped with their degree-two projections
${\mathbb {C}}$, equipped with their degree-two projections ![]() $\pi _i: E_i\to {\mathbb {P}}^1$, there exists a Möbius transformation
$\pi _i: E_i\to {\mathbb {P}}^1$, there exists a Möbius transformation ![]() $A \in \operatorname {Aut}{\mathbb {P}}^1$ and an
$A \in \operatorname {Aut}{\mathbb {P}}^1$ and an ![]() $s \in S({\mathbb {C}})$ so that
$s \in S({\mathbb {C}})$ so that
Observing also that ![]() $\pi _1(E_1[2]) = \pi _2(E_2[2])$ if and only if
$\pi _1(E_1[2]) = \pi _2(E_2[2])$ if and only if ![]() $\pi _1(E_1^{\mathrm {tors}}) = \pi _2(E_2^{\mathrm {tors}})$ if and only
$\pi _1(E_1^{\mathrm {tors}}) = \pi _2(E_2^{\mathrm {tors}})$ if and only ![]() $\mathrm {Preper}(f_s) = \mathrm {Preper}(g_s)$, the proof is complete.
$\mathrm {Preper}(f_s) = \mathrm {Preper}(g_s)$, the proof is complete.
Proof of Corollary 8.3 We apply Theorem 8.1 to the algebraic family of pairs ![]() $\Phi = (f,g)$ for
$\Phi = (f,g)$ for ![]() $f \in {\mathcal {L}}$ and
$f \in {\mathcal {L}}$ and ![]() $g$ the family of all conjugates of the map
$g$ the family of all conjugates of the map ![]() $g_0(z) = z^2$. More precisely, let
$g_0(z) = z^2$. More precisely, let ![]() $V \subset \mathrm {Rat}_2$ be the
$V \subset \mathrm {Rat}_2$ be the ![]() $\operatorname {Aut}{\mathbb {P}}^1$-orbit of
$\operatorname {Aut}{\mathbb {P}}^1$-orbit of ![]() $g_0$. Note that
$g_0$. Note that ![]() $\mathrm {Preper}(g_0) \supset \mu _\infty$, the set of all roots of unity. Let
$\mathrm {Preper}(g_0) \supset \mu _\infty$, the set of all roots of unity. Let ![]() $S = {\mathcal {L}} \times V$. For any elliptic curve
$S = {\mathcal {L}} \times V$. For any elliptic curve ![]() $E$ over
$E$ over ![]() ${\mathbb {C}}$, equipped with its degree-two projection
${\mathbb {C}}$, equipped with its degree-two projection ![]() $\pi : E \to {\mathbb {P}}^1$, there exists a Möbius transformation
$\pi : E \to {\mathbb {P}}^1$, there exists a Möbius transformation ![]() $A \in \operatorname {Aut}{\mathbb {P}}^1$ and an
$A \in \operatorname {Aut}{\mathbb {P}}^1$ and an ![]() $s \in S({\mathbb {C}})$ so that
$s \in S({\mathbb {C}})$ so that
Note that we cannot have ![]() $\mathrm {Preper}(f_s) = \mathrm {Preper}(g_s)$ for any
$\mathrm {Preper}(f_s) = \mathrm {Preper}(g_s)$ for any ![]() $s \in S({\mathbb {C}})$, because the Julia set of
$s \in S({\mathbb {C}})$, because the Julia set of ![]() $g_s$ is a circle while
$g_s$ is a circle while ![]() $J(f_s) = {\mathbb {P}}^1$. We apply Theorem 8.1 to complete the proof.
$J(f_s) = {\mathbb {P}}^1$. We apply Theorem 8.1 to complete the proof.
Acknowledgements
We would like to thank Thomas Gauthier, Trevor Hyde, Harry Schmidt, and Gabriel Vigny for many helpful discussions during the preparation of this article. We also thank the referee for his careful reading and interesting questions. The authors were supported by grants DMS-2050037 and DMS-2200981 from the National Science Foundation.
Conflicts of interest
None.