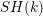1 Introduction
By the celebrated Serre finiteness theorem [Reference SerreSer53] the positive stable homotopy groups of the classical sphere spectrum with rational coefficients are zero. This implies that the stable homotopy category of
![]() $S^{1}$
-spectra with rational coefficients
$S^{1}$
-spectra with rational coefficients
![]() $SH_{\mathbb{Q}}$
is naturally equivalent to the homotopy category of
$SH_{\mathbb{Q}}$
is naturally equivalent to the homotopy category of
![]() $H\mathbb{Q}$
-modules
$H\mathbb{Q}$
-modules
![]() $\operatorname{Ho}(\operatorname{Mod}H\mathbb{Q})$
, where
$\operatorname{Ho}(\operatorname{Mod}H\mathbb{Q})$
, where
![]() $H\mathbb{Q}$
is the Eilenberg–Mac Lane symmetric spectrum of
$H\mathbb{Q}$
is the Eilenberg–Mac Lane symmetric spectrum of
![]() $\mathbb{Q}$
. By the Robinson theorem [Reference RobinsonRob87] the homotopy category of
$\mathbb{Q}$
. By the Robinson theorem [Reference RobinsonRob87] the homotopy category of
![]() $HA$
-modules
$HA$
-modules
![]() $\operatorname{Ho}(\operatorname{Mod}HA)$
, where
$\operatorname{Ho}(\operatorname{Mod}HA)$
, where
![]() $A$
is a ring with identity, is equivalent to the derived category
$A$
is a ring with identity, is equivalent to the derived category
![]() $D(A)$
of
$D(A)$
of
![]() $A$
. Thus
$A$
. Thus
![]() $SH_{\mathbb{Q}}$
is naturally equivalent to the derived category of rational vector spaces
$SH_{\mathbb{Q}}$
is naturally equivalent to the derived category of rational vector spaces
![]() $D(\mathbb{Q})$
.
$D(\mathbb{Q})$
.
In the motivic world the role of a ring is played by a ‘preadditive category of correspondences’
![]() ${\mathcal{A}}$
whose objects are the smooth algebraic varieties
${\mathcal{A}}$
whose objects are the smooth algebraic varieties
![]() $Sm/k$
over a field
$Sm/k$
over a field
![]() $k$
. Using the category theory terminology,
$k$
. Using the category theory terminology,
![]() ${\mathcal{A}}$
is a ring with several objects, whose objects are those of
${\mathcal{A}}$
is a ring with several objects, whose objects are those of
![]() $Sm/k$
. In turn, the role of the classical derived category over a ring is played by the category
$Sm/k$
. In turn, the role of the classical derived category over a ring is played by the category
![]() $DM_{{\mathcal{A}}}(k)$
, which is just an extension of the celebrated Voevodsky triangulated category [Reference Voevodsky, Voevodsky, Suslin and FriedlanderVoe00b]
$DM_{{\mathcal{A}}}(k)$
, which is just an extension of the celebrated Voevodsky triangulated category [Reference Voevodsky, Voevodsky, Suslin and FriedlanderVoe00b]
![]() $DM(k)$
to general correspondences. Since motivic homotopy theory requires the Nisnevich topology and contractability of the affine line
$DM(k)$
to general correspondences. Since motivic homotopy theory requires the Nisnevich topology and contractability of the affine line
![]() $\mathbb{A}^{1}$
, we require the relevant properties for
$\mathbb{A}^{1}$
, we require the relevant properties for
![]() ${\mathcal{A}}$
to satisfy (see § 2 for details).
${\mathcal{A}}$
to satisfy (see § 2 for details).
The rational stable motivic homotopy theory
![]() $SH(k)_{\mathbb{Q}}$
splits in two parts:
$SH(k)_{\mathbb{Q}}$
splits in two parts:
![]() $SH^{+}(k)_{\mathbb{Q}}$
and
$SH^{+}(k)_{\mathbb{Q}}$
and
![]() $SH^{-}(k)_{\mathbb{Q}}$
. The plus part
$SH^{-}(k)_{\mathbb{Q}}$
. The plus part
![]() $SH^{+}(k)_{\mathbb{Q}}$
is equivalent to Voevodsky’s
$SH^{+}(k)_{\mathbb{Q}}$
is equivalent to Voevodsky’s
![]() $DM(k)_{\mathbb{Q}}$
(this follows from a theorem of Cisinski and Déglise [Reference Cisinski and DégliseCD12, Theorem 16.2.13]). Ananyevskiy, Levine and Panin [Reference Ananyevskiy, Levine and PaninALP17] have computed
$DM(k)_{\mathbb{Q}}$
(this follows from a theorem of Cisinski and Déglise [Reference Cisinski and DégliseCD12, Theorem 16.2.13]). Ananyevskiy, Levine and Panin [Reference Ananyevskiy, Levine and PaninALP17] have computed
![]() $SH^{-}(k)_{\mathbb{Q}}$
as the category of Witt motives with rational coefficients (see also Bachmann [Reference BachmannBac18]). Using these results, we show in Theorem 4.2 that the rational motivic sphere spectrum
$SH^{-}(k)_{\mathbb{Q}}$
as the category of Witt motives with rational coefficients (see also Bachmann [Reference BachmannBac18]). Using these results, we show in Theorem 4.2 that the rational motivic sphere spectrum
![]() $\mathbb{S}\otimes \mathbb{Q}$
is naturally equivalent to the ‘additive motivic sphere spectrum’
$\mathbb{S}\otimes \mathbb{Q}$
is naturally equivalent to the ‘additive motivic sphere spectrum’
![]() $\mathbb{S}^{\text{MW}}\otimes \mathbb{Q}$
associated with the additive category of finite Milnor–Witt correspondences
$\mathbb{S}^{\text{MW}}\otimes \mathbb{Q}$
associated with the additive category of finite Milnor–Witt correspondences
![]() $\widetilde{\operatorname{Cor}}$
in the sense of Calmès and Fasel [Reference Calmès and FaselCF14].
$\widetilde{\operatorname{Cor}}$
in the sense of Calmès and Fasel [Reference Calmès and FaselCF14].
Next, we extend the Röndigs–Østvær theorem [Reference Röndigs and ØstværRØ08a, Theorem 1] to the triangulated category
![]() $DM_{{\mathcal{A}}}(k)$
(see Theorem 5.3). This extension is of independent interest. For example, it is of great utility to compare various triangulated categories of motives in [Reference GarkushaGar18]. The generalized Röndigs–Østvær theorem can also be regarded as a motivic counterpart of the Robinson theorem [Reference RobinsonRob87].
$DM_{{\mathcal{A}}}(k)$
(see Theorem 5.3). This extension is of independent interest. For example, it is of great utility to compare various triangulated categories of motives in [Reference GarkushaGar18]. The generalized Röndigs–Østvær theorem can also be regarded as a motivic counterpart of the Robinson theorem [Reference RobinsonRob87].
Theorem 4.2 computing
![]() $\mathbb{S}\,\otimes \,\mathbb{Q}$
and the generalized Röndigs–Østvær’s theorem (Theorem 5.3) together lead to the proof of the main result of the paper which is formulated as follows (see Theorem 5.5).
$\mathbb{S}\,\otimes \,\mathbb{Q}$
and the generalized Röndigs–Østvær’s theorem (Theorem 5.3) together lead to the proof of the main result of the paper which is formulated as follows (see Theorem 5.5).
Theorem (Reconstruction). If
![]() $k$
is an infinite perfect field of characteristic not
$k$
is an infinite perfect field of characteristic not
![]() $2$
, then
$2$
, then
![]() $SH(k)_{\mathbb{Q}}$
is equivalent to the triangulated category of Milnor–Witt motives with rational coefficients
$SH(k)_{\mathbb{Q}}$
is equivalent to the triangulated category of Milnor–Witt motives with rational coefficients
![]() $DM_{\text{MW}}(k)_{\mathbb{Q}}$
in the sense of [Reference Déglise and FaselDF17]. The equivalence preserves the triangulated structure.
$DM_{\text{MW}}(k)_{\mathbb{Q}}$
in the sense of [Reference Déglise and FaselDF17]. The equivalence preserves the triangulated structure.
One of the approaches to constructing motivic homotopy theory, pioneered by Voevodsky, is to use various correspondences on smooth algebraic varieties. This approach has many computational advantages. Voevodsky [Reference Voevodsky, Voevodsky, Suslin and FriedlanderVoe00b] constructed the category of motives
![]() $DM(k)$
by using finite correspondences. Later he developed the theory of framed correspondences [Reference VoevodskyVoe01]. One of the aims was to suggest another framework for Morel and Voevodsky’s stable motivic homotopy theory
$DM(k)$
by using finite correspondences. Later he developed the theory of framed correspondences [Reference VoevodskyVoe01]. One of the aims was to suggest another framework for Morel and Voevodsky’s stable motivic homotopy theory
![]() $SH(k)$
. In [Reference Garkusha and PaninGP14b] the author and Panin use Voevodsky’s theory to develop the theory of big framed motives which converts the classical Morel–Voevodsky stable motivic homotopy theory into an equivalent local theory of framed bispectra.
$SH(k)$
. In [Reference Garkusha and PaninGP14b] the author and Panin use Voevodsky’s theory to develop the theory of big framed motives which converts the classical Morel–Voevodsky stable motivic homotopy theory into an equivalent local theory of framed bispectra.
One of the central objects of the theory of (big) framed motives in the sense of [Reference Garkusha and PaninGP14b] is linear framed motives of algebraic varieties. These are explicitly constructed complexes of Nisnevich sheaves with framed correspondences
![]() $\mathbb{Z}F(-\times \unicode[STIX]{x1D6E5}^{\bullet },X)$
, where
$\mathbb{Z}F(-\times \unicode[STIX]{x1D6E5}^{\bullet },X)$
, where
![]() $X\in Sm/k$
. As an application of the reconstruction theorem we prove the following result comparing motivic complexes with framed and Milnor–Witt correspondences respectively (see Theorem 6.1).
$X\in Sm/k$
. As an application of the reconstruction theorem we prove the following result comparing motivic complexes with framed and Milnor–Witt correspondences respectively (see Theorem 6.1).
Theorem (Comparison). Given an infinite perfect field of characteristic not
![]() $2$
and a
$2$
and a
![]() $k$
-smooth scheme
$k$
-smooth scheme
![]() $X$
, each morphism of complexes of Nisnevich sheaves
$X$
, each morphism of complexes of Nisnevich sheaves
is a quasi-isomorphism, where the left complex is the
![]() $n$
-twisted linear framed motive of
$n$
-twisted linear framed motive of
![]() $X$
with rational coefficients in the sense of [Reference Garkusha and PaninGP14b].
$X$
with rational coefficients in the sense of [Reference Garkusha and PaninGP14b].
Throughout the paper we denote by
![]() $Sm/k$
the category of smooth separated schemes of finite type over the base field
$Sm/k$
the category of smooth separated schemes of finite type over the base field
![]() $k$
.
$k$
.
2 Additive categories of correspondences
In this section we set up a framework within which we shall work later.
Definition 2.1. We say that a preadditive category
![]() ${\mathcal{A}}$
is a category of correspondences if the following conditions apply.
${\mathcal{A}}$
is a category of correspondences if the following conditions apply.
(i) Its objects are those of
![]() $Sm/k$
. Its morphisms are also referred to as
$Sm/k$
. Its morphisms are also referred to as
![]() ${\mathcal{A}}$
-correspondences or just correspondences.
${\mathcal{A}}$
-correspondences or just correspondences.
(ii) There is a functor
![]() $\unicode[STIX]{x1D70C}:Sm/k\rightarrow {\mathcal{A}}$
which is the identity map on objects. The image
$\unicode[STIX]{x1D70C}:Sm/k\rightarrow {\mathcal{A}}$
which is the identity map on objects. The image
![]() $\unicode[STIX]{x1D70C}(f)$
of a morphism of smooth schemes
$\unicode[STIX]{x1D70C}(f)$
of a morphism of smooth schemes
![]() $f:X\rightarrow Y$
will be referred to as the graph of
$f:X\rightarrow Y$
will be referred to as the graph of
![]() $f$
and denoted by
$f$
and denoted by
![]() $\unicode[STIX]{x1D6E4}_{f}$
. We have, in particular, that
$\unicode[STIX]{x1D6E4}_{f}$
. We have, in particular, that
![]() $\unicode[STIX]{x1D6E4}_{gf}=\unicode[STIX]{x1D6E4}_{g}\circ \unicode[STIX]{x1D6E4}_{f}$
and
$\unicode[STIX]{x1D6E4}_{gf}=\unicode[STIX]{x1D6E4}_{g}\circ \unicode[STIX]{x1D6E4}_{f}$
and
![]() $\unicode[STIX]{x1D6E4}_{\operatorname{id}}=\operatorname{id}$
. Thus we have a functor
$\unicode[STIX]{x1D6E4}_{\operatorname{id}}=\operatorname{id}$
. Thus we have a functor
such that
![]() ${\mathcal{A}}(1_{X},g)=\unicode[STIX]{x1D6E4}_{g}\circ -$
and
${\mathcal{A}}(1_{X},g)=\unicode[STIX]{x1D6E4}_{g}\circ -$
and
![]() ${\mathcal{A}}(h,1_{Y})=-\circ \unicode[STIX]{x1D6E4}_{h}$
.
${\mathcal{A}}(h,1_{Y})=-\circ \unicode[STIX]{x1D6E4}_{h}$
.
(iii) For every elementary Nisnevich square

the sequence of Nisnevich sheaves
is exact. Moreover, we require
![]() ${\mathcal{A}}(-,\emptyset )_{\operatorname{nis}}=0$
(corresponding to the ‘degenerate distinguished square’,
${\mathcal{A}}(-,\emptyset )_{\operatorname{nis}}=0$
(corresponding to the ‘degenerate distinguished square’,
![]() $\emptyset$
, with only one entry in the lower right-hand corner).
$\emptyset$
, with only one entry in the lower right-hand corner).
(iv) For every
![]() ${\mathcal{A}}$
-presheaf
${\mathcal{A}}$
-presheaf
![]() ${\mathcal{F}}$
(i.e. an additive contravariant functor from
${\mathcal{F}}$
(i.e. an additive contravariant functor from
![]() ${\mathcal{A}}$
to Abelian groups Ab) the associated Nisnevich sheaf
${\mathcal{A}}$
to Abelian groups Ab) the associated Nisnevich sheaf
![]() ${\mathcal{F}}_{\operatorname{nis}}$
has a unique structure of an
${\mathcal{F}}_{\operatorname{nis}}$
has a unique structure of an
![]() ${\mathcal{A}}$
-presheaf for which the canonical morphism
${\mathcal{A}}$
-presheaf for which the canonical morphism
![]() ${\mathcal{F}}\rightarrow {\mathcal{F}}_{\operatorname{nis}}$
is a morphism of
${\mathcal{F}}\rightarrow {\mathcal{F}}_{\operatorname{nis}}$
is a morphism of
![]() ${\mathcal{A}}$
-presheaves.
${\mathcal{A}}$
-presheaves.
(v) There is an action of
![]() $Sm/k$
on
$Sm/k$
on
![]() ${\mathcal{A}}$
in the following sense. Given
${\mathcal{A}}$
in the following sense. Given
![]() $U\in Sm/k$
, there is a homomorphism
$U\in Sm/k$
, there is a homomorphism
functorial in
![]() $X$
and
$X$
and
![]() $Y$
, such that for any morphism
$Y$
, such that for any morphism
![]() $f:U\rightarrow V$
in
$f:U\rightarrow V$
in
![]() $Sm/k$
the following square of abelian groups is commutative:
$Sm/k$
the following square of abelian groups is commutative:

We require
![]() $\unicode[STIX]{x1D6FC}_{U}(\operatorname{id}_{X})=\operatorname{id}_{X\times U}$
for all
$\unicode[STIX]{x1D6FC}_{U}(\operatorname{id}_{X})=\operatorname{id}_{X\times U}$
for all
![]() $U,Z\in Sm/k$
. By the functoriality of
$U,Z\in Sm/k$
. By the functoriality of
![]() $\unicode[STIX]{x1D6FC}_{U}$
in
$\unicode[STIX]{x1D6FC}_{U}$
in
![]() $X$
we mean that the following square of Abelian groups is commutative for any
$X$
we mean that the following square of Abelian groups is commutative for any
![]() $Y\in Sm/k$
and any morphism
$Y\in Sm/k$
and any morphism
![]() $f:X^{\prime }\rightarrow X$
in
$f:X^{\prime }\rightarrow X$
in
![]() ${\mathcal{A}}$
:
${\mathcal{A}}$
:

By the functoriality of
![]() $\unicode[STIX]{x1D6FC}_{U}$
in
$\unicode[STIX]{x1D6FC}_{U}$
in
![]() $Y$
we mean that the following square of additive functors is commutative for any
$Y$
we mean that the following square of additive functors is commutative for any
![]() $X\in Sm/k$
and any morphism
$X\in Sm/k$
and any morphism
![]() $g:Y\rightarrow Y^{\prime }$
in
$g:Y\rightarrow Y^{\prime }$
in
![]() ${\mathcal{A}}$
:
${\mathcal{A}}$
:

In other words, we have a functor
sending
![]() $(X,U)\in Sm/k\times Sm/k$
to
$(X,U)\in Sm/k\times Sm/k$
to
![]() $X\times U\in Sm/k$
and such that
$X\times U\in Sm/k$
and such that
![]() $1_{X}\boxtimes f=\unicode[STIX]{x1D6E4}_{1_{X}\times f}$
,
$1_{X}\boxtimes f=\unicode[STIX]{x1D6E4}_{1_{X}\times f}$
,
![]() $(u+v)\boxtimes f=u\boxtimes f+v\boxtimes f$
for all
$(u+v)\boxtimes f=u\boxtimes f+v\boxtimes f$
for all
![]() $f\in \operatorname{Mor}(Sm/k)$
and
$f\in \operatorname{Mor}(Sm/k)$
and
![]() $u,v\in \operatorname{Mor}({\mathcal{A}})$
.
$u,v\in \operatorname{Mor}({\mathcal{A}})$
.
Remark 2.2. It follows from Definition 2.1(iii) that the canonical morphism
is an isomorphism of Nisnevich sheaves.
Observe that for any category of correspondences
![]() ${\mathcal{A}}$
, an
${\mathcal{A}}$
, an
![]() ${\mathcal{A}}$
-presheaf
${\mathcal{A}}$
-presheaf
![]() ${\mathcal{F}}$
and
${\mathcal{F}}$
and
![]() $U\in Sm/k$
the presheaf
$U\in Sm/k$
the presheaf
is an
![]() ${\mathcal{A}}$
-presheaf. Moreover, it is functorial in
${\mathcal{A}}$
-presheaf. Moreover, it is functorial in
![]() $U$
.
$U$
.
For instance,
![]() ${\mathcal{A}}$
can be given by the naive preadditive category of correspondences
${\mathcal{A}}$
can be given by the naive preadditive category of correspondences
![]() ${\mathcal{A}}_{\text{naive}}$
, with
${\mathcal{A}}_{\text{naive}}$
, with
![]() ${\mathcal{A}}_{\text{naive}}(X,Y)$
being the free abelian group generated by
${\mathcal{A}}_{\text{naive}}(X,Y)$
being the free abelian group generated by
![]() $\operatorname{Hom}_{Sm/k}(X,Y)$
. Non-trivial examples are given by finite correspondences
$\operatorname{Hom}_{Sm/k}(X,Y)$
. Non-trivial examples are given by finite correspondences
![]() $\operatorname{Cor}$
in the sense of Voevodsky [Reference Voevodsky, Voevodsky, Suslin and FriedlanderVoe00b], finite Milnor–Witt correspondences
$\operatorname{Cor}$
in the sense of Voevodsky [Reference Voevodsky, Voevodsky, Suslin and FriedlanderVoe00b], finite Milnor–Witt correspondences
![]() $\widetilde{\operatorname{Cor}}$
in the sense of Calmès and Fasel [Reference Calmès and FaselCF14] or
$\widetilde{\operatorname{Cor}}$
in the sense of Calmès and Fasel [Reference Calmès and FaselCF14] or
![]() $K_{0}^{\oplus }$
in the sense of Walker [Reference WalkerWal96]. Given a ring
$K_{0}^{\oplus }$
in the sense of Walker [Reference WalkerWal96]. Given a ring
![]() $R$
(not necessarily commutative) which is flat as a
$R$
(not necessarily commutative) which is flat as a
![]() $\mathbb{Z}$
-algebra and a category of correspondences
$\mathbb{Z}$
-algebra and a category of correspondences
![]() ${\mathcal{A}}$
, we can form an additive category of correspondences
${\mathcal{A}}$
, we can form an additive category of correspondences
![]() ${\mathcal{A}}_{R}$
with coefficients in
${\mathcal{A}}_{R}$
with coefficients in
![]() $R$
. By definition,
$R$
. By definition,
![]() ${\mathcal{A}}_{R}(X,Y):={\mathcal{A}}(X,Y)\otimes R$
for all
${\mathcal{A}}_{R}(X,Y):={\mathcal{A}}(X,Y)\otimes R$
for all
![]() $X,Y\in Sm/k$
.
$X,Y\in Sm/k$
.
Definition 2.3. We say that a category of correspondences
![]() ${\mathcal{A}}$
is a
${\mathcal{A}}$
is a
![]() $V$
-category of correspondences (‘
$V$
-category of correspondences (‘
![]() $V$
’ for Voevodsky) if for any
$V$
’ for Voevodsky) if for any
![]() $\mathbb{A}^{1}$
-invariant
$\mathbb{A}^{1}$
-invariant
![]() ${\mathcal{A}}$
-presheaf of abelian groups
${\mathcal{A}}$
-presheaf of abelian groups
![]() ${\mathcal{F}}$
the associated Nisnevich sheaf
${\mathcal{F}}$
the associated Nisnevich sheaf
![]() ${\mathcal{F}}_{\operatorname{nis}}$
is
${\mathcal{F}}_{\operatorname{nis}}$
is
![]() $\mathbb{A}^{1}$
-invariant. Recall that a Nisnevich sheaf
$\mathbb{A}^{1}$
-invariant. Recall that a Nisnevich sheaf
![]() ${\mathcal{F}}$
of abelian groups is strictly
${\mathcal{F}}$
of abelian groups is strictly
![]() $\mathbb{A}^{1}$
-invariant if for any
$\mathbb{A}^{1}$
-invariant if for any
![]() $X\in Sm/k$
the canonical morphism
$X\in Sm/k$
the canonical morphism
is an isomorphism. A
![]() $V$
-category of correspondences
$V$
-category of correspondences
![]() ${\mathcal{A}}$
is a strict
${\mathcal{A}}$
is a strict
![]() $V$
-category of correspondences if for any
$V$
-category of correspondences if for any
![]() $\mathbb{A}^{1}$
-invariant
$\mathbb{A}^{1}$
-invariant
![]() ${\mathcal{A}}$
-presheaf of abelian groups
${\mathcal{A}}$
-presheaf of abelian groups
![]() ${\mathcal{F}}$
the associated Nisnevich sheaf
${\mathcal{F}}$
the associated Nisnevich sheaf
![]() ${\mathcal{F}}_{\operatorname{nis}}$
is strictly
${\mathcal{F}}_{\operatorname{nis}}$
is strictly
![]() $\mathbb{A}^{1}$
-invariant.
$\mathbb{A}^{1}$
-invariant.
Observe that any (strict)
![]() $V$
-category of correspondences is a (strict)
$V$
-category of correspondences is a (strict)
![]() $V$
-ringoid in the sense of [Reference Garkusha and PaninGP14a]. For example,
$V$
-ringoid in the sense of [Reference Garkusha and PaninGP14a]. For example,
![]() $\operatorname{Cor}$
and
$\operatorname{Cor}$
and
![]() $K_{0}^{\oplus }$
are
$K_{0}^{\oplus }$
are
![]() $V$
-categories of correspondences, which are strict whenever the base field
$V$
-categories of correspondences, which are strict whenever the base field
![]() $k$
is perfect (see [Reference Voevodsky, Voevodsky, Suslin and FriedlanderVoe00a, Reference WalkerWal96]). The category
$k$
is perfect (see [Reference Voevodsky, Voevodsky, Suslin and FriedlanderVoe00a, Reference WalkerWal96]). The category
![]() $\widetilde{\operatorname{Cor}}$
is a
$\widetilde{\operatorname{Cor}}$
is a
![]() $V$
-category of correspondences, which is strict if
$V$
-category of correspondences, which is strict if
![]() $k$
is infinite and perfect with
$k$
is infinite and perfect with
![]() $\operatorname{char}k\not =2$
(see [Reference Déglise and FaselDF17, Reference KolderupKol17]). Observe that if
$\operatorname{char}k\not =2$
(see [Reference Déglise and FaselDF17, Reference KolderupKol17]). Observe that if
![]() ${\mathcal{A}}$
is a
${\mathcal{A}}$
is a
![]() $V$
-category of correspondences then so is
$V$
-category of correspondences then so is
![]() ${\mathcal{A}}_{R}$
with
${\mathcal{A}}_{R}$
with
![]() $R$
commutative flat as a
$R$
commutative flat as a
![]() $\mathbb{Z}$
-algebra. Moreover, if
$\mathbb{Z}$
-algebra. Moreover, if
![]() $R$
is a ring of fractions of
$R$
is a ring of fractions of
![]() $\mathbb{Z}$
like, for example,
$\mathbb{Z}$
like, for example,
![]() $\mathbb{Z}[1/p]$
or
$\mathbb{Z}[1/p]$
or
![]() $\mathbb{Q}$
, then
$\mathbb{Q}$
, then
![]() ${\mathcal{A}}_{R}$
is a strict
${\mathcal{A}}_{R}$
is a strict
![]() $V$
-category of correspondences whenever
$V$
-category of correspondences whenever
![]() ${\mathcal{A}}$
is.
${\mathcal{A}}$
is.
Let
![]() ${\mathcal{A}}$
be a category of correspondences. Let
${\mathcal{A}}$
be a category of correspondences. Let
![]() $Sh(Sm/k)$
(respectively,
$Sh(Sm/k)$
(respectively,
![]() $Sh({\mathcal{A}})$
) denote the category of Nisnevich sheaves on
$Sh({\mathcal{A}})$
) denote the category of Nisnevich sheaves on
![]() $Sm/k$
(respectively, Nisnevich
$Sm/k$
(respectively, Nisnevich
![]() ${\mathcal{A}}$
-sheaves). Similar to [Reference Garkusha and PaninGP12, Corollary 6.4],
${\mathcal{A}}$
-sheaves). Similar to [Reference Garkusha and PaninGP12, Corollary 6.4],
![]() $Sh({\mathcal{A}})$
is a Grothendieck category such that
$Sh({\mathcal{A}})$
is a Grothendieck category such that
![]() $\{{\mathcal{A}}{(-,X)_{\operatorname{nis}}\}}_{X\in Sm/k}$
is a family of generators of
$\{{\mathcal{A}}{(-,X)_{\operatorname{nis}}\}}_{X\in Sm/k}$
is a family of generators of
![]() $Sh({\mathcal{A}})$
. Denote by
$Sh({\mathcal{A}})$
. Denote by
![]() $D(Sh(Sm/k))$
and
$D(Sh(Sm/k))$
and
![]() $D(Sh({\mathcal{A}}))$
the corresponding derived categories of unbounded complexes. Note that
$D(Sh({\mathcal{A}}))$
the corresponding derived categories of unbounded complexes. Note that
![]() $D(Sh(Sm/k))=D(Sh({\mathcal{A}}_{\text{naive}}))$
.
$D(Sh(Sm/k))=D(Sh({\mathcal{A}}_{\text{naive}}))$
.
The category
![]() $\mathbb{M}$
of motivic spaces consists of contravariant functors from
$\mathbb{M}$
of motivic spaces consists of contravariant functors from
![]() $Sm/k$
to pointed simplicial sets. We refer the reader to [Reference JardineJar00, Reference Morel and VoevodskyMV99] for the definition of motivic weak equivalences between motivic spaces.
$Sm/k$
to pointed simplicial sets. We refer the reader to [Reference JardineJar00, Reference Morel and VoevodskyMV99] for the definition of motivic weak equivalences between motivic spaces.
Lemma 2.4. Given any field
![]() $k$
, let
$k$
, let
![]() ${\mathcal{A}}$
be a category of correspondences. Then the natural map
${\mathcal{A}}$
be a category of correspondences. Then the natural map
is a motivic weak equivalence in the category of motivic spaces
![]() $\mathbb{M}$
.
$\mathbb{M}$
.
Proof. We follow an argument of [Reference Röndigs and ØstværRØ08a, p. 694]. As in classical algebraic topology, an inclusion of pointed motivic spaces
![]() $g:A\rightarrow B$
is an
$g:A\rightarrow B$
is an
![]() $\mathbb{A}^{1}$
-deformation retract if there exist a map
$\mathbb{A}^{1}$
-deformation retract if there exist a map
![]() $r:B\rightarrow A$
such that
$r:B\rightarrow A$
such that
![]() $rg=\operatorname{id}_{A}$
and an
$rg=\operatorname{id}_{A}$
and an
![]() $\mathbb{A}^{1}$
-homotopy
$\mathbb{A}^{1}$
-homotopy
![]() $H:B\wedge \mathbb{A}_{+}^{1}\rightarrow B$
between
$H:B\wedge \mathbb{A}_{+}^{1}\rightarrow B$
between
![]() $gr$
and
$gr$
and
![]() $\operatorname{id}_{B}$
which is constant on
$\operatorname{id}_{B}$
which is constant on
![]() $A$
. Then
$A$
. Then
![]() $\mathbb{A}^{1}$
-deformation retracts are motivic weak equivalences.
$\mathbb{A}^{1}$
-deformation retracts are motivic weak equivalences.
There is an obvious map
![]() $r:{\mathcal{A}}(-,X)\rightarrow {\mathcal{A}}(-,X\times \mathbb{A}^{1})$
such that
$r:{\mathcal{A}}(-,X)\rightarrow {\mathcal{A}}(-,X\times \mathbb{A}^{1})$
such that
![]() $fr=1$
. Since
$fr=1$
. Since
![]() $Sm/k$
naturally acts on
$Sm/k$
naturally acts on
![]() ${\mathcal{A}}$
, it follows that
${\mathcal{A}}$
, it follows that
![]() ${\mathcal{A}}(-\times \mathbb{A}^{1},X\times \mathbb{A}^{1})$
is an
${\mathcal{A}}(-\times \mathbb{A}^{1},X\times \mathbb{A}^{1})$
is an
![]() ${\mathcal{A}}$
-presheaf.
${\mathcal{A}}$
-presheaf.
There is a natural isomorphism
where the Hom-set on the left is taken in the category of
![]() ${\mathcal{A}}$
-presheaves. Consider the functor
${\mathcal{A}}$
-presheaves. Consider the functor
![]() $\unicode[STIX]{x1D70C}:Sm/k\rightarrow {\mathcal{A}}$
. Denote by
$\unicode[STIX]{x1D70C}:Sm/k\rightarrow {\mathcal{A}}$
. Denote by
![]() $\unicode[STIX]{x1D6FC}$
the obvious map
$\unicode[STIX]{x1D6FC}$
the obvious map
![]() $\mathbb{A}^{1}\times \mathbb{A}^{1}\rightarrow \mathbb{A}^{1}$
. We set
$\mathbb{A}^{1}\times \mathbb{A}^{1}\rightarrow \mathbb{A}^{1}$
. We set
![]() $h=\unicode[STIX]{x1D70C}(1_{X}\times \unicode[STIX]{x1D6FC})$
; then
$h=\unicode[STIX]{x1D70C}(1_{X}\times \unicode[STIX]{x1D6FC})$
; then
![]() $h$
uniquely determines a morphism of
$h$
uniquely determines a morphism of
![]() ${\mathcal{A}}$
-presheaves
${\mathcal{A}}$
-presheaves
This morphism can be regarded as a morphism in
![]() $\mathbb{M}$
, denoted by the same letter. By adjointness
$\mathbb{M}$
, denoted by the same letter. By adjointness
![]() $h^{\prime }$
uniquely determines a map in
$h^{\prime }$
uniquely determines a map in
![]() $\mathbb{M}$
,
$\mathbb{M}$
,
Then
![]() $H$
yields an
$H$
yields an
![]() $\mathbb{A}^{1}$
-homotopy between the identity map and
$\mathbb{A}^{1}$
-homotopy between the identity map and
![]() $rf$
. We see that
$rf$
. We see that
![]() $f$
is a motivic weak equivalence, as required.◻
$f$
is a motivic weak equivalence, as required.◻
By the general localization theory of compactly generated triangulated categories [Reference NeemanNee96] one can localize
![]() $D(Sh({\mathcal{A}}))$
with respect to the localizing subcategory
$D(Sh({\mathcal{A}}))$
with respect to the localizing subcategory
![]() ${\mathcal{L}}$
generated by complexes of the form
${\mathcal{L}}$
generated by complexes of the form
The resulting quotient category
![]() $D(Sh({\mathcal{A}}))/{\mathcal{L}}$
is denoted by
$D(Sh({\mathcal{A}}))/{\mathcal{L}}$
is denoted by
![]() $D_{\mathbb{A}^{1}}(Sh({\mathcal{A}}))$
.
$D_{\mathbb{A}^{1}}(Sh({\mathcal{A}}))$
.
If we denote by
![]() $DM_{{\mathcal{A}}}^{\text{eff}}(k)$
the full subcategory of
$DM_{{\mathcal{A}}}^{\text{eff}}(k)$
the full subcategory of
![]() $D(Sh({\mathcal{A}}))$
consisting of the complexes with strictly
$D(Sh({\mathcal{A}}))$
consisting of the complexes with strictly
![]() $\mathbb{A}^{1}$
-invariant homology sheaves, then, similarly to a theorem of Voevodsky [Reference Voevodsky, Voevodsky, Suslin and FriedlanderVoe00a], the composite functor
$\mathbb{A}^{1}$
-invariant homology sheaves, then, similarly to a theorem of Voevodsky [Reference Voevodsky, Voevodsky, Suslin and FriedlanderVoe00a], the composite functor
is an equivalence of triangulated categories whenever
![]() ${\mathcal{A}}$
is a strict
${\mathcal{A}}$
is a strict
![]() $V$
-category of correspondences. Moreover, the functor
$V$
-category of correspondences. Moreover, the functor
lands in
![]() $DM_{{\mathcal{A}}}^{\text{eff}}(k)$
. The kernel of
$DM_{{\mathcal{A}}}^{\text{eff}}(k)$
. The kernel of
![]() $C_{\ast }$
is
$C_{\ast }$
is
![]() ${\mathcal{L}}$
and
${\mathcal{L}}$
and
![]() $C_{\ast }$
is left adjoint to the inclusion functor
$C_{\ast }$
is left adjoint to the inclusion functor
(see [Reference Voevodsky, Voevodsky, Suslin and FriedlanderVoe00a] for details or [Reference Garkusha and PaninGP14a, Theorem 3.5]).
Let
![]() $(\mathbb{G}_{m},1)\in \mathbb{M}$
denote
$(\mathbb{G}_{m},1)\in \mathbb{M}$
denote
![]() $\mathbb{G}_{m}$
pointed at 1 and let
$\mathbb{G}_{m}$
pointed at 1 and let
![]() $\mathbb{G}_{m}^{{\mathcal{A}}}$
be the sheaf
$\mathbb{G}_{m}^{{\mathcal{A}}}$
be the sheaf
induced by the map
![]() $pt\mapsto 1\in \mathbb{G}_{m}$
in
$pt\mapsto 1\in \mathbb{G}_{m}$
in
![]() $Sm/k$
. Regarding it as a complex concentrated in zeroth degree, we have an endofunctor
$Sm/k$
. Regarding it as a complex concentrated in zeroth degree, we have an endofunctor
induced by the action of
![]() $Sm/k$
on
$Sm/k$
on
![]() ${\mathcal{A}}$
. In more detail, by [Reference Al Hwaeer and GarkushaAG16, Proposition 3.4],
${\mathcal{A}}$
. In more detail, by [Reference Al Hwaeer and GarkushaAG16, Proposition 3.4],
![]() $\operatorname{Ch}(Sh({\mathcal{A}}))$
is a Grothendieck category with generators of the form
$\operatorname{Ch}(Sh({\mathcal{A}}))$
is a Grothendieck category with generators of the form
![]() $\{D^{n}{\mathcal{A}}{(-,U)_{\operatorname{nis}}\}}_{n\in \mathbb{Z},U\in Sm/k}$
. Here
$\{D^{n}{\mathcal{A}}{(-,U)_{\operatorname{nis}}\}}_{n\in \mathbb{Z},U\in Sm/k}$
. Here
![]() $D^{n}{\mathcal{A}}(-,U)_{\operatorname{nis}}$
is the complex which is
$D^{n}{\mathcal{A}}(-,U)_{\operatorname{nis}}$
is the complex which is
![]() ${\mathcal{A}}(-,U)_{\operatorname{nis}}$
in degrees
${\mathcal{A}}(-,U)_{\operatorname{nis}}$
in degrees
![]() $n$
and
$n$
and
![]() $n-1$
and 0 elsewhere, with interesting differential being the identity map. Every complex
$n-1$
and 0 elsewhere, with interesting differential being the identity map. Every complex
![]() $X\in \operatorname{Ch}(Sh({\mathcal{A}}))$
is written as a colimit of generators,
$X\in \operatorname{Ch}(Sh({\mathcal{A}}))$
is written as a colimit of generators,
We set
where the sheaf
![]() ${\mathcal{A}}(-,U\wedge \mathbb{G}_{m}^{\wedge 1})_{\operatorname{nis}}:=\operatorname{Coker}({\mathcal{A}}(-,U\times pt)_{\operatorname{nis}}\rightarrow {\mathcal{A}}(-,U\times \mathbb{G}_{m})_{\operatorname{nis}})$
.
${\mathcal{A}}(-,U\wedge \mathbb{G}_{m}^{\wedge 1})_{\operatorname{nis}}:=\operatorname{Coker}({\mathcal{A}}(-,U\times pt)_{\operatorname{nis}}\rightarrow {\mathcal{A}}(-,U\times \mathbb{G}_{m})_{\operatorname{nis}})$
.
Stabilizing
![]() $D_{\mathbb{A}^{1}}(Sh({\mathcal{A}}))$
in the
$D_{\mathbb{A}^{1}}(Sh({\mathcal{A}}))$
in the
![]() $\mathbb{G}_{m}$
-direction with respect to this endofunctor, we arrive at the category
$\mathbb{G}_{m}$
-direction with respect to this endofunctor, we arrive at the category
![]() $D_{\mathbb{A}^{1}}^{\text{st}}(Sh({\mathcal{A}}))$
. If
$D_{\mathbb{A}^{1}}^{\text{st}}(Sh({\mathcal{A}}))$
. If
![]() ${\mathcal{A}}$
is a strict
${\mathcal{A}}$
is a strict
![]() $V$
-category of correspondences, we can likewise stabilize
$V$
-category of correspondences, we can likewise stabilize
![]() $DM_{{\mathcal{A}}}^{\text{eff}}(k)$
in the
$DM_{{\mathcal{A}}}^{\text{eff}}(k)$
in the
![]() $\mathbb{G}_{m}$
-direction. The resulting category is denoted by
$\mathbb{G}_{m}$
-direction. The resulting category is denoted by
![]() $DM_{{\mathcal{A}}}(k)$
. The triangulated equivalence
$DM_{{\mathcal{A}}}(k)$
. The triangulated equivalence
![]() $C_{\ast }:D_{\mathbb{A}^{1}}(Sh({\mathcal{A}}))\rightarrow DM_{{\mathcal{A}}}^{\text{eff}}(k)$
extends to a triangulated equivalence
$C_{\ast }:D_{\mathbb{A}^{1}}(Sh({\mathcal{A}}))\rightarrow DM_{{\mathcal{A}}}^{\text{eff}}(k)$
extends to a triangulated equivalence
Given a category of correspondences
![]() ${\mathcal{A}}$
and
${\mathcal{A}}$
and
![]() $p>0$
, we shall write
$p>0$
, we shall write
![]() $D_{\mathbb{A}^{1}}^{\text{st}}(Sh({\mathcal{A}}))[p^{-1}]$
(respectively,
$D_{\mathbb{A}^{1}}^{\text{st}}(Sh({\mathcal{A}}))[p^{-1}]$
(respectively,
![]() $D_{\mathbb{A}^{1}}^{\text{st}}(Sh({\mathcal{A}}))_{\mathbb{ Q}}$
) to denote the category
$D_{\mathbb{A}^{1}}^{\text{st}}(Sh({\mathcal{A}}))_{\mathbb{ Q}}$
) to denote the category
![]() $D_{\mathbb{A}^{1}}^{\text{st}}(Sh({\mathcal{A}}\otimes \mathbb{Z}[1/p]))(k)$
(respectively,
$D_{\mathbb{A}^{1}}^{\text{st}}(Sh({\mathcal{A}}\otimes \mathbb{Z}[1/p]))(k)$
(respectively,
![]() $D_{\mathbb{A}^{1}}^{\text{st}}(Sh({\mathcal{A}}\otimes \mathbb{Q}))(k)$
). Note that
$D_{\mathbb{A}^{1}}^{\text{st}}(Sh({\mathcal{A}}\otimes \mathbb{Q}))(k)$
). Note that
![]() ${\mathcal{A}}\otimes \mathbb{Z}[1/p]$
and
${\mathcal{A}}\otimes \mathbb{Z}[1/p]$
and
![]() ${\mathcal{A}}\otimes \mathbb{Q}$
are categories of correspondences.
${\mathcal{A}}\otimes \mathbb{Q}$
are categories of correspondences.
Definition 2.5. We say that a category of correspondences
![]() ${\mathcal{A}}$
is symmetric monoidal if the usual product of schemes defines a symmetric monoidal structure on
${\mathcal{A}}$
is symmetric monoidal if the usual product of schemes defines a symmetric monoidal structure on
![]() ${\mathcal{A}}$
.
${\mathcal{A}}$
.
The categories
![]() $\operatorname{Cor}$
,
$\operatorname{Cor}$
,
![]() $\widetilde{\operatorname{Cor}}$
,
$\widetilde{\operatorname{Cor}}$
,
![]() $K_{0}^{\oplus }$
are examples of symmetric monoidal
$K_{0}^{\oplus }$
are examples of symmetric monoidal
![]() $V$
-categories (see [Reference Calmès and FaselCF14, Reference Déglise and FaselDF17, Reference SuslinSus03, Reference Suslin and VoevodskySV00, Reference WalkerWal96] for more details).
$V$
-categories (see [Reference Calmès and FaselCF14, Reference Déglise and FaselDF17, Reference SuslinSus03, Reference Suslin and VoevodskySV00, Reference WalkerWal96] for more details).
![]() ${\mathcal{A}}_{\text{naive}}$
is obviously symmetric monoidal.
${\mathcal{A}}_{\text{naive}}$
is obviously symmetric monoidal.
Given a symmetric monoidal category of correspondences
![]() ${\mathcal{A}}$
, a theorem of Day [Reference DayDay70] implies that the category of
${\mathcal{A}}$
, a theorem of Day [Reference DayDay70] implies that the category of
![]() ${\mathcal{A}}$
-presheaves
${\mathcal{A}}$
-presheaves
![]() $PSh({\mathcal{A}})$
is a closed symmetric monoidal category with a tensor product defined as
$PSh({\mathcal{A}})$
is a closed symmetric monoidal category with a tensor product defined as
The monoidal unit equals
![]() ${\mathcal{A}}(-,pt)$
with
${\mathcal{A}}(-,pt)$
with
![]() $pt=\operatorname{Spec}k$
.
$pt=\operatorname{Spec}k$
.
The tensor product is then extended to a tensor product
![]() $\widetilde{\otimes }$
on
$\widetilde{\otimes }$
on
![]() $Sh({\mathcal{A}})$
. Namely, for all
$Sh({\mathcal{A}})$
. Namely, for all
![]() $F,G\in Sh({\mathcal{A}})$
we set
$F,G\in Sh({\mathcal{A}})$
we set
![]() $F\,\widetilde{\otimes }\,G$
to be the sheaf associated with the presheaf
$F\,\widetilde{\otimes }\,G$
to be the sheaf associated with the presheaf
![]() $F\otimes G$
defined above. With this tensor product
$F\otimes G$
defined above. With this tensor product
![]() $Sh({\mathcal{A}})$
is a closed symmetric monoidal category with
$Sh({\mathcal{A}})$
is a closed symmetric monoidal category with
![]() ${\mathcal{A}}(-,pt)_{\operatorname{nis}}$
a monoidal unit. Likewise,
${\mathcal{A}}(-,pt)_{\operatorname{nis}}$
a monoidal unit. Likewise,
![]() $\widetilde{\otimes }$
is extended to chain complexes
$\widetilde{\otimes }$
is extended to chain complexes
![]() $\operatorname{Ch}(Sh({\mathcal{A}}))$
, which also defines a closed symmetric monoidal structure on the derived category
$\operatorname{Ch}(Sh({\mathcal{A}}))$
, which also defines a closed symmetric monoidal structure on the derived category
![]() $D(Sh({\mathcal{A}}))$
with respect to the derived tensor product
$D(Sh({\mathcal{A}}))$
with respect to the derived tensor product
![]() $\widetilde{\otimes }^{L}$
(we also refer the reader to [Reference Suslin and VoevodskySV00, § 2] and [Reference Cisinski and DégliseCD09, Example 3.3]). It is straightforward to show that the localizing subcategory
$\widetilde{\otimes }^{L}$
(we also refer the reader to [Reference Suslin and VoevodskySV00, § 2] and [Reference Cisinski and DégliseCD09, Example 3.3]). It is straightforward to show that the localizing subcategory
![]() ${\mathcal{L}}$
of
${\mathcal{L}}$
of
![]() $D(Sh({\mathcal{A}}))$
defined above is closed under the derived tensor product
$D(Sh({\mathcal{A}}))$
defined above is closed under the derived tensor product
![]() $\widetilde{\otimes }^{L}$
. As a result, one obtains a symmetric monoidal product on
$\widetilde{\otimes }^{L}$
. As a result, one obtains a symmetric monoidal product on
![]() $D_{\mathbb{A}^{1}}^{\text{st}}(Sh({\mathcal{A}}))$
(and on
$D_{\mathbb{A}^{1}}^{\text{st}}(Sh({\mathcal{A}}))$
(and on
![]() $DM_{{\mathcal{A}}}^{\text{eff}}(k)$
,
$DM_{{\mathcal{A}}}^{\text{eff}}(k)$
,
![]() $DM_{{\mathcal{A}}}(k)$
if
$DM_{{\mathcal{A}}}(k)$
if
![]() ${\mathcal{A}}$
is a strict
${\mathcal{A}}$
is a strict
![]() $V$
-category).
$V$
-category).
Remark 2.6. Let
![]() ${\mathcal{A}}$
be a symmetric monoidal strict
${\mathcal{A}}$
be a symmetric monoidal strict
![]() $V$
-category of correspondences. With a little extra care we describe the tensor product in
$V$
-category of correspondences. With a little extra care we describe the tensor product in
![]() $DM_{{\mathcal{A}}}(k)$
explicitly as follows. The endofunctor
$DM_{{\mathcal{A}}}(k)$
explicitly as follows. The endofunctor
![]() $-\boxtimes \mathbb{G}_{m}^{{\mathcal{A}}}:\operatorname{Ch}(Sh({\mathcal{A}}))\rightarrow \operatorname{Ch}(Sh({\mathcal{A}}))$
equals
$-\boxtimes \mathbb{G}_{m}^{{\mathcal{A}}}:\operatorname{Ch}(Sh({\mathcal{A}}))\rightarrow \operatorname{Ch}(Sh({\mathcal{A}}))$
equals
![]() $-\,\widetilde{\otimes }\,\mathbb{G}_{m}^{{\mathcal{A}}}$
.
$-\,\widetilde{\otimes }\,\mathbb{G}_{m}^{{\mathcal{A}}}$
.
![]() $DM_{{\mathcal{A}}}(k)$
is equivalent to the homotopy category of the symmetric
$DM_{{\mathcal{A}}}(k)$
is equivalent to the homotopy category of the symmetric
![]() $\mathbb{G}_{m}^{{\mathcal{A}}}$
-spectra associated to a monoidal motivic model category structure on
$\mathbb{G}_{m}^{{\mathcal{A}}}$
-spectra associated to a monoidal motivic model category structure on
![]() $\operatorname{Ch}(Sh({\mathcal{A}}))$
. We also refer the reader to [Reference Déglise and FaselDF17], where a monoidal model structure is defined in the case of
$\operatorname{Ch}(Sh({\mathcal{A}}))$
. We also refer the reader to [Reference Déglise and FaselDF17], where a monoidal model structure is defined in the case of
![]() $MW$
-correspondences.
$MW$
-correspondences.
3 The additive motivic sphere spectrum
 $\mathbb{S}^{{\mathcal{A}}}$
$\mathbb{S}^{{\mathcal{A}}}$
Let
![]() $Sp_{S^{1},\mathbb{G}_{m}}(k)$
denote the category of symmetric
$Sp_{S^{1},\mathbb{G}_{m}}(k)$
denote the category of symmetric
![]() $(S^{1},\mathbb{G}_{m})$
-bispectra, where the
$(S^{1},\mathbb{G}_{m})$
-bispectra, where the
![]() $\mathbb{G}_{m}$
-direction is associated with the pointed motivic space
$\mathbb{G}_{m}$
-direction is associated with the pointed motivic space
![]() $(\mathbb{G}_{m},1)$
. It is equipped with a stable motivic model category structure [Reference JardineJar00]. Denote by
$(\mathbb{G}_{m},1)$
. It is equipped with a stable motivic model category structure [Reference JardineJar00]. Denote by
![]() $SH(k)$
its homotopy category. The category
$SH(k)$
its homotopy category. The category
![]() $SH(k)$
has a closed symmetric monoidal structure with the motivic sphere spectrum
$SH(k)$
has a closed symmetric monoidal structure with the motivic sphere spectrum
![]() $\mathbb{S}$
as monoidal unit (see [Reference JardineJar00] for details). Given
$\mathbb{S}$
as monoidal unit (see [Reference JardineJar00] for details). Given
![]() $p>0$
, the category
$p>0$
, the category
![]() $Sp_{S^{1},\mathbb{G}_{m}}(k)$
has a further model structure whose weak equivalences are the maps of bispectra
$Sp_{S^{1},\mathbb{G}_{m}}(k)$
has a further model structure whose weak equivalences are the maps of bispectra
![]() $f:X\rightarrow Y$
such that the induced map of bigraded Nisnevich sheaves
$f:X\rightarrow Y$
such that the induced map of bigraded Nisnevich sheaves
![]() $f_{\ast }:\text{}\underline{\unicode[STIX]{x1D70B}}_{\ast ,\ast }^{\mathbb{A}^{1}}(X)\otimes \mathbb{Z}[1/p]\rightarrow \text{}\underline{\unicode[STIX]{x1D70B}}_{\ast ,\ast }^{\mathbb{A}^{1}}(Y)\otimes \mathbb{Z}[1/p]$
is an isomorphism. In what follows we denote its homotopy category by
$f_{\ast }:\text{}\underline{\unicode[STIX]{x1D70B}}_{\ast ,\ast }^{\mathbb{A}^{1}}(X)\otimes \mathbb{Z}[1/p]\rightarrow \text{}\underline{\unicode[STIX]{x1D70B}}_{\ast ,\ast }^{\mathbb{A}^{1}}(Y)\otimes \mathbb{Z}[1/p]$
is an isomorphism. In what follows we denote its homotopy category by
![]() $SH(k)[p^{-1}]$
. The category
$SH(k)[p^{-1}]$
. The category
![]() $SH(k)_{\mathbb{Q}}$
is defined in a similar fashion. The corresponding classes of weak equivalences are also called
$SH(k)_{\mathbb{Q}}$
is defined in a similar fashion. The corresponding classes of weak equivalences are also called
![]() $p^{-1}$
-stable/
$p^{-1}$
-stable/
![]() $\mathbb{Q}$
-stable motivic weak equivalences. We also refer the reader to [Reference Röndigs and ØstværRØ08b, Appendix A] for general localization theory of motivic spectra.
$\mathbb{Q}$
-stable motivic weak equivalences. We also refer the reader to [Reference Röndigs and ØstværRØ08b, Appendix A] for general localization theory of motivic spectra.
It is worth mentioning that any other kind of motivic spectra or motivic functors in the sense of [Reference Dundas, Röndigs and ØstværDRØ03] together with the stable motivic model structure lead to equivalent definitions of
![]() $SH(k)[p^{-1}]$
and
$SH(k)[p^{-1}]$
and
![]() $SH(k)_{\mathbb{Q}}$
, respectively.
$SH(k)_{\mathbb{Q}}$
, respectively.
The isomorphism
![]() $\operatorname{tw}:(\mathbb{G}_{m},1)\wedge (\mathbb{G}_{m},1)\overset{\cong }{\longrightarrow }(\mathbb{G}_{m},1)\wedge (\mathbb{G}_{m},1)$
permuting factors is an involution, that is,
$\operatorname{tw}:(\mathbb{G}_{m},1)\wedge (\mathbb{G}_{m},1)\overset{\cong }{\longrightarrow }(\mathbb{G}_{m},1)\wedge (\mathbb{G}_{m},1)$
permuting factors is an involution, that is,
![]() $\operatorname{tw}^{2}=\operatorname{id}$
. It gives an endomorphism
$\operatorname{tw}^{2}=\operatorname{id}$
. It gives an endomorphism
![]() $\unicode[STIX]{x1D700}:\mathbb{S}\rightarrow \mathbb{S}$
such that
$\unicode[STIX]{x1D700}:\mathbb{S}\rightarrow \mathbb{S}$
such that
![]() $\unicode[STIX]{x1D700}^{2}=\operatorname{id}$
. If we denote by
$\unicode[STIX]{x1D700}^{2}=\operatorname{id}$
. If we denote by
![]() $SH(k)[2^{-1}]$
the stable motivic homotopy theory with
$SH(k)[2^{-1}]$
the stable motivic homotopy theory with
![]() $\mathbb{Z}[1/2]$
-coefficients, then
$\mathbb{Z}[1/2]$
-coefficients, then
are two orthogonal idempotent endomorphisms of
![]() $\mathbb{S}[2^{-1}]$
such that
$\mathbb{S}[2^{-1}]$
such that
![]() $\unicode[STIX]{x1D700}_{+}+\unicode[STIX]{x1D700}_{-}=\operatorname{id}$
and
$\unicode[STIX]{x1D700}_{+}+\unicode[STIX]{x1D700}_{-}=\operatorname{id}$
and
![]() $\unicode[STIX]{x1D700}=\unicode[STIX]{x1D700}_{-}-\unicode[STIX]{x1D700}_{+}$
. It follows that
$\unicode[STIX]{x1D700}=\unicode[STIX]{x1D700}_{-}-\unicode[STIX]{x1D700}_{+}$
. It follows that
where
![]() $\mathbb{S}_{+}$
(respectively,
$\mathbb{S}_{+}$
(respectively,
![]() $\mathbb{S}_{-}$
) corresponds to the idempotent
$\mathbb{S}_{-}$
) corresponds to the idempotent
![]() $\unicode[STIX]{x1D700}_{+}$
(respectively,
$\unicode[STIX]{x1D700}_{+}$
(respectively,
![]() $\unicode[STIX]{x1D700}_{-}$
).
$\unicode[STIX]{x1D700}_{-}$
).
By [Reference MorelMor03, § 6] the stable algebraic Hopf map
![]() $\unicode[STIX]{x1D702}:\mathbb{S}\rightarrow \mathbb{S}^{-1,-1}$
satisfies
$\unicode[STIX]{x1D702}:\mathbb{S}\rightarrow \mathbb{S}^{-1,-1}$
satisfies
![]() $\unicode[STIX]{x1D702}\unicode[STIX]{x1D700}_{+}=0$
,
$\unicode[STIX]{x1D702}\unicode[STIX]{x1D700}_{+}=0$
,
![]() $\unicode[STIX]{x1D702}\unicode[STIX]{x1D700}=\unicode[STIX]{x1D702}$
in
$\unicode[STIX]{x1D702}\unicode[STIX]{x1D700}=\unicode[STIX]{x1D702}$
in
![]() $SH(k)[2^{-1}]$
. Moreover,
$SH(k)[2^{-1}]$
. Moreover,
is an isomorphism in
![]() $SH(k)[2^{-1}]$
, denoted by the same letter
$SH(k)[2^{-1}]$
, denoted by the same letter
![]() $\unicode[STIX]{x1D702}$
. In particular, there is an isomorphism
$\unicode[STIX]{x1D702}$
. In particular, there is an isomorphism
The decomposition
![]() $\mathbb{S}[2^{-1}]=\mathbb{S}_{+}\oplus \mathbb{S}_{-}$
of the monoidal unit of
$\mathbb{S}[2^{-1}]=\mathbb{S}_{+}\oplus \mathbb{S}_{-}$
of the monoidal unit of
![]() $SH(k)[2^{-1}]$
implies
$SH(k)[2^{-1}]$
implies
![]() $SH(k)[2^{-1}]$
is a product of symmetric monoidal triangulated categories
$SH(k)[2^{-1}]$
is a product of symmetric monoidal triangulated categories
where
![]() $\mathbb{S}_{+}$
and
$\mathbb{S}_{+}$
and
![]() $\mathbb{S}_{-}$
are monoidal units for
$\mathbb{S}_{-}$
are monoidal units for
![]() $SH(k)_{+}$
and
$SH(k)_{+}$
and
![]() $SH(k)_{-}$
, respectively.
$SH(k)_{-}$
, respectively.
Consider a category of correspondences
![]() ${\mathcal{A}}$
. There is a natural triangulated functor
${\mathcal{A}}$
. There is a natural triangulated functor
In more detail, there is an adjoint pair [Reference Garkusha and PaninGP12, § 6]
where
![]() $\operatorname{Mod}{\mathcal{A}}^{\text{EM}}$
is the category of
$\operatorname{Mod}{\mathcal{A}}^{\text{EM}}$
is the category of
![]() ${\mathcal{A}}^{\text{EM}}$
-modules equipped with the stable projective motivic model structure over the Eilenberg–Mac Lane spectral category
${\mathcal{A}}^{\text{EM}}$
-modules equipped with the stable projective motivic model structure over the Eilenberg–Mac Lane spectral category
![]() ${\mathcal{A}}^{\text{EM}}$
associated with
${\mathcal{A}}^{\text{EM}}$
associated with
![]() ${\mathcal{A}}$
. Also, there is a zig-zag of triangulated equivalences between
${\mathcal{A}}$
. Also, there is a zig-zag of triangulated equivalences between
![]() $\operatorname{Ho}(\operatorname{Mod}{\mathcal{A}}^{\text{EM}})$
and
$\operatorname{Ho}(\operatorname{Mod}{\mathcal{A}}^{\text{EM}})$
and
![]() $D_{\mathbb{A}^{1}}(Sh({\mathcal{A}}))$
. Then the resulting functor
$D_{\mathbb{A}^{1}}(Sh({\mathcal{A}}))$
. Then the resulting functor
is naturally extended to
![]() $\mathbb{G}_{m}$
-spectra in both categories.
$\mathbb{G}_{m}$
-spectra in both categories.
The functor
![]() $F$
sends each bispectrum
$F$
sends each bispectrum
![]() $\unicode[STIX]{x1D6F4}_{S^{1}}^{\infty }\unicode[STIX]{x1D6F4}_{\mathbb{G}_{m}}^{\infty }X_{+}$
,
$\unicode[STIX]{x1D6F4}_{S^{1}}^{\infty }\unicode[STIX]{x1D6F4}_{\mathbb{G}_{m}}^{\infty }X_{+}$
,
![]() $X\in Sm/k$
, to a
$X\in Sm/k$
, to a
![]() $\mathbb{G}_{m}$
-spectrum isomorphic to
$\mathbb{G}_{m}$
-spectrum isomorphic to
Here each entry is a complex in degree
![]() $0$
, each
$0$
, each
![]() ${\mathcal{A}}(-,X\wedge \mathbb{G}_{m}^{\wedge n})_{\operatorname{nis}}$
is a sheaf associated to the presheaf
${\mathcal{A}}(-,X\wedge \mathbb{G}_{m}^{\wedge n})_{\operatorname{nis}}$
is a sheaf associated to the presheaf
where the natural additive functors
![]() $i_{s}:{\mathcal{A}}(-,X\times \mathbb{G}_{m}^{\times (\ell -1)})\rightarrow {\mathcal{A}}(-,X\times \mathbb{G}_{m}^{\times \ell })$
are induced by the embeddings
$i_{s}:{\mathcal{A}}(-,X\times \mathbb{G}_{m}^{\times (\ell -1)})\rightarrow {\mathcal{A}}(-,X\times \mathbb{G}_{m}^{\times \ell })$
are induced by the embeddings
![]() $i_{s}:\mathbb{G}_{m}^{\times (\ell -1)}\rightarrow \mathbb{G}_{m}^{\times \ell }$
of the form
$i_{s}:\mathbb{G}_{m}^{\times (\ell -1)}\rightarrow \mathbb{G}_{m}^{\times \ell }$
of the form
in which 1 is the
![]() $s$
th coordinate.
$s$
th coordinate.
Note that
![]() $F$
factors through the stable
$F$
factors through the stable
![]() $\mathbb{A}^{1}$
-derived category
$\mathbb{A}^{1}$
-derived category
![]() $D_{\mathbb{A}^{1}}(k):=D_{\mathbb{A}^{1}}^{\text{st}}(Sh({\mathcal{A}}_{\text{naive}}))$
in the sense of Morel [Reference MorelMor04] (see also [Reference Cisinski and DégliseCD12, § 5.3]). In what follows we shall denote by
$D_{\mathbb{A}^{1}}(k):=D_{\mathbb{A}^{1}}^{\text{st}}(Sh({\mathcal{A}}_{\text{naive}}))$
in the sense of Morel [Reference MorelMor04] (see also [Reference Cisinski and DégliseCD12, § 5.3]). In what follows we shall denote by
![]() $H_{\mathbb{A}^{1}}\mathbb{Z}$
its monoidal unit. Note that
$H_{\mathbb{A}^{1}}\mathbb{Z}$
its monoidal unit. Note that
![]() $H_{\mathbb{A}^{1}}\mathbb{Z}$
is the image of
$H_{\mathbb{A}^{1}}\mathbb{Z}$
is the image of
![]() $\mathbb{S}$
under the canonical functor
$\mathbb{S}$
under the canonical functor
As above, one has decompositions
In what follows we shall write
![]() $\mathbb{S}^{{\mathcal{A}}}$
to denote the spectrum
$\mathbb{S}^{{\mathcal{A}}}$
to denote the spectrum
![]() ${\mathcal{A}}(pt)_{\mathbb{G}_{m}}^{\infty }$
and call it the additive motivic
${\mathcal{A}}(pt)_{\mathbb{G}_{m}}^{\infty }$
and call it the additive motivic
![]() ${\mathcal{A}}$
-sphere spectrum. Taking the Eilenberg–Mac Lane
${\mathcal{A}}$
-sphere spectrum. Taking the Eilenberg–Mac Lane
![]() $S^{1}$
-spectra for each sheaf
$S^{1}$
-spectra for each sheaf
![]() ${\mathcal{A}}(-,X\wedge \mathbb{G}_{m}^{\wedge n})_{\operatorname{nis}}$
(see, for example, [Reference MorelMor06, § 3.2]), we can regard
${\mathcal{A}}(-,X\wedge \mathbb{G}_{m}^{\wedge n})_{\operatorname{nis}}$
(see, for example, [Reference MorelMor06, § 3.2]), we can regard
![]() $\mathbb{S}^{{\mathcal{A}}}$
as an ordinary
$\mathbb{S}^{{\mathcal{A}}}$
as an ordinary
![]() $(S^{1},\mathbb{G}_{m})$
-bispectrum (and denote it by the same letter if there is no likelihood of confusion).
$(S^{1},\mathbb{G}_{m})$
-bispectrum (and denote it by the same letter if there is no likelihood of confusion).
The canonical triangulated functor
takes the ordinary motivic sphere
![]() $\mathbb{S}$
to a spectrum isomorphic to
$\mathbb{S}$
to a spectrum isomorphic to
![]() $\mathbb{S}^{{\mathcal{A}}}$
.
$\mathbb{S}^{{\mathcal{A}}}$
.
![]() $F(\unicode[STIX]{x1D702})$
induces a morphism
$F(\unicode[STIX]{x1D702})$
induces a morphism
We also set
and
![]() $\mathbb{S}_{-}^{{\mathcal{A}}}\cong F(\mathbb{S}_{-})$
,
$\mathbb{S}_{-}^{{\mathcal{A}}}\cong F(\mathbb{S}_{-})$
,
![]() $\mathbb{S}_{+}^{{\mathcal{A}}}\cong F(\mathbb{S}_{+})$
. Then we have the following relations in
$\mathbb{S}_{+}^{{\mathcal{A}}}\cong F(\mathbb{S}_{+})$
. Then we have the following relations in
![]() $D_{\mathbb{A}^{1}}^{\text{st}}(Sh({\mathcal{A}}))$
:
$D_{\mathbb{A}^{1}}^{\text{st}}(Sh({\mathcal{A}}))$
:
As above,
![]() $\unicode[STIX]{x1D702}_{{\mathcal{A}}}$
annihilates
$\unicode[STIX]{x1D702}_{{\mathcal{A}}}$
annihilates
![]() $\mathbb{S}_{+}^{{\mathcal{A}}}$
and is an isomorphism on
$\mathbb{S}_{+}^{{\mathcal{A}}}$
and is an isomorphism on
![]() $\mathbb{S}_{-}^{{\mathcal{A}}}$
.
$\mathbb{S}_{-}^{{\mathcal{A}}}$
.
Remark 3.1. Following an equivalent description of
![]() $DM_{{\mathcal{A}}}(k)$
over a symmetric monoidal strict
$DM_{{\mathcal{A}}}(k)$
over a symmetric monoidal strict
![]() $V$
-category of correspondences in Remark 2.6 in terms of
$V$
-category of correspondences in Remark 2.6 in terms of
![]() $\mathbb{G}_{m}^{{\mathcal{A}}}$
-symmetric spectra (in this case
$\mathbb{G}_{m}^{{\mathcal{A}}}$
-symmetric spectra (in this case
![]() $D_{\mathbb{A}^{1}}^{\text{st}}(Sh({\mathcal{A}})),DM_{{\mathcal{A}}}(k)$
are canonically equivalent), the additive motivic
$D_{\mathbb{A}^{1}}^{\text{st}}(Sh({\mathcal{A}})),DM_{{\mathcal{A}}}(k)$
are canonically equivalent), the additive motivic
![]() ${\mathcal{A}}$
-sphere spectrum
${\mathcal{A}}$
-sphere spectrum
![]() $\mathbb{S}^{{\mathcal{A}}}$
is nothing but the symmetric sequence
$\mathbb{S}^{{\mathcal{A}}}$
is nothing but the symmetric sequence
where
![]() $\unicode[STIX]{x1D6F4}_{n}$
acts on
$\unicode[STIX]{x1D6F4}_{n}$
acts on
![]() $(\mathbb{G}_{m}^{{\mathcal{A}}})^{\widetilde{\otimes }n}$
by permutation. It is a commutative monoid in the category of symmetric sequences in
$(\mathbb{G}_{m}^{{\mathcal{A}}})^{\widetilde{\otimes }n}$
by permutation. It is a commutative monoid in the category of symmetric sequences in
![]() $\operatorname{Ch}(Sh({\mathcal{A}}))$
(see [Reference HoveyHov01, § 7]). Moreover, the motivic model category
$\operatorname{Ch}(Sh({\mathcal{A}}))$
(see [Reference HoveyHov01, § 7]). Moreover, the motivic model category
![]() $Sp^{\unicode[STIX]{x1D6F4}}(\operatorname{Ch}(Sh{\mathcal{A}}),\mathbb{G}_{m}^{{\mathcal{A}}})$
of symmetric
$Sp^{\unicode[STIX]{x1D6F4}}(\operatorname{Ch}(Sh{\mathcal{A}}),\mathbb{G}_{m}^{{\mathcal{A}}})$
of symmetric
![]() $\mathbb{G}_{m}^{{\mathcal{A}}}$
-spectra associated with the motivic model category structure on
$\mathbb{G}_{m}^{{\mathcal{A}}}$
-spectra associated with the motivic model category structure on
![]() $\operatorname{Ch}(Sh{\mathcal{A}})$
is the category of modules in the category of symmetric sequences over the commutative monoid
$\operatorname{Ch}(Sh{\mathcal{A}})$
is the category of modules in the category of symmetric sequences over the commutative monoid
![]() $\mathbb{S}^{{\mathcal{A}}}$
. The homotopy category of
$\mathbb{S}^{{\mathcal{A}}}$
. The homotopy category of
![]() $Sp^{\unicode[STIX]{x1D6F4}}(\operatorname{Ch}(Sh{\mathcal{A}}),\mathbb{G}_{m}^{{\mathcal{A}}})$
, which is equivalent to
$Sp^{\unicode[STIX]{x1D6F4}}(\operatorname{Ch}(Sh{\mathcal{A}}),\mathbb{G}_{m}^{{\mathcal{A}}})$
, which is equivalent to
![]() $DM_{{\mathcal{A}}}(k)$
, is a closed symmetric monoidal category with
$DM_{{\mathcal{A}}}(k)$
, is a closed symmetric monoidal category with
![]() $\mathbb{S}^{{\mathcal{A}}}$
a monoidal unit.
$\mathbb{S}^{{\mathcal{A}}}$
a monoidal unit.
Definition 3.2. Let
![]() ${\mathcal{A}}$
be a category of
${\mathcal{A}}$
be a category of
![]() $V$
-correspondences. Following [Reference Voevodsky, Voevodsky, Suslin and FriedlanderVoe00b, Reference Suslin and VoevodskySV00, Reference SuslinSus03], the
$V$
-correspondences. Following [Reference Voevodsky, Voevodsky, Suslin and FriedlanderVoe00b, Reference Suslin and VoevodskySV00, Reference SuslinSus03], the
![]() ${\mathcal{A}}$
-motive of a smooth algebraic variety
${\mathcal{A}}$
-motive of a smooth algebraic variety
![]() $X\in Sm/k$
, denoted by
$X\in Sm/k$
, denoted by
![]() $M_{{\mathcal{A}}}(X)$
, is the complex associated to the simplicial Nisnevich sheaf
$M_{{\mathcal{A}}}(X)$
, is the complex associated to the simplicial Nisnevich sheaf
Lemma 3.3. Let
![]() ${\mathcal{A}}$
be a strict category of
${\mathcal{A}}$
be a strict category of
![]() $V$
-correspondences and
$V$
-correspondences and
![]() ${\mathcal{X}}$
a motivic
${\mathcal{X}}$
a motivic
![]() $S^{1}$
-spectrum such that its presheaves
$S^{1}$
-spectrum such that its presheaves
![]() $\unicode[STIX]{x1D70B}_{\ast }({\mathcal{X}})$
of homotopy groups are homotopy invariant
$\unicode[STIX]{x1D70B}_{\ast }({\mathcal{X}})$
of homotopy groups are homotopy invariant
![]() ${\mathcal{A}}$
-presheaves. Then every Nisnevich local fibrant replacement
${\mathcal{A}}$
-presheaves. Then every Nisnevich local fibrant replacement
![]() ${\mathcal{X}}_{f}$
of
${\mathcal{X}}_{f}$
of
![]() ${\mathcal{X}}$
is motivically fibrant.
${\mathcal{X}}$
is motivically fibrant.
Proof. Since
![]() ${\mathcal{A}}$
is a strict category of
${\mathcal{A}}$
is a strict category of
![]() $V$
-correspondences, the sheaves
$V$
-correspondences, the sheaves
![]() $\unicode[STIX]{x1D70B}_{\ast }({\mathcal{X}})_{\operatorname{nis}}$
are strictly
$\unicode[STIX]{x1D70B}_{\ast }({\mathcal{X}})_{\operatorname{nis}}$
are strictly
![]() $\mathbb{A}^{1}$
-invariant. Our claim now follows from [Reference MorelMor06, Theorem 6.2.7].◻
$\mathbb{A}^{1}$
-invariant. Our claim now follows from [Reference MorelMor06, Theorem 6.2.7].◻
Remark 3.4. It is worth mentioning that Lemma 3.3 does not depend on Morel’s connectivity theorem [Reference MorelMor06, Theorem 6.1.8]. Indeed, it easily follows for connected spectra from the Brown–Gersten spectral sequence. Then we use the fact that
![]() ${\mathcal{X}}_{f}=\operatorname{hocolim}_{n\rightarrow -\infty }({\mathcal{X}}_{{\geqslant}n})_{f}$
, where
${\mathcal{X}}_{f}=\operatorname{hocolim}_{n\rightarrow -\infty }({\mathcal{X}}_{{\geqslant}n})_{f}$
, where
![]() ${\mathcal{X}}_{{\geqslant}n}$
is the naive
${\mathcal{X}}_{{\geqslant}n}$
is the naive
![]() $n$
th truncation of
$n$
th truncation of
![]() ${\mathcal{X}}$
.
${\mathcal{X}}$
.
The spectrum
![]() ${\mathcal{A}}(X)_{\mathbb{G}_{m}}^{\infty }$
is motivically equivalent to the spectrum
${\mathcal{A}}(X)_{\mathbb{G}_{m}}^{\infty }$
is motivically equivalent to the spectrum
consisting of complexes of Nisnevich
![]() ${\mathcal{A}}$
-sheaves associated with the simplicial sheaves
${\mathcal{A}}$
-sheaves associated with the simplicial sheaves
![]() $n\longmapsto {\mathcal{A}}(-\times \unicode[STIX]{x1D6E5}^{n},X\wedge \mathbb{G}_{m}^{\wedge q})_{\operatorname{nis}}$
.
$n\longmapsto {\mathcal{A}}(-\times \unicode[STIX]{x1D6E5}^{n},X\wedge \mathbb{G}_{m}^{\wedge q})_{\operatorname{nis}}$
.
Definition 3.5. Let
![]() ${\mathcal{A}}$
be a category of
${\mathcal{A}}$
be a category of
![]() $V$
-correspondences. The bivariant
$V$
-correspondences. The bivariant
![]() ${\mathcal{A}}$
-motivic cohomology groups are defined by
${\mathcal{A}}$
-motivic cohomology groups are defined by
where the right-hand side stands for Nisnevich hypercohomology groups of
![]() $X$
with coefficients in
$X$
with coefficients in
![]() ${\mathcal{A}}(-\times \unicode[STIX]{x1D6E5}^{\bullet },Y\wedge \mathbb{G}_{m}^{\wedge q})_{\operatorname{nis}}[-q]$
(the shift is cohomological).
${\mathcal{A}}(-\times \unicode[STIX]{x1D6E5}^{\bullet },Y\wedge \mathbb{G}_{m}^{\wedge q})_{\operatorname{nis}}[-q]$
(the shift is cohomological).
Following [Reference Garkusha and PaninGP18], we say that the bigraded presheaves
![]() $H_{{\mathcal{A}}}^{\ast ,\ast }(-,Y)$
satisfy the cancellation property if all maps
$H_{{\mathcal{A}}}^{\ast ,\ast }(-,Y)$
satisfy the cancellation property if all maps
induced by the structure maps of the spectrum
![]() $M_{{\mathcal{A}}}^{\mathbb{G}_{m}}(Y)$
are isomorphisms.
$M_{{\mathcal{A}}}^{\mathbb{G}_{m}}(Y)$
are isomorphisms.
Given
![]() $Y\in Sm/k$
, write
$Y\in Sm/k$
, write
where each
![]() $M_{{\mathcal{A}}}(Y\wedge \mathbb{G}_{m}^{\wedge n})_{f}$
is a fibrant Nisnevich local replacement of
$M_{{\mathcal{A}}}(Y\wedge \mathbb{G}_{m}^{\wedge n})_{f}$
is a fibrant Nisnevich local replacement of
![]() $M_{{\mathcal{A}}}(Y\wedge \mathbb{G}_{m}^{\wedge n})$
. It is important to note that each
$M_{{\mathcal{A}}}(Y\wedge \mathbb{G}_{m}^{\wedge n})$
. It is important to note that each
![]() $M_{{\mathcal{A}}}(Y\wedge \mathbb{G}_{m}^{\wedge n})_{f}$
can be constructed within
$M_{{\mathcal{A}}}(Y\wedge \mathbb{G}_{m}^{\wedge n})_{f}$
can be constructed within
![]() $\operatorname{Ch}(Sh({\mathcal{A}}))$
whenever
$\operatorname{Ch}(Sh({\mathcal{A}}))$
whenever
![]() ${\mathcal{A}}$
is a strict category of
${\mathcal{A}}$
is a strict category of
![]() $V$
-correspondences (this can be shown similarly to [Reference Garkusha and PaninGP12, Theorem 5.12]). Observe as well that
$V$
-correspondences (this can be shown similarly to [Reference Garkusha and PaninGP12, Theorem 5.12]). Observe as well that
![]() ${\mathcal{A}}(Y)_{\mathbb{G}_{m}}^{\infty }$
is motivically equivalent to
${\mathcal{A}}(Y)_{\mathbb{G}_{m}}^{\infty }$
is motivically equivalent to
![]() $M_{{\mathcal{A}}}^{\mathbb{G}_{m}}(Y)_{f}$
.
$M_{{\mathcal{A}}}^{\mathbb{G}_{m}}(Y)_{f}$
.
Lemma 3.6. Suppose
![]() ${\mathcal{A}}$
is a strict
${\mathcal{A}}$
is a strict
![]() $V$
-category of correspondences. The bigraded presheaves
$V$
-category of correspondences. The bigraded presheaves
![]() $H_{{\mathcal{A}}}^{\ast ,\ast }(-,Y)$
satisfy the cancellation property if and only if
$H_{{\mathcal{A}}}^{\ast ,\ast }(-,Y)$
satisfy the cancellation property if and only if
![]() $M_{{\mathcal{A}}}^{\mathbb{G}_{m}}(Y)_{f}$
is motivically fibrant as an ordinary motivic bispectrum.
$M_{{\mathcal{A}}}^{\mathbb{G}_{m}}(Y)_{f}$
is motivically fibrant as an ordinary motivic bispectrum.
Proof. Using Lemma 3.3, this is proved similarly to [Reference Garkusha and PaninGP18, Lemma 4.5]. ◻
Corollary 3.7. Suppose
![]() ${\mathcal{A}}$
is a strict
${\mathcal{A}}$
is a strict
![]() $V$
-category of correspondences satisfying the cancellation property. Then the presheaves
$V$
-category of correspondences satisfying the cancellation property. Then the presheaves
![]() $H_{{\mathcal{A}}}^{\ast ,\ast }(-,Y)$
are represented in
$H_{{\mathcal{A}}}^{\ast ,\ast }(-,Y)$
are represented in
![]() $SH(k)$
by the bispectrum
$SH(k)$
by the bispectrum
![]() $M_{{\mathcal{A}}}^{\mathbb{G}_{m}}(Y)_{f}$
. Specifically,
$M_{{\mathcal{A}}}^{\mathbb{G}_{m}}(Y)_{f}$
. Specifically,
where
![]() $S^{p,q}=S^{p-q}\wedge (\mathbb{G}_{m},1)^{\wedge q}$
.
$S^{p,q}=S^{p-q}\wedge (\mathbb{G}_{m},1)^{\wedge q}$
.
Under the assumptions of Corollary 3.7 we can compute
![]() $\mathbb{S}^{{\mathcal{A}}}[\unicode[STIX]{x1D702}_{{\mathcal{A}}}^{-1}]$
up to an isomorphism in
$\mathbb{S}^{{\mathcal{A}}}[\unicode[STIX]{x1D702}_{{\mathcal{A}}}^{-1}]$
up to an isomorphism in
![]() $D_{\mathbb{A}^{1}}^{\text{st}}(Sh({\mathcal{A}}))$
as follows:
$D_{\mathbb{A}^{1}}^{\text{st}}(Sh({\mathcal{A}}))$
as follows:
Here the maps of the colimit are induced by
![]() $\unicode[STIX]{x1D702}_{{\mathcal{A}}}$
. Denote the right-hand side by
$\unicode[STIX]{x1D702}_{{\mathcal{A}}}$
. Denote the right-hand side by
![]() $M_{{\mathcal{A}}}^{\mathbb{G}_{m}}(pt)_{f}[\unicode[STIX]{x1D702}^{-1}]$
. This is termwise a spectrum,
$M_{{\mathcal{A}}}^{\mathbb{G}_{m}}(pt)_{f}[\unicode[STIX]{x1D702}^{-1}]$
. This is termwise a spectrum,
where each
Since the structure maps of
![]() $M_{{\mathcal{A}}}^{\mathbb{G}_{m}}(pt)_{f}[\unicode[STIX]{x1D702}^{-1}]$
are schemewise equivalences by the cancellation property, it follows from the construction of
$M_{{\mathcal{A}}}^{\mathbb{G}_{m}}(pt)_{f}[\unicode[STIX]{x1D702}^{-1}]$
are schemewise equivalences by the cancellation property, it follows from the construction of
![]() $M_{{\mathcal{A}}}^{\mathbb{G}_{m}}(pt)_{f}[\unicode[STIX]{x1D702}^{-1}]$
that all homotopy sheaves
$M_{{\mathcal{A}}}^{\mathbb{G}_{m}}(pt)_{f}[\unicode[STIX]{x1D702}^{-1}]$
that all homotopy sheaves
![]() $\unicode[STIX]{x1D70B}_{i,j}^{\mathbb{A}^{1}}(M_{{\mathcal{A}}}^{\mathbb{G}_{m}}(pt)_{f}[\unicode[STIX]{x1D702}^{-1}])$
are concentrated in weight
$\unicode[STIX]{x1D70B}_{i,j}^{\mathbb{A}^{1}}(M_{{\mathcal{A}}}^{\mathbb{G}_{m}}(pt)_{f}[\unicode[STIX]{x1D702}^{-1}])$
are concentrated in weight
![]() $0$
only. By [Reference MorelMor03, Lemma 4.3.11], the canonical map of sheaves
$0$
only. By [Reference MorelMor03, Lemma 4.3.11], the canonical map of sheaves
is an isomorphism, hence the composite map of sheaves is an isomorphism for all
![]() $n\geqslant 0$
$n\geqslant 0$
where the left map is induced by the structure map.
Denote by
![]() ${\mathcal{W}}^{{\mathcal{A}}}$
the strictly
${\mathcal{W}}^{{\mathcal{A}}}$
the strictly
![]() $\mathbb{A}^{1}$
-invariant sheaf
$\mathbb{A}^{1}$
-invariant sheaf
![]() $\unicode[STIX]{x1D70B}_{0,0}^{\mathbb{A}^{1}}(M_{{\mathcal{A}}}^{\mathbb{G}_{m}}(pt)_{f}[\unicode[STIX]{x1D702}^{-1}])$
. If we regard it as a complex concentrated in zeroth degree, then the collection of complexes
$\unicode[STIX]{x1D70B}_{0,0}^{\mathbb{A}^{1}}(M_{{\mathcal{A}}}^{\mathbb{G}_{m}}(pt)_{f}[\unicode[STIX]{x1D702}^{-1}])$
. If we regard it as a complex concentrated in zeroth degree, then the collection of complexes
together with isomorphisms
![]() $\unicode[STIX]{x1D6FD}_{0}:{\mathcal{W}}^{{\mathcal{A}}}\rightarrow ({\mathcal{W}}^{{\mathcal{A}}})_{-1}$
, is an object of
$\unicode[STIX]{x1D6FD}_{0}:{\mathcal{W}}^{{\mathcal{A}}}\rightarrow ({\mathcal{W}}^{{\mathcal{A}}})_{-1}$
, is an object of
![]() $DM_{{\mathcal{A}}}(k)$
, which is
$DM_{{\mathcal{A}}}(k)$
, which is
![]() $\mathbb{A}^{1}$
-local as an ordinary bispectrum (after taking the Eilenberg–Mac Lane spectrum of each sheaf
$\mathbb{A}^{1}$
-local as an ordinary bispectrum (after taking the Eilenberg–Mac Lane spectrum of each sheaf
![]() ${\mathcal{W}}^{{\mathcal{A}}}$
). Notice that the homotopy module of
${\mathcal{W}}^{{\mathcal{A}}}$
). Notice that the homotopy module of
![]() ${\mathcal{W}}_{\mathbb{G}_{m}}^{{\mathcal{A}}}$
in the sense of [Reference MorelMor03, Definition 5.2.4] is given by
${\mathcal{W}}_{\mathbb{G}_{m}}^{{\mathcal{A}}}$
in the sense of [Reference MorelMor03, Definition 5.2.4] is given by
![]() $(M_{\ast },\unicode[STIX]{x1D707}_{\ast })$
with each
$(M_{\ast },\unicode[STIX]{x1D707}_{\ast })$
with each
![]() $M_{n}={\mathcal{W}}^{{\mathcal{A}}}$
and
$M_{n}={\mathcal{W}}^{{\mathcal{A}}}$
and
![]() $\unicode[STIX]{x1D707}_{n}=\unicode[STIX]{x1D6FD}_{0}$
,
$\unicode[STIX]{x1D707}_{n}=\unicode[STIX]{x1D6FD}_{0}$
,
![]() $n\in \mathbb{Z}$
. There is a canonical morphism of spectra
$n\in \mathbb{Z}$
. There is a canonical morphism of spectra
induced by taking the zeroth homology sheaf of each complex
![]() $\unicode[STIX]{x1D6FA}_{(\mathbb{G}_{m},1)}^{\infty -n}(M_{{\mathcal{A}}}(pt)_{f})$
.
$\unicode[STIX]{x1D6FA}_{(\mathbb{G}_{m},1)}^{\infty -n}(M_{{\mathcal{A}}}(pt)_{f})$
.
Let
![]() $\text{}\underline{W}$
be the Nisnevich sheaf of Witt rings on
$\text{}\underline{W}$
be the Nisnevich sheaf of Witt rings on
![]() $Sm/k$
. Following [Reference Ananyevskiy, Levine and PaninALP17, p. 380], we take the model
$Sm/k$
. Following [Reference Ananyevskiy, Levine and PaninALP17, p. 380], we take the model
![]() $\text{}\underline{W}:=\text{}\underline{K}_{0}^{\text{MW}}/h$
. The isomorphism
$\text{}\underline{W}:=\text{}\underline{K}_{0}^{\text{MW}}/h$
. The isomorphism
![]() $\text{}\underline{W}\cong \unicode[STIX]{x1D70B}_{n>0,n>0}^{\mathbb{A}^{1}}(\mathbb{S})$
gives the canonical isomorphism of sheaves
$\text{}\underline{W}\cong \unicode[STIX]{x1D70B}_{n>0,n>0}^{\mathbb{A}^{1}}(\mathbb{S})$
gives the canonical isomorphism of sheaves
![]() $\unicode[STIX]{x1D700}:\text{}\underline{W}\cong \text{}\underline{\operatorname{Hom}}((\mathbb{G}_{m},1),\text{}\underline{W})$
. More precisely, it takes
$\unicode[STIX]{x1D700}:\text{}\underline{W}\cong \text{}\underline{\operatorname{Hom}}((\mathbb{G}_{m},1),\text{}\underline{W})$
. More precisely, it takes
![]() $w\in \text{}\underline{W}(U)$
to
$w\in \text{}\underline{W}(U)$
to
![]() $p_{1}^{\ast }(\unicode[STIX]{x1D702}\cdot [t])\cdot p_{2}^{\ast }(w)\in \text{}\underline{W}(U\wedge (\mathbb{G}_{m},1))$
, where
$p_{1}^{\ast }(\unicode[STIX]{x1D702}\cdot [t])\cdot p_{2}^{\ast }(w)\in \text{}\underline{W}(U\wedge (\mathbb{G}_{m},1))$
, where
![]() $t$
is the canonical unit on
$t$
is the canonical unit on
![]() $\mathbb{G}_{m}$
and
$\mathbb{G}_{m}$
and
![]() $[t]\in \text{}\underline{K}_{1}^{\text{MW}}(\mathbb{G}_{m})$
the corresponding section.
$[t]\in \text{}\underline{K}_{1}^{\text{MW}}(\mathbb{G}_{m})$
the corresponding section.
Definition 3.8. Suppose
![]() ${\mathcal{A}}$
is a strict
${\mathcal{A}}$
is a strict
![]() $V$
-category of correspondences satisfying the cancellation property and
$V$
-category of correspondences satisfying the cancellation property and
![]() $R$
a flat
$R$
a flat
![]() $\mathbb{Z}$
-algebra. We say that the spectrum
$\mathbb{Z}$
-algebra. We say that the spectrum
![]() $\mathbb{S}^{{\mathcal{A}}}[\unicode[STIX]{x1D702}_{{\mathcal{A}}}^{-1}]$
is of Witt type with
$\mathbb{S}^{{\mathcal{A}}}[\unicode[STIX]{x1D702}_{{\mathcal{A}}}^{-1}]$
is of Witt type with
![]() $R$
-coefficients if the zeroth cohomology sheaf
$R$
-coefficients if the zeroth cohomology sheaf
![]() ${\mathcal{W}}_{R}^{{\mathcal{A}}}=\unicode[STIX]{x1D70B}_{0,0}^{\mathbb{A}^{1}}(M_{{\mathcal{A}}}^{\mathbb{G}_{m}}(pt)_{f}[\unicode[STIX]{x1D702}^{-1}])\otimes R$
of the complex
${\mathcal{W}}_{R}^{{\mathcal{A}}}=\unicode[STIX]{x1D70B}_{0,0}^{\mathbb{A}^{1}}(M_{{\mathcal{A}}}^{\mathbb{G}_{m}}(pt)_{f}[\unicode[STIX]{x1D702}^{-1}])\otimes R$
of the complex
![]() $\unicode[STIX]{x1D6FA}_{(\mathbb{G}_{m},1)}^{\infty }(M_{{\mathcal{A}}}(pt)_{f})\otimes R$
is the only non-zero cohomology sheaf (the other cohomology sheaves are required to be zero) and
$\unicode[STIX]{x1D6FA}_{(\mathbb{G}_{m},1)}^{\infty }(M_{{\mathcal{A}}}(pt)_{f})\otimes R$
is the only non-zero cohomology sheaf (the other cohomology sheaves are required to be zero) and
![]() ${\mathcal{W}}_{R}^{{\mathcal{A}}}$
is isomorphic to the Nisnevich sheaf
${\mathcal{W}}_{R}^{{\mathcal{A}}}$
is isomorphic to the Nisnevich sheaf
![]() $\text{}\underline{W}_{R}=\text{}\underline{W}\otimes R$
. We also require the diagram
$\text{}\underline{W}_{R}=\text{}\underline{W}\otimes R$
. We also require the diagram

to be commutative. If
![]() $R=\mathbb{Z}$
then we just say that
$R=\mathbb{Z}$
then we just say that
![]() $\mathbb{S}^{{\mathcal{A}}}[\unicode[STIX]{x1D702}_{{\mathcal{A}}}^{-1}]$
is of Witt type.
$\mathbb{S}^{{\mathcal{A}}}[\unicode[STIX]{x1D702}_{{\mathcal{A}}}^{-1}]$
is of Witt type.
Lemma 3.9. Suppose
![]() ${\mathcal{A}}$
is a strict
${\mathcal{A}}$
is a strict
![]() $V$
-category of correspondences satisfying the cancellation property and
$V$
-category of correspondences satisfying the cancellation property and
![]() $R$
a ring of fractions of
$R$
a ring of fractions of
![]() $\mathbb{Z}$
. If the spectrum
$\mathbb{Z}$
. If the spectrum
![]() $\mathbb{S}^{{\mathcal{A}}}[\unicode[STIX]{x1D702}_{{\mathcal{A}}}^{-1}]$
is of Witt type with
$\mathbb{S}^{{\mathcal{A}}}[\unicode[STIX]{x1D702}_{{\mathcal{A}}}^{-1}]$
is of Witt type with
![]() $R$
-coefficients then it is isomorphic in
$R$
-coefficients then it is isomorphic in
![]() $SH(k)$
to the bispectrum
$SH(k)$
to the bispectrum
in which every structure map is induced by
![]() $\unicode[STIX]{x1D700}$
.
$\unicode[STIX]{x1D700}$
.
Proof. This immediately follows from Definition 3.8 and the observation that the morphism of spectra (1) is a motivic equivalence. ◻
We are now in a position to prove the main result of this section.
Theorem 3.10. Suppose
![]() ${\mathcal{A}}$
is a strict
${\mathcal{A}}$
is a strict
![]() $V$
-category of correspondences satisfying the cancellation property.
$V$
-category of correspondences satisfying the cancellation property.
(1) If the spectrum
 $\mathbb{S}^{{\mathcal{A}}}[\unicode[STIX]{x1D702}_{{\mathcal{A}}}^{-1}]$
is of Witt type with
$\mathbb{S}^{{\mathcal{A}}}[\unicode[STIX]{x1D702}_{{\mathcal{A}}}^{-1}]$
is of Witt type with
 $\mathbb{Q}$
-coefficients then the canonical morphism is an isomorphism in
$\mathbb{Q}$
-coefficients then the canonical morphism is an isomorphism in $$\begin{eqnarray}\mathbb{S}_{-}\otimes \mathbb{Q}\rightarrow \mathbb{S}_{-}^{{\mathcal{A}}}\otimes \mathbb{Q}\end{eqnarray}$$
$$\begin{eqnarray}\mathbb{S}_{-}\otimes \mathbb{Q}\rightarrow \mathbb{S}_{-}^{{\mathcal{A}}}\otimes \mathbb{Q}\end{eqnarray}$$
 $SH(k)$
.
$SH(k)$
.(2) If the spectrum
 $\mathbb{S}^{{\mathcal{A}}}[\unicode[STIX]{x1D702}_{{\mathcal{A}}}^{-1}]$
is of Witt type with
$\mathbb{S}^{{\mathcal{A}}}[\unicode[STIX]{x1D702}_{{\mathcal{A}}}^{-1}]$
is of Witt type with
 $\mathbb{Z}[1/2]$
-coefficients then the canonical morphism is an isomorphism in
$\mathbb{Z}[1/2]$
-coefficients then the canonical morphism is an isomorphism in $$\begin{eqnarray}H_{\mathbb{A}^{1}}\mathbb{Z}_{-}\rightarrow \mathbb{S}_{-}^{{\mathcal{A}}}\end{eqnarray}$$
$$\begin{eqnarray}H_{\mathbb{A}^{1}}\mathbb{Z}_{-}\rightarrow \mathbb{S}_{-}^{{\mathcal{A}}}\end{eqnarray}$$
 $SH(k)$
.
$SH(k)$
.
Proof. (1) It follows from [Reference Ananyevskiy, Levine and PaninALP17] that the composite morphism
is an isomorphism in
![]() $SH(k)$
. By Lemma 3.9 the right morphism is an isomorphism in
$SH(k)$
. By Lemma 3.9 the right morphism is an isomorphism in
![]() $SH(k)$
, and hence so is the left one.
$SH(k)$
, and hence so is the left one.
(2) It follows from [Reference BachmannBac18, Proposition 37] that the composite morphism
is an isomorphism in
![]() $SH(k)$
. By Lemma 3.9 the right morphism is an isomorphism in
$SH(k)$
. By Lemma 3.9 the right morphism is an isomorphism in
![]() $SH(k)$
, and hence so is the left one.◻
$SH(k)$
, and hence so is the left one.◻
4 The Milnor–Witt sphere spectrum
 $\mathbb{S}^{\text{MW}}$
$\mathbb{S}^{\text{MW}}$
Throughout this section
![]() $k$
is an infinite perfect field with
$k$
is an infinite perfect field with
![]() $\operatorname{char}k\not =2$
. We refer the reader to [Reference Calmès and FaselCF14] for basic facts and definitions on the category of finite Milnor–Witt correspondences
$\operatorname{char}k\not =2$
. We refer the reader to [Reference Calmès and FaselCF14] for basic facts and definitions on the category of finite Milnor–Witt correspondences
![]() $\widetilde{\operatorname{Cor}}$
. It is a strict
$\widetilde{\operatorname{Cor}}$
. It is a strict
![]() $V$
-category of correspondences by [Reference Déglise and FaselDF17]. It follows from [Reference Fasel and ØstværFØ17] that
$V$
-category of correspondences by [Reference Déglise and FaselDF17]. It follows from [Reference Fasel and ØstværFØ17] that
![]() $\widetilde{\operatorname{Cor}}$
has the cancellation property. We denote the additive sphere spectrum associated with
$\widetilde{\operatorname{Cor}}$
has the cancellation property. We denote the additive sphere spectrum associated with
![]() $\widetilde{\operatorname{Cor}}$
by
$\widetilde{\operatorname{Cor}}$
by
![]() $\mathbb{S}^{\text{MW}}$
.
$\mathbb{S}^{\text{MW}}$
.
By [Reference Calmès and FaselCF14, Proposition 5.11]
![]() $\widetilde{\operatorname{Cor}}(-,Y)$
is a Zariski sheaf, but not a Nisnevich sheaf in general [Reference Calmès and FaselCF14, Example 5.12]. However,
$\widetilde{\operatorname{Cor}}(-,Y)$
is a Zariski sheaf, but not a Nisnevich sheaf in general [Reference Calmès and FaselCF14, Example 5.12]. However,
![]() $\widetilde{\operatorname{Cor}}(-,pt)$
is the Nisnevich sheaf
$\widetilde{\operatorname{Cor}}(-,pt)$
is the Nisnevich sheaf
![]() $\text{}\underline{K}_{0}^{\text{MW}}$
[Reference Calmès and FaselCF14, Example 4.5], which is homotopy invariant by [Reference FaselFas08, Corollaire 11.3.3]. Since
$\text{}\underline{K}_{0}^{\text{MW}}$
[Reference Calmès and FaselCF14, Example 4.5], which is homotopy invariant by [Reference FaselFas08, Corollaire 11.3.3]. Since
![]() $\widetilde{\operatorname{Cor}}$
is a strict additive
$\widetilde{\operatorname{Cor}}$
is a strict additive
![]() $V$
-category of correspondences by [Reference Déglise and FaselDF17], we see that the Nisnevich sheaf
$V$
-category of correspondences by [Reference Déglise and FaselDF17], we see that the Nisnevich sheaf
![]() $\widetilde{\operatorname{Cor}}(-,pt)$
is strictly homotopy invariant. In particular, the normalized complex
$\widetilde{\operatorname{Cor}}(-,pt)$
is strictly homotopy invariant. In particular, the normalized complex
![]() $M_{\text{MW}}(pt)$
associated to the simplicial sheaf
$M_{\text{MW}}(pt)$
associated to the simplicial sheaf
![]() $\widetilde{\operatorname{Cor}}(-\times \unicode[STIX]{x1D6E5}^{\bullet },pt)$
has only one non-trivial homology sheaf
$\widetilde{\operatorname{Cor}}(-\times \unicode[STIX]{x1D6E5}^{\bullet },pt)$
has only one non-trivial homology sheaf
![]() $\text{}\underline{K}_{0}^{\text{MW}}$
. It follows from [Reference Calmès and FaselCF14, Proposition 5.34] that
$\text{}\underline{K}_{0}^{\text{MW}}$
. It follows from [Reference Calmès and FaselCF14, Proposition 5.34] that
![]() $\unicode[STIX]{x1D70B}_{0}^{\mathbb{A}^{1}}(\operatorname{Hom}((\mathbb{G}_{m},1)^{\wedge n},M_{\text{MW}}(pt)))$
is isomorphic to the sheaf
$\unicode[STIX]{x1D70B}_{0}^{\mathbb{A}^{1}}(\operatorname{Hom}((\mathbb{G}_{m},1)^{\wedge n},M_{\text{MW}}(pt)))$
is isomorphic to the sheaf
![]() $\text{}\underline{W}$
of Witt rings. Thus the spectrum
$\text{}\underline{W}$
of Witt rings. Thus the spectrum
![]() $\mathbb{S}^{\text{MW}}[\unicode[STIX]{x1D702}^{-1}]$
is of Witt type. Theorem 3.10 now implies the following result.
$\mathbb{S}^{\text{MW}}[\unicode[STIX]{x1D702}^{-1}]$
is of Witt type. Theorem 3.10 now implies the following result.
Proposition 4.1. The canonical morphisms
are isomorphisms in
![]() $SH(k)$
.
$SH(k)$
.
It follows from properties of finite Milnor–Witt correspondences [Reference Calmès and FaselCF14] that
![]() $\mathbb{S}_{+}^{\text{MW}}$
is isomorphic to
$\mathbb{S}_{+}^{\text{MW}}$
is isomorphic to
![]() $\mathbb{S}^{\operatorname{Cor}}[2^{-1}]$
in
$\mathbb{S}^{\operatorname{Cor}}[2^{-1}]$
in
![]() $DM_{\text{MW}}(k)[2^{-1}]:=DM_{\widetilde{\operatorname{Cor}}}(k)[2^{-1}]$
. Thus we have a splitting,
$DM_{\text{MW}}(k)[2^{-1}]:=DM_{\widetilde{\operatorname{Cor}}}(k)[2^{-1}]$
. Thus we have a splitting,
A theorem of Cisinski and Déglise [Reference Cisinski and DégliseCD12, Theorem 16.2.13] shows that the canonical map
![]() $\mathbb{S}_{+}\otimes \mathbb{Q}\rightarrow \mathbb{S}^{\operatorname{Cor}}\otimes \mathbb{Q}$
is an isomorphism in
$\mathbb{S}_{+}\otimes \mathbb{Q}\rightarrow \mathbb{S}^{\operatorname{Cor}}\otimes \mathbb{Q}$
is an isomorphism in
![]() $SH(k)$
. Combining this with Proposition 4.1, we have proved the following theorem, which is the main result of the section.
$SH(k)$
. Combining this with Proposition 4.1, we have proved the following theorem, which is the main result of the section.
Theorem 4.2. Given an infinite perfect field
![]() $k$
of characteristic not
$k$
of characteristic not
![]() $2$
, the canonical morphism of bispectra
$2$
, the canonical morphism of bispectra
is an isomorphism in
![]() $SH(k)$
.
$SH(k)$
.
Let
![]() $H_{\mathbb{A}^{1}}^{\ast ,\ast }(X)$
be the cohomology theory represented in
$H_{\mathbb{A}^{1}}^{\ast ,\ast }(X)$
be the cohomology theory represented in
![]() $SH(k)$
by the bispectrum
$SH(k)$
by the bispectrum
![]() $H_{\mathbb{A}^{1}}\mathbb{Z}$
. The following statement is a consequence of the preceding theorem and a result of Déglise and Fasel [Reference Déglise and FaselDF17, Corollary 4.2.6],
$H_{\mathbb{A}^{1}}\mathbb{Z}$
. The following statement is a consequence of the preceding theorem and a result of Déglise and Fasel [Reference Déglise and FaselDF17, Corollary 4.2.6],
Corollary 4.3. Given an infinite perfect field
![]() $k$
of characteristic not
$k$
of characteristic not
![]() $2$
,
$2$
,
![]() $n\geqslant 0$
and
$n\geqslant 0$
and
![]() $X\in Sm/k$
, there is a natural isomorphism
$X\in Sm/k$
, there is a natural isomorphism
where the right-hand side is the
![]() $n$
th rational Chow–Witt group of
$n$
th rational Chow–Witt group of
![]() $X$
. In particular, if
$X$
. In particular, if
![]() $-1$
is a sum of squares in
$-1$
is a sum of squares in
![]() $k$
, then
$k$
, then
![]() $H_{\mathbb{A}^{1}}^{2n,n}(X)\otimes \mathbb{Q}\cong CH^{n}(X)\otimes \mathbb{Q},$
where
$H_{\mathbb{A}^{1}}^{2n,n}(X)\otimes \mathbb{Q}\cong CH^{n}(X)\otimes \mathbb{Q},$
where
![]() $CH^{n}(X)\otimes \mathbb{Q}$
is the
$CH^{n}(X)\otimes \mathbb{Q}$
is the
![]() $n$
th rational Chow group of
$n$
th rational Chow group of
![]() $X$
.
$X$
.
5 Reconstructing
 $SH(k)_{\mathbb{Q}}$
from finite Milnor–Witt correspondences
$SH(k)_{\mathbb{Q}}$
from finite Milnor–Witt correspondences
In this section we prove the main result of the paper stating that
![]() $SH(k)_{\mathbb{Q}}$
is recovered as
$SH(k)_{\mathbb{Q}}$
is recovered as
![]() $DM_{\text{MW}}(k)_{\mathbb{Q}}$
whenever the base field
$DM_{\text{MW}}(k)_{\mathbb{Q}}$
whenever the base field
![]() $k$
is infinite perfect of characteristic not
$k$
is infinite perfect of characteristic not
![]() $2$
. To this end, we need to extend Röndigs and Østvær’s theorem [Reference Röndigs and ØstværRØ08a] to preadditive categories of correspondences. Throughout this section
$2$
. To this end, we need to extend Röndigs and Østvær’s theorem [Reference Röndigs and ØstværRØ08a] to preadditive categories of correspondences. Throughout this section
![]() ${\mathcal{A}}$
is a category of correspondences.
${\mathcal{A}}$
is a category of correspondences.
Following [Reference Röndigs and ØstværRØ08a, § 2], define the category
![]() $\mathbb{M}^{{\mathcal{A}}}$
of motivic spaces with
$\mathbb{M}^{{\mathcal{A}}}$
of motivic spaces with
![]() ${\mathcal{A}}$
-correspondences as all contravariant additive functors from
${\mathcal{A}}$
-correspondences as all contravariant additive functors from
![]() ${\mathcal{A}}$
to simplicial abelian groups. A scheme
${\mathcal{A}}$
to simplicial abelian groups. A scheme
![]() $U$
in
$U$
in
![]() $Sm/k$
defines a representable motivic space
$Sm/k$
defines a representable motivic space
![]() ${\mathcal{A}}(-,U)\in \mathbb{M}^{{\mathcal{A}}}$
. Let
${\mathcal{A}}(-,U)\in \mathbb{M}^{{\mathcal{A}}}$
. Let
![]() ${\mathcal{U}}:\mathbb{M}^{{\mathcal{A}}}\rightarrow \mathbb{M}$
denote the evident forgetful functor induced by the graph
${\mathcal{U}}:\mathbb{M}^{{\mathcal{A}}}\rightarrow \mathbb{M}$
denote the evident forgetful functor induced by the graph
![]() $Sm/k\rightarrow {\mathcal{A}}$
. It has a left adjoint
$Sm/k\rightarrow {\mathcal{A}}$
. It has a left adjoint
![]() $\mathbb{Z}^{{\mathcal{A}}}:\mathbb{M}\rightarrow \mathbb{M}^{{\mathcal{A}}}$
defined as the left Kan extension functor determined by
$\mathbb{Z}^{{\mathcal{A}}}:\mathbb{M}\rightarrow \mathbb{M}^{{\mathcal{A}}}$
defined as the left Kan extension functor determined by
If
![]() $X$
is a motivic space, let
$X$
is a motivic space, let
![]() $X^{{\mathcal{A}}}$
be short for
$X^{{\mathcal{A}}}$
be short for
![]() $\mathbb{Z}^{{\mathcal{A}}}(X)$
.
$\mathbb{Z}^{{\mathcal{A}}}(X)$
.
Similarly to [Reference Röndigs and ØstværRØ08a, § 2.1], we define a projective motivic model category structure on
![]() $\mathbb{M}^{{\mathcal{A}}}$
. This model category is denoted by
$\mathbb{M}^{{\mathcal{A}}}$
. This model category is denoted by
![]() $\mathbb{M}_{\operatorname{mot}}^{{\mathcal{A}}}$
. The projective motivic model category of motivic spaces is denoted by
$\mathbb{M}_{\operatorname{mot}}^{{\mathcal{A}}}$
. The projective motivic model category of motivic spaces is denoted by
![]() $\mathbb{M}_{\operatorname{mot}}$
. We have a Quillen pair
$\mathbb{M}_{\operatorname{mot}}$
. We have a Quillen pair
Using Definition 2.3(1) and Lemma 2.4, the proof of the following lemma literally repeats [Reference Röndigs and ØstværRØ08a, Lemma 9].
Lemma 5.1. A map between motivic spaces with
![]() ${\mathcal{A}}$
-correspondences is a motivic weak equivalence in
${\mathcal{A}}$
-correspondences is a motivic weak equivalence in
![]() $\mathbb{M}_{\operatorname{mot}}^{{\mathcal{A}}}$
if and only if it is so when considered as a map between ordinary motivic spaces.
$\mathbb{M}_{\operatorname{mot}}^{{\mathcal{A}}}$
if and only if it is so when considered as a map between ordinary motivic spaces.
Let
![]() $\unicode[STIX]{x1D704}:pt=\operatorname{Spec}k\rightarrow \mathbb{G}_{m}$
be the embedding
$\unicode[STIX]{x1D704}:pt=\operatorname{Spec}k\rightarrow \mathbb{G}_{m}$
be the embedding
![]() $\unicode[STIX]{x1D704}(pt)=1\in \mathbb{G}_{m}$
. The mapping cylinder yields a factorization of the induced map
$\unicode[STIX]{x1D704}(pt)=1\in \mathbb{G}_{m}$
. The mapping cylinder yields a factorization of the induced map
into a projective cofibration and a simplicial homotopy equivalence in
![]() $\mathbb{M}$
. Let
$\mathbb{M}$
. Let
![]() $\mathbb{G}$
denote the cofibrant pointed presheaf
$\mathbb{G}$
denote the cofibrant pointed presheaf
![]() $\operatorname{Cyl}(\unicode[STIX]{x1D704})/\operatorname{Spec}k_{+}$
and
$\operatorname{Cyl}(\unicode[STIX]{x1D704})/\operatorname{Spec}k_{+}$
and
![]() $T:=S^{1}\wedge \mathbb{G}$
.
$T:=S^{1}\wedge \mathbb{G}$
.
Following [Reference Röndigs and ØstværRØ08a, § 2.4], we define a motivic spectrum
The structure maps are induced by morphisms
(recall that
![]() $Sm/k$
acts on
$Sm/k$
acts on
![]() ${\mathcal{A}}$
).
${\mathcal{A}}$
).
Given a symmetric monoidal category of correspondences
![]() ${\mathcal{A}}$
, a theorem of Day [Reference DayDay70] implies that
${\mathcal{A}}$
, a theorem of Day [Reference DayDay70] implies that
![]() $\mathbb{M}^{{\mathcal{A}}}$
is a closed symmetric monoidal category with a tensor product defined as
$\mathbb{M}^{{\mathcal{A}}}$
is a closed symmetric monoidal category with a tensor product defined as
As an example,
![]() ${\mathcal{A}}(-,U)\odot {\mathcal{A}}(-,V)={\mathcal{A}}(-,U\times V)$
. The monoidal unit equals
${\mathcal{A}}(-,U)\odot {\mathcal{A}}(-,V)={\mathcal{A}}(-,U\times V)$
. The monoidal unit equals
![]() ${\mathcal{A}}(-,pt)$
with
${\mathcal{A}}(-,pt)$
with
![]() $pt=\operatorname{Spec}k$
. Similarly to [Reference Dundas, Röndigs and ØstværDRØ03, Example 3.4],
$pt=\operatorname{Spec}k$
. Similarly to [Reference Dundas, Röndigs and ØstværDRØ03, Example 3.4],
![]() $H{\mathcal{A}}$
is a commutative motivic symmetric ring spectrum.
$H{\mathcal{A}}$
is a commutative motivic symmetric ring spectrum.
Suppose
![]() ${\mathcal{A}}$
is a symmetric monoidal category of correspondences. Repeating the proof of [Reference Röndigs and ØstværRØ08a, Lemma 10] word for word, the projective motivic model structure on
${\mathcal{A}}$
is a symmetric monoidal category of correspondences. Repeating the proof of [Reference Röndigs and ØstværRØ08a, Lemma 10] word for word, the projective motivic model structure on
![]() $\mathbb{M}_{\operatorname{mot}}^{{\mathcal{A}}}$
is symmetric monoidal. Following [Reference HoveyHov01, Reference Röndigs and ØstværRØ08a], one can define the stable monoidal model category of symmetric
$\mathbb{M}_{\operatorname{mot}}^{{\mathcal{A}}}$
is symmetric monoidal. Following [Reference HoveyHov01, Reference Röndigs and ØstværRØ08a], one can define the stable monoidal model category of symmetric
![]() $T$
-spectra
$T$
-spectra
![]() $\mathbb{MSS}^{{\mathcal{A}}}$
associated to
$\mathbb{MSS}^{{\mathcal{A}}}$
associated to
![]() $\mathbb{M}_{\operatorname{mot}}^{{\mathcal{A}}}$
(with projective model structure). The homotopy category of
$\mathbb{M}_{\operatorname{mot}}^{{\mathcal{A}}}$
(with projective model structure). The homotopy category of
![]() $\mathbb{MSS}^{{\mathcal{A}}}$
is a model for
$\mathbb{MSS}^{{\mathcal{A}}}$
is a model for
![]() $D_{\mathbb{A}^{1}}^{\text{st}}(Sh({\mathcal{A}}))(k)$
. It is also a model for
$D_{\mathbb{A}^{1}}^{\text{st}}(Sh({\mathcal{A}}))(k)$
. It is also a model for
![]() $DM_{{\mathcal{A}}}(k)$
whenever
$DM_{{\mathcal{A}}}(k)$
whenever
![]() ${\mathcal{A}}$
is a strict
${\mathcal{A}}$
is a strict
![]() $V$
-category of correspondences (for this, repeat the proof of [Reference Röndigs and ØstværRØ08a, Theorem 11] word for word).
$V$
-category of correspondences (for this, repeat the proof of [Reference Röndigs and ØstværRØ08a, Theorem 11] word for word).
Below we shall need the following theorem proved by Riou in [Reference Levine, Yang and ZhaoLYZ13, Appendix B] (see also the proof of [Reference Hoyois, Kelly and ØstværHKØ17, Theorem 5.8]).
Theorem 5.2 (Riou).
Let
![]() $k$
be a perfect field. Let
$k$
be a perfect field. Let
![]() $p$
denote the caracteristic exponent of
$p$
denote the caracteristic exponent of
![]() $k$
(i.e.
$k$
(i.e.
![]() $p>0$
or
$p>0$
or
![]() $p=1$
if the characteristic of
$p=1$
if the characteristic of
![]() $k$
is zero). Then, for any smooth finite type
$k$
is zero). Then, for any smooth finite type
![]() $k$
-scheme
$k$
-scheme
![]() $U$
, the suspension spectrum
$U$
, the suspension spectrum
![]() $\unicode[STIX]{x1D6F4}_{T}^{\infty }U_{+}$
is strongly dualizable in
$\unicode[STIX]{x1D6F4}_{T}^{\infty }U_{+}$
is strongly dualizable in
![]() $SH(k)[1/p]$
.
$SH(k)[1/p]$
.
We are now in a position to prove the Röndigs–Østvær theorem for
![]() ${\mathcal{A}}$
-correspondences. Notice that in all known examples a
${\mathcal{A}}$
-correspondences. Notice that in all known examples a
![]() $V$
-category of correspondences is strict whenever the base field
$V$
-category of correspondences is strict whenever the base field
![]() $k$
is (infinite) perfect (of characteristic not
$k$
is (infinite) perfect (of characteristic not
![]() $2$
if
$2$
if
![]() ${\mathcal{A}}=\widetilde{\text{Cor}}$
). We also remind the reader that the category
${\mathcal{A}}=\widetilde{\text{Cor}}$
). We also remind the reader that the category
![]() $SH(k)[p^{-1}]$
is defined on p. 1430. It is the homotopy category of the stable model category of motivic functors with weak equivalences being
$SH(k)[p^{-1}]$
is defined on p. 1430. It is the homotopy category of the stable model category of motivic functors with weak equivalences being
![]() $p^{-1}$
-stable motivic equivalences.
$p^{-1}$
-stable motivic equivalences.
Theorem 5.3 (Röndigs and Østvær).
If
![]() $k$
is a perfect field of exponential characteristic
$k$
is a perfect field of exponential characteristic
![]() $p$
and
$p$
and
![]() ${\mathcal{A}}$
is a symmetric monoidal category of correspondences, then the homotopy category of
${\mathcal{A}}$
is a symmetric monoidal category of correspondences, then the homotopy category of
![]() $\operatorname{Mod}H{\mathcal{A}}_{\mathbb{Z}[1/p]}$
(respectively,
$\operatorname{Mod}H{\mathcal{A}}_{\mathbb{Z}[1/p]}$
(respectively,
![]() $\operatorname{Mod}H{\mathcal{A}}_{\mathbb{Q}}$
) is equivalent to
$\operatorname{Mod}H{\mathcal{A}}_{\mathbb{Q}}$
) is equivalent to
![]() $D_{\mathbb{A}^{1}}^{\text{st}}(Sh({\mathcal{A}}))(k)[1/p]$
(respectively,
$D_{\mathbb{A}^{1}}^{\text{st}}(Sh({\mathcal{A}}))(k)[1/p]$
(respectively,
![]() $D_{\mathbb{A}^{1}}^{\text{st}}(Sh({\mathcal{A}}))(k)\otimes \mathbb{Q}$
). The equivalence preserves the triangulated structure. In particular,
$D_{\mathbb{A}^{1}}^{\text{st}}(Sh({\mathcal{A}}))(k)\otimes \mathbb{Q}$
). The equivalence preserves the triangulated structure. In particular,
![]() $\operatorname{Ho}(\operatorname{Mod}H{\mathcal{A}}_{\mathbb{Z}[1/p]})$
(respectively,
$\operatorname{Ho}(\operatorname{Mod}H{\mathcal{A}}_{\mathbb{Z}[1/p]})$
(respectively,
![]() $\operatorname{Ho}(\operatorname{Mod}H{\mathcal{A}}_{\mathbb{Q}})$
) is equivalent to
$\operatorname{Ho}(\operatorname{Mod}H{\mathcal{A}}_{\mathbb{Q}})$
) is equivalent to
![]() $DM_{{\mathcal{A}}}(k)[1/p]$
(respectively,
$DM_{{\mathcal{A}}}(k)[1/p]$
(respectively,
![]() $DM_{{\mathcal{A}}}(k)\otimes \mathbb{Q}$
) if
$DM_{{\mathcal{A}}}(k)\otimes \mathbb{Q}$
) if
![]() ${\mathcal{A}}$
is a symmetric monoidal strict
${\mathcal{A}}$
is a symmetric monoidal strict
![]() $V$
-category of correspondences.
$V$
-category of correspondences.
Proof. We verify the theorem for categories with
![]() $\mathbb{Z}[1/p]$
-coefficients, because the proof of the statement for categories with rational coefficients repeats that for
$\mathbb{Z}[1/p]$
-coefficients, because the proof of the statement for categories with rational coefficients repeats that for
![]() $\mathbb{Z}[1/p]$
-coefficients word for word. The proof of the theorem for categories with
$\mathbb{Z}[1/p]$
-coefficients word for word. The proof of the theorem for categories with
![]() $\mathbb{Z}[1/p]$
-coefficients is the same with the original Röndigs–Østvær theorem [Reference Röndigs and ØstværRØ08a]. The only difference is that we shall have to deal somewhere with
$\mathbb{Z}[1/p]$
-coefficients is the same with the original Röndigs–Østvær theorem [Reference Röndigs and ØstværRØ08a]. The only difference is that we shall have to deal somewhere with
![]() $p^{-1}$
-stable weak equivalences of motivic functors instead of ordinary stable weak equivalences.
$p^{-1}$
-stable weak equivalences of motivic functors instead of ordinary stable weak equivalences.
We must show that the canonical pair of adjoint (triangulated) functors
is a Quillen equivalence (
![]() $\unicode[STIX]{x1D6F9}$
forgets correspondences).
$\unicode[STIX]{x1D6F9}$
forgets correspondences).
Similarly to [Reference Röndigs and ØstværRØ08a, Lemma 43], it suffices to prove that the unit of the adjunction
is a stable motivic weak equivalence of motivic symmetric spectra for every smooth scheme
![]() $U$
. Note that
$U$
. Note that
![]() $\unicode[STIX]{x1D6F9}\unicode[STIX]{x1D6F7}(H{\mathcal{A}}_{\mathbb{Z}[1/p]}\wedge U_{+})$
is the symmetric spectrum
$\unicode[STIX]{x1D6F9}\unicode[STIX]{x1D6F7}(H{\mathcal{A}}_{\mathbb{Z}[1/p]}\wedge U_{+})$
is the symmetric spectrum
![]() $({\mathcal{A}}(-,U)\otimes \mathbb{Z}[1/p],(U_{+}\wedge T)^{{\mathcal{A}}\otimes \mathbb{Z}[1/p]},(U_{+}\wedge T^{\wedge 2})^{{\mathcal{A}}\otimes \mathbb{Z}[1/p]},\ldots )$
.
$({\mathcal{A}}(-,U)\otimes \mathbb{Z}[1/p],(U_{+}\wedge T)^{{\mathcal{A}}\otimes \mathbb{Z}[1/p]},(U_{+}\wedge T^{\wedge 2})^{{\mathcal{A}}\otimes \mathbb{Z}[1/p]},\ldots )$
.
By Theorem 5.2,
![]() $U_{+}$
is dualizable in
$U_{+}$
is dualizable in
![]() $SH(k)[p^{-1}]$
for every
$SH(k)[p^{-1}]$
for every
![]() $k$
-smooth scheme
$k$
-smooth scheme
![]() $U$
. Suppose
$U$
. Suppose
![]() $X$
is a motivic functor in the sense of [Reference Dundas, Röndigs and ØstværDRØ03] and
$X$
is a motivic functor in the sense of [Reference Dundas, Röndigs and ØstværDRØ03] and
![]() $B$
is a cofibrant finitely presentable motivic space such that
$B$
is a cofibrant finitely presentable motivic space such that
![]() $-\wedge B$
is dualizable in
$-\wedge B$
is dualizable in
![]() $SH(k)[p^{-1}]$
. When
$SH(k)[p^{-1}]$
. When
![]() $X$
preserves motivic weak equivalences of cofibrant finitely presentable motivic spaces, then the evaluation of the assembly map
$X$
preserves motivic weak equivalences of cofibrant finitely presentable motivic spaces, then the evaluation of the assembly map
is a
![]() $p^{-1}$
-stable weak equivalence between motivic symmetric spectra by [Reference Röndigs and ØstværRØ08a, Corollary 56] (though [Reference Röndigs and ØstværRØ08a, Corollary 56] is proved within an ordinary stable motivic model structure of motivic functors, it is also true within the
$p^{-1}$
-stable weak equivalence between motivic symmetric spectra by [Reference Röndigs and ØstværRØ08a, Corollary 56] (though [Reference Röndigs and ØstværRØ08a, Corollary 56] is proved within an ordinary stable motivic model structure of motivic functors, it is also true within the
![]() $p^{-1}$
-stable model structure). We use here the notation and terminology of [Reference Dundas, Röndigs and ØstværDRØ03]. Recall that motivic functors give a model for motivic symmetric spectra, and hence for
$p^{-1}$
-stable model structure). We use here the notation and terminology of [Reference Dundas, Röndigs and ØstværDRØ03]. Recall that motivic functors give a model for motivic symmetric spectra, and hence for
![]() $SH(k)$
[Reference Dundas, Röndigs and ØstværDRØ03].
$SH(k)$
[Reference Dundas, Röndigs and ØstværDRØ03].
Consider a motivic functor associated with
![]() $H{\mathcal{A}}$
(denoted by the same letters)
$H{\mathcal{A}}$
(denoted by the same letters)
Here
![]() $c\mathbb{M}$
is the full subcategory of
$c\mathbb{M}$
is the full subcategory of
![]() $\mathbb{M}$
of cofibrant finitely presentable motivic spaces.
$\mathbb{M}$
of cofibrant finitely presentable motivic spaces.
![]() $\mathbb{Z}^{{\mathcal{A}}}:\mathbb{M}_{\operatorname{mot}}\rightarrow \mathbb{M}_{\operatorname{mot}}^{{\mathcal{A}}}$
is a left Quillen functor, hence it preserves motivic weak equivalences between cofibrant motivic spaces. By Lemma 5.1,
$\mathbb{Z}^{{\mathcal{A}}}:\mathbb{M}_{\operatorname{mot}}\rightarrow \mathbb{M}_{\operatorname{mot}}^{{\mathcal{A}}}$
is a left Quillen functor, hence it preserves motivic weak equivalences between cofibrant motivic spaces. By Lemma 5.1,
![]() ${\mathcal{U}}$
preserves weak equivalences in
${\mathcal{U}}$
preserves weak equivalences in
![]() $\mathbb{M}_{\operatorname{mot}}^{{\mathcal{A}}}$
. It follows that
$\mathbb{M}_{\operatorname{mot}}^{{\mathcal{A}}}$
. It follows that
![]() $H{\mathcal{A}}$
preserves motivic equivalences of cofibrant finitely presentable motivic spaces. Hence,
$H{\mathcal{A}}$
preserves motivic equivalences of cofibrant finitely presentable motivic spaces. Hence,
is a
![]() $p^{-1}$
-stable weak equivalence between motivic symmetric spectra by [Reference Röndigs and ØstværRØ08a, Corollary 56]. Similarly,
$p^{-1}$
-stable weak equivalence between motivic symmetric spectra by [Reference Röndigs and ØstværRØ08a, Corollary 56]. Similarly,
is a
![]() $p^{-1}$
-stable weak equivalence between motivic symmetric spectra. Obviously,
$p^{-1}$
-stable weak equivalence between motivic symmetric spectra. Obviously,
This is because fibrant replacements of the
![]() $T$
-spectrum
$T$
-spectrum
![]() $H{\mathcal{A}}_{\mathbb{Z}[1/p]}\circ (\mathbb{S}_{k}\wedge U_{+})$
, where
$H{\mathcal{A}}_{\mathbb{Z}[1/p]}\circ (\mathbb{S}_{k}\wedge U_{+})$
, where
![]() $\mathbb{S}_{k}$
is the motivic sphere spectrum, can be computed in
$\mathbb{S}_{k}$
is the motivic sphere spectrum, can be computed in
![]() $\mathbb{MSS}^{{\mathcal{A}}_{\mathbb{Z}[1/p]}}$
.
$\mathbb{MSS}^{{\mathcal{A}}_{\mathbb{Z}[1/p]}}$
.
We claim that
Indeed, this follows from an isomorphism in
![]() $SH(k)$
,
$SH(k)$
,
We see that (3) is not only a
![]() $p^{-1}$
-stable weak equivalence between motivic symmetric spectra, but also an ordinary stable motivic equivalence.
$p^{-1}$
-stable weak equivalence between motivic symmetric spectra, but also an ordinary stable motivic equivalence.
Ordinary symmetric
![]() $T$
-spectra are obtained from motivic spaces by evaluating them at spheres
$T$
-spectra are obtained from motivic spaces by evaluating them at spheres
![]() $S^{0},T,T^{\wedge 2},\ldots$
(see [Reference Dundas, Röndigs and ØstværDRØ03, §3.2]). The evaluation of the motivic space
$S^{0},T,T^{\wedge 2},\ldots$
(see [Reference Dundas, Röndigs and ØstværDRØ03, §3.2]). The evaluation of the motivic space
![]() $H{\mathcal{A}}_{\mathbb{Z}[1/p]}\wedge U_{+}$
is the symmetric
$H{\mathcal{A}}_{\mathbb{Z}[1/p]}\wedge U_{+}$
is the symmetric
![]() $T$
-spectrum
$T$
-spectrum
The evaluation of the motivic space
![]() $H{\mathcal{A}}_{\mathbb{Z}[1/p]}\circ (-\wedge U_{+})$
is the symmetric
$H{\mathcal{A}}_{\mathbb{Z}[1/p]}\circ (-\wedge U_{+})$
is the symmetric
![]() $T$
-spectrum
$T$
-spectrum
Furthermore, the evaluation of the morphism (3) is the morphism (2). We see that the morphism (2) is a stable motivic equivalence of motivic symmetric spectra, as was to be shown. ◻
Remark 5.4. Very recently Elmanto and Kolderup [Reference Elmanto and KolderupEK17] have suggested another approach to the Röndigs–Østvær theorem for
![]() ${\mathcal{A}}=\widetilde{\text{Cor}}$
that uses Lurie’s
${\mathcal{A}}=\widetilde{\text{Cor}}$
that uses Lurie’s
![]() $\infty$
-categorical version of the Barr–Beck theorem.
$\infty$
-categorical version of the Barr–Beck theorem.
Theorem 5.5 (Reconstruction).
If
![]() $k$
is an infinite perfect field with
$k$
is an infinite perfect field with
![]() $\operatorname{char}k\not =2$
, then
$\operatorname{char}k\not =2$
, then
![]() $SH(k)_{\mathbb{Q}}$
is equivalent to
$SH(k)_{\mathbb{Q}}$
is equivalent to
![]() $DM_{\text{MW}}(k)_{\mathbb{Q}}$
. The equivalence preserves the triangulated structure.
$DM_{\text{MW}}(k)_{\mathbb{Q}}$
. The equivalence preserves the triangulated structure.
Proof.
![]() $SH(k)_{\mathbb{Q}}$
is equivalent to
$SH(k)_{\mathbb{Q}}$
is equivalent to
![]() $D_{\mathbb{A}^{1}}(k)_{\mathbb{Q}}$
(see [Reference MorelMor04]). By Theorem 5.3, the latter is equivalent to the homotopy category of
$D_{\mathbb{A}^{1}}(k)_{\mathbb{Q}}$
(see [Reference MorelMor04]). By Theorem 5.3, the latter is equivalent to the homotopy category of
![]() $\mathbb{S}^{{\mathcal{A}}_{\text{naive}}}\otimes \mathbb{Q}$
-modules.
$\mathbb{S}^{{\mathcal{A}}_{\text{naive}}}\otimes \mathbb{Q}$
-modules.
![]() $\mathbb{S}^{{\mathcal{A}}_{\text{naive}}}\otimes \mathbb{Q}$
is motivically equivalent to the commutative monoid spectrum
$\mathbb{S}^{{\mathcal{A}}_{\text{naive}}}\otimes \mathbb{Q}$
is motivically equivalent to the commutative monoid spectrum
![]() $\mathbb{S}\otimes \mathbb{Q}$
. By [Reference Schwede and ShipleySS00, Theorem 4.3], the homotopy category of
$\mathbb{S}\otimes \mathbb{Q}$
. By [Reference Schwede and ShipleySS00, Theorem 4.3], the homotopy category of
![]() $\mathbb{S}^{{\mathcal{A}}_{\text{naive}}}\otimes \mathbb{Q}$
-modules is equivalent to the homotopy category of
$\mathbb{S}^{{\mathcal{A}}_{\text{naive}}}\otimes \mathbb{Q}$
-modules is equivalent to the homotopy category of
![]() $\mathbb{S}\otimes \mathbb{Q}$
-modules. By Theorem 4.2,
$\mathbb{S}\otimes \mathbb{Q}$
-modules. By Theorem 4.2,
![]() $\mathbb{S}\otimes \mathbb{Q}$
is motivically equivalent to the commutative monoid spectrum
$\mathbb{S}\otimes \mathbb{Q}$
is motivically equivalent to the commutative monoid spectrum
![]() $\mathbb{S}^{\text{MW}}\otimes \mathbb{Q}$
. By [Reference Schwede and ShipleySS00, Theorem 4.3], the homotopy category of
$\mathbb{S}^{\text{MW}}\otimes \mathbb{Q}$
. By [Reference Schwede and ShipleySS00, Theorem 4.3], the homotopy category of
![]() $\mathbb{S}\otimes \mathbb{Q}$
-modules is equivalent to the homotopy category of
$\mathbb{S}\otimes \mathbb{Q}$
-modules is equivalent to the homotopy category of
![]() $\mathbb{S}^{\text{MW}}\otimes \mathbb{Q}$
-modules. We see that
$\mathbb{S}^{\text{MW}}\otimes \mathbb{Q}$
-modules. We see that
![]() $SH(k)_{\mathbb{Q}}$
is equivalent to the homotopy category of
$SH(k)_{\mathbb{Q}}$
is equivalent to the homotopy category of
![]() $\mathbb{S}^{\text{MW}}\otimes \mathbb{Q}$
-modules. By Theorem 5.3, the latter category is triangle equivalent to
$\mathbb{S}^{\text{MW}}\otimes \mathbb{Q}$
-modules. By Theorem 5.3, the latter category is triangle equivalent to
![]() $DM_{\text{MW}}(k)_{\mathbb{Q}}$
, as was to be shown.◻
$DM_{\text{MW}}(k)_{\mathbb{Q}}$
, as was to be shown.◻
Remark 5.6. The triangulated equivalence of Theorem 5.5 is in fact symmetric monoidal. The main point here is that the natural functor between categories of correspondences
![]() ${\mathcal{A}}_{\text{naive}}\rightarrow \widetilde{\text{Cor}}$
is extended to a symmetric monoidal triangulated functor
${\mathcal{A}}_{\text{naive}}\rightarrow \widetilde{\text{Cor}}$
is extended to a symmetric monoidal triangulated functor
![]() $D_{\mathbb{A}^{1}}(k)\rightarrow DM_{\text{MW}}(k)$
(see also [Reference Déglise and FaselDF17, Section 3.3]). Consider a commutative diagram of natural triangulated functors
$D_{\mathbb{A}^{1}}(k)\rightarrow DM_{\text{MW}}(k)$
(see also [Reference Déglise and FaselDF17, Section 3.3]). Consider a commutative diagram of natural triangulated functors

The proof of the preceding theorem implies that the lower and the vertical functors are equivalences. We see that the upper functor is an equivalence. It is right adjoint to the functor
![]() $D_{\mathbb{A}^{1}}(k)_{\mathbb{Q}}\rightarrow DM_{\text{MW}}(k)_{\mathbb{Q}}$
. It follows that the latter functor is an equivalence, too. It is plainly symmetric monoidal.
$D_{\mathbb{A}^{1}}(k)_{\mathbb{Q}}\rightarrow DM_{\text{MW}}(k)_{\mathbb{Q}}$
. It follows that the latter functor is an equivalence, too. It is plainly symmetric monoidal.
6 Comparing motivic complexes with framed and
 $MW$
-correspondences
$MW$
-correspondences
In this section we apply the reconstruction theorem (Theorem 5.5) to compare rational motives with framed and Milnor–Witt correspondences respectively. Throughout this section the base field
![]() $k$
is infinite perfect of characteristic different from
$k$
is infinite perfect of characteristic different from
![]() $2$
.
$2$
.
It is shown in [Reference Garkusha and PaninGP14b] that the suspension bispectrum
![]() $\unicode[STIX]{x1D6F4}_{S^{1}}^{\infty }\unicode[STIX]{x1D6F4}_{\mathbb{G}}^{\infty }X_{+}\in SH(k)$
of a
$\unicode[STIX]{x1D6F4}_{S^{1}}^{\infty }\unicode[STIX]{x1D6F4}_{\mathbb{G}}^{\infty }X_{+}\in SH(k)$
of a
![]() $k$
-smooth algebraic variety
$k$
-smooth algebraic variety
![]() $X$
is stably equivalent to the bispectrum
$X$
is stably equivalent to the bispectrum
each term of which is a twisted framed motive of
![]() $X$
. Since the functor
$X$
. Since the functor
![]() $\widetilde{\mathbb{Z}}:{\mathcal{X}}\mapsto \widetilde{\mathbb{Z}}[{\mathcal{X}}]$
respects stable weak equivalences of bispectra, it follows that the bispectrum
$\widetilde{\mathbb{Z}}:{\mathcal{X}}\mapsto \widetilde{\mathbb{Z}}[{\mathcal{X}}]$
respects stable weak equivalences of bispectra, it follows that the bispectrum
![]() $\widetilde{\mathbb{Z}}[\unicode[STIX]{x1D6F4}_{S^{1}}^{\infty }\unicode[STIX]{x1D6F4}_{\mathbb{G}}^{\infty }X_{+}]\in SH(k)$
is stably equivalent to the bispectrum
$\widetilde{\mathbb{Z}}[\unicode[STIX]{x1D6F4}_{S^{1}}^{\infty }\unicode[STIX]{x1D6F4}_{\mathbb{G}}^{\infty }X_{+}]\in SH(k)$
is stably equivalent to the bispectrum
By [Reference Garkusha, Neshitov and PaninGPN16, Theorem 1.2], the latter bispectrum is stably equivalent to the bispectrum
consisting of twisted linear framed motives in the sense of [Reference Garkusha and PaninGP14b]. If we take a levelwise Nisnevich local fibrant replacement of
![]() $LM_{fr}(X\times \mathbb{G}_{m}^{\wedge n})$
, we get a bispectrum
$LM_{fr}(X\times \mathbb{G}_{m}^{\wedge n})$
, we get a bispectrum
where each
![]() $LM_{fr}(X\times \mathbb{G}_{m}^{\wedge n})_{f}$
is a Nisnevich local fibrant replacement of the
$LM_{fr}(X\times \mathbb{G}_{m}^{\wedge n})_{f}$
is a Nisnevich local fibrant replacement of the
![]() $S^{1}$
-spectrum
$S^{1}$
-spectrum
![]() $LM_{fr}(X\times \mathbb{G}_{m}^{\wedge n})$
. It follows from the cancellation theorem for linear framed motives [Reference Ananyevskiy, Garkusha and PaninAGP16] that
$LM_{fr}(X\times \mathbb{G}_{m}^{\wedge n})$
. It follows from the cancellation theorem for linear framed motives [Reference Ananyevskiy, Garkusha and PaninAGP16] that
![]() $LM_{fr}^{\mathbb{G}}(X)_{f}$
is a motivically fibrant bispectrum. In particular,
$LM_{fr}^{\mathbb{G}}(X)_{f}$
is a motivically fibrant bispectrum. In particular,
![]() $(\mathbb{S}\wedge X_{+})\otimes \mathbb{Q}$
is computed locally in the Nisnevich topology as the bispectrum
$(\mathbb{S}\wedge X_{+})\otimes \mathbb{Q}$
is computed locally in the Nisnevich topology as the bispectrum
consisting of twisted rational linear framed motives of
![]() $X$
. Each
$X$
. Each
![]() $S^{1}$
-spectrum
$S^{1}$
-spectrum
![]() $LM_{fr}(X\times \mathbb{G}_{m}^{\wedge n})$
is the Eilenberg–Mac Lane spectrum associated with the simplicial Nisnevich sheaf
$LM_{fr}(X\times \mathbb{G}_{m}^{\wedge n})$
is the Eilenberg–Mac Lane spectrum associated with the simplicial Nisnevich sheaf
![]() $\mathbb{Z}F(-\times \unicode[STIX]{x1D6E5}^{\bullet },X\times \mathbb{G}_{m}^{\wedge n})$
defined in terms of the category of linear framed correspondences
$\mathbb{Z}F(-\times \unicode[STIX]{x1D6E5}^{\bullet },X\times \mathbb{G}_{m}^{\wedge n})$
defined in terms of the category of linear framed correspondences
![]() $\mathbb{Z}F_{\ast }(k)$
and stabilized in the
$\mathbb{Z}F_{\ast }(k)$
and stabilized in the
![]() $\unicode[STIX]{x1D70E}$
-direction (see [Reference Garkusha and PaninGP14b] for details).
$\unicode[STIX]{x1D70E}$
-direction (see [Reference Garkusha and PaninGP14b] for details).
It is natural to compare twisted complexes defined by various categories of correspondences. There is constructed a functor in [Reference Déglise and FaselDF17],
It induces morphisms of twisted complexes
A question, originally due to Calmès and Fasel, is whether the
![]() $f_{n}$
are quasi-isomorphisms of complexes of Nisnevich sheaves. The following theorem answers this question in the affirmative with rational coefficients.
$f_{n}$
are quasi-isomorphisms of complexes of Nisnevich sheaves. The following theorem answers this question in the affirmative with rational coefficients.
Theorem 6.1 (Comparison).
Given an infinite perfect field of characteristic not
![]() $2$
and a
$2$
and a
![]() $k$
-smooth scheme
$k$
-smooth scheme
![]() $X$
, each morphism of complexes of Nisnevich sheaves
$X$
, each morphism of complexes of Nisnevich sheaves
is a quasi-isomorphism.
Proof. We defined the bispectrum
![]() $M_{\text{MW}}^{\mathbb{G}_{m}}(X)$
on p. 1432. Taking levelwise Nisnevich local fibrant replacements, we get a bispectrum
$M_{\text{MW}}^{\mathbb{G}_{m}}(X)$
on p. 1432. Taking levelwise Nisnevich local fibrant replacements, we get a bispectrum
![]() $M_{\text{MW}}^{\mathbb{G}_{m}}(X)_{f}$
. The canonical morphism of bispectra
$M_{\text{MW}}^{\mathbb{G}_{m}}(X)_{f}$
. The canonical morphism of bispectra
![]() $\unicode[STIX]{x1D6F4}_{S^{1}}^{\infty }\unicode[STIX]{x1D6F4}_{\mathbb{G}}^{\infty }X_{+}\rightarrow M_{\text{MW}}(X)_{f}$
factors as
$\unicode[STIX]{x1D6F4}_{S^{1}}^{\infty }\unicode[STIX]{x1D6F4}_{\mathbb{G}}^{\infty }X_{+}\rightarrow M_{\text{MW}}(X)_{f}$
factors as
As we have shown above, the left arrow is rationally a stable motivic equivalence.
![]() $F$
is a map between fibrant bispectra which are both locally given by twisted complexes with linear framed and finite Milnor–Witt correspondences, respectively. It follows that the morphisms of the corollary are quasi-isomorphisms if and only
$F$
is a map between fibrant bispectra which are both locally given by twisted complexes with linear framed and finite Milnor–Witt correspondences, respectively. It follows that the morphisms of the corollary are quasi-isomorphisms if and only
![]() $(F\circ \ell )\otimes \mathbb{Q}$
is an isomorphism in
$(F\circ \ell )\otimes \mathbb{Q}$
is an isomorphism in
![]() $SH(k)$
. But the latter follows from Theorem 5.5.◻
$SH(k)$
. But the latter follows from Theorem 5.5.◻
Remark 6.2. Bachmann and Ananyevskiy recently pointed out to the author that Theorem 6.1 cannot be true with integer coefficients even for
![]() $X=pt$
. Moreover, it is not true with
$X=pt$
. Moreover, it is not true with
![]() $\mathbb{Z}[1/p_{1},\ldots ,1/p_{s}]$
-coefficients for any finite collection of primes
$\mathbb{Z}[1/p_{1},\ldots ,1/p_{s}]$
-coefficients for any finite collection of primes
![]() $p_{1},\ldots ,p_{s}$
. Therefore the quasi-isomorphism of the comparison theorem is genuinely rational.
$p_{1},\ldots ,p_{s}$
. Therefore the quasi-isomorphism of the comparison theorem is genuinely rational.
7 Concluding remarks
The methods developed in the previous sections should also be applicable to compute
![]() $SH(k)_{\mathbb{Q}}$
in terms of the hypothetical category of ‘Hermitian correspondences’
$SH(k)_{\mathbb{Q}}$
in terms of the hypothetical category of ‘Hermitian correspondences’
![]() $K_{0}^{h}$
. Its objects are those of
$K_{0}^{h}$
. Its objects are those of
![]() $Sm/k$
and morphisms are given by certain bimodules with duality with/without coefficients in some line bundles.
$Sm/k$
and morphisms are given by certain bimodules with duality with/without coefficients in some line bundles.
![]() $K_{0}^{h}$
is expected to be a symmetric monoidal strict
$K_{0}^{h}$
is expected to be a symmetric monoidal strict
![]() $V$
-category of correspondences satisfying the cancellation property. It is also expected that
$V$
-category of correspondences satisfying the cancellation property. It is also expected that
Suslin’s theorem [Reference SuslinSus03] together with [Reference Ananyevskiy, Levine and PaninALP17, Theorem 3.4] and [Reference Cisinski and DégliseCD12, Theorem 16.2.13] then would imply that
![]() $\mathbb{S}\otimes \mathbb{Q}$
is isomorphic to
$\mathbb{S}\otimes \mathbb{Q}$
is isomorphic to
![]() $\mathbb{S}^{K_{0}^{h}}\otimes \mathbb{Q}$
. The proof of Theorem 5.5 would then be the same for showing that
$\mathbb{S}^{K_{0}^{h}}\otimes \mathbb{Q}$
. The proof of Theorem 5.5 would then be the same for showing that
![]() $SH(k)_{\mathbb{Q}}$
is equivalent to
$SH(k)_{\mathbb{Q}}$
is equivalent to
![]() $DM_{K_{0}^{h}}(k)_{\mathbb{Q}}$
.
$DM_{K_{0}^{h}}(k)_{\mathbb{Q}}$
.
The Suslin theorem [Reference SuslinSus03] comparing Grayson’s cohomology with motivic cohomology is then extended to finite Milnor–Witt correspondences as follows. It states that there is a natural functor between categories of
![]() $V$
-correspondences
$V$
-correspondences
such that the induced morphism of twisted complexes of Nisnevich sheaves
is locally a quasi-isomorphism (at least over infinite perfect fields of characteristic not
![]() $2$
). The extension of the Suslin theorem should be reduced to the original Suslin theorem.
$2$
). The extension of the Suslin theorem should be reduced to the original Suslin theorem.
We invite the interested reader to construct the category of ‘Hermitian correspondences’
![]() $K_{0}^{h}$
with the desired properties.
$K_{0}^{h}$
with the desired properties.
Acknowledgements
I would like to thank I. Panin for numerous discussions on motivic homotopy theory. I am also grateful to A. Druzhinin, J. Fasel and A. Neshitov for helpful discussions on Milnor–Witt correspondences. I thank D.-C. Cisinski for pointing out results of Riou, thanks to which the main theorem of this paper has been improved. This paper was written during my visit to IHES in September 2016. I would like to thank the Institute for its kind hospitality.