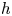1. Introduction
Let ![]() $f(x)=0$ be an algebraic differential equation in a single indeterminate
$f(x)=0$ be an algebraic differential equation in a single indeterminate ![]() $x$ with coefficients in a differential field
$x$ with coefficients in a differential field ![]() $(K, \delta )$ of characteristic zero. In this paper we are particularly interested in the case that
$(K, \delta )$ of characteristic zero. In this paper we are particularly interested in the case that ![]() $f(x)$ is nonlinear and of order at least two. The central property we study is the strong minimality of the solution set of
$f(x)$ is nonlinear and of order at least two. The central property we study is the strong minimality of the solution set of ![]() $f(x)=0$. The notion of strong minimality comes from model theory; in general, a definable set
$f(x)=0$. The notion of strong minimality comes from model theory; in general, a definable set ![]() $X$ is strongly minimal if every definable subset is finite or cofinite, uniformly in parameters. In our setting, we are interested in the situation in which
$X$ is strongly minimal if every definable subset is finite or cofinite, uniformly in parameters. In our setting, we are interested in the situation in which ![]() $X = \{ x \in \mathcal {U} \mid f(x) =0 \}$ is the set of solutions to an algebraic differential equation where
$X = \{ x \in \mathcal {U} \mid f(x) =0 \}$ is the set of solutions to an algebraic differential equation where ![]() $\mathcal {U}$ is a differentially closed field. Let
$\mathcal {U}$ is a differentially closed field. Let ![]() $h$ be the order of
$h$ be the order of ![]() $f$, that is, the highest derivative of
$f$, that is, the highest derivative of ![]() $x$ appearing in
$x$ appearing in ![]() $f$. In this context,
$f$. In this context, ![]() $X$ is strongly minimal if and only if the multivariate polynomial
$X$ is strongly minimal if and only if the multivariate polynomial ![]() $f$ is irreducible over
$f$ is irreducible over ![]() $K^{\mathrm {alg}}$, and given any
$K^{\mathrm {alg}}$, and given any ![]() $a \in \mathcal {U}$ with
$a \in \mathcal {U}$ with ![]() $f(a) = 0$, and any differential field
$f(a) = 0$, and any differential field ![]() $K_1 \leq \mathcal {U}$ with
$K_1 \leq \mathcal {U}$ with ![]() $K \leq K_1$, the transcendence degree of
$K \leq K_1$, the transcendence degree of ![]() $K_1 \langle a \rangle$ over
$K_1 \langle a \rangle$ over ![]() $K_1$ is either zero or
$K_1$ is either zero or ![]() $h$.
$h$.
Strong minimality is an intensively studied property of definable sets, and has been at the center of many important number-theoretic applications of model theory and differential algebra [Reference Casale, Freitag and NaglooCFN20, Reference Freitag and ScanlonFS17, Reference HrushovskiHru96, Reference Nagloo and PillayNP17]. Despite this, there are relatively few (classes of) equations which have been shown to satisfy the property – so few, that we are in fact able to give below what we believe to be (at the moment) a comprehensive list of those equations which have been shown to be strongly minimal. Showing the strong minimality of a given equation is itself sometimes a motivational goal, but often it is an important piece of a more elaborate application, since it allows one to use powerful tools from geometric stability theory. The existing strategies to prove strong minimality are widely disparate but apply only to very special cases. In roughly chronological order:
(1) Poizat established that the set of non-constant solutions of
 $x \cdot x'' =x'$ is strongly minimal (see [Reference Marker, Messmer and PillayMMP05] for an explanation). Poizat's arguments were generalized by Brestovski [Reference BrestovskiBre89] to a class of very specifically chosen differential equations of order two with constant coefficients.
$x \cdot x'' =x'$ is strongly minimal (see [Reference Marker, Messmer and PillayMMP05] for an explanation). Poizat's arguments were generalized by Brestovski [Reference BrestovskiBre89] to a class of very specifically chosen differential equations of order two with constant coefficients.(2) Hrushovski's work [Reference HrushovskiHru96] around the Mordell–Lang conjecture proved the strong minimality of Manin kernels of non-isotrivial simple abelian varieties. It uses specific properties of abelian varieties as well as model-theoretic techniques around modularity of strongly minimal sets.
(3) Nagloo and Pillay [Reference Nagloo and PillayNP17] show that results of the Japanese school of differential algebra [Reference MurataMur95, Reference Ohyama, Kawamuko, Sakai and OkamotoOKSO06, Reference OkamotoOka86, Reference OkamotoOka87a, Reference OkamotoOka87b, Reference Umemura and WatanabeUW97, Reference Umemura and WatanabeUW98, Reference WatanabeWat95, Reference WatanabeWat98] imply that Painlevé equations with generic coefficients are strongly minimal. The techniques employed are differential-algebraic and valuation-theoretic, relying on very specific properties of the equations.
(4) Work of Freitag and Scanlon [Reference Freitag and ScanlonFS17] shows that the differential equation satisfied by the
 $j$-function is strongly minimal. This result ultimately relies on point-counting and o-minimality via the Pila–Wilkie theorem as applied in [Reference PilaPil11, Reference PilaPil13]; the argument there is very specific to the third order nonlinear differential equation satisfied by the
$j$-function is strongly minimal. This result ultimately relies on point-counting and o-minimality via the Pila–Wilkie theorem as applied in [Reference PilaPil11, Reference PilaPil13]; the argument there is very specific to the third order nonlinear differential equation satisfied by the  $j$-function. Later, Aslanyan [Reference AslanyanAsl20] produced another proof, ultimately relying on similar (stronger) inputs of [Reference Pila and TsimermanPT16].
$j$-function. Later, Aslanyan [Reference AslanyanAsl20] produced another proof, ultimately relying on similar (stronger) inputs of [Reference Pila and TsimermanPT16].(5) Casale et al. [Reference Casale, Freitag and NaglooCFN20] show that equations satisfied by
 $\Gamma$-automorphic functions on the upper half-plane for
$\Gamma$-automorphic functions on the upper half-plane for  $\Gamma$ a Fuchsian group of the first kind are strongly minimal. The arguments use differential Galois theory with some additional analytic geometry, and the techniques again are very specific to the third order equations of this specific form.
$\Gamma$ a Fuchsian group of the first kind are strongly minimal. The arguments use differential Galois theory with some additional analytic geometry, and the techniques again are very specific to the third order equations of this specific form.(6) Jaoui shows that generic planar vector fields over the constants give rise to strongly minimal order two differential varieties [Reference JaouiJao22]. The arguments rely on various sophisticated analytic techniques and results from foliation theory, some of which are particular to the specific class of equations considered.
(7) Blázquez-Sanz et al. [Reference Blázquez-Sanz, Casale, Freitag and NaglooBCFN20] prove the strong minimality of certain general Schwarzian differential equations.
(8) Freitag et al. [Reference Freitag, Jaoui, Marker and NaglooFJMN22] show that various equations of Liénard-type are strongly minimal, using techniques from valuation theory.
We should also mention that strong minimality in this context was perhaps first studied by Painlevé using different language in [Reference PainlevéPai97]. Painlevé conjectured the strong minimality of various classes of differential equations, where the notion is equivalent to Umemura's condition (J). See [Reference Nagloo and PillayNP17] for a discussion of these connections. We believe that the above list, together with a specific example of [Reference FreitagFre12], constitutes the entire list of differential equations (of order at least two) which have been proven to be strongly minimal. Most of the techniques in the above listed results apply only to specific equations or narrow classes of equations and rely on specific properties of those classes in proving strong minimality. Our goal in this article is to develop a rather more general approach which applies widely to equations with at least one differentially transcendental coefficient.
1.1 Our approach and results
Let ![]() $f \in k\{ x \}$. Generally speaking, when attempting to prove strong minimalityFootnote 1 of some differential variety
$f \in k\{ x \}$. Generally speaking, when attempting to prove strong minimalityFootnote 1 of some differential variety
there are two phenomena which make the task difficult.
(1) There is no a priori upper bound on the degree of the differential polynomials which define a differential subvariety of
 $V$.
$V$.(2) The differential polynomials used to define a differential subvariety might (necessarily) have coefficients from a differential field extension of the field of
 $k$.
$k$.
There are structure theorems related to (1), but only in special cases. See, for instance, [Reference Freitag and MoosaFM17] when the subvarieties are co-order one in ![]() $V$. Controlling the field extension in (2) is a key step in various recent works [Reference Freitag and ScanlonFS17, Reference JaouiJao22, Reference Nagloo and PillayNP17]. This is most often accomplished by noting that stable embeddedness of the generic type of
$V$. Controlling the field extension in (2) is a key step in various recent works [Reference Freitag and ScanlonFS17, Reference JaouiJao22, Reference Nagloo and PillayNP17]. This is most often accomplished by noting that stable embeddedness of the generic type of ![]() $V$ implies that the generators of the field of definition of a forking extension can be assumed to themselves realize the generic type of
$V$ implies that the generators of the field of definition of a forking extension can be assumed to themselves realize the generic type of ![]() $V$ – see explanations in [Reference Casale, Freitag and NaglooCFN20, Reference Freitag and ScanlonFS17]. In recent work, Freitag and Moosa [Reference Freitag and MoosaFM21] introduce a new invariant of a type, which more closely controls the structure over which the forking extension of a type is defined:
$V$ – see explanations in [Reference Casale, Freitag and NaglooCFN20, Reference Freitag and ScanlonFS17]. In recent work, Freitag and Moosa [Reference Freitag and MoosaFM21] introduce a new invariant of a type, which more closely controls the structure over which the forking extension of a type is defined:
Definition 1.1 Suppose ![]() $p\in S(A)$ is a stationary type of
$p\in S(A)$ is a stationary type of ![]() $U$-rank greater than one. By the degree of non-minimality of
$U$-rank greater than one. By the degree of non-minimality of ![]() $p$, denoted by
$p$, denoted by ![]() $\operatorname {nmdeg}(p)$, we mean the least positive integer
$\operatorname {nmdeg}(p)$, we mean the least positive integer ![]() $k$ such that for a Morley sequence of
$k$ such that for a Morley sequence of ![]() $p$ of length
$p$ of length ![]() $k$, say
$k$, say ![]() $(a_1,\dots,a_k)$,
$(a_1,\dots,a_k)$, ![]() $p$ has a non-algebraic forking extension over
$p$ has a non-algebraic forking extension over ![]() $A,a_1,\dots,a_k$. If
$A,a_1,\dots,a_k$. If ![]() $\operatorname {RU}(p)\leq 1$ then we set
$\operatorname {RU}(p)\leq 1$ then we set ![]() $\operatorname {nmdeg}(p)=0$.
$\operatorname {nmdeg}(p)=0$.
In the theory of differentially closed fields of characteristic zero, Freitag and Moosa [Reference Freitag and MoosaFM21] give an upper bound for the degree of non-minimality in terms of Lascar rank.
Theorem 1.2 Let ![]() $p \in S(k)$ have finite rank. Then
$p \in S(k)$ have finite rank. Then ![]() $\operatorname {nmdeg}(p) \leq \operatorname {RU}(p)+1.$
$\operatorname {nmdeg}(p) \leq \operatorname {RU}(p)+1.$
Let ![]() $a \models p$. We will call the transcendence degree of the differential field
$a \models p$. We will call the transcendence degree of the differential field ![]() $k\langle a \rangle /k$ the order of
$k\langle a \rangle /k$ the order of ![]() $p$. When
$p$. When ![]() $p$ is the generic type of a differential variety
$p$ is the generic type of a differential variety ![]() $V$, we also call this the orderFootnote 2 of
$V$, we also call this the orderFootnote 2 of ![]() $V$. The order of
$V$. The order of ![]() $p$ is an upper bound for the Morley rank of
$p$ is an upper bound for the Morley rank of ![]() $p$. The Morley rank of
$p$. The Morley rank of ![]() $p$ is a bound for the Lascar rank of
$p$ is a bound for the Lascar rank of ![]() $p$. For proofs of these facts, see [Reference Marker, Messmer and PillayMMP05]. It follows that if the type
$p$. For proofs of these facts, see [Reference Marker, Messmer and PillayMMP05]. It follows that if the type ![]() $p$ of a generic solution of an order
$p$ of a generic solution of an order ![]() $n$ differential equation over
$n$ differential equation over ![]() $k$ has a non-algebraic forking extension over some differential field extension, then already
$k$ has a non-algebraic forking extension over some differential field extension, then already ![]() $p$ has such a forking extension over
$p$ has such a forking extension over ![]() $k\langle a_1, \ldots, a_{n+1} \rangle$ where the
$k\langle a_1, \ldots, a_{n+1} \rangle$ where the ![]() $a_i$ are from a Morley sequence in the type of
$a_i$ are from a Morley sequence in the type of ![]() $p$ over
$p$ over ![]() $k$. This consequence of Theorem 1.2 will be essential to our approach to handling issue (2) above.
$k$. This consequence of Theorem 1.2 will be essential to our approach to handling issue (2) above.
Our approach to issue (1) follows a familiar general strategy of reducing certain problems for nonlinear differential equations to related problems for associated linear differential equations. For instance, [Reference Pillay and ZieglerPZ03] applies a strategy of this nature to establish results around the Zilber trichotomy, while [Reference Casale, Freitag and NaglooCFN20, Reference NaglooNag19] use this strategy to establish irreducibility of solutions to automorphic and Painlevé equations using certain associated Riccati equations. Our technique fits into this general framework and relies on Kolchin's differential tangent space, which will provide the linear equations associated with the original nonlinear differential variety ![]() $V$. Our approach to the associated linear equations has been under development in the thesis of Wolf [Reference WolfWol19] and the forthcoming thesis of DeVilbiss which gives an approach to calculating the Lascar rank of underdetermined systems of linear differential equations.
$V$. Our approach to the associated linear equations has been under development in the thesis of Wolf [Reference WolfWol19] and the forthcoming thesis of DeVilbiss which gives an approach to calculating the Lascar rank of underdetermined systems of linear differential equations.
We call a differential polynomial ![]() $f(x)$ generic of order
$f(x)$ generic of order ![]() $h$ and degree
$h$ and degree ![]() $d$, if
$d$, if ![]() $f$ is a linear combination of all monomials of degree no more than
$f$ is a linear combination of all monomials of degree no more than ![]() $d$ on the variables
$d$ on the variables ![]() $x, x' ,\ldots, x^{(h)}$ with independent differentially transcendental coefficients.
$x, x' ,\ldots, x^{(h)}$ with independent differentially transcendental coefficients.
We now state our main theorem.
Theorem 1.3 Let ![]() $f(x)$ be a generic differential polynomial of order
$f(x)$ be a generic differential polynomial of order ![]() $h>1$ and degree
$h>1$ and degree ![]() $d$. Let
$d$. Let ![]() $p$ be the type of a generic solution to
$p$ be the type of a generic solution to ![]() $Z(f)$. If
$Z(f)$. If ![]() $d \geq 2 \cdot (\operatorname {nmdeg}(p)+1),$ then
$d \geq 2 \cdot (\operatorname {nmdeg}(p)+1),$ then ![]() $Z(f)$ is strongly minimal.
$Z(f)$ is strongly minimal.
Since ![]() $\operatorname {nmdeg}(p)\leq \operatorname {RU}(p) +1 \leq \operatorname {ord}(f)+1$, the following corollary is immediate.
$\operatorname {nmdeg}(p)\leq \operatorname {RU}(p) +1 \leq \operatorname {ord}(f)+1$, the following corollary is immediate.
Corollary 1.4 Let ![]() $f(x)$ be a generic differential polynomial of order
$f(x)$ be a generic differential polynomial of order ![]() $h>1$ and degree
$h>1$ and degree ![]() $d$. If
$d$. If ![]() $d \geq 2 \cdot (h+2),$ then
$d \geq 2 \cdot (h+2),$ then ![]() $Z(f)$ is strongly minimal.
$Z(f)$ is strongly minimal.
This answers Question 7 of [Reference PoizatPoi80] for sufficiently large degree, any order, and non-constant coefficients. As described above, Jaoui [Reference JaouiJao22] has recently answered the order two case of Question 7 of [Reference PoizatPoi80] for constant coefficients. We conjecture a more general form of Theorem 1.3.
Conjecture 1.5 Generic differential equations of fixed order and degree greater than one are strongly minimal.
To the non-model theorist, it does not seem obvious why strong minimality plays a central role in the theory of algebraic differential equations, but there seem to be two important factors behind this.
• Once strong minimality of an equation is established, powerful results having their origins in geometric stability theory can be employed (e.g. the Zilber trichotomy, discussed next).
• Among nonlinear equations, the results of this paper and those of [Reference JaouiJao22] show that strong minimality holds ubiquitously.
Even when an equation is not strongly minimal, it is often true that questions about the solutions can be reduced to questions about solutions of certain associated minimal equations coming from a notion called semi-minimal analysis; for instance, see [Reference Freitag, Jaoui and MoosaFJM22b]. We now state the Zilber trichotomy for strongly minimal sets adapted to the setting of differentially closed fields:
Fact 1.6 [Reference Hrushovski and SokolovićHS94, Reference Pillay and ZieglerPZ03]
Let ![]() $X$ be a strongly minimal set. Then exactly one of the following assertions holds.
$X$ be a strongly minimal set. Then exactly one of the following assertions holds.
(1) (non-locally modular)
 $X$ is non-orthogonal to
$X$ is non-orthogonal to  $\mathbb {C}$.
$\mathbb {C}$.(2) (locally modular, non-trivial)
 $X$ is non-orthogonal to the (unique) smallest Zariski-dense definable subgroup of a simple abelian variety
$X$ is non-orthogonal to the (unique) smallest Zariski-dense definable subgroup of a simple abelian variety  $A$ which does not descend to
$A$ which does not descend to  $\mathbb {C}$.
$\mathbb {C}$.(3) (trivial)
 $X$ is geometrically trivial.
$X$ is geometrically trivial.
Nonorthogonality is a natural equivalence relation on strongly minimal sets. For strongly minimal sets ![]() $X$ and
$X$ and ![]() $Y$,
$Y$, ![]() $X$ is non-orthogonal to
$X$ is non-orthogonal to ![]() $Y$ if and only if there is a generic finite-to-finite definable correspondence between
$Y$ if and only if there is a generic finite-to-finite definable correspondence between ![]() $X$ and
$X$ and ![]() $Y$. A strongly minimal set is geometrically trivial if whenever
$Y$. A strongly minimal set is geometrically trivial if whenever ![]() $a_1, \ldots, a_n \in X$ are dependent in the sense of forking, there is a pair of distinct
$a_1, \ldots, a_n \in X$ are dependent in the sense of forking, there is a pair of distinct ![]() $a_i, a_j$ which is dependent. In terms of algebraic relations in our setting, whenever
$a_i, a_j$ which is dependent. In terms of algebraic relations in our setting, whenever ![]() $a_1, \ldots, a_n \in X$ are generic solutions of the differential equation
$a_1, \ldots, a_n \in X$ are generic solutions of the differential equation ![]() $X$, if
$X$, if
then there is a distinct pair ![]() $a_i,a_j$ such that
$a_i,a_j$ such that
By strong minimality, the previous inequality implies that
While Fact 1.6 gives a rather complete classification of strongly minimal sets in the non-trivial cases of the Zilber trichotomy, there is no general classification of the geometrically trivial strongly minimal sets in differentially closed fields.
We conjecture that generic differential equations are geometrically trivial in a strong form.
Conjecture 1.7 Any two solutions of a generic differential equation of fixed order and degree greater than one are (differentially) algebraically independent.
In this paper our techniques are applied to equations with differentially transcendental coefficients, but this is not an inherent restriction of the methods. For instance, in forthcoming work using these techniques joint with Casale and Nagloo, we give a fundamentally new proof of the main theorem of [Reference Freitag and ScanlonFS17], proving that the equation satisfied by the ![]() $j$-function is strongly minimal. See § 5 for additional discussion.
$j$-function is strongly minimal. See § 5 for additional discussion.
1.2 Organization
In § 2 we set up the notation and background results we require. Section 3 gives a new sufficient condition for the strong minimality of a differential variety. Section 4 applies this condition to show that generic differential equations are strongly minimal. Section 5 shows how one can establish a weaker condition than strong minimality in a more computationally straightforward manner and gives some open problems.
2. Notation
Let ![]() $\mathcal {U}$ be a countably saturated differentially closed field of characteristic zero and let
$\mathcal {U}$ be a countably saturated differentially closed field of characteristic zero and let ![]() $\mathcal {C}$ be the field of constants of
$\mathcal {C}$ be the field of constants of ![]() $\mathcal {U}$. All of the fields we consider will be subfields of
$\mathcal {U}$. All of the fields we consider will be subfields of ![]() $\mathcal {U}$. An affine differential variety is the zero set of a (finite) system of irreducible differential polynomial equations over (a finitely generated subfield of)
$\mathcal {U}$. An affine differential variety is the zero set of a (finite) system of irreducible differential polynomial equations over (a finitely generated subfield of) ![]() $\mathcal {U}$.
$\mathcal {U}$.
Let ![]() $(y_1, \ldots, y_n)$ be a finite set of differential indeterminants over
$(y_1, \ldots, y_n)$ be a finite set of differential indeterminants over ![]() $\mathcal {U}$ and let
$\mathcal {U}$ and let ![]() $\Theta$ denote the set of derivative operators on
$\Theta$ denote the set of derivative operators on ![]() $\mathcal {U}$. Since we are interested in differential fields with a single derivation,
$\mathcal {U}$. Since we are interested in differential fields with a single derivation, ![]() $\Theta =\{\delta ^{k}:k\geq 0\}$. A ranking on
$\Theta =\{\delta ^{k}:k\geq 0\}$. A ranking on ![]() $(y_1, \ldots y_n)$ is a total ordering on the derivatives
$(y_1, \ldots y_n)$ is a total ordering on the derivatives ![]() $\{\theta y_j: \theta \in \Theta, 1\leq j \leq n\}$ such that for all such derivatives
$\{\theta y_j: \theta \in \Theta, 1\leq j \leq n\}$ such that for all such derivatives ![]() $u$,
$u$, ![]() $v$, and all
$v$, and all ![]() $\theta \in \Theta$, we have
$\theta \in \Theta$, we have
A ranking is orderly if whenever the order of ![]() $\theta _1$ is lower than the order of
$\theta _1$ is lower than the order of ![]() $\theta _2$, we have
$\theta _2$, we have ![]() $\theta _1 y_i < \theta _2 y_j$ for any
$\theta _1 y_i < \theta _2 y_j$ for any ![]() $i, j$. An elimination ranking is a ranking in which
$i, j$. An elimination ranking is a ranking in which ![]() $y_i < y_j$ implies
$y_i < y_j$ implies ![]() $\theta _1 y_i < \theta _2 y_j$ for any
$\theta _1 y_i < \theta _2 y_j$ for any ![]() $\theta _1,\theta _2\in \Theta$. For a
$\theta _1,\theta _2\in \Theta$. For a ![]() $\delta$-polynomial
$\delta$-polynomial ![]() $f(y_1, \ldots, y_n)$, the highest ranking
$f(y_1, \ldots, y_n)$, the highest ranking ![]() $\theta y_j$ appearing in
$\theta y_j$ appearing in ![]() $f$ is the leader of
$f$ is the leader of ![]() $f$, denoted
$f$, denoted ![]() $u_f$. If
$u_f$. If ![]() $u_f$ has degree
$u_f$ has degree ![]() $d$ in
$d$ in ![]() $f$, we can rewrite
$f$, we can rewrite ![]() $f$ as a polynomial in
$f$ as a polynomial in ![]() $u_f$,
$u_f$, ![]() $f= \sum _{i=0}^d I_i u_f^i$, where the initial of
$f= \sum _{i=0}^d I_i u_f^i$, where the initial of ![]() $f$,
$f$, ![]() $I_d$, is not zero. The separant of
$I_d$, is not zero. The separant of ![]() $f$ is the formal derivative
$f$ is the formal derivative ![]() ${\partial f}/{\partial u_f}$. Note that the leader, initial, and separant of a differential polynomial are defined only after choosing a specific ranking. A detailed treatment of these definitions can be found in [Reference KolchinKol76, p. 75].
${\partial f}/{\partial u_f}$. Note that the leader, initial, and separant of a differential polynomial are defined only after choosing a specific ranking. A detailed treatment of these definitions can be found in [Reference KolchinKol76, p. 75].
Let ![]() $\bar a \in \mathcal {U}$, and
$\bar a \in \mathcal {U}$, and ![]() $F$ be a differential subfield of
$F$ be a differential subfield of ![]() $\mathcal {U}$. There is a numerical polynomial
$\mathcal {U}$. There is a numerical polynomial ![]() $\omega (\bar a /F)$ called the Kolchin polynomial of
$\omega (\bar a /F)$ called the Kolchin polynomial of ![]() $\bar a$ over
$\bar a$ over ![]() $F$ such that for sufficiently large
$F$ such that for sufficiently large ![]() $s\in \mathbb {N}$,
$s\in \mathbb {N}$,
(see [Reference KolchinKol76, Theorem 6, p. 115]). When ![]() $X$ is a differential variety, that is, a closed irreducible set in the Kolchin topology,
$X$ is a differential variety, that is, a closed irreducible set in the Kolchin topology, ![]() $\omega (X/F):=\omega (\bar a /F)$ where
$\omega (X/F):=\omega (\bar a /F)$ where ![]() $\bar a$ is a generic point on
$\bar a$ is a generic point on ![]() $X$ over
$X$ over ![]() $F$. Since we are only concerned with differential fields with a single derivation, the degree of
$F$. Since we are only concerned with differential fields with a single derivation, the degree of ![]() $\omega (X/F)$, sometimes called the differential type, is either zero or one. The leading coefficient of
$\omega (X/F)$, sometimes called the differential type, is either zero or one. The leading coefficient of ![]() $\omega (X/F)$ is called the typical differential dimension. Crucially for our purposes, the Kolchin polynomial witnesses forking in the sense of model theory, that is,
$\omega (X/F)$ is called the typical differential dimension. Crucially for our purposes, the Kolchin polynomial witnesses forking in the sense of model theory, that is,
Proof of this fact can be found in Theorem 4.3.10 of [Reference McGrailMcG00] and in Proposition 2.8 of [Reference PongPon03].
Let ![]() $X\subset \mathcal {U}^n$ be a differential variety and let
$X\subset \mathcal {U}^n$ be a differential variety and let ![]() $I(X)$ be the ideal of differential polynomials vanishing on
$I(X)$ be the ideal of differential polynomials vanishing on ![]() $X$. The differential tangent bundle
$X$. The differential tangent bundle ![]() $T^\Delta X$ is the differential variety given by
$T^\Delta X$ is the differential variety given by
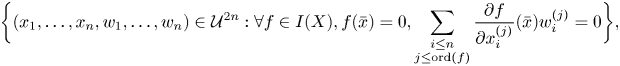 \[ \bigg\{ (x_1,\ldots, x_n, w_1, \ldots, w_n)\in \mathcal{U}^{2n}: \forall f\in I(X), f(\bar{x})=0, \sum_{\substack{i\leq n\\ j\leq \operatorname{ord}(f)}} \frac{\partial f}{\partial x_i^{(j)}}(\bar{x})w_i^{(j)}=0\bigg\}, \]
\[ \bigg\{ (x_1,\ldots, x_n, w_1, \ldots, w_n)\in \mathcal{U}^{2n}: \forall f\in I(X), f(\bar{x})=0, \sum_{\substack{i\leq n\\ j\leq \operatorname{ord}(f)}} \frac{\partial f}{\partial x_i^{(j)}}(\bar{x})w_i^{(j)}=0\bigg\}, \]
where ![]() $({\partial f}/{\partial x_i^{(j)}})(\bar {x})$ is a formal partial derivative where the
$({\partial f}/{\partial x_i^{(j)}})(\bar {x})$ is a formal partial derivative where the ![]() $x_i^{(j)}$ are considered as algebraic variables. Given
$x_i^{(j)}$ are considered as algebraic variables. Given ![]() $\bar {a}\in X$, the differential tangent space of
$\bar {a}\in X$, the differential tangent space of ![]() $X$ over
$X$ over ![]() $\bar {a}$, denoted by
$\bar {a}$, denoted by ![]() $T_{\bar {a}}^\Delta X$, is the fiber of
$T_{\bar {a}}^\Delta X$, is the fiber of ![]() $T^\Delta X$ over
$T^\Delta X$ over ![]() $\bar {a}$. We now state a few basic properties of
$\bar {a}$. We now state a few basic properties of ![]() $T^\Delta X$ which will be used later.
$T^\Delta X$ which will be used later.
• The fibers
 $T_{\bar a}^\Delta X$ are (possibly infinite-dimensional)
$T_{\bar a}^\Delta X$ are (possibly infinite-dimensional)  $\mathcal {C}$-vector spaces where
$\mathcal {C}$-vector spaces where  $\mathcal {C}$ is the field of constant elements in
$\mathcal {C}$ is the field of constant elements in  $\mathcal {U}$.
$\mathcal {U}$.• If
 $Y$ is a closed differential subvariety of
$Y$ is a closed differential subvariety of  $X$ and
$X$ and  $\bar a\in Y$, then
$\bar a\in Y$, then  $T_{\bar a}^\Delta Y$ is a closed
$T_{\bar a}^\Delta Y$ is a closed  $\mathcal {C}$-vector subspace of
$\mathcal {C}$-vector subspace of  $T_{\bar a}^\Delta X$.
$T_{\bar a}^\Delta X$.
The following lemma appears as a corollary of [Reference KolchinKol84, Theorem 1, p. 199]. The sentence involving a single differential variable is an improvement on Kolchin's corollary and follows immediately from Kolchin's proof.
Lemma 2.1 Let ![]() $F$ be a differential field,
$F$ be a differential field, ![]() $X$ a differential variety defined over
$X$ a differential variety defined over ![]() $F$. Then there is a Kolchin open set
$F$. Then there is a Kolchin open set ![]() $U\subseteq X$ such that for every
$U\subseteq X$ such that for every ![]() $\bar {a}\in U$, the Kolchin polynomial
$\bar {a}\in U$, the Kolchin polynomial ![]() $\omega \big (X/F \big ) = \omega \big ( T^\Delta _{\bar {a}} (X) / F\langle \bar {a} \rangle \big )$. Moreover, if
$\omega \big (X/F \big ) = \omega \big ( T^\Delta _{\bar {a}} (X) / F\langle \bar {a} \rangle \big )$. Moreover, if ![]() $X$ is defined by the vanishing of a single differential polynomial
$X$ is defined by the vanishing of a single differential polynomial ![]() $f\in F\{x_1, \ldots, x_n\}$, then
$f\in F\{x_1, \ldots, x_n\}$, then ![]() $U$ can be taken to be the open set defined by
$U$ can be taken to be the open set defined by ![]() $I_fs_f\neq 0$ where
$I_fs_f\neq 0$ where ![]() $I_f$ is the initial of
$I_f$ is the initial of ![]() $f$ and
$f$ and ![]() $s_f$ is the separant of
$s_f$ is the separant of ![]() $f$ with respect to some orderly ranking.
$f$ with respect to some orderly ranking.
3. A general sufficient criterion for strong minimality
Let ![]() $f(x)$ be an order
$f(x)$ be an order ![]() $n\geq 1$ nonlinear differential polynomial in one variable without a constant term. Let
$n\geq 1$ nonlinear differential polynomial in one variable without a constant term. Let ![]() $\bar {\alpha }$ denote the coefficients of
$\bar {\alpha }$ denote the coefficients of ![]() $f$ and let
$f$ and let ![]() $\alpha _0$ be differentially transcendental over
$\alpha _0$ be differentially transcendental over ![]() $\bar {\alpha }$. Let
$\bar {\alpha }$. Let ![]() $V_0$ be the differential variety corresponding to
$V_0$ be the differential variety corresponding to ![]() $f(x)=\alpha _0$. Our goal in this section is to find sufficient conditions under which such a variety
$f(x)=\alpha _0$. Our goal in this section is to find sufficient conditions under which such a variety ![]() $V_0$ is strongly minimal.
$V_0$ is strongly minimal.
Our next proposition shows that when ![]() $\alpha _0$ is differentially transcendental over
$\alpha _0$ is differentially transcendental over ![]() $\mathbb {Q}\langle \bar {\alpha }\rangle$, there are no proper subvarieties of
$\mathbb {Q}\langle \bar {\alpha }\rangle$, there are no proper subvarieties of ![]() $V_0$ which are defined over the field
$V_0$ which are defined over the field ![]() $\mathbb {Q} \langle \bar \alpha, \alpha _0 \rangle.$ Though the argument is simple, an elaboration of the technique in the proof will be used in the more difficult general case where one extends the field of coefficients.
$\mathbb {Q} \langle \bar \alpha, \alpha _0 \rangle.$ Though the argument is simple, an elaboration of the technique in the proof will be used in the more difficult general case where one extends the field of coefficients.
Proposition 3.1 Let ![]() $f(x)$ be a nonlinear order
$f(x)$ be a nonlinear order ![]() $h\geq 1$ differential polynomial with coefficients
$h\geq 1$ differential polynomial with coefficients ![]() $\bar {\alpha }$, let
$\bar {\alpha }$, let ![]() $\alpha _0$ be differentially transcendental over
$\alpha _0$ be differentially transcendental over ![]() $\mathbb {Q}\langle \bar {\alpha }\rangle$, and let
$\mathbb {Q}\langle \bar {\alpha }\rangle$, and let ![]() $V_0$ be the differential variety defined by
$V_0$ be the differential variety defined by ![]() $f(x)=\alpha _0$. Then
$f(x)=\alpha _0$. Then ![]() $V_0$ has no infinite proper subvarieties that are defined over
$V_0$ has no infinite proper subvarieties that are defined over ![]() $\mathbb {Q}\langle \bar {\alpha },\alpha _0\rangle$.
$\mathbb {Q}\langle \bar {\alpha },\alpha _0\rangle$.
Proof. Suppose towards a contradiction that ![]() $W_0$ is an infinite proper subvariety of
$W_0$ is an infinite proper subvariety of ![]() $V_0$ defined over
$V_0$ defined over ![]() $\mathbb {Q}\langle \bar {\alpha }, \alpha _0 \rangle$. Then
$\mathbb {Q}\langle \bar {\alpha }, \alpha _0 \rangle$. Then ![]() $W_0$ is given by some positive-order
$W_0$ is given by some positive-order ![]() $\delta$-polynomial
$\delta$-polynomial ![]() $g(x)\in \mathbb {Q}\langle \bar {\alpha }, \alpha _0 \rangle \{x\}$. By clearing the denominators of
$g(x)\in \mathbb {Q}\langle \bar {\alpha }, \alpha _0 \rangle \{x\}$. By clearing the denominators of ![]() $\alpha _0$, we can write
$\alpha _0$, we can write ![]() $g(x,\alpha _0) \in \mathbb {Q}\langle \bar {\alpha }\rangle \{x, \alpha _0\}$. For ease of notation, let
$g(x,\alpha _0) \in \mathbb {Q}\langle \bar {\alpha }\rangle \{x, \alpha _0\}$. For ease of notation, let ![]() $k=\mathbb {Q}\langle \bar {\alpha }\rangle$.
$k=\mathbb {Q}\langle \bar {\alpha }\rangle$.
Let ![]() $V$ be the differential variety given by
$V$ be the differential variety given by ![]() $f(x)=y$ and let
$f(x)=y$ and let ![]() $W$ be given by
$W$ be given by ![]() $g(x,y)=0$ so that each instance of
$g(x,y)=0$ so that each instance of ![]() $\alpha _0$ is replaced with the variable
$\alpha _0$ is replaced with the variable ![]() $y$. These varieties are now defined by
$y$. These varieties are now defined by ![]() $\delta$-polynomials in two variables with coefficients in
$\delta$-polynomials in two variables with coefficients in ![]() $k$ and
$k$ and ![]() $W \subsetneq V$. Let
$W \subsetneq V$. Let ![]() $a=(a_1,a_2)$ be a generic point of
$a=(a_1,a_2)$ be a generic point of ![]() $W$ over
$W$ over ![]() $k$. Since
$k$. Since ![]() $\alpha _0$ is differentially transcendental over
$\alpha _0$ is differentially transcendental over ![]() $\bar \alpha$ the locus of
$\bar \alpha$ the locus of ![]() $y$ over
$y$ over ![]() $k$ is
$k$ is ![]() $\mathbb {A}^1$, so it follows that
$\mathbb {A}^1$, so it follows that ![]() $W$ is an infinite-rank (proper) subvariety of
$W$ is an infinite-rank (proper) subvariety of ![]() $V$. Consider the orderly ranking with
$V$. Consider the orderly ranking with ![]() $x$ ranked higher than
$x$ ranked higher than ![]() $y$.
$y$.
We claim that the generic point ![]() $a$ of
$a$ of ![]() $W$ lies outside the locus on
$W$ lies outside the locus on ![]() $V$ where the separant of
$V$ where the separant of ![]() $f(x)-y$ vanishes (we will call this the singular locus of
$f(x)-y$ vanishes (we will call this the singular locus of ![]() $V$). This follows because the locus of the separant of
$V$). This follows because the locus of the separant of ![]() $f$ inside of
$f$ inside of ![]() $V$ is of finite rank (to see this, note that the separant is a differential polynomial in
$V$ is of finite rank (to see this, note that the separant is a differential polynomial in ![]() $k\{x\}$ so its generic solution has
$k\{x\}$ so its generic solution has ![]() $x$-coordinate differentially algebraic over
$x$-coordinate differentially algebraic over ![]() $k$). From the fact that
$k$). From the fact that ![]() $a$ lies outside the singular locus of
$a$ lies outside the singular locus of ![]() $V$ and the singular locus of
$V$ and the singular locus of ![]() $W$ (since
$W$ (since ![]() $a$ is generic on
$a$ is generic on ![]() $W$), it follows that the Kolchin polynomials of
$W$), it follows that the Kolchin polynomials of ![]() $T^\Delta _{a} W$ and
$T^\Delta _{a} W$ and ![]() $T^\Delta _{a} V$ are equal to the Kolchin polynomials of
$T^\Delta _{a} V$ are equal to the Kolchin polynomials of ![]() $W$ and
$W$ and ![]() $V$, respectively, and so
$V$, respectively, and so ![]() $T^\Delta _{a} W \subsetneq T^\Delta _{a} V$.
$T^\Delta _{a} W \subsetneq T^\Delta _{a} V$.
For ![]() $0\leq i \leq n$, let
$0\leq i \leq n$, let
denote the formal derivative of ![]() $f$ with respect to the
$f$ with respect to the ![]() $i$th derivative of
$i$th derivative of ![]() $x$. Using this notation, the differential tangent space
$x$. Using this notation, the differential tangent space ![]() $T^\Delta _a V$ is the set of
$T^\Delta _a V$ is the set of ![]() $(w,z)$ satisfying the linear differential equation
$(w,z)$ satisfying the linear differential equation
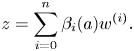 \[ z=\sum_{i=0}^n \beta_i(a)w^{(i)}. \]
\[ z=\sum_{i=0}^n \beta_i(a)w^{(i)}. \]
From this equation, we can see that ![]() $z$ is determined by our choice of
$z$ is determined by our choice of ![]() $w$, but
$w$, but ![]() $w$ may be chosen freely. This gives a definable bijection between
$w$ may be chosen freely. This gives a definable bijection between ![]() $T^\Delta _a V$ and
$T^\Delta _a V$ and ![]() $\mathbb {A}^1(\mathcal {U})$. Further, it follows that
$\mathbb {A}^1(\mathcal {U})$. Further, it follows that ![]() $T^\Delta _a V$ has no infinite-rank subspaces over
$T^\Delta _a V$ has no infinite-rank subspaces over ![]() $k\langle a \rangle$, since if it did, we could consider the image of this subvariety under the definable bijection to
$k\langle a \rangle$, since if it did, we could consider the image of this subvariety under the definable bijection to ![]() $\mathbb {A}^1(\mathcal {U})$. However,
$\mathbb {A}^1(\mathcal {U})$. However, ![]() $\mathbb {A}^1(\mathcal {U})$ has no infinite-rank subsets, so the image must have finite rank. Therefore,
$\mathbb {A}^1(\mathcal {U})$ has no infinite-rank subsets, so the image must have finite rank. Therefore, ![]() $\omega \big (T^\Delta _a W /k\langle a \rangle \big )$ is finite, a contradiction.
$\omega \big (T^\Delta _a W /k\langle a \rangle \big )$ is finite, a contradiction.
Remark 3.2 For ![]() $X$ a differential variety over a differential field
$X$ a differential variety over a differential field ![]() $\mathbb {Q}\langle \bar {\alpha }\rangle$, the following conditions on the differential tangent space
$\mathbb {Q}\langle \bar {\alpha }\rangle$, the following conditions on the differential tangent space ![]() $T_{\bar {a}}^\Delta X$ are equivalent.
$T_{\bar {a}}^\Delta X$ are equivalent.
(1) The Lascar rank
 $\operatorname {RU}\bigl (T^\Delta _{\bar {a}} V\bigr )=\omega$.
$\operatorname {RU}\bigl (T^\Delta _{\bar {a}} V\bigr )=\omega$.(2) The Morley rank
 $\operatorname {RM}\bigl (T^\Delta _{\bar {a}} X\bigr )=\omega$.
$\operatorname {RM}\bigl (T^\Delta _{\bar {a}} X\bigr )=\omega$.(3) The differential tangent space
 $T^\Delta _{\bar {a}} X$ has no proper infinite-rank
$T^\Delta _{\bar {a}} X$ has no proper infinite-rank  $\mathcal {C}$-vector subspaces definable over
$\mathcal {C}$-vector subspaces definable over  $\mathbb {Q}\langle \bar {a},\bar {\alpha }\rangle$.
$\mathbb {Q}\langle \bar {a},\bar {\alpha }\rangle$.(4) The differential tangent space
 $T^\Delta _{\bar {a}} X$ has no proper infinite-rank
$T^\Delta _{\bar {a}} X$ has no proper infinite-rank  $\mathcal {C}$-vector subspaces definable over
$\mathcal {C}$-vector subspaces definable over  $\mathcal {U}$.
$\mathcal {U}$.(5) The differential tangent space
 $T^\Delta _{\bar {a}} X$ has no proper infinite-rank subvarieties definable over
$T^\Delta _{\bar {a}} X$ has no proper infinite-rank subvarieties definable over  $\mathbb {Q}\langle \bar {a},\bar {\alpha }\rangle$.
$\mathbb {Q}\langle \bar {a},\bar {\alpha }\rangle$.(6) The differential tangent space
 $T^\Delta _{\bar {a}} X$ has no proper infinite-rank subvarieties definable over
$T^\Delta _{\bar {a}} X$ has no proper infinite-rank subvarieties definable over  $\mathcal {U}$.
$\mathcal {U}$.
The equivalence of (1) and (2) is proved in [Reference Pillay and PongPP02] and the equivalence of the others follows from the Berline–Lascar decomposition [Reference PoizatPoi87, Theorem 6.7]. By the argument at the end of the previous proof, each of these properties is implied by the existence of a definable bijection between the differential tangent space ![]() $T^\Delta _{\bar {a}} X$ and
$T^\Delta _{\bar {a}} X$ and ![]() $\mathbb {A}^1(\mathcal {U})$.
$\mathbb {A}^1(\mathcal {U})$.
Remark 3.3 The previous result shows that under very general circumstances, for instance when any single coefficient is differentially transcendental over the others, the equation has no subvarieties over the coefficients of the equation itself. We state the following result, but omit its proof, as it is analogous to the previous proof and will not be used later in this paper.
Proposition 3.4 Let ![]() $f$ be a differential polynomial in one variable and
$f$ be a differential polynomial in one variable and ![]() $V$ the zero set of
$V$ the zero set of ![]() $f$. Let
$f$. Let ![]() $\bar \alpha$ denote the tuple of coefficients in
$\bar \alpha$ denote the tuple of coefficients in ![]() $f$. If
$f$. If ![]() $\bar {\alpha }$ has some element
$\bar {\alpha }$ has some element ![]() ${\alpha _1}$ such that
${\alpha _1}$ such that ![]() $\alpha _1$ is differentially transcendental over
$\alpha _1$ is differentially transcendental over ![]() $\mathbb {Q} \langle \bar \alpha _{-1} \rangle$,Footnote 3 then
$\mathbb {Q} \langle \bar \alpha _{-1} \rangle$,Footnote 3 then ![]() $V$ has no differential subvarieties over
$V$ has no differential subvarieties over ![]() $\mathbb {Q} \langle \bar \alpha \rangle$ except perhaps the zero set given by the monomial of which
$\mathbb {Q} \langle \bar \alpha \rangle$ except perhaps the zero set given by the monomial of which ![]() $\alpha _1$ is a coefficient.
$\alpha _1$ is a coefficient.
The previous proposition works in such generality, in part because we have restricted the coefficient field. In various situations, identifying differential subvarieties defined over the field of definition of a variety ![]() $V$ is a much easier problem than identifying differential subvarieties of
$V$ is a much easier problem than identifying differential subvarieties of ![]() $V$ defined over differential field extensions. For instance, in [Reference NishiokaNis89], Nishioka shows that the equations corresponding to automorphic functions of dense subgroups of
$V$ defined over differential field extensions. For instance, in [Reference NishiokaNis89], Nishioka shows that the equations corresponding to automorphic functions of dense subgroups of ![]() $SL_2$ have no differential subvarieties over
$SL_2$ have no differential subvarieties over ![]() $\mathbb {C}$. In the special case of genus zero Fuchsian functions, a much more difficult argument was required to extend the result to differential subvarieties over differential field extensions [Reference Casale, Freitag and NaglooCFN20], answering a long-standing open problem of Painlevé.
$\mathbb {C}$. In the special case of genus zero Fuchsian functions, a much more difficult argument was required to extend the result to differential subvarieties over differential field extensions [Reference Casale, Freitag and NaglooCFN20], answering a long-standing open problem of Painlevé.
There is one general-purpose model-theoretic tool which restricts the field extensions one needs to consider. We will use a principle in stability theory, generally related to stable embeddedness (see, for instance, [Reference Chatzidakis and HrushovskiCH08] where this general type of result is referred to as the Shelah reflection principle). For the following result, see [Reference PillayPil96, Lemma 2.28].
Lemma 3.5 In a superstable theory, let ![]() $A\subseteq B$ and
$A\subseteq B$ and ![]() $p\in S(B)$ which forks over
$p\in S(B)$ which forks over ![]() $A$. Then there is an indiscernible sequence
$A$. Then there is an indiscernible sequence ![]() $(a_i:i\in \mathbb {N})$ such that the canonical base of
$(a_i:i\in \mathbb {N})$ such that the canonical base of ![]() $p$ is contained in the definable closure of
$p$ is contained in the definable closure of ![]() $A, a_1, \ldots, a_d$, where
$A, a_1, \ldots, a_d$, where ![]() $a_1, \ldots, a_d$ is a finite initial segment of this indiscernible sequence.
$a_1, \ldots, a_d$ is a finite initial segment of this indiscernible sequence.
Let ![]() $f$ and
$f$ and ![]() $V_0$ be as before and let
$V_0$ be as before and let ![]() $d\in \mathbb {N}$. Consider
$d\in \mathbb {N}$. Consider ![]() $V_0^{[d]}$, the set of
$V_0^{[d]}$, the set of ![]() $d$-tuples so that each coordinate
$d$-tuples so that each coordinate ![]() $x_i$ satisfies
$x_i$ satisfies ![]() $f(x_i)=\alpha _0$. As before, we can replace each instance of
$f(x_i)=\alpha _0$. As before, we can replace each instance of ![]() $\alpha _0$ with a new variable
$\alpha _0$ with a new variable ![]() $y$, resulting in a differential variety
$y$, resulting in a differential variety ![]() $V^{[d]}$ defined by the system of equations:
$V^{[d]}$ defined by the system of equations:
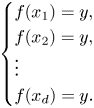 \[ \begin{cases} f(x_1) = y, \\ f(x_2) = y, \\ \vdots \\ f(x_d) = y. \end{cases} \]
\[ \begin{cases} f(x_1) = y, \\ f(x_2) = y, \\ \vdots \\ f(x_d) = y. \end{cases} \]
Proposition 3.6 Let ![]() $f(x)$ be a nonlinear order
$f(x)$ be a nonlinear order ![]() $h\geq 1$ differential polynomial with coefficients
$h\geq 1$ differential polynomial with coefficients ![]() $\bar {\alpha }$, let
$\bar {\alpha }$, let ![]() $\alpha _0$ be differentially transcendental over
$\alpha _0$ be differentially transcendental over ![]() $\mathbb {Q}\langle \bar {\alpha }\rangle$, and let
$\mathbb {Q}\langle \bar {\alpha }\rangle$, and let ![]() $V_0$ be the differential variety defined by
$V_0$ be the differential variety defined by ![]() $f(x)=\alpha _0$. Suppose that for all
$f(x)=\alpha _0$. Suppose that for all ![]() $d\in \mathbb {N}$ and for all indiscernible sequences
$d\in \mathbb {N}$ and for all indiscernible sequences ![]() $\bar {a}=(a_1,\ldots, a_d)$ in the generic type of
$\bar {a}=(a_1,\ldots, a_d)$ in the generic type of ![]() $V_0$ with
$V_0$ with ![]() $a_1, \ldots a_d$ algebraically independent over
$a_1, \ldots a_d$ algebraically independent over ![]() $\mathbb {Q}\langle \bar {\alpha }\rangle$, we have that the differential tangent space
$\mathbb {Q}\langle \bar {\alpha }\rangle$, we have that the differential tangent space ![]() $T^\Delta _{\bar {a}}\big ( V^{[d]} \big )$ has no proper infinite-rank
$T^\Delta _{\bar {a}}\big ( V^{[d]} \big )$ has no proper infinite-rank ![]() $\mathcal {C}$-vector subspaces definable over
$\mathcal {C}$-vector subspaces definable over ![]() $\mathbb {Q}\langle \bar {\alpha }, \bar {a}\rangle$. Then
$\mathbb {Q}\langle \bar {\alpha }, \bar {a}\rangle$. Then ![]() $V_0$ is strongly minimal.
$V_0$ is strongly minimal.
Proof. Suppose ![]() $V_0$ is not strongly minimal and let
$V_0$ is not strongly minimal and let ![]() $p(x)\in S_1\big (\mathbb {Q}\langle \bar {\alpha },\alpha _0 \rangle \big )$ be the type of a generic solution of
$p(x)\in S_1\big (\mathbb {Q}\langle \bar {\alpha },\alpha _0 \rangle \big )$ be the type of a generic solution of ![]() $V_0$. By Proposition 3.1,
$V_0$. By Proposition 3.1, ![]() $V_0$ does not have any infinite subvarieties defined over
$V_0$ does not have any infinite subvarieties defined over ![]() $\mathbb {Q}\langle \bar {\alpha },\alpha _0 \rangle$, so
$\mathbb {Q}\langle \bar {\alpha },\alpha _0 \rangle$, so ![]() $p$ has a forking extension
$p$ has a forking extension ![]() $q$ over a differential field extension
$q$ over a differential field extension ![]() $K>\mathbb {Q}\langle \bar {\alpha },\alpha _0 \rangle$. By Lemma 3.5, there exist some finite
$K>\mathbb {Q}\langle \bar {\alpha },\alpha _0 \rangle$. By Lemma 3.5, there exist some finite ![]() $d$ and a Morley sequence
$d$ and a Morley sequence ![]() $(a_1, \ldots, a_d)$ for
$(a_1, \ldots, a_d)$ for ![]() $q$ such that
$q$ such that ![]() $(a_1, \ldots, a_d)$ is not
$(a_1, \ldots, a_d)$ is not ![]() $\mathbb {Q}\langle \bar {\alpha },\alpha _0 \rangle$-independent. Consider the minimal such
$\mathbb {Q}\langle \bar {\alpha },\alpha _0 \rangle$-independent. Consider the minimal such ![]() $d$. Then
$d$. Then ![]() $\operatorname {tp}\big (a_1/ \mathbb {Q} \langle \bar \alpha, \alpha _0, a_2, a_3, \ldots, a_d \rangle \big )$ forks over
$\operatorname {tp}\big (a_1/ \mathbb {Q} \langle \bar \alpha, \alpha _0, a_2, a_3, \ldots, a_d \rangle \big )$ forks over ![]() $\mathbb {Q}\langle \bar {\alpha },\alpha _0 \rangle$. Since these are types over differential fields, this happens exactly when the Kolchin polynomial of
$\mathbb {Q}\langle \bar {\alpha },\alpha _0 \rangle$. Since these are types over differential fields, this happens exactly when the Kolchin polynomial of ![]() $\big (a_1/ \mathbb {Q} \langle \bar \alpha, \alpha _0, a_2, a_3, \ldots, a_d \rangle \big )$ is strictly less than the Kolchin polynomial of
$\big (a_1/ \mathbb {Q} \langle \bar \alpha, \alpha _0, a_2, a_3, \ldots, a_d \rangle \big )$ is strictly less than the Kolchin polynomial of ![]() $\big (a_1/\mathbb {Q}\langle \bar {\alpha },\alpha _0 \rangle \big )$ because the Kolchin polynomial witnesses forking.
$\big (a_1/\mathbb {Q}\langle \bar {\alpha },\alpha _0 \rangle \big )$ because the Kolchin polynomial witnesses forking.
Thus, there is a differential polynomial ![]() $g(x)\in \mathbb {Q}\langle \bar {\alpha },\alpha _0,a_2, \ldots, a_d\rangle \{x\}$ such that
$g(x)\in \mathbb {Q}\langle \bar {\alpha },\alpha _0,a_2, \ldots, a_d\rangle \{x\}$ such that ![]() ${g(a_1)=0}$ and
${g(a_1)=0}$ and ![]() $g$ has order strictly less than the order of
$g$ has order strictly less than the order of ![]() $f$. By clearing denominators, we can write
$f$. By clearing denominators, we can write ![]() $g(x_1, \ldots, x_d ) \in \mathbb {Q} \langle \bar {\alpha }, \alpha _0 \rangle \{x_1 , \ldots, x_d\}$ such that
$g(x_1, \ldots, x_d ) \in \mathbb {Q} \langle \bar {\alpha }, \alpha _0 \rangle \{x_1 , \ldots, x_d\}$ such that ![]() $g(a_1, \ldots, a_d)=0$. Let
$g(a_1, \ldots, a_d)=0$. Let ![]() $U_0\subset V_0^{[d]}$ be the vanishing set of
$U_0\subset V_0^{[d]}$ be the vanishing set of ![]() $g(x_1,\ldots, x_d)$. Just as with
$g(x_1,\ldots, x_d)$. Just as with ![]() $V$, we can replace
$V$, we can replace ![]() $\alpha _0$ with a new variable
$\alpha _0$ with a new variable ![]() $y$ after clearing denominators again, giving a
$y$ after clearing denominators again, giving a ![]() $\mathbb {Q}\langle \bar {\alpha }\rangle$-polynomial
$\mathbb {Q}\langle \bar {\alpha }\rangle$-polynomial ![]() $g(x_1,\ldots, x_d, y)$ and the corresponding variety
$g(x_1,\ldots, x_d, y)$ and the corresponding variety ![]() $U\subset V^{[d]}$. The Kolchin polynomial
$U\subset V^{[d]}$. The Kolchin polynomial ![]() $\omega \big ( U / \mathbb {Q}\langle \bar {\alpha }\rangle \big )$ is non-constant. Let
$\omega \big ( U / \mathbb {Q}\langle \bar {\alpha }\rangle \big )$ is non-constant. Let ![]() ${\bar {a}=(a_1, \ldots, a_d, \alpha _0)}$ and notice that
${\bar {a}=(a_1, \ldots, a_d, \alpha _0)}$ and notice that ![]() $\bar {a}$ is a generic point of
$\bar {a}$ is a generic point of ![]() $U$ over
$U$ over ![]() $\mathbb {Q}\langle \alpha \rangle$. By Lemma 2.1, the Kolchin polynomial of the differential tangent space
$\mathbb {Q}\langle \alpha \rangle$. By Lemma 2.1, the Kolchin polynomial of the differential tangent space ![]() $\omega \big ( T^\Delta _{\bar {a}} (U)/\mathbb {Q}\langle \bar {\alpha }, \bar {a}\rangle \big )$ is also non-constant, so
$\omega \big ( T^\Delta _{\bar {a}} (U)/\mathbb {Q}\langle \bar {\alpha }, \bar {a}\rangle \big )$ is also non-constant, so ![]() $T^\Delta _{\bar {a}} (V^{[d]})$ has an infinite-rank subspace over
$T^\Delta _{\bar {a}} (V^{[d]})$ has an infinite-rank subspace over ![]() $\mathbb {Q}\langle \bar {\alpha,} \bar {a}\rangle$, a contradiction to our assumption.
$\mathbb {Q}\langle \bar {\alpha,} \bar {a}\rangle$, a contradiction to our assumption.
Remark 3.7 Using Lemma 3.5 together with Proposition 3.6 gives a strategy for establishing the strong minimality of nonlinear differential equations with generic coefficients, but only if one can verify the hypothesis of Proposition 3.6. A priori, this looks quite hard since it would require the analysis of systems of linear differential equations in ![]() $n$ variables for all
$n$ variables for all ![]() $n \in \mathbb {N}.$ This may be possible via a clever inductive argument for specially selected classes of equations, but Theorem 1.2 gives a bound for the number of variables we need to consider.
$n \in \mathbb {N}.$ This may be possible via a clever inductive argument for specially selected classes of equations, but Theorem 1.2 gives a bound for the number of variables we need to consider.
Theorem 3.8 Let ![]() $f(x)$ be a nonlinear order
$f(x)$ be a nonlinear order ![]() $h\geq 1$ differential polynomial with coefficients
$h\geq 1$ differential polynomial with coefficients ![]() $\bar {\alpha }$, let
$\bar {\alpha }$, let ![]() $\alpha _0$ be differentially transcendental over
$\alpha _0$ be differentially transcendental over ![]() $\mathbb {Q}\langle \bar {\alpha }\rangle$, and let
$\mathbb {Q}\langle \bar {\alpha }\rangle$, and let ![]() $V_0$ be the differential variety defined by
$V_0$ be the differential variety defined by ![]() $f(x)=\alpha _0$. Let
$f(x)=\alpha _0$. Let ![]() $p$ be the generic type of
$p$ be the generic type of ![]() $V_0$. Suppose that for some
$V_0$. Suppose that for some ![]() $d \geq \operatorname {nmdeg}{p}+1$, the following property holds: for any
$d \geq \operatorname {nmdeg}{p}+1$, the following property holds: for any ![]() $\bar {a} = (a_1, \ldots, a_{d} )$ realizing the generic type of
$\bar {a} = (a_1, \ldots, a_{d} )$ realizing the generic type of ![]() $V_0$ with
$V_0$ with ![]() $a_1, \ldots, a_d$ algebraically independent over
$a_1, \ldots, a_d$ algebraically independent over ![]() $\mathbb {Q}\langle \bar {\alpha }\rangle$, the differential tangent space
$\mathbb {Q}\langle \bar {\alpha }\rangle$, the differential tangent space ![]() $T^\Delta _{\bar {a}}\big ( V^{[d]} \big )$ has no definable proper infinite-rank
$T^\Delta _{\bar {a}}\big ( V^{[d]} \big )$ has no definable proper infinite-rank ![]() $\mathcal {C}$-vector subspace over
$\mathcal {C}$-vector subspace over ![]() $\mathbb {Q}\langle \bar {\alpha }, \bar {a}\rangle$. Then
$\mathbb {Q}\langle \bar {\alpha }, \bar {a}\rangle$. Then ![]() $V_0$ is strongly minimal.
$V_0$ is strongly minimal.
Proof. By Proposition 3.1, there are no subvarieties of ![]() $V_0$ defined over the differential field generated by the coefficients of
$V_0$ defined over the differential field generated by the coefficients of ![]() $f$. So, we need only consider forking extensions of the generic type of
$f$. So, we need only consider forking extensions of the generic type of ![]() $V_0$. By definition of non-minimality degree, if there is an infinite proper differential subvariety of
$V_0$. By definition of non-minimality degree, if there is an infinite proper differential subvariety of ![]() $V_0$, then it is defined over (the algebraic closure of) a Morley sequence of length at most
$V_0$, then it is defined over (the algebraic closure of) a Morley sequence of length at most ![]() $\operatorname {nmdeg}(p)$. Thus, there is a proper subvariety of
$\operatorname {nmdeg}(p)$. Thus, there is a proper subvariety of ![]() $W_0 \subset V_0^{[d]}$ which surjects onto the first
$W_0 \subset V_0^{[d]}$ which surjects onto the first ![]() $d-1$ coordinates such that the fiber over a generic point in the first
$d-1$ coordinates such that the fiber over a generic point in the first ![]() $d-1$ coordinates is a forking extension of the generic type of
$d-1$ coordinates is a forking extension of the generic type of ![]() $V_0$. But then by the argument of Proposition 3.6, there is a definable proper infinite-rank subspace of
$V_0$. But then by the argument of Proposition 3.6, there is a definable proper infinite-rank subspace of ![]() $T^\Delta _{\bar {a}}\big ( V^{[d]} \big )$ over
$T^\Delta _{\bar {a}}\big ( V^{[d]} \big )$ over ![]() $\mathbb {Q}\langle \bar {\alpha }, \bar {a}\rangle$.
$\mathbb {Q}\langle \bar {\alpha }, \bar {a}\rangle$.
4. Strong minimality of generic equations
4.1 A first example
Theorem 4.1 Let ![]() $X_\alpha$ be the differential variety given by
$X_\alpha$ be the differential variety given by
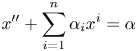 \begin{equation} x'' + \sum _{i=1} ^n \alpha _i x^i =\alpha \end{equation}
\begin{equation} x'' + \sum _{i=1} ^n \alpha _i x^i =\alpha \end{equation}
for some ![]() $n \geq 8$, where
$n \geq 8$, where ![]() $(\alpha, \alpha _0,\ldots, \alpha _n)$ is a tuple of independent differential transcendentals over
$(\alpha, \alpha _0,\ldots, \alpha _n)$ is a tuple of independent differential transcendentals over ![]() $\mathbb {Q}.$ Then
$\mathbb {Q}.$ Then ![]() $X_\alpha$ is strongly minimal.
$X_\alpha$ is strongly minimal.
Proof. By Theorem 1.2, we know that the degree of non-minimality of the generic type of ![]() $X_\alpha$ is at most three, so it suffices to verify the hypotheses of Theorem 3.8 for
$X_\alpha$ is at most three, so it suffices to verify the hypotheses of Theorem 3.8 for ![]() $d=4$. Thus, we need to show that given any solutions
$d=4$. Thus, we need to show that given any solutions ![]() $a_1, a_2, a_3 ,a_4$ to (1) that are algebraically independent over
$a_1, a_2, a_3 ,a_4$ to (1) that are algebraically independent over ![]() $\mathbb {Q} \langle \alpha, \alpha _1 , \ldots, \alpha _n \rangle$,Footnote 4 we cannot have that the transcendence degree of
$\mathbb {Q} \langle \alpha, \alpha _1 , \ldots, \alpha _n \rangle$,Footnote 4 we cannot have that the transcendence degree of ![]() $\mathbb {Q} \langle a_1, \alpha, \alpha _1, \ldots, \alpha _n, a_2, \ldots, a_4 \rangle$ over
$\mathbb {Q} \langle a_1, \alpha, \alpha _1, \ldots, \alpha _n, a_2, \ldots, a_4 \rangle$ over ![]() $\mathbb {Q} \langle \alpha, \alpha _1, \ldots, \alpha _n, a_2, \ldots, a_4 \rangle$ is one.
$\mathbb {Q} \langle \alpha, \alpha _1, \ldots, \alpha _n, a_2, \ldots, a_4 \rangle$ is one.
Observe that the differential tangent space ![]() $T_{\bar {a}}^\Delta \big (X^{[4]}\big )$ after eliminating
$T_{\bar {a}}^\Delta \big (X^{[4]}\big )$ after eliminating ![]() $y$ is given by the system
$y$ is given by the system
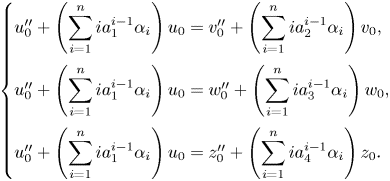 \[\begin{cases}
u_0'' + \left(\displaystyle\sum _{i=1}^n i a_1^{i-1} \alpha_i \right) u_0 = v_0'' +
\left(\displaystyle\sum _{i=1}^n i a_2^{i-1} \alpha_i \right) v_0,\\
u_0'' + \left(\displaystyle\sum _{i=1}^n i a_1^{i-1} \alpha_i \right)
u_0 = w_0'' + \left(\displaystyle\sum _{i=1}^n i a_3^{i-1} \alpha_i \right) w_0,\\
u_0'' + \left(\displaystyle\sum _{i=1}^n i a_1^{i-1} \alpha_i \right) u_0 = z_0'' +
\left(\displaystyle\sum _{i=1}^n i a_4^{i-1} \alpha_i \right) z_0. \end{cases} \]
\[\begin{cases}
u_0'' + \left(\displaystyle\sum _{i=1}^n i a_1^{i-1} \alpha_i \right) u_0 = v_0'' +
\left(\displaystyle\sum _{i=1}^n i a_2^{i-1} \alpha_i \right) v_0,\\
u_0'' + \left(\displaystyle\sum _{i=1}^n i a_1^{i-1} \alpha_i \right)
u_0 = w_0'' + \left(\displaystyle\sum _{i=1}^n i a_3^{i-1} \alpha_i \right) w_0,\\
u_0'' + \left(\displaystyle\sum _{i=1}^n i a_1^{i-1} \alpha_i \right) u_0 = z_0'' +
\left(\displaystyle\sum _{i=1}^n i a_4^{i-1} \alpha_i \right) z_0. \end{cases} \]
For ![]() $j=1, \ldots, 4$, we let
$j=1, \ldots, 4$, we let ![]() $\beta _j= \sum _{i=0}^n i a_j^{i-1} \alpha _i$. We argue that
$\beta _j= \sum _{i=0}^n i a_j^{i-1} \alpha _i$. We argue that ![]() $\beta _1, \ldots, \beta _4$ are independent differential transcendentals. Note that
$\beta _1, \ldots, \beta _4$ are independent differential transcendentals. Note that
 \[ \left( \begin{matrix} n a_1^{n-1} &
(n-1)a_1^{n-2} & \ldots & 2a_1 & 1\\ n a_2^{n-1} &
(n-1)a_2^{n-2} & \ldots & 2a_2 & 1\\ n a_3^{n-1} &
(n-1)a_3^{n-2} & \ldots & 2a_3 & 1\\ n a_4^{n-1} &
(n-1)a_4^{n-2} & \ldots & 2a_4 & 1\\ \end{matrix}\right)
\left( \begin{matrix} \alpha_n \\ \alpha_{n-1}\\ \vdots \\
\alpha_1 \end{matrix}\right) = \left( \begin{matrix}
\beta_1 \\ \beta_2 \\ \beta_3 \\ \beta_4 \end{matrix}
\right). \]
\[ \left( \begin{matrix} n a_1^{n-1} &
(n-1)a_1^{n-2} & \ldots & 2a_1 & 1\\ n a_2^{n-1} &
(n-1)a_2^{n-2} & \ldots & 2a_2 & 1\\ n a_3^{n-1} &
(n-1)a_3^{n-2} & \ldots & 2a_3 & 1\\ n a_4^{n-1} &
(n-1)a_4^{n-2} & \ldots & 2a_4 & 1\\ \end{matrix}\right)
\left( \begin{matrix} \alpha_n \\ \alpha_{n-1}\\ \vdots \\
\alpha_1 \end{matrix}\right) = \left( \begin{matrix}
\beta_1 \\ \beta_2 \\ \beta_3 \\ \beta_4 \end{matrix}
\right). \]
We claim that any four columns of the matrix of ![]() $a_i$ are linearly independent. To see this, note that if not then the vanishing of the corresponding determinant shows that there is a non-trivial polynomial relation which holds of
$a_i$ are linearly independent. To see this, note that if not then the vanishing of the corresponding determinant shows that there is a non-trivial polynomial relation which holds of ![]() $a_1, \ldots, a_4.$ This contradicts the fact that
$a_1, \ldots, a_4.$ This contradicts the fact that ![]() $a_1, \ldots a_4$ are algebraically independent over
$a_1, \ldots a_4$ are algebraically independent over ![]() $\mathbb {Q}$. By the independence of
$\mathbb {Q}$. By the independence of ![]() $\alpha _1, \ldots, \alpha _n$, and since
$\alpha _1, \ldots, \alpha _n$, and since ![]() $n\geq 8$, there are at least four of the
$n\geq 8$, there are at least four of the ![]() $\alpha _i$ which are independent differential transcendentals over the other
$\alpha _i$ which are independent differential transcendentals over the other ![]() $\alpha _i$ and
$\alpha _i$ and ![]() $a_1, \ldots, a_4.$ Without loss of generality, assume
$a_1, \ldots, a_4.$ Without loss of generality, assume ![]() $\alpha _1, \ldots, \alpha _4$ are independent differential transcendentals over
$\alpha _1, \ldots, \alpha _4$ are independent differential transcendentals over ![]() $\mathbb {Q} \langle \alpha _5, \ldots, \alpha _n , a_1, \ldots, a_4 \rangle$. Then since the last four columns of the above matrix of
$\mathbb {Q} \langle \alpha _5, \ldots, \alpha _n , a_1, \ldots, a_4 \rangle$. Then since the last four columns of the above matrix of ![]() $a_i$ are linearly independent, it follows that
$a_i$ are linearly independent, it follows that ![]() $\alpha _1, \ldots, \alpha _4$ are interalgebraic with
$\alpha _1, \ldots, \alpha _4$ are interalgebraic with ![]() $\beta _1, \ldots, \beta _4$ over
$\beta _1, \ldots, \beta _4$ over ![]() $\mathbb {Q} \langle a_1, \ldots, a_4, \alpha _5, \ldots, \alpha _n \rangle.$ It follows that
$\mathbb {Q} \langle a_1, \ldots, a_4, \alpha _5, \ldots, \alpha _n \rangle.$ It follows that ![]() $\beta _1, \ldots, \beta _4$ are independent differential transcendentals over
$\beta _1, \ldots, \beta _4$ are independent differential transcendentals over ![]() $\mathbb {Q} \langle a_1, \ldots, a_4, \alpha _5, \ldots, \alpha _n \rangle$.
$\mathbb {Q} \langle a_1, \ldots, a_4, \alpha _5, \ldots, \alpha _n \rangle$.
Lemma 4.2 A linear system of the form
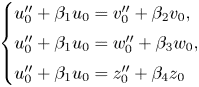 \[\begin{cases}
u_0'' + \beta_1 u_0 = v_0'' + \beta_2 v_0,\\
u_0'' + \beta_1 u_0 = w_0'' + \beta_3 w_0,\\ u_0'' + \beta_1 u_0 = z_0'' + \beta_4 z_0
\end{cases}\]
\[\begin{cases}
u_0'' + \beta_1 u_0 = v_0'' + \beta_2 v_0,\\
u_0'' + \beta_1 u_0 = w_0'' + \beta_3 w_0,\\ u_0'' + \beta_1 u_0 = z_0'' + \beta_4 z_0
\end{cases}\]
with ![]() $\beta _1, \ldots, \beta _4$ independent differential transcendentals has no proper infinite rank
$\beta _1, \ldots, \beta _4$ independent differential transcendentals has no proper infinite rank ![]() $\mathcal {C}$-vector subspaces definable over
$\mathcal {C}$-vector subspaces definable over ![]() $\mathcal {U}$.
$\mathcal {U}$.
Proof. We will prove that this system has no infinite-rank subvarieties by proving that the solution set is in definable bijection with ![]() $\mathbb {A}^1(\mathcal {U})$. This is constructed by composing a series of linear substitutions.
$\mathbb {A}^1(\mathcal {U})$. This is constructed by composing a series of linear substitutions.
First, we substitute ![]() $u_1$ for
$u_1$ for ![]() $u_0$, where
$u_0$, where ![]() $u_0=u_1+v_0$. This reduces the order of
$u_0=u_1+v_0$. This reduces the order of ![]() $v_0$ in the top equation, resulting in the system
$v_0$ in the top equation, resulting in the system
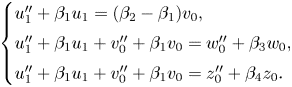 \[ \begin{cases} u_1'' +
\beta_1 u_1 = (\beta_2-\beta_1) v_0,\\ u_1'' +
\beta_1 u_1 +v_0'' +\beta_1 v_0 = w_0'' + \beta_3
w_0,\\ u_1'' + \beta_1 u_1 +v_0'' +\beta_1 v_0 =
z_0'' + \beta_4 z_0.
\end{cases}\]
\[ \begin{cases} u_1'' +
\beta_1 u_1 = (\beta_2-\beta_1) v_0,\\ u_1'' +
\beta_1 u_1 +v_0'' +\beta_1 v_0 = w_0'' + \beta_3
w_0,\\ u_1'' + \beta_1 u_1 +v_0'' +\beta_1 v_0 =
z_0'' + \beta_4 z_0.
\end{cases}\]
To reduce the order ![]() $v_0$ in the lower equations we substitute
$v_0$ in the lower equations we substitute ![]() $w_1,z_1$ for
$w_1,z_1$ for ![]() $w_0,z_0$, where
$w_0,z_0$, where ![]() $w_0=w_1+v_0,z_0=z_1+v_0$. Then we have
$w_0=w_1+v_0,z_0=z_1+v_0$. Then we have
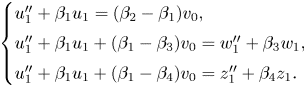 \[ \begin{cases} u_1'' +
\beta_1 u_1 = (\beta_2-\beta_1) v_0,\\ u_1'' +
\beta_1 u_1 +(\beta_1-\beta_3) v_0 = w_1'' + \beta_3
w_1,\\ u_1'' + \beta_1 u_1 +(\beta_1-\beta_4) v_0
= z_1'' + \beta_4 z_1. \end{cases}
\]
\[ \begin{cases} u_1'' +
\beta_1 u_1 = (\beta_2-\beta_1) v_0,\\ u_1'' +
\beta_1 u_1 +(\beta_1-\beta_3) v_0 = w_1'' + \beta_3
w_1,\\ u_1'' + \beta_1 u_1 +(\beta_1-\beta_4) v_0
= z_1'' + \beta_4 z_1. \end{cases}
\]
Solving the top equation for ![]() $v_0$ in terms of
$v_0$ in terms of ![]() $u_1$ and plugging this in for
$u_1$ and plugging this in for ![]() $v_0$ allows us to eliminate
$v_0$ allows us to eliminate ![]() $v_0$ from lower equations, resulting in the system
$v_0$ from lower equations, resulting in the system
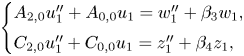 \[ \begin{cases} A_{2,0}u_1''
+ A_{0,0} u_1 = w_1'' + \beta_3 w_1,\\
C_{2,0}u_1'' + C_{0,0} u_1 = z_1'' + \beta_4 z_1,
\end{cases} \]
\[ \begin{cases} A_{2,0}u_1''
+ A_{0,0} u_1 = w_1'' + \beta_3 w_1,\\
C_{2,0}u_1'' + C_{0,0} u_1 = z_1'' + \beta_4 z_1,
\end{cases} \]
where (after some simplification)
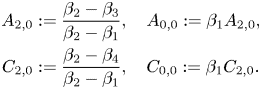 \begin{align*} A_{2,0}&:=\frac{\beta_2-\beta_3}{\beta_2-\beta_1}, \quad A_{0,0}:=\beta_1 A_{2,0},\\ C_{2,0}&:=\frac{\beta_2-\beta_4}{\beta_2-\beta_1}, \quad C_{0,0}:=\beta_1 C_{2,0}. \end{align*}
\begin{align*} A_{2,0}&:=\frac{\beta_2-\beta_3}{\beta_2-\beta_1}, \quad A_{0,0}:=\beta_1 A_{2,0},\\ C_{2,0}&:=\frac{\beta_2-\beta_4}{\beta_2-\beta_1}, \quad C_{0,0}:=\beta_1 C_{2,0}. \end{align*}
We again reduce the order of the variable in the top equation by substituting ![]() $u_2$ for
$u_2$ for ![]() $u_1$ defined by
$u_1$ defined by ![]() $u_1=u_2+({1}/{A_{2,0}})w_1$, resulting in the system
$u_1=u_2+({1}/{A_{2,0}})w_1$, resulting in the system
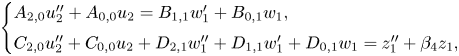 \[ \begin{cases} A_{2,0}u_2''
+ A_{0,0} u_2 = B_{1,1}w_1'+B_{0,1} w_1,\\
C_{2,0}u_2'' + C_{0,0} u_2 + D_{2,1} w_1''+
D_{1,1}w_1'+D_{0,1}w_1 = z_1'' + \beta_4 z_1,
\end{cases} \]
\[ \begin{cases} A_{2,0}u_2''
+ A_{0,0} u_2 = B_{1,1}w_1'+B_{0,1} w_1,\\
C_{2,0}u_2'' + C_{0,0} u_2 + D_{2,1} w_1''+
D_{1,1}w_1'+D_{0,1}w_1 = z_1'' + \beta_4 z_1,
\end{cases} \]
where
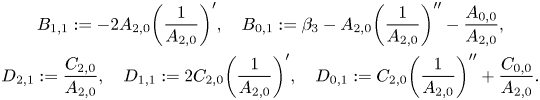 \begin{gather*} B_{1,1}:=-2
A_{2,0}\biggl(\frac{1}{A_{2,0}}\biggr)', \quad
B_{0,1}:=\beta_3 - A_{2,0}\biggl(\frac{1}{A_{2,0}}\biggr)''
-\frac{A_{0,0}}{A_{2,0}},\\
D_{2,1}:=\frac{C_{2,0}}{A_{2,0}},\quad
D_{1,1}:=2C_{2,0}\biggl(\frac{1}{A_{2,0}}\biggr)', \quad
D_{0,1}:=C_{2,0}\biggl(\frac{1}{A_{2,0}}\biggr)''+\frac{C_{0,0}}{A_{2,0}}.
\end{gather*}
\begin{gather*} B_{1,1}:=-2
A_{2,0}\biggl(\frac{1}{A_{2,0}}\biggr)', \quad
B_{0,1}:=\beta_3 - A_{2,0}\biggl(\frac{1}{A_{2,0}}\biggr)''
-\frac{A_{0,0}}{A_{2,0}},\\
D_{2,1}:=\frac{C_{2,0}}{A_{2,0}},\quad
D_{1,1}:=2C_{2,0}\biggl(\frac{1}{A_{2,0}}\biggr)', \quad
D_{0,1}:=C_{2,0}\biggl(\frac{1}{A_{2,0}}\biggr)''+\frac{C_{0,0}}{A_{2,0}}.
\end{gather*}
We next reduce the order of ![]() $w_1$ in lower equations with the substitution
$w_1$ in lower equations with the substitution ![]() $z_2$ for
$z_2$ for ![]() $z_1$ defined by
$z_1$ defined by ![]() $z_1=z_2+D_{2,1}w_1$. Now we have the system
$z_1=z_2+D_{2,1}w_1$. Now we have the system
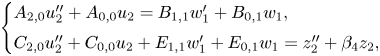 \[ \begin{cases} A_{2,0}u_2''
+ A_{0,0} u_2 = B_{1,1}w_1'+B_{0,1} w_1,\\
C_{2,0}u_2'' + C_{0,0} u_2 + E_{1,1}w_1'+E_{0,1}w_1 = z_2''
+ \beta_4 z_2, \end{cases}
\]
\[ \begin{cases} A_{2,0}u_2''
+ A_{0,0} u_2 = B_{1,1}w_1'+B_{0,1} w_1,\\
C_{2,0}u_2'' + C_{0,0} u_2 + E_{1,1}w_1'+E_{0,1}w_1 = z_2''
+ \beta_4 z_2, \end{cases}
\]
where
Next we reduce the order of ![]() $u_2$ in the top equation by substituting
$u_2$ in the top equation by substituting ![]() $w_2$ for
$w_2$ for ![]() $w_1$ with
$w_1$ with ![]() $w_1=w_2 + ({A_{2,0}}/{B_{1,1}})u_2'$, resulting in the system
$w_1=w_2 + ({A_{2,0}}/{B_{1,1}})u_2'$, resulting in the system
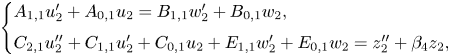 \[ \left\{ \begin{array}{@{}l} A_{1,1}u_2' + A_{0,1} u_2 = B_{1,1}w_2'+B_{0,1} w_2,\\ C_{2,1}u_2'' +C_{1,1}u_2'+ C_{0,1} u_2 + E_{1,1}w_2'+E_{0,1}w_2= z_2'' + \beta_4 z_2, \end{array} \right. \]
\[ \left\{ \begin{array}{@{}l} A_{1,1}u_2' + A_{0,1} u_2 = B_{1,1}w_2'+B_{0,1} w_2,\\ C_{2,1}u_2'' +C_{1,1}u_2'+ C_{0,1} u_2 + E_{1,1}w_2'+E_{0,1}w_2= z_2'' + \beta_4 z_2, \end{array} \right. \]
where
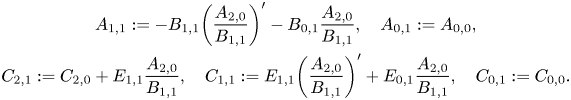 \begin{gather*}
A_{1,1}:=-B_{1,1}\biggl(\frac{A_{2,0}}{B_{1,1}}\biggr)'-B_{0,1}\frac{A_{2,0}}{B_{1,1}},
\quad A_{0,1}:= A_{0,0},\\
C_{2,1}:=C_{2,0}+E_{1,1}\frac{A_{2,0}}{B_{1,1}}, \quad
C_{1,1}:=E_{1,1}\biggl(\frac{A_{2,0}}{B_{1,1}}\biggr)'+E_{0,1}\frac{A_{2,0}}{B_{1,1}},
\quad C_{0,1}:=C_{0,0}. \end{gather*}
\begin{gather*}
A_{1,1}:=-B_{1,1}\biggl(\frac{A_{2,0}}{B_{1,1}}\biggr)'-B_{0,1}\frac{A_{2,0}}{B_{1,1}},
\quad A_{0,1}:= A_{0,0},\\
C_{2,1}:=C_{2,0}+E_{1,1}\frac{A_{2,0}}{B_{1,1}}, \quad
C_{1,1}:=E_{1,1}\biggl(\frac{A_{2,0}}{B_{1,1}}\biggr)'+E_{0,1}\frac{A_{2,0}}{B_{1,1}},
\quad C_{0,1}:=C_{0,0}. \end{gather*}
The reduction in order of the top equation continues with the replacement of ![]() $u_2$ with
$u_2$ with ![]() $u_3$ given by
$u_3$ given by ![]() $u_2=u_3+({B_{1,1}}/{A_{1,1}})w_2$. This results in the system
$u_2=u_3+({B_{1,1}}/{A_{1,1}})w_2$. This results in the system
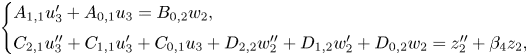 \[ \begin{cases} A_{1,1}u_3'
+ A_{0,1} u_3 = B_{0,2} w_2,\\ C_{2,1}u_3''
+C_{1,1}u_3'+ C_{0,1} u_3 + D_{2,2}w_2''+
D_{1,2}w_2'+D_{0,2}w_2 = z_2'' + \beta_4z_2,
\end{cases} \]
\[ \begin{cases} A_{1,1}u_3'
+ A_{0,1} u_3 = B_{0,2} w_2,\\ C_{2,1}u_3''
+C_{1,1}u_3'+ C_{0,1} u_3 + D_{2,2}w_2''+
D_{1,2}w_2'+D_{0,2}w_2 = z_2'' + \beta_4z_2,
\end{cases} \]
where
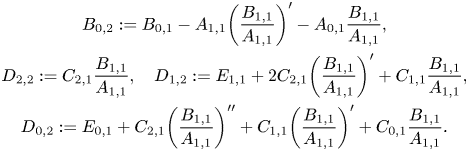 \begin{gather*} B_{0,2}:=B_{0,1}-
A_{1,1}\biggl(\frac{B_{1,1}}{A_{1,1}}\biggr)'-A_{0,1}\frac{B_{1,1}}{A_{1,1}},\\
D_{2,2}:= C_{2,1}\frac{B_{1,1}}{A_{1,1}}, \quad
D_{1,2}:=E_{1,1}+2
C_{2,1}\biggl(\frac{B_{1,1}}{A_{1,1}}\biggr)'+C_{1,1}\frac{B_{1,1}}{A_{1,1}},\\
D_{0,2}:=E_{0,1}+
C_{2,1}\biggl(\frac{B_{1,1}}{A_{1,1}}\biggr)''
+C_{1,1}\biggl(\frac{B_{1,1}}{A_{1,1}}\biggr)'
+C_{0,1}\frac{B_{1,1}}{A_{1,1}}. \end{gather*}
\begin{gather*} B_{0,2}:=B_{0,1}-
A_{1,1}\biggl(\frac{B_{1,1}}{A_{1,1}}\biggr)'-A_{0,1}\frac{B_{1,1}}{A_{1,1}},\\
D_{2,2}:= C_{2,1}\frac{B_{1,1}}{A_{1,1}}, \quad
D_{1,2}:=E_{1,1}+2
C_{2,1}\biggl(\frac{B_{1,1}}{A_{1,1}}\biggr)'+C_{1,1}\frac{B_{1,1}}{A_{1,1}},\\
D_{0,2}:=E_{0,1}+
C_{2,1}\biggl(\frac{B_{1,1}}{A_{1,1}}\biggr)''
+C_{1,1}\biggl(\frac{B_{1,1}}{A_{1,1}}\biggr)'
+C_{0,1}\frac{B_{1,1}}{A_{1,1}}. \end{gather*}
Next we replace ![]() $z_2$ with
$z_2$ with ![]() $z_3$ given by
$z_3$ given by ![]() $z_2=z_3 + D_{2,2}w_2$ to arrive at
$z_2=z_3 + D_{2,2}w_2$ to arrive at
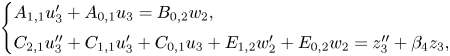 \[ \begin{cases} A_{1,1}u_3'
+ A_{0,1} u_3 = B_{0,2} w_2,\\ C_{2,1}u_3''
+C_{1,1}u_3'+ C_{0,1} u_3 + E_{1,2}w_2'+E_{0,2}w_2 = z_3''
+ \beta_4 z_3, \end{cases}
\]
\[ \begin{cases} A_{1,1}u_3'
+ A_{0,1} u_3 = B_{0,2} w_2,\\ C_{2,1}u_3''
+C_{1,1}u_3'+ C_{0,1} u_3 + E_{1,2}w_2'+E_{0,2}w_2 = z_3''
+ \beta_4 z_3, \end{cases}
\]
where
Now we can solve the top equation for ![]() $w_2$ in terms of
$w_2$ in terms of ![]() $u_3$ and plug the resulting expression into the lower equations:
$u_3$ and plug the resulting expression into the lower equations:
where
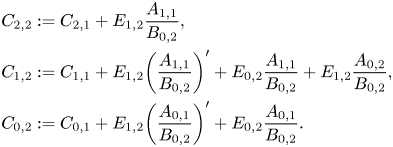 \begin{align*} C_{2,2}&:= C_{2,1}+E_{1,2}\frac{A_{1,1}}{B_{0,2}}, \\ C_{1,2}&:= C_{1,1}+E_{1,2}\biggl(\frac{A_{1,1}}{B_{0,2}}\biggr)' + E_{0,2}\frac{A_{1,1}}{B_{0,2}} + E_{1,2}\frac{A_{0,2}}{B_{0,2}},\\ C_{0,2}&:=C_{0,1}+E_{1,2}\biggl(\frac{A_{0,1}}{B_{0,2}}\biggr)'+E_{0,2}\frac{A_{0,1}}{B_{0,2}}. \end{align*}
\begin{align*} C_{2,2}&:= C_{2,1}+E_{1,2}\frac{A_{1,1}}{B_{0,2}}, \\ C_{1,2}&:= C_{1,1}+E_{1,2}\biggl(\frac{A_{1,1}}{B_{0,2}}\biggr)' + E_{0,2}\frac{A_{1,1}}{B_{0,2}} + E_{1,2}\frac{A_{0,2}}{B_{0,2}},\\ C_{0,2}&:=C_{0,1}+E_{1,2}\biggl(\frac{A_{0,1}}{B_{0,2}}\biggr)'+E_{0,2}\frac{A_{0,1}}{B_{0,2}}. \end{align*}
Next we perform analogous substitutions to eliminate ![]() $z_3$ from the top equation, beginning with substituting
$z_3$ from the top equation, beginning with substituting ![]() $u_4$ for
$u_4$ for ![]() $u_3$ defined by
$u_3$ defined by ![]() $u_3=u_4+({1}/{C_{2,2}})z_3$, so we have
$u_3=u_4+({1}/{C_{2,2}})z_3$, so we have
where
Next, substitute ![]() $z_4$ for
$z_4$ for ![]() $z_3$, where
$z_3$, where ![]() $z_3=z_4+({C_{2,2}}/{F_{1,1}})u_4'$. This will result in the equation
$z_3=z_4+({C_{2,2}}/{F_{1,1}})u_4'$. This will result in the equation
where
Replace ![]() $u_4$ with
$u_4$ with ![]() $u_5$ defined by
$u_5$ defined by ![]() $u_4=u_5+({F_{1,1}}/{C_{1,3}})z_4$, giving us the equation
$u_4=u_5+({F_{1,1}}/{C_{1,3}})z_4$, giving us the equation
where
Any solution to (3) is determined by the value of ![]() $u_5$, so the solution set is in definable bijection with
$u_5$, so the solution set is in definable bijection with ![]() $\mathbb {A}^1(\mathcal {U})$. Each of these linear substitutions gives rise to a definable bijection between systems so long as the substitutions are well defined, that is, the denominators of the coefficients are all non-zero. For this procedure to give a definable bijection from the original system (2) to
$\mathbb {A}^1(\mathcal {U})$. Each of these linear substitutions gives rise to a definable bijection between systems so long as the substitutions are well defined, that is, the denominators of the coefficients are all non-zero. For this procedure to give a definable bijection from the original system (2) to ![]() $\mathbb {A}^1(\mathcal {U})$, we must verify that the following expressions are not zero:
$\mathbb {A}^1(\mathcal {U})$, we must verify that the following expressions are not zero:
The expression ![]() $\beta _2-\beta _1$ is non-zero because
$\beta _2-\beta _1$ is non-zero because ![]() $\beta _1,\beta _2,\beta _3,\beta _4$ are all distinct. Each of these coefficients can be considered as a differential rational function in terms of
$\beta _1,\beta _2,\beta _3,\beta _4$ are all distinct. Each of these coefficients can be considered as a differential rational function in terms of ![]() $\beta _1,\beta _2, \beta _3,\beta _4$, and so they can be analyzed according to a ranking on
$\beta _1,\beta _2, \beta _3,\beta _4$, and so they can be analyzed according to a ranking on ![]() $\bar {\beta }$. We will show that these coefficients are non-zero by showing that the initials of each are non-zero in some elimination ranking. It then follows that the coefficients themselves are non-zero because
$\bar {\beta }$. We will show that these coefficients are non-zero by showing that the initials of each are non-zero in some elimination ranking. It then follows that the coefficients themselves are non-zero because ![]() $\beta _1, \beta _2, \beta _3, \beta _4$ are independent differential transcendentals.
$\beta _1, \beta _2, \beta _3, \beta _4$ are independent differential transcendentals.
Consider the terms of these expressions ordered by some elimination ranking on ![]() $\bar {\beta }$ with
$\bar {\beta }$ with ![]() $\beta _3$ ranked highest. The leading term in this ranking of each expression can be calculated using the definitions of previous coefficients. The following table shows that these leading terms are non-zero:
$\beta _3$ ranked highest. The leading term in this ranking of each expression can be calculated using the definitions of previous coefficients. The following table shows that these leading terms are non-zero:
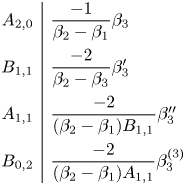 \begin{align*}
\begin{array}{c|l}
A_{2,0} & \dfrac{-1}{\beta_2-\beta_{1_{\vphantom{\frac{A}{A}}}}}\beta_3 \\
B_{1,1} & \dfrac{-2}{\beta_2-\beta_{3_{\vphantom{\frac{A}{A}}}}}\beta_3' \\
A_{1,1} & \dfrac{-2}{(\beta_2-\beta_1)B_{1,1_{\vphantom{\frac{A}{A}}}}}\beta_3'' \\
B_{0,2} & \dfrac{-2}{(\beta_2-\beta_1)A_{1,1}}\beta_3^{(3)}
\end{array} \end{align*}
\begin{align*}
\begin{array}{c|l}
A_{2,0} & \dfrac{-1}{\beta_2-\beta_{1_{\vphantom{\frac{A}{A}}}}}\beta_3 \\
B_{1,1} & \dfrac{-2}{\beta_2-\beta_{3_{\vphantom{\frac{A}{A}}}}}\beta_3' \\
A_{1,1} & \dfrac{-2}{(\beta_2-\beta_1)B_{1,1_{\vphantom{\frac{A}{A}}}}}\beta_3'' \\
B_{0,2} & \dfrac{-2}{(\beta_2-\beta_1)A_{1,1}}\beta_3^{(3)}
\end{array} \end{align*}
We turn our attention to an elimination ranking with ![]() $\beta _4$ ranked highest to prove that the remaining coefficients are non-zero. The following table shows that the leading terms of these coefficients are also non-zero:
$\beta _4$ ranked highest to prove that the remaining coefficients are non-zero. The following table shows that the leading terms of these coefficients are also non-zero:
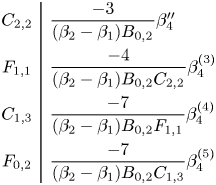 \[
\begin{array}{c|l} C_{2,2} & \dfrac{-3}{(\beta_2-\beta_1)B_{0,2_{\vphantom{\frac{A}{A}}}}}\beta_4''\\
F_{1,1} & \dfrac{-4}{(\beta_2-\beta_1)B_{0,2}C_{2,2_{\vphantom{\frac{A}{A}}}}}\beta_4^{(3)}\\
C_{1,3} & \dfrac{-7}{(\beta_2-\beta_1)B_{0,2}F_{1,1_{\vphantom{\frac{A}{A}}}}}\beta_4^{(4)} \\
F_{0,2} & \dfrac{-7}{(\beta_2-\beta_1)B_{0,2}C_{1,3}}\beta_4^{(5)}
\end{array} \]
\[
\begin{array}{c|l} C_{2,2} & \dfrac{-3}{(\beta_2-\beta_1)B_{0,2_{\vphantom{\frac{A}{A}}}}}\beta_4''\\
F_{1,1} & \dfrac{-4}{(\beta_2-\beta_1)B_{0,2}C_{2,2_{\vphantom{\frac{A}{A}}}}}\beta_4^{(3)}\\
C_{1,3} & \dfrac{-7}{(\beta_2-\beta_1)B_{0,2}F_{1,1_{\vphantom{\frac{A}{A}}}}}\beta_4^{(4)} \\
F_{0,2} & \dfrac{-7}{(\beta_2-\beta_1)B_{0,2}C_{1,3}}\beta_4^{(5)}
\end{array} \]
We have shown that each substitution is well defined, and therefore we have constructed a definable bijection between system (2) and ![]() $\mathbb {A}^1(\mathcal {U})$. Since
$\mathbb {A}^1(\mathcal {U})$. Since ![]() $\mathbb {A}^1(\mathcal {U})$ has no infinite-rank subspaces, neither does our original system, completing the proof of the proposition.
$\mathbb {A}^1(\mathcal {U})$ has no infinite-rank subspaces, neither does our original system, completing the proof of the proposition.
We now finish the proof of Theorem 4.1. Since the differential tangent space ![]() $T_{\bar {a}}^\Delta \big ( X^{[4]}\big )$ satisfies the conditions of Lemma 4.2, it has no infinite-rank subspaces over
$T_{\bar {a}}^\Delta \big ( X^{[4]}\big )$ satisfies the conditions of Lemma 4.2, it has no infinite-rank subspaces over ![]() $\mathbb {Q}\langle \bar {\alpha },\bar {a}\rangle$. Therefore,
$\mathbb {Q}\langle \bar {\alpha },\bar {a}\rangle$. Therefore, ![]() $X_\alpha$ is strongly minimal by Theorem 3.8.
$X_\alpha$ is strongly minimal by Theorem 3.8.
4.2 Generic higher-order equations
The technique used in the previous example can be applied to more general classes of equations. In this section we use analogous techniques to show that generic equations with high enough degree have differential tangent spaces cut out by linear equations with generic coefficients and that these tangent spaces have no proper infinite-rank ![]() $\mathcal {C}$-vector subspace definable over
$\mathcal {C}$-vector subspace definable over ![]() $\mathcal {U}$.
$\mathcal {U}$.
Let
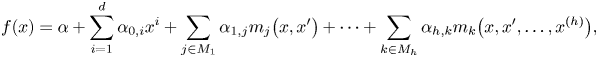 \[ f(x)=\alpha + \sum_{i=1}^d \alpha_{0,i} x^i + \sum_{j\in M_1} \alpha_{1,j} m_j\bigl(x,x'\bigr) + \cdots + \sum _{k\in M_h} \alpha_{h,k} m_k \bigl(x,x',\ldots , x^{(h)}\bigr), \]
\[ f(x)=\alpha + \sum_{i=1}^d \alpha_{0,i} x^i + \sum_{j\in M_1} \alpha_{1,j} m_j\bigl(x,x'\bigr) + \cdots + \sum _{k\in M_h} \alpha_{h,k} m_k \bigl(x,x',\ldots , x^{(h)}\bigr), \]
where ![]() $M_n$ indexes the set of all order
$M_n$ indexes the set of all order ![]() $n$ monomials of degree at most
$n$ monomials of degree at most ![]() $d$ and the entire collection of coefficients
$d$ and the entire collection of coefficients ![]() $\alpha, \alpha _{i,j}$ are independent differential transcendentals over
$\alpha, \alpha _{i,j}$ are independent differential transcendentals over ![]() $\mathbb {Q}$. Let
$\mathbb {Q}$. Let ![]() $V_\alpha$ be the zero set of
$V_\alpha$ be the zero set of ![]() $f(x)$ and let
$f(x)$ and let ![]() $m$ be the degree of non-minimality of
$m$ be the degree of non-minimality of ![]() $f$ plus one. Following the notation of § 3, we let
$f$ plus one. Following the notation of § 3, we let ![]() $V^{[m]}$ be the following system of equations in
$V^{[m]}$ be the following system of equations in ![]() $x_1, \ldots, x_m , y$:
$x_1, \ldots, x_m , y$:
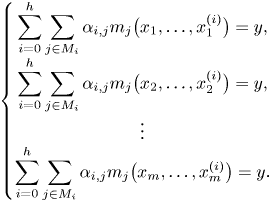 \[ \left\{ \begin{array}{@{}c} \displaystyle\sum_{i=0}^h \sum_{j\in M_i}\alpha_{i,j} m_j\bigl(x_1, \ldots, x_1^{(i)}\bigr) = y, \\ \displaystyle\sum_{i=0}^h \sum_{j\in M_i}\alpha_{i,j} m_j\bigl(x_2, \ldots, x_2^{(i)}\bigr) = y, \\ \vdots \\ \displaystyle\sum_{i=0}^h \sum_{j\in M_i}\alpha_{i,j} m_j\bigl(x_m, \ldots, x_m^{(i)}\bigr) = y. \end{array} \right. \]
\[ \left\{ \begin{array}{@{}c} \displaystyle\sum_{i=0}^h \sum_{j\in M_i}\alpha_{i,j} m_j\bigl(x_1, \ldots, x_1^{(i)}\bigr) = y, \\ \displaystyle\sum_{i=0}^h \sum_{j\in M_i}\alpha_{i,j} m_j\bigl(x_2, \ldots, x_2^{(i)}\bigr) = y, \\ \vdots \\ \displaystyle\sum_{i=0}^h \sum_{j\in M_i}\alpha_{i,j} m_j\bigl(x_m, \ldots, x_m^{(i)}\bigr) = y. \end{array} \right. \]
Let ![]() $\bar a = (a_1, \ldots, a_m)$ be an indiscernible sequence in
$\bar a = (a_1, \ldots, a_m)$ be an indiscernible sequence in ![]() $V_\alpha$ such that
$V_\alpha$ such that ![]() $a_m$ forks over
$a_m$ forks over ![]() $a_1, \ldots, a_{m-1}$ and
$a_1, \ldots, a_{m-1}$ and ![]() $tp(a_m/ \mathbb {Q} \langle \alpha, \alpha _{i,j} , a_1, \ldots, a_{m-1} \rangle _{i=0, \ldots, h, j\in M_i }$ has rank between one and
$tp(a_m/ \mathbb {Q} \langle \alpha, \alpha _{i,j} , a_1, \ldots, a_{m-1} \rangle _{i=0, \ldots, h, j\in M_i }$ has rank between one and ![]() $h-1$. That is,
$h-1$. That is, ![]() $a_m$ satisfies a differential equation of order at least one but no more than
$a_m$ satisfies a differential equation of order at least one but no more than ![]() $h-1$ over
$h-1$ over ![]() $\mathbb {Q} \langle \alpha, \alpha _{i,j} , a_1, \ldots, a_{m-1} \rangle _{i=0, \ldots, h, j\in M_i }$. Crucially for this proof, we note that
$\mathbb {Q} \langle \alpha, \alpha _{i,j} , a_1, \ldots, a_{m-1} \rangle _{i=0, \ldots, h, j\in M_i }$. Crucially for this proof, we note that ![]() $a_1, \ldots, a_m$ are algebraically independent over
$a_1, \ldots, a_m$ are algebraically independent over ![]() $\mathbb {Q} \langle \alpha, \alpha _{i,j} \rangle$.
$\mathbb {Q} \langle \alpha, \alpha _{i,j} \rangle$.
Let ![]() $T^\Delta _{(\bar {a}, \alpha )}\big ( V^{[m]} \big )$ denote the differential tangent space of
$T^\Delta _{(\bar {a}, \alpha )}\big ( V^{[m]} \big )$ denote the differential tangent space of ![]() $V^{[m]}$ over
$V^{[m]}$ over ![]() $(\bar a, \alpha )$. Then
$(\bar a, \alpha )$. Then ![]() $T^\Delta _{(\bar {a}, \alpha )}\big ( V^{[m]} \big )$ is given by
$T^\Delta _{(\bar {a}, \alpha )}\big ( V^{[m]} \big )$ is given by
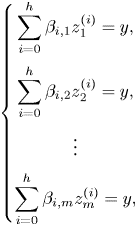 \begin{align*} \left\{ \begin{array}{@{}c} \displaystyle\sum_{i=0}^h \beta_{i,1} z_1^{(i)} = y, \\ \displaystyle\sum_{i=0}^h \beta_{i,2} z_2^{(i)} = y, \\ \vdots \\ \displaystyle\sum_{i=0}^h \beta_{i,m} z_m^{(i)} = y, \end{array} \right. \end{align*}
\begin{align*} \left\{ \begin{array}{@{}c} \displaystyle\sum_{i=0}^h \beta_{i,1} z_1^{(i)} = y, \\ \displaystyle\sum_{i=0}^h \beta_{i,2} z_2^{(i)} = y, \\ \vdots \\ \displaystyle\sum_{i=0}^h \beta_{i,m} z_m^{(i)} = y, \end{array} \right. \end{align*}
where ![]() $\beta _{i,j}=({\partial f}/{\partial x^{(i)}})(a_j)$ as used in previous sections.
$\beta _{i,j}=({\partial f}/{\partial x^{(i)}})(a_j)$ as used in previous sections.
Lemma 4.3 Let ![]() $V$ be a differential variety cut out by a generic differential polynomial of order
$V$ be a differential variety cut out by a generic differential polynomial of order ![]() $h$, degree
$h$, degree ![]() $d$ and non-minimality degree no more than
$d$ and non-minimality degree no more than ![]() $m-1$. If
$m-1$. If ![]() $\bar a = (a_1, \ldots, a_m)$ are realizations of the generic type of
$\bar a = (a_1, \ldots, a_m)$ are realizations of the generic type of ![]() $V_0$ such that
$V_0$ such that ![]() $a_1,\ldots, a_m$ are algebraically independent over
$a_1,\ldots, a_m$ are algebraically independent over ![]() $\mathbb {Q}\langle \bar {\alpha }\rangle$, then the variety
$\mathbb {Q}\langle \bar {\alpha }\rangle$, then the variety ![]() $T^\Delta _{(\bar {a}, \alpha )}\big ( V^{[m]} \big )$ has coefficients which are independent differential transcendentals over
$T^\Delta _{(\bar {a}, \alpha )}\big ( V^{[m]} \big )$ has coefficients which are independent differential transcendentals over ![]() $\mathbb {Q}$ whenever
$\mathbb {Q}$ whenever ![]() $d \geq 2m.$
$d \geq 2m.$
Proof. We proceed by induction on the order, beginning with ![]() $\beta _{0,1}, \beta _{0,2}, \ldots, \beta _{0,m}$. Since
$\beta _{0,1}, \beta _{0,2}, \ldots, \beta _{0,m}$. Since ![]() $d \geq 2m,$ there are
$d \geq 2m,$ there are ![]() $j_1, \ldots, j_m$ such that
$j_1, \ldots, j_m$ such that ![]() $\alpha _{0,j_1}, \ldots, \alpha _{0,j_m}$ are independent differential transcendentals over
$\alpha _{0,j_1}, \ldots, \alpha _{0,j_m}$ are independent differential transcendentals over ![]() $\mathbb {Q} \langle \mathcal {A}_0 a_1 \cdots a_{m} \rangle$ where
$\mathbb {Q} \langle \mathcal {A}_0 a_1 \cdots a_{m} \rangle$ where ![]() $\mathcal {A}_0=\{\alpha _{i,j}:0\leq i \leq h, j\in M_i\}\setminus \{\alpha _{0,j_1}, \ldots, \alpha _{0,j_m}\}$. Note that
$\mathcal {A}_0=\{\alpha _{i,j}:0\leq i \leq h, j\in M_i\}\setminus \{\alpha _{0,j_1}, \ldots, \alpha _{0,j_m}\}$. Note that
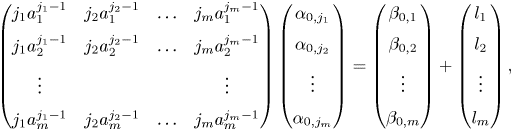 \[ \left( \begin{matrix} j_1 a_{1}^{j_1-1} & j_2 a_{1}^{j_2-1} & \ldots & j_m a_{1} ^{j_m -1}\\ j_1 a_{2}^{j_1-1} & j_2 a_{2}^{j_2-1} & \ldots & j_m a_{2} ^{j_m -1}\\ \vdots & & & \vdots \\ j_1 a_{m}^{j_1-1} & j_2 a_{m}^{j_2-1} & \ldots & j_m a_{m} ^{j_m -1} \end{matrix}\right) \left( \begin{matrix} \alpha_{0,j_1} \\ \alpha_{0,j_2}\\ \vdots \\ \alpha_{0,j_m} \end{matrix}\right) = \left( \begin{matrix} \beta_{0,1} \\ \beta_{0,2} \\ \vdots \\ \beta_{0,m} \end{matrix} \right) + \left( \begin{matrix} l_1 \\ l_2 \\ \vdots \\ l_m \end{matrix} \right), \]
\[ \left( \begin{matrix} j_1 a_{1}^{j_1-1} & j_2 a_{1}^{j_2-1} & \ldots & j_m a_{1} ^{j_m -1}\\ j_1 a_{2}^{j_1-1} & j_2 a_{2}^{j_2-1} & \ldots & j_m a_{2} ^{j_m -1}\\ \vdots & & & \vdots \\ j_1 a_{m}^{j_1-1} & j_2 a_{m}^{j_2-1} & \ldots & j_m a_{m} ^{j_m -1} \end{matrix}\right) \left( \begin{matrix} \alpha_{0,j_1} \\ \alpha_{0,j_2}\\ \vdots \\ \alpha_{0,j_m} \end{matrix}\right) = \left( \begin{matrix} \beta_{0,1} \\ \beta_{0,2} \\ \vdots \\ \beta_{0,m} \end{matrix} \right) + \left( \begin{matrix} l_1 \\ l_2 \\ \vdots \\ l_m \end{matrix} \right), \]
where ![]() $l_i \in \mathbb {Q} \langle \mathcal {A}_0 a_1 \cdots a_{m} \rangle$.
$l_i \in \mathbb {Q} \langle \mathcal {A}_0 a_1 \cdots a_{m} \rangle$.
The above matrix is invertible, as the vanishing of its determinant imposes a non-trivial algebraic relation among ![]() $a_1, \ldots, a_m$, which are, by assumption, algebraically independent. It follows that
$a_1, \ldots, a_m$, which are, by assumption, algebraically independent. It follows that ![]() $\beta _{0,1}, \ldots, \beta _{0,m}$ are interdefinable with
$\beta _{0,1}, \ldots, \beta _{0,m}$ are interdefinable with ![]() $\alpha _{0,j_1}, \ldots, \alpha _{0,j_m}$ over
$\alpha _{0,j_1}, \ldots, \alpha _{0,j_m}$ over ![]() $\mathbb {Q} \langle \mathcal {A}_0 a_1 \cdots a_{m} \rangle.$ Thus,
$\mathbb {Q} \langle \mathcal {A}_0 a_1 \cdots a_{m} \rangle.$ Thus, ![]() $\beta _{0,1}, \ldots, \beta _{0,m}$ are independent and differentially transcendental over
$\beta _{0,1}, \ldots, \beta _{0,m}$ are independent and differentially transcendental over ![]() $\mathbb {Q} \langle \mathcal {A}_0 a_1 \cdots a_{m} \rangle.$ Note that the coefficients
$\mathbb {Q} \langle \mathcal {A}_0 a_1 \cdots a_{m} \rangle.$ Note that the coefficients ![]() $\{\beta _{i,j}:1\leq i \leq h, 1\leq j \leq m\}$ are contained in the field
$\{\beta _{i,j}:1\leq i \leq h, 1\leq j \leq m\}$ are contained in the field ![]() $\mathbb {Q} \langle \mathcal {A}_0 a_1 \cdots a_{m} \rangle,$ so we have shown that
$\mathbb {Q} \langle \mathcal {A}_0 a_1 \cdots a_{m} \rangle,$ so we have shown that ![]() $\beta _{0,1}, \ldots, \beta _{0,m}$ are independent differential transcendentals over
$\beta _{0,1}, \ldots, \beta _{0,m}$ are independent differential transcendentals over ![]() $\mathbb {Q} \langle \beta _{i,j}:1\leq i \leq h, 1\leq j \leq m\rangle$.
$\mathbb {Q} \langle \beta _{i,j}:1\leq i \leq h, 1\leq j \leq m\rangle$.
Suppose we have already shown that ![]() $\beta _{n,1}, \ldots, \beta _{n,m}$ are independent differential transcendentals over
$\beta _{n,1}, \ldots, \beta _{n,m}$ are independent differential transcendentals over ![]() $\mathbb {Q} \langle \beta _{i,j}:n+1\leq i \leq h, 1\leq j \leq m\rangle$ for some
$\mathbb {Q} \langle \beta _{i,j}:n+1\leq i \leq h, 1\leq j \leq m\rangle$ for some ![]() $n< h$. Let
$n< h$. Let ![]() $M^*_{n+1}$ index the collection of order
$M^*_{n+1}$ index the collection of order ![]() $n+1$ monomials of order no more than
$n+1$ monomials of order no more than ![]() $d$ excluding the monomials of the form
$d$ excluding the monomials of the form ![]() $\{x^{(n+1)}x^r:0\leq r \leq d-1\}$. Assume the order
$\{x^{(n+1)}x^r:0\leq r \leq d-1\}$. Assume the order ![]() $n+1$ terms in
$n+1$ terms in ![]() $f(x)$ are ordered so that
$f(x)$ are ordered so that
 \[ \sum _{k\in M_{n+1}} \alpha_{n+1,k} m_k (x,x',\ldots , x^{(n+1)}) = \sum _{k=0}^{d-1} \alpha_{n+1,k} x^{(n+1)} x^k + \sum_{j \in M^*_{n+1}} \alpha_{n+1,j} m_j \bigl(x,x', \ldots, x^{(n+1)}\bigr). \]
\[ \sum _{k\in M_{n+1}} \alpha_{n+1,k} m_k (x,x',\ldots , x^{(n+1)}) = \sum _{k=0}^{d-1} \alpha_{n+1,k} x^{(n+1)} x^k + \sum_{j \in M^*_{n+1}} \alpha_{n+1,j} m_j \bigl(x,x', \ldots, x^{(n+1)}\bigr). \]
Since ![]() $d \geq 2m,$ there are
$d \geq 2m,$ there are ![]() $k_1, \ldots, k_m < d$ such that
$k_1, \ldots, k_m < d$ such that ![]() $\alpha _{n+1,k_1}, \ldots, \alpha _{n+1,k_m}$ are independent and differentially transcendental over
$\alpha _{n+1,k_1}, \ldots, \alpha _{n+1,k_m}$ are independent and differentially transcendental over ![]() $\mathbb {Q} \langle \mathcal {A}_{n+1} a_1 \cdots a_m \rangle$, where
$\mathbb {Q} \langle \mathcal {A}_{n+1} a_1 \cdots a_m \rangle$, where ![]() $\mathcal {A}_{n+1}=\{\alpha _{i,j}: n+1\leq i\leq h,j\in M_{i}\}\setminus \{\alpha _{n+1,k_1}, \ldots, \alpha _{n+1,k_m}\}$. Note that
$\mathcal {A}_{n+1}=\{\alpha _{i,j}: n+1\leq i\leq h,j\in M_{i}\}\setminus \{\alpha _{n+1,k_1}, \ldots, \alpha _{n+1,k_m}\}$. Note that
 \[ \left( \begin{matrix} a_{1}^{k_1} &
a_{1}^{k_2} & \ldots & a_{1} ^{k_m }\\ a_{2}^{k_1} &
a_{2}^{k_2} & \ldots & a_{2} ^{k_m }\\ \vdots & & & \vdots
\\ a_{m}^{k_1} & a_{m}^{k_2} & \ldots & a_{m} ^{k_m }
\end{matrix}\right) \left( \begin{matrix} \alpha_{n+1,k_1}
\\ \alpha_{n+1,k_2}\\ \vdots \\ \alpha_{n+1,k_m}
\end{matrix}\right) = \left( \begin{matrix} \beta_{n+1,1}
\\ \beta_{n+1,2} \\ \vdots \\ \beta_{n+1,m} \end{matrix}
\right) + \left( \begin{matrix} r_1 \\ r_2 \\ \vdots \\ r_m
\end{matrix} \right), \]
\[ \left( \begin{matrix} a_{1}^{k_1} &
a_{1}^{k_2} & \ldots & a_{1} ^{k_m }\\ a_{2}^{k_1} &
a_{2}^{k_2} & \ldots & a_{2} ^{k_m }\\ \vdots & & & \vdots
\\ a_{m}^{k_1} & a_{m}^{k_2} & \ldots & a_{m} ^{k_m }
\end{matrix}\right) \left( \begin{matrix} \alpha_{n+1,k_1}
\\ \alpha_{n+1,k_2}\\ \vdots \\ \alpha_{n+1,k_m}
\end{matrix}\right) = \left( \begin{matrix} \beta_{n+1,1}
\\ \beta_{n+1,2} \\ \vdots \\ \beta_{n+1,m} \end{matrix}
\right) + \left( \begin{matrix} r_1 \\ r_2 \\ \vdots \\ r_m
\end{matrix} \right), \]
where ![]() $r_i \in \mathbb {Q} \langle \mathcal {A}_{n+1} a_1 \cdots a_m \rangle$. The above matrix is invertible, since we are assuming that
$r_i \in \mathbb {Q} \langle \mathcal {A}_{n+1} a_1 \cdots a_m \rangle$. The above matrix is invertible, since we are assuming that ![]() $a_1, \ldots, a_m$ are algebraically independent. Thus,
$a_1, \ldots, a_m$ are algebraically independent. Thus, ![]() $\alpha _{n+1,k_1}, \ldots, \alpha _{n+1,k_m}$ are interdefinable with
$\alpha _{n+1,k_1}, \ldots, \alpha _{n+1,k_m}$ are interdefinable with ![]() $\beta _{n+1,1}, \ldots, \beta _{n+1,m}$ over
$\beta _{n+1,1}, \ldots, \beta _{n+1,m}$ over ![]() $\mathbb {Q} \langle \mathcal {A}_{n+1} a_1 \cdots a_m \rangle$. Since
$\mathbb {Q} \langle \mathcal {A}_{n+1} a_1 \cdots a_m \rangle$. Since ![]() $\{\beta _{i,j}:n+1< i\leq h, 1\leq j \leq m\}$ are contained in the field
$\{\beta _{i,j}:n+1< i\leq h, 1\leq j \leq m\}$ are contained in the field ![]() $\mathbb {Q} \langle \mathcal {A}_{n+1} a_1 \cdots a_m \rangle$, it follows that
$\mathbb {Q} \langle \mathcal {A}_{n+1} a_1 \cdots a_m \rangle$, it follows that ![]() $\beta _{n+1,1}, \ldots, \beta _{n+1,m}$ are independent and differentially transcendental over
$\beta _{n+1,1}, \ldots, \beta _{n+1,m}$ are independent and differentially transcendental over ![]() $\{\beta _{i,j}:n+1< i\leq h, 1\leq j \leq m\}$.
$\{\beta _{i,j}:n+1< i\leq h, 1\leq j \leq m\}$.
Putting together the above analysis, we have proved that the set of coefficients ![]() $\{\beta _{i,j}:0\leq i \leq h, 1\leq j \leq m\}$ are independent and differentially transcendental over
$\{\beta _{i,j}:0\leq i \leq h, 1\leq j \leq m\}$ are independent and differentially transcendental over ![]() $\mathbb {Q} \langle a_1, \ldots, a_m \rangle$ and thus over
$\mathbb {Q} \langle a_1, \ldots, a_m \rangle$ and thus over ![]() $\mathbb {Q}.$
$\mathbb {Q}.$
Eliminating the variable ![]() $y$ from
$y$ from ![]() $T^\Delta _{(\bar {a}, \alpha )}\big ( V^{[m]} \big )$ results in a system of
$T^\Delta _{(\bar {a}, \alpha )}\big ( V^{[m]} \big )$ results in a system of ![]() $m-1$ linear equations in
$m-1$ linear equations in ![]() $m$ variables as described in the following theorem.
$m$ variables as described in the following theorem.
Theorem 4.4 Consider a system of ![]() $m-1$ linear differential equations of order
$m-1$ linear differential equations of order ![]() $h$ in variables
$h$ in variables ![]() $(z_1,\ldots, z_m)$ of the form
$(z_1,\ldots, z_m)$ of the form
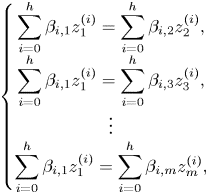 \begin{equation} \left\{ \begin{array}{@{}c} \displaystyle\sum_{i=0}^h \beta_{i,1} z_1^{(i)} = \sum_{i=0}^h \beta_{i,2} z_2^{(i)}, \\ \displaystyle\sum_{i=0}^h \beta_{i,1} z_1^{(i)} = \sum_{i=0}^h \beta_{i,3} z_3^{(i)}, \\ \vdots \\ \displaystyle\sum_{i=0}^h \beta_{i,1} z_1^{(i)} = \sum_{i=0}^h \beta_{i,m} z_m^{(i)}, \end{array} \right. \end{equation}
\begin{equation} \left\{ \begin{array}{@{}c} \displaystyle\sum_{i=0}^h \beta_{i,1} z_1^{(i)} = \sum_{i=0}^h \beta_{i,2} z_2^{(i)}, \\ \displaystyle\sum_{i=0}^h \beta_{i,1} z_1^{(i)} = \sum_{i=0}^h \beta_{i,3} z_3^{(i)}, \\ \vdots \\ \displaystyle\sum_{i=0}^h \beta_{i,1} z_1^{(i)} = \sum_{i=0}^h \beta_{i,m} z_m^{(i)}, \end{array} \right. \end{equation}
where the entire set of coefficients ![]() $\{\beta _{i,j}:0\leq i \leq h, 1\leq j \leq m\}$ are independent differential transcendentals. Then the solution set of such a system has no proper infinite-rank
$\{\beta _{i,j}:0\leq i \leq h, 1\leq j \leq m\}$ are independent differential transcendentals. Then the solution set of such a system has no proper infinite-rank ![]() $\mathcal {C}$-vector subspaces definable over
$\mathcal {C}$-vector subspaces definable over ![]() $\mathcal {U}$ for
$\mathcal {U}$ for ![]() $h>1$ and
$h>1$ and ![]() $m>1$.
$m>1$.
As in Lemma 4.2, we show that such a system has no infinite-rank subspaces by constructing a definable bijection to ![]() $\mathbb {A}^1(\mathcal {U})$. This is accomplished through two algorithms: Algorithm A will apply a sequence of linear substitutions which will lower the order of the top equation by one, and Algorithm B will apply Algorithm A inductively to reduce the number of equations and variables by one.
$\mathbb {A}^1(\mathcal {U})$. This is accomplished through two algorithms: Algorithm A will apply a sequence of linear substitutions which will lower the order of the top equation by one, and Algorithm B will apply Algorithm A inductively to reduce the number of equations and variables by one.
Algorithm A We begin with a system of equations of the form
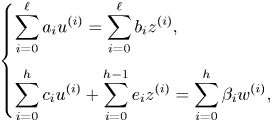 \[ \left\{ \begin{array}{@{}l} \displaystyle\sum_{i=0}^{\ell} a_i u^{(i)} = \sum_{i=0}^{\ell} b_i z^{(i)}, \\ \displaystyle\sum_{i=0}^h c_i u^{(i)} + \sum_{i=0}^{h-1} e_i z^{(i)} = \sum_{i=0}^h \beta_i w^{(i)}, \end{array} \right. \]
\[ \left\{ \begin{array}{@{}l} \displaystyle\sum_{i=0}^{\ell} a_i u^{(i)} = \sum_{i=0}^{\ell} b_i z^{(i)}, \\ \displaystyle\sum_{i=0}^h c_i u^{(i)} + \sum_{i=0}^{h-1} e_i z^{(i)} = \sum_{i=0}^h \beta_i w^{(i)}, \end{array} \right. \]
with ![]() $1\leq \ell \leq h$. We lower the order of the top equation by applying a trio of substitutions. The first substitution replaces the variable
$1\leq \ell \leq h$. We lower the order of the top equation by applying a trio of substitutions. The first substitution replaces the variable ![]() $u$ with
$u$ with ![]() $\tilde {u}$ where
$\tilde {u}$ where ![]() $u=\tilde {u} + ({b_\ell }/{a_\ell })z$, which reduces the order of
$u=\tilde {u} + ({b_\ell }/{a_\ell })z$, which reduces the order of ![]() $z$ in the top equation by one. This results in the new system:
$z$ in the top equation by one. This results in the new system:
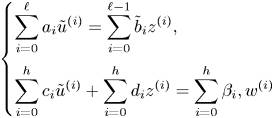 \[ \left\{ \begin{array}{@{}l} \displaystyle\sum_{i=0}^{\ell} a_i \tilde{u}^{(i)} = \sum_{i=0}^{\ell-1} \tilde{b}_i z^{(i)},\\ \displaystyle\sum_{i=0}^h c_i \tilde{u}^{(i)} + \sum_{i=0}^{h} d_i z^{(i)} = \sum_{i=0}^h \beta_i, w^{(i)} \end{array} \right. \]
\[ \left\{ \begin{array}{@{}l} \displaystyle\sum_{i=0}^{\ell} a_i \tilde{u}^{(i)} = \sum_{i=0}^{\ell-1} \tilde{b}_i z^{(i)},\\ \displaystyle\sum_{i=0}^h c_i \tilde{u}^{(i)} + \sum_{i=0}^{h} d_i z^{(i)} = \sum_{i=0}^h \beta_i, w^{(i)} \end{array} \right. \]
where
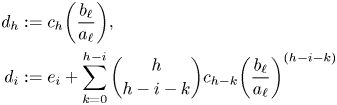 \begin{align*}d_h& :=
c_h\biggl(\frac{b_{\ell}}{a_{\ell}}\biggr),\\ d_{i}&:=
e_{i}+\sum_{k=0}^{h-i}\binom{h}{h-i-k}c_{h-k}\biggl(\frac{b_{\ell}}{a_\ell}\biggr)^{(h-i-k)}
\end{align*}
\begin{align*}d_h& :=
c_h\biggl(\frac{b_{\ell}}{a_{\ell}}\biggr),\\ d_{i}&:=
e_{i}+\sum_{k=0}^{h-i}\binom{h}{h-i-k}c_{h-k}\biggl(\frac{b_{\ell}}{a_\ell}\biggr)^{(h-i-k)}
\end{align*}
for ![]() $0\leq i \leq h-1$, and
$0\leq i \leq h-1$, and
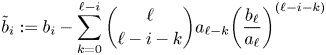 \[ \tilde{b}_{i}:= b_{i}-\sum_{k=0}^{\ell-i}\binom{\ell}{\ell-i-k}a_{\ell-k}\biggl( \frac{b_{\ell}}{a_{\ell}}\biggr)^{(\ell-i-k)} \]
\[ \tilde{b}_{i}:= b_{i}-\sum_{k=0}^{\ell-i}\binom{\ell}{\ell-i-k}a_{\ell-k}\biggl( \frac{b_{\ell}}{a_{\ell}}\biggr)^{(\ell-i-k)} \]
for ![]() $0\leq i \leq \ell -1$.
$0\leq i \leq \ell -1$.
The next substitution replaces ![]() $v$ with
$v$ with ![]() $\tilde {v}$, defined by
$\tilde {v}$, defined by ![]() $v=\tilde {v}+({d_{h}}/{\beta _{h}})z$, reducing the order of
$v=\tilde {v}+({d_{h}}/{\beta _{h}})z$, reducing the order of ![]() $z$ in the lower equation by one. This results in the system of equations
$z$ in the lower equation by one. This results in the system of equations
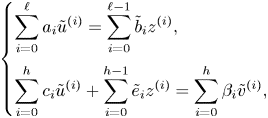 \[ \left\{ \begin{array}{@{}l}
\displaystyle\sum_{i=0}^{\ell} a_{i} \tilde{u}^{(i)} =
\sum_{i=0}^{\ell-1} \tilde{b}_{i} z^{(i)},\\
\displaystyle\sum_{i=0}^h c_{i} \tilde{u}^{(i)} +
\sum_{i=0}^{h-1} \tilde{e}_{i} z^{(i)} = \sum_{i=0}^h
\beta_{i} \tilde{v}^{(i)}, \end{array} \right.
\]
\[ \left\{ \begin{array}{@{}l}
\displaystyle\sum_{i=0}^{\ell} a_{i} \tilde{u}^{(i)} =
\sum_{i=0}^{\ell-1} \tilde{b}_{i} z^{(i)},\\
\displaystyle\sum_{i=0}^h c_{i} \tilde{u}^{(i)} +
\sum_{i=0}^{h-1} \tilde{e}_{i} z^{(i)} = \sum_{i=0}^h
\beta_{i} \tilde{v}^{(i)}, \end{array} \right.
\]
where
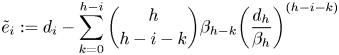 \[ \tilde{e}_{i}:= d_{i}- \sum_{k=0}^{h-i}\binom{h}{h-i-k}\beta_{h-k}\biggl(\frac{d_{h}}{\beta_{h}}\biggr)^{(h-i-k)} \]
\[ \tilde{e}_{i}:= d_{i}- \sum_{k=0}^{h-i}\binom{h}{h-i-k}\beta_{h-k}\biggl(\frac{d_{h}}{\beta_{h}}\biggr)^{(h-i-k)} \]
for ![]() $0\leq i \leq h-1$.
$0\leq i \leq h-1$.
To complete the trio, we substitute ![]() $\tilde {z}$ for
$\tilde {z}$ for ![]() $z$ defined by
$z$ defined by ![]() $z=\tilde {z}+({a_{\ell }}/{\tilde {b}_{\ell -1}})\tilde {u}'$. Now we have the system
$z=\tilde {z}+({a_{\ell }}/{\tilde {b}_{\ell -1}})\tilde {u}'$. Now we have the system
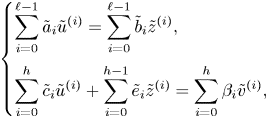 \[ \left\{ \begin{array}{@{}l} \displaystyle\sum_{i=0}^{\ell-1} \tilde{a}_{i} \tilde{u}^{(i)} = \sum_{i=0}^{\ell-1} \tilde{b}_{i} \tilde{z}^{(i)},\\ \displaystyle\sum_{i=0}^h \tilde{c}_{i} \tilde{u}^{(i)} + \sum_{i=0}^{h-1} \tilde{e}_{i} \tilde{z}^{(i)} = \sum_{i=0}^h \beta_{i} \tilde{v}^{(i)}, \end{array} \right. \]
\[ \left\{ \begin{array}{@{}l} \displaystyle\sum_{i=0}^{\ell-1} \tilde{a}_{i} \tilde{u}^{(i)} = \sum_{i=0}^{\ell-1} \tilde{b}_{i} \tilde{z}^{(i)},\\ \displaystyle\sum_{i=0}^h \tilde{c}_{i} \tilde{u}^{(i)} + \sum_{i=0}^{h-1} \tilde{e}_{i} \tilde{z}^{(i)} = \sum_{i=0}^h \beta_{i} \tilde{v}^{(i)}, \end{array} \right. \]
where
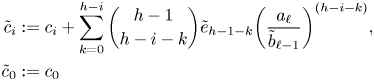 \begin{align*} \tilde{c}_{i}&:= c_{i} + \sum_{k=0}^{h-i} \binom{h-1}{h-i-k} \tilde{e}_{h-1-k} \biggl( \frac{a_{\ell}}{\tilde{b}_{\ell-1}}\biggr)^{(h-i-k)},\\ \tilde{c}_{0}&:=c_{0} \end{align*}
\begin{align*} \tilde{c}_{i}&:= c_{i} + \sum_{k=0}^{h-i} \binom{h-1}{h-i-k} \tilde{e}_{h-1-k} \biggl( \frac{a_{\ell}}{\tilde{b}_{\ell-1}}\biggr)^{(h-i-k)},\\ \tilde{c}_{0}&:=c_{0} \end{align*}
for ![]() $1\leq i \leq h$, and
$1\leq i \leq h$, and
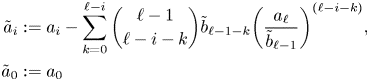 \begin{align*} \tilde{a}_{i}&:= a_{i}-\sum_{k=0}^{\ell-i}\binom{\ell-1}{\ell-i-k}\tilde{b}_{\ell-1-k}\biggl( \frac{a_{\ell}}{\tilde{b}_{\ell-1}}\biggr)^{(\ell-i-k)},\\ \tilde{a}_{0}&:=a_{0} \end{align*}
\begin{align*} \tilde{a}_{i}&:= a_{i}-\sum_{k=0}^{\ell-i}\binom{\ell-1}{\ell-i-k}\tilde{b}_{\ell-1-k}\biggl( \frac{a_{\ell}}{\tilde{b}_{\ell-1}}\biggr)^{(\ell-i-k)},\\ \tilde{a}_{0}&:=a_{0} \end{align*}
for ![]() $1\leq i\leq \ell -1$.
$1\leq i\leq \ell -1$.
We must first prove that each of these linear substitutions is well defined under the assumptions of Theorem 4.4, that is, that the coefficients ![]() $a_\ell$,
$a_\ell$, ![]() $\beta _h$, and
$\beta _h$, and ![]() $\tilde {b}_{\ell -1}$ which appear in the denominators of substitutions are all non-zero.
$\tilde {b}_{\ell -1}$ which appear in the denominators of substitutions are all non-zero.
Lemma 4.5 The tuple ![]() $(b_{i}, a_{i}:0\leq i \leq \ell )$ is interdefinable with
$(b_{i}, a_{i}:0\leq i \leq \ell )$ is interdefinable with ![]() $(b_\ell, a_\ell, \tilde {b}_{i}, \tilde {a}_{i}:0\leq i \leq \ell -1 )$ as defined in Algorithm A.
$(b_\ell, a_\ell, \tilde {b}_{i}, \tilde {a}_{i}:0\leq i \leq \ell -1 )$ as defined in Algorithm A.
Proof. It is clear from the definition of ![]() $\tilde {b}_{i}$ that
$\tilde {b}_{i}$ that ![]() $(b_{i}:0\leq i \leq \ell -1)$ is interdefinable with
$(b_{i}:0\leq i \leq \ell -1)$ is interdefinable with ![]() $(\tilde {b}_{i}:0\leq i \leq \ell -1)$ over
$(\tilde {b}_{i}:0\leq i \leq \ell -1)$ over ![]() $b_\ell$ and
$b_\ell$ and ![]() $\{a_{i}:0\leq i \leq \ell \}$. By adding the parameters themselves, we have that
$\{a_{i}:0\leq i \leq \ell \}$. By adding the parameters themselves, we have that ![]() $(b_{i}, a_{i}:0\leq i \leq \ell )$ is interdefinable with
$(b_{i}, a_{i}:0\leq i \leq \ell )$ is interdefinable with ![]() $(b_{\ell }, \tilde {b}_{i}:0\leq i \leq \ell -1)\cup ( a_{i}:0\leq i \leq \ell )$. It is also clear from the definition of
$(b_{\ell }, \tilde {b}_{i}:0\leq i \leq \ell -1)\cup ( a_{i}:0\leq i \leq \ell )$. It is also clear from the definition of ![]() $\tilde {a}_{i}$ that
$\tilde {a}_{i}$ that ![]() $(a_{i}: 0\leq i \leq \ell -1)$ is interdefinable with
$(a_{i}: 0\leq i \leq \ell -1)$ is interdefinable with ![]() $(\tilde {a}_{i}:0\leq i \leq \ell -1)$ over
$(\tilde {a}_{i}:0\leq i \leq \ell -1)$ over ![]() $a_{\ell }$ and
$a_{\ell }$ and ![]() $\{\tilde {b}_{i}:0\leq i \leq \ell -1\}$. Combining these two facts, we conclude that the desired tuples are interdefinable.
$\{\tilde {b}_{i}:0\leq i \leq \ell -1\}$. Combining these two facts, we conclude that the desired tuples are interdefinable.
Assuming the initial coefficients ![]() $\{a_i,b_i:0\leq i \leq \ell \}\cup \{\beta _i:0\leq i \leq h\}$ constitute an independent set of differential transcendentals, Lemma 4.5 shows that
$\{a_i,b_i:0\leq i \leq \ell \}\cup \{\beta _i:0\leq i \leq h\}$ constitute an independent set of differential transcendentals, Lemma 4.5 shows that ![]() $\{\tilde {a}_i,\tilde {b}_i:0\leq i \leq \ell -1\}\cup \{\beta _i:0\leq i \leq h\}\cup \{a_\ell,b_\ell \}$ are also independent differential transcendentals, and hence non-zero. It follows that the substitutions in Algorithm A are well defined as long as the initial coefficients have this property.
$\{\tilde {a}_i,\tilde {b}_i:0\leq i \leq \ell -1\}\cup \{\beta _i:0\leq i \leq h\}\cup \{a_\ell,b_\ell \}$ are also independent differential transcendentals, and hence non-zero. It follows that the substitutions in Algorithm A are well defined as long as the initial coefficients have this property.
Lemma 4.6 Suppose that ![]() $(e_i:0\leq i \leq h-1)$ is differentially algebraic over
$(e_i:0\leq i \leq h-1)$ is differentially algebraic over ![]() $\{c_i:0\leq i \leq h\}\cup \{a_\ell, b_\ell, \tilde {a}_{\ell -1}, \tilde {b}_{\ell -1}, \}\cup \{\beta _i:0 \leq i \leq h\}$. Then
$\{c_i:0\leq i \leq h\}\cup \{a_\ell, b_\ell, \tilde {a}_{\ell -1}, \tilde {b}_{\ell -1}, \}\cup \{\beta _i:0 \leq i \leq h\}$. Then ![]() $(c_i:0\leq i \leq h)$ is interdifferentially algebraic with
$(c_i:0\leq i \leq h)$ is interdifferentially algebraic with ![]() $(\tilde {c}_i:0\leq i \leq h)$ over
$(\tilde {c}_i:0\leq i \leq h)$ over ![]() $\{a_i,b_i:0\leq i \leq \ell \}\cup \{\beta _i:0\leq i \leq \ell \}$, and
$\{a_i,b_i:0\leq i \leq \ell \}\cup \{\beta _i:0\leq i \leq \ell \}$, and ![]() $(\tilde {e}_i:0\leq i \leq h-1)$ is differentially algebraic over
$(\tilde {e}_i:0\leq i \leq h-1)$ is differentially algebraic over ![]() $\{\tilde {c}_i:0\leq i \leq h\}\cup \{a_\ell, b_\ell, \tilde {a}_{\ell -1}, \tilde {b}_{\ell -1}, \}\cup \{\beta _i:0 \leq i \leq h\}$.
$\{\tilde {c}_i:0\leq i \leq h\}\cup \{a_\ell, b_\ell, \tilde {a}_{\ell -1}, \tilde {b}_{\ell -1}, \}\cup \{\beta _i:0 \leq i \leq h\}$.
Proof. From the definitions, it is clear that ![]() $(\tilde {c}_i:0\leq i \leq h)$ is differentially algebraic over
$(\tilde {c}_i:0\leq i \leq h)$ is differentially algebraic over ![]() $(c_i:0\leq i \leq h)$. To prove the other direction, we combine the definitions of
$(c_i:0\leq i \leq h)$. To prove the other direction, we combine the definitions of ![]() $\tilde {c}_i$,
$\tilde {c}_i$, ![]() $\tilde {e}_i$, and
$\tilde {e}_i$, and ![]() $d_i$, and we can write
$d_i$, and we can write ![]() $\tilde {c}_i$ in terms of
$\tilde {c}_i$ in terms of ![]() $(c_i:0\leq i \leq h)$ (as well as other terms). Doing this for
$(c_i:0\leq i \leq h)$ (as well as other terms). Doing this for ![]() $\tilde {c}_h$ (and performing some simplifications), we have
$\tilde {c}_h$ (and performing some simplifications), we have
Doing the same to the other ![]() $\tilde {c}$s, we see that
$\tilde {c}$s, we see that ![]() $c_h$ appears with order at least one, but each
$c_h$ appears with order at least one, but each ![]() $c_i$ is order zero and linear over
$c_i$ is order zero and linear over ![]() $\mathbb {Q}\langle a_\ell, \tilde {a}_{\ell -1},b_\ell, \tilde {b}_{\ell -1}\rangle$ for
$\mathbb {Q}\langle a_\ell, \tilde {a}_{\ell -1},b_\ell, \tilde {b}_{\ell -1}\rangle$ for ![]() $i< h$. This is represented in the following matrix equation:
$i< h$. This is represented in the following matrix equation:
 \begin{equation} \begin{bmatrix} M_1 & M_0 & 0 & \cdots & 0 & 0 & 0 & 0\\ M_2 & M_1 & M_0 & \cdots & 0 & 0 & 0 & 0\\ M_3 & M_2 & M_1 & \cdots & 0 & 0 & 0 & 0\\ \vdots & \vdots & \vdots & \ddots & \vdots & \vdots & \vdots & \vdots\\ M_{h-3} & M_{h-4} & M_{h-5} & \cdots & M_1 & M_0 & 0 & 0\\ M_{h-2} & M_{h-3} & M_{h-4} & \cdots & M_2 & M_1 & M_0 & 0\\ M_{h-1} & M_{h-2} & M_{h-3} & \cdots & M_3 & M_2 & M_1 & M_0\\ 0 & 0 & 0 & \cdots & 0 & 0 & 0 & 1 \end{bmatrix} \begin{bmatrix} c_{h-1} \\ c_{h-2} \\ c_{h-3} \\ \vdots \\ c_{3} \\ c_{2} \\ c_{1} \\ c_{0} \end{bmatrix} = \begin{bmatrix} \tilde{c}_{h-1} \\ \tilde{c}_{h-2} \\ \tilde{c}_{h-3} \\ \vdots \\ \tilde{c}_{3} \\ \tilde{c}_{2} \\ \tilde{c}_{1} \\ \tilde{c}_{0} \end{bmatrix} - \begin{bmatrix} L_{h-1} \\ L_{h-2} \\ L_{h-3} \\ \vdots \\ L_{3} \\ L_{2} \\ L_{1} \\ 0 \end{bmatrix}, \end{equation}
\begin{equation} \begin{bmatrix} M_1 & M_0 & 0 & \cdots & 0 & 0 & 0 & 0\\ M_2 & M_1 & M_0 & \cdots & 0 & 0 & 0 & 0\\ M_3 & M_2 & M_1 & \cdots & 0 & 0 & 0 & 0\\ \vdots & \vdots & \vdots & \ddots & \vdots & \vdots & \vdots & \vdots\\ M_{h-3} & M_{h-4} & M_{h-5} & \cdots & M_1 & M_0 & 0 & 0\\ M_{h-2} & M_{h-3} & M_{h-4} & \cdots & M_2 & M_1 & M_0 & 0\\ M_{h-1} & M_{h-2} & M_{h-3} & \cdots & M_3 & M_2 & M_1 & M_0\\ 0 & 0 & 0 & \cdots & 0 & 0 & 0 & 1 \end{bmatrix} \begin{bmatrix} c_{h-1} \\ c_{h-2} \\ c_{h-3} \\ \vdots \\ c_{3} \\ c_{2} \\ c_{1} \\ c_{0} \end{bmatrix} = \begin{bmatrix} \tilde{c}_{h-1} \\ \tilde{c}_{h-2} \\ \tilde{c}_{h-3} \\ \vdots \\ \tilde{c}_{3} \\ \tilde{c}_{2} \\ \tilde{c}_{1} \\ \tilde{c}_{0} \end{bmatrix} - \begin{bmatrix} L_{h-1} \\ L_{h-2} \\ L_{h-3} \\ \vdots \\ L_{3} \\ L_{2} \\ L_{1} \\ 0 \end{bmatrix}, \end{equation}
where ![]() $L_i\in \mathbb {Q}\langle \{c_{h},a_{\ell },b_{\ell },\tilde {a}_{\ell -1}, \tilde {b}_{\ell -1}\}\cup \{\beta _i:0 \leq i \leq h\}\cup \{e_i:0\leq i \leq h-1\}\rangle$. The matrix entries can be computed as follows:
$L_i\in \mathbb {Q}\langle \{c_{h},a_{\ell },b_{\ell },\tilde {a}_{\ell -1}, \tilde {b}_{\ell -1}\}\cup \{\beta _i:0 \leq i \leq h\}\cup \{e_i:0\leq i \leq h-1\}\rangle$. The matrix entries can be computed as follows:
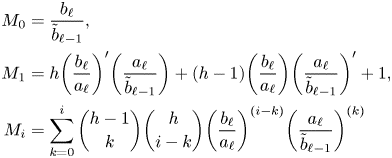 \begin{align*} M_0 &= \frac{b_{\ell}}{\tilde{b}_{\ell-1}},\\ M_1 &= h \biggl(\frac{b_{\ell}}{a_{\ell}}\biggr)' \biggl(\frac{a_{\ell}}{\tilde{b}_{\ell-1}}\biggr) + (h-1)\biggl(\frac{b_{\ell}}{a_{\ell}}\biggr)\biggl(\frac{a_{\ell}}{\tilde{b}_{\ell-1}}\biggr)'+1,\\ M_i &= \sum_{k=0}^i\binom{h-1}{k}\binom{h}{i-k}\biggl(\frac{b_{\ell}}{a_{\ell}}\biggr)^{(i-k)} \biggl(\frac{a_{\ell}}{\tilde{b}_{\ell-1}}\biggr)^{(k)} \end{align*}
\begin{align*} M_0 &= \frac{b_{\ell}}{\tilde{b}_{\ell-1}},\\ M_1 &= h \biggl(\frac{b_{\ell}}{a_{\ell}}\biggr)' \biggl(\frac{a_{\ell}}{\tilde{b}_{\ell-1}}\biggr) + (h-1)\biggl(\frac{b_{\ell}}{a_{\ell}}\biggr)\biggl(\frac{a_{\ell}}{\tilde{b}_{\ell-1}}\biggr)'+1,\\ M_i &= \sum_{k=0}^i\binom{h-1}{k}\binom{h}{i-k}\biggl(\frac{b_{\ell}}{a_{\ell}}\biggr)^{(i-k)} \biggl(\frac{a_{\ell}}{\tilde{b}_{\ell-1}}\biggr)^{(k)} \end{align*}
for ![]() $i>1$. Using Gaussian elimination, we can make this matrix lower triangular:
$i>1$. Using Gaussian elimination, we can make this matrix lower triangular:
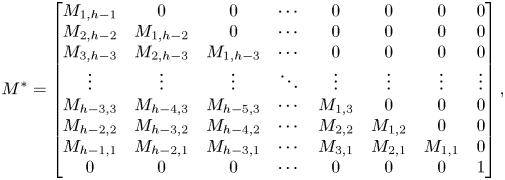 \[ M^*=\begin{bmatrix} M_{1,h-1} & 0 & 0 & \cdots & 0 & 0 & 0 & 0\\ M_{2,h-2} & M_{1,h-2} & 0 & \cdots & 0 & 0 & 0 & 0\\ M_{3,h-3} & M_{2,h-3} & M_{1,h-3} & \cdots & 0 & 0 & 0 & 0\\ \vdots & \vdots & \vdots & \ddots & \vdots & \vdots & \vdots & \vdots\\ M_{h-3,3} & M_{h-4,3} & M_{h-5,3} & \cdots & M_{1,3} & 0 & 0 & 0\\ M_{h-2,2} & M_{h-3,2} & M_{h-4,2} & \cdots & M_{2,2} & M_{1,2} & 0 & 0\\ M_{h-1,1} & M_{h-2,1} & M_{h-3,1} & \cdots & M_{3,1} & M_{2,1} & M_{1,1} & 0\\ 0 & 0 & 0 & \cdots & 0 & 0 & 0 & 1 \end{bmatrix}, \]
\[ M^*=\begin{bmatrix} M_{1,h-1} & 0 & 0 & \cdots & 0 & 0 & 0 & 0\\ M_{2,h-2} & M_{1,h-2} & 0 & \cdots & 0 & 0 & 0 & 0\\ M_{3,h-3} & M_{2,h-3} & M_{1,h-3} & \cdots & 0 & 0 & 0 & 0\\ \vdots & \vdots & \vdots & \ddots & \vdots & \vdots & \vdots & \vdots\\ M_{h-3,3} & M_{h-4,3} & M_{h-5,3} & \cdots & M_{1,3} & 0 & 0 & 0\\ M_{h-2,2} & M_{h-3,2} & M_{h-4,2} & \cdots & M_{2,2} & M_{1,2} & 0 & 0\\ M_{h-1,1} & M_{h-2,1} & M_{h-3,1} & \cdots & M_{3,1} & M_{2,1} & M_{1,1} & 0\\ 0 & 0 & 0 & \cdots & 0 & 0 & 0 & 1 \end{bmatrix}, \]
where the new matrix entries can be computed recursively for ![]() $2\leq j\leq h-1$ and
$2\leq j\leq h-1$ and ![]() $1\leq i \leq h-j$:
$1\leq i \leq h-j$:
Claim 4.7 For all ![]() $1\leq j\leq h-1$ and
$1\leq j\leq h-1$ and ![]() $1\leq i \leq h-j$,
$1\leq i \leq h-j$, ![]() $M_{i,j}\neq 0$, and therefore, the determinant of
$M_{i,j}\neq 0$, and therefore, the determinant of ![]() $M^*$ is non-zero.
$M^*$ is non-zero.
Proof. We prove this by showing that ![]() $M_{i,j}$ is order
$M_{i,j}$ is order ![]() $i+j-1$ in
$i+j-1$ in ![]() $a_{\ell }$ using induction on
$a_{\ell }$ using induction on ![]() $j$. It follows from Claim 4.5 that
$j$. It follows from Claim 4.5 that ![]() $M_{i,1}$ is order
$M_{i,1}$ is order ![]() $i$ in
$i$ in ![]() $a_{\ell }$ for each
$a_{\ell }$ for each ![]() $i$. Now suppose the claim holds for
$i$. Now suppose the claim holds for ![]() $j$. Since
$j$. Since ![]() $M_{i,j+1}=M_{i}-({M_0}/{M_{1,j}}) M_{i+1,j}$, we can see that
$M_{i,j+1}=M_{i}-({M_0}/{M_{1,j}}) M_{i+1,j}$, we can see that ![]() $M_{i,j+1}$ is order
$M_{i,j+1}$ is order ![]() $i+j$ since
$i+j$ since ![]() $M_{i+1,j}$ is order
$M_{i+1,j}$ is order ![]() $i+j$ by assumption, and all other terms in the definition have strictly smaller order. Thus the determinant is non-zero.
$i+j$ by assumption, and all other terms in the definition have strictly smaller order. Thus the determinant is non-zero.
Since ![]() $M^*$ is non-singular, it follows also that the original matrix in (6) is non-singular. Therefore,
$M^*$ is non-singular, it follows also that the original matrix in (6) is non-singular. Therefore, ![]() $(c_{i}:0\leq i \leq h-1)$ and
$(c_{i}:0\leq i \leq h-1)$ and ![]() $(\tilde {c}_{i}:0\leq i \leq h-1)$ are interdefinable over
$(\tilde {c}_{i}:0\leq i \leq h-1)$ are interdefinable over ![]() $\{c_{h},a_{\ell },b_{\ell },\tilde {a}_{\ell -1}, \tilde {b}_{\ell -1}\}\cup \{\beta _i:0 \leq i \leq h\}\cup \{e_i:0\leq i \leq h-1\}$.
$\{c_{h},a_{\ell },b_{\ell },\tilde {a}_{\ell -1}, \tilde {b}_{\ell -1}\}\cup \{\beta _i:0 \leq i \leq h\}\cup \{e_i:0\leq i \leq h-1\}$.
Turning our attention once more to (5), we use this interdefinability to substitute ![]() $c_{h-1}$ for an expression involving
$c_{h-1}$ for an expression involving ![]() $c_h$ and
$c_h$ and ![]() $(\tilde {c}_i:0\leq i \leq h)$. The resulting equation establishes a differential relation between
$(\tilde {c}_i:0\leq i \leq h)$. The resulting equation establishes a differential relation between ![]() $c_h$ and
$c_h$ and ![]() $(\tilde {c}_i:0\leq i \leq h)$. It follows that
$(\tilde {c}_i:0\leq i \leq h)$. It follows that ![]() $(c_i:0\leq i \leq h)$ is differentially algebraic over
$(c_i:0\leq i \leq h)$ is differentially algebraic over ![]() $\tilde {c}_i:0\leq i \leq h)$ along with
$\tilde {c}_i:0\leq i \leq h)$ along with ![]() $\{a_\ell, b_\ell, \tilde {a}_{\ell -1}, \tilde {b}_{\ell -1}\}\cup \{\beta _i:0 \leq i \leq h\}\cup \{e_i:0\leq i \leq h-1\}$. By assumption,
$\{a_\ell, b_\ell, \tilde {a}_{\ell -1}, \tilde {b}_{\ell -1}\}\cup \{\beta _i:0 \leq i \leq h\}\cup \{e_i:0\leq i \leq h-1\}$. By assumption, ![]() $(e_i:0\leq i \leq h-1)$ is identically 0 or differentially algebraic over
$(e_i:0\leq i \leq h-1)$ is identically 0 or differentially algebraic over ![]() $\{c_i:0\leq i \leq h\}\cup \{a_\ell, b_\ell, \tilde {a}_{\ell -1}, \tilde {b}_{\ell -1}, \}\cup \{\beta _i:0 \leq i \leq h\}$. In either case, it follows that
$\{c_i:0\leq i \leq h\}\cup \{a_\ell, b_\ell, \tilde {a}_{\ell -1}, \tilde {b}_{\ell -1}, \}\cup \{\beta _i:0 \leq i \leq h\}$. In either case, it follows that ![]() $(c_i:0\leq i \leq h)$ and
$(c_i:0\leq i \leq h)$ and ![]() $\tilde {c}_i:0\leq i \leq h)$ are interdifferentially algebraic over
$\tilde {c}_i:0\leq i \leq h)$ are interdifferentially algebraic over ![]() $\{a_\ell, b_\ell, \tilde {a}_{\ell -1}, \tilde {b}_{\ell -1}\}\cup \{\beta _i:0 \leq i \leq h\}$.
$\{a_\ell, b_\ell, \tilde {a}_{\ell -1}, \tilde {b}_{\ell -1}\}\cup \{\beta _i:0 \leq i \leq h\}$.
So that this lemma can be applied inductively, we show that ![]() $(\tilde {e}_i:0\leq i \leq h-1)$ is differentially algebraic over
$(\tilde {e}_i:0\leq i \leq h-1)$ is differentially algebraic over ![]() $\{\tilde {c}_i:0\leq i \leq h\}\cup \{a_\ell, b_\ell, \tilde {a}_{\ell -1}, \tilde {b}_{\ell -1}, \}\cup \{\beta _i:0 \leq i \leq h\}$. If
$\{\tilde {c}_i:0\leq i \leq h\}\cup \{a_\ell, b_\ell, \tilde {a}_{\ell -1}, \tilde {b}_{\ell -1}, \}\cup \{\beta _i:0 \leq i \leq h\}$. If ![]() $e_i=0$ for all
$e_i=0$ for all ![]() $i$, this result follows from the definition of
$i$, this result follows from the definition of ![]() $\tilde {e}_i$. Suppose otherwise, and we can see that
$\tilde {e}_i$. Suppose otherwise, and we can see that ![]() $\tilde {e}_{i}$ is defined by
$\tilde {e}_{i}$ is defined by ![]() $(c_{i}:0\leq i\leq h)$,
$(c_{i}:0\leq i\leq h)$, ![]() $(e_{i}:0\leq i\leq h-1)$, and
$(e_{i}:0\leq i\leq h-1)$, and ![]() $\{a_\ell, b_\ell, \tilde {b}_{\ell -1}, \tilde {a}_{\ell -1}\}\cup \{\beta _i:0 \leq i \leq h\}$. By assumption on
$\{a_\ell, b_\ell, \tilde {b}_{\ell -1}, \tilde {a}_{\ell -1}\}\cup \{\beta _i:0 \leq i \leq h\}$. By assumption on ![]() $e_i$, we can see that
$e_i$, we can see that ![]() $(\tilde {e}_{i}:0\leq i\leq h-1)$ is differentially algebraic over
$(\tilde {e}_{i}:0\leq i\leq h-1)$ is differentially algebraic over ![]() $(c_{i}:0\leq i\leq h)$ and
$(c_{i}:0\leq i\leq h)$ and ![]() $\{a_\ell, b_\ell, \tilde {b}_{\ell -1}, \tilde {a}_{\ell -1}\}\cup \{\beta _i:0 \leq i \leq h\}$. We have already shown that
$\{a_\ell, b_\ell, \tilde {b}_{\ell -1}, \tilde {a}_{\ell -1}\}\cup \{\beta _i:0 \leq i \leq h\}$. We have already shown that ![]() $(c_{i}:0\leq i\leq h)$ and
$(c_{i}:0\leq i\leq h)$ and ![]() $(\tilde {c}_{i}:0\leq i\leq h)$ are interdifferentially algebraic, so
$(\tilde {c}_{i}:0\leq i\leq h)$ are interdifferentially algebraic, so ![]() $(\tilde {e}_{i}:0\leq i\leq h-1)$ is differentially algebraic over
$(\tilde {e}_{i}:0\leq i\leq h-1)$ is differentially algebraic over ![]() $(\tilde {c}_{i}:0\leq i\leq h)$, and
$(\tilde {c}_{i}:0\leq i\leq h)$, and ![]() $\{a_\ell, b_\ell, \tilde {b}_{\ell -1}, \tilde {a}_{\ell -1}\}\cup \{\beta _i:0 \leq i \leq h\}$.
$\{a_\ell, b_\ell, \tilde {b}_{\ell -1}, \tilde {a}_{\ell -1}\}\cup \{\beta _i:0 \leq i \leq h\}$.
Algorithm B We begin with a system of equations of the form
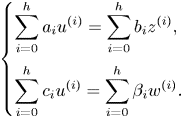 \begin{equation} \left\{
\begin{array}{@{}l} \displaystyle\sum_{i=0}^{h} a_i u^{(i)} =
\sum_{i=0}^{h} b_i z^{(i)}, \\
\displaystyle\sum_{i=0}^h c_i u^{(i)} = \sum_{i=0}^h
\beta_i w^{(i)}. \\ \end{array} \right.
\end{equation}
\begin{equation} \left\{
\begin{array}{@{}l} \displaystyle\sum_{i=0}^{h} a_i u^{(i)} =
\sum_{i=0}^{h} b_i z^{(i)}, \\
\displaystyle\sum_{i=0}^h c_i u^{(i)} = \sum_{i=0}^h
\beta_i w^{(i)}. \\ \end{array} \right.
\end{equation} Algorithm B will eliminate the top equation in this system by first applying Algorithm A ![]() $h$ times, reducing the order of the top equation to zero:
$h$ times, reducing the order of the top equation to zero:
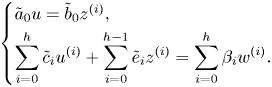 \[ \left\{ \begin{array}{@{}l} \tilde{a}_0
u = \tilde{b}_0 z^{(i)}, \\ \displaystyle
\sum_{i=0}^h \tilde{c}_i u^{(i)} + \sum_{i=0}^{h-1}
\tilde{e}_i z^{(i)} = \sum_{i=0}^h \beta_i
w^{(i)}. \end{array} \right. \]
\[ \left\{ \begin{array}{@{}l} \tilde{a}_0
u = \tilde{b}_0 z^{(i)}, \\ \displaystyle
\sum_{i=0}^h \tilde{c}_i u^{(i)} + \sum_{i=0}^{h-1}
\tilde{e}_i z^{(i)} = \sum_{i=0}^h \beta_i
w^{(i)}. \end{array} \right. \]
Finally, ![]() $z=({\tilde {a}_0}/{\tilde {b}_0})u$, so we substitute this expression for
$z=({\tilde {a}_0}/{\tilde {b}_0})u$, so we substitute this expression for ![]() $z$ in the lower equation, eliminating
$z$ in the lower equation, eliminating ![]() $z$ from the system:
$z$ from the system:
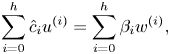 \begin{equation} \sum_{i=0}^h \hat{c}_i u^{(i)} = \sum_{i=0}^h \beta_i w^{(i)}, \end{equation}
\begin{equation} \sum_{i=0}^h \hat{c}_i u^{(i)} = \sum_{i=0}^h \beta_i w^{(i)}, \end{equation}where
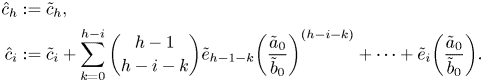 \begin{align*} \hat{c}_{h}&:=\tilde{c}_{h},\\ \hat{c}_{i}&:=\tilde{c}_{i}+\sum_{k=0}^{h-i} \binom{h-1}{h-i-k}\tilde{e}_{h-1-k}\biggl(\frac{\tilde{a}_{0}}{\tilde{b}_{0}}\biggr)^{(h-i-k)}+ \cdots + \tilde{e}_{i}\biggl(\frac{\tilde{a}_{0}}{\tilde{b}_{0}}\biggr). \end{align*}
\begin{align*} \hat{c}_{h}&:=\tilde{c}_{h},\\ \hat{c}_{i}&:=\tilde{c}_{i}+\sum_{k=0}^{h-i} \binom{h-1}{h-i-k}\tilde{e}_{h-1-k}\biggl(\frac{\tilde{a}_{0}}{\tilde{b}_{0}}\biggr)^{(h-i-k)}+ \cdots + \tilde{e}_{i}\biggl(\frac{\tilde{a}_{0}}{\tilde{b}_{0}}\biggr). \end{align*}
Lemma 4.8 For ![]() $a_i$,
$a_i$, ![]() $b_i$,
$b_i$, ![]() $c_i$,
$c_i$, ![]() $\hat {c}_i$, and
$\hat {c}_i$, and ![]() $\beta _i$ as defined in Algorithm B, suppose
$\beta _i$ as defined in Algorithm B, suppose ![]() $\{a_i, b_i, \beta _i:0\leq i \leq h\}$ is an independent set of differential transcendentals and suppose
$\{a_i, b_i, \beta _i:0\leq i \leq h\}$ is an independent set of differential transcendentals and suppose ![]() $(a_i:0\leq i \leq h)$ and
$(a_i:0\leq i \leq h)$ and ![]() $(c_i:0\leq i \leq h)$ are interdifferentially algebraic over the other coefficients
$(c_i:0\leq i \leq h)$ are interdifferentially algebraic over the other coefficients ![]() $\{b_i, \beta _i:0\leq i \leq h\}$. Then
$\{b_i, \beta _i:0\leq i \leq h\}$. Then ![]() ${(c_i:0\leq i \leq h)}$ and
${(c_i:0\leq i \leq h)}$ and ![]() $(\hat {c}_i:0\leq i \leq h)$ are interdifferentially algebraic over
$(\hat {c}_i:0\leq i \leq h)$ are interdifferentially algebraic over ![]() $\{b_i, \beta _i:0\leq i \leq h\}$.
$\{b_i, \beta _i:0\leq i \leq h\}$.
Proof. By Lemmas 4.6 and 4.5, we see that ![]() $(c_i:0\leq i \leq h)$ is interdifferentially algebraic with
$(c_i:0\leq i \leq h)$ is interdifferentially algebraic with ![]() $(\tilde {c}_i:0\leq i \leq h)$ over
$(\tilde {c}_i:0\leq i \leq h)$ over ![]() $\{a_i,b_i:0\leq i \leq h\}\cup \{\beta _i:0\leq i \leq \ell \}$. Since
$\{a_i,b_i:0\leq i \leq h\}\cup \{\beta _i:0\leq i \leq \ell \}$. Since ![]() $(a_i:0\leq i \leq h )$ is interdifferentially algebraic with
$(a_i:0\leq i \leq h )$ is interdifferentially algebraic with ![]() $(c_i:0\leq i \leq h)$ by assumption, it follows that
$(c_i:0\leq i \leq h)$ by assumption, it follows that ![]() $(c_i:0\leq i \leq h)$ is interdifferentially algebraic with
$(c_i:0\leq i \leq h)$ is interdifferentially algebraic with ![]() $(\tilde {c}_i:0\leq i \leq h)$ over
$(\tilde {c}_i:0\leq i \leq h)$ over ![]() $\{b_i:0\leq i \leq h\}\cup \{\beta _i:0\leq i \leq \ell \}$. Consequently,
$\{b_i:0\leq i \leq h\}\cup \{\beta _i:0\leq i \leq \ell \}$. Consequently, ![]() $(\tilde {c}_i:0\leq i \leq h)$ is independent over
$(\tilde {c}_i:0\leq i \leq h)$ is independent over ![]() $\{b_i:0\leq i \leq h\}\cup \{\beta _i:0\leq i \leq \ell \}$.
$\{b_i:0\leq i \leq h\}\cup \{\beta _i:0\leq i \leq \ell \}$.
It follows from the definition that ![]() $(\tilde {c}_{i}:0\leq i \leq h)$ is interdefinable with
$(\tilde {c}_{i}:0\leq i \leq h)$ is interdefinable with ![]() $(\hat {c}_{i}:0\leq i \leq h)$ over
$(\hat {c}_{i}:0\leq i \leq h)$ over ![]() $\{a_{i}, b_{i}:0\leq i\leq h, \}\cup \{\beta _i:0 \leq i \leq h\}\cup \{\tilde {e}_{i}:0\leq i\leq h-1\}$. By Lemma 4.6,
$\{a_{i}, b_{i}:0\leq i\leq h, \}\cup \{\beta _i:0 \leq i \leq h\}\cup \{\tilde {e}_{i}:0\leq i\leq h-1\}$. By Lemma 4.6, ![]() $(\tilde {e}_{i}:0\leq i\leq h-1)$ is differentially algebraic over
$(\tilde {e}_{i}:0\leq i\leq h-1)$ is differentially algebraic over ![]() $\{\tilde {c}_i:0\leq i \leq h\}\cup \{a_i,b_i:0\leq i \leq h\}\cup \{\beta _i:0 \leq i \leq h\}$, and we have already seen that
$\{\tilde {c}_i:0\leq i \leq h\}\cup \{a_i,b_i:0\leq i \leq h\}\cup \{\beta _i:0 \leq i \leq h\}$, and we have already seen that ![]() $(a_i:0\leq i \leq h)$ is interdifferentially algebraic with
$(a_i:0\leq i \leq h)$ is interdifferentially algebraic with ![]() $(\tilde {c}_i:0\leq i \leq h)$. Thus,
$(\tilde {c}_i:0\leq i \leq h)$. Thus, ![]() $(\hat {c}_{i}:0\leq i \leq h)$ is interdefinable with
$(\hat {c}_{i}:0\leq i \leq h)$ is interdefinable with ![]() $(\tilde {c}_{i}:0\leq i \leq h)$, and hence with
$(\tilde {c}_{i}:0\leq i \leq h)$, and hence with ![]() $(c_i:0\leq i \leq h)$ over
$(c_i:0\leq i \leq h)$ over ![]() $\{b_i:0\leq i \leq h\}\cup \{\beta _i:0\leq i \leq \ell \}$.
$\{b_i:0\leq i \leq h\}\cup \{\beta _i:0\leq i \leq \ell \}$.
Remark 4.9 Due to the nature of the substitutions defining Algorithms A and B, only coefficients from the first equation influence the lower equation, and not vice versa. For simplicity, Algorithms A and B have been defined for systems of two equations, although due to this lack of interaction these algorithms can be easily applied to systems of many equations. The only change that need be made is that an analogous form of the middle substitution in Algorithm A must be applied to all lower equations simultaneously (lowering the order of ![]() $z$ in all of these equations by one).
$z$ in all of these equations by one).
Using Lemma 4.8, we can apply Algorithm B recursively to system (4) until all but one variables have been eliminated. This results in a definable bijection between system (4) and ![]() $\mathbb {A}^1(\mathcal {U})$, resulting in a proof of Theorem 4.4.
$\mathbb {A}^1(\mathcal {U})$, resulting in a proof of Theorem 4.4.
Proof of Theorem 1.3 Let ![]() $f(x)$ be a generic differential polynomial of order
$f(x)$ be a generic differential polynomial of order ![]() $h>1$ and degree
$h>1$ and degree ![]() $d$. Let
$d$. Let ![]() $\bar {a}$ be the coefficients of
$\bar {a}$ be the coefficients of ![]() $f$ and let
$f$ and let ![]() $p$ be the type of a generic solution to
$p$ be the type of a generic solution to ![]() $f(x)=0$. Suppose that
$f(x)=0$. Suppose that ![]() $d\geq 2 \cdot (\operatorname {nmdeg}(p)+1)$. Let
$d\geq 2 \cdot (\operatorname {nmdeg}(p)+1)$. Let ![]() $\bar {a}=(a_1,\ldots a_m)$ be realizations of
$\bar {a}=(a_1,\ldots a_m)$ be realizations of ![]() $p$ which are algebraically independent over
$p$ which are algebraically independent over ![]() $\mathbb {Q}\langle \bar {\alpha }\rangle$ where
$\mathbb {Q}\langle \bar {\alpha }\rangle$ where ![]() $m\leq {d}/{2}$. By Lemma 4.3, the differential tangent space
$m\leq {d}/{2}$. By Lemma 4.3, the differential tangent space ![]() $T^\Delta _{(\bar {a},\bar {\alpha })}\big (V^{[m]}\big )$ has coefficients which are independent differential transcendentals over
$T^\Delta _{(\bar {a},\bar {\alpha })}\big (V^{[m]}\big )$ has coefficients which are independent differential transcendentals over ![]() $\mathbb {Q}$. This differential tangent space satisfies the hypotheses of Theorem 4.4, so the solution set of
$\mathbb {Q}$. This differential tangent space satisfies the hypotheses of Theorem 4.4, so the solution set of ![]() $T^\Delta _{(\bar {a},\bar {\alpha })}\big (V^{[m]}\big )$ has no infinite-rank proper
$T^\Delta _{(\bar {a},\bar {\alpha })}\big (V^{[m]}\big )$ has no infinite-rank proper ![]() $\mathcal {C}$-vector subspaces definable over
$\mathcal {C}$-vector subspaces definable over ![]() $\mathbb {Q}\langle \bar {a},\bar {\alpha }\rangle$. By Theorem 3.8, we conclude that the differential variety defined by
$\mathbb {Q}\langle \bar {a},\bar {\alpha }\rangle$. By Theorem 3.8, we conclude that the differential variety defined by ![]() $f(x)=0$ is strongly minimal.
$f(x)=0$ is strongly minimal.
Finally, we present an example of a system of equations which does not have transcendental coefficients where the substitutions of Algorithms A and B are not well defined.
Example 4.10 Consider a generic fiber of the differential equation satisfied by the ![]() $j$-function
$j$-function
where ![]() $\alpha$ is a differential transcendental,
$\alpha$ is a differential transcendental, ![]() $S(x)$ is the Schwarzian derivative
$S(x)$ is the Schwarzian derivative
and
Following the procedure laid out in § 3, let ![]() $(a_1,a_2)$ be a Morley sequenceFootnote 5 for
$(a_1,a_2)$ be a Morley sequenceFootnote 5 for ![]() $E_\alpha$. We replace the transcendental
$E_\alpha$. We replace the transcendental ![]() $\alpha$ with a variable
$\alpha$ with a variable ![]() $y$, compute the differential tangent space, and eliminate
$y$, compute the differential tangent space, and eliminate ![]() $y$, resulting in the equation
$y$, resulting in the equation
where
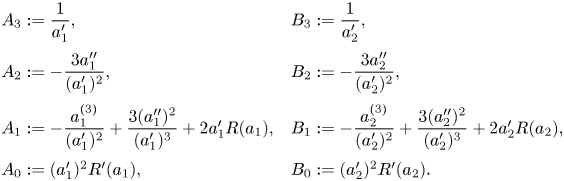 \[ \begin{array}{ll} A_{3} :=
\dfrac{1}{a_1'}, & B_{3} := \dfrac{1}{a_2'},\\ A_{2} :=
-\dfrac{3 a_1''}{(a_1')^2}, & B_{2} := -\dfrac{3
a_2''}{(a_2')^2},\\ A_{1} :=
-\dfrac{a_1^{(3)}}{(a_1')^2}+\dfrac{3(a_1'')^2}{(a_1')^3}
+2a_1'R(a_1), & B_{1} :=
-\dfrac{a_2^{(3)}}{(a_2')^2}+\dfrac{3(a_2'')^2}{(a_2')^3}
+2a_2'R(a_2),\\ A_{0} :=(a_1')^2 R'(a_1), & B_{0}
:=(a_2')^2 R'(a_2). \end{array} \]
\[ \begin{array}{ll} A_{3} :=
\dfrac{1}{a_1'}, & B_{3} := \dfrac{1}{a_2'},\\ A_{2} :=
-\dfrac{3 a_1''}{(a_1')^2}, & B_{2} := -\dfrac{3
a_2''}{(a_2')^2},\\ A_{1} :=
-\dfrac{a_1^{(3)}}{(a_1')^2}+\dfrac{3(a_1'')^2}{(a_1')^3}
+2a_1'R(a_1), & B_{1} :=
-\dfrac{a_2^{(3)}}{(a_2')^2}+\dfrac{3(a_2'')^2}{(a_2')^3}
+2a_2'R(a_2),\\ A_{0} :=(a_1')^2 R'(a_1), & B_{0}
:=(a_2')^2 R'(a_2). \end{array} \]
Unlike in § 4, these coefficients are not independent differential transcendentals. In fact, ![]() $A_{2}=3A_{3}'$ and
$A_{2}=3A_{3}'$ and ![]() $B_{2}=3B_{3}'$. We now apply the sequence of substitutions found in Algorithm A. First
$B_{2}=3B_{3}'$. We now apply the sequence of substitutions found in Algorithm A. First ![]() $(u,v)\mapsto (\tilde {u},v)$ where
$(u,v)\mapsto (\tilde {u},v)$ where ![]() $\tilde {u}=u-({B_{3}}/{A_{3}})v$, resulting in the equation
$\tilde {u}=u-({B_{3}}/{A_{3}})v$, resulting in the equation
where
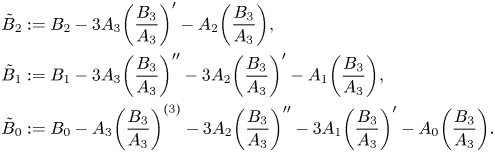 \begin{align*} \tilde{B}_2 &:= B_{2} - 3 A_{3}\biggl(\frac{B_{3}}{A_{3}}\biggr)' -A_{2}\biggl(\frac{B_{3}}{A_{3}}\biggr),\\ \tilde{B}_1 &:= B_{1} - 3 A_{3}\biggl(\frac{B_{3}}{A_{3}}\biggr)''-3A_{2}\biggl(\frac{B_{3}}{A_{3}}\biggr)'- A_{1}\biggl(\frac{B_{3}}{A_{3}}\biggr),\\ \tilde{B}_0 &:= B_{0} - A_{3}\biggl(\frac{B_{3}}{A_{3}}\biggr)^{(3)}-3A_{2}\biggl(\frac{B_{3}}{A_{3}}\biggr)'' -3A_{1}\biggl(\frac{B_{3}}{A_{3}}\biggr)'-A_{0}\biggl(\frac{B_{3}}{A_{3}}\biggr). \end{align*}
\begin{align*} \tilde{B}_2 &:= B_{2} - 3 A_{3}\biggl(\frac{B_{3}}{A_{3}}\biggr)' -A_{2}\biggl(\frac{B_{3}}{A_{3}}\biggr),\\ \tilde{B}_1 &:= B_{1} - 3 A_{3}\biggl(\frac{B_{3}}{A_{3}}\biggr)''-3A_{2}\biggl(\frac{B_{3}}{A_{3}}\biggr)'- A_{1}\biggl(\frac{B_{3}}{A_{3}}\biggr),\\ \tilde{B}_0 &:= B_{0} - A_{3}\biggl(\frac{B_{3}}{A_{3}}\biggr)^{(3)}-3A_{2}\biggl(\frac{B_{3}}{A_{3}}\biggr)'' -3A_{1}\biggl(\frac{B_{3}}{A_{3}}\biggr)'-A_{0}\biggl(\frac{B_{3}}{A_{3}}\biggr). \end{align*}
The next substitution would replace ![]() $v$ with
$v$ with ![]() $\tilde {v}$ where
$\tilde {v}$ where ![]() $v=\tilde {v}+( {A_3}/{\tilde {B}_2} )\tilde {u}'$, which would reduce the order of the
$v=\tilde {v}+( {A_3}/{\tilde {B}_2} )\tilde {u}'$, which would reduce the order of the ![]() $\tilde {u}$. However, this substitution is not well defined because
$\tilde {u}$. However, this substitution is not well defined because ![]() $\tilde {B}_2=0$:
$\tilde {B}_2=0$:
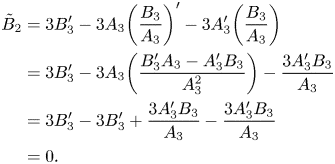 \begin{align*} \tilde{B}_2 &= 3B_{3}' - 3A_{3}\biggl(\frac{B_{3}}{A_{3}}\biggr)' -3A_{3}'\biggl(\frac{B_{3}}{A_{3}}\biggr)\\ &=3B_{3}' - 3A_{3}\biggl(\frac{B_{3}'A_{3}-A_{3}'B_{3}}{A_{3}^2}\biggr) -\frac{3A_{3}'B_{3}}{A_{3}}\\ &= 3B_{3}'-3B_{3}'+ \frac{3A_{3}'B_{3}}{A_{3}} - \frac{3A_{3}'B_{3}}{A_{3}} \\ &= 0. \end{align*}
\begin{align*} \tilde{B}_2 &= 3B_{3}' - 3A_{3}\biggl(\frac{B_{3}}{A_{3}}\biggr)' -3A_{3}'\biggl(\frac{B_{3}}{A_{3}}\biggr)\\ &=3B_{3}' - 3A_{3}\biggl(\frac{B_{3}'A_{3}-A_{3}'B_{3}}{A_{3}^2}\biggr) -\frac{3A_{3}'B_{3}}{A_{3}}\\ &= 3B_{3}'-3B_{3}'+ \frac{3A_{3}'B_{3}}{A_{3}} - \frac{3A_{3}'B_{3}}{A_{3}} \\ &= 0. \end{align*}
While this specific substitution does not yield a definable bijection, one can use another substitution ![]() $(\tilde {v}=v-({A_{3}}/{\tilde {B}_{1}})\tilde {u}'')$, and in this case the fact that
$(\tilde {v}=v-({A_{3}}/{\tilde {B}_{1}})\tilde {u}'')$, and in this case the fact that ![]() $\tilde {B}_2=0$ results in fewer substitutions being necessary to reach the desired result.
$\tilde {B}_2=0$ results in fewer substitutions being necessary to reach the desired result.
5. Orthogonality to the constants
We have seen that bounds of [Reference Freitag and MoosaFM21] on the degree of non-minimality can be used in conjunction with linearization techniques to establish the strong minimality of general classes of differential equations. There are two main obstacles to the wide application of these techniques for establishing strong minimality of many classical nonlinear equations.
(1) The methods developed in the previous sections seem to require at least one coefficient of the equation in question to be differentially transcendental.
(2) For a given equation, even of small order, the computations required to verify strong minimality are quite involved.
In this section we will show how the computational demands can be significantly reduced if a weaker condition than strong minimality is the goal: ![]() $V$ is either strongly minimal or almost internal to the constants. In [Reference Freitag and MoosaFM21] it is shown that if
$V$ is either strongly minimal or almost internal to the constants. In [Reference Freitag and MoosaFM21] it is shown that if ![]() $\operatorname {nmdeg}(p) > 1,$ then
$\operatorname {nmdeg}(p) > 1,$ then ![]() $p$ is an isolated type which is almost internal to a non-locally modular type. In differentially closed fields, this means that
$p$ is an isolated type which is almost internal to a non-locally modular type. In differentially closed fields, this means that ![]() $p$ is almost internal to the constant field whenever
$p$ is almost internal to the constant field whenever ![]() $\operatorname {nmdeg}(p) > 1.$ Thus, verifying the weaker condition only requires an analysis of forking extensions over one new solution – the computations need only involve two unknown variables in this case.
$\operatorname {nmdeg}(p) > 1.$ Thus, verifying the weaker condition only requires an analysis of forking extensions over one new solution – the computations need only involve two unknown variables in this case.
Example 5.1 We will show that the equation
where ![]() $\alpha$ is a differential transcendental, is either strongly minimal or internal to the constants. If the equation is not internal to the constants and not strongly minimal, then by the results of [Reference Freitag and MoosaFM21] there is an indiscernible sequence of length two
$\alpha$ is a differential transcendental, is either strongly minimal or internal to the constants. If the equation is not internal to the constants and not strongly minimal, then by the results of [Reference Freitag and MoosaFM21] there is an indiscernible sequence of length two ![]() $(x_1,x_2)$, which would satisfy the system
$(x_1,x_2)$, which would satisfy the system
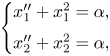 \[ \left\{ \begin{array}{@{}l} x_1''+x_1^2
= \alpha,\\ x_2''+x_2^2 = \alpha,
\end{array} \right. \]
\[ \left\{ \begin{array}{@{}l} x_1''+x_1^2
= \alpha,\\ x_2''+x_2^2 = \alpha,
\end{array} \right. \]
such that ![]() $x_2$ satisfies an order one equation over
$x_2$ satisfies an order one equation over ![]() $x_1.$ Using the same strategy as in the previous sections, we replace
$x_1.$ Using the same strategy as in the previous sections, we replace ![]() $\alpha$ with a variable
$\alpha$ with a variable ![]() $y$ in both equations, and then compute the differential tangent space:
$y$ in both equations, and then compute the differential tangent space:
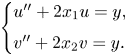 \[ \left\{ \begin{array}{@{}l} u''+2 x_1 u
= y, \\ v''+2 x_2 v = y. \end{array} \right.
\]
\[ \left\{ \begin{array}{@{}l} u''+2 x_1 u
= y, \\ v''+2 x_2 v = y. \end{array} \right.
\]
Eliminating ![]() $y$, we are left with the single equation
$y$, we are left with the single equation
Consider the definable bijection given by the substitution ![]() $(u,v)\mapsto (w,v)$ where
$(u,v)\mapsto (w,v)$ where ![]() $u=w+v$. This transforms the above equation into
$u=w+v$. This transforms the above equation into
which can be solved for ![]() $v$ since
$v$ since ![]() $x_1\neq x_2$. Therefore the differential tangent space has no infinite-rank subvarieties, a contradiction, so
$x_1\neq x_2$. Therefore the differential tangent space has no infinite-rank subvarieties, a contradiction, so ![]() $x''+x^2-\alpha =0$ is either strongly minimal or almost internal to the constants.
$x''+x^2-\alpha =0$ is either strongly minimal or almost internal to the constants.
Question 5.2 Varieties which are internal to the constants have certain stronger properties that may, in general, allow one show via some additional argument the strong minimality of specific equations. For instance, by [Reference Freitag and MoosaFM17], if ![]() $X$ is non-orthogonal to the constants, then there are infinitely many subvarieties of
$X$ is non-orthogonal to the constants, then there are infinitely many subvarieties of ![]() $X$ of co-order one. Thus, in this setting, showing strong minimality (after an argument like that of the example above) is equivalent to ruling out subvarieties of co-order one. Are there interesting classes of equations in which one can successfully employ this strategy?
$X$ of co-order one. Thus, in this setting, showing strong minimality (after an argument like that of the example above) is equivalent to ruling out subvarieties of co-order one. Are there interesting classes of equations in which one can successfully employ this strategy?
After the completion of this work, the authors, together with Guy Casale and Joel Nagloo, were able to give an affirmative answer to Question 5.2 in the case of the equation satisfied by the ![]() $j$-function. This gives a new proof of the main theorem of [Reference Freitag and ScanlonFS17]: the differential equation satisfied by the
$j$-function. This gives a new proof of the main theorem of [Reference Freitag and ScanlonFS17]: the differential equation satisfied by the ![]() $j$-function
$j$-function
is strongly minimal. We also employ the strategy to establish the strong minimality of several new equations. Nevertheless, we have left Question 5.2 as stated above, since we feel pursuing this approach is an important direction for future research.
During the revisions of this paper, the bounds on the degree of non-minimality in differentially closed fields were improved dramatically [Reference Freitag, Jaoui and MoosaFJM22a]: the degree of non-minimality in differentially closed fields is at most two. This does not affect the statement of our main result, Theorem 1.3, but does widen the scope of the result as pointed out in [Reference Freitag, Jaoui and MoosaFJM22a]: generic differential equations of degree at least six are strongly minimal.
Acknowledgements
The authors thank D. Marker, R. Nagloo, A. Pillay, and especially R. Moosa for useful conversations around this work. The techniques developed in this paper build on the thesis of J. Wolf cited below. The authors also wish to acknowledge the extremely detailed and useful remarks of the referee.
Conflicts of Interest
None.