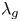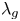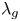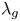1. Introduction
1.1 The Hodge bundle
Let ![]() $\overline {\mathcal {M}}_g$ be the moduli space of Deligne–Mumford stable curves, and let
$\overline {\mathcal {M}}_g$ be the moduli space of Deligne–Mumford stable curves, and let
be the universal curve with relative dualizing sheaf ![]() $\omega _\pi$. The rank
$\omega _\pi$. The rank ![]() $g$ Hodge bundle
$g$ Hodge bundle ![]() $\mathbb {E}_g$ on
$\mathbb {E}_g$ on ![]() $\overline {\mathcal {M}}_g$ is defined by
$\overline {\mathcal {M}}_g$ is defined by
The study of the Chern classes of the Hodge bundle goes back at least to Mumford's Grothendieck–Riemann–Roch calculation [Reference MumfordMum83] in the 1980s. Starting in the late 1990s, the connection of the Hodge bundle to the deformation theory of the moduli space of stable maps has led to an exploration of Hodge integrals in various contexts (see [Reference Aganagic, Klemm, Mariño and VafaAKMV05, Reference Ekdahl, Lando, Shapiro and VainshteinELSV01, Reference Faber and PandharipandeFP00a, Reference Graber and PandharipandeGP99, Reference Li, Liu, Liu and ZhouLLLZ09, Reference Liu, Liu and ZhouLLZ03, Reference Maulik, Oblomkov, Okounkov and PandharipandeMOOP11, Reference Okounkov and PandharipandeOP04, Reference PandharipandePan99]).
The top Chern classFootnote 1 of the Hodge bundle
plays a special role for several reasons.
(i) Two vanishing properties hold:
where \[ \lambda_g^2=0 \in \mathsf{CH}^{2g}(\overline{\mathcal{M}}_g) \quad \text{and}\quad \lambda_g|_{\Delta_0}= 0 \in \mathsf{CH}^g(\Delta_0), \]
\[ \lambda_g^2=0 \in \mathsf{CH}^{2g}(\overline{\mathcal{M}}_g) \quad \text{and}\quad \lambda_g|_{\Delta_0}= 0 \in \mathsf{CH}^g(\Delta_0), \]
 $\Delta _0\subset \overline {\mathcal {M}}_g$ is the divisor of curves with a non-separating node. The first vanishing follows from the highest graded part of Mumford's relation
proven in [Reference MumfordMum83, equations (5.4), (5.5)]. The second follows from the existence of a trivial quotientFootnote 2
$\Delta _0\subset \overline {\mathcal {M}}_g$ is the divisor of curves with a non-separating node. The first vanishing follows from the highest graded part of Mumford's relation
proven in [Reference MumfordMum83, equations (5.4), (5.5)]. The second follows from the existence of a trivial quotientFootnote 2 \[ c(\mathbb{E}_g)\cdot c(\mathbb{E}_g^*)= 1, \]
determined by the residue at (a branch of) the node (see [Reference Faber and PandharipandeFP00b, § 0.4]).
\[ c(\mathbb{E}_g)\cdot c(\mathbb{E}_g^*)= 1, \]
determined by the residue at (a branch of) the node (see [Reference Faber and PandharipandeFP00b, § 0.4]). \[ \mathbb{E}_g \twoheadrightarrow \mathbb{C} \]
\[ \mathbb{E}_g \twoheadrightarrow \mathbb{C} \]
(ii) The class
 $(-1)^g \lambda _g$ appears in the virtual fundamental class of the moduli of contracted maps in the Gromov–Witten theory of target curves. Since the double ramification cycle in the degree 0 case is defined via contracted maps, we have
where
$(-1)^g \lambda _g$ appears in the virtual fundamental class of the moduli of contracted maps in the Gromov–Witten theory of target curves. Since the double ramification cycle in the degree 0 case is defined via contracted maps, we have
where \[ \mathsf{DR}_{g,(0,\ldots,0)} = (-1)^g\lambda_g \in \mathsf{CH}^g(\overline{\mathcal{M}}_{g,n}), \]
\[ \mathsf{DR}_{g,(0,\ldots,0)} = (-1)^g\lambda_g \in \mathsf{CH}^g(\overline{\mathcal{M}}_{g,n}), \]
 $\overline {\mathcal {M}}_{g,n}$ is the moduli space of stable pointed curves. See [Reference Janda, Pandharipande, Pixton and ZvonkineJPPZ17, §§ 0.5.3 and 3.1].
$\overline {\mathcal {M}}_{g,n}$ is the moduli space of stable pointed curves. See [Reference Janda, Pandharipande, Pixton and ZvonkineJPPZ17, §§ 0.5.3 and 3.1].
Another basic consequence is the
 $\lambda _g$-formula [Reference Faber and PandharipandeFP03],
predicted by the Virasoro constraints for degree 0 maps to curves [Reference Getzler and PandharipandeGP98]. Here
$\lambda _g$-formula [Reference Faber and PandharipandeFP03],
predicted by the Virasoro constraints for degree 0 maps to curves [Reference Getzler and PandharipandeGP98]. Here \[ \int_{\overline{\mathcal{M}}_{g,n}} \psi_1^{k_1} \cdots \psi_n^{k_n} \lambda_g = \binom{2g+n-3}{k_1,\ldots, k_n} \cdot \int_{\overline{\mathcal{M}}_{g,1}} \psi_1^{2g-2} \lambda_g, \]
is the Chern class of the cotangent line at the
\[ \int_{\overline{\mathcal{M}}_{g,n}} \psi_1^{k_1} \cdots \psi_n^{k_n} \lambda_g = \binom{2g+n-3}{k_1,\ldots, k_n} \cdot \int_{\overline{\mathcal{M}}_{g,1}} \psi_1^{2g-2} \lambda_g, \]
is the Chern class of the cotangent line at the \[ \psi_i = c_1(\mathbb{L}_i) \in \mathsf{CH}^1(\overline{\mathcal{M}}_{g,n}) \]
\[ \psi_i = c_1(\mathbb{L}_i) \in \mathsf{CH}^1(\overline{\mathcal{M}}_{g,n}) \]
 $i$th point. The
$i$th point. The  $\lambda _g$-formula plays a central role in the study of the tautological ring
$\lambda _g$-formula plays a central role in the study of the tautological ring  $\mathsf {R}^\star (\mathcal {M}^{\mathsf {ct}}_{g,n})$ of the moduli space of curves of compact type [Reference PandharipandePan12].
$\mathsf {R}^\star (\mathcal {M}^{\mathsf {ct}}_{g,n})$ of the moduli space of curves of compact type [Reference PandharipandePan12].(iii) Again as an excess class,
 $(-1)^g\lambda _g$ appears fundamentally in the local Gromov–Witten theory of surfaces. For example, the Katz–Klemm–Vafa formula [Reference Katz, Klemm and VafaKKV99] proven in [Reference Maulik, Pandharipande and ThomasMPT10, Reference Pandharipande and ThomasPT16] concerns integrals
against the reduced virtual fundamental class of the moduli space of stable maps to
$(-1)^g\lambda _g$ appears fundamentally in the local Gromov–Witten theory of surfaces. For example, the Katz–Klemm–Vafa formula [Reference Katz, Klemm and VafaKKV99] proven in [Reference Maulik, Pandharipande and ThomasMPT10, Reference Pandharipande and ThomasPT16] concerns integrals
against the reduced virtual fundamental class of the moduli space of stable maps to \[ \int_{[\overline{\mathcal{M}}_g(S,\beta)]^{\mathsf{red}}} (-1)^g \lambda_g \]
\[ \int_{[\overline{\mathcal{M}}_g(S,\beta)]^{\mathsf{red}}} (-1)^g \lambda_g \]
 $K3$ surfaces. For a recent study of the parallel problem for local log Calabi–Yau surfaces (with integrand
$K3$ surfaces. For a recent study of the parallel problem for local log Calabi–Yau surfaces (with integrand  $(-1)^g \lambda _g$); see [Reference BousseauBou20].
$(-1)^g \lambda _g$); see [Reference BousseauBou20].(iv) The class
 $(-1)^g\lambda _g$ arises via the pull-back of the universal
$(-1)^g\lambda _g$ arises via the pull-back of the universal  $0$-section of the moduli space of principally polarized abelian varieties (PPAVs). Over the moduli space of compact type curves, the connection to PPAVs shows a third vanishing property,
(see [Reference van der GeervdG99]). We will discuss PPAVs further in § 1.2 below.
$0$-section of the moduli space of principally polarized abelian varieties (PPAVs). Over the moduli space of compact type curves, the connection to PPAVs shows a third vanishing property,
(see [Reference van der GeervdG99]). We will discuss PPAVs further in § 1.2 below. \[ \lambda_g |_{\mathcal{M}_{g}^{\mathsf{ct}}} = 0 \]
\[ \lambda_g |_{\mathcal{M}_{g}^{\mathsf{ct}}} = 0 \]
Our main results here concern the complexity of the class ![]() $\lambda _g$ in the Chow ring. For
$\lambda _g$ in the Chow ring. For ![]() $\overline {\mathcal {M}}_g$, we bound from below the complexity of formulas for
$\overline {\mathcal {M}}_g$, we bound from below the complexity of formulas for
As a consequence of the connection to the moduli of PPAVs, we also bound from below the complexity of formulas for the universal ![]() $0$-section.
$0$-section.
The log Chow ring of ![]() $(\overline {\mathcal {M}}_g,\partial \overline {\mathcal {M}}_g)$ is defined as a colimit over all iterated blow-ups of boundary strata. The usual Chow ring is naturally a subalgebra
$(\overline {\mathcal {M}}_g,\partial \overline {\mathcal {M}}_g)$ is defined as a colimit over all iterated blow-ups of boundary strata. The usual Chow ring is naturally a subalgebra
The main positive result of the paper is the simplicity of ![]() $\lambda _g$ in the log Chow ring. We prove
$\lambda _g$ in the log Chow ring. We prove
where
is the subalgebra generated by logarithmic boundary divisors. While ![]() $\lambda _g$ in Chow is complicated,
$\lambda _g$ in Chow is complicated, ![]() $\lambda _g$ in log Chow is as simple as possible! We present several related open questions.
$\lambda _g$ in log Chow is as simple as possible! We present several related open questions.
1.2 The 0-section
Let ![]() $\mathcal {A}_g$ be the moduli space of PPAVs of dimension
$\mathcal {A}_g$ be the moduli space of PPAVs of dimension ![]() $g$, and let
$g$, and let
be the universal abelian variety ![]() $\pi$ equipped with a universal
$\pi$ equipped with a universal ![]() $0$-section
$0$-section
The image of the ![]() $0$-section determines an algebraic cycle class
$0$-section determines an algebraic cycle class
The second Voronoi compactification of ![]() $\mathcal {A}_g$ has been given a modular interpretation by Alekseev:
$\mathcal {A}_g$ has been given a modular interpretation by Alekseev:
Olsson [Reference OlssonOls12] provided a modular interpretation for the normalization
Our approach here will be equally valid for both ![]() $\overline {\mathcal {A}}^{\mathsf {Olsson}}$ and
$\overline {\mathcal {A}}^{\mathsf {Olsson}}$ and ![]() $\overline {\mathcal {A}}_g^{\mathsf {Alekseev}}$. We will simply denote the compactification by
$\overline {\mathcal {A}}_g^{\mathsf {Alekseev}}$. We will simply denote the compactification by
where ![]() $\overline {\mathcal {A}}_g$ stands for either the space of Alekseev or the space of Olsson.
$\overline {\mathcal {A}}_g$ stands for either the space of Alekseev or the space of Olsson.
The four important propertiesFootnote 3 of the compactification ![]() $\overline {\mathcal {A}}_g$ which we will require are as follows.
$\overline {\mathcal {A}}_g$ which we will require are as follows.
• The points of
 $\overline {\mathcal {A}}_g$ parameterize (before normalization) stable semiabelic pairs which are quadruples
$\overline {\mathcal {A}}_g$ parameterize (before normalization) stable semiabelic pairs which are quadruples  $(G,P,L,\theta )$ where
$(G,P,L,\theta )$ where  $G$ is a semiabelian variety,
$G$ is a semiabelian variety,  $P$ is a projective variety equipped with a
$P$ is a projective variety equipped with a  $G$-action,
$G$-action,  $L$ is an ample line bundle on
$L$ is an ample line bundle on  $P$, and
$P$, and  $\theta \in H^0(P,L)$. The data
$\theta \in H^0(P,L)$. The data  $(G,P,L,\theta )$ satisfy several further conditions (see § 4.2.16 of [Reference OlssonOls12]).
$(G,P,L,\theta )$ satisfy several further conditions (see § 4.2.16 of [Reference OlssonOls12]).• There is a universal semiabelian variety
with a \[ \overline{\pi}: \overline{\mathcal{X}}_g \rightarrow \overline{\mathcal{A}}_g \]
\[ \overline{\pi}: \overline{\mathcal{X}}_g \rightarrow \overline{\mathcal{A}}_g \]
 $0$-section
corresponding to the semiabelian variety which is the first piece of data of a stable semiabelic pair (the rest of the pair data will not play a role in our study).
$0$-section
corresponding to the semiabelian variety which is the first piece of data of a stable semiabelic pair (the rest of the pair data will not play a role in our study). \[ \overline{s}: \overline{\mathcal{A}}_g \rightarrow \overline{\mathcal{X}}_g \]
\[ \overline{s}: \overline{\mathcal{A}}_g \rightarrow \overline{\mathcal{X}}_g \]
• The usual Torelli map
 $\tau : \mathcal {M}_g \rightarrow \mathcal {A}_g$ extends canonically,
(see [Reference AlekseevAle04]).
$\tau : \mathcal {M}_g \rightarrow \mathcal {A}_g$ extends canonically,
(see [Reference AlekseevAle04]). \[ \overline{\tau}: \overline{\mathcal{M}}_g \rightarrow \overline{\mathcal{A}}_g \]
\[ \overline{\tau}: \overline{\mathcal{M}}_g \rightarrow \overline{\mathcal{A}}_g \]
• The
 $\overline {\tau }$-pull-back to
$\overline {\tau }$-pull-back to  $\overline {\mathcal {M}}_g$ of
$\overline {\mathcal {M}}_g$ of  $\overline {\mathcal {X}}_g$ is the universal family
parameterizing line bundles on the fibers of the universal curve
$\overline {\mathcal {X}}_g$ is the universal family
parameterizing line bundles on the fibers of the universal curve \[ \mathsf{Pic}_\epsilon^0 \rightarrow \overline{\mathcal{M}}_g \]
which have degree 0 on every component of any fiber [Reference AlekseevAle04].
\[ \mathsf{Pic}_\epsilon^0 \rightarrow \overline{\mathcal{M}}_g \]
which have degree 0 on every component of any fiber [Reference AlekseevAle04]. \[ \epsilon:\mathcal{C}_g \rightarrow \overline{\mathcal{M}}_g \]
\[ \epsilon:\mathcal{C}_g \rightarrow \overline{\mathcal{M}}_g \]
The image of the ![]() $0$-section
$0$-section ![]() $\overline {s}$ determines an operational Chow class
$\overline {s}$ determines an operational Chow class
since the image is an étale local complete intersection in ![]() $\overline {\mathcal {X}}_g$. The class
$\overline {\mathcal {X}}_g$. The class ![]() $\overline {Z}_g$ is related to
$\overline {Z}_g$ is related to ![]() $(-1)^g\lambda _g$ via a pull-back construction. Let
$(-1)^g\lambda _g$ via a pull-back construction. Let
be the ![]() $0$-section defined by the trivial line bundle. By the properties of
$0$-section defined by the trivial line bundle. By the properties of
discussed above,
By the standard analysis of the vertical tangent bundle of ![]() $\mathsf {Pic}_\epsilon ^0$,
$\mathsf {Pic}_\epsilon ^0$,
Indeed, by the excess intersection formula the class ![]() $t^*(t_*[\overline {\mathcal {M}}_g])$ equals the top Chern class of the normal bundle of the
$t^*(t_*[\overline {\mathcal {M}}_g])$ equals the top Chern class of the normal bundle of the ![]() $0$-section of
$0$-section of ![]() $\mathsf {Pic}_\epsilon ^0$. Over
$\mathsf {Pic}_\epsilon ^0$. Over ![]() $[C]\in \overline {\mathcal {M}}_g$, the fiber of the normal bundle is the first-order deformation space of the trivial line bundle on
$[C]\in \overline {\mathcal {M}}_g$, the fiber of the normal bundle is the first-order deformation space of the trivial line bundle on ![]() $C$. The deformation space is given by
$C$. The deformation space is given by
the fiber of the dual of the Hodge bundle ![]() $\mathbb {E}_g^\vee$ with top Chern class
$\mathbb {E}_g^\vee$ with top Chern class ![]() $(-1)^g \lambda _g$. We conclude that
$(-1)^g \lambda _g$. We conclude that
1.3 Complexity of the  $0$-section
$0$-section
The study the ![]() $0$-section over
$0$-section over ![]() $\mathcal {A}_g$ is related to the double ramification cycle (especially over curves of compact type) (see Hain [Reference HainHai13] and Grushevsky-Zakharov [Reference Grushevsky and ZakharovGZ14a]). A central idea there is to use the beautiful formula
$\mathcal {A}_g$ is related to the double ramification cycle (especially over curves of compact type) (see Hain [Reference HainHai13] and Grushevsky-Zakharov [Reference Grushevsky and ZakharovGZ14a]). A central idea there is to use the beautiful formula
where ![]() $\Theta \in \mathsf {CH}^1(\mathcal {X}_g)$ is the universal symmetric theta divisor trivialized along the
$\Theta \in \mathsf {CH}^1(\mathcal {X}_g)$ is the universal symmetric theta divisor trivialized along the ![]() $0$-section. The proof of (2) in Chow uses the Fourier–Mukai transformation and work of Deninger and Murre [Reference Deninger and MurreDM91] (see [Reference Birkenhake and LangeBL04, Reference VoisinVoi14]). The article [Reference Grushevsky and ZakharovGZ14a] provides a more detailed discussion of the history of (2).
$0$-section. The proof of (2) in Chow uses the Fourier–Mukai transformation and work of Deninger and Murre [Reference Deninger and MurreDM91] (see [Reference Birkenhake and LangeBL04, Reference VoisinVoi14]). The article [Reference Grushevsky and ZakharovGZ14a] provides a more detailed discussion of the history of (2).
We are interested in the following question: to what extent is an equation of the form of (2) possible over ![]() $\overline {\mathcal {A}}_g$? A result by Grushevsky and Zakharov along these lines appears in [Reference Grushevsky and ZakharovGZ14b]. As before, let
$\overline {\mathcal {A}}_g$? A result by Grushevsky and Zakharov along these lines appears in [Reference Grushevsky and ZakharovGZ14b]. As before, let
be the class of the ![]() $0$-section
$0$-section ![]() $\overline {s}$. Grushevsky and Zakharov calculate the restriction
$\overline {s}$. Grushevsky and Zakharov calculate the restriction ![]() $\overline {Z}_g|_{\mathcal {U}_g}$ of
$\overline {Z}_g|_{\mathcal {U}_g}$ of ![]() $\overline {Z}_g$ over a particular open setFootnote 4
$\overline {Z}_g$ over a particular open setFootnote 4
in terms of ![]() $\Theta$, a boundary divisor
$\Theta$, a boundary divisor ![]() $D\in \mathsf {CH}^1(\overline {\mathcal {X}}_g|_{\mathcal {U}_g})$, and a class
$D\in \mathsf {CH}^1(\overline {\mathcal {X}}_g|_{\mathcal {U}_g})$, and a class
The result of Grushevsky and Zakharov shows that while the naive extension of (2) does not hold over ![]() $\mathcal {U}_g$, the class
$\mathcal {U}_g$, the class ![]() $\overline {Z}_g|_{\mathcal {U}_g}$ lies in the subalgebra of
$\overline {Z}_g|_{\mathcal {U}_g}$ lies in the subalgebra of ![]() $\mathsf {CH}^\star (\overline {\mathcal {X}}_g|_{\mathcal {U}_g})$ generated by classes of degrees 1 and 2. The formula of [Reference Grushevsky and ZakharovGZ14b] is a useful extension of (2).
$\mathsf {CH}^\star (\overline {\mathcal {X}}_g|_{\mathcal {U}_g})$ generated by classes of degrees 1 and 2. The formula of [Reference Grushevsky and ZakharovGZ14b] is a useful extension of (2).
The divisor classes ![]() $\mathsf {CH}^1_{\mathsf {op}}(\overline {\mathcal {X}}_g)$ generate a subalgebra
$\mathsf {CH}^1_{\mathsf {op}}(\overline {\mathcal {X}}_g)$ generate a subalgebra
The first bound from below of the complexity of the class of the ![]() $0$-section is the following result.
$0$-section is the following result.
Theorem 1 For all ![]() $g\geq 3$, we have
$g\geq 3$, we have ![]() $\overline {Z}_g\notin \mathsf {divCH}^\star _{\mathsf {op}}(\overline {\mathcal {X}}_g)$.
$\overline {Z}_g\notin \mathsf {divCH}^\star _{\mathsf {op}}(\overline {\mathcal {X}}_g)$.
As a consequence, no divisor formula extending (2) is possible for ![]() $\overline {\mathcal {A}}_g$. Though not stated, the analysis of [Reference Grushevsky and ZakharovGZ14b] over
$\overline {\mathcal {A}}_g$. Though not stated, the analysis of [Reference Grushevsky and ZakharovGZ14b] over ![]() $\mathcal {U}_g$ can be used to show that
$\mathcal {U}_g$ can be used to show that ![]() $\overline {Z}_g|_{\mathcal {U}_g}$ is not in the subalgebra of
$\overline {Z}_g|_{\mathcal {U}_g}$ is not in the subalgebra of ![]() $\mathsf {CH}^\star (\overline {\mathcal {X}}_g|_{\mathcal {U}_g})$ generated by classes of degree 1. Theorem 1 can therefore also be obtained from [Reference Grushevsky and ZakharovGZ14b].Footnote 5
$\mathsf {CH}^\star (\overline {\mathcal {X}}_g|_{\mathcal {U}_g})$ generated by classes of degree 1. Theorem 1 can therefore also be obtained from [Reference Grushevsky and ZakharovGZ14b].Footnote 5
In fact, we can go further. Let
be the subalgebra generated by all elements of degree at most ![]() $k$, so that
$k$, so that
Theorem 2 For all ![]() $g\geq 7$, we have
$g\geq 7$, we have ![]() $\overline {Z}_g\notin \mathsf {CH}^\star _{\leq 2}(\overline {\mathcal {X}}_g)$.
$\overline {Z}_g\notin \mathsf {CH}^\star _{\leq 2}(\overline {\mathcal {X}}_g)$.
By Theorem 2, the Grushevsky–Zakharov formula for ![]() $\overline {Z}_g |_{{\mathcal {U}}_g}$ will require corrections by higher-degree classes when extended over
$\overline {Z}_g |_{{\mathcal {U}}_g}$ will require corrections by higher-degree classes when extended over ![]() $\overline {\mathcal {A}}_g$. We propose the following conjecture about the complexity of the class
$\overline {\mathcal {A}}_g$. We propose the following conjecture about the complexity of the class ![]() $\overline {Z}_g$.
$\overline {Z}_g$.
Conjecture A No extension of (2) over ![]() $\overline {\mathcal {A}}_g$ for all
$\overline {\mathcal {A}}_g$ for all ![]() $g$ can be written in terms of classes of uniformly bounded degree.
$g$ can be written in terms of classes of uniformly bounded degree.
The pull-back relation (1) relates the complexity of the class
to the complexity of ![]() $\overline {Z}_g\in \mathsf {CH}^\star _{\mathsf {op}}(\overline {\mathcal {X}}_g)$. Theorems 1 and 2 will be the immediate consequence of parallelFootnote 6 complexity bounds for
$\overline {Z}_g\in \mathsf {CH}^\star _{\mathsf {op}}(\overline {\mathcal {X}}_g)$. Theorems 1 and 2 will be the immediate consequence of parallelFootnote 6 complexity bounds for ![]() $\lambda _g$.
$\lambda _g$.
1.4 Complexity of  $\lambda _g$
$\lambda _g$
The divisor classes ![]() $\mathsf {CH}^1(\overline {\mathcal {M}}_g)$ generate a subalgebra
$\mathsf {CH}^1(\overline {\mathcal {M}}_g)$ generate a subalgebra
The first bound from below of the complexity of ![]() $\lambda _g$ is the following result.
$\lambda _g$ is the following result.
Theorem 3 For all ![]() $g\geq 3$, we have
$g\geq 3$, we have ![]() $\lambda _g\notin \mathsf {divCH}^\star (\overline {\mathcal {M}}_g)$.
$\lambda _g\notin \mathsf {divCH}^\star (\overline {\mathcal {M}}_g)$.
Via the pull-back relation (1), Theorem 3 immediately implies Theorem 1. The proof of Theorem 3, presented in § 2, starts with explicit calculations in the tautological ring in genera ![]() $3$ and
$3$ and ![]() $4$ using the Sage package admcycles [Reference Delecroix, Schmitt and van ZelmDSvZ21]. A boundary restriction argument is then used to inductively control all higher genera.
$4$ using the Sage package admcycles [Reference Delecroix, Schmitt and van ZelmDSvZ21]. A boundary restriction argument is then used to inductively control all higher genera.
For the analogue of Theorem 2, let
be the subalgebra generated by all elements of degree at most ![]() $k$. A similar strategy (with a much more complicated initial calculation in genus 5) yields the following result which implies Theorem 2.
$k$. A similar strategy (with a much more complicated initial calculation in genus 5) yields the following result which implies Theorem 2.
Theorem 4 For all ![]() $g\geq 7$, we have
$g\geq 7$, we have ![]() $\lambda _g\notin \mathsf {CH}^\star _{\leq 2}(\overline {\mathcal {M}}_g)$.
$\lambda _g\notin \mathsf {CH}^\star _{\leq 2}(\overline {\mathcal {M}}_g)$.
The proofs of Theorems 3 and 4 require new cases of Pixton's conjecture about the ideal of relations in the tautological ring
Proposition 5 Pixton's relations generate all relations among tautological classes in ![]() $\mathsf {R}^4(\overline {\mathcal {M}}_{4,1})$ and
$\mathsf {R}^4(\overline {\mathcal {M}}_{4,1})$ and ![]() $\mathsf {R}^5(\overline {\mathcal {M}}_{5,1})$.
$\mathsf {R}^5(\overline {\mathcal {M}}_{5,1})$.
While the above arguments become harder to pursue in general for ![]() $\mathsf {CH}^\star _{\leq k}(\overline {\mathcal {M}}_g)$, we expect the following assertion to hold.
$\mathsf {CH}^\star _{\leq k}(\overline {\mathcal {M}}_g)$, we expect the following assertion to hold.
Conjecture B For fixed ![]() $k$,
$k$, ![]() $\lambda _g \in \mathsf {CH}^\star _{\leq k}(\overline {\mathcal {M}}_g)$ holds only for finitely many
$\lambda _g \in \mathsf {CH}^\star _{\leq k}(\overline {\mathcal {M}}_g)$ holds only for finitely many ![]() $g$.
$g$.
1.5 Log Chow
Theorems 1–4 about the classes ![]() $\overline {Z}_g$ and
$\overline {Z}_g$ and ![]() $\lambda _g$ are in a sense negative results since formula types are excluded. Our main positive result about
$\lambda _g$ are in a sense negative results since formula types are excluded. Our main positive result about ![]() $\lambda _g$ concerns the larger log Chow ring
$\lambda _g$ concerns the larger log Chow ring
The log Chow ring and the subalgebra
generated by logarithmic boundary divisors are defined carefully in § 3. Our perspective, using limits over log blow-ups, requires the least background in log geometry. A more intrinsic approach to the definitions can be found in [Reference BarrottBar18].
Theorem 6 For all ![]() $g\geq 2$, we have
$g\geq 2$, we have ![]() $\lambda _g \in \mathsf {divlogCH}^\star (\overline {\mathcal {M}}_g, \partial \overline {\mathcal {M}}_g)$.
$\lambda _g \in \mathsf {divlogCH}^\star (\overline {\mathcal {M}}_g, \partial \overline {\mathcal {M}}_g)$.
Our proof of Theorem 6 is constructive: we start with Pixton's formula for the double ramification cycle for constant maps [Reference Janda, Pandharipande, Pixton and ZvonkineJPPZ17] and show that each term lies in ![]() $\mathsf {divlogCH}^\star (\overline {\mathcal {M}}_g)$. In principle, it is possible to obtain bounds for the necessary log blow-ups from the proof, but these will certainly not be optimal. Finding a minimal (or efficient) sequence of log-blows of
$\mathsf {divlogCH}^\star (\overline {\mathcal {M}}_g)$. In principle, it is possible to obtain bounds for the necessary log blow-ups from the proof, but these will certainly not be optimal. Finding a minimal (or efficient) sequence of log-blows of ![]() $(\overline {\mathcal {M}}_g, \partial \overline {\mathcal {M}}_g)$ after which
$(\overline {\mathcal {M}}_g, \partial \overline {\mathcal {M}}_g)$ after which ![]() $\lambda _g$ lies in the subalgebra of logarithmic boundary divisors is an interesting question.
$\lambda _g$ lies in the subalgebra of logarithmic boundary divisors is an interesting question.
A crucial part of the proof of Theorem 6 is the study in § 5 of the logarithmic tautological ring,
defined by a normal crossings divisor ![]() $D\subset X$ in a non-singular variety
$D\subset X$ in a non-singular variety ![]() $X$. Tautological classes are defined here using the Chern roots of the normal bundle of logarithmic strata
$X$. Tautological classes are defined here using the Chern roots of the normal bundle of logarithmic strata ![]() $S\subset X$. The precise definitions are given in § 5.1.
$S\subset X$. The precise definitions are given in § 5.1.
We prove three main structural results about logarithmic tautological classes.
(i)
 $\mathsf {R}^\star (X,D) \subset \mathsf {divlogCH}^\star (X,D)$.
$\mathsf {R}^\star (X,D) \subset \mathsf {divlogCH}^\star (X,D)$.(ii) pull-backs of tautological classes under log blow-ups are tautological.
(iii) push-forwards of tautological classes under log blow-ups are tautological.
Our first proof of (i) is presented in § 5.2 via an explicit analysis of explosions: sequences of blow-ups associated to logarithmic strata of ![]() $X$. A second approach to (i)–(iii), via the geometry of the Artin fan of
$X$. A second approach to (i)–(iii), via the geometry of the Artin fan of ![]() $(X,D)$, is given in § 5.5. The Artin fan perspective, advocated by D. Ranganathan,Footnote 7 is theoretically more flexible.
$(X,D)$, is given in § 5.5. The Artin fan perspective, advocated by D. Ranganathan,Footnote 7 is theoretically more flexible.
After Pixton's formula for the double ramification cycle for constant maps is shown to lie in ![]() $\mathsf {R}^\star (\overline {\mathcal {M}}_g, \partial \overline {\mathcal {M}}_g)$, property (i) implies Theorem 6. Since Pixton's formula and the proof of (i) are both effective, it is possible in principle to compute divisor expressions for
$\mathsf {R}^\star (\overline {\mathcal {M}}_g, \partial \overline {\mathcal {M}}_g)$, property (i) implies Theorem 6. Since Pixton's formula and the proof of (i) are both effective, it is possible in principle to compute divisor expressions for ![]() $\lambda _g$. The result reveals the essential simplicity of
$\lambda _g$. The result reveals the essential simplicity of ![]() $\lambda _g$ and opens the door to the search for a simpler formula in divisors.
$\lambda _g$ and opens the door to the search for a simpler formula in divisors.
The proof of Theorem 6 yields a refined result: only logarithmic boundary divisors over
are needed to generate ![]() $\lambda _g$. The parallel result is also true for pointed curves:
$\lambda _g$. The parallel result is also true for pointed curves:
for ![]() $2g-2+n>0$.
$2g-2+n>0$.
We have seen that ![]() $(-1)^g \lambda _g$ is a special case of the double ramification cycle. The general double ramification cycle
$(-1)^g \lambda _g$ is a special case of the double ramification cycle. The general double ramification cycle
is defined with respect to a vector of integers ![]() $A=(a_1,\ldots,a_n)$ satisfying
$A=(a_1,\ldots,a_n)$ satisfying
 \[ \sum_{i=1}^n a_i =0. \]
\[ \sum_{i=1}^n a_i =0. \]
In [Reference Holmes, Pixton and SchmittHPS19, Appendix A], the double ramification cycle was lifted to log Chow,Footnote 8
Motivated by Theorem 6, we conjectureFootnote 9 a uniform divisorial property of the lifted double ramification cycle (3).
Conjecture C For all ![]() $g$ and
$g$ and ![]() $A$, we have
$A$, we have ![]() $\widetilde {\mathsf {DR}}_{g,A} \in \underline {\mathsf {div}}\mathsf {logCH}^\star (\overline {\mathcal {M}}_{g,n})$ where
$\widetilde {\mathsf {DR}}_{g,A} \in \underline {\mathsf {div}}\mathsf {logCH}^\star (\overline {\mathcal {M}}_{g,n})$ where
is the subalgebra generated by logarithmic boundary divisors together with the cotangent line classes ![]() $\psi _1,\ldots, \psi _n$.
$\psi _1,\ldots, \psi _n$.
Finally, we return to the ![]() $\Theta$-formula (2) for
$\Theta$-formula (2) for ![]() $Z_g$. Is an extension of the
$Z_g$. Is an extension of the ![]() $\Theta$-formula possible over
$\Theta$-formula possible over ![]() $\overline {\mathcal {M}}_g$ in
$\overline {\mathcal {M}}_g$ in ![]() $\mathsf {logCH}^\star (\overline {\mathcal {M}}_g)$? More specifically, can we find
$\mathsf {logCH}^\star (\overline {\mathcal {M}}_g)$? More specifically, can we find
which satisfies the following two properties?
(i) The restriction of
 $\mathsf {T}$ over the moduli of curves
$\mathsf {T}$ over the moduli of curves  $\mathcal {M}^{\mathsf {ct}}_g$ of compact type is
$\mathcal {M}^{\mathsf {ct}}_g$ of compact type is  $0$.
$0$.(ii)
 $(-1)^g\lambda _g = \frac {\mathsf {T}^g}{g!} \in \mathsf {logCH}^g(\overline {\mathcal {M}}_g)$.
$(-1)^g\lambda _g = \frac {\mathsf {T}^g}{g!} \in \mathsf {logCH}^g(\overline {\mathcal {M}}_g)$.
Property (i) is imposed since
by the trivialization condition for ![]() $\Theta$. Unfortunately, the answer is no even for genus
$\Theta$. Unfortunately, the answer is no even for genus ![]() $2$.
$2$.
Proposition 7 There does not exist a class ![]() $\mathsf {T}\in \mathsf {logCH}^1(\overline {\mathcal {M}}_2)$ satisfying the restriction property (i) and
$\mathsf {T}\in \mathsf {logCH}^1(\overline {\mathcal {M}}_2)$ satisfying the restriction property (i) and
The ![]() $\Theta$-formula for
$\Theta$-formula for ![]() $(-1)^g\lambda _g$ can not be extended in a straightforward way in
$(-1)^g\lambda _g$ can not be extended in a straightforward way in ![]() $\mathsf {CH}^g(\overline {\mathcal {M}}_g)$ or
$\mathsf {CH}^g(\overline {\mathcal {M}}_g)$ or ![]() $\mathsf {logCH}^g(\overline {\mathcal {M}}_g)$. However,
$\mathsf {logCH}^g(\overline {\mathcal {M}}_g)$. However,
is a degree ![]() $g$ polynomial in the logarithmic boundary divisors over
$g$ polynomial in the logarithmic boundary divisors over ![]() $\Delta _0\subset \overline {\mathcal {M}}_g$.
$\Delta _0\subset \overline {\mathcal {M}}_g$.
Question D Find a polynomial formula in logarithmic boundary divisors for ![]() $\lambda _g$ in log Chow (without using Pixton's formula).
$\lambda _g$ in log Chow (without using Pixton's formula).
The larger bChow ring of ![]() $\overline {\mathcal {M}}_g$ is defined as a limit over all blow-ups:
$\overline {\mathcal {M}}_g$ is defined as a limit over all blow-ups:
The bChow ring is by far the largest of the three Chow constructions. In § 7, we show that the main questions of the paper become trivial in bChow. In fact, for every non-singular variety ![]() $X$, we have
$X$, we have
The logarithmic geometry of ![]() $\overline {\mathcal {M}}_g$ is therefore the natural place to study Question D for
$\overline {\mathcal {M}}_g$ is therefore the natural place to study Question D for ![]() $\lambda _g$.
$\lambda _g$.
2.  $\lambda _g$ in the Chow ring
$\lambda _g$ in the Chow ring
2.1 Proof of Theorem 3
Recall that the tautological rings ![]() $(R^\star (\overline {\mathcal {M}}_{g,n}))_{g,n}$ are defined as the smallest system of
$(R^\star (\overline {\mathcal {M}}_{g,n}))_{g,n}$ are defined as the smallest system of ![]() $\mathbb {Q}$-subalgebras with unit of the Chow rings
$\mathbb {Q}$-subalgebras with unit of the Chow rings ![]() $(\mathsf {CH}^\star (\overline {\mathcal {M}}_{g,n}))_{g,n}$ closed under push-forwards by gluing and forgetful maps (see [Reference Faber and PandharipandeFP00b, Reference PandharipandePan18] for more details). The tautological subring
$(\mathsf {CH}^\star (\overline {\mathcal {M}}_{g,n}))_{g,n}$ closed under push-forwards by gluing and forgetful maps (see [Reference Faber and PandharipandeFP00b, Reference PandharipandePan18] for more details). The tautological subring ![]() $\mathsf {RH}^\star (\overline {\mathcal {M}}_{g,n})$ is defined as the image of the cycle map
$\mathsf {RH}^\star (\overline {\mathcal {M}}_{g,n})$ is defined as the image of the cycle map
We will use the complex degree grading for ![]() $\mathsf {RH}^\star$ and the real degree grading (as usual) for
$\mathsf {RH}^\star$ and the real degree grading (as usual) for ![]() $\mathsf {H}^\star$. Let
$\mathsf {H}^\star$. Let
be the subrings generated respectively by ![]() $\mathsf {RH}^1(\overline {\mathcal {M}}_{g,n})$ and
$\mathsf {RH}^1(\overline {\mathcal {M}}_{g,n})$ and ![]() $\mathsf {H}^2(\overline {\mathcal {M}}_{g,n})$. Since
$\mathsf {H}^2(\overline {\mathcal {M}}_{g,n})$. Since
by [Reference Arbarello and CornalbaAC98, Theorem 2.2] we have
We will use the complex degree grading for both ![]() $\mathsf {divRH}^\star$ and
$\mathsf {divRH}^\star$ and ![]() $\mathsf {divH}^\star$. Since
$\mathsf {divH}^\star$. Since
via the cycle class map, we obtain a surjection
The following stronger result implies Theorem 3.
Theorem 3/Cohomology. For all ![]() $g\geq 3$, we have
$g\geq 3$, we have ![]() $\lambda _g\notin \mathsf {divH}^\star (\overline {\mathcal {M}}_g)$.
$\lambda _g\notin \mathsf {divH}^\star (\overline {\mathcal {M}}_g)$.
Proof. For ![]() $g=3$, we have complete control of the tautological rings in Chow and cohomology since the intersection pairing to
$g=3$, we have complete control of the tautological rings in Chow and cohomology since the intersection pairing to ![]() $\mathsf {R}_0(\overline {\mathcal {M}}_g) \stackrel {\sim }= \mathbb {Q}$ is non-degenerate for tautological classes (see [Reference FaberFab90]). In particular,
$\mathsf {R}_0(\overline {\mathcal {M}}_g) \stackrel {\sim }= \mathbb {Q}$ is non-degenerate for tautological classes (see [Reference FaberFab90]). In particular,
In degree 3,
is a nine-dimensional subspace of a 10-dimensional space. Explicit calculations with the Sage program admcycles [Reference Delecroix, Schmitt and van ZelmDSvZ21] show that ![]() $\lambda _3 \notin \mathsf {divRH}^3(\overline {\mathcal {M}}_3)$. We conclude that
$\lambda _3 \notin \mathsf {divRH}^3(\overline {\mathcal {M}}_3)$. We conclude that ![]() $\lambda _3 \notin \mathsf {divH}^\star (\overline {\mathcal {M}}_3)$ by (4).
$\lambda _3 \notin \mathsf {divH}^\star (\overline {\mathcal {M}}_3)$ by (4).
Adding one marked point, we can consider the case of ![]() $\overline {\mathcal {M}}_{3,1}$. Again it is known that all (even) cohomology classes on
$\overline {\mathcal {M}}_{3,1}$. Again it is known that all (even) cohomology classes on ![]() $\overline {\mathcal {M}}_{3,1}$ are tautological (see [Reference Schmitt and van ZelmSvZ20, § 5.1]). Thus, again by Poincaré duality, the intersection pairing on
$\overline {\mathcal {M}}_{3,1}$ are tautological (see [Reference Schmitt and van ZelmSvZ20, § 5.1]). Thus, again by Poincaré duality, the intersection pairing on ![]() $\mathsf {RH}^*(\overline {\mathcal {M}}_{3,1})$ is perfect and hence we can completely identify these groups in terms of generators and relations. One finds that
$\mathsf {RH}^*(\overline {\mathcal {M}}_{3,1})$ is perfect and hence we can completely identify these groups in terms of generators and relations. One finds that
is a 28-dimensional subspace of a 29-dimensional space. But remarkably, a calculation by admcycles shows
The containment appears miraculous. Is there a geometric explanation?
The tautological ring ![]() $\mathsf {RH}^*(\overline {\mathcal {M}}_{4,1})$ is also completely under control in codimension 4:
$\mathsf {RH}^*(\overline {\mathcal {M}}_{4,1})$ is also completely under control in codimension 4:
is a 103-dimensional subspace of a 191-dimensional space. An admcycles calculation shows that
Result (5) implies ![]() $\lambda _4 \notin \mathsf {divRH}^4(\overline {\mathcal {M}}_{4})$ by a pull-back argument and
$\lambda _4 \notin \mathsf {divRH}^4(\overline {\mathcal {M}}_{4})$ by a pull-back argument and
since divisor classes are tautological.
For ![]() $g\geq 5$, a boundary restriction argument is pursued. Suppose, for contradiction, that
$g\geq 5$, a boundary restriction argument is pursued. Suppose, for contradiction, that
Then, by pull-back, we have
Consider the standard boundary inclusion
As usual, we have
Then (7) implies
Since ![]() $\mathsf {H}^1(\overline {\mathcal {M}}_{g-1,1})$ and
$\mathsf {H}^1(\overline {\mathcal {M}}_{g-1,1})$ and ![]() $\mathsf {H}^1(\overline {\mathcal {M}}_{1,2})$ both vanish,
$\mathsf {H}^1(\overline {\mathcal {M}}_{1,2})$ both vanish,
We can therefore write ![]() $\mathsf {divH}^g( \overline {\mathcal {M}}_{g-1,1} \times \overline {\mathcal {M}}_{1,2} )$ as
$\mathsf {divH}^g( \overline {\mathcal {M}}_{g-1,1} \times \overline {\mathcal {M}}_{1,2} )$ as
 \begin{align} \mathsf{divH}^{g}(\overline{\mathcal{M}}_{g-1,1})&\otimes \mathsf{divH}^{0}(\overline{\mathcal{M}}_{1,2}) \nonumber\\ \oplus\quad \mathsf{divH}^{g-1}(\overline{\mathcal{M}}_{g-1,1}) &\otimes \mathsf{divH}^{1}(\overline{\mathcal{M}}_{1,2}) \nonumber\\ \oplus\quad \mathsf{divH}^{g-2}(\overline{\mathcal{M}}_{g-1,1}) &\otimes \mathsf{divH}^{2}(\overline{\mathcal{M}}_{1,2}). \end{align}
\begin{align} \mathsf{divH}^{g}(\overline{\mathcal{M}}_{g-1,1})&\otimes \mathsf{divH}^{0}(\overline{\mathcal{M}}_{1,2}) \nonumber\\ \oplus\quad \mathsf{divH}^{g-1}(\overline{\mathcal{M}}_{g-1,1}) &\otimes \mathsf{divH}^{1}(\overline{\mathcal{M}}_{1,2}) \nonumber\\ \oplus\quad \mathsf{divH}^{g-2}(\overline{\mathcal{M}}_{g-1,1}) &\otimes \mathsf{divH}^{2}(\overline{\mathcal{M}}_{1,2}). \end{align}
Since by (8) the degree of ![]() $\delta ^*(\lambda _g)$ splits as
$\delta ^*(\lambda _g)$ splits as ![]() $(g-1)+1$ on the two factors, we conclude that
$(g-1)+1$ on the two factors, we conclude that
 \begin{align*} \lambda_{g-1}\otimes \lambda_1 &\in \mathsf{divH}^{g-1} (\overline{\mathcal{M}}_{g-1,1}) \otimes \mathsf{divH}^{1} (\overline{\mathcal{M}}_{1,2})\\ \implies \lambda_{g-1} &\in \mathsf{divH}^{g-1}(\overline{\mathcal{M}}_{g-1,1}), \end{align*}
\begin{align*} \lambda_{g-1}\otimes \lambda_1 &\in \mathsf{divH}^{g-1} (\overline{\mathcal{M}}_{g-1,1}) \otimes \mathsf{divH}^{1} (\overline{\mathcal{M}}_{1,2})\\ \implies \lambda_{g-1} &\in \mathsf{divH}^{g-1}(\overline{\mathcal{M}}_{g-1,1}), \end{align*}
using that ![]() $\lambda _1 \neq 0 \in \mathsf {divH}^{1}(\overline {\mathcal {M}}_{1,2})$. By descending induction, we contradict (5). Therefore (7) and hence also (6) must be false.
$\lambda _1 \neq 0 \in \mathsf {divH}^{1}(\overline {\mathcal {M}}_{1,2})$. By descending induction, we contradict (5). Therefore (7) and hence also (6) must be false.
2.2 With marked points
The proof of Theorem 3 in cohomology shows that
for ![]() $g\geq 4$. By using (11) as a starting point, we can study
$g\geq 4$. By using (11) as a starting point, we can study
for ![]() $g\geq 4$ and
$g\geq 4$ and ![]() $n\geq 2$ using the boundary restrictions
$n\geq 2$ using the boundary restrictions
The argument used in the proof then easily yields the following statement with markings.
Theorem 3/Markings. For all ![]() $g\geq 4$ and
$g\geq 4$ and ![]() $n\geq 0$, we have
$n\geq 0$, we have
2.3 Proof of Theorem 4
Define the subalgebra of tautological classes
generated by classes of complex degrees less than or equal to ![]() $k$. Since all divisors are tautological,
$k$. Since all divisors are tautological,
The arguments in §§ 2.1 and 2.2 naturally generalize to address the following question: when does
hold?
A crucial case of the question (from the point of view of boundary restriction arguments) is for ![]() $n=1$. Let
$n=1$. Let ![]() $\mathsf {Q}_g(r,k)$ be the statement
$\mathsf {Q}_g(r,k)$ be the statement
which may be true or false.
For example, ![]() $\mathsf {Q}_g(r,g-r)$ is false essentially by definition. In fact,
$\mathsf {Q}_g(r,g-r)$ is false essentially by definition. In fact,
for the same reason. In fact, depending on the parity of ![]() $g-r$, it is also false for
$g-r$, it is also false for ![]() $s$ slightly below
$s$ slightly below ![]() $r$:
$r$:
To see this, note that the even Chern character ![]() $\mathrm {ch}_{g-(r-1)}(\mathbb {E}_g)$ vanishes by [Reference MumfordMum83, Corollary (5.3)]. Expressing it in terms of Chern classes
$\mathrm {ch}_{g-(r-1)}(\mathbb {E}_g)$ vanishes by [Reference MumfordMum83, Corollary (5.3)]. Expressing it in terms of Chern classes ![]() $\lambda _i = c_i(\mathbb {E}_g)$ using Newton's identities, we have
$\lambda _i = c_i(\mathbb {E}_g)$ using Newton's identities, we have
This proves that ![]() $\lambda _{g-r+1}$ can be written in terms of tautological classes of degrees
$\lambda _{g-r+1}$ can be written in terms of tautological classes of degrees ![]() $1, \ldots, g-r$, showing
$1, \ldots, g-r$, showing ![]() $\mathsf {Q}_g(r-1,g-r)$ to be false.
$\mathsf {Q}_g(r-1,g-r)$ to be false.
The boundary arguments used in §§ 2.1 and 2.2 yield the following two results.
Proposition 8 If ![]() $\mathsf {Q}_g(r,k)$ is true, then
$\mathsf {Q}_g(r,k)$ is true, then ![]() $\mathsf {Q}_{g+1}(r,k)$ and
$\mathsf {Q}_{g+1}(r,k)$ and ![]() $\mathsf {Q}_{g+1}(r+1,k)$ are true.
$\mathsf {Q}_{g+1}(r+1,k)$ are true.
Proposition 9 If ![]() $\mathsf {Q}_g(r,k)$ is true, then
$\mathsf {Q}_g(r,k)$ is true, then
for all ![]() $n\geq 0$.
$n\geq 0$.
Since the ![]() $k=1$ case has already been analyzed, we now consider
$k=1$ case has already been analyzed, we now consider ![]() $k= 2$. The first relevant admcycles calculation is
$k= 2$. The first relevant admcycles calculation is
so ![]() $\mathsf {Q}_4(1,2)$ is true. The corresponding subspace here is of dimension 91 inside a 93-dimensional space. As a consequence of Propositions 8 and 9, we obtain the following result.
$\mathsf {Q}_4(1,2)$ is true. The corresponding subspace here is of dimension 91 inside a 93-dimensional space. As a consequence of Propositions 8 and 9, we obtain the following result.
Proposition 10 For all ![]() $g\geq 4$ and
$g\geq 4$ and ![]() $n\geq 0$, we have
$n\geq 0$, we have
A much more complicated admcycles calculation shows that
so ![]() $\mathsf {Q}_5(0,2)$ is true. The corresponding subspace here is of dimension 1314 inside a 1371-dimensional space. As a consequence of Propositions 8 and 9, we find that
$\mathsf {Q}_5(0,2)$ is true. The corresponding subspace here is of dimension 1314 inside a 1371-dimensional space. As a consequence of Propositions 8 and 9, we find that
for all ![]() $g\geq 5$ and
$g\geq 5$ and ![]() $n\geq 0$. For
$n\geq 0$. For ![]() $g\geq 7$, the equality
$g\geq 7$, the equality
is shown by combining results of Edidin [Reference EdidinEdi92] and Boldsen [Reference BoldsenBol12]. We provide a summary of the argument in Appendix A. For ![]() $g\geq 7$, the cycle map
$g\geq 7$, the cycle map
therefore factors through ![]() $\mathsf {RH}_{\leq 2}^\star (\overline {\mathcal {M}}_g)$. Then the non-containment (12) completes the proof of Theorem 4.
$\mathsf {RH}_{\leq 2}^\star (\overline {\mathcal {M}}_g)$. Then the non-containment (12) completes the proof of Theorem 4.
2.4 Cases of Pixton's conjecture (Proposition 5)
For the proofs of Theorem 3 and 4, dimensions and bases of the following graded parts of tautological rings are required:
 \begin{align*} & \mathsf{RH}^4(\overline{\mathcal{M}}_{4,1}),\quad \text{dim}_{\mathbb{Q}} = 191, \\ & \mathsf{RH}^5(\overline{\mathcal{M}}_{5,1}),\quad \text{dim}_{\mathbb{Q}} = 1314. \end{align*}
\begin{align*} & \mathsf{RH}^4(\overline{\mathcal{M}}_{4,1}),\quad \text{dim}_{\mathbb{Q}} = 191, \\ & \mathsf{RH}^5(\overline{\mathcal{M}}_{5,1}),\quad \text{dim}_{\mathbb{Q}} = 1314. \end{align*}
These cases can be analyzed (via admcycles) since the dual pairings are found to have kernels exactly spanned by Pixton's relations. A discussion of the admcycles calculation is presented in Appendix B.
Pixton has conjectured that his relations always provide all tautological relations. Dual pairings are known to be insufficient to prove Pixton's conjecture in all cases; see [Reference PandharipandePan18, Reference Pandharipande, Pixton and ZvonkinePPZ15] for a more complete discussion.
3. The log Chow ring
3.1 Definitions
Let ![]() $(X,D)$ be a non-singular varietyFootnote 10
$(X,D)$ be a non-singular varietyFootnote 10 ![]() $X$ with a normal crossings divisor
$X$ with a normal crossings divisor
with ![]() $\ell$ irreducible components. The divisor
$\ell$ irreducible components. The divisor ![]() $D\subset X$ is called the logarithmic boundary. An open stratum
$D\subset X$ is called the logarithmic boundary. An open stratum
is an irreducible quasi-projective subvariety satisfying two properties.
(i)
 $S$ is étale locally the transverse intersections of the branches of the
$S$ is étale locally the transverse intersections of the branches of the  $D_i$ which meet
$D_i$ which meet  $S$.
$S$.(ii)
 $S$ is maximal with respect to (i).
$S$ is maximal with respect to (i).
The set ![]() $U=X{\setminus} D$ is an open stratum. Every open stratum is non-singular. A closed stratum is the closure of an open stratum.
$U=X{\setminus} D$ is an open stratum. Every open stratum is non-singular. A closed stratum is the closure of an open stratum.
If all ![]() $D_i$ are non-singular and all intersections
$D_i$ are non-singular and all intersections
are irreducible and non-empty, then there are exactly ![]() $2^\ell$ open strata.
$2^\ell$ open strata.
Our main interest will be in the case ![]() $(\overline {\mathcal {M}}_{g,n}, \partial \overline {\mathcal {M}}_{g,n})$ where the normal crossings divisors have self-intersections. The open strata defined above for
$(\overline {\mathcal {M}}_{g,n}, \partial \overline {\mathcal {M}}_{g,n})$ where the normal crossings divisors have self-intersections. The open strata defined above for ![]() $(\overline {\mathcal {M}}_{g,n}, \partial \overline {\mathcal {M}}_{g,n})$ are the same as the usual open strata of the moduli space of stable curves.
$(\overline {\mathcal {M}}_{g,n}, \partial \overline {\mathcal {M}}_{g,n})$ are the same as the usual open strata of the moduli space of stable curves.
An open stratum ![]() $S\subset X$ is simple if the closure
$S\subset X$ is simple if the closure
is non-singular. A simple blow-up of ![]() $(X,D)$ is a blow-up of
$(X,D)$ is a blow-up of ![]() $X$ along the closure
$X$ along the closure ![]() $\overline {S}\subset X$ of a simple stratum. Let
$\overline {S}\subset X$ of a simple stratum. Let
be a simple blow-up along ![]() $\overline {S}$. Let
$\overline {S}$. Let
be the union of the strict transforms ![]() $\widetilde {D}_i$ of
$\widetilde {D}_i$ of ![]() $D_i$ along with the exceptional divisor
$D_i$ along with the exceptional divisor ![]() $E$ of the blow-up (13). Then
$E$ of the blow-up (13). Then ![]() $(\widetilde {X},\widetilde {D})$ is also a non-singular variety with a normal crossings divisor. An iterated blow-up
$(\widetilde {X},\widetilde {D})$ is also a non-singular variety with a normal crossings divisor. An iterated blow-up
is a finite sequence of simple blow-ups of varieties with normal crossings divisors.Footnote 11
The log Chow group of ![]() $(X,D)$ is defined as a colimit over all iterated blow-ups,
$(X,D)$ is defined as a colimit over all iterated blow-ups,
Here, ![]() $\mathsf {logB}(X,D)$ is the category of iterated blow-ups of
$\mathsf {logB}(X,D)$ is the category of iterated blow-ups of ![]() $(X,D)$: objects in
$(X,D)$: objects in ![]() $\mathsf {logB}(X,D)$ are iterated blow-ups of
$\mathsf {logB}(X,D)$ are iterated blow-ups of ![]() $(X,D)$ and morphisms in
$(X,D)$ and morphisms in ![]() $\mathsf {logB}(X,D)$ are iterated blow-ups.
$\mathsf {logB}(X,D)$ are iterated blow-ups.
Since ![]() $(X,D)$ is the trivial iterated blow-up of itself, there is canonical algebra homomorphism
$(X,D)$ is the trivial iterated blow-up of itself, there is canonical algebra homomorphism
which is injective (since an inverse map of ![]() $\mathbb {Q}$-vectors spaces is obtained by proper push-forward). We therefore view
$\mathbb {Q}$-vectors spaces is obtained by proper push-forward). We therefore view ![]() $\mathsf {CH}^\star (X)$ as a subalgebra of
$\mathsf {CH}^\star (X)$ as a subalgebra of ![]() $\mathsf {logCH}^\star (X,D)$. Every Chow class on
$\mathsf {logCH}^\star (X,D)$. Every Chow class on ![]() $X$ canonically determines a log Chow class for
$X$ canonically determines a log Chow class for ![]() $(X,D)$.
$(X,D)$.
3.2 Calculation in genus 2
We will prove Proposition 7: there does not exist a class ![]() $\mathsf {T}\in \mathsf {logCH}^1(\overline {\mathcal {M}}_2)$ satisfying
$\mathsf {T}\in \mathsf {logCH}^1(\overline {\mathcal {M}}_2)$ satisfying
Proof. Denote by ![]() $\pi _* : \mathsf {logCH}^\star (\overline {\mathcal {M}}_{2}) \to \mathsf {CH}^\star (\overline {\mathcal {M}}_{2})$ the push-forward from log Chow to ordinary Chow. We will prove a stronger claim: there does not exist a class
$\pi _* : \mathsf {logCH}^\star (\overline {\mathcal {M}}_{2}) \to \mathsf {CH}^\star (\overline {\mathcal {M}}_{2})$ the push-forward from log Chow to ordinary Chow. We will prove a stronger claim: there does not exist a class ![]() $\mathsf {T}\in \mathsf {logCH}^1(\overline {\mathcal {M}}_{2})$ satisfying
$\mathsf {T}\in \mathsf {logCH}^1(\overline {\mathcal {M}}_{2})$ satisfying
Denote by ![]() $U_2 \subseteq \overline {\mathcal {M}}_{2}$ the open subset obtained by removing all closed strata of codimension at least
$U_2 \subseteq \overline {\mathcal {M}}_{2}$ the open subset obtained by removing all closed strata of codimension at least ![]() $3$. By the excision exact sequence of Chow groups, we have
$3$. By the excision exact sequence of Chow groups, we have
and thus we can verify the stronger claim by working over ![]() $U_2$.
$U_2$.
The open set ![]() $U_2$ has open strata of codimension 1 and 2. Since blow-ups along codimension 1 strata do not change
$U_2$ has open strata of codimension 1 and 2. Since blow-ups along codimension 1 strata do not change ![]() $U_2$, the only simple blow-ups
$U_2$, the only simple blow-ups
are along codimension 2 open strata (all of which are special in ![]() $U_2$). Since the codimension 2 open strata of
$U_2$). Since the codimension 2 open strata of ![]() $U_2$ do not intersect (or self-intersect), we obtain a
$U_2$ do not intersect (or self-intersect), we obtain a ![]() $\mathbb {P}^1$-bundle as an exceptional divisor which contains
$\mathbb {P}^1$-bundle as an exceptional divisor which contains ![]() $0$- and
$0$- and ![]() $\infty$-sectionsFootnote 12 which are codimension 2 strata of
$\infty$-sectionsFootnote 12 which are codimension 2 strata of ![]() $U'_2$. The iterated blow-ups
$U'_2$. The iterated blow-ups
are then simply towers of blow-ups of these codimension 2 toric strata in successive exceptional divisors.
Assume ![]() $\mathsf {T} \in \mathsf {logCH}^1(U_{2})$ satisfies the conditions (14). Since
$\mathsf {T} \in \mathsf {logCH}^1(U_{2})$ satisfies the conditions (14). Since ![]() $\mathsf {T}$ restricts to zero over the compact type locus,
$\mathsf {T}$ restricts to zero over the compact type locus, ![]() $\mathsf {T}$ can be represented as
$\mathsf {T}$ can be represented as
on an iterated blow-up
with all blow-up centers living over strata in the complement of the compact type locus.
There are a single codimension 1 stratum ![]() $\Delta _0\subset U_2$ and two codimension 2 strata
$\Delta _0\subset U_2$ and two codimension 2 strata ![]() $B,C \subset U_2$ contained in the complement of the compact type locus (see Figure 1).
$B,C \subset U_2$ contained in the complement of the compact type locus (see Figure 1).

Figure 1. The stable graphs associated to the codimension ![]() $2$ boundary strata
$2$ boundary strata ![]() $B$ and
$B$ and ![]() $C$ contained in
$C$ contained in ![]() $U_2$.
$U_2$.
Denote by ![]() $E_B^1, \ldots, E_B^\ell$ and
$E_B^1, \ldots, E_B^\ell$ and ![]() $E_C^1, \ldots, E_C^m$ the exceptional divisors of blow-ups with centers lying over
$E_C^1, \ldots, E_C^m$ the exceptional divisors of blow-ups with centers lying over ![]() $B$ and
$B$ and ![]() $C$. Then
$C$. Then ![]() $\mathsf {T}$ has a representationFootnote 13
$\mathsf {T}$ has a representationFootnote 13
 \[ \mathsf{T} = a \cdot [\Delta_0] + \sum_{i=1}^\ell b_i [E_B^i] + \sum_{j=1}^m c_j [E_C^j]. \]
\[ \mathsf{T} = a \cdot [\Delta_0] + \sum_{i=1}^\ell b_i [E_B^i] + \sum_{j=1}^m c_j [E_C^j]. \]
After taking the square and pushing forward, we claim that
with ![]() $x, y, z \in \mathbb {Q}$ satisfying
$x, y, z \in \mathbb {Q}$ satisfying
The claim follows from the following observations.
• In
 $\mathsf {T}^2$, all mixed terms
$\mathsf {T}^2$, all mixed terms  $[\Delta _0] \cdot [E_B^i]$ and
$[\Delta _0] \cdot [E_B^i]$ and  $[\Delta _0] \cdot [E_C^j]$ vanish after push-forward to
$[\Delta _0] \cdot [E_C^j]$ vanish after push-forward to  $U_{2}$, since
$U_{2}$, since
 \[ \pi_*([\Delta_0] \cdot [E_B^i]) = [\Delta_0] \cdot \pi_* [E_B^i] =[\Delta_0] \cdot 0 = 0. \]
\[ \pi_*([\Delta_0] \cdot [E_B^i]) = [\Delta_0] \cdot \pi_* [E_B^i] =[\Delta_0] \cdot 0 = 0. \]
• Similarly, since
 $B \cap C = \emptyset$ in
$B \cap C = \emptyset$ in  $U_2$ (as we have removed the codimension
$U_2$ (as we have removed the codimension  $3$ stratum of
$3$ stratum of  $\overline {\mathcal {M}}_2$), we have
$\overline {\mathcal {M}}_2$), we have  $[E_B^i] \cdot [E_C^j] = 0$.
$[E_B^i] \cdot [E_C^j] = 0$.• Denote by
 $\textbf {M} \in \mathsf {Mat}_{\mathbb {Q}, m \times m}$ the matrix defined by
A basic fact is that
$\textbf {M} \in \mathsf {Mat}_{\mathbb {Q}, m \times m}$ the matrix defined by
A basic fact is that \[ \pi_*([E_C^{j_1}] \cdot [E_C^{j_2}]) = \textbf{M}_{j_1, j_2} [C]. \]
\[ \pi_*([E_C^{j_1}] \cdot [E_C^{j_2}]) = \textbf{M}_{j_1, j_2} [C]. \]
 $\textbf {M}$ is negative definite (see [Reference MumfordMum61, § 1]). Therefore, for
$\textbf {M}$ is negative definite (see [Reference MumfordMum61, § 1]). Therefore, for  $\textbf {b} = (b_i)_{i=1}^\ell$, we have
$\textbf {b} = (b_i)_{i=1}^\ell$, we have
 \[ \pi_* \bigg(\sum_{j=1}^m b_j [E_C^j]\bigg)^2 = \underbrace{( \textbf{b}^\top \textbf{M} \textbf{b} )}_{= z \leq 0} [C]. \]
\[ \pi_* \bigg(\sum_{j=1}^m b_j [E_C^j]\bigg)^2 = \underbrace{( \textbf{b}^\top \textbf{M} \textbf{b} )}_{= z \leq 0} [C]. \]
• The push-forward
is supported on \[ \pi_* \bigg(\sum_{i=1}^\ell b_i [E_B^i]\bigg)^2 \]
\[ \pi_* \bigg(\sum_{i=1}^\ell b_i [E_B^i]\bigg)^2 \]
 $B$ and thus is a multiple
$B$ and thus is a multiple  $y \cdot [B]$ of the fundamental class of
$y \cdot [B]$ of the fundamental class of  $B$.
$B$.
After substituting (15) in the second condition of (14), we conclude the existence of ![]() $x, y, z \in \mathbb {Q}$ with
$x, y, z \in \mathbb {Q}$ with ![]() $x \geq 0$ and
$x \geq 0$ and ![]() $z \leq 0$ satisfying
$z \leq 0$ satisfying
Using admcycles (see Appendix B.3), we can explicitly identify all classes in (16) in
The corresponding affine linear equation has the solution space
But for ![]() $z \leq 0$, we have
$z \leq 0$, we have
which contradicts the assumption that ![]() $x \geq 0$. Therefore, there cannot exist a class
$x \geq 0$. Therefore, there cannot exist a class
satisfying conditions (14).
4. Relationship with logarithmic geometry
4.1 Overview
The definitions of § 3 are natural from the perspective of logarithmic geometry. The choice of the divisor ![]() $D$ on
$D$ on ![]() $X$ can be seen as the choice of a log structure on
$X$ can be seen as the choice of a log structure on ![]() $X$. We briefly recall the relevant definitions and constructions of logarithmic geometry.
$X$. We briefly recall the relevant definitions and constructions of logarithmic geometry.
4.2 Definitions
A log structure on a scheme ![]() $X$ is a sheaf of monoids
$X$ is a sheaf of monoids ![]() $M_X$ on the étale site of
$M_X$ on the étale site of ![]() $X$ together with a homomorphismFootnote 14
$X$ together with a homomorphismFootnote 14
which induces an isomorphism ![]() ${\rm exp}^{-1}(\mathcal {O}_X^*) \cong \mathcal {O}_X^*$ on units.
${\rm exp}^{-1}(\mathcal {O}_X^*) \cong \mathcal {O}_X^*$ on units.
• Morphisms of log schemes
 $(X,M_X) \rightarrow (Y,M_Y)$ are morphisms of schemes
together with homomorphisms of sheaves of monoids
$(X,M_X) \rightarrow (Y,M_Y)$ are morphisms of schemes
together with homomorphisms of sheaves of monoids \[ f:X \to Y \]
\[ f:X \to Y \]
 $f^{-1}M_Y \to M_X$ which are compatible with the structure map
$f^{-1}M_Y \to M_X$ which are compatible with the structure map  $f^{-1}\mathcal {O}_Y \to \mathcal {O}_X$ in the obvious sense.
$f^{-1}\mathcal {O}_Y \to \mathcal {O}_X$ in the obvious sense.• Log structures can be pulled back. Given a morphism of schemes
and a log structure \[ f: X \to Y \]
\[ f: X \to Y \]
 $M_Y$ on
$M_Y$ on  $Y$, there is an induced log structure
$Y$, there is an induced log structure  $f^*M_Y$ on
$f^*M_Y$ on  $X$, generated by
$X$, generated by  $f^{-1}M_Y$ and the units
$f^{-1}M_Y$ and the units  $\mathcal {O}_X^*$.
$\mathcal {O}_X^*$.
The basics of log schemes can be found in Kato's original article on the subject [Reference KatoKat89].
The category of log schemes is, in practice, too large for geometric study. It is therefore common to work in smaller categories by requiring additional properties to hold. For our purposes, we will work only with in the category of fine and saturated log schemes, usually termed f.s. log schemes. The prototype of such a log scheme is
the spectrum of the algebra generated by a fine and saturated monoid ![]() $P$: a finitely generated monoid
$P$: a finitely generated monoid ![]() $P$ which injects into its Grothendieck group
$P$ which injects into its Grothendieck group ![]() $P^{\rm gp}$ and which is saturated there,
$P^{\rm gp}$ and which is saturated there,
The sheaf ![]() $M_{A_P}$ here is the subsheaf of
$M_{A_P}$ here is the subsheaf of ![]() $\mathcal {O}_{A_P}$ generated by
$\mathcal {O}_{A_P}$ generated by ![]() $P$ and the units of
$P$ and the units of ![]() $\mathcal {O}_{A_P}$.
$\mathcal {O}_{A_P}$.
All of the log schemes which arise for us will be comparable to ![]() $A_P$ on the level of log structures. More precisely, we require our log schemes
$A_P$ on the level of log structures. More precisely, we require our log schemes ![]() $X$ to admit the following local charts: for each
$X$ to admit the following local charts: for each ![]() $x \in X$, there must be an étale neighborhood
$x \in X$, there must be an étale neighborhood
an f.s. monoid ![]() $P$, and a map
$P$, and a map ![]() $g: U \to A_P$ such that
$g: U \to A_P$ such that
Since we are always working with f.s. log schemes, the chart ![]() $P$ at
$P$ at ![]() $x$ can in fact always be chosen to be isomorphic to the characteristic monoidFootnote 15
$x$ can in fact always be chosen to be isomorphic to the characteristic monoidFootnote 15
at ![]() $x$.
$x$.
4.3 Normal crossings pairs
Let us now return to the situation of interest for this paper: a pair ![]() $(X,D)$ of a non-singular scheme (or Deligne–Mumford stack) with a normal crossings divisor
$(X,D)$ of a non-singular scheme (or Deligne–Mumford stack) with a normal crossings divisor ![]() $D\subset X$. The pair
$D\subset X$. The pair ![]() $(X,D)$ determines a sheaf
$(X,D)$ determines a sheaf ![]() $M_X$ on the étale site of
$M_X$ on the étale site of ![]() $X$ by setting
$X$ by setting
for each étale map ![]() $p:U \rightarrow X$. The sheaf of units
$p:U \rightarrow X$. The sheaf of units ![]() $\mathcal {O}_X^*$ is a subsheaf of
$\mathcal {O}_X^*$ is a subsheaf of ![]() $M_X$. We write
$M_X$. We write
for the characteristic monoid of ![]() $X$. Normal crossings pairs
$X$. Normal crossings pairs ![]() $(X,D)$, with the log structure described above, are precisely the log schemes which are log smooth over the base field
$(X,D)$, with the log structure described above, are precisely the log schemes which are log smooth over the base field ![]() ${\rm Spec } k$ with trivial log structure.
${\rm Spec } k$ with trivial log structure.
When the irreducible components of ![]() $D$ do not have self-intersections, the log structure
$D$ do not have self-intersections, the log structure ![]() $M_X$ of
$M_X$ of ![]() $(X,D)$ can be defined on the Zariski topology of
$(X,D)$ can be defined on the Zariski topology of ![]() $X$. The result is a technically simpler theory. The pair
$X$. The result is a technically simpler theory. The pair ![]() $(X,D)$ is then called a toroidal embedding (without self-intersection) in [Reference Kempf, Knudsen, Mumford and Saint-DonatKKMS73]. However, for a general pair
$(X,D)$ is then called a toroidal embedding (without self-intersection) in [Reference Kempf, Knudsen, Mumford and Saint-DonatKKMS73]. However, for a general pair ![]() $(X,D)$,
$(X,D)$, ![]() $M_X$ can only be defined on the étale site of
$M_X$ can only be defined on the étale site of ![]() $X$. The general étale case differs from the Zariski case in two key aspects: the irreducible components of
$X$. The general étale case differs from the Zariski case in two key aspects: the irreducible components of ![]() $D$ can self-intersect, and the characteristic monoid
$D$ can self-intersect, and the characteristic monoid ![]() $\overline {M}_X$, while locally constant on a stratum, can globally acquire monodromy.
$\overline {M}_X$, while locally constant on a stratum, can globally acquire monodromy.
The characteristic monoid ![]() $\overline {M}_X$ is a constructible sheaf on
$\overline {M}_X$ is a constructible sheaf on ![]() $X$. The connected components of the loci on which
$X$. The connected components of the loci on which ![]() $\overline {M}_X$ is locally constant define a stratification of
$\overline {M}_X$ is locally constant define a stratification of ![]() $X$, which is precisely the stratification of § 3.1. Indeed, for a geometric point
$X$, which is precisely the stratification of § 3.1. Indeed, for a geometric point ![]() $x \in X$,
$x \in X$,
where ![]() $r$ is the number of branches (in the étale topology) of
$r$ is the number of branches (in the étale topology) of ![]() $D$ that contain
$D$ that contain ![]() $x$.
$x$.
A combinatorial space can be built from the information contained in ![]() $\overline {M}_{X}$. There are two basic approaches. The first, which is more geometric and more evidently combinatorial, is to build the cone complex
$\overline {M}_{X}$. There are two basic approaches. The first, which is more geometric and more evidently combinatorial, is to build the cone complex ![]() $C(X,D)$ of
$C(X,D)$ of ![]() $(X,D)$. We briefly outline the construction (details can be found in [Reference Cavalieri, Chan, Ulirsch and WiseCCUW20, Reference Abramovich, Chen, Marcus, Ulirsch and WiseACMUW16]).
$(X,D)$. We briefly outline the construction (details can be found in [Reference Cavalieri, Chan, Ulirsch and WiseCCUW20, Reference Abramovich, Chen, Marcus, Ulirsch and WiseACMUW16]).
We begin with the case where ![]() $M_X$ is defined Zariski locally on
$M_X$ is defined Zariski locally on ![]() $X$ (when the irreducible components of
$X$ (when the irreducible components of ![]() $D$ do not have self-intersections). Then
$D$ do not have self-intersections). Then ![]() $C(X,D)$ is a rational polyhedral cone complex (see [Reference Kempf, Knudsen, Mumford and Saint-DonatKKMS73]).
$C(X,D)$ is a rational polyhedral cone complex (see [Reference Kempf, Knudsen, Mumford and Saint-DonatKKMS73]).
• For each point
 $x \in X$, the characteristic monoid
$x \in X$, the characteristic monoid  $\overline {M}_{X,\overline {x}}$ determines a rational polyhedral cone
together with an integral structure
$\overline {M}_{X,\overline {x}}$ determines a rational polyhedral cone
together with an integral structure \[ \sigma_{X,x} = {\rm Hom}_{{\rm Monoids}}(\overline{M}_{X,\overline{x}}, \mathbb{R}_{\ge 0}) \]
\[ \sigma_{X,x} = {\rm Hom}_{{\rm Monoids}}(\overline{M}_{X,\overline{x}}, \mathbb{R}_{\ge 0}) \]
 \[ N_{X,x} = {\rm Hom}(\overline{M}_{X,\overline{x}}^{\rm gp},\mathbb{Z}). \]
\[ N_{X,x} = {\rm Hom}(\overline{M}_{X,\overline{x}}^{\rm gp},\mathbb{Z}). \]
• When
 $x$ belongs to a stratum
$x$ belongs to a stratum  $S \subset X$ and
$S \subset X$ and  $y$ belongs to the closure
$y$ belongs to the closure  $\overline {S}\subset X$, there are canonical inclusions
$\overline {S}\subset X$, there are canonical inclusions
 \[ \sigma_{X,x} \subset \sigma_{X,y},\quad N_{X,x} \subset N_{X,y}. \]
\[ \sigma_{X,x} \subset \sigma_{X,y},\quad N_{X,x} \subset N_{X,y}. \]
• We glue the cones
 $\sigma _{X,x}$ together with their integral structures to form the complex
$\sigma _{X,x}$ together with their integral structures to form the complex
 \[ C(X,D) = \varinjlim_{x \in X} (\sigma_{X,x}, \sigma_{X,x} \cap N_{X,x}). \]
\[ C(X,D) = \varinjlim_{x \in X} (\sigma_{X,x}, \sigma_{X,x} \cap N_{X,x}). \]
• More effectively, instead of working with all points
 $x \in X$, we can take the finite set
$x \in X$, we can take the finite set  $\{x_S \}$ of the generic points of the strata of
$\{x_S \}$ of the generic points of the strata of  $(X,D)$. Then
In other words,
$(X,D)$. Then
In other words, \[ C(X,D) = \varinjlim_{x_S}(\sigma_{X,x_S}, \sigma_{X,x_S} \cap N_{X,x_S}). \]
\[ C(X,D) = \varinjlim_{x_S}(\sigma_{X,x_S}, \sigma_{X,x_S} \cap N_{X,x_S}). \]
 $C(X,D)$ is the dual intersection complex of
$C(X,D)$ is the dual intersection complex of  $(X,D)$.
$(X,D)$.
When ![]() $M_X$ is defined only on the étale site, we build the cone complex
$M_X$ is defined only on the étale site, we build the cone complex ![]() $C(X,D)$ by descent.
$C(X,D)$ by descent.
• We find an étale (but not necessarily proper), strict (
 $f^*M_X = M_Y)$ cover
$f^*M_X = M_Y)$ cover  $f: Y \to X$ which is as fine as possible (called atomic or small in the literature): the log structure on
$f: Y \to X$ which is as fine as possible (called atomic or small in the literature): the log structure on  $Y$ is defined on the Zariski site of
$Y$ is defined on the Zariski site of  $Y$, and each connected component of
$Y$, and each connected component of  $Y$ has a unique closed stratum. Taking a further such cover
$Y$ has a unique closed stratum. Taking a further such cover  $V$ of the fiber product
$V$ of the fiber product  $Y \times _X Y$ if necessary, we find a groupoid presentation
$Y \times _X Y$ if necessary, we find a groupoid presentation
 \[ V \rightrightarrows Y \rightarrow X. \]
\[ V \rightrightarrows Y \rightarrow X. \]
• We define
in the category of stacks (with respect to the topology generated by face inclusions) over cone complexes. The construction is carried out in detail in [Reference Cavalieri, Chan, Ulirsch and WiseCCUW20], where it is also shown that it is independent of the choice of groupoid presentation. \[ C(X,D) = \varinjlim [C(V) \rightrightarrows C(Y)] \]
\[ C(X,D) = \varinjlim [C(V) \rightrightarrows C(Y)] \]
Moreover, ![]() $C(X,D)$ is a complex of cones, but no longer a rational polyhedral cone complex. For each point
$C(X,D)$ is a complex of cones, but no longer a rational polyhedral cone complex. For each point ![]() $x \in X$, there is a canonical map
$x \in X$, there is a canonical map
but the map may no longer be injective. As the étale local branches of the divisor ![]() $D$ may be connected globally on
$D$ may be connected globally on ![]() $X$, the faces of the cones
$X$, the faces of the cones ![]() $\sigma _{X,x}$ may be glued to each other in
$\sigma _{X,x}$ may be glued to each other in ![]() $C(X,D)$, and they may naturally acquire automorphisms coming from the monodromy of the branches of
$C(X,D)$, and they may naturally acquire automorphisms coming from the monodromy of the branches of ![]() $D$.
$D$.
4.4 Artin fans
An equivalent combinatorial space is the Artin fan ![]() $\mathcal {A}_X$ of
$\mathcal {A}_X$ of ![]() $(X,D)$. The Artin fan is defined by gluing, instead of the dual cones
$(X,D)$. The Artin fan is defined by gluing, instead of the dual cones ![]() $\sigma _{X,x}$ of
$\sigma _{X,x}$ of ![]() $\overline {M}_{X,\overline {x}}$, the quotient stacks
$\overline {M}_{X,\overline {x}}$, the quotient stacks
The gluing is exactly the same as for ![]() $C(X,D)$ as explained above. When
$C(X,D)$ as explained above. When ![]() $M_X$ is defined on the Zariski site of
$M_X$ is defined on the Zariski site of ![]() $X$,
$X$,
and when ![]() $M_X$ is defined only on the étale site of
$M_X$ is defined only on the étale site of ![]() $X$,
$X$,
for an atomic presentation ![]() $\varinjlim [V \rightrightarrows Y] = X$ as before.
$\varinjlim [V \rightrightarrows Y] = X$ as before.
The Artin fan ![]() $\mathcal {A}_X$ captures exactly the same combinatorial information as the cone complex
$\mathcal {A}_X$ captures exactly the same combinatorial information as the cone complex ![]() $C(X,D)$, but is geometrically less intuitive. Nevertheless, the Artin fan has the advantage of coming with a smooth morphism of stacks
$C(X,D)$, but is geometrically less intuitive. Nevertheless, the Artin fan has the advantage of coming with a smooth morphism of stacks
4.5 Logarithmic modifications
The cone complex ![]() $C(X,D)$ encodes an important operation: logarithmic modification of
$C(X,D)$ encodes an important operation: logarithmic modification of ![]() $X$. Logarithmic modifications correspond to subdivisions of
$X$. Logarithmic modifications correspond to subdivisions of ![]() $C(X,D)$. A subdivision of
$C(X,D)$. A subdivision of ![]() $C(X,D)$ is, by definition, a compatible subdivision of all the cones
$C(X,D)$ is, by definition, a compatible subdivision of all the cones ![]() $\sigma _{X,x}$ compatible with the gluing relations. Each cone in the subdivision
$\sigma _{X,x}$ compatible with the gluing relations. Each cone in the subdivision ![]() $\sigma _{X,x}' \rightarrow \sigma _{X,x}$ determines dually a map
$\sigma _{X,x}' \rightarrow \sigma _{X,x}$ determines dually a map ![]() $\overline {M}_{X,\overline {x}} \rightarrow \overline {M}_{X,\overline {x}}'$, and so a map
$\overline {M}_{X,\overline {x}} \rightarrow \overline {M}_{X,\overline {x}}'$, and so a map
The compatibility of the subdivisions with respect to the gluing relations in ![]() $C(X,D)$ implies that these maps glue to a proper and birational representable map
$C(X,D)$ implies that these maps glue to a proper and birational representable map
Then we define
which is proper, birational, and representable over ![]() $X$. Moreover,
$X$. Moreover, ![]() $X'$ has an induced log structure, and there is a map
$X'$ has an induced log structure, and there is a map
which is proper, Deligne–Mumford type, étale, and bijective.
The map ![]() $\mathcal {A}_{X}' \to \mathcal {A}_{X'}$ – called the relative Artin fan of
$\mathcal {A}_{X}' \to \mathcal {A}_{X'}$ – called the relative Artin fan of ![]() $X'$ over
$X'$ over ![]() $X$ in the literature – is not necessarily representable, as the various monodromy groups of the strata of
$X$ in the literature – is not necessarily representable, as the various monodromy groups of the strata of ![]() $\mathcal {A}_X$ may act non-faithfully on the strata of
$\mathcal {A}_X$ may act non-faithfully on the strata of ![]() $\mathcal {A}_{X}'$, whereas the monodromy groups of the strata of
$\mathcal {A}_{X}'$, whereas the monodromy groups of the strata of ![]() $X'$ act faithfully on
$X'$ act faithfully on ![]() $\mathcal {A}_{X'}$ by definition. In this way the strata of
$\mathcal {A}_{X'}$ by definition. In this way the strata of ![]() $\mathcal {A}_{X}'$ become trivial gerbes over the strata of
$\mathcal {A}_{X}'$ become trivial gerbes over the strata of ![]() $\mathcal {A}_{X'}$. In a sense,
$\mathcal {A}_{X'}$. In a sense, ![]() $\mathcal {A}_{X'}$ can be considered as a relative coarse moduli space for
$\mathcal {A}_{X'}$ can be considered as a relative coarse moduli space for ![]() $\mathcal {A}_{X}'$.Footnote 16
$\mathcal {A}_{X}'$.Footnote 16
Geometrically, subdivisions come in three levels of generality as follows.
• General subdivisions simply produce proper birational maps
 $X' \to X$, which are isomorphisms over
$X' \to X$, which are isomorphisms over  $X - D$. Such maps are called logarithmic modifications
$X - D$. Such maps are called logarithmic modifications• Log blow-ups are a special kind of subdivision. They are the subdivisions of
 $C(X,D)$ into the domains of linearity of a piecewise linear function on
$C(X,D)$ into the domains of linearity of a piecewise linear function on  $C(X,D)$, and they correspond to a sheaf of monomial ideals,
The map
$C(X,D)$, and they correspond to a sheaf of monomial ideals,
The map \[ I \subset M_X. \]
\[ I \subset M_X. \]
 $X' \to X$ is then projective and is the normalization of the blow-up of
$X' \to X$ is then projective and is the normalization of the blow-up of  $X$ along the sheaf of ideals
$X$ along the sheaf of ideals  ${\rm exp}(I) \subset \mathcal {O}_X$.
${\rm exp}(I) \subset \mathcal {O}_X$.• Star subdivisions along simple strata
 $S$ correspond to the most basic logarithmic modifications. The strata of
$S$ correspond to the most basic logarithmic modifications. The strata of  $X$ are, by construction, in bijection with the cones of
$X$ are, by construction, in bijection with the cones of  $C(X,D)$. We obtain a subdivision by subdividing
$C(X,D)$. We obtain a subdivision by subdividing  $\sigma _{X,x_S}$ along its barycenter (see [Reference Cox, Little and SchenckCLS11, Definition 3.3.13]). A simple blow-up along
$\sigma _{X,x_S}$ along its barycenter (see [Reference Cox, Little and SchenckCLS11, Definition 3.3.13]). A simple blow-up along  $\overline {S}$ corresponds precisely to the star subdivision of the cone
$\overline {S}$ corresponds precisely to the star subdivision of the cone  $\sigma _{X,x_S}$. Further applications of the star subdivision operation are discussed in § 5.3.
$\sigma _{X,x_S}$. Further applications of the star subdivision operation are discussed in § 5.3.
Although star subdivisions are the simplest and most basic subdivisions, we need not consider more general subdivisions for our purposes. We are only concerned with statements that are valid over some arbitrarily fine subdivision, and the star subdivisions along simple strata are cofinal in this setting: for each subdivision
there is a further subdivision ![]() $C(X,D)'' \to C(X,D)'$ such that the composition
$C(X,D)'' \to C(X,D)'$ such that the composition ![]() $C(X,D)'' \to C(X,D)$ is the composition of star subdivisions along simple strata (see [Reference OdaOda88, Chapter 1.7]). So the reader can restrict attention to simple blow-ups without any loss of generality.
$C(X,D)'' \to C(X,D)$ is the composition of star subdivisions along simple strata (see [Reference OdaOda88, Chapter 1.7]). So the reader can restrict attention to simple blow-ups without any loss of generality.
We define a category ![]() $\mathsf {logM}(X,D)$ whose objects are log modifications
$\mathsf {logM}(X,D)$ whose objects are log modifications
obtained via subdivisions of ![]() $C(X,D)$. There is a unique morphism
$C(X,D)$. There is a unique morphism ![]() $X'' \to X'$ if and only if
$X'' \to X'$ if and only if ![]() $X''$ is a log modification of
$X''$ is a log modification of ![]() $X'$. Following [Reference BarrottBar18], we then define
$X'$. Following [Reference BarrottBar18], we then define
As simple blow-ups are cofinal among log modifications, we have, equivalently,
as defined in § 3.1.
5. The divisor subalgebra of log Chow
5.1 Definitions
Let ![]() $(X,D)$ be a non-singular variety
$(X,D)$ be a non-singular variety ![]() $X$ with a normal crossings divisor
$X$ with a normal crossings divisor
with ![]() $\ell$ irreducible components. Let
$\ell$ irreducible components. Let
be the subalgebra generated by the classes of all the components of the associated normal crossings divisors of all iterated blow-ups of ![]() $X$.
$X$.
Let ![]() $S\subset X$ be an open stratum of codimension
$S\subset X$ be an open stratum of codimension ![]() $s$, let
$s$, let ![]() $\overline {S} \subset X$ be the closure, and let
$\overline {S} \subset X$ be the closure, and let
be the normalization of ![]() $\overline {S}$ equipped with a canonical map
$\overline {S}$ equipped with a canonical map ![]() $\epsilon$ to
$\epsilon$ to ![]() $X$. The normalization
$X$. The normalization ![]() $\widetilde {S}$ is non-singular and separates the branches of the self-intersections of
$\widetilde {S}$ is non-singular and separates the branches of the self-intersections of ![]() $\overline {S}$. The map
$\overline {S}$. The map ![]() $\epsilon$ is an immersion locally on the source and therefore has a well-defined normal bundle
$\epsilon$ is an immersion locally on the source and therefore has a well-defined normal bundle
of rank ![]() $s$.
$s$.
An open stratum ![]() $S\subset X$ of codimension
$S\subset X$ of codimension ![]() $s$ is étale locally cut out by
$s$ is étale locally cut out by ![]() $s$ branches of the full divisor
$s$ branches of the full divisor ![]() $D$. These
$D$. These ![]() $s$ branches are partitioned by monodromy orbits over
$s$ branches are partitioned by monodromy orbits over ![]() $S$. Each monodromy orbit determines a summand of
$S$. Each monodromy orbit determines a summand of ![]() $\mathsf {N}_\epsilon$. We obtain a canonical splitting of
$\mathsf {N}_\epsilon$. We obtain a canonical splitting of ![]() $\mathsf {N}_\epsilon$ corresponding to monodromy orbits
$\mathsf {N}_\epsilon$ corresponding to monodromy orbits
where ![]() $\mathsf {Orb}(S)$ is the set of monodromy orbits of the branches of
$\mathsf {Orb}(S)$ is the set of monodromy orbits of the branches of ![]() $D$ cutting out
$D$ cutting out ![]() $S$, and
$S$, and ![]() $|\gamma |$ is the number of branches in the orbit
$|\gamma |$ is the number of branches in the orbit ![]() $\gamma$. For polynomials
$\gamma$. For polynomials ![]() $P_\gamma$ in the Chern classes of
$P_\gamma$ in the Chern classes of ![]() $\mathsf {N}^\gamma _\epsilon$, we define
$\mathsf {N}^\gamma _\epsilon$, we define
 \begin{equation} [S, \{P_\gamma\}_{\gamma\in \mathsf{Orb}(S)}] = \epsilon_*\bigg(\prod_{\gamma\in \mathsf{Orb}(S)} P_\gamma( \mathsf{N}^\gamma_\epsilon)\bigg) \in \mathsf{CH}^\star(X). \end{equation}
\begin{equation} [S, \{P_\gamma\}_{\gamma\in \mathsf{Orb}(S)}] = \epsilon_*\bigg(\prod_{\gamma\in \mathsf{Orb}(S)} P_\gamma( \mathsf{N}^\gamma_\epsilon)\bigg) \in \mathsf{CH}^\star(X). \end{equation} We define normally decorated classes by the following more general construction. Let ![]() $G$ be the monodromy group of the
$G$ be the monodromy group of the ![]() $s$ branches of
$s$ branches of ![]() $D$ which cut out
$D$ which cut out ![]() $S$. Over
$S$. Over ![]() $\widetilde {S}$, there is a principal
$\widetilde {S}$, there is a principal ![]() $G$-bundle
$G$-bundle
over which the ![]() $s$ branches determine
$s$ branches determine ![]() $s$ line bundles
$s$ line bundles
The ![]() $G$-action on
$G$-action on ![]() $\widetilde {P}$ permutes the line bundles (18) via the original monodromy representation. Let
$\widetilde {P}$ permutes the line bundles (18) via the original monodromy representation. Let ![]() $P_G$ be any
$P_G$ be any ![]() $G$-invariant polynomial in the Chern classes
$G$-invariant polynomial in the Chern classes ![]() $c_1(N_i)$. Since
$c_1(N_i)$. Since ![]() $P_G(c_1(N_1), \ldots,c_1(N_s))$ is
$P_G(c_1(N_1), \ldots,c_1(N_s))$ is ![]() $G$-invariant,
$G$-invariant,
We define a normally decorated strata class by
Construction (17) is a special case of a normally decorated strata class.
A fundamental result about the log Chow ring of ![]() $(X,D)$ is the following inclusion.
$(X,D)$ is the following inclusion.
Theorem 11 Let ![]() $(X,D)$ be a non-singular variety with a normal crossings divisor. Let
$(X,D)$ be a non-singular variety with a normal crossings divisor. Let ![]() $S\subset X$ be an open stratum. Every normally decorated class associated to
$S\subset X$ be an open stratum. Every normally decorated class associated to ![]() $S$ lies in
$S$ lies in ![]() $\mathsf {divlogCH}^\star (X,D)$.
$\mathsf {divlogCH}^\star (X,D)$.
We give two proofs of Theorem 11. In § 5.2 we give a very concrete iterated blow-up of ![]() $X$ and an explicit computation expressing the normally decorated class as a sum of products of divisors. On the other hand, in Corollary 16 we give a more conceptual explanation based on the study of the Chow group of the Artin fan of the pair
$X$ and an explicit computation expressing the normally decorated class as a sum of products of divisors. On the other hand, in Corollary 16 we give a more conceptual explanation based on the study of the Chow group of the Artin fan of the pair ![]() $(X,D)$.
$(X,D)$.
5.2 Proof of Theorem 11
Theorem 11 is almost trivial if every irreducible component ![]() $D_i$ of
$D_i$ of ![]() $D$ is non-singular. The complexity of the argument occurs only if there are irreducible components with self-intersections.
$D$ is non-singular. The complexity of the argument occurs only if there are irreducible components with self-intersections.
Proof. Let ![]() $S\subset X$ be an open stratum of codimension
$S\subset X$ be an open stratum of codimension ![]() $s$. The first case to consider is when
$s$. The first case to consider is when ![]() $S$ is simple. Then the closure
$S$ is simple. Then the closure
in non-singular and no normalization is needed,
Let ![]() $G$ be the monodromy of the
$G$ be the monodromy of the ![]() $s$ branches of
$s$ branches of ![]() $D$ which cut out
$D$ which cut out ![]() $S$. We must prove
$S$. We must prove
for every ![]() $G$-invariant polynomial
$G$-invariant polynomial ![]() $P_G$.
$P_G$.
We argue by induction on the degree of ![]() $P_G$. The base case is when
$P_G$. The base case is when ![]() $P_G$ is of degree 0. We can take
$P_G$ is of degree 0. We can take ![]() $P_G=1$, and we must prove
$P_G=1$, and we must prove
Our argument requires a blow-up construction which we term an explosion.
The explosion of ![]() $(X,D)$ along a simple stratum
$(X,D)$ along a simple stratum ![]() $S$,
$S$,
is defined by a sequence of blow-ups of ![]() $X$. To describe the blow-ups locallyFootnote 17 near a point
$X$. To describe the blow-ups locallyFootnote 17 near a point ![]() $p\in S$, let
$p\in S$, let
be the branches of ![]() $D$ cutting out
$D$ cutting out ![]() $S$ near
$S$ near ![]() $p$.
$p$.
• At the zeroth stage, we blow up
 $S$, the intersection of all
$S$, the intersection of all  $s$ branches
$s$ branches  $B_1,\ldots,B_s$.
$B_1,\ldots,B_s$.
Consider next the strict transform of the intersection of ![]() $s-1$ branches. For each choice of
$s-1$ branches. For each choice of ![]() $s-1$ branches, the strict transform of the intersection is non-singular of codimension
$s-1$ branches, the strict transform of the intersection is non-singular of codimension ![]() $s-1$ over an open set of
$s-1$ over an open set of ![]() $p\in X$. Moreover, the strict transforms of the intersections of different sets of
$p\in X$. Moreover, the strict transforms of the intersections of different sets of ![]() $s-1$ branches are disjoint over an open set of
$s-1$ branches are disjoint over an open set of ![]() $p\in X$.
$p\in X$.
• At the first stage, we blow up all
 $s$ of these strict transforms of intersections of
$s$ of these strict transforms of intersections of  $s-1$ branches.
$s-1$ branches.
Then the strict transforms of the intersections of ![]() $s-2$ branches among
$s-2$ branches among ![]() $B_1,\ldots, B_s$ are non-singular of codimension
$B_1,\ldots, B_s$ are non-singular of codimension ![]() $s-2$ and disjoint over an open set of
$s-2$ and disjoint over an open set of ![]() $p\in X$.
$p\in X$.
• At the second stage, we blow up all
 $\binom {s}{2}$ of these strict transforms of intersections of
$\binom {s}{2}$ of these strict transforms of intersections of  $s-2$ branches.
$s-2$ branches.
We proceed in the above pattern until we have completed ![]() $s-1$ stages.
$s-1$ stages.
• At the
 $j$th stage, we blow up all
$j$th stage, we blow up all  $\binom {s}{j}$ strict transforms of intersections of
$\binom {s}{j}$ strict transforms of intersections of  $s-j$ branches.
$s-j$ branches.
The explosion (20) is the result after stage ![]() $j=s-1$.Footnote 18 Since the above blow-ups are defined symmetrically with respect to the branches
$j=s-1$.Footnote 18 Since the above blow-ups are defined symmetrically with respect to the branches ![]() $B_i$, the definition is well defined globally on
$B_i$, the definition is well defined globally on ![]() $X$.
$X$.
Near ![]() $S$, all the prescribed blow-ups are of simple loci, but non-simplicity may occur away from
$S$, all the prescribed blow-ups are of simple loci, but non-simplicity may occur away from ![]() $S$. In order for the explosion to be a sequence of simple blow-ups, some extra blow-ups may be required far from
$S$. In order for the explosion to be a sequence of simple blow-ups, some extra blow-ups may be required far from ![]() $S$. Since we will only be interested in the geometry near
$S$. Since we will only be interested in the geometry near ![]() $S$, the blow-ups related to non-simplicity away from
$S$, the blow-ups related to non-simplicity away from ![]() $S$ are not important for our argument (and are not included in our notation).
$S$ are not important for our argument (and are not included in our notation).
A local study shows the following properties of the explosion
near ![]() $S$.
$S$.
(i) The inverse image
 $e^{-1}(S) \subset \mathsf {E}_S(X,D)$ is a non-singular irreducible subvariety which we denote by
$e^{-1}(S) \subset \mathsf {E}_S(X,D)$ is a non-singular irreducible subvariety which we denote by  $\mathsf {E}_S(S)$ and call the exceptional divisor of the explosion. We denote the inclusion by
$\mathsf {E}_S(S)$ and call the exceptional divisor of the explosion. We denote the inclusion by
 \[ \iota: \mathsf{E}_S(S) \rightarrow \mathsf{E}_S(X,D). \]
\[ \iota: \mathsf{E}_S(S) \rightarrow \mathsf{E}_S(X,D). \]
(ii) Let
 $\mathsf {N}_S$ be the rank
$\mathsf {N}_S$ be the rank  $s$ normal bundle of
$s$ normal bundle of  $S$ in
$S$ in  $X$. The fibers of the projective normal bundle
(21)have a canonical (unordered) set of
$X$. The fibers of the projective normal bundle
(21)have a canonical (unordered) set of \begin{equation} \mathsf{P}(\mathsf{N}_S) \rightarrow S \end{equation}
\begin{equation} \mathsf{P}(\mathsf{N}_S) \rightarrow S \end{equation} $s$ coordinate hyperplanes determined by the
$s$ coordinate hyperplanes determined by the  $s$ local branches of
$s$ local branches of  $D$ cutting out
$D$ cutting out  $S$. In the fibers of (21), these relative hyperplanes determine
$S$. In the fibers of (21), these relative hyperplanes determine  $s$ coordinate points,
$s$ coordinate points,  $\binom {s}{2}$ coordinate lines,
$\binom {s}{2}$ coordinate lines,  $\binom {s}{3}$ coordinate planes, and so on.
$\binom {s}{3}$ coordinate planes, and so on.(iii) The restriction of the explosion morphism to the exceptional divisor
is obtained from \[ e_S: \mathsf{E}_S(S) \rightarrow S \]
\[ e_S: \mathsf{E}_S(S) \rightarrow S \]
 $\mathsf {P}(\mathsf {N}_S) \rightarrow S$ by first blowing up the coordinate points, and then blowing up the strict transforms of the coordinate lines, and so on. For
the
$\mathsf {P}(\mathsf {N}_S) \rightarrow S$ by first blowing up the coordinate points, and then blowing up the strict transforms of the coordinate lines, and so on. For
the \[ 1\leq j \leq s-1, \]
\[ 1\leq j \leq s-1, \]
 $j$th stage of the construction of the explosion restricts to the blow-up of the strict transform of the
$j$th stage of the construction of the explosion restricts to the blow-up of the strict transform of the  $(j-1)$-dimensional coordinate linear spaces of the fibers of (21).
$(j-1)$-dimensional coordinate linear spaces of the fibers of (21).(iv) On
 $\mathsf {E}_S(S)$, we have a distinguished set of divisors
Here,
$\mathsf {E}_S(S)$, we have a distinguished set of divisors
Here, \[ E_0, E_1, \ldots, E_{s-1} \in \mathsf{CH}^1(\mathsf{E}_S(S)). \]
\[ E_0, E_1, \ldots, E_{s-1} \in \mathsf{CH}^1(\mathsf{E}_S(S)). \]
 $E_0$ is the pull-back to
$E_0$ is the pull-back to  $\mathsf {E}_S(S)$ of
determined by the zeroth stage of the construction of the explosion. Then
$\mathsf {E}_S(S)$ of
determined by the zeroth stage of the construction of the explosion. Then \[ \mathcal{O}_{\mathsf{P}(\mathsf{N}_S)}(-1) \rightarrow \mathsf{P}(\mathsf{N}_S) \]
\[ \mathcal{O}_{\mathsf{P}(\mathsf{N}_S)}(-1) \rightarrow \mathsf{P}(\mathsf{N}_S) \]
 $E_j \in \mathsf {CH}^1( \mathsf {E}_S(S))$ is the pull-back to
$E_j \in \mathsf {CH}^1( \mathsf {E}_S(S))$ is the pull-back to  $\mathsf {E}_S(S)$ of the exceptional divisor obtained from the blow-up of the strict transform of the
$\mathsf {E}_S(S)$ of the exceptional divisor obtained from the blow-up of the strict transform of the  $(j-1)$-dimensional coordinate linear spaces in the fibers of (21).
$(j-1)$-dimensional coordinate linear spaces in the fibers of (21).(v) Every class of the form
where \[ [\mathsf{E}_S(S)]\cdot \mathsf{F}(E_0,\ldots,E_{s-1}) \in \mathsf{CH}^*(\mathsf{E}_S(X,D)), \]
\[ [\mathsf{E}_S(S)]\cdot \mathsf{F}(E_0,\ldots,E_{s-1}) \in \mathsf{CH}^*(\mathsf{E}_S(X,D)), \]
 $\mathsf {F}$ is a polynomial, lies in the divisor ring of log Chow,
The claim follows from the geometric construction of the explosion. To start,
$\mathsf {F}$ is a polynomial, lies in the divisor ring of log Chow,
The claim follows from the geometric construction of the explosion. To start, \[ [\mathsf{E}_S(S)]\cdot \mathsf{F}(E_0,\ldots,E_{s-1}) \in \mathsf{divlogCH}^*(X,D). \]
\[ [\mathsf{E}_S(S)]\cdot \mathsf{F}(E_0,\ldots,E_{s-1}) \in \mathsf{divlogCH}^*(X,D). \]
 $\mathsf {E}_S(S)$ is a component of the associated normal crossings divisor of
$\mathsf {E}_S(S)$ is a component of the associated normal crossings divisor of  $\mathsf {E}_S(X,D)$. For each
$\mathsf {E}_S(X,D)$. For each  $0\leq j \leq s-1$,
$0\leq j \leq s-1$,  $E_j$ comes from the pull-back of a divisor stratum of the blow-up at the
$E_j$ comes from the pull-back of a divisor stratum of the blow-up at the  $j$th stage.
$j$th stage.
To the explosion geometry, we can apply Fulton's excess intersection formula. We start with the zeroth stage:
is the blow-up along ![]() $S$, and
$S$, and
When we pull back ![]() $e_0^*[S]$ all the way to
$e_0^*[S]$ all the way to ![]() $\mathsf {E}_S(X,D)$, we obtainFootnote 19
$\mathsf {E}_S(X,D)$, we obtainFootnote 19
By definition, we have
By property (v) above for the explosion geometry, to prove
we need only show that
for polynomials ![]() $\mathsf {F}_k$,
$\mathsf {F}_k$, ![]() $1\leq k \leq s-1$.
$1\leq k \leq s-1$.
Claim (23) is established directly by the following basic formula of the explosion geometry. For ![]() $0\leq j\leq s-1$, let
$0\leq j\leq s-1$, let
 \[ \mathsf{L_j} = \sum_{i=0}^j E_i. \]
\[ \mathsf{L_j} = \sum_{i=0}^j E_i. \]
Let ![]() $\sigma _k$ be the
$\sigma _k$ be the ![]() $k$th elementary symmetric polynomial. Then we claim that
$k$th elementary symmetric polynomial. Then we claim that
Once we prove (24), this immediately shows (23) and thus, as explained above, establishes (22). We remind ourselves that (22) represents the base case ![]() $P_G=1$ of our inductive proof that
$P_G=1$ of our inductive proof that ![]() $[S, P_G] \in \mathsf {divlogCH}^*(X)$.
$[S, P_G] \in \mathsf {divlogCH}^*(X)$.
Let ![]() $\mathsf {T}=(\mathbb {C}^*)^s$ and let
$\mathsf {T}=(\mathbb {C}^*)^s$ and let ![]() $t_i : T \to \mathbb {C}^*$ be the projection to the
$t_i : T \to \mathbb {C}^*$ be the projection to the ![]() $i$th factor, which we interpret as the weight of the standard representation of this
$i$th factor, which we interpret as the weight of the standard representation of this ![]() $i$th factor. To show formula (24), we consider the universal
$i$th factor. To show formula (24), we consider the universal ![]() $\mathsf {T}$-equivariant model where
$\mathsf {T}$-equivariant model where ![]() $S\subset X$ is
$S\subset X$ is
and the logarithmic boundary ![]() $H\subset \mathbb {C}^s$ is the union of the
$H\subset \mathbb {C}^s$ is the union of the ![]() $s$ coordinate hyperplanes. Then the
$s$ coordinate hyperplanes. Then the ![]() $\mathsf {T}$-action on
$\mathsf {T}$-action on
has ![]() $s!$ isolated
$s!$ isolated ![]() $\mathsf {T}$-fixed points naturally indexed by elements of the symmetric group
$\mathsf {T}$-fixed points naturally indexed by elements of the symmetric group ![]() $\Sigma _s$. The weights of the divisors
$\Sigma _s$. The weights of the divisors
with their canonical ![]() $\mathsf {T}$-equivariant lifts at the
$\mathsf {T}$-equivariant lifts at the ![]() $\mathsf {T}$-fixed point
$\mathsf {T}$-fixed point ![]() $\gamma \in \Sigma _s$ are
$\gamma \in \Sigma _s$ are
respectively. Formula (24) then follows immediately for the ![]() $\mathsf {T}$-equivariant model. The general case of (24) is a formal consequence.
$\mathsf {T}$-equivariant model. The general case of (24) is a formal consequence.
We now will establish the induction step. Let ![]() $S\subset X$ be a simple stratum of codimension
$S\subset X$ be a simple stratum of codimension ![]() $s$ with monodromy groupFootnote 20
$s$ with monodromy groupFootnote 20 ![]() $G$ of the branches of
$G$ of the branches of ![]() $D$ cutting out
$D$ cutting out ![]() $S$. We must prove
$S$. We must prove
for every ![]() $G$-invariant polynomial
$G$-invariant polynomial ![]() $P_G$. By induction, we assume the truth of the statement for polynomials of lower degree.
$P_G$. By induction, we assume the truth of the statement for polynomials of lower degree.
Let ![]() $P_G$ be a
$P_G$ be a ![]() $G$-equivariant polynomial in
$G$-equivariant polynomial in ![]() $c_1(N_1), \ldots, c_1(N_s)$ of degree
$c_1(N_1), \ldots, c_1(N_s)$ of degree ![]() $d>0$. We will prove a stronger property for the induction argument:
$d>0$. We will prove a stronger property for the induction argument:
can be expressed as a linear combination of terms of the form
where the ![]() $\widehat {D}_i$ are components of the logarithmic boundary of an iterated blow-up of the explosion
$\widehat {D}_i$ are components of the logarithmic boundary of an iterated blow-up of the explosion ![]() $\mathsf {E}_S(X,D)$ and
$\mathsf {E}_S(X,D)$ and ![]() $\widehat {D}_1$ lies over
$\widehat {D}_1$ lies over
Our proof of the base of the induction establishes the stronger property.
We can assume ![]() $P_G$ is the summationFootnote 21
$P_G$ is the summationFootnote 21 ![]() $M_G$ of the
$M_G$ of the ![]() $G$-orbit of a degree
$G$-orbit of a degree ![]() $d$ monomial
$d$ monomial ![]() $M$,
$M$,
 \[ M_G=\frac{1}{|\mathsf{Stab}(M)|}\sum_{g\in G} g(M). \]
\[ M_G=\frac{1}{|\mathsf{Stab}(M)|}\sum_{g\in G} g(M). \]
We will study the geometry of the exceptional divisor of the explosion
locally over an analytic open set ![]() $U_p \subset S$ of
$U_p \subset S$ of ![]() $p\in S$.
$p\in S$.
Over small enough ![]() $U_p$, we can separate all the branches
$U_p$, we can separate all the branches ![]() $B_1,\ldots, B_s$ of
$B_1,\ldots, B_s$ of ![]() $D$ which cut out
$D$ which cut out ![]() $S$, and we can write
$S$, and we can write
Over ![]() $U_p$, we can separate all the exceptional divisors of all the blow-ups in the construction of
$U_p$, we can separate all the exceptional divisors of all the blow-ups in the construction of
explained in (iii) above. There are ![]() $2^{s}-2$ such exceptional divisors in bijective correspondence to all the proper non-zero coordinate linear subspaces of the fiber
$2^{s}-2$ such exceptional divisors in bijective correspondence to all the proper non-zero coordinate linear subspaces of the fiber ![]() $\mathsf {N}_{S}|_p$ of
$\mathsf {N}_{S}|_p$ of ![]() $\mathsf {N}_S$ at
$\mathsf {N}_S$ at ![]() $p$. We denote these
$p$. We denote these ![]() $2^{s}-2$ exceptional divisors by
$2^{s}-2$ exceptional divisors by ![]() $E_\Lambda$, where
$E_\Lambda$, where
is a proper coordinate linear space. As before, we denote the pull-back of ![]() $\mathcal {O}_{\mathsf {P}(\mathsf {N}_S)}(-1)$ to
$\mathcal {O}_{\mathsf {P}(\mathsf {N}_S)}(-1)$ to ![]() $\mathsf {E}_S(S)$ by
$\mathsf {E}_S(S)$ by ![]() $E_0$.
$E_0$.
Via the pull-back formula for ![]() $B_i$, we have
$B_i$, we have
where ![]() $H_i \subset \mathsf {N}_{S}|_p$ is the hyperplane associated to
$H_i \subset \mathsf {N}_{S}|_p$ is the hyperplane associated to ![]() $B_i$. We now substitute formula (26) into (25) to find that
$B_i$. We now substitute formula (26) into (25) to find that
Of course, ![]() $M$ has degree
$M$ has degree ![]() $d$ in the divisors
$d$ in the divisors ![]() $E_0$ and
$E_0$ and ![]() $\{ E_\Lambda \}_\Lambda$.
$\{ E_\Lambda \}_\Lambda$.
Let ![]() $M^E$ be a monomial of degree
$M^E$ be a monomial of degree ![]() $d$ in the divisors
$d$ in the divisors
The monodromy group ![]() $G$ actsFootnote 22 canonically on the set (27) leaving
$G$ actsFootnote 22 canonically on the set (27) leaving ![]() $E_0$ fixed. Let
$E_0$ fixed. Let
 \[ M^E_G=\frac{1}{|\mathsf{Stab}(M^E)|}\sum_{g\in G} g(M^E) \]
\[ M^E_G=\frac{1}{|\mathsf{Stab}(M^E)|}\sum_{g\in G} g(M^E) \]
be the summation over the ![]() $G$-orbit of
$G$-orbit of ![]() $M^E$. Since
$M^E$. Since ![]() $M^E_G$ is
$M^E_G$ is ![]() $G$-invariant,
$G$-invariant, ![]() $M^E_G$ is a well-defined class
$M^E_G$ is a well-defined class
To prove the stronger induction step, we need only proveFootnote 23 that
can be expressed as a linear combination of terms of the form
where the ![]() $\widehat {D}_i$ are components of the logarithmic boundary of an iterated blow-up of the explosion
$\widehat {D}_i$ are components of the logarithmic boundary of an iterated blow-up of the explosion ![]() $\mathsf {E}_S(X,D)$ and
$\mathsf {E}_S(X,D)$ and ![]() $\widehat {D}_1$ lies over
$\widehat {D}_1$ lies over ![]() $\mathsf {E}_S(S)$. To see why the claim for (28) is enough, we write
$\mathsf {E}_S(S)$. To see why the claim for (28) is enough, we write
 \begin{align*} e^*[S,M_G] &= \sum_{M^E_G} e^*[S] \cdot M^E_G\\ &= \sum_{M^E_G}[\mathsf{E}_S(S)]\cdot c_{s-1} \bigg(\frac{\mathsf{N}_S}{ \mathcal{O}_{\mathsf{P}(\mathsf{N}_S)}(-1)}\bigg)\cdot M^E_G\\ &= \sum_{M^E_G}\iota_*\bigg(M^E_G \cdot c_{s-1}\bigg(\frac{\mathsf{N}_S}{ \mathcal{O}_{\mathsf{P}(\mathsf{N}_S)}(-1)}\bigg)\bigg). \end{align*}
\begin{align*} e^*[S,M_G] &= \sum_{M^E_G} e^*[S] \cdot M^E_G\\ &= \sum_{M^E_G}[\mathsf{E}_S(S)]\cdot c_{s-1} \bigg(\frac{\mathsf{N}_S}{ \mathcal{O}_{\mathsf{P}(\mathsf{N}_S)}(-1)}\bigg)\cdot M^E_G\\ &= \sum_{M^E_G}\iota_*\bigg(M^E_G \cdot c_{s-1}\bigg(\frac{\mathsf{N}_S}{ \mathcal{O}_{\mathsf{P}(\mathsf{N}_S)}(-1)}\bigg)\bigg). \end{align*}
The first equality is written with the understanding that ![]() $e^*[S]$ is supported on
$e^*[S]$ is supported on ![]() $\mathsf {E}_S(S)$.
$\mathsf {E}_S(S)$.
To study ![]() $M^E_G$, we take a geometric approach. If
$M^E_G$, we take a geometric approach. If ![]() $M^E$ is just
$M^E$ is just ![]() $E_0^d$, then (28) is already of the claimed form by our analysis in the base case. Otherwise,
$E_0^d$, then (28) is already of the claimed form by our analysis in the base case. Otherwise, ![]() $M^E$ has at least one factor
$M^E$ has at least one factor ![]() $E_\Lambda$. Since
$E_\Lambda$. Since ![]() $\{E_\Lambda \}_\Lambda$ is a set of simple normal crossings divisors on
$\{E_\Lambda \}_\Lambda$ is a set of simple normal crossings divisors on ![]() $\mathsf {E}_S(S)$, we claim that we can write
$\mathsf {E}_S(S)$, we claim that we can write ![]() $M^E$ (if non-zero) as
$M^E$ (if non-zero) as
where ![]() $E_{\Lambda _1},\ldots,E_{\Lambda _t}$ are distinct divisors with a non-empty transverse intersection
$E_{\Lambda _1},\ldots,E_{\Lambda _t}$ are distinct divisors with a non-empty transverse intersection
Moreover, we can assume every divisor of the monomial ![]() $\widetilde {M}^E$ contains
$\widetilde {M}^E$ contains ![]() $I_{U_p}$. Indeed, we construct inductively for
$I_{U_p}$. Indeed, we construct inductively for ![]() $i=1,2, \ldots$ a representation
$i=1,2, \ldots$ a representation
such that the ![]() $E_{\Lambda _j}$ are distinct and have non-zero transverse intersection. For
$E_{\Lambda _j}$ are distinct and have non-zero transverse intersection. For ![]() $i=1$ this is just our assumption that
$i=1$ this is just our assumption that ![]() $M^E$ has some factor
$M^E$ has some factor ![]() $E_{\Lambda }=:E_{\Lambda _1}$. On the other hand, given the representation above for some
$E_{\Lambda }=:E_{\Lambda _1}$. On the other hand, given the representation above for some ![]() $i$, if all factors
$i$, if all factors ![]() $E_{\Lambda '}$ of
$E_{\Lambda '}$ of ![]() $\widetilde {M}_i^E$ contain
$\widetilde {M}_i^E$ contain ![]() $E_{\Lambda _1} \cap \cdots \cap E_{\Lambda _i}$, we are done, setting
$E_{\Lambda _1} \cap \cdots \cap E_{\Lambda _i}$, we are done, setting ![]() ${t=i}$. If there is an
${t=i}$. If there is an ![]() $E_{\Lambda '}$ not satisfying this, we set
$E_{\Lambda '}$ not satisfying this, we set ![]() $E_{\Lambda _{i+1}}=E_{\Lambda '}$. If the intersection
$E_{\Lambda _{i+1}}=E_{\Lambda '}$. If the intersection ![]() $E_{\Lambda _1} \cap \cdots \cap E_{\Lambda _{i+1}}$ was empty, then
$E_{\Lambda _1} \cap \cdots \cap E_{\Lambda _{i+1}}$ was empty, then ![]() $M^E=0$, giving a contradiction. Thus, the intersection is non-empty, and transverse by the fact that the
$M^E=0$, giving a contradiction. Thus, the intersection is non-empty, and transverse by the fact that the ![]() $E_{\Lambda }$ are a normal crossings divisor. We continue inductively, and this construction concludes after at most
$E_{\Lambda }$ are a normal crossings divisor. We continue inductively, and this construction concludes after at most ![]() $d$ steps.
$d$ steps.
When the monodromy invariant ![]() $M^E_G$ is considered, we obtain a non-singular subvariety of
$M^E_G$ is considered, we obtain a non-singular subvariety of ![]() $\mathsf {E}_S(S)$ of codimension
$\mathsf {E}_S(S)$ of codimension ![]() $t$,
$t$,
which is a simple stratum of ![]() $\mathsf {E}_S(X,D)$,
$\mathsf {E}_S(X,D)$,
Over ![]() $U_p$, the subvariety
$U_p$, the subvariety ![]() $V$ restricts to the unionFootnote 24 of the distinct
$V$ restricts to the unionFootnote 24 of the distinct ![]() $G$-translates of
$G$-translates of ![]() $I_{U_p}$. The crucial geometric observation is
$I_{U_p}$. The crucial geometric observation is
where ![]() $\widetilde {P}$ is defined by
$\widetilde {P}$ is defined by ![]() $\widetilde {M}^E$ and is of degree at most
$\widetilde {M}^E$ and is of degree at most ![]() $d-1$.
$d-1$.
We can apply the strong induction property: the class
can be expressed as a linear combination of terms of the form
where the ![]() $\widehat {D}_i$ are components of the logarithmic boundary of an iterated blow-up of the explosion of
$\widehat {D}_i$ are components of the logarithmic boundary of an iterated blow-up of the explosion of ![]() $V$ in
$V$ in ![]() $\mathsf {E}_S(X,D)$ and
$\mathsf {E}_S(X,D)$ and ![]() $\widehat {D}_1$ lies over
$\widehat {D}_1$ lies over
Then the claim
holds by the analysis of
on ![]() $\mathsf {E}_S(S)$ in the base case of the induction. Since each monomial
$\mathsf {E}_S(S)$ in the base case of the induction. Since each monomial
of ![]() $\epsilon ^V_*(\widetilde {P})$ lies over
$\epsilon ^V_*(\widetilde {P})$ lies over ![]() $\mathsf {E}_V(V)$, which in turn lies over
$\mathsf {E}_V(V)$, which in turn lies over ![]() $\mathsf {E}_{S}(S)$, the analysis of the base case yields the desired result (29).
$\mathsf {E}_{S}(S)$, the analysis of the base case yields the desired result (29).
The induction argument is complete, so we have proven Theorem 11 in the case where ![]() $S$ is a simple stratum of
$S$ is a simple stratum of ![]() $(X,D)$. The general case follows by repeated application of the result for a simple stratum.
$(X,D)$. The general case follows by repeated application of the result for a simple stratum.
Let ![]() $S\subset X$ be a stratum with a singular closure
$S\subset X$ be a stratum with a singular closure
The first step is to blow up simple strata in ![]() $\overline {S}$,
$\overline {S}$,
until the strict transform of ![]() $\overline {S}$,
$\overline {S}$,
is non-singular. Since ![]() $S$ is simple stratum of the blow-up
$S$ is simple stratum of the blow-up ![]() $\widehat {X}$, we can apply Theorem 11 to
$\widehat {X}$, we can apply Theorem 11 to ![]() ${S} \subset \widehat {X}$.
${S} \subset \widehat {X}$.
Via the blow-down map, we have
There are two discrepancies to handle before deducing Theorem 11 for normally decorated classes associated to ![]() $S\subset X$ from the result for normally decorated classes associated to
$S\subset X$ from the result for normally decorated classes associated to ![]() $S\subset \widehat {X}$.
$S\subset \widehat {X}$.
(i) The fundamental class
 $[\widehat {S}]\in \mathsf {CH}^\star (\widehat {X})$ is not the pull-back of
$[\widehat {S}]\in \mathsf {CH}^\star (\widehat {X})$ is not the pull-back of  $[\overline {S}]\in \mathsf {CH}^\star ({X})$.
$[\overline {S}]\in \mathsf {CH}^\star ({X})$.(ii) The normal directions of
 $\widehat {S}\subset \widehat {X}$ differ from the pull-backs of the normal directions of
$\widehat {S}\subset \widehat {X}$ differ from the pull-backs of the normal directions of  $\overline {S}\subset {X}$.
$\overline {S}\subset {X}$.
However, both discrepancies are corrected by applying the simple stratum result to the lower-dimensional strata occurring in ![]() $\widehat {S}\,{\setminus}\, S$.
$\widehat {S}\,{\setminus}\, S$.
5.3 Explosion geometry and barycentric subdivision
The explosion operation ![]() $E(X,D)$ along a simple stratum
$E(X,D)$ along a simple stratum ![]() $S\subset X$, which appeared in the proof § 5.2, is an essentially combinatorial operation that has a natural interpretation in terms of the geometry of the cone complex
$S\subset X$, which appeared in the proof § 5.2, is an essentially combinatorial operation that has a natural interpretation in terms of the geometry of the cone complex ![]() $C(X,D)$.
$C(X,D)$.
Consider first a cone ![]() $\sigma$ of dimension
$\sigma$ of dimension ![]() $n$ in a lattice
$n$ in a lattice ![]() $N$, and let
$N$, and let ![]() $A_\sigma$ be the associated toric variety. Let
$A_\sigma$ be the associated toric variety. Let ![]() $\mathcal {A}_\sigma$ be the associated Artin fan, which is simply the stack quotient of
$\mathcal {A}_\sigma$ be the associated Artin fan, which is simply the stack quotient of ![]() $A_\sigma$ by the corresponding dense torus
$A_\sigma$ by the corresponding dense torus ![]() $T_\sigma$. The logarithmic stratification of
$T_\sigma$. The logarithmic stratification of ![]() $A_\sigma$ is precisely the stratification defined by the orbits of
$A_\sigma$ is precisely the stratification defined by the orbits of ![]() $T_\sigma$, and there is a bijective dimension-reversing correspondence between faces of
$T_\sigma$, and there is a bijective dimension-reversing correspondence between faces of ![]() $\sigma$ and strata. We write
$\sigma$ and strata. We write ![]() $\sigma (k)$ for the
$\sigma (k)$ for the ![]() $k$-dimensional faces of
$k$-dimensional faces of ![]() $\sigma$ and thus the codimension
$\sigma$ and thus the codimension ![]() $k$ strata of
$k$ strata of ![]() $A_\sigma$.
$A_\sigma$.
For each face ![]() $\tau$ of
$\tau$ of ![]() $\sigma$, the barycenter
$\sigma$, the barycenter ![]() $b_\tau$ of
$b_\tau$ of ![]() $\tau$ is the sum
$\tau$ is the sum
of the primitive vectors along the extremal rays of ![]() $\tau$. For any flag
$\tau$. For any flag
of faces of ![]() $\sigma$, the barycenters
$\sigma$, the barycenters ![]() $b_{\tau _0}, \ldots, b_{\tau _k}$ span a cone. The set of all such cones, for all flags in
$b_{\tau _0}, \ldots, b_{\tau _k}$ span a cone. The set of all such cones, for all flags in ![]() $\sigma$, forms a subdivision of
$\sigma$, forms a subdivision of ![]() $\sigma$, which we call the barycentric subdivision
$\sigma$, which we call the barycentric subdivision ![]() $\widetilde {\sigma }$ of
$\widetilde {\sigma }$ of ![]() $\sigma$.
$\sigma$.
Alternatively, we can build the barycentric subdivision inductively: at step ![]() $1$, we start with the star subdivision over the barycenter of faces in
$1$, we start with the star subdivision over the barycenter of faces in ![]() $\sigma (n)$ (where
$\sigma (n)$ (where ![]() $\sigma$ has dimension
$\sigma$ has dimension ![]() $n$), then take the star subdivision over faces in
$n$), then take the star subdivision over faces in ![]() $\sigma (n-1)$, and so on, terminating after
$\sigma (n-1)$, and so on, terminating after ![]() $n-1$ steps with
$n-1$ steps with ![]() $\sigma (2)$, after which the operation no longer has any effect. We thus produce a sequence of
$\sigma (2)$, after which the operation no longer has any effect. We thus produce a sequence of ![]() $n-1$ subdivisions
$n-1$ subdivisions
When ![]() $\sigma = \mathbb {R}_{\ge 0}^n$, which is our main case of interest, the barycentric subdivision has
$\sigma = \mathbb {R}_{\ge 0}^n$, which is our main case of interest, the barycentric subdivision has ![]() $n!$ maximal cones.
$n!$ maximal cones.
The barycentric subdivision of ![]() $\sigma$ produces a log modification
$\sigma$ produces a log modification
which is in fact a log blow-up. More precisely, we have constructed the subdivision ![]() $\widetilde {A}_\sigma \to A_\sigma$ as a sequence
$\widetilde {A}_\sigma \to A_\sigma$ as a sequence
and the map ![]() $A_k \to A_{k-1}$ is determined by the subdivision
$A_k \to A_{k-1}$ is determined by the subdivision ![]() $\sigma _k \to \sigma _{k-1}$, which is the subdivision corresponding to the domains of linearity of a piecewise linear function (see [Reference Kempf, Knudsen, Mumford and Saint-DonatKKMS73] for the construction). In the case of interest,
$\sigma _k \to \sigma _{k-1}$, which is the subdivision corresponding to the domains of linearity of a piecewise linear function (see [Reference Kempf, Knudsen, Mumford and Saint-DonatKKMS73] for the construction). In the case of interest,
the map ![]() $A_1 \to A_0$ is the blow-up of
$A_1 \to A_0$ is the blow-up of ![]() $\mathbb {A}^n$ at the origin,
$\mathbb {A}^n$ at the origin, ![]() $A_2 \to A_1$ is the blow-up along the strict transforms of the coordinate lines, and in general
$A_2 \to A_1$ is the blow-up along the strict transforms of the coordinate lines, and in general ![]() $A_k \to A_{k-1}$ is the blow-up along the strict transforms of the dimension
$A_k \to A_{k-1}$ is the blow-up along the strict transforms of the dimension ![]() $k-1$ hyperplanes of
$k-1$ hyperplanes of ![]() $\mathbb {A}^n$ in
$\mathbb {A}^n$ in ![]() $A_{k-1}$. Thus, the barycentric subdivision of
$A_{k-1}$. Thus, the barycentric subdivision of ![]() $\mathbb {A}^n$ is precisely the explosion of
$\mathbb {A}^n$ is precisely the explosion of ![]() $\mathbb {A}^n$ along the origin.
$\mathbb {A}^n$ along the origin.
The barycentric subdivision construction is clearly equivariant and therefore descends to the Artin fan ![]() $\mathcal {A}_\sigma$ of
$\mathcal {A}_\sigma$ of ![]() $A_\sigma$. Furthermore, the subdivision is the same on isomorphic faces of
$A_\sigma$. Furthermore, the subdivision is the same on isomorphic faces of ![]() $\sigma$ and invariant with respect to automorphisms of
$\sigma$ and invariant with respect to automorphisms of ![]() $\sigma$. Consequently, given any cone complex
$\sigma$. Consequently, given any cone complex ![]() $C$, the barycentric subdivisions of individual cones glue to a global subdivision of
$C$, the barycentric subdivisions of individual cones glue to a global subdivision of ![]() $C$, and that is true even if faces of
$C$, and that is true even if faces of ![]() $C$ are identified or if there is monodromy in
$C$ are identified or if there is monodromy in ![]() $C$. Thus, for a normal crossings pair
$C$. Thus, for a normal crossings pair ![]() $(X,D)$, we can define the barycentric subdivision
$(X,D)$, we can define the barycentric subdivision ![]() $\widetilde {C}(X,D)$ of the cone complex
$\widetilde {C}(X,D)$ of the cone complex ![]() $C(X,D)$, and equivalently, a log blow-up
$C(X,D)$, and equivalently, a log blow-up
of the Artin fan. We also obtain globally a log blow-up
with Artin fan ![]() $\mathcal {A}_{\widetilde {X}} = \widetilde {\mathcal {A}}_X$.
$\mathcal {A}_{\widetilde {X}} = \widetilde {\mathcal {A}}_X$.
The explosion of § 5.2 can only be defined locally around a simple stratum ![]() $S$. A quasi-projective stratum
$S$. A quasi-projective stratum ![]() $S$ (not necessarily simple) of a normal crossings pair
$S$ (not necessarily simple) of a normal crossings pair ![]() $(X,D)$ corresponds to a cone
$(X,D)$ corresponds to a cone ![]() $\sigma$ of
$\sigma$ of ![]() $C(X,D)$. More precisely, the quasi-projective stratum
$C(X,D)$. More precisely, the quasi-projective stratum ![]() $S$ corresponds to the interior of
$S$ corresponds to the interior of ![]() $\sigma$, and the whole of
$\sigma$, and the whole of ![]() $\sigma$ corresponds to a canonical open set
$\sigma$ corresponds to a canonical open set ![]() $U$ in
$U$ in ![]() $X$ that contains
$X$ that contains ![]() $S$ as its minimal stratum: the open set
$S$ as its minimal stratum: the open set ![]() $U$ consists of all quasi-projective strata whose closure contains
$U$ consists of all quasi-projective strata whose closure contains ![]() $S$. The explosion
$S$. The explosion ![]() $\mathsf {E}_S(U, D|_U))$ is well defined.
$\mathsf {E}_S(U, D|_U))$ is well defined.
The cone ![]() $\sigma$ has a cover by
$\sigma$ has a cover by ![]() $\mathbb {R}^n_{\ge 0}$, and, more precisely, by a quotient of
$\mathbb {R}^n_{\ge 0}$, and, more precisely, by a quotient of ![]() $\mathbb {R}^n_{\ge 0}$ obtained by potentially identifying faces and taking a quotient by a group
$\mathbb {R}^n_{\ge 0}$ obtained by potentially identifying faces and taking a quotient by a group ![]() $G$. The group
$G$. The group ![]() $G$ is precisely the monodromy group of the divisors
$G$ is precisely the monodromy group of the divisors ![]() $D$ that cut out
$D$ that cut out ![]() $S$ considered in § 5, and the interior
$S$ considered in § 5, and the interior ![]() $\sigma ^\circ$ of
$\sigma ^\circ$ of ![]() $\sigma$ is in fact the stack quotient
$\sigma$ is in fact the stack quotient ![]() $[\mathbb {R}_{>0}^n/G]$. Similarly, the Artin fan
$[\mathbb {R}_{>0}^n/G]$. Similarly, the Artin fan ![]() $\mathcal {U}$ of
$\mathcal {U}$ of ![]() $U$ has an analogous étale cover by the groupoid quotient of
$U$ has an analogous étale cover by the groupoid quotient of ![]() $[\mathbb {A}^n/\mathbb {G}_m^n \rtimes G]$, with
$[\mathbb {A}^n/\mathbb {G}_m^n \rtimes G]$, with ![]() $S$ corresponding to the minimal stratum
$S$ corresponding to the minimal stratum
The cover is not representable, but is representable over ![]() $S$. From the discussion of the barycentric subdivision of
$S$. From the discussion of the barycentric subdivision of ![]() $\mathbb {A}^n$, we see that
$\mathbb {A}^n$, we see that ![]() $\mathsf {E}_S(U,D_U)$ is precisely the barycentric subdivision
$\mathsf {E}_S(U,D_U)$ is precisely the barycentric subdivision ![]() $\widetilde {X} \to X$ restricted to
$\widetilde {X} \to X$ restricted to ![]() $U$. We may thus view the barycentric subdivision as globalizing the explosion geometry.
$U$. We may thus view the barycentric subdivision as globalizing the explosion geometry.
If the stratum ![]() $S$ is simple, the explosion of § 5.2 is defined over a neighborhood of
$S$ is simple, the explosion of § 5.2 is defined over a neighborhood of ![]() $\overline {S}$. However, the extension no longer coincides with the barycentric subdivision. The barycentric subdivision performs additional blow-ups, first blowing up all minimal strata in the closure of
$\overline {S}$. However, the extension no longer coincides with the barycentric subdivision. The barycentric subdivision performs additional blow-ups, first blowing up all minimal strata in the closure of ![]() $S$ (and also strata around
$S$ (and also strata around ![]() $\overline {S}$ whose closure does not necessarily meet
$\overline {S}$ whose closure does not necessarily meet ![]() $S$).
$S$).
We illustrate the concepts discussed above through an example. Let ![]() $(X,D)$ be a log scheme whose cone complex is the cone over an equilateral triangle, with all edges identified and with monodromy
$(X,D)$ be a log scheme whose cone complex is the cone over an equilateral triangle, with all edges identified and with monodromy ![]() $\mathbb {Z}/3\mathbb {Z}$. For example, we can construct
$\mathbb {Z}/3\mathbb {Z}$. For example, we can construct ![]() $(X,D)$ by taking
$(X,D)$ by taking
to be a family with fiber ![]() $\mathbb {A}^3$ over a non-singular base
$\mathbb {A}^3$ over a non-singular base ![]() $B$ satisfying
$B$ satisfying ![]() $\pi _1(B) = \mathbb {Z}$, so that the generator of
$\pi _1(B) = \mathbb {Z}$, so that the generator of ![]() $\pi _1(B)$ cyclically permutes the coordinate hyperplanes of
$\pi _1(B)$ cyclically permutes the coordinate hyperplanes of ![]() $\mathbb {A}^3$. The divisor
$\mathbb {A}^3$. The divisor ![]() $D\subset X$ is then the union of these coordinate hyperplanes over
$D\subset X$ is then the union of these coordinate hyperplanes over ![]() $B$.
$B$.

The log scheme ![]() $(X,D)$ has four strata: the open set
$(X,D)$ has four strata: the open set ![]() $X-D$, corresponding to the empty face of the triangle (or, equivalently, the vertex of the cone over the triangle); the interior of the divisor
$X-D$, corresponding to the empty face of the triangle (or, equivalently, the vertex of the cone over the triangle); the interior of the divisor ![]() $D$ corresponding to the vertex
$D$ corresponding to the vertex
the locus which is étale locally the intersection of exactly two irreducible components of ![]() $D$ corresponding to edge
$D$ corresponding to edge
and the triple point singularity of ![]() $D$ corresponding to the whole triangle. We name the strata
$D$ corresponding to the whole triangle. We name the strata ![]() $Q,R,S,T$, respectively. While
$Q,R,S,T$, respectively. While ![]() $T$ is simple,
$T$ is simple, ![]() $S$ is not, since
$S$ is not, since
is not normal. The strata are taken bijectively to points of the Artin fan via the map
We depict the Artin fan as four points, each isomorphic to ![]() $B\mathbb {G}_m^k \rtimes G$ as indicated, with points drawn increasingly bigger to describe the topology (the closure contains all smaller points).
$B\mathbb {G}_m^k \rtimes G$ as indicated, with points drawn increasingly bigger to describe the topology (the closure contains all smaller points).

Consider the explosion of the quasi-projective stratum ![]() $S$ depicted by the open line segment
$S$ depicted by the open line segment ![]() $\overline {e_1e_2}$. The open set
$\overline {e_1e_2}$. The open set ![]() $U$ over which the explosion is defined is
$U$ over which the explosion is defined is ![]() $Q \cup R \cup S$. The explosion of
$Q \cup R \cup S$. The explosion of ![]() $S$ is the barycentric subdivision of
$S$ is the barycentric subdivision of ![]() $\overline {e_1e_2}$:
$\overline {e_1e_2}$:

However, the above explosion does not extend away from ![]() $U$. The blow-up of
$U$. The blow-up of ![]() $\overline {S}$, over an étale cover of
$\overline {S}$, over an étale cover of ![]() $X$ is depicted as
$X$ is depicted as

But the blow-up does not descend to ![]() $X$ as it does not respect the face identifications/ automorphisms of
$X$ as it does not respect the face identifications/ automorphisms of ![]() $C(X,D)$. The barycentric subdivision is depicted as
$C(X,D)$. The barycentric subdivision is depicted as

The corresponding log blow-up restricts to the explosion over ![]() $U$. Over
$U$. Over ![]() $X$, the log blow-up is not the blow-up of
$X$, the log blow-up is not the blow-up of ![]() $\overline {S}$, but the explosion of
$\overline {S}$, but the explosion of ![]() $T$.
$T$.
5.4 Tautological classes
Let ![]() $(X,D)$ be a non-singular variety with a normal crossings divisor. We define the logarithmic tautological ring
$(X,D)$ be a non-singular variety with a normal crossings divisor. We define the logarithmic tautological ring
to be the ![]() $\mathbb {Q}$-linear subspace spanned by all normally decorated strata classes (which is easily seen to be closed under the intersection product). Theorem 11 can then be written as
$\mathbb {Q}$-linear subspace spanned by all normally decorated strata classes (which is easily seen to be closed under the intersection product). Theorem 11 can then be written as
The logarithmic tautological ring of ![]() $(X,D)$ depends strongly on the divisor
$(X,D)$ depends strongly on the divisor ![]() $D$. For example, if
$D$. For example, if ![]() $X$ is irreducible and
$X$ is irreducible and ![]() $D=\emptyset$, then there is only one stratum and
$D=\emptyset$, then there is only one stratum and
For the moduli space of curves, the inclusion
is proper for ![]() $g\geq 2$. Furthermore, the inclusion
$g\geq 2$. Furthermore, the inclusion
in the standard tautological ringFootnote 25 is proper for ![]() $g\geq 3$ since
$g\geq 3$ since ![]() $\mathsf {R}^\star (\overline {\mathcal {M}}_g)$ contains
$\mathsf {R}^\star (\overline {\mathcal {M}}_g)$ contains ![]() $\kappa$ and
$\kappa$ and ![]() $\psi$ classes which do not appear in the logarithmic constructions.
$\psi$ classes which do not appear in the logarithmic constructions.
Let ![]() $(X,D)$ be a non-singular variety with a normal crossings divisor. Let
$(X,D)$ be a non-singular variety with a normal crossings divisor. Let
be a simple blow-up of ![]() $(X,D)$. Let
$(X,D)$. Let ![]() $\widetilde {D}\subset \widetilde {X}$ be the associated normal crossings divisor. We will prove the following two basic properties of logarithmic tautological rings.
$\widetilde {D}\subset \widetilde {X}$ be the associated normal crossings divisor. We will prove the following two basic properties of logarithmic tautological rings.
Theorem 12 The pull-back
has image in ![]() $\mathsf {R}^\star (\widetilde {X}, \widetilde {D})$.
$\mathsf {R}^\star (\widetilde {X}, \widetilde {D})$.
Theorem 13 The push-forward
has image in ![]() $\mathsf {R}^\star (X,D)$.
$\mathsf {R}^\star (X,D)$.
By Theorems 12 and 13, we can simply write
Theorems 12 and 13 will proven in § 5.6 via the geometry of the Artin fan. As a consequence, we will present a more conceptual (but less constructive) proof of Theorem 11.
5.5 The Chow ring of the Artin fan
Let ![]() $(X,D)$ be a non-singular variety with a normal crossings divisor. We relate here the normally decorated strata classes of
$(X,D)$ be a non-singular variety with a normal crossings divisor. We relate here the normally decorated strata classes of ![]() $(X,D)$ to Chow classes on the Artin fan
$(X,D)$ to Chow classes on the Artin fan ![]() $\mathcal {A}_X$ of
$\mathcal {A}_X$ of ![]() $(X,D)$. Here, since
$(X,D)$. Here, since ![]() $\mathcal {A}_X$ is a smooth, finite type algebraic stack stratified by quotient stacks, it has well-defined Chow groups
$\mathcal {A}_X$ is a smooth, finite type algebraic stack stratified by quotient stacks, it has well-defined Chow groups ![]() $\mathsf {CH}^\star (\mathcal {A}_X)$ with an intersection product as defined in [Reference KreschKre99]. Note that for our proof below it will not be necessary to recall the precise definition from [Reference KreschKre99], since we only use some properties and examples of these Chow groups (such as the existence of an excision sequence) that we recall when needed. Also, we stress again that all Chow groups below are with
$\mathsf {CH}^\star (\mathcal {A}_X)$ with an intersection product as defined in [Reference KreschKre99]. Note that for our proof below it will not be necessary to recall the precise definition from [Reference KreschKre99], since we only use some properties and examples of these Chow groups (such as the existence of an excision sequence) that we recall when needed. Also, we stress again that all Chow groups below are with ![]() $\mathbb {Q}$-coefficients.
$\mathbb {Q}$-coefficients.
As we explain in § 4.4, there is a smooth morphism to the Artin fan,
Theorem 14 There is a canonical isomorphism
between the Chow ring of ![]() $\mathcal {A}_X$ and the algebra of piecewise polynomial functions on the cone complex
$\mathcal {A}_X$ and the algebra of piecewise polynomial functions on the cone complex ![]() $C(X,D)$.
$C(X,D)$.
Proof. By construction, the Artin fan ![]() $\mathcal {A}_X$ has a presentation as a colimit
$\mathcal {A}_X$ has a presentation as a colimit
where ![]() $\mathcal {S}$ is a finite diagram, each map
$\mathcal {S}$ is a finite diagram, each map ![]() $\mathcal {A}_x$ is a stack of the form
$\mathcal {A}_x$ is a stack of the form ![]() $[\mathbb {A}^n/\mathbb {G}_m^n]$, and all maps in the diagram are étale. First, we note that for the individual stacks
$[\mathbb {A}^n/\mathbb {G}_m^n]$, and all maps in the diagram are étale. First, we note that for the individual stacks ![]() $\mathcal {A}_x = [\mathbb {A}^n/\mathbb {G}_m^n]$ we have
$\mathcal {A}_x = [\mathbb {A}^n/\mathbb {G}_m^n]$ we have
The first equality is because
is a vector bundle and induces an isomorphism of Chow groups by [Reference KreschKre99, Theorem 2.1.12 (vi)]. The second equality is because the equivariant Chow ring of a product of tori is a polynomial algebra [Reference Edidin and GrahamEG98, § 3.2], which can be identified with polynomials on the cone ![]() $\sigma _{X,x}$ associated to
$\sigma _{X,x}$ associated to ![]() $\mathcal {A}_x$ (appearing in the colimit presentation of
$\mathcal {A}_x$ (appearing in the colimit presentation of ![]() $C(X,D)$).
$C(X,D)$).
For the entire Artin fan ![]() $\mathcal {A}_X$, we claim
$\mathcal {A}_X$, we claim
If we can show equality (31), then Theorem 14 will follow since the result holds for each term on the right-hand side by (30). Piecewise polynomial functions on ![]() $C(X,D)$ are defined by the corresponding limit presentation.
$C(X,D)$ are defined by the corresponding limit presentation.
All the stacks appearing in (31) are very special: they are non-singular and have a stratification with strata isomorphic to
where ![]() $G$ is a finite group. For the argument below, it will be more convenient to index Chow groups by the dimension of the cycles (instead of the codimension) and proveFootnote 26
$G$ is a finite group. For the argument below, it will be more convenient to index Chow groups by the dimension of the cycles (instead of the codimension) and proveFootnote 26
Let ![]() $\mathcal {C}$ denote the full 2-subcategory of the 2-category of algebraic stacks with Ob(
$\mathcal {C}$ denote the full 2-subcategory of the 2-category of algebraic stacks with Ob(![]() $\mathcal {C}$) given by algebraic stacks
$\mathcal {C}$) given by algebraic stacks ![]() $\mathcal {A}$ with a stratification by stacks of the form
$\mathcal {A}$ with a stratification by stacks of the form ![]() $B (\mathbb {G}_m^n \rtimes G)$, with
$B (\mathbb {G}_m^n \rtimes G)$, with ![]() $G$ a finite group. Similarly, let
$G$ a finite group. Similarly, let ![]() $\mathcal {C}^\circ$ be the full 2-subcategory of
$\mathcal {C}^\circ$ be the full 2-subcategory of ![]() $\mathcal {C}$ with objects given by stacks of the form
$\mathcal {C}$ with objects given by stacks of the form ![]() $B \mathbb {G}_m^n$. We start with a stackFootnote 27
$B \mathbb {G}_m^n$. We start with a stackFootnote 27 ![]() $\mathcal {A}_X \in \mathcal {C}$ with a colimit presentation
$\mathcal {A}_X \in \mathcal {C}$ with a colimit presentation
where ![]() $\mathcal {A}_x \in \mathcal {C}^\circ$ and all maps in the diagram are étale. We will prove (32) by induction on the number of strata of
$\mathcal {A}_x \in \mathcal {C}^\circ$ and all maps in the diagram are étale. We will prove (32) by induction on the number of strata of ![]() $\mathcal {A}_X$.
$\mathcal {A}_X$.
Assume first that there is a unique stratum,
and all maps in the diagram ![]() $\mathcal {S}$ are isomorphisms. Then the groupoid
$\mathcal {S}$ are isomorphisms. Then the groupoid
is equivalent to the quotient ![]() $B\mathbb {G}_m^n/G$, and the statement is equivalent to
$B\mathbb {G}_m^n/G$, and the statement is equivalent to
which is true (see [Reference Bae and SchmittBS21, Lemma 2.20]). In general, we pick an open stratum ![]() $U \in \mathcal {A}_X$ with preimage
$U \in \mathcal {A}_X$ with preimage ![]() $U_x \in \mathcal {A}_x$. Then, by [Reference KreschKre99, Proposition 4.2.1], we have an exact sequence
$U_x \in \mathcal {A}_x$. Then, by [Reference KreschKre99, Proposition 4.2.1], we have an exact sequence
with ![]() $Z = \mathcal {A}_X - U$. Since
$Z = \mathcal {A}_X - U$. Since ![]() $U$ is of the form
$U$ is of the form ![]() $U = B(\mathbb {G}_m^n \rtimes G)$, we can use [Reference Bae and SchmittBS21, Proposition 2.14, Remark 2.21] to see that
$U = B(\mathbb {G}_m^n \rtimes G)$, we can use [Reference Bae and SchmittBS21, Proposition 2.14, Remark 2.21] to see that
Then, by [Reference Bae and SchmittBS21, Remark 2.18], the connecting homomorphism ![]() $\mathsf {CH}(U,1) \to \mathsf {CH}(Z)$ vanishes. So we obtain an exact sequence
$\mathsf {CH}(U,1) \to \mathsf {CH}(Z)$ vanishes. So we obtain an exact sequence
and the same sequence holds with ![]() $\mathcal {A}_X$ replaced by
$\mathcal {A}_X$ replaced by ![]() $\mathcal {A}_x$,
$\mathcal {A}_x$, ![]() $U$ by
$U$ by ![]() $U_x$, and
$U_x$, and ![]() $Z$ by
$Z$ by ![]() $Z_x = \mathcal {A}_x - U_x$. As projective limits are left exact, we obtain the following diagram.
$Z_x = \mathcal {A}_x - U_x$. As projective limits are left exact, we obtain the following diagram.

By induction, the left and right vertical arrows are isomorphisms. But the bottom row is exact as well: the composed map
is surjective and factors through ![]() $\varprojlim _{x \in \mathcal {S}}\mathsf {CH}(\mathcal {A}_x)$. Thus, the map
$\varprojlim _{x \in \mathcal {S}}\mathsf {CH}(\mathcal {A}_x)$. Thus, the map
is an isomorphism as well.
Theorem 14 has clear precursors in the toric context by Payne [Reference PaynePay06] and Brion [Reference BrionBri94]. In the logarithmic context, we were directly motivated by ideas of Ranganathan. A development of the theory for general log schemes can be found in [Reference Molcho and RanganathanMR21].
Theorem 15 The logarithmic tautological ring
coincides with the image ![]() $\alpha ^*\mathsf {CH}^\star (\mathcal {A}_X) \subset \mathsf {CH}^\star (X)$.
$\alpha ^*\mathsf {CH}^\star (\mathcal {A}_X) \subset \mathsf {CH}^\star (X)$.
Proof. Fix a stratum ![]() $S\subset X$ with closure
$S\subset X$ with closure ![]() $\overline {S}\subset X$, and normalization
$\overline {S}\subset X$, and normalization
Consider the cone complex ![]() $C(X,D)$ and the Artin fan
$C(X,D)$ and the Artin fan ![]() $\mathcal {A}_X$ of
$\mathcal {A}_X$ of ![]() $(X,D)$ with
$(X,D)$ with
Let ![]() $\widetilde {P}$ be the total space of the principal
$\widetilde {P}$ be the total space of the principal ![]() $G$-bundle over the normalization
$G$-bundle over the normalization ![]() $\widetilde {S}$ defined by the branches of
$\widetilde {S}$ defined by the branches of ![]() $D$ in § 5.1,
$D$ in § 5.1,
We observe that all the relevant geometry is pulled back from the Artin fan ![]() $\mathcal {A}_X$: the stratum
$\mathcal {A}_X$: the stratum ![]() $S$ corresponds to the stratum
$S$ corresponds to the stratum
with closure ![]() $\overline {\mathcal {S}} = \alpha (\overline {S})$. Let
$\overline {\mathcal {S}} = \alpha (\overline {S})$. Let ![]() $\widetilde {\mathcal {S}}$ be the normalization of
$\widetilde {\mathcal {S}}$ be the normalization of ![]() $\overline {\mathcal {S}}$, and let
$\overline {\mathcal {S}}$, and let
be the total space of the principal ![]() $G$-bundle over
$G$-bundle over ![]() $\widetilde {\mathcal {S}}$. Then
$\widetilde {\mathcal {S}}$. Then
Furthermore, since the map ![]() $\alpha$ is smooth, we find that
$\alpha$ is smooth, we find that ![]() $N_{\widetilde {S}/X}$ is the pull-back of
$N_{\widetilde {S}/X}$ is the pull-back of ![]() $N_{\widetilde {\mathcal {S}}/\mathcal {A}_X}$, and the splitting of
$N_{\widetilde {\mathcal {S}}/\mathcal {A}_X}$, and the splitting of ![]() $N_{\widetilde {S}/X}$ on
$N_{\widetilde {S}/X}$ on ![]() $\widetilde {P}$ into line bundles is pulled back from the splitting of
$\widetilde {P}$ into line bundles is pulled back from the splitting of ![]() $N_{\widetilde {\mathcal {S}}/\mathcal {A}_X}$ on
$N_{\widetilde {\mathcal {S}}/\mathcal {A}_X}$ on ![]() $\widetilde {\mathcal {P}}$. In other words, we have the following Cartesian diagram.
$\widetilde {\mathcal {P}}$. In other words, we have the following Cartesian diagram.

Normally decorated strata classes on ![]() $\overline {S}$ have the form
$\overline {S}$ have the form ![]() $\mu _{X*}\alpha _P^*(\gamma )$ for
$\mu _{X*}\alpha _P^*(\gamma )$ for ![]() $\gamma \in \mathsf {CH}^\star (\widetilde {\mathcal {P}})$. As
$\gamma \in \mathsf {CH}^\star (\widetilde {\mathcal {P}})$. As ![]() $\alpha,\alpha _P$ are smooth,
$\alpha,\alpha _P$ are smooth, ![]() $\mu _{X*}\alpha _P^*= \alpha ^*\mu _{\mathcal {A}*}$. Therefore,
$\mu _{X*}\alpha _P^*= \alpha ^*\mu _{\mathcal {A}*}$. Therefore,
In fact, the argument shows more precisely that
for ![]() $\mathcal {D} = \alpha (D)$ the corresponding divisor in
$\mathcal {D} = \alpha (D)$ the corresponding divisor in ![]() $\mathcal {A}_X$. In other words, the logarithmic tautological ring of
$\mathcal {A}_X$. In other words, the logarithmic tautological ring of ![]() $(X,D)$, which is generated by the Chern roots of the normal bundles on the various monodromy torsors of the strata of
$(X,D)$, which is generated by the Chern roots of the normal bundles on the various monodromy torsors of the strata of ![]() $(X,D)$, is the pull-back of the logarithmic tautological ring of
$(X,D)$, is the pull-back of the logarithmic tautological ring of ![]() $\mathcal {A}_X$, generated by the analogous constructions over the strata of
$\mathcal {A}_X$, generated by the analogous constructions over the strata of ![]() $\mathcal {A}_X$. Thus, it suffices to show that the normally decorated strata classes of
$\mathcal {A}_X$. Thus, it suffices to show that the normally decorated strata classes of ![]() $\mathcal {A}_X$ generate the Chow ring of
$\mathcal {A}_X$ generate the Chow ring of ![]() $\mathcal {A}_X$. We may thus reduce to proving the theorem for
$\mathcal {A}_X$. We may thus reduce to proving the theorem for ![]() $\mathcal {A}_X$.
$\mathcal {A}_X$.
So let ![]() $\gamma$ be a class in
$\gamma$ be a class in ![]() $\mathsf {CH}^\star (\mathcal {A}_X)$. We must show that
$\mathsf {CH}^\star (\mathcal {A}_X)$. We must show that
We may assume that ![]() $\gamma$ is supported on
$\gamma$ is supported on ![]() $\overline {\mathcal {S}}$ for some stratum
$\overline {\mathcal {S}}$ for some stratum ![]() $\mathcal {S}\subset \mathcal {A}_X$. Suppose, by induction, we have shown that every such class supported on a stratum
$\mathcal {S}\subset \mathcal {A}_X$. Suppose, by induction, we have shown that every such class supported on a stratum ![]() $\overline {\mathcal {S}'}$ with
$\overline {\mathcal {S}'}$ with
is in ![]() $R(\mathcal {A}_X,\mathcal {D})$. Suppose further that we can find a class
$R(\mathcal {A}_X,\mathcal {D})$. Suppose further that we can find a class ![]() $\delta \in R(\mathcal {A}_X,\mathcal {D})$ such that
$\delta \in R(\mathcal {A}_X,\mathcal {D})$ such that ![]() $\gamma$ equals
$\gamma$ equals ![]() $\delta$ on
$\delta$ on ![]() $\mathcal {S}$. Then
$\mathcal {S}$. Then
is supported on lower-dimensional strata and therefore lies in ![]() $R(\mathcal {A}_X,\mathcal {D})$, so that we have
$R(\mathcal {A}_X,\mathcal {D})$, so that we have ![]() $\gamma \in R(\mathcal {A}_X,\mathcal {D})$ as well. Thus, the induction hypothesis ensures that, for a given dimension
$\gamma \in R(\mathcal {A}_X,\mathcal {D})$ as well. Thus, the induction hypothesis ensures that, for a given dimension ![]() $\dim \mathcal {S}$, we can remove strata
$\dim \mathcal {S}$, we can remove strata ![]() $\mathcal {S}'$ with
$\mathcal {S}'$ with ![]() $\dim \mathcal {S}' < \dim \mathcal {S}$, and thus it suffices to prove the statement with the additional assumption that
$\dim \mathcal {S}' < \dim \mathcal {S}$, and thus it suffices to prove the statement with the additional assumption that ![]() $\mathcal {S}$ is closed in
$\mathcal {S}$ is closed in ![]() $\mathcal {A}_X$. Note that this reduction also suffices to handle the base of the induction: the minimal dimensional strata of
$\mathcal {A}_X$. Note that this reduction also suffices to handle the base of the induction: the minimal dimensional strata of ![]() $\mathcal {A}_X$ are automatically closed.
$\mathcal {A}_X$ are automatically closed.
Suppose then that ![]() $\gamma$ is a class supported on
$\gamma$ is a class supported on ![]() $\mathcal {S}$, and
$\mathcal {S}$, and ![]() $\mathcal {S}$ is closed of codimension
$\mathcal {S}$ is closed of codimension ![]() $n$ in
$n$ in ![]() $\mathcal {A}_X$. Then
$\mathcal {A}_X$. Then ![]() $\mathcal {S} \cong B(\mathbb {G}_m^n \rtimes G)$,
$\mathcal {S} \cong B(\mathbb {G}_m^n \rtimes G)$, ![]() $\mathcal {A}_X$ is a quotient of
$\mathcal {A}_X$ is a quotient of ![]() $[\mathbb {A}^n/\mathbb {G}_m^n]$ by an étale equivalence relation in a neighborhood of
$[\mathbb {A}^n/\mathbb {G}_m^n]$ by an étale equivalence relation in a neighborhood of ![]() $\mathcal {S}$, and the monodromy torsor
$\mathcal {S}$, and the monodromy torsor ![]() $\mu : \tilde {\mathcal {P}} \to \mathcal {S}$ is isomorphic to
$\mu : \tilde {\mathcal {P}} \to \mathcal {S}$ is isomorphic to ![]() $B\mathbb {G}_m^n$.
$B\mathbb {G}_m^n$.
We can use this to describe the normal bundle ![]() $N_{\mathcal {S}/\mathcal {A}_X}$ on
$N_{\mathcal {S}/\mathcal {A}_X}$ on ![]() $\mathcal {S}$: the data of this vector bundle on
$\mathcal {S}$: the data of this vector bundle on ![]() $\mathcal {S}$ are equivalent to specifying the bundle
$\mathcal {S}$ are equivalent to specifying the bundle ![]() $\mu ^* N_{\mathcal {S}/\mathcal {A}_X}$ on
$\mu ^* N_{\mathcal {S}/\mathcal {A}_X}$ on ![]() $\tilde {\mathcal {P}}$ together with a
$\tilde {\mathcal {P}}$ together with a ![]() $G$-action. It is given by
$G$-action. It is given by
where ![]() $\mathcal {D}_i$ is the
$\mathcal {D}_i$ is the ![]() $i$th hyperplane divisor in
$i$th hyperplane divisor in ![]() $[\mathbb {A}^n/\mathbb {G}_m^n]$. The monodromy group
$[\mathbb {A}^n/\mathbb {G}_m^n]$. The monodromy group ![]() $G$ acts by permuting the hyperplanes
$G$ acts by permuting the hyperplanes ![]() $\mathcal {D}_i$ cutting out
$\mathcal {D}_i$ cutting out ![]() $S$, and this action lifts to a corresponding action permuting the direct summands
$S$, and this action lifts to a corresponding action permuting the direct summands ![]() $N_i$ above. In particular, while the pull-back
$N_i$ above. In particular, while the pull-back ![]() $\mu ^* N_{\mathcal {S}/\mathcal {A}_X}$ is a direct sum, the individual direct summands are in general not invariant under the
$\mu ^* N_{\mathcal {S}/\mathcal {A}_X}$ is a direct sum, the individual direct summands are in general not invariant under the ![]() $G$-action, and thus
$G$-action, and thus ![]() $N_{\mathcal {S}/\mathcal {A}_X}$ is not actually split on
$N_{\mathcal {S}/\mathcal {A}_X}$ is not actually split on ![]() $\mathcal {S}$.
$\mathcal {S}$.
Still, on ![]() $\tilde {\mathcal {P}}$ we have that the classes
$\tilde {\mathcal {P}}$ we have that the classes ![]() $x_i:=c_1(N_i)$ form a generating set for the algebra
$x_i:=c_1(N_i)$ form a generating set for the algebra
On the other hand, the map ![]() $\mu$ gives an isomorphism
$\mu$ gives an isomorphism
with inverse ![]() $ ({1}/{|G|})\mu _*$, since we are working with rational Chow groups. Thus,
$ ({1}/{|G|})\mu _*$, since we are working with rational Chow groups. Thus, ![]() $\gamma$ is the image of
$\gamma$ is the image of ![]() $ ({1}/{|G|})\mu ^*\gamma$ under
$ ({1}/{|G|})\mu ^*\gamma$ under ![]() $\mu _*$, which is a
$\mu _*$, which is a ![]() $G$-invariant polynomial in the
$G$-invariant polynomial in the ![]() $x_i$. This shows that
$x_i$. This shows that ![]() $\gamma$ is a normally decorated strata class, completing the proof.
$\gamma$ is a normally decorated strata class, completing the proof.
Theorem 15 immediately implies that ![]() $\mathsf {R}^\star (X,D)\subset \mathsf {CH}^\star (X)$ is closed under the intersection product (a claim which was left to the reader in § 5.4). On the other hand, it is not immediate to see which piecewise polynomial corresponds to which normally decorated strata class. The precise correspondence between piecewise polynomials and normally decorated strata classes has now been established in [Reference Holmes, Molcho, Pandharipande, Pixton and SchmittHMPPS22, § 6].
$\mathsf {R}^\star (X,D)\subset \mathsf {CH}^\star (X)$ is closed under the intersection product (a claim which was left to the reader in § 5.4). On the other hand, it is not immediate to see which piecewise polynomial corresponds to which normally decorated strata class. The precise correspondence between piecewise polynomials and normally decorated strata classes has now been established in [Reference Holmes, Molcho, Pandharipande, Pixton and SchmittHMPPS22, § 6].
5.6 Proofs of Theorems 12 and 13
Fix a normal crossings pair ![]() $(X,D)$ with Artin fan
$(X,D)$ with Artin fan ![]() $\mathcal {A}_X$ and map
$\mathcal {A}_X$ and map
Consider an arbitrary smooth log modification
necessarily of the form ![]() $(\widetilde {X},\widetilde {D})$, with an associated map
$(\widetilde {X},\widetilde {D})$, with an associated map
By definition, the log modification ![]() $\widetilde {X} \to X$ is pulled back to
$\widetilde {X} \to X$ is pulled back to ![]() $X$ from a log modification
$X$ from a log modification ![]() $\widetilde {\mathcal {A}}_{X} \to \mathcal {A}_X$ of Artin fans, and we have a diagram
$\widetilde {\mathcal {A}}_{X} \to \mathcal {A}_X$ of Artin fans, and we have a diagram

with the square being Cartesian, the map ![]() $c$ proper, Deligne-Mumford type, étale and bijective, and
$c$ proper, Deligne-Mumford type, étale and bijective, and ![]() $\widetilde {\alpha } = c \circ \beta$. By Theorem 15,
$\widetilde {\alpha } = c \circ \beta$. By Theorem 15,
Since the map ![]() $c$ is proper, Deligne–Mumford type, étale and bijective, it induces an isomorphism
$c$ is proper, Deligne–Mumford type, étale and bijective, it induces an isomorphism
between rational Chow groups, and thus we also have
As ![]() $f_*{\beta }^*(\widetilde {\delta }) = \alpha ^*g_*(\widetilde {\delta })$, we have
$f_*{\beta }^*(\widetilde {\delta }) = \alpha ^*g_*(\widetilde {\delta })$, we have
where we conclude equality instead of inclusion since ![]() $g_*$ is surjective.Footnote 28 Similarly, since
$g_*$ is surjective.Footnote 28 Similarly, since ![]() $f^*\alpha ^*(\delta ) = \beta ^*g^*(\delta )$, we have
$f^*\alpha ^*(\delta ) = \beta ^*g^*(\delta )$, we have ![]() $f^*\mathsf {R}^\star (X,D) \subset \mathsf {R}^\star (\widetilde {X},\widetilde {D})$.
$f^*\mathsf {R}^\star (X,D) \subset \mathsf {R}^\star (\widetilde {X},\widetilde {D})$.
Combining Theorem 15 with the techniques used in the proof above also provides a second proof of Theorem 11 based on the study of the Artin fan. The crucial observation is as follows. Suppose ![]() $(X,D)$ is a normal crossings pair with
$(X,D)$ is a normal crossings pair with ![]() $D$ ‘as simple as possible’:
$D$ ‘as simple as possible’: ![]() $D$ is normal crossings in the Zariski topology, and the non-empty intersections of the branches of
$D$ is normal crossings in the Zariski topology, and the non-empty intersections of the branches of ![]() $D$ are connected. Equivalently, this means that
$D$ are connected. Equivalently, this means that ![]() $C(X,D)$ is the cone over an abstract simplicial complex, that is, can be piecewise linearly embedded into a vector space. Then the ring of piecewise polynomials on
$C(X,D)$ is the cone over an abstract simplicial complex, that is, can be piecewise linearly embedded into a vector space. Then the ring of piecewise polynomials on ![]() $C(X,D)$ has a global description in terms of the Stanley–Reisner ring,
$C(X,D)$ has a global description in terms of the Stanley–Reisner ring,
where the variables ![]() $x_r$ range over the rays of
$x_r$ range over the rays of ![]() $C(X,D)$, and
$C(X,D)$, and ![]() $N$ is the ideal of non-faces, that is, generated by monomials
$N$ is the ideal of non-faces, that is, generated by monomials ![]() $x_{i_1}\cdots x_{i_k}$ ranging over the collections
$x_{i_1}\cdots x_{i_k}$ ranging over the collections ![]() $i_1,\ldots,i_k$ of rays which do not form a cone in
$i_1,\ldots,i_k$ of rays which do not form a cone in ![]() $C(X,D)$. A fortiori, this presentation implies that
$C(X,D)$. A fortiori, this presentation implies that ![]() $\mathsf {CH}(\mathcal {A}_X)$ is generated by divisors.
$\mathsf {CH}(\mathcal {A}_X)$ is generated by divisors.
While the piecewise polynomials of a general ![]() $(X,D)$ do not admit this simple description, the observation is relevant in our context because any sufficiently fine log blow-up of
$(X,D)$ do not admit this simple description, the observation is relevant in our context because any sufficiently fine log blow-up of ![]() $(X,D)$ has this form. For example, the double barycentric subdivision
$(X,D)$ has this form. For example, the double barycentric subdivision ![]() $(\widehat {X},\widehat {D})$ of
$(\widehat {X},\widehat {D})$ of ![]() $(X,D)$ always has this form. Applying barycentric subdivision once on an arbitrary
$(X,D)$ always has this form. Applying barycentric subdivision once on an arbitrary ![]() $C(X,D)$ produces a cone complex with no self-intersection (and thus no monodromy), but where two cones possibly share the same set of rays (i.e. the intersection of a set of branches of the divisor is disconnected). Applying barycentric subdivision a second time separates such cones, ensuring that each cone is uniquely characterized by its set of rays, and thus produces a cone complex
$C(X,D)$ produces a cone complex with no self-intersection (and thus no monodromy), but where two cones possibly share the same set of rays (i.e. the intersection of a set of branches of the divisor is disconnected). Applying barycentric subdivision a second time separates such cones, ensuring that each cone is uniquely characterized by its set of rays, and thus produces a cone complex ![]() $C(\widehat {X},\widehat {D})$ which is the cone over a simplicial complex.
$C(\widehat {X},\widehat {D})$ which is the cone over a simplicial complex.
Corollary 16 We have ![]() $\mathsf {R}^\star (X,D)\subset \mathsf {divlogCH}^\star (X,D)$.
$\mathsf {R}^\star (X,D)\subset \mathsf {divlogCH}^\star (X,D)$.
Proof. Let ![]() $(\widehat {X},\widehat {D})$ be the log blow-up corresponding to the double barycentric subdivision,
$(\widehat {X},\widehat {D})$ be the log blow-up corresponding to the double barycentric subdivision,

As above, ![]() $\widehat {\mathcal {A}}_X$ is the relative Artin fan of
$\widehat {\mathcal {A}}_X$ is the relative Artin fan of ![]() $\widehat {X} \to X$, and the Artin fan
$\widehat {X} \to X$, and the Artin fan ![]() $\mathcal {A}_{\widehat {X}}$ has the same rational Chow ring as
$\mathcal {A}_{\widehat {X}}$ has the same rational Chow ring as ![]() $\widehat {\mathcal {A}}_X$. Let
$\widehat {\mathcal {A}}_X$. Let ![]() $\gamma \in \mathsf {R}^\star (X,D)$. By Theorem 15,
$\gamma \in \mathsf {R}^\star (X,D)$. By Theorem 15, ![]() $\gamma \in \alpha ^*\mathsf {CH}^\star (\mathcal {A}_X)$ and therefore
$\gamma \in \alpha ^*\mathsf {CH}^\star (\mathcal {A}_X)$ and therefore
Since ![]() $\mathsf {CH}^\star (\mathcal {A}_{\widehat {X}})$ is generated by divisors, we have
$\mathsf {CH}^\star (\mathcal {A}_{\widehat {X}})$ is generated by divisors, we have ![]() $f^*(\gamma ) \in \mathsf {divCH}^\star (\widehat {X})$.
$f^*(\gamma ) \in \mathsf {divCH}^\star (\widehat {X})$.
The proof of Theorem 15 immediately yields a finer statement: ![]() $\mathsf {R}^\star (X,D)$ lies in the subalgebra generated by logarithmic divisors of the log blow-up associated to the second barycentric subdivision of the Artin fan of
$\mathsf {R}^\star (X,D)$ lies in the subalgebra generated by logarithmic divisors of the log blow-up associated to the second barycentric subdivision of the Artin fan of ![]() $(X,D)$; in fact, the subalgebra generated by logarithmic divisors of the log blow-up associated to any log blow-up
$(X,D)$; in fact, the subalgebra generated by logarithmic divisors of the log blow-up associated to any log blow-up ![]() $(\tilde {X},\tilde {D})$ with
$(\tilde {X},\tilde {D})$ with ![]() $C(\tilde {X},\tilde {D})$ the cone over a simplicial complex. The double barycentric subdivision of any normal crossings pair
$C(\tilde {X},\tilde {D})$ the cone over a simplicial complex. The double barycentric subdivision of any normal crossings pair ![]() $(X,D)$ is always a canonical such choice, but, for any given example, a much more efficient choice
$(X,D)$ is always a canonical such choice, but, for any given example, a much more efficient choice ![]() $(\widetilde {X},\widetilde {D})$ may be available.
$(\widetilde {X},\widetilde {D})$ may be available.
6. Pixton's formula for  $\lambda _g\in \mathsf {CH}^\star (\overline {\mathcal {M}}_g)$
$\lambda _g\in \mathsf {CH}^\star (\overline {\mathcal {M}}_g)$
6.1 Strata
Pixton's formula for the double ramification cycle ![]() $\mathsf {DR}_{g,A}\in \mathsf {CH}^g(\overline {\mathcal {M}}_{g,n})$ is expressed as a sum over strata of
$\mathsf {DR}_{g,A}\in \mathsf {CH}^g(\overline {\mathcal {M}}_{g,n})$ is expressed as a sum over strata of ![]() $(\overline {\mathcal {M}}_{g,n},\partial \overline {\mathcal {M}}_{g,n})$ indexed by the set
$(\overline {\mathcal {M}}_{g,n},\partial \overline {\mathcal {M}}_{g,n})$ indexed by the set ![]() $\mathsf {G}_{g,n}$ of stable graphs. We present here Pixton's formula with an emphasis on the special case
$\mathsf {G}_{g,n}$ of stable graphs. We present here Pixton's formula with an emphasis on the special case
We refer the reader to [Reference Janda, Pandharipande, Pixton and ZvonkineJPPZ17, Reference PandharipandePan99] for a more detailed discussion about double ramification cycles, stable graphs, Pixton's formula, and the relation to classical Abel–Jacobi theory.
6.2 Weightings
Let ![]() $A=(a_1,\ldots,a_n)\in \mathbb {Z}^n$ satisfy
$A=(a_1,\ldots,a_n)\in \mathbb {Z}^n$ satisfy ![]() $\sum _{i=1}^n a_i=0$. Let
$\sum _{i=1}^n a_i=0$. Let
be a stable graphFootnote 29 of genus ![]() $g$ with
$g$ with ![]() $n$ legs. A weighting of
$n$ legs. A weighting of ![]() $\Gamma$ is a function on the set of half-edges,
$\Gamma$ is a function on the set of half-edges,
which satisfies the following three properties:
(i) for all
 $h_i\in \mathrm {L}(\Gamma )$, corresponding to the marking
$h_i\in \mathrm {L}(\Gamma )$, corresponding to the marking  $i\in \{1,\ldots, n\}$,
$i\in \{1,\ldots, n\}$,
 \[ w(h_i)=a_i; \]
\[ w(h_i)=a_i; \]
(ii) for all
 $e \in \mathrm {E}(\Gamma )$, corresponding to two half-edges
$e \in \mathrm {E}(\Gamma )$, corresponding to two half-edges  $h,h' \in \mathrm {H}(\Gamma )$;
$h,h' \in \mathrm {H}(\Gamma )$;
 \[ w(h)+w(h')=0, \]
\[ w(h)+w(h')=0, \]
(iii) for all
 $v\in \mathrm {V}(\Gamma )$,
where the sum is taken over all
$v\in \mathrm {V}(\Gamma )$,
where the sum is taken over all \[ \sum_{v(h)= v} w(h)=0, \]
\[ \sum_{v(h)= v} w(h)=0, \]
 $n(v)$ half-edges incident to
$n(v)$ half-edges incident to  $v$.
$v$.
In the case ![]() $A=\emptyset$, the set of half-edges
$A=\emptyset$, the set of half-edges ![]() $\mathrm {H}(\Gamma )$ has no legs (
$\mathrm {H}(\Gamma )$ has no legs (![]() $n=0$).
$n=0$).
Let ![]() $r$ be a positive integer. A weighting mod
$r$ be a positive integer. A weighting mod ![]() $r$ of
$r$ of ![]() $\Gamma$ is a function,
$\Gamma$ is a function,
which satisfies exactly properties (i)–(iii) above, but with the equalities replaced, in each case, by the condition of congruence ![]() $mod$
$mod$ ![]() $r$. The set
$r$. The set ![]() $\mathsf {W}_{\Gamma,r}$ of such weightings
$\mathsf {W}_{\Gamma,r}$ of such weightings ![]() $w$ is finite, with cardinality
$w$ is finite, with cardinality ![]() $r^{h^1(\Gamma )}$.
$r^{h^1(\Gamma )}$.
6.3 Formula for double ramification cycles
Let ![]() $A=(a_1,\ldots,a_n)\in \mathbb {Z}^n$ satisfy
$A=(a_1,\ldots,a_n)\in \mathbb {Z}^n$ satisfy ![]() $\sum _{i=1}^n a_i=0$. Let
$\sum _{i=1}^n a_i=0$. Let ![]() $r$ be a positive integer. We denote by
$r$ be a positive integer. We denote by
the degree ![]() $d$ component of the tautological class
$d$ component of the tautological class
 \begin{align} & \sum_{\Gamma\in \mathsf{G}_{g,n}}\sum_{w\in \mathsf{W}_{\Gamma,r}} \frac1{|{\rm Aut}(\Gamma)|}\frac1{r^{h^1(\Gamma)}}\xi_{\Gamma*} \Bigg[\prod_{i=1}^n \exp(a_i^2 \psi_{h_i}) \nonumber\\ &\quad \cdot\prod_{e=(h,h')\in \mathrm{E}(\Gamma)} \frac{1-\exp(-w(h)w(h')(\psi_h+\psi_{h'}))}{\psi_h + \psi_{h'}}\Bigg] \end{align}
\begin{align} & \sum_{\Gamma\in \mathsf{G}_{g,n}}\sum_{w\in \mathsf{W}_{\Gamma,r}} \frac1{|{\rm Aut}(\Gamma)|}\frac1{r^{h^1(\Gamma)}}\xi_{\Gamma*} \Bigg[\prod_{i=1}^n \exp(a_i^2 \psi_{h_i}) \nonumber\\ &\quad \cdot\prod_{e=(h,h')\in \mathrm{E}(\Gamma)} \frac{1-\exp(-w(h)w(h')(\psi_h+\psi_{h'}))}{\psi_h + \psi_{h'}}\Bigg] \end{align}
in ![]() $R^*(\overline {\mathcal {M}}_{g,n})$.
$R^*(\overline {\mathcal {M}}_{g,n})$.
The following fundamental polynomiality property of ![]() $\mathsf {P}_g^{d,r}(A)$ has been proven by Pixton (see [Reference Janda, Pandharipande, Pixton and ZvonkineJPPZ17, Appendix]).
$\mathsf {P}_g^{d,r}(A)$ has been proven by Pixton (see [Reference Janda, Pandharipande, Pixton and ZvonkineJPPZ17, Appendix]).
Proposition 17 (Pixton)
For fixed ![]() $g$,
$g$, ![]() $A$, and
$A$, and ![]() $d$, the class
$d$, the class
is polynomial in ![]() $r$ (for all sufficiently large
$r$ (for all sufficiently large ![]() $r$).
$r$).
We denote by ![]() $\mathsf {P}_g^d(A)$ the value at
$\mathsf {P}_g^d(A)$ the value at ![]() $r=0$ of the polynomial associated to
$r=0$ of the polynomial associated to ![]() $\mathsf {P}_g^{d,r}(A)$ by Proposition 17. In other words,
$\mathsf {P}_g^{d,r}(A)$ by Proposition 17. In other words, ![]() $\mathsf {P}_g^d(A)$ is the constant term of the associated polynomial in
$\mathsf {P}_g^d(A)$ is the constant term of the associated polynomial in ![]() $r$. Pixton's formula for double ramification cycles is
$r$. Pixton's formula for double ramification cycles is
6.4 Examples in the  $A=\emptyset$ case
$A=\emptyset$ case
For the reader's convenience, we present in Figure 2 the first few examplesFootnote 30 of Pixton's formula for ![]() $\lambda _g$ obtained by calculating
$\lambda _g$ obtained by calculating ![]() $(-1)^g \mathsf {DR}_{g,\emptyset }$.
$(-1)^g \mathsf {DR}_{g,\emptyset }$.

Figure 2. Formulas for the classes ![]() $\lambda_g$ for
$\lambda_g$ for ![]() $g=1, \ldots, 4$.
$g=1, \ldots, 4$.
Each labeled graph ![]() $\Gamma$ describes a moduli space
$\Gamma$ describes a moduli space ![]() $\overline {\mathcal {M}}_\Gamma$ (a product of moduli spaces associated with the vertices of
$\overline {\mathcal {M}}_\Gamma$ (a product of moduli spaces associated with the vertices of ![]() $\Gamma$), a tautological class
$\Gamma$), a tautological class ![]() $\alpha \in R^*(\overline {\mathcal {M}}_\Gamma )$, and a natural map
$\alpha \in R^*(\overline {\mathcal {M}}_\Gamma )$, and a natural map
Our convention in the formulas below is that the graph ![]() $\Gamma$ represents the cycle class
$\Gamma$ represents the cycle class ![]() $(\xi _\Gamma )_* \alpha$. For instance, assume the graph carries no
$(\xi _\Gamma )_* \alpha$. For instance, assume the graph carries no ![]() $\psi$-classes and the class
$\psi$-classes and the class ![]() $\alpha$ equals 1. Since the map
$\alpha$ equals 1. Since the map ![]() $\xi _\Gamma$ is of degree
$\xi _\Gamma$ is of degree ![]() $|{\rm Aut} (\Gamma )|$ onto its image, the cycle class represented by
$|{\rm Aut} (\Gamma )|$ onto its image, the cycle class represented by ![]() $\Gamma$ is then
$\Gamma$ is then ![]() $|{\rm Aut} (\Gamma )|$ times the class of the image of
$|{\rm Aut} (\Gamma )|$ times the class of the image of ![]() $\xi _\Gamma$.
$\xi _\Gamma$.
6.5 Proof of Theorem 6
We analyze Pixton's formula in the ![]() $A=\emptyset$ case,
$A=\emptyset$ case,
Since ![]() $A=\emptyset$, the sum (33) is over stable graphs
$A=\emptyset$, the sum (33) is over stable graphs ![]() $\Gamma \in \mathsf {G}_{g}$ corresponding to strata of
$\Gamma \in \mathsf {G}_{g}$ corresponding to strata of ![]() $(\overline {\mathcal {M}}_{g},\partial \overline {\mathcal {M}}_{g})$.
$(\overline {\mathcal {M}}_{g},\partial \overline {\mathcal {M}}_{g})$.
• By the definition of a weighting mod
 $r$, the weights
on the two halves of every separating edge
$r$, the weights
on the two halves of every separating edge \[ w(h),\quad w(h') \]
\[ w(h),\quad w(h') \]
 $e$ of
$e$ of  $\Gamma$ must both be
$\Gamma$ must both be  $0$. The factor in Pixton's formula for
$0$. The factor in Pixton's formula for  $e$,
then vanishes and kills the contribution of
$e$,
then vanishes and kills the contribution of \[ \frac{1-\exp(-w(h)w(h')(\psi_h+\psi_{h'}))}{\psi_h + \psi_{h'}}, \]
\[ \frac{1-\exp(-w(h)w(h')(\psi_h+\psi_{h'}))}{\psi_h + \psi_{h'}}, \]
 $\Gamma$ to
$\Gamma$ to  $\mathsf {P}_g^g(\emptyset )$. Therefore, non-vanishing terms in the sum (33) must correspond to graphs with no separating edges.
$\mathsf {P}_g^g(\emptyset )$. Therefore, non-vanishing terms in the sum (33) must correspond to graphs with no separating edges.• Since
 $A=\emptyset$, the term
drops out of (33).
$A=\emptyset$, the term
drops out of (33). \[ \prod_{i=1}^n \exp(a_i^2 \psi_{h_i}) \]
\[ \prod_{i=1}^n \exp(a_i^2 \psi_{h_i}) \]
• The classes which do appear in (33) are the normal bundle terms
 $\psi _h+\psi _{h'}$ at each edge of
$\psi _h+\psi _{h'}$ at each edge of  $\Gamma$.
$\Gamma$.
Since the formula (33) respects the automorphisms of the stable graph ![]() $\Gamma$, we obtain the following result.
$\Gamma$, we obtain the following result.
Proposition 18 The class ![]() $\lambda _g\in \mathsf {CH}^g(\overline {\mathcal {M}}_{g})$ is a sum of normally decorated classes associated to strata of
$\lambda _g\in \mathsf {CH}^g(\overline {\mathcal {M}}_{g})$ is a sum of normally decorated classes associated to strata of ![]() $(\overline {\mathcal {M}}_{g},\partial \overline {\mathcal {M}}_{g})$ corresponding to stable graphs
$(\overline {\mathcal {M}}_{g},\partial \overline {\mathcal {M}}_{g})$ corresponding to stable graphs ![]() $\Gamma \in \mathsf {G}_{g}$ with no separating edges.
$\Gamma \in \mathsf {G}_{g}$ with no separating edges.
Theorem 6 is then an immediate consequence of Proposition 18 and Theorem 11. Proposition 18 reflects a very special property of ![]() $\lambda _g$ obtained from Pixton's formula. Since every edge of every stable graph
$\lambda _g$ obtained from Pixton's formula. Since every edge of every stable graph ![]() $\Gamma \in \mathsf {G}_g$ which appears in Pixton's formula for
$\Gamma \in \mathsf {G}_g$ which appears in Pixton's formula for ![]() $\lambda _g$ is non-separating, we actually have
$\lambda _g$ is non-separating, we actually have
Theorem 11 then implies a refinement of Theorem 6,
By applying Pixton's formula for the double ramification cycle
an identical argument yields
for ![]() $2g-2+n>0$.
$2g-2+n>0$.
6.6 More general double ramification cycles
Let ![]() $A=(a_1,\ldots,a_n)$ be a vector of integers satisfying
$A=(a_1,\ldots,a_n)$ be a vector of integers satisfying ![]() $\sum _{i=1}^n a_i =0$. Pixton's formula for the double ramification cycle
$\sum _{i=1}^n a_i =0$. Pixton's formula for the double ramification cycle
together with Theorem 11, yields the following result (the proof of which is exactly the same as the proof of Theorem 6).
Theorem 19 We have ![]() $\mathsf {DR}_{g,A}\in \underline {\mathsf {div}}\mathsf {logCH}^\star (\overline {\mathcal {M}}_{g,n})$ where
$\mathsf {DR}_{g,A}\in \underline {\mathsf {div}}\mathsf {logCH}^\star (\overline {\mathcal {M}}_{g,n})$ where
is the subalgebra generated by logarithmic boundary divisors together with the cotangent line classes ![]() $\psi _1,\ldots, \psi _n$.
$\psi _1,\ldots, \psi _n$.
Theorem 19 provides half of the proof of Conjecture C concerning the lifted double ramification cycle ![]() $\widetilde {\mathsf {DR}}_{g,A}$. There are now three proofs of the other half of the conjecture via three different approaches. The first two are by Abel–Jacobi theory in [Reference Holmes and SchwarzHS22] and by controlling the difference between
$\widetilde {\mathsf {DR}}_{g,A}$. There are now three proofs of the other half of the conjecture via three different approaches. The first two are by Abel–Jacobi theory in [Reference Holmes and SchwarzHS22] and by controlling the difference between ![]() $\mathsf {DR}_{g,A}$ and
$\mathsf {DR}_{g,A}$ and ![]() $\widetilde {\mathsf {DR}}_{g,A}$ in an appropriate blow-up of
$\widetilde {\mathsf {DR}}_{g,A}$ in an appropriate blow-up of ![]() $\overline {\mathcal {M}}_{g,n}$ in [Reference Molcho and RanganathanMR21]. The third, presented in [Reference Holmes, Molcho, Pandharipande, Pixton and SchmittHMPPS22], proves the conjecture directly by giving a formula for (a representative of)
$\overline {\mathcal {M}}_{g,n}$ in [Reference Molcho and RanganathanMR21]. The third, presented in [Reference Holmes, Molcho, Pandharipande, Pixton and SchmittHMPPS22], proves the conjecture directly by giving a formula for (a representative of) ![]() $\widetilde {\mathsf {DR}}_{g,A}$ in terms of
$\widetilde {\mathsf {DR}}_{g,A}$ in terms of ![]() $\psi$-classes and piecewise polynomials.
$\psi$-classes and piecewise polynomials.
The special case ![]() $A=(0,\ldots,0)$ related to the class
$A=(0,\ldots,0)$ related to the class ![]() $\lambda _g$ is simpler since no cotangent line classes appear at the markings in Pixton's formula. Moreover, there is no change in the lift for
$\lambda _g$ is simpler since no cotangent line classes appear at the markings in Pixton's formula. Moreover, there is no change in the lift for ![]() $A=(0,\ldots,0)$:
$A=(0,\ldots,0)$:
The ![]() $\omega ^k$-twisted double ramification cycle [Reference HolmesHol19] is also governed by Pixton's formula [Reference Bae, Holmes, Pandharipande, Schmitt and SchwarzBHPSS20],
$\omega ^k$-twisted double ramification cycle [Reference HolmesHol19] is also governed by Pixton's formula [Reference Bae, Holmes, Pandharipande, Schmitt and SchwarzBHPSS20],
 \[ \mathsf{DR}^k_{g,A}\in \mathsf{R}^\star(\overline{\mathcal{M}}_{g,n}),\quad \sum_{i=1}^n a_i = k(2g-2). \]
\[ \mathsf{DR}^k_{g,A}\in \mathsf{R}^\star(\overline{\mathcal{M}}_{g,n}),\quad \sum_{i=1}^n a_i = k(2g-2). \]
The analogue of Theorem 19 can be proven for the ![]() $\omega ^k$-twisted double ramification cycle, but the divisor subalgebra of
$\omega ^k$-twisted double ramification cycle, but the divisor subalgebra of ![]() $\mathsf {logCH}^\star (\overline {\mathcal {M}}_{g,n})$ must include
$\mathsf {logCH}^\star (\overline {\mathcal {M}}_{g,n})$ must include ![]() $\kappa _1$ together with the cotangent line classes
$\kappa _1$ together with the cotangent line classes ![]() $\psi _i$ and the logarithmic boundary divisors. Conjecture C can then also be promoted to a statement for the lifted
$\psi _i$ and the logarithmic boundary divisors. Conjecture C can then also be promoted to a statement for the lifted ![]() $\omega ^k$-twisted double ramification cycle (again including
$\omega ^k$-twisted double ramification cycle (again including ![]() $\kappa _1$ in the subalgebra).
$\kappa _1$ in the subalgebra).
6.7 Pixton's generalized boundary strata classes
In [Reference PixtonPix18], Pixton defined a subalgebra of the tautological ring ![]() $\mathsf {R}^*(\overline {\mathcal {M}}_{g,n})$ spanned by generalized boundary strata classes: tautological classes
$\mathsf {R}^*(\overline {\mathcal {M}}_{g,n})$ spanned by generalized boundary strata classes: tautological classes ![]() $[\Gamma ]$ associated to prestable graphs
$[\Gamma ]$ associated to prestable graphs ![]() $\Gamma$ of genus
$\Gamma$ of genus ![]() $g$ with
$g$ with ![]() $n$ legs.
$n$ legs.
If ![]() $\Gamma$ is a semistable graph (every genus
$\Gamma$ is a semistable graph (every genus ![]() $0$ vertex is incident to at least two legs or half-edges), then Pixton's definition takes a simple form. Let
$0$ vertex is incident to at least two legs or half-edges), then Pixton's definition takes a simple form. Let ![]() $\Gamma '$ be the stabilization of
$\Gamma '$ be the stabilization of ![]() $\Gamma$. The class
$\Gamma$. The class ![]() $[\Gamma ]$ is defined as a push-forward under the gluing map
$[\Gamma ]$ is defined as a push-forward under the gluing map ![]() $\xi _{\Gamma '}$ of products of classes
$\xi _{\Gamma '}$ of products of classes ![]() $\psi _1,\ldots, \psi _n$ and classes
$\psi _1,\ldots, \psi _n$ and classes ![]() $\psi _h + \psi _{h'}$ for half-edges
$\psi _h + \psi _{h'}$ for half-edges ![]() $(h,h')$ forming an edge of
$(h,h')$ forming an edge of ![]() $\Gamma '$. The analysis of § 6.5 then implies
$\Gamma '$. The analysis of § 6.5 then implies
in the semistable case.
Pixton's boundary class for more general unstable graphs has ![]() $\kappa$ classes and will likely not lie in any version of
$\kappa$ classes and will likely not lie in any version of ![]() $\mathsf {divlogCH}^\star (\overline {\mathcal {M}}_g, \partial \overline {\mathcal {M}}_g)$.
$\mathsf {divlogCH}^\star (\overline {\mathcal {M}}_g, \partial \overline {\mathcal {M}}_g)$.
7. The bChow ring
Let ![]() $X$ be a non-singular variety. Given the additional data of a normal crossings divisor
$X$ be a non-singular variety. Given the additional data of a normal crossings divisor ![]() $D \subset X$, we defined the log Chow ring of the pair
$D \subset X$, we defined the log Chow ring of the pair ![]() $(X,D)$. This is a variant of a much larger ring, the bChow ring of
$(X,D)$. This is a variant of a much larger ring, the bChow ring of ![]() $X$. We define
$X$. We define
where ![]() $\mathsf {B}(X)$ is the category of non-singular blow-ups of
$\mathsf {B}(X)$ is the category of non-singular blow-ups of ![]() $X$: objects in
$X$: objects in ![]() $\mathsf {B}(X)$ are proper birational maps
$\mathsf {B}(X)$ are proper birational maps
with ![]() $Y$ non-singular, and morphisms in
$Y$ non-singular, and morphisms in ![]() $\mathsf {B}(X)$ are proper birational maps over
$\mathsf {B}(X)$ are proper birational maps over ![]() $X$. For a longer introduction to the bChow ring, see [Reference Holmes, Pixton and SchmittHPS19]. Some of the ideas involved go back to papers of Shokurov [Reference ShokurovSho96, Reference ShokurovSho03]. See also Aluffi [Reference AluffiAlu05] for similar constructions.
$X$. For a longer introduction to the bChow ring, see [Reference Holmes, Pixton and SchmittHPS19]. Some of the ideas involved go back to papers of Shokurov [Reference ShokurovSho96, Reference ShokurovSho03]. See also Aluffi [Reference AluffiAlu05] for similar constructions.
Let ![]() $[Z\to X]$ and
$[Z\to X]$ and ![]() $[Y\to X]$ be objects of
$[Y\to X]$ be objects of ![]() $\mathsf {B}(X)$. If
$\mathsf {B}(X)$. If ![]() $Z \to X$ factors as
$Z \to X$ factors as
then there is a unique morphism from ![]() $[Z \to X]$ to
$[Z \to X]$ to ![]() $[Y \to X]$ in
$[Y \to X]$ in ![]() $\mathsf {B}(X)$, and we call
$\mathsf {B}(X)$, and we call ![]() $Z \to X$ a refinement of
$Z \to X$ a refinement of ![]() $Y \to X$. The transition maps in the above colimit are given by pull-backs
$Y \to X$. The transition maps in the above colimit are given by pull-backs
for refinements ![]() $Z \stackrel {f}{\to } Y\to X$.
$Z \stackrel {f}{\to } Y\to X$.
Unlike ![]() $\mathsf {logCH}^\star (X)$, the bChow ring does not depend upon the choice of a normal crossings divisor
$\mathsf {logCH}^\star (X)$, the bChow ring does not depend upon the choice of a normal crossings divisor ![]() $D\subset X$. However, given such a choice there is always a tower of natural inclusions
$D\subset X$. However, given such a choice there is always a tower of natural inclusions
Since the centers of the blow-up are so restricted in the definition of ![]() $\mathsf {logCH}^\star (X)$, we view
$\mathsf {logCH}^\star (X)$, we view ![]() $\mathsf {CH}^\star (X)$ and
$\mathsf {CH}^\star (X)$ and ![]() $\mathsf {logCH}^\star (X)$ as relatively close in size. On the other hand,
$\mathsf {logCH}^\star (X)$ as relatively close in size. On the other hand, ![]() $\mathsf {bCH}^\star (X)$ is very much larger.
$\mathsf {bCH}^\star (X)$ is very much larger.
Let ![]() $\mathsf {divbCH}^\star (X)$ be the subalgebra of
$\mathsf {divbCH}^\star (X)$ be the subalgebra of ![]() $\mathsf {bCH}^\star (X)$ generated by divisors. More precisely,
$\mathsf {bCH}^\star (X)$ generated by divisors. More precisely,
While the proof of the claim
depended upon special properties of ![]() $\lambda _g$, the parallel bChow statement
$\lambda _g$, the parallel bChow statement
immediately follows from a general result.
Theorem 20 For every non-singular quasi-projective varietyFootnote 31 ![]() $X$, bChow is generated by divisor classes,
$X$, bChow is generated by divisor classes,
Proof. Let ![]() $\alpha \in \mathsf {CH}^\star (Y)$ for an object
$\alpha \in \mathsf {CH}^\star (Y)$ for an object ![]() $[Y \to X]$ in
$[Y \to X]$ in ![]() $\mathsf {B}(X)$. We will find a refinement
$\mathsf {B}(X)$. We will find a refinement ![]() $Z \to Y$ for which
$Z \to Y$ for which
Since ![]() $Y$ is non-singular and quasi-projective, the Chern classes of vector bundles generate
$Y$ is non-singular and quasi-projective, the Chern classes of vector bundles generate ![]() $\mathsf {CH}^\star (Y)$. We can assume
$\mathsf {CH}^\star (Y)$. We can assume ![]() $\alpha = c_i(E)$ for a vector bundle
$\alpha = c_i(E)$ for a vector bundle ![]() $E$ on
$E$ on ![]() $Y$. By [Reference HironakaHir64, Corollary 2], there is a blow-up
$Y$. By [Reference HironakaHir64, Corollary 2], there is a blow-up
where ![]() $W$ is non-singular and
$W$ is non-singular and ![]() $g^*E$ contains a subline bundle
$g^*E$ contains a subline bundle ![]() $L$,
$L$,
Applying the same argument to the quotient bundle ![]() $g^*E/L$, we find inductively a non-singular blow-up
$g^*E/L$, we find inductively a non-singular blow-up
for which ![]() $f^*E$ has a filtration with line bundles as quotients. Therefore,
$f^*E$ has a filtration with line bundles as quotients. Therefore,
is in ![]() $\mathsf {divCH}^\star (Z)$.
$\mathsf {divCH}^\star (Z)$.
The quasi-projective hypothesis is used only for vector bundle resolutions. In fact, the hypothesis is not necessary. Theorem 20 can be proven locally near any cycle
by successive blow-ups along non-singular centers to resolve ![]() $S$ and appropriately modify the Chern classes of the normal bundle of
$S$ and appropriately modify the Chern classes of the normal bundle of ![]() $S$. We leave the details for the interested reader.
$S$. We leave the details for the interested reader.
Acknowledgements
D. Holmes, D. Ranganathan, and J. Wise have suggested that the ![]() $\Theta$-formula (2) should extend over the moduli of curves in some form in log geometry (based on their understanding of the logarithmic Picard stack [Reference Molcho and WiseMW22]). Our initial motivation here was to study geometric obstructions to such an extension. While the simplest form is excluded, Theorem 6 supports the idea of the existence of some perturbed extension of (2) in log Chow. Our development of the logarithmic tautological ring of
$\Theta$-formula (2) should extend over the moduli of curves in some form in log geometry (based on their understanding of the logarithmic Picard stack [Reference Molcho and WiseMW22]). Our initial motivation here was to study geometric obstructions to such an extension. While the simplest form is excluded, Theorem 6 supports the idea of the existence of some perturbed extension of (2) in log Chow. Our development of the logarithmic tautological ring of ![]() $(X,D)$ emerged from the proof of Theorem 6. We are very grateful to Holmes, Ranganathan, and Wise for extensive discussions of these topics. We have also benefited from related conversations with Y. Bae, C. Faber, T. Graber, S. Grushevsky, M. Olsson, A. Pixton, R. Vakil, and D. Zakharov. The results of the paper were presented at the Algebraic Geometry Seminar at Stanford in the fall of 2020 (with a lively and very helpful discussion afterwards). Finally, we wish to thank the referee for a very careful reading and many suggestions that helped to improve the text. S.M. was supported by ERC-2017-AdG-786580-MACI. R.P. was supported by SNF-200020-182181, ERC-2017-AdG-786580-MACI, and SwissMAP. J.S. was supported by the SNF Early Postdoc Mobility grant 184245, the grant SNF-184613, and thanks the Max Planck Institute for Mathematics in Bonn for its hospitality. This project has received funding from the European Research Council (ERC) under the European Union Horizon 2020 research and innovation program (grant agreement No 786580).
$(X,D)$ emerged from the proof of Theorem 6. We are very grateful to Holmes, Ranganathan, and Wise for extensive discussions of these topics. We have also benefited from related conversations with Y. Bae, C. Faber, T. Graber, S. Grushevsky, M. Olsson, A. Pixton, R. Vakil, and D. Zakharov. The results of the paper were presented at the Algebraic Geometry Seminar at Stanford in the fall of 2020 (with a lively and very helpful discussion afterwards). Finally, we wish to thank the referee for a very careful reading and many suggestions that helped to improve the text. S.M. was supported by ERC-2017-AdG-786580-MACI. R.P. was supported by SNF-200020-182181, ERC-2017-AdG-786580-MACI, and SwissMAP. J.S. was supported by the SNF Early Postdoc Mobility grant 184245, the grant SNF-184613, and thanks the Max Planck Institute for Mathematics in Bonn for its hospitality. This project has received funding from the European Research Council (ERC) under the European Union Horizon 2020 research and innovation program (grant agreement No 786580).
Appendix A. The fourth cohomology group of  $\overline {\mathcal {M}}_{g}$
$\overline {\mathcal {M}}_{g}$
In the proof of Theorem 4, we require the equalityFootnote 32
for sufficiently large ![]() $g$, In other words, the fourth cohomology group of
$g$, In other words, the fourth cohomology group of ![]() $\overline {\mathcal {M}}_{g}$ is spanned by tautological classes for sufficiently high
$\overline {\mathcal {M}}_{g}$ is spanned by tautological classes for sufficiently high ![]() $g$.
$g$.
Equality (A.1) was first proven by Edidin [Reference EdidinEdi92] for ![]() $g \geq 12$. Edidin bounded the Betti number
$g \geq 12$. Edidin bounded the Betti number ![]() $\mathsf {h}^4(\overline {\mathcal {M}}_g)$ from above and then showed by intersection calculations that the span of the tautological classesFootnote 33 in codimension 2 achieves the required rank. Edidin used the interior result
$\mathsf {h}^4(\overline {\mathcal {M}}_g)$ from above and then showed by intersection calculations that the span of the tautological classesFootnote 33 in codimension 2 achieves the required rank. Edidin used the interior result
proven by Harer [Reference HarerHar85] for ![]() $g\geq 12$. The interior statement (A.2) was later proven for
$g\geq 12$. The interior statement (A.2) was later proven for ![]() $g\geq 9$ by Ivanov [Reference IvanovIva93] and strengthened further to
$g\geq 9$ by Ivanov [Reference IvanovIva93] and strengthened further to ![]() $g \geq 7$ by Boldsen [Reference BoldsenBol12] which improved Edidin's bound.
$g \geq 7$ by Boldsen [Reference BoldsenBol12] which improved Edidin's bound.
Theorem A.1 [Reference EdidinEdi92, Reference IvanovIva93, Reference BoldsenBol12]
We have ![]() $\mathsf {H}^4(\overline {\mathcal {M}}_{g}) = \mathsf {RH}^2(\overline {\mathcal {M}}_{g})$ for
$\mathsf {H}^4(\overline {\mathcal {M}}_{g}) = \mathsf {RH}^2(\overline {\mathcal {M}}_{g})$ for ![]() $g \geq 7$.
$g \geq 7$.
Appendix B. Computations in admcycles
B.1 Verification of Pixton's conjecture
In [Reference PixtonPix12], Pixton proposed a set of relations between tautological classes on the moduli spaces ![]() $\overline {\mathcal {M}}_{g,n}$ of stable curves. These were proven to hold in cohomology [Reference Pandharipande, Pixton and ZvonkinePPZ15] and in Chow [Reference JandaJan17]. Furthermore, Pixton conjectured that his relations span the complete set of relations among tautological classes. The relations were implemented by Pixton in the mathematical software SageMath [Sag20] and later incorporated in the SageMath package admcycles. Assuming Pixton's conjecture, the software computes a basis of the
$\overline {\mathcal {M}}_{g,n}$ of stable curves. These were proven to hold in cohomology [Reference Pandharipande, Pixton and ZvonkinePPZ15] and in Chow [Reference JandaJan17]. Furthermore, Pixton conjectured that his relations span the complete set of relations among tautological classes. The relations were implemented by Pixton in the mathematical software SageMath [Sag20] and later incorporated in the SageMath package admcycles. Assuming Pixton's conjecture, the software computes a basis of the ![]() $\mathbb {Q}$-vector spaces
$\mathbb {Q}$-vector spaces ![]() $\mathsf {R}^d(\overline {\mathcal {M}}_{g,n})$ and express tautological classes in the basis.
$\mathsf {R}^d(\overline {\mathcal {M}}_{g,n})$ and express tautological classes in the basis.
In Proposition 5, we state that Pixton's conjecture holds for the spaces
Assuming the conjecture, admcycles computes the rank of these two spaces to be ![]() $191$ and
$191$ and ![]() $1371$, respectively. If the conjecture were false, the rank of one (or both) of the groups would have to be strictly smaller. However, using admcycles, we verify that the ranks of the intersection pairings
$1371$, respectively. If the conjecture were false, the rank of one (or both) of the groups would have to be strictly smaller. However, using admcycles, we verify that the ranks of the intersection pairings
are bounded from below by ![]() $191$ and
$191$ and ![]() $1371$, respectively. The rank bounds are obtained by taking generating sets of
$1371$, respectively. The rank bounds are obtained by taking generating sets of ![]() $\mathsf {R}^4(\overline {\mathcal {M}}_{4,1})$ and
$\mathsf {R}^4(\overline {\mathcal {M}}_{4,1})$ and ![]() $\mathsf {R}^5(\overline {\mathcal {M}}_{5,1})$ and computing the matrix of pairings with generators in
$\mathsf {R}^5(\overline {\mathcal {M}}_{5,1})$ and computing the matrix of pairings with generators in ![]() $\mathsf {R}^6(\overline {\mathcal {M}}_{4,1})$ and
$\mathsf {R}^6(\overline {\mathcal {M}}_{4,1})$ and ![]() $\mathsf {R}^8(\overline {\mathcal {M}}_{5,1})$, respectively. For the rank bounds of pairing, we do not assume anything about the relations between the above generators, though we are allowed to use the known relations [Reference Pandharipande, Pixton and ZvonkinePPZ15] to reduce the size of the generating sets.
$\mathsf {R}^8(\overline {\mathcal {M}}_{5,1})$, respectively. For the rank bounds of pairing, we do not assume anything about the relations between the above generators, though we are allowed to use the known relations [Reference Pandharipande, Pixton and ZvonkinePPZ15] to reduce the size of the generating sets.
The computations were performed on a server of the Max Planck Institute for Mathematics in Bonn,Footnote 34 taking two days in the case of ![]() $\overline {\mathcal {M}}_{4,1}$ and
$\overline {\mathcal {M}}_{4,1}$ and ![]() $31$ days for
$31$ days for ![]() $\overline {\mathcal {M}}_{5,1}$. Without substantial improvements to the algorithm, it is thus unlikely that Pixton's conjecture can be verified in this way for significantly larger
$\overline {\mathcal {M}}_{5,1}$. Without substantial improvements to the algorithm, it is thus unlikely that Pixton's conjecture can be verified in this way for significantly larger ![]() $g$,
$g$, ![]() $n$, and
$n$, and ![]() $d$. We warmly thank the Max Planck Institute for providing the computer infrastructure for our computations.
$d$. We warmly thank the Max Planck Institute for providing the computer infrastructure for our computations.
B.2 Computations in proofs of Theorems 3 and 4
Once we have verified Pixton's conjecture (as above)Footnote 35 for ![]() $\mathsf {RH}^d(\overline {\mathcal {M}}_{g,n})$, we can explicitly check whether
$\mathsf {RH}^d(\overline {\mathcal {M}}_{g,n})$, we can explicitly check whether
Several such checks used in the proofs of Theorems 3 and 4 were made using admcycles.
We provide below an example of the computation showing that the class ![]() $\lambda _3$ is not contained in the space
$\lambda _3$ is not contained in the space
which is a nine-dimensional subspace of a 10-dimensional space. We first create the list divcl of divisor classes on ![]() $\overline {\mathcal {M}}_3$, compute the set of triple products of such classes, and then take the span divR of the vectors representing them in a basis of
$\overline {\mathcal {M}}_3$, compute the set of triple products of such classes, and then take the span divR of the vectors representing them in a basis of ![]() $\mathsf {RH}^3(\overline {\mathcal {M}}_3)$. We verify that divR is
$\mathsf {RH}^3(\overline {\mathcal {M}}_3)$. We verify that divR is ![]() $9$-dimensional inside the
$9$-dimensional inside the ![]() $10$-dimensional ambient space
$10$-dimensional ambient space ![]() $\mathsf {RH}^3(\overline {\mathcal {M}}_3)$. Finally, we compute the class
$\mathsf {RH}^3(\overline {\mathcal {M}}_3)$. Finally, we compute the class ![]() $\lambda _3$ and verify that the associated vector Lv is not contained in divR.
$\lambda _3$ and verify that the associated vector Lv is not contained in divR.
sage: from admcycles import *
sage: divcl = tautgens(3,0,1)
sage: divp = [a*b*c for a in divcl for b in divcl for c in divcl]
sage: divR = span(u.toTautbasis() for u in divp)
sage: (divR.rank(), divR.degree())
(9, 10)
sage: L = lambdaclass(3,3,0)
sage: Lv = L.toTautbasis()
sage: Lv in divR
False
B.3 Proof of Proposition 7
We record below the computation in admcycles used in the proof of Proposition 7. We create the classes ![]() $\lambda _2, [\Delta _0], [B]$, and
$\lambda _2, [\Delta _0], [B]$, and ![]() $[C]$ and represent the class defined by
$[C]$ and represent the class defined by
in the vector diff with respect to a basis of ![]() $\mathsf {CH}^2(\overline {\mathcal {M}}_2) = {\mathsf {R}}^2(\overline {\mathcal {M}}_2)$. We then solve the equation diff=0 to find the formula for
$\mathsf {CH}^2(\overline {\mathcal {M}}_2) = {\mathsf {R}}^2(\overline {\mathcal {M}}_2)$. We then solve the equation diff=0 to find the formula for ![]() $x$ and
$x$ and ![]() $y$ in terms of the variable
$y$ in terms of the variable ![]() $z$ used in the proof.
$z$ used in the proof.
We remark that in the definition of the class Delta0 we need to divide by ![]() $2$ since this is the degree of the gluing morphism parameterizing the boundary divisor
$2$ since this is the degree of the gluing morphism parameterizing the boundary divisor ![]() $\Delta _0$.
$\Delta _0$.
sage: from admcycles import *
sage: lambda2 = lambdaclass(2,2,0)
sage: Delta0 = 1/2 * irrbdiv(2,0)
sage: gammaB = StableGraph([0],[[1,2,3,4]],[(1,2),(3,4)])
sage: B = gammaB.boundary_pushforward()
sage: gammaC = StableGraph([0,1],[[1,2,3],[4]],[(1,2),(3,4)])
sage: C = gammaC.boundary_pushforward()
sage: x, y, z = var('x, y, z')
sage: diff = (2*lambda2 - x*Delta0^2 - y*B - z*C).toTautbasis()
sage: diff
(476*x + 1824*y - 96*z - 3, -144*x - 576*y + 24*z + 1)
sage: solve([diff[i]==0 for i in (0,1)], x,y,z)
[[x == r1 - 1/120, y == -5/24*r1 + 11/2880, z == r1]]