1. Introduction
Inertial waves play an important role in rotating fluid mechanics, especially in geophysical flows, where they are often responsible for the maintenance of quasi-geostrophic motion (Greenspan Reference Greenspan1968), and in rapidly-rotating turbulence, where they generate and maintain columnar structures aligned with the rotation axis (Davidson Reference Davidson2013). Their dispersion relationship is ![]() $\varpi = 2\varOmega \cos \varphi$, where
$\varpi = 2\varOmega \cos \varphi$, where ![]() $\varpi$ is the wave frequency,
$\varpi$ is the wave frequency, ![]() $\varOmega$ the background rotation rate and
$\varOmega$ the background rotation rate and ![]() $\varphi$ the angle between
$\varphi$ the angle between ![]() $\boldsymbol {\varOmega }$ and the wavevector
$\boldsymbol {\varOmega }$ and the wavevector ![]() $\boldsymbol {k}$. Evidently, inertial waves are anisotropic and dispersive, with a frequency limited to the range
$\boldsymbol {k}$. Evidently, inertial waves are anisotropic and dispersive, with a frequency limited to the range ![]() $0 < \varpi < 2\varOmega$. The case of low-frequency waves,
$0 < \varpi < 2\varOmega$. The case of low-frequency waves, ![]() $\varpi \ll 2\varOmega$, has been extensively studied, in part because these have the largest group velocity, and in part because such waves are responsible for the formation of columnar motion (Greenspan Reference Greenspan1968; Davidson Reference Davidson2013). There has been less interest in the limit
$\varpi \ll 2\varOmega$, has been extensively studied, in part because these have the largest group velocity, and in part because such waves are responsible for the formation of columnar motion (Greenspan Reference Greenspan1968; Davidson Reference Davidson2013). There has been less interest in the limit ![]() $\varpi \rightarrow 2\varOmega$, possibly because such waves have a vanishingly small group velocity, and almost no interest in evanescent disturbances, for which
$\varpi \rightarrow 2\varOmega$, possibly because such waves have a vanishingly small group velocity, and almost no interest in evanescent disturbances, for which ![]() $\varpi > 2\varOmega$. This lies in contrast to the case of internal gravity waves, where the properties of evanescent gravity waves are well known (Sutherland Reference Sutherland2010). Yet, disturbances near twice the rotation frequency might occur in the liquid fuel tank of satellites, resulting from rotation and mechanical instabilities. In a geophysical context topography may also result in energy injection at frequencies near or above
$\varpi > 2\varOmega$. This lies in contrast to the case of internal gravity waves, where the properties of evanescent gravity waves are well known (Sutherland Reference Sutherland2010). Yet, disturbances near twice the rotation frequency might occur in the liquid fuel tank of satellites, resulting from rotation and mechanical instabilities. In a geophysical context topography may also result in energy injection at frequencies near or above ![]() $2\varOmega$ due to the Doppler shift resulting from a differential motion between the core and the mantle or a subsurface ocean and the surrounding shells.
$2\varOmega$ due to the Doppler shift resulting from a differential motion between the core and the mantle or a subsurface ocean and the surrounding shells.
In many systems, evanescent disturbances are of limited interest, as they are localized around the boundary at which they are generated, with an amplitude that falls off exponentially with distance from that surface. However, this is not true of internal gravity waves in the limit as ![]() $\varpi$ approaches the Brunt–Väisälä frequency from above, or for tidally driven gravito inertial-waves (Ogilvie & Lin Reference Ogilvie and Lin2004; Richet, Chomaz & Muller Reference Richet, Chomaz and Muller2018). In this limit, an evanescent disturbance extends over large distances above and below its source, limited only by viscosity. Given the similarities between internal gravity waves and inertial waves, we might expect a similar phenomenon in the limit of
$\varpi$ approaches the Brunt–Väisälä frequency from above, or for tidally driven gravito inertial-waves (Ogilvie & Lin Reference Ogilvie and Lin2004; Richet, Chomaz & Muller Reference Richet, Chomaz and Muller2018). In this limit, an evanescent disturbance extends over large distances above and below its source, limited only by viscosity. Given the similarities between internal gravity waves and inertial waves, we might expect a similar phenomenon in the limit of ![]() $\varpi \rightarrow 2\varOmega$, and we shall see that this is indeed the case. In particular, as
$\varpi \rightarrow 2\varOmega$, and we shall see that this is indeed the case. In particular, as ![]() $\varpi$ approaches
$\varpi$ approaches ![]() $2\varOmega$ from above, an evanescent disturbance in a rotating fluid is predicted to extend over very large horizontal distances. Given the counterintuitive nature of this phenomenon, it seems appropriate to investigate this limit experimentally, and this provides much of the motivation for our study. Consequently, we provide here a detailed experimental investigation of evanescent inertial waves in which measurements and theory are compared. This represents the first quantitative experimental study of evanescent inertial waves, though see McEwan (Reference McEwan1970) for a qualitative study.
$2\varOmega$ from above, an evanescent disturbance in a rotating fluid is predicted to extend over very large horizontal distances. Given the counterintuitive nature of this phenomenon, it seems appropriate to investigate this limit experimentally, and this provides much of the motivation for our study. Consequently, we provide here a detailed experimental investigation of evanescent inertial waves in which measurements and theory are compared. This represents the first quantitative experimental study of evanescent inertial waves, though see McEwan (Reference McEwan1970) for a qualitative study.
We focus on the simplest case of evanescent disturbances which are linear and axisymmetric, with emphasis on the limit of ![]() $\varpi \rightarrow 2\varOmega$. We shall see that the link between inviscid theory and experiment is remarkably close, with spatially extended evanescent disturbances emerging near the cross-over frequency
$\varpi \rightarrow 2\varOmega$. We shall see that the link between inviscid theory and experiment is remarkably close, with spatially extended evanescent disturbances emerging near the cross-over frequency ![]() $\varpi = 2\varOmega$. For completeness, we also consider the case where
$\varpi = 2\varOmega$. For completeness, we also consider the case where ![]() $\varpi$ approaches
$\varpi$ approaches ![]() $2\varOmega$ from below, where conventional inertial waves exist, but their group velocity is horizontal and vanishingly small. Not surprisingly, we find the same behaviour at
$2\varOmega$ from below, where conventional inertial waves exist, but their group velocity is horizontal and vanishingly small. Not surprisingly, we find the same behaviour at ![]() $\varpi = 2\varOmega$, irrespective of whether the limit is approached from above or from below. Although the evanescent disturbances in our experiment are more or less independent of viscosity, the same cannot be said for the inertial waves generated when
$\varpi = 2\varOmega$, irrespective of whether the limit is approached from above or from below. Although the evanescent disturbances in our experiment are more or less independent of viscosity, the same cannot be said for the inertial waves generated when ![]() $\varpi < 2\varOmega$. This is because, in a closed domain, standing inertial waves can exhibit resonances, and in such cases viscosity plays an important role in controlling the amplitude of the motion (Greenspan Reference Greenspan1968). This is precisely what we find in our experiment, where we observe a geometrical resonance at a frequency just below
$\varpi < 2\varOmega$. This is because, in a closed domain, standing inertial waves can exhibit resonances, and in such cases viscosity plays an important role in controlling the amplitude of the motion (Greenspan Reference Greenspan1968). This is precisely what we find in our experiment, where we observe a geometrical resonance at a frequency just below ![]() $\varpi = 2\varOmega$. Let us start, however, with the inviscid theory of linear evanescent disturbances.
$\varpi = 2\varOmega$. Let us start, however, with the inviscid theory of linear evanescent disturbances.
2. Inviscid, axisymmetric, evanescent inertial waves of small amplitude
Consider axisymmetric motion in a rotating fluid confined to an annulus. We use cylindrical polar coordinates, (![]() $r,\theta ,z$), with
$r,\theta ,z$), with ![]() $R_1$ and
$R_1$ and ![]() $R_2$ the inner and outer radii of the annulus (see figure 1). The angular momentum density is
$R_2$ the inner and outer radii of the annulus (see figure 1). The angular momentum density is ![]() $\varGamma = ru_\theta$ and the Stokes stream-function
$\varGamma = ru_\theta$ and the Stokes stream-function ![]() $\varPsi$ is defined by
$\varPsi$ is defined by
The inner boundary is assumed to oscillate with the radial displacement
and this excites standing waves or evanescent disturbances through the boundary condition
In the linear approximation, (2.3) is applied at ![]() $r=R_1$, rather than at
$r=R_1$, rather than at ![]() $r = R_1 + \eta$.
$r = R_1 + \eta$.

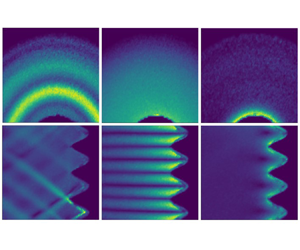
Figure 1. (a) Sketch of the experimental apparatus, showing all principal parts of the experiment. A wave generator with sinusoidal topography is used to excite inertial waves with angular frequency ![]() $\varpi$. (b) Amplitude of the velocity in vertical (left column) and horizontal (right column) planes for three oscillation frequencies:
$\varpi$. (b) Amplitude of the velocity in vertical (left column) and horizontal (right column) planes for three oscillation frequencies: ![]() $\varpi /2\varOmega \approx 0.72$ (top),
$\varpi /2\varOmega \approx 0.72$ (top), ![]() $\varpi /2\varOmega \approx 1$ (middle) and
$\varpi /2\varOmega \approx 1$ (middle) and ![]() $\varpi /2\varOmega \approx 1.5$ (bottom). We have normalized each panel by its maximum amplitude of velocity.
$\varpi /2\varOmega \approx 1.5$ (bottom). We have normalized each panel by its maximum amplitude of velocity.
The inviscid vorticity equation in the rotating frame is (Davidson Reference Davidson2013)
where ![]() $\boldsymbol {\omega }$ denotes the vorticity, and the application of the operator
$\boldsymbol {\omega }$ denotes the vorticity, and the application of the operator ![]() $\boldsymbol {\nabla } \times (\partial /\partial t)$ to (2.4) yields the well-known wave-like equation for inertial waves,
$\boldsymbol {\nabla } \times (\partial /\partial t)$ to (2.4) yields the well-known wave-like equation for inertial waves,
with dispersion relation ![]() $\varpi /2\varOmega =k_z/|\boldsymbol {k}|$. For axisymmetric flows the
$\varpi /2\varOmega =k_z/|\boldsymbol {k}|$. For axisymmetric flows the ![]() $\theta$ component of
$\theta$ component of ![]() $\nabla ^2 \boldsymbol {u}$ is
$\nabla ^2 \boldsymbol {u}$ is
and so the azimuthal component of our wave equation can be written in the form
where
is the Stokes operator. It is readily confirmed that ![]() $\varPsi$ is governed by exactly the same equation.
$\varPsi$ is governed by exactly the same equation.
Consider first the evanescent case of ![]() $\varpi > 2\varOmega$. Given the boundary condition (2.3), we look for disturbances of the form
$\varpi > 2\varOmega$. Given the boundary condition (2.3), we look for disturbances of the form
and (2.7) then yields
where
This can be rewritten as
which has the general solution
where ![]() $K_1$ and
$K_1$ and ![]() $I_1$ are the usual exponential-like modified Bessel functions and
$I_1$ are the usual exponential-like modified Bessel functions and ![]() $A$ and
$A$ and ![]() $B$ are constants. Moreover,
$B$ are constants. Moreover, ![]() $u_r$ can be found from
$u_r$ can be found from ![]() $u_\theta$ using the azimuthal component of the Euler equation:
$u_\theta$ using the azimuthal component of the Euler equation:
It remains to combine (2.14) with (2.3) to give the boundary condition at ![]() $R_1$,
$R_1$,
which, along with the boundary condition ![]() $u_r = u_\theta = 0$ at
$u_r = u_\theta = 0$ at ![]() $R_2$ , allows us to determine the two unknown coefficients in (2.13). In particular,
$R_2$ , allows us to determine the two unknown coefficients in (2.13). In particular, ![]() $u_\theta = 0$ at
$u_\theta = 0$ at ![]() $R_2$ demands
$R_2$ demands
while (2.15a,b) yields
Finally, (2.14) gives us
which we integrate to give
These expressions all relate to evanescent disturbances. The equivalent results for inertial waves can be obtained by returning to (2.7) and (2.10) and taking ![]() $\varpi <2\varOmega$. Introducing
$\varpi <2\varOmega$. Introducing
and following the same steps as above, we find
where ![]() $Y_1$ and
$Y_1$ and ![]() $J_1$ are the usual oscillatory Bessel functions and
$J_1$ are the usual oscillatory Bessel functions and
Finally, it is of interest to consider what happens as we approach the cross-over frequency ![]() $\varpi = 2\varOmega$ from above and below. It is readily confirmed that, if we let
$\varpi = 2\varOmega$ from above and below. It is readily confirmed that, if we let ![]() $\varpi \rightarrow 2\varOmega$ in either (2.16) or (2.21), we find
$\varpi \rightarrow 2\varOmega$ in either (2.16) or (2.21), we find
Evidently, there is a smooth transition from inertial waves to evanescent disturbances at ![]() $\varpi = 2\varOmega$. Moreover, at the cross-over frequency, the radial variation in velocity is neither oscillatory nor exponential, but a simple power law. For example, the angular momentum density,
$\varpi = 2\varOmega$. Moreover, at the cross-over frequency, the radial variation in velocity is neither oscillatory nor exponential, but a simple power law. For example, the angular momentum density, ![]() $\varGamma$, falls monotonically from a maximum at the inner boundary to zero at the outer boundary, according to
$\varGamma$, falls monotonically from a maximum at the inner boundary to zero at the outer boundary, according to ![]() $\varGamma \sim (R^2_2 -r^2)\cos (k_z z)\cos (2\varOmega t)$.
$\varGamma \sim (R^2_2 -r^2)\cos (k_z z)\cos (2\varOmega t)$.
3. The experimental set-up
Let us now turn to the experiment. Figure 1(a) shows the experimental set-up. A closed cylindrical tank of radius ![]() $R_2 = 14$ cm and height
$R_2 = 14$ cm and height ![]() $H = 28.5$ cm is completely filled with water and mounted on a turntable rotating at an angular velocity of
$H = 28.5$ cm is completely filled with water and mounted on a turntable rotating at an angular velocity of ![]() $\varOmega = 3.14$ rad s
$\varOmega = 3.14$ rad s![]() $^{-1}$. To excite wave motion, we use a wave generator in the form of a cylindrically-shaped shaft of mean radius
$^{-1}$. To excite wave motion, we use a wave generator in the form of a cylindrically-shaped shaft of mean radius ![]() $R_1 = 3.99$ cm, and with a sinusoidal surface of vertical wavelength
$R_1 = 3.99$ cm, and with a sinusoidal surface of vertical wavelength ![]() $\lambda = 2.86$ cm and radial amplitude
$\lambda = 2.86$ cm and radial amplitude ![]() $\eta _0 = 0.79$ cm. The wave generator is oscillated up and down the rotation axis with a frequency of
$\eta _0 = 0.79$ cm. The wave generator is oscillated up and down the rotation axis with a frequency of ![]() $4.52\ \text {rad}\ \text {s}^{-1} < \varpi < 9.42$ rad s
$4.52\ \text {rad}\ \text {s}^{-1} < \varpi < 9.42$ rad s![]() $^{-1}$ and amplitude
$^{-1}$ and amplitude ![]() $z_0 = 0.5$ mm by a servo motor and a cam. The choice of a small displacement amplitude is motivated by our interest in studying the laminar flow response without inducing any instabilities, which should be a safe assumption at our Rossby numbers
$z_0 = 0.5$ mm by a servo motor and a cam. The choice of a small displacement amplitude is motivated by our interest in studying the laminar flow response without inducing any instabilities, which should be a safe assumption at our Rossby numbers ![]() $Ro=\varpi \hat {\eta }/(\varOmega R_1) < 0.02$.
$Ro=\varpi \hat {\eta }/(\varOmega R_1) < 0.02$.
As a consequence of this oscillation, the inner boundary is perturbed radially according to
where ![]() $k_z = 2{\rm \pi} /\lambda$. For
$k_z = 2{\rm \pi} /\lambda$. For ![]() $k_z z_0 \ll 1$, the inner boundary condition can be linearized to give
$k_z z_0 \ll 1$, the inner boundary condition can be linearized to give
the time-dependant part of which we rewrite as
For quantitative flow visualization we use Particle Image Velocimetry (PIV) in horizontal and vertical planes. We seed the fluid with hollow glass spheres of diameter ![]() $15\ \mathrm {\mu }\text {m}$ and density
$15\ \mathrm {\mu }\text {m}$ and density ![]() $1050$ kg m
$1050$ kg m![]() $^{-3}$. The particles are illuminated by a 1 watt continuous green laser and a line generator lens, which can provide a horizontal and vertical laser light sheet. We position the horizontal laser light sheet at mid-height and the vertical laser light sheet along a meridional plane of the cylinder. Note that we align the horizontal laser light sheet with the plane of maximum velocity of the excited waves. A MicroVec camera equipped with a Nikon
$^{-3}$. The particles are illuminated by a 1 watt continuous green laser and a line generator lens, which can provide a horizontal and vertical laser light sheet. We position the horizontal laser light sheet at mid-height and the vertical laser light sheet along a meridional plane of the cylinder. Note that we align the horizontal laser light sheet with the plane of maximum velocity of the excited waves. A MicroVec camera equipped with a Nikon![]() $^\text {TM}$
$^\text {TM}$ ![]() $50$ mm lens is used to record images of
$50$ mm lens is used to record images of ![]() $2592\times 2048$ pixels at 30 frames per second. We use the PIV package DPIVsoft2010 (Meunier & Leweke Reference Meunier and Leweke2003) to calculate velocity fields with
$2592\times 2048$ pixels at 30 frames per second. We use the PIV package DPIVsoft2010 (Meunier & Leweke Reference Meunier and Leweke2003) to calculate velocity fields with ![]() $320\times 232$ vectors over an area equivalent of
$320\times 232$ vectors over an area equivalent of ![]() $14.5\times 11.5$ cm.
$14.5\times 11.5$ cm.
Our experimental protocol is as follows: we set the turntable into rotation at ![]() $3.14$ rad s
$3.14$ rad s![]() $^{-1}$ and wait until the fluid is co-rotating with the container. We then start the motion of the wave generator at angular frequency
$^{-1}$ and wait until the fluid is co-rotating with the container. We then start the motion of the wave generator at angular frequency ![]() $\varpi$ and wait for the initial transient motion to be dissipated. Finally, we start our PIV measurements and sample a time series of 1200 images, typically
$\varpi$ and wait for the initial transient motion to be dissipated. Finally, we start our PIV measurements and sample a time series of 1200 images, typically ![]() ${\sim }40$ oscillations of the wave generator.
${\sim }40$ oscillations of the wave generator.
In figure 1, we provide a qualitative impression of the flow excited by the wave generator at three different frequencies, to illustrate the three different regimes. For ![]() $\varpi < 2\varOmega$, we see inertial waves with a characteristic ray pattern orthogonal to the wavevector
$\varpi < 2\varOmega$, we see inertial waves with a characteristic ray pattern orthogonal to the wavevector ![]() $\boldsymbol {k}$, which in turn satisfies the dispersion relation
$\boldsymbol {k}$, which in turn satisfies the dispersion relation ![]() $\varpi /2\varOmega = k_z/|\boldsymbol {k}| = \cos \varphi$. As the excitation frequency approaches the limit
$\varpi /2\varOmega = k_z/|\boldsymbol {k}| = \cos \varphi$. As the excitation frequency approaches the limit ![]() $\varpi \rightarrow 2\varOmega$, the group velocity
$\varpi \rightarrow 2\varOmega$, the group velocity ![]() $\boldsymbol {c}_g$ becomes horizontal, and so the characteristic surfaces along which the energy travels are also horizontal, with a wavevector parallel to the rotation axis,
$\boldsymbol {c}_g$ becomes horizontal, and so the characteristic surfaces along which the energy travels are also horizontal, with a wavevector parallel to the rotation axis, ![]() $\varphi = 0$. Note that the same disturbance pattern is obtained if we approach
$\varphi = 0$. Note that the same disturbance pattern is obtained if we approach ![]() $\varpi = 2\varOmega$ from above, so we could equally regard the horizontal striations in this image as indicative of evanescent waves. Finally, for
$\varpi = 2\varOmega$ from above, so we could equally regard the horizontal striations in this image as indicative of evanescent waves. Finally, for ![]() $\varpi > 2\varOmega$ the energy does not propagate into the bulk but remains confined to the vicinity of the wave generator, except, of course, as we approach the limit
$\varpi > 2\varOmega$ the energy does not propagate into the bulk but remains confined to the vicinity of the wave generator, except, of course, as we approach the limit ![]() $\varpi \rightarrow 2\varOmega$.
$\varpi \rightarrow 2\varOmega$.
4. Evanescent disturbances and standing waves near the cross-over frequency
To compare the inviscid predictions with our experimental results, we first consider the radial profile of kinetic energy density in the equatorial plane. We construct radial profiles of the kinetic energy by averaging the kinetic energy density over the azimuth in each PIV frame. The average is calculated over thin concentric rings of radial thickness ![]() $1$ mm, resulting in a radial profile of the kinetic energy density with 90 data points. Each data point represents the azimuthal average of at least 300 individual points close to the wave generator and up to 800 points in the outer regions. Finally, we average the time-resolved radial profiles over approximately 40 cycles of the wave generator motion. The resulting radial profiles are displayed in figure 2.
$1$ mm, resulting in a radial profile of the kinetic energy density with 90 data points. Each data point represents the azimuthal average of at least 300 individual points close to the wave generator and up to 800 points in the outer regions. Finally, we average the time-resolved radial profiles over approximately 40 cycles of the wave generator motion. The resulting radial profiles are displayed in figure 2.

Figure 2. Kinetic energy density as a function of the radial distance for different driving frequencies. The value above each line represents the ratio ![]() $\varpi /2\varOmega$. Each curve on the left is offset by
$\varpi /2\varOmega$. Each curve on the left is offset by ![]() $0.4$, while those in the middle and right are offset by
$0.4$, while those in the middle and right are offset by ![]() $0.6$, to achieve better visibility. Crossed points depict the measurements. The dashed lines represent the inviscid solution, while solid lines represent the solution with a viscous correction, as discussed in §§ 5 and 6.
$0.6$, to achieve better visibility. Crossed points depict the measurements. The dashed lines represent the inviscid solution, while solid lines represent the solution with a viscous correction, as discussed in §§ 5 and 6.
The inviscid analysis described in § 2 predicts exponentially decaying evanescent waves for ![]() $\varpi > 2 \varOmega$. Consistent with this, the experimental data for excitation frequencies significantly above
$\varpi > 2 \varOmega$. Consistent with this, the experimental data for excitation frequencies significantly above ![]() $2\varOmega$ (figure 2a) shows that the kinetic energy is mostly confined to the vicinity of the wave generator, from where it decays exponentially with the radius. However, even at
$2\varOmega$ (figure 2a) shows that the kinetic energy is mostly confined to the vicinity of the wave generator, from where it decays exponentially with the radius. However, even at ![]() $\varpi /2\varOmega \sim 1.5$, the energy of the evanescent waves still penetrates into the bulk up to around 10 % of the fluid gap. All in all, the predicted inviscid solution for
$\varpi /2\varOmega \sim 1.5$, the energy of the evanescent waves still penetrates into the bulk up to around 10 % of the fluid gap. All in all, the predicted inviscid solution for ![]() $\boldsymbol {u}$ is in good agreement with the radial structure of the measured kinetic energy, as displayed in figure 2(a).
$\boldsymbol {u}$ is in good agreement with the radial structure of the measured kinetic energy, as displayed in figure 2(a).
We now turn to excitation frequencies which are close to, but above, the critical value of ![]() $\varpi = 2\varOmega$ (figure 2b). Again, there is a close link between theory and measurements, with the radial profiles of the kinetic energy becoming flatter as we approach the cross-over frequency, which means that the motion progressively spreads away from the wave generator. This observation, while consistent with our inviscid analysis, contrasts with the early study of Morgan (Reference Morgan1951). Morgan investigated theoretically the problem of an oscillating disk in a cylindrical geometry and found that, as the excitation frequency gets close to the critical value of
$\varpi = 2\varOmega$ (figure 2b). Again, there is a close link between theory and measurements, with the radial profiles of the kinetic energy becoming flatter as we approach the cross-over frequency, which means that the motion progressively spreads away from the wave generator. This observation, while consistent with our inviscid analysis, contrasts with the early study of Morgan (Reference Morgan1951). Morgan investigated theoretically the problem of an oscillating disk in a cylindrical geometry and found that, as the excitation frequency gets close to the critical value of ![]() $2\varOmega$, the fluid motion is mostly confined to the vicinity of the disk. He speculates about a resonant behaviour resulting in ‘violent motion’ when the system is excited at exactly the critical frequency. Baines (Reference Baines1967), on the other hand, concludes that no steady-state solution exists in this limit. In contrast to these statements, we observe a smooth transition from evanescent waves with radially decaying velocity to a standing-wave profile as
$2\varOmega$, the fluid motion is mostly confined to the vicinity of the disk. He speculates about a resonant behaviour resulting in ‘violent motion’ when the system is excited at exactly the critical frequency. Baines (Reference Baines1967), on the other hand, concludes that no steady-state solution exists in this limit. In contrast to these statements, we observe a smooth transition from evanescent waves with radially decaying velocity to a standing-wave profile as ![]() $\varpi$ passes through the cross-over frequency of
$\varpi$ passes through the cross-over frequency of ![]() $2\varOmega$ (figure 2c). We therefore conclude that, at least for the type of forcing used in our experiment, there is no unusual behaviour at
$2\varOmega$ (figure 2c). We therefore conclude that, at least for the type of forcing used in our experiment, there is no unusual behaviour at ![]() $\varpi = 2\varOmega$. Rather, there is a smooth transition, exactly as predicted by the inviscid analysis. Interestingly, figure 2(c) shows a significant discrepancy between the inviscid analysis and the measurements when
$\varpi = 2\varOmega$. Rather, there is a smooth transition, exactly as predicted by the inviscid analysis. Interestingly, figure 2(c) shows a significant discrepancy between the inviscid analysis and the measurements when ![]() $\varpi < 2\varOmega$, particularly at
$\varpi < 2\varOmega$, particularly at ![]() $\varpi /2\varOmega = 0.991$. We shall see shortly that this is due to a standing-wave resonance whose amplitude is controlled by viscosity.
$\varpi /2\varOmega = 0.991$. We shall see shortly that this is due to a standing-wave resonance whose amplitude is controlled by viscosity.
Also shown in figure 2(a–c) are the viscous corrections to the inviscid theory. These corrections are negligible in the evanescent regime, but important below the cross-over frequency. We shall discuss these corrections, as well as the discrepancy between the inviscid theory and observations for ![]() $\varpi < 2\varOmega$, in § 6.
$\varpi < 2\varOmega$, in § 6.
5. Corrections due to viscous action in the bulk
When viscosity is finite, (2.14) generalizes to
while the azimuthal component of
combines with
to yield
It is convenient to introduce the Stokes streamfunction, ![]() $\varPsi$, defined by (2.1). This gives us
$\varPsi$, defined by (2.1). This gives us
These, in turn, yield
which is the viscous generalization of (2.7), as well as
As with the inviscid analysis, we can work with either ![]() $\varGamma$ or
$\varGamma$ or ![]() $\varPsi$, but for the viscous case it is easier to work with
$\varPsi$, but for the viscous case it is easier to work with ![]() $\varPsi$. The boundary condition (2.3) can be rewritten in terms of
$\varPsi$. The boundary condition (2.3) can be rewritten in terms of ![]() $\varPsi$ as
$\varPsi$ as
which combines with (2.2) to give
We therefore look for standing waves or evanescent disturbances of the form
where ![]() $\hat {\varPsi }$ is complex. The expression (5.12) combines with (5.9) to give
$\hat {\varPsi }$ is complex. The expression (5.12) combines with (5.9) to give
 \begin{equation} \left[1+j\left(\frac{\nu k_z^2}{\varpi}\right)(\hat{\nabla}^2_*-1)\right]^2 (\hat{\nabla}^2_*-1)\hat{\varPsi} + \left(\frac{2\varOmega}{\varpi}\right)^2 \hat{\varPsi} = 0, \end{equation}
\begin{equation} \left[1+j\left(\frac{\nu k_z^2}{\varpi}\right)(\hat{\nabla}^2_*-1)\right]^2 (\hat{\nabla}^2_*-1)\hat{\varPsi} + \left(\frac{2\varOmega}{\varpi}\right)^2 \hat{\varPsi} = 0, \end{equation}where the dimensionless operator is
At this point we can look for either evanescent disturbances or standing inertial waves. Let us consider evanescent disturbances. For ![]() $\varpi > 2\varOmega$, (5.13) admits solutions of the form
$\varpi > 2\varOmega$, (5.13) admits solutions of the form
provided
 \begin{equation} \left[1+{j}\left(\frac{\nu k_z^2}{\varpi}\right)(\kappa^2-1)\right]^2(\kappa^2-1)+ \left(\frac{2\varOmega}{\varpi}\right)^2 = 0. \end{equation}
\begin{equation} \left[1+{j}\left(\frac{\nu k_z^2}{\varpi}\right)(\kappa^2-1)\right]^2(\kappa^2-1)+ \left(\frac{2\varOmega}{\varpi}\right)^2 = 0. \end{equation}
Note that, when ![]() $\nu = 0$, (5.16) reduces to
$\nu = 0$, (5.16) reduces to
and so we recover the inviscid solution. For small ![]() $\nu k^2_z / \varpi$, which is the case in our experiment, (5.16) has the solution
$\nu k^2_z / \varpi$, which is the case in our experiment, (5.16) has the solution
 \begin{equation} \kappa^2 = \left[1-\left(\frac{2\varOmega}{\varpi}\right)^2\right] - 2{j}\left(\frac{\nu k^2_z}{\varpi}\right)\left(\frac{2\varOmega}{\varpi}\right)^4 + O ((\nu k_z^2/\varpi)^2). \end{equation}
\begin{equation} \kappa^2 = \left[1-\left(\frac{2\varOmega}{\varpi}\right)^2\right] - 2{j}\left(\frac{\nu k^2_z}{\varpi}\right)\left(\frac{2\varOmega}{\varpi}\right)^4 + O ((\nu k_z^2/\varpi)^2). \end{equation}
We can use this estimate of ![]() $\kappa$, along with (5.15), to estimate the effects of viscosity on evanescent disturbances. The equivalent results for inertial waves may be found in exactly the same way.
$\kappa$, along with (5.15), to estimate the effects of viscosity on evanescent disturbances. The equivalent results for inertial waves may be found in exactly the same way.
6. A comparison of the measurements with the viscously corrected theory
We can use the analysis above to estimate the effects of viscosity on the propagation of both inertial waves and evanescent disturbances. We shall do this while ignoring the viscous boundary layer on the wave generator, of which an estimate of the thickness and local Reynolds number are ![]() $\delta \sim \sqrt {\nu /\varOmega } \approx 0.6$ mm and
$\delta \sim \sqrt {\nu /\varOmega } \approx 0.6$ mm and ![]() $Re = u \delta /\nu = (\varpi \hat {\eta })\delta /\nu \approx 1.8$. That is to say, we shall assume, and then check retrospectively, that viscosity does not strongly influence the generation of inertial waves or evanescent disturbances, only their subsequent behaviour in the bulk. To that end, we use (5.18) to evaluate
$Re = u \delta /\nu = (\varpi \hat {\eta })\delta /\nu \approx 1.8$. That is to say, we shall assume, and then check retrospectively, that viscosity does not strongly influence the generation of inertial waves or evanescent disturbances, only their subsequent behaviour in the bulk. To that end, we use (5.18) to evaluate ![]() $\kappa$, substitute this into (5.15), and then use the inviscid estimates for the coefficients
$\kappa$, substitute this into (5.15), and then use the inviscid estimates for the coefficients ![]() $C$ and
$C$ and ![]() $D$ taken from (2.19). A similar procedure can be followed for inertial waves. A comparison of these viscous corrections with the experimental data is shown in figure 2, where the viscously-corrected predictions are the solid lines.
$D$ taken from (2.19). A similar procedure can be followed for inertial waves. A comparison of these viscous corrections with the experimental data is shown in figure 2, where the viscously-corrected predictions are the solid lines.
In our experiment we have ![]() $\nu k_z^2 / \varpi \approx 0.008$ and so we might expect the viscous corrections to be modest for
$\nu k_z^2 / \varpi \approx 0.008$ and so we might expect the viscous corrections to be modest for ![]() $\varpi = 2\varOmega$. Moreover, the inviscid and viscously corrected theory seem to capture equally well the experimental data in the evanescent regime,
$\varpi = 2\varOmega$. Moreover, the inviscid and viscously corrected theory seem to capture equally well the experimental data in the evanescent regime, ![]() $\varpi > 2\varOmega$. This suggests that the evanescent disturbances are not strongly influenced by viscosity, at least not in our experiment. However, the superiority of the viscously corrected solutions over the inviscid predictions is particularly clear when
$\varpi > 2\varOmega$. This suggests that the evanescent disturbances are not strongly influenced by viscosity, at least not in our experiment. However, the superiority of the viscously corrected solutions over the inviscid predictions is particularly clear when ![]() $\varpi$ is somewhat less than
$\varpi$ is somewhat less than ![]() $2\varOmega$ (figure 2c). Here the inviscid solution is less successful at capturing the radial structure of the flow, and this is especially true when we are close to a resonance of the standing waves, as is the case for
$2\varOmega$ (figure 2c). Here the inviscid solution is less successful at capturing the radial structure of the flow, and this is especially true when we are close to a resonance of the standing waves, as is the case for ![]() $\varpi /2\varOmega = 0.991$.
$\varpi /2\varOmega = 0.991$.
To show that this discrepancy between the inviscid theory and the observations arises from a resonance, we investigate the dependence of the total kinetic energy on ![]() $\varpi /2\varOmega$. We consider the total mean kinetic energy over the entire PIV image averaged over 40 oscillation periods and plot it against its analytical counterpart for various excitation frequencies. The results are presented in figure 3(a), where the dashed line represents the inviscid theory and the solid line the viscously corrected prediction. Evidently, there is a quantitative agreement between the viscous theory and experiments, but a large discrepancy with the inviscid theory at around
$\varpi /2\varOmega$. We consider the total mean kinetic energy over the entire PIV image averaged over 40 oscillation periods and plot it against its analytical counterpart for various excitation frequencies. The results are presented in figure 3(a), where the dashed line represents the inviscid theory and the solid line the viscously corrected prediction. Evidently, there is a quantitative agreement between the viscous theory and experiments, but a large discrepancy with the inviscid theory at around ![]() $\varpi /2\varOmega \approx 0.99$. This frequency corresponds to the denominator in (2.17) falling to zero, and so represents a geometrical resonance in the standing wave pattern. Clearly, this resonance is smoothed out by viscosity.
$\varpi /2\varOmega \approx 0.99$. This frequency corresponds to the denominator in (2.17) falling to zero, and so represents a geometrical resonance in the standing wave pattern. Clearly, this resonance is smoothed out by viscosity.

Figure 3. (a) The kinetic energy calculated from the velocity amplitude over the PIV area as a function of ![]() $\varpi /2\varOmega$. The solid line represents the viscous prediction, the coloured dots the measurements, and the dashed line the inviscid solution. (b) The peak in energy at
$\varpi /2\varOmega$. The solid line represents the viscous prediction, the coloured dots the measurements, and the dashed line the inviscid solution. (b) The peak in energy at ![]() $\varpi / 2\varOmega \approx 0.99$ corresponds to a geometric resonance between emitted and reflected waves at critical angle
$\varpi / 2\varOmega \approx 0.99$ corresponds to a geometric resonance between emitted and reflected waves at critical angle ![]() $\varphi _1$.
$\varphi _1$.
Physically, this resonant frequency corresponds to inertial waves reflected from the outer wall interfering constructively with outgoing waves, according to the expression
This is illustrated in figure 3(b). Further resonances are expected with the frequencies
7. Conclusions
To the best of our knowledge, our experiments represent the first quantitative experimental investigation of evanescent inertial waves. The comparison with inviscid theory is excellent, especially the smooth transition from inertial waves to evanescent disturbances, and the prediction that evanescent disturbances are spatially extensive near the cross-over frequency, ![]() $\varpi = 2\varOmega$. While the evanescent disturbances in our experiment are insensitive to viscosity, the same is not true of the inertial waves generated for
$\varpi = 2\varOmega$. While the evanescent disturbances in our experiment are insensitive to viscosity, the same is not true of the inertial waves generated for ![]() $\varpi < 2\varOmega$. We attribute this sensitivity to geometrical resonances associated with standing inertial waves, resonances whose amplitudes are limited by viscosity. We have modified the inviscid theory to allow for the effects of viscosity on the propagation of inertial waves, while simultaneously assuming that viscosity has negligible influence on the generation of such waves. Somewhat surprisingly, despite the neglect of the boundary layer on the wave generator, our viscously modified theory captures well the measured amplitude of inertial waves, even near resonance.
$\varpi < 2\varOmega$. We attribute this sensitivity to geometrical resonances associated with standing inertial waves, resonances whose amplitudes are limited by viscosity. We have modified the inviscid theory to allow for the effects of viscosity on the propagation of inertial waves, while simultaneously assuming that viscosity has negligible influence on the generation of such waves. Somewhat surprisingly, despite the neglect of the boundary layer on the wave generator, our viscously modified theory captures well the measured amplitude of inertial waves, even near resonance.
Acknowledgements
We thank three anonymous reviewers for their thoughtful comments on our manuscript.
Funding
The work of Z.N. is supported by Swiss National Science Foundation grant no. 200021_185088 and that of F.B. by Swiss National Science Foundation grant no. 200021_165641.
Declaration of interest
The authors report no conflict of interest.