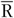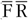Despite efforts to develop innovative ways to estimate habitual dietary intake using new emerging technologies, nutrition research and especially large epidemiological studies still rely heavily on traditional dietary assessment tools such as the FFQ, specifically developed for assessing habitual dietary intakes, and 24 h recalls (24hR) and dietary records, aiming at estimating actual dietary intakes. These methods all have their strengths and limitations( Reference Willett 1 ). The FFQ is, for example, relatively cheap and easy to administer, but relies on memory and can be subject to social desirability bias, while a limited set of aggregated food items leads to loss of precision and portion sizes are difficult to assess accurately. The 24hR and dietary records assess all foods consumed on one or more days, but can also lead to social desirability bias, rely often on memory and dietary records can influence actual intake due to reactivity( Reference Willett 1 ). Furthermore, recalls and records of several days or weeks or the addition of a food propensity questionnaire are necessary if one wants to assess individual habitual intake. Altogether, dietary intake estimates assessed with the FFQ, 24hR or dietary records are known to be biased due to systematic and random measurement error( Reference Kipnis, Subar and Midthune 2 , Reference Prentice, Mossavar-Rahmani and Huang 3 ).
Measurement error leads to bias, usually attenuation of estimated diet–health associations, loss of precision of estimated associations and loss of power to detect diet–chronic disease associations( Reference Freedman, Schatzkin and Midthune 4 ). Bias in these detected diet–chronic disease associations introduced by measurement errors can be corrected with statistical methods. To do so, statistical methods rely on intake estimates from a second (superior) assessment method, i.e. a reference method( Reference Willett 1 ). The reference method is allowed to have random error, but should be unbiased, i.e. free of systematic error. Regression calibration (RC) is the most well-known method, which performs the regression of dietary intake estimates obtained with a reference instrument (e.g. biomarker, 24hR) v. dietary intake estimates obtained with the main method (e.g. FFQ) to correct detect diet–disease associations( Reference Rosner, Willett and Spiegelman 5 – Reference Rosner, Spiegelman and Willett 9 ). RC is relatively intuitive and simple to use and is applicable in many situations, such as linear, logistic and Cox regression.
An unbiased biomarker serves as the ideal reference instrument. However, in practice the 24hR is often used as reference instrument because unbiased biomarkers of intake are available for only a limited number of nutrients and very costly to collect. Since the development of web-based 24hR and dietary records( Reference Timon, van den Barg and Blain 10 ) it is less burdensome for researchers and cheaper to obtain recalls or records from (a sub-sample of) a study population. Therefore, RC can be used more often to correct for measurement error by combining information obtained with the reference instrument and main method. With RC, equations are obtained that will give predicted dietary intake estimates based on reported intake estimates from the main instrument. However, the calibrated values from the prediction equations only incorporate individual information assessed with the main method, while individual information from the 24hR measurement is only used to fit the calibration model. This means that two individuals scoring the same on the main method assessment, but having a different reference method value, are assigned the same calibrated value. This is unavoidable when 24hR measurements are present only for a sub-sample. However, when both the main method (usually FFQ) and the reference instrument (usually 24hR or dietary records) are used in the entire study population, this implies unnecessary loss of information. Dietary intake estimates obtained from both methods can be combined in other ways to obtain better and more precise estimates( Reference Carroll, Midthune and Subar 11 ).
The aim of the current study was to demonstrate the impact of combining FFQ and 24hR estimates by using standard RC and a relatively simple extension of RC using all available information, i.e. enhanced regression calibration (ERC), on diet–chronic disease associations.
Methods
Study design and population
In the present study, we compare protein and K intake estimates from RC and ERC with more naïve approaches, i.e. using only the 24hR as measured, only the FFQ as measured and from averaging 24hR and FFQ. In our study, the FFQ is used as the main instrument for estimating habitual dietary intake and the average of two telephone-administered 24hR is considered as the superior reference instrument, as is commonly done in nutritional epidemiology. The extent of the measurement error in the resulting diet–disease associations is assessed for each of the five approaches by estimating the association between the intake estimate and a truly unbiased intake measurement obtained with urinary recovery biomarkers for protein and K (i.e. attenuation factors (AF)). With perfect adjustment, the AF would be 1.
For these analyses, data from the National Dietary Assessment Reference Database (NDARD) were used. The aim and design of the NDARD have been described elsewhere( Reference Brouwer-Brolsma, Streppel and van Lee 12 ). Briefly, a total of 2048 men and women were included between May 2011 and February 2013. They were aged between 20 and 70 years and randomly selected inhabitants of the cities Wageningen, Renkum, Ede, Arnhem and Veenendaal, which are located in the central part of the Netherlands. All participants gave written informed consent before the start of the study. The NDARD study was approved by the Medical Ethical Committee of Wageningen University and was conducted according to the guidelines of the Declaration of Helsinki( 13 ).
Baseline measurements consisted of, among others, a physical examination, dietary assessment with multiple telephone-administered 24hR and an FFQ, and a 24 h urine collection. For the present study, we selected participants with data of two 24hR, a baseline FFQ and biomarker data of protein and K (n 236). The 24 h urines were collected in the first year of the study (on average 5 months (interquartile range: 3–6 months) after the start of the study) on both weekdays (Monday–Thursday; 52 %) and weekend days (Friday–Sunday; 48 %). The FFQ was administered on average 7·5 months after the start of the study (interquartile range: 5–10 months). The first 24hR was administered on average 7·8 months after the start of the study (interquartile range: 4–16 months); whereas the second recall was administered on average after 15 months (interquartile range: 10–20 months). The 24hR data collection comprised both weekdays (Monday–Thursday; 56 %) and weekend days (Friday–Sunday; 44 %). Recalls of the same participant were at least one month apart. An overview of the time frame of the different assessments is presented in Fig. 1.

Fig. 1 Schematic overview of the time frame of the different dietary assessments and urine collection. The black line represents the median, the grey box represents the interquartile range (25th percentile–75th percentile) and the horizontal bars the minimum and maximum
Dietary assessment
24 h recall
Trained dietitians of the Division of Human Nutrition of Wageningen University made an unannounced phone call to the participant. They asked about foods and drinks consumed the previous day according to a standardized protocol based on the five-step multiple-pass method( Reference Conway, Ingwersen and Vinyard 14 ). The recalls were transcribed into food codes and amounts( Reference Donders-Engelen, Van der Heijden and Hulshof 15 , 16 ). Portion sizes were estimated using natural portions (bread shapes) and commonly used household measures (e.g. spoon and cup). Regular meetings with all dietitians ensured the quality of the interviews and the food coding. All dietitians coded the same 24hR and differences in coding were discussed during these meetings. At least one interview per dietitian was tape-recorded with the participant’s permission and reviewed for quality by a senior research dietitian. Energy and nutrient intakes were estimated using the 2011 Dutch food composition table( 16 ). For various outcomes (energy, nutrients and foods) the highest and lowest ten values were checked for errors, such as errors in coding number or amounts (e.g. 150 cups instead of 150 g of milk).
FFQ
A 180-item semi-quantitative FFQ was self-administered to all participants using the open-source online survey tool LimesurveyTM (LimeSurvey project team/Carsten Schmitz, Hamburg, Germany, 2012). The FFQ has been previously evaluated for energy intake, macronutrients, dietary fibre and selected vitamins( Reference Siebelink, Geelen and de Vries 17 , Reference Verkleij-Hagoort, de Vries and Stegers 18 ). Portion sizes were estimated using natural portions (bread shapes) and commonly used household measures (e.g. spoon and cup). The reference period for reporting was the past month. Average daily nutrient intakes were calculated by multiplying frequency of consumption by portion size and nutrient content per gram using the 2011 Dutch food composition table( 16 ).
Biomarker assessment
Participants received supplies, including urine collection boxes, and verbal and written instructions for the 24 h urine collection. The urine collection started after discarding the first voiding on the morning of the collection day and ended after the first voiding on the morning of the next day. To check for completeness of the urine collection, participants were instructed to ingest a tablet containing 80 mg p-aminobenzoic acid during breakfast, lunch and dinner on the day of the collection. Possible deviations from the protocol (e.g. missing urine) were registered by the participant. The urine collections were mixed, weighed, aliquoted and stored at –20 °C until further analysis at the study centre.
The N content of the urine was assessed with the Kjeldahl technique( Reference Hambleton and Noel 19 ). The amount of protein was calculated using an N to protein conversion factor of 6·25( Reference Jones 20 ) and an average ratio of urinary-N excretion to dietary-N of 0·81( Reference Bingham and Cummings 21 ) was assumed. K in urine was determined with an ion-selective electrode and K intake was calculated taking into account extra-renal and faecal K losses of 19 %( Reference Freisling, van Bakel and Biessy 22 ). p-Aminobenzoic acid in urine was assessed by the HPLC method. Incomplete urines, based on the cut-off value of 78 % p-aminobenzoic acid recovery( Reference Jakobsen, Ovesen and Fagt 23 ), were excluded from the analysis (n 16).
Combining FFQ and 24 h recalls
Measurement error model
A diet–chronic disease model is usually structured in the following way:
with disease Y related to dietary exposure of interest T through a linear regression model. E denotes the expectation of developing disease Y given consumption of T. β 0 and β 1 are parameters representing the shape of the relationship between Y and T.
However, as stated previously, dietary exposures are rarely measured without measurement error. Therefore, the true value of T cannot be measured. Instead, we use the following calibration model to express the expected dietary exposure measured with measurement instrument Q, e.g. FFQ:
where ϑ 0 and ϑ 1 represent the systematic errors.
If we replace T with E(T|Q) in our diet–disease model we obtain:
Performing the regression of Y v. E(T|Q) gives the parameter of interest. If the disease model is not linear, but for instance a logistic or loglinear model, this parameter is the relative risk or odds ratio.
Furthermore, in order to satisfy the conditions of RC, one needs to include all confounders C used in the disease model that also predict T given Q. In other words, one needs to use E(T|Q,C) instead of E(T|Q). For simplicity, we included no such relevant confounders, but they can easily be added. For our assessment using biomarkers as outcome, we considered the presence of strong bias from such confounders unlikely.
Approaches to combine FFQ and 24 h recall
In the present study, we used the FFQ as main instrument and the average of two 24hR (
![]() $\overline {\it R}$
) as reference instrument. We assumed that the average of two 24hR provides unbiased estimates of usual intake on a group level and contains only random within-person error (classical error) while the FFQ is assumed to be subject to systematic error. We present five approaches to obtain intake estimates for use in diet–disease associations (Table 1). First, we used the uncalibrated FFQ estimates (FFQ). For the second approach the mean of two 24hR (
$\overline {\it R}$
) as reference instrument. We assumed that the average of two 24hR provides unbiased estimates of usual intake on a group level and contains only random within-person error (classical error) while the FFQ is assumed to be subject to systematic error. We present five approaches to obtain intake estimates for use in diet–disease associations (Table 1). First, we used the uncalibrated FFQ estimates (FFQ). For the second approach the mean of two 24hR (
![]() $\overline {\it R}$
) is used. The third approach is simply the average of the FFQ and
$\overline {\it R}$
) is used. The third approach is simply the average of the FFQ and
![]() $\overline R$
(
$\overline R$
(
![]() $\overline F\,\overline R$
). This approach has no real justification and therefore we do not advise to use it in practice due to the differences in method, bias and, in our case, different intake periods. It is included only for illustration purposes. Fourth is a calibrated value as would be used in standard RC, which is the predicted value from performing the regression of the average value of both 24hR measurements per person v. FFQ, resulting in an estimate of E(R|Q), i.e. the expectation of the value R that is measured with the reference instrument (e.g. average of two 24hR) given the value Q, measured with the main measurement instrument (e.g. FFQ). When R is unbiased, this is equal to E(T|Q). The fifth and last approach is the ERC. ERC is an extension of RC in which the FFQ estimate is included in the measurement error model as described by Freedman et al.
(
Reference Freedman, Schatzkin and Midthune
4
). We used the ERC calculation as described by Midthune, resulting in a calibrated value that includes the individual random effect(
Reference Midthune
24
). While RC can be used if intake data from a second method are available for a sub-sample of the population, ERC needs data from two methods for all individuals in a population. The following formula is used for the ERC:
$\overline F\,\overline R$
). This approach has no real justification and therefore we do not advise to use it in practice due to the differences in method, bias and, in our case, different intake periods. It is included only for illustration purposes. Fourth is a calibrated value as would be used in standard RC, which is the predicted value from performing the regression of the average value of both 24hR measurements per person v. FFQ, resulting in an estimate of E(R|Q), i.e. the expectation of the value R that is measured with the reference instrument (e.g. average of two 24hR) given the value Q, measured with the main measurement instrument (e.g. FFQ). When R is unbiased, this is equal to E(T|Q). The fifth and last approach is the ERC. ERC is an extension of RC in which the FFQ estimate is included in the measurement error model as described by Freedman et al.
(
Reference Freedman, Schatzkin and Midthune
4
). We used the ERC calculation as described by Midthune, resulting in a calibrated value that includes the individual random effect(
Reference Midthune
24
). While RC can be used if intake data from a second method are available for a sub-sample of the population, ERC needs data from two methods for all individuals in a population. The following formula is used for the ERC:
Table 1 Overview of the five approaches used in the current study

where
![]() $\overline R$
is the average of two 24hR (R1 and R2), E(T|Q) is set equal to E(R|Q), assuming that R is unbiased, and w is var(u)/(var(u)+var(e)/2), where var(u) is between person-variance in 24hR (conditional on all covariates included in the measurement error model) and var(e) is within-person variance in 24hR.
$\overline R$
is the average of two 24hR (R1 and R2), E(T|Q) is set equal to E(R|Q), assuming that R is unbiased, and w is var(u)/(var(u)+var(e)/2), where var(u) is between person-variance in 24hR (conditional on all covariates included in the measurement error model) and var(e) is within-person variance in 24hR.
Proc Reg was used to obtain RC estimates and Proc Mixed was used to obtain estimates for ERC. The SAS syntax is given in the online supplementary material, Supplemental File 1.
It should be noted that, if available, the biomarkers (assuming classical error) would be the preferred reference instrument rather than 24hR for the RC and ERC. We use the biomarker in estimating the AF to illustrate what may happen in the more usual case when biomarkers are not available and, therefore, the 24hR is used as reference instrument. The regression coefficient in the regression of biomarker v. FFQ is the resulting AF if we would use the biomarker as reference instrument.
Statistical analysis
Descriptive statistics were presented in percentages and as means with their standard deviations. Intake and biomarker estimates were on approximation normally distributed. The percentage bias was calculated by dividing the difference between the intake assessed by one of the approaches and the intake as estimated from the biomarker, divided by the intake from the biomarker. A linear regression model was used to calculate empirical AF values by performing the regression of the biomarker v. the intake estimate obtained by each approach. The AF provides information on the extent to which diet–disease associations are affected by measurement error. Regression of a recovery biomarker v. a perfect unbiased dietary intake estimate should result in a regression coefficient (i.e. AF) of 1. The subsequent use of an unbiased estimate in a diet–disease association should deliver an unbiased estimate, e.g. relative risk (RR). An AF lower than 1 indicates attenuation of the diet–disease association due to measurement error, with a larger deviation from 1 indicating more attenuation. An AF higher than 1 indicates a possible overcorrection, with a larger deviation from 1 indicating more overcorrection. To test whether empirical AF values of the different approaches differed statistically significantly from each other, we used a bootstrap approach (1000 replicates). To correct for multiple testing, we used the Bonferroni correction and thus considered a P value <0·01 statistically significant for the comparison of AF values between the five approaches. Finally, we used the obtained AF values to illustrate the impact of measurement error present in the dietary estimates of the five approaches. An example diet–disease association with an assumed true RR of 2·0 was used in this illustration. We estimated the observed RR that would have been found when using the dietary estimates from the five approaches, i.e. observed RR, with the following formula: RRtrue = (RRobserved)1/AF. Rewriting the formula gives: RRobserved = (RRtrue)AF. All statistical tests were performed using the statistical software package SAS version 9.3.
Results
At baseline, participants (n 236; eighty-nine men and 147 women) were on average 54·0 (sd 10·9) years old, had a mean BMI of 25·4 (sd 4·0) kg/m2 and 68·5 % was classified as highly educated (university or college degree).
The mean intakes estimated using the RC and ERC approaches were similar to
![]() $\overline {\rm R}$
, as this is the reference method used (Table 2). The sd of the intake distribution of the ERC was larger compared with that of RC, thus theoretically the ERC has more power to detect an association with disease or other outcome than RC. However, the sd was still considerably smaller than the sd of
$\overline {\rm R}$
, as this is the reference method used (Table 2). The sd of the intake distribution of the ERC was larger compared with that of RC, thus theoretically the ERC has more power to detect an association with disease or other outcome than RC. However, the sd was still considerably smaller than the sd of
![]() $\overline {\rm R}$
and the biomarker, which are high due to random day-to-day error.
$\overline {\rm R}$
and the biomarker, which are high due to random day-to-day error.
Table 2 Mean estimated intake and bias per approach
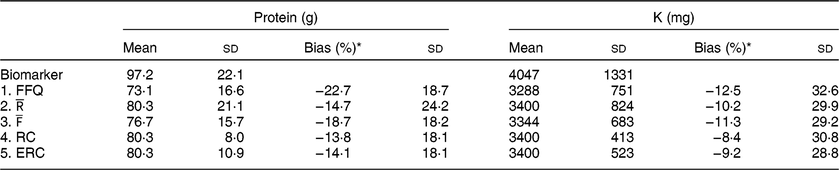
* Percentage bias was calculated on the individual level using the biomarker as the true intake and is displayed as mean and SD.
Both the FFQ and
![]() $\overline {\rm R}$
underestimated protein and K intake compared with their respective urinary biomarkers (Table 2), with FFQ showing the largest underestimation. Protein intake was underestimated by 22·7 % when using FFQ estimates and 14·7 % when using
$\overline {\rm R}$
underestimated protein and K intake compared with their respective urinary biomarkers (Table 2), with FFQ showing the largest underestimation. Protein intake was underestimated by 22·7 % when using FFQ estimates and 14·7 % when using
![]() $\overline {\rm R}$
estimates as compared with protein intake based on urinary-N. Averaging FFQ and 24hR (
$\overline {\rm R}$
estimates as compared with protein intake based on urinary-N. Averaging FFQ and 24hR (
![]() $\overline {\rm F}\,\overline {\rm R}$
) resulted in an average underestimation of 18·7 %, whereas estimates based on RC underestimated by 13·8 % and ERC estimates underestimated protein intake by 14·1 %. For K, the FFQ underestimated K intake the most, with an average bias of 12·5 %. For
$\overline {\rm F}\,\overline {\rm R}$
) resulted in an average underestimation of 18·7 %, whereas estimates based on RC underestimated by 13·8 % and ERC estimates underestimated protein intake by 14·1 %. For K, the FFQ underestimated K intake the most, with an average bias of 12·5 %. For
![]() $\overline {\rm R}$
the underestimation was 10·2 % on average, whereas for
$\overline {\rm R}$
the underestimation was 10·2 % on average, whereas for
![]() $\overline {\rm F}\,\overline {\rm R}$
this was 11·3 %. RC and ERC underestimated K intake the least with 8·4 % underestimation for RC and 9·2 % for ERC.
$\overline {\rm F}\,\overline {\rm R}$
this was 11·3 %. RC and ERC underestimated K intake the least with 8·4 % underestimation for RC and 9·2 % for ERC.
For protein intake estimates, the empirical AF was smallest for
![]() $\overline {\rm R}$
estimates (0·40) and slightly but not significantly higher for FFQ intake estimates (0·55; Fig. 2(a)). The average of FFQ and
$\overline {\rm R}$
estimates (0·40) and slightly but not significantly higher for FFQ intake estimates (0·55; Fig. 2(a)). The average of FFQ and
![]() $\overline {\rm R}$
(
$\overline {\rm R}$
(
![]() $\overline {\rm F}\,\overline {\rm R}$
) had an AF of 0·66 and therewith performed significantly better than FFQ and
$\overline {\rm F}\,\overline {\rm R}$
) had an AF of 0·66 and therewith performed significantly better than FFQ and
![]() $\overline {\rm R}$
intake estimates. The RC and ERC intake estimates produced significantly higher AF values, being 1·14 and 0·95, respectively. For K, AF values were smallest for FFQ estimates (0·70) and slightly but not significantly higher for
$\overline {\rm R}$
intake estimates. The RC and ERC intake estimates produced significantly higher AF values, being 1·14 and 0·95, respectively. For K, AF values were smallest for FFQ estimates (0·70) and slightly but not significantly higher for
![]() $\overline {\rm R}$
intake estimates (0·80; Fig. 2(b)). The AF was 1·01 for the
$\overline {\rm R}$
intake estimates (0·80; Fig. 2(b)). The AF was 1·01 for the
![]() $\overline {\rm F}\,\overline {\rm R}$
estimates of K, whereas the AF for RC and ERC was higher than 1 (1·28 and 1·34, respectively). The latter value differs statistically significantly from 1, indicating that a correction using ERC based on the average of two 24hR as reference value could lead to an overestimation of the strength of the association between K intake and health effect. For protein, however, an ERC correction using the average of two 24hR from our data seems to yield an approximately correct strength of association.
$\overline {\rm F}\,\overline {\rm R}$
estimates of K, whereas the AF for RC and ERC was higher than 1 (1·28 and 1·34, respectively). The latter value differs statistically significantly from 1, indicating that a correction using ERC based on the average of two 24hR as reference value could lead to an overestimation of the strength of the association between K intake and health effect. For protein, however, an ERC correction using the average of two 24hR from our data seems to yield an approximately correct strength of association.

Fig. 2 Empirical attenuation factors (AF), with their 95% CI indicated by horizontal bars, for the five approaches for (a) protein and (b) potassium from regression of the biomarker v. the intake estimates. a,b,cUnlike superscript letters indicate statistically significant AF: P < 0·01 (FFQ, FFQ estimate;
![]() $\overline {\rm R}$
, mean of two telephone-based 24 h recalls (24hR);
$\overline {\rm R}$
, mean of two telephone-based 24 h recalls (24hR);
![]() $\overline {\rm F}\,\overline {\rm R}$
, mean of FFQ and two telephone-based 24hR; RC, regression calibration with the FFQ as main instrument and two telephone-based 24hR as superior instrument; ERC, enhanced regression calibration with the FFQ as main instrument and two telephone-based 24hR recalls as superior instrument)
$\overline {\rm F}\,\overline {\rm R}$
, mean of FFQ and two telephone-based 24hR; RC, regression calibration with the FFQ as main instrument and two telephone-based 24hR as superior instrument; ERC, enhanced regression calibration with the FFQ as main instrument and two telephone-based 24hR recalls as superior instrument)
While for both nutrients RC and ERC AF values did not differ statistically significantly from each other, the ERC estimate had the smallest 95% CI, indicating higher precision of the AF and potentially more power to detect diet–disease associations.
To illustrate the impact of applying RC or ERC on dietary intake estimates used to assess diet–disease associations, we give an example using AF values obtained for the five approaches for protein and K. We assume to have a hypothetical diet–disease association with a true RR of 2·0. If we would use the FFQ estimate for protein, we would obtain an observed RR of 1·46 (i.e. 2·00·55), whereas with the
![]() $\overline {\rm R}$
estimate an RR of 1·36 (i.e. 2·00·40) would be obtained (Fig. 3, left side). Please note that the mentioned observed RR are on average, the actual observed RR in any given study might be rather different. For the
$\overline {\rm R}$
estimate an RR of 1·36 (i.e. 2·00·40) would be obtained (Fig. 3, left side). Please note that the mentioned observed RR are on average, the actual observed RR in any given study might be rather different. For the
![]() $\overline {\rm F}\,\overline {\rm R}$
an RR of 1·58 (i.e. 2·00·66) would be observed. Using RC intake estimates for protein would give an RR of 2·20 (i.e. 2·01·14). For the ERC the observed RR would be 1·93 (i.e. 2·00·95), which is closest to the true RR. For K, the observed RR would be 1·62 (i.e. 2·00·70) when using FFQ intake estimates and 1·74 (i.e. 2·00·80) when using
$\overline {\rm F}\,\overline {\rm R}$
an RR of 1·58 (i.e. 2·00·66) would be observed. Using RC intake estimates for protein would give an RR of 2·20 (i.e. 2·01·14). For the ERC the observed RR would be 1·93 (i.e. 2·00·95), which is closest to the true RR. For K, the observed RR would be 1·62 (i.e. 2·00·70) when using FFQ intake estimates and 1·74 (i.e. 2·00·80) when using
![]() $\overline R$
intake estimates (Fig. 3, right side). Using
$\overline R$
intake estimates (Fig. 3, right side). Using
![]() $\overline {\rm F}\,\overline {\rm R}$
intake estimates would result in an observed RR of 2·01 (i.e. 2·01·01), which is closest to the true RR. Using RC and ERC would lead to an observed RR of 2·45 (i.e. 2·01·28) and 2·53 (i.e. 2·01·34), respectively, indicating overcorrection as these are higher than the true RR of 2·0.
$\overline {\rm F}\,\overline {\rm R}$
intake estimates would result in an observed RR of 2·01 (i.e. 2·01·01), which is closest to the true RR. Using RC and ERC would lead to an observed RR of 2·45 (i.e. 2·01·28) and 2·53 (i.e. 2·01·34), respectively, indicating overcorrection as these are higher than the true RR of 2·0.

Fig. 3 Visualization of the impact of the five presented approaches on diet–disease relative risk (RR) assuming a hypothetical true RR risk (![]() ) of 2·0:
) of 2·0: ![]() , FFQ (FFQ estimate);
, FFQ (FFQ estimate); ![]() ,
,
![]() $\overline {\rm R}$
(mean of two telephone-based 24 h recalls (24hR));
$\overline {\rm R}$
(mean of two telephone-based 24 h recalls (24hR)); ![]() ,
,
![]() $\overline {\rm F}\,\overline {\rm R}$
(mean of FFQ and two telephone-based 24hR);
$\overline {\rm F}\,\overline {\rm R}$
(mean of FFQ and two telephone-based 24hR); ![]() , RC (regression calibration with the FFQ as main instrument and two telephone-based 24hR as superior instrument);
, RC (regression calibration with the FFQ as main instrument and two telephone-based 24hR as superior instrument); ![]() , ERC (enhanced regression calibration with the FFQ as main instrument and two telephone-based 24hR as superior instrument)
, ERC (enhanced regression calibration with the FFQ as main instrument and two telephone-based 24hR as superior instrument)
Discussion
RC and ERC significantly reduced bias in estimates of diet–chronic disease associations, as demonstrated by AF values approaching 1, as compared with simply averaging estimates from two different assessment methods and uncorrected estimates. For both K and protein, RC and ERC AF values did not differ statistically significantly from each other. The ERC AF, however, had the narrowest 95% CI, indicating higher precision of the AF and potentially more power to detect diet–disease associations than the RC approach.
Although our finding of substantial measurement error is not new( Reference Kipnis, Subar and Midthune 2 , Reference Geelen, Souverein and Busstra 25 ), it does underscore the importance of validation studies and statistical methods that reduce bias in diet–disease associations. In our study, we used the average of two 24hR as reference instrument for the RC and ERC approaches, as this is common practice in nutritional epidemiology. However, this requires the assumption that 24hR intakes are unbiased, which often does not hold( Reference Freedman, Commins and Willett 26 ). Also in our study we can see that this assumption is violated, as there is an average under-reporting of 14·7% for protein and 10·2% for K intake estimates based on two 24hR compared with intake estimates based on urinary recovery biomarkers. The impact of bias in 24hR and its subsequent use in calibration models is described in the paper of Freedman et al. ( Reference Freedman, Commins and Willett 26 ). Even though the 24hR does not fulfil the assumption of unbiasedness, Freedman et al. showed that diet–disease estimates were less biased when calibrated dietary intake estimates were used than uncalibrated dietary intake estimates.
An important consideration that should be noted is that RC and ERC calibrate the main instrument (i.e. the FFQ) to the reference instrument (i.e. 24hR) to obtain calibrated intakes that can be used to assess diet–disease associations. Estimates obtained with RC and ERC do not reflect correct individual intake levels and cannot be used as such. However, the aim of our study was not to correct individual intake levels, but to assess if using combined FFQ and 24hR estimates using RC or ERC leads to less bias in resulting diet–disease associations. Diet–disease associations are usually the main interest in nutritional epidemiology. In our study, we used AF as a measure for bias in resulting diet–disease associations, with an AF of 1 indicating no bias present. AF values for the FFQ and 24hR showed that there was substantial bias, especially for protein intake, that would result in attenuation of diet–disease associations (i.e.
![]() ${\mathop{\rm AF}\nolimits} \ll 1$
). Averaging FFQ and 24hR resulted in AF values closer to 1, while using RC and ERC improved protein estimates with resulting AF close to 1. However, for K, using RC and ERC led to overcorrection, as indicated by AF > 1. This overcorrection is likely the result of systematic bias present in the used reference instrument, i.e. 24hR. Therefore, the use of unbiased reference instruments, e.g. biomarkers of intake, remains the preferred option.
${\mathop{\rm AF}\nolimits} \ll 1$
). Averaging FFQ and 24hR resulted in AF values closer to 1, while using RC and ERC improved protein estimates with resulting AF close to 1. However, for K, using RC and ERC led to overcorrection, as indicated by AF > 1. This overcorrection is likely the result of systematic bias present in the used reference instrument, i.e. 24hR. Therefore, the use of unbiased reference instruments, e.g. biomarkers of intake, remains the preferred option.
The mean intake estimates and the AF values for RC and ERC did not differ much, which could raise the question whether ERC has additional benefits to RC, as it implies a lot of extra effort and labour to collect two 24hR for each participant instead of only a sub-sample. However, the sd of RC is smaller than the sd of the ERC, indicating a narrower distribution of RC values than of ERC values. This narrower distribution of the RC values makes it more difficult to discriminate between individuals and indicates a loss of power. The wider distribution of the ERC intake estimates thus underlines the theoretical advantage of the ERC having more power to detect diet–disease associations than RC. Another example can be found in the 95% CI of the AF values being narrower for ERC than for RC, indicating more precision with the ERC in estimating diet–disease associations.
In the current study, we used the average of two telephone-administered 24hR as reference instrument, as this is a well-documented commonly used reference instrument. However, this method is too labour-intensive and expensive to administer in the entire study population of large epidemiological studies. Using recalls as reference method would thus be limited to validation studies, excluding the possibility to use the proposed ERC method. However, with the availability of 24hR administered via the Internet (e.g. ASA24( Reference Subar, Kirkpatrick and Mittl 27 ), Compl-eat( Reference Meijboom, Van Houts-Streppel and Perenboom 28 )) costs of collecting 24hR are substantially reduced, making the web-based 24hR a viable option for large epidemiological studies. Evaluations indicated that web-based 24hR are in general in good agreement with interview-administered 24hR( Reference Timon, van den Barg and Blain 10 ). For example, the ASA24 had an average relative mean difference of 1·6 % for energy intake, 2·9 to 11·1 % for macronutrients and −4·2 to 11·9 % for micronutrients, compared with the telephone-administered 24hR( Reference Thompson, Dixit-Joshi and Potischman 29 ). Furthermore, the Dutch web-based 24hR tool Compl-eat underestimated macronutrients on average by 8 % and micronutrients by 13 % compared with telephone-administered 24hR( Reference Meijboom, Van Houts-Streppel and Perenboom 28 ). These results indicate that web-based 24hR could also be used as reference instruments for the RC and ERC.
We propose a rather simple method, i.e. ERC, to combine the 24hR and FFQ dietary intake estimates. In the presented calibration model, we did not include covariates, to keep the calibration model as simple as possible and to be able to illustrate the potential impact of RC and ERC on bias in resulting diet–disease associations. In theory, RC should include all covariates in the diet–disease model. Otherwise, it will lead to biased results. This would apply to the ERC, as well( Reference Kipnis, Midthune and Buckman 30 ). Others have shown that adding covariates such as BMI to the model might improve the RC( Reference Prentice, Pettinger and Tinker 31 , Reference Prentice and Huang 32 ). However, adding covariates in addition to those in the outcome model should be done under the condition that they are related to the true exposure of interest, but not related to the outcome given the true exposure and other covariates in the outcome model( Reference Kipnis, Midthune and Buckman 30 ). Furthermore, these covariates should be measured accurately and without bias to prevent introducing additional bias( Reference Agogo, van der Voet and van’t Veer 33 ). Energy adjustment is commonly used to reduce bias in diet–disease associations. However, it depends on the dietary assessment method and nutrient, whether energy adjustment reduces bias substantially or not( Reference Freedman, Commins and Moler 34 , Reference Freedman, Commins and Moler 35 ). Another method suggested including biomarker measures in the RC model to provide unbiased diet–disease estimates( Reference Freedman, Midthune and Carroll 36 ). The advantage of using biomarkers is that they are objectively measured and are assumed to have uncorrelated errors with the self-report instrument, in contrast to using two self-report dietary assessment tools such as FFQ and 24hR. Additionally, recovery biomarkers are free of intake-related bias. A limitation is the limited availability of biomarkers for nutrient intake, and the substantial burden and costs associated with biomarker measurements. Therefore, combining two self-report dietary assessment tools has much more potential in the field of nutritional epidemiology.
A limitation of the current study is that recovery biomarkers were needed for validation of the proposed approaches. Therefore, we were limited to studying protein and K intake estimates as no other recovery biomarkers were available. We can only speculate whether the proposed approaches also improve estimates for intakes of other (micro) nutrients, energy and foods. It must be noted that AF values observed for protein and K showed different results, with the ERC being the closest to 1 for protein, whereas the RC and ERC were higher than 1 for K. Thus, different results were obtained for different nutrients and this must be kept in mind when studying other nutrients. The study of Carroll et al. demonstrated a large gain in power and precision when combining FFQ and 24hR data for micronutrients and food groups compared with only two 24hR or one FFQ( Reference Carroll, Midthune and Subar 11 ). They used the National Cancer Institute method to obtain usual intake estimates( Reference Freedman, Guenther and Krebs-Smith 37 , Reference Freedman, Guenther and Dodd 38 ) using the frequency information from the FFQ as covariate in the RC( Reference Kipnis, Midthune and Buckman 30 ). Although the National Cancer Institute method is capable of combining FFQ and 24hR data, this method requires more advanced computations, whereas the ERC is a rather simple extension of a commonly used method to calibrate intake estimates and consequently reduce bias in diet–disease associations. The benefits of combining FFQ and 24hR demonstrated by Carroll et al. should also apply to the ERC approach in our study, suggesting the suitability of the ERC for micronutrients and food groups. It should be noted that RC and thus also ERC are based on the assumption that measurement error in the exposure is non-differential with respect to the outcome, thus the use of RC and ERC in case–control and interventions should be applied with caution.
Another limitation of the current study is that we had only one biomarker measurement available, whereas two measurements would be more desirable to study usual intake. It is likely that by using only one biomarker measurement more random error due to day-to-day variation is present, leading to less precise estimates.
Furthermore, the period in which dietary intake was assessed for the various methods was quite broad and differed per individual. A larger time between assessment methods may have led to more variation in the dietary intakes and might allow for changes due to seasonality as well as changes in dietary habits over time. However, analysis stratified for the time between 24hR and FFQ assessment did not indicate a difference in protein and K intake.
Future research should focus on validating the error structures of intake estimates implicit in the RC and ERC approach. This information can be used to further improve the RC models, possibly by including other covariates. However, keeping the simplicity of the suggested ERC approach is desirable.
Conclusions
Measurement error is a serious problem in nutrition research. Our study highlights the potential of combining FFQ and 24hR data using RC and ERC, simple approaches, with substantial impact on correcting diet–disease associations. The availability of web-based 24hR reduces burden and costs, making it easier to use in large population study. Preferably, FFQ and 24hR data are collected for the entire study population and ERC is used.
Acknowledgements
Acknowledgements: The authors thank all participants in the NDARD study for their time and contributions, and the research staff and students for collecting the data of NDARD. Financial support: NDARD was funded by Wageningen University and ZonMW (grant number 911100030), The Netherlands Organization for Health Research and Development, The Hague. The funders had no role in the design, analysis or writing of this article. Conflict of interest: The authors declare that they have no conflict of interest. Authorship: M.L., A.G. and H.C.B. designed the study and formulated the research question; M.L. analysed the data and drafted the manuscript. All authors critically revised the manuscript for important intellectual content and approved of the final version to be published. Ethics of human subject participation: The NDARD was approved by the Medical Ethical Committee of Wageningen University and was conducted according to the guidelines of the Declaration of Helsinki. All participants gave written informed consent before the start of the study.
Supplementary material
To view supplementary material for this article, please visit https://doi.org/10.1017/S1368980019001563
Author ORCID
Moniek Looman, 0000-0002-9258-3340.