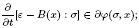We establish new existence results for multiple positive solutions of fourth-order nonlinear equations which model deflections of an elastic beam. We consider the widely studied boundary conditions corresponding to clamped and hinged ends and many non-local boundary conditions, with a unified approach. Our method is to show that each boundary-value problem can be written as the same type of perturbed integral equation, in the space $C[0,1]$, involving a linear functional $\alpha[u]$ but, although we seek positive solutions, the functional is not assumed to be positive for all positive $u$. The results are new even for the classic boundary conditions of clamped or hinged ends when $\alpha[u]=0$, because we obtain sharp results for the existence of one positive solution; for multiple solutions we seek optimal values of some of the constants that occur in the theory, which allows us to impose weaker assumptions on the nonlinear term than in previous works. Our non-local boundary conditions contain multi-point problems as special cases and, for the first time in fourth-order problems, we allow coefficients of both signs.

A convergence result is proved for the equilibrium configurations of a three-dimensional thin elastic beam, as the diameter $h$ of the cross-section tends to zero. More precisely, we show that stationary points of the nonlinear elastic functional $E^h$, whose energies (per unit cross-section) are bounded by $Ch^2$, converge to stationary points of the $\varGamma$-limit of $E^h/h^2$. This corresponds to a nonlinear one-dimensional model for inextensible rods, describing bending and torsion effects. The proof is based on the rigidity estimate for low-energy deformations by Friesecke, James and Müller and on a compensated compactness argument in a singular geometry. In addition, possible concentration effects of the strain are controlled by a careful truncation argument.

This paper deals with processes in nonlinear inelastic materials whose constitutive behaviour is represented by the inclusion

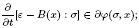
here we denote by σ the stress tensor, by ε the linearized strain tensor, by B(x) the compliance tensor and by ∂ϕ(·, x) the subdifferential of a convex function ϕ(·, x). This relation accounts for elasto-viscoplasticity, including a nonlinear version of the classical Maxwell model of viscoelasticity and the Prandtl—Reuss model of elastoplasticity.

The constitutive law is coupled with the equation of continuum dynamics, and well-posedness is proved for an initial- and boundary-value problem. The function ϕ and the tensor B are then assumed to oscillate periodically with respect to x and, as this period vanishes, a two-scale model of the asymptotic behaviour is derived via Nguetseng's notion of two-scale convergence. A fully homogenized single-scale model is also retrieved, and its equivalence with the two-scale problem is proved. This formulation is non-local in time and is at variance with that based on so-called analogical models that rest on a mean-field-type hypothesis.

We prove weighted norm inequalities for vector-valued commutators of multilinear operators. We first consider the strong $(p,p)$ case with $p>0$ and then the case weak-type estimate.

By Karamata regular variation theory, a perturbation method and construction of comparison functions, we show the exact asymptotic behaviour of solutions near the boundary to nonlinear elliptic problems Δu ± |Δu|q = b(x)g(u), u > 0 in Ω, u|∂Ω = ∞, where Ω is a bounded domain with smooth boundary in ℝN, q > 0, g ∈ C1[0, ∞) is increasing on [0, ∞), g(0) = 0, g′ is regularly varying at infinity with positive index ρ and b is non-negative in Ω and is singular on the boundary.

This paper concerns the asymptotic behaviours of pulse-like solutions for a 3 × 3 semilinear hyperbolic system in the limit of short wavelength ε. When two pulses interact with each other, we construct a pulse-like approximate solution up to Ο(ε), at which order a new pulse appears. The existence of a solution to the 3 × 3 semilinear problem with the initial data being the interaction of two pulses in a domain independent of the wavelength is proved in the space of co-normal distributions. Meanwhile, we obtain that the error between this exact solution and the approximate solution is of Ο(ε2) as ε → 0, which rigorously shows that there are three pulses propagated after the interaction of two pulses for the 3 × 3 semilinear system.