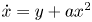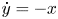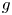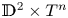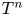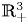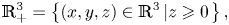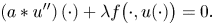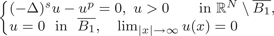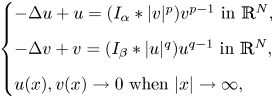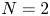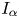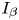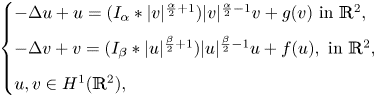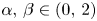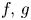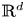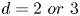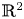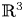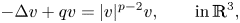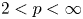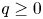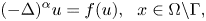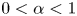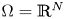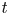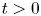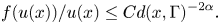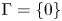Research Article
The cyclicity of the period annulus of a reversible quadratic system
- Part of:
-
- Published online by Cambridge University Press:
- 10 February 2021, pp. 281-290
-
- Article
- Export citation
Generalized small cancellation conditions, non-positive curvature and diagrammatic reducibility
- Part of:
-
- Published online by Cambridge University Press:
- 02 March 2021, pp. 545-566
-
- Article
- Export citation
Parrondo's paradox for homoeomorphisms
- Part of:
-
- Published online by Cambridge University Press:
- 16 June 2021, pp. 817-825
-
- Article
- Export citation
Discs area-minimizing in mean convex Riemannian n-manifolds
- Part of:
-
- Published online by Cambridge University Press:
- 06 September 2021, pp. 1361-1382
-
- Article
- Export citation
On the Cauchy problem associated with the Brinkman flow in
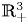 $\mathbb {R}_{+}^{3}$
$\mathbb {R}_{+}^{3}$
- Part of:
-
- Published online by Cambridge University Press:
- 07 September 2021, pp. 1089-1108
-
- Article
- Export citation
Existence and monotonicity of nonlocal boundary value problems: the one-dimensional case
- Part of:
-
- Published online by Cambridge University Press:
- 23 December 2020, pp. 1-27
-
- Article
- Export citation
Recollements, comma categories and morphic enhancements
- Part of:
-
- Published online by Cambridge University Press:
- 09 March 2021, pp. 567-591
-
- Article
- Export citation
Fast and slow decay solutions for supercritical fractional elliptic problems in exterior domains
- Part of:
-
- Published online by Cambridge University Press:
- 18 January 2021, pp. 28-53
-
- Article
- Export citation
Existence and nonexistence results for a class of Hamiltonian Choquard-type elliptic systems with lower critical growth on ℝ2
- Part of:
-
- Published online by Cambridge University Press:
- 28 September 2021, pp. 1383-1410
-
- Article
- Export citation
Existence of solution for elliptic equations with supercritical Trudinger–Moser growth
- Part of:
-
- Published online by Cambridge University Press:
- 16 February 2021, pp. 291-310
-
- Article
- Export citation
Global regularity for the micropolar Rayleigh-Bénard problem with only velocity dissipation
- Part of:
-
- Published online by Cambridge University Press:
- 26 August 2021, pp. 1109-1138
-
- Article
- Export citation
Global well-posedness and nonlinear stability of a chemotaxis system modelling multiple sclerosis
- Part of:
-
- Published online by Cambridge University Press:
- 28 July 2021, pp. 826-856
-
- Article
- Export citation
Concentrating standing waves for Davey–Stewartson systems
- Part of:
-
- Published online by Cambridge University Press:
- 01 October 2021, pp. 1411-1450
-
- Article
- Export citation
The second moment of symmetric square L-functions over Gaussian integers
- Part of:
-
- Published online by Cambridge University Press:
- 11 January 2021, pp. 54-80
-
- Article
- Export citation
Spiraling solutions of nonlinear Schrödinger equations
-
- Published online by Cambridge University Press:
- 24 May 2021, pp. 592-625
-
- Article
- Export citation
On the first eigenvalue of the Laplace operator for compact spacelike submanifolds in Lorentz–Minkowski spacetime 𝕃m
- Part of:
-
- Published online by Cambridge University Press:
- 11 February 2021, pp. 311-330
-
- Article
- Export citation
Lorentz and Gale–Ryser theorems on general measure spaces
- Part of:
-
- Published online by Cambridge University Press:
- 09 August 2021, pp. 857-878
-
- Article
- Export citation
Riemannian approximation in Carnot groups
- Part of:
-
- Published online by Cambridge University Press:
- 06 September 2021, pp. 1139-1154
-
- Article
- Export citation
Qualitative properties of singular solutions to fractional elliptic equations
- Part of:
-
- Published online by Cambridge University Press:
- 14 September 2021, pp. 1155-1190
-
- Article
- Export citation
The homotopy classification of four-dimensional toric orbifolds
- Part of:
-
- Published online by Cambridge University Press:
- 25 May 2021, pp. 626-648
-
- Article
- Export citation