Hostname: page-component-8448b6f56d-mp689 Total loading time: 0 Render date: 2024-04-24T17:53:11.980Z Has data issue: false hasContentIssue false
  • English
  • Français

Existence and nonexistence results for a class of Hamiltonian Choquard-type elliptic systems with lower critical growth on ℝ2

Part of: Elliptic equations and systems Partial differential equations

Published online by Cambridge University Press:  28 September 2021

B. B. V. Maia Open the ORCID record for B. B. V. Maia [Opens in a new window]  and
O. H. Miyagaki Open the ORCID record for O. H. Miyagaki [Opens in a new window]
B. B. V. Maia
Affiliation:
Universidade Federal Rural da Amazônia, campus de Capitão-Poço, Capitão-Poço, PA, Brazil (braulio.maia@ufra.edu.br)
O. H. Miyagaki
Affiliation:
Departmento de Matemática, Universidade Federal de São Carlos, São Carlos, SP, Brazil (olimpio@dm.ufscar.br)
Get access Rights & Permissions [Opens in a new window]

Abstract

In this paper, we investigate the existence and nonexistence of results for a class of Hamiltonian-Choquard-type elliptic systems. We show the nonexistence of classical nontrivial solutions for the problem

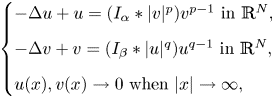\[ \begin{cases} -\Delta u + u= ( I_{\alpha} \ast |v|^{p} )v^{p-1} \text{ in } \mathbb{R}^{N},\\ -\Delta v + v= ( I_{\beta} \ast |u|^{q} )u^{q-1} \text{ in } \mathbb{R}^{N}, \\ u(x),v(x) \rightarrow 0 \text{ when } |x|\rightarrow \infty, \end{cases} \]
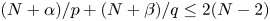when $(N+\alpha )/p + (N+\beta )/q \leq 2(N-2)$ (if 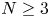$N\geq 3$) and 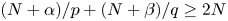$(N+\alpha )/p + (N+\beta )/q \geq 2N$ (if 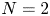$N=2$), where 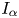$I_{\alpha }$ and 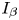$I_{\beta }$ denote the Riesz potential. Second, via variational methods and the generalized Nehari manifold, we show the existence of a nontrivial non-negative solution or a Nehari-type ground state solution for the problem
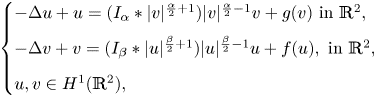\[ \begin{cases} -\Delta u + u= (I_{\alpha} \ast |v|^{\frac{\alpha}{2}+1})|v|^{\frac{\alpha}{2}-1}v + g(v) \hbox{ in } \mathbb{R}^{2},\\ - \Delta v + v= (I_{\beta} \ast |u|^{\frac{\beta}{2}+1})|u|^{\frac{\beta}{2}-1}u + f(u), \hbox{ in } \mathbb{R}^{2},\\ u,v \in H^{1}(\mathbb{R}^{2}), \end{cases} \]
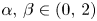where $\alpha ,\,\beta \in (0,\,2)$ and 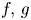$f,\,g$ have exponential critical growth in the Trudinger–Moser sense.

Keywords

Hamiltonian elliptic systemChoquard equationsexponential critical growthnonexistence

MSC classification

Primary: 35J50: Variational methods for elliptic systems
Secondary: 35B33: Critical exponents 35J60: Nonlinear elliptic equations
Type
Research Article
Information
Proceedings of the Royal Society of Edinburgh Section A: Mathematics , Volume 152 , Issue 6 , December 2022 , pp. 1383 - 1410
Check for updates
Copyright
Copyright © The Author(s), 2021. Published by Cambridge University Press on behalf of The Royal Society of Edinburgh

Access options

Get access to the full version of this content by using one of the access options below. (Log in options will check for institutional or personal access. Content may require purchase if you do not have access.)

References

Cao, D. M.. Nontrivial solution of semilinear elliptic equation with critical exponent in $\mathbb {R}^{2}$. Comm. Partial Differ. Eqs. 17 (1992), 407–435.CrossRefGoogle Scholar
Chen, S., Tang, X. and Wei, J.. Nehari-type ground state solutions for a Choquard equation with doubly critical exponents. Adv. Nonlinear Anal. 10 (2021), 152–171.CrossRefGoogle Scholar
Diósi, L.. Gravitation and quantum-mechanical localization of macro-objects. Phys. Lett. A 105 (1984), 199–202.CrossRefGoogle Scholar
de Figueiredo, D. G, do Ó, J. M. and Zhang, J.. Ground state solutions of Hamiltonian elliptic systems in dimension two. Proc. R. Soc. Edinburgh: Sect. Math. 150 (2020), 1737–1760.CrossRefGoogle Scholar
de Figueiredo, D. G., do Ó, J. M. and Ruf, B.. Critical and subcritical elliptic systems in dimension two. Indiana Univ. Math. J. 53 (2004), 1037–1054.CrossRefGoogle Scholar
de Figueiredo, D. G., Miyagaki, O. H. and Ruf, B.. Elliptic equations in $\mathbb {R}^{2}$ with nonlinearities in the critical growth range. Calc. Var. Partial Differ. Eqs. 3 (1995), 139–153.CrossRefGoogle Scholar
de Figueiredo, D. G. and Yang, J.. Decay, symmetry and existence of solutions of semilinear elliptic systems. Nonlinear Anal. 33 (1998), 211–234.CrossRefGoogle Scholar
do Ó, J. M., Medeiros, E. and Severo, U.. A nonhomogeneous elliptic problem involving critical growth in dimension two. J. Math. Anal. Appl. 345 (2008), 286–304.CrossRefGoogle Scholar
Jones, K. R. W.. Gravitational self-energy as the litmus of reality. Modern Phys. Lett. 10 (1995), 657–667.CrossRefGoogle Scholar
Moroz, I. M., Penrose, R. and Tod, P.. Spherically-symmetric solutions of the Schrödinger-Newton equations. Class. Quantum Gravity 15 (1998), 2733–2742.CrossRefGoogle Scholar
Korman, P.. Pohozaev's identity and non-existence of solutions for elliptic systems. Comm. Appl. Nonlinear Anal. 17 (2010), 81–88.Google Scholar
Li, G. and Yang, J.. Asymptotically linear elliptic systems. Comm. Partial Differ. Eqs. 29 (2004), 925–954.CrossRefGoogle Scholar
Lieb, E. and Loss, M.. Analysis, Graduate Studies in Mathematics (Providence, Rhode Island: AMS, 2001).Google Scholar
Lions, P. L.. The Choquard equation and related questions. Nonlinear Anal. 4 (1980), 1063–1072.CrossRefGoogle Scholar
Lions, P. L.. Compactness and topological methods for some nonlinear variational problems of mathematical physics. Nonlinear Probl.: Present Future 61 (1982), 17–34.Google Scholar
Maia, B. B. V. and Miyagaki, O. H.. On a class of Hamiltonian Choquard-type elliptic systems. J. Math. Phys. 61 (2020), 011502.CrossRefGoogle Scholar
Moroz, V. and Van Schaftingen, J.. Ground states of nonlinear Choquard equations: existence, qualitative properties and decay asymptotics. J. Funct. Anal. 265 (2013), 153–184.CrossRefGoogle Scholar
Pankov, A.. Periodic nonlinear Schrödinger equation with application to photonic crystals. Milan J. Math. 73 (2005), 259–287.CrossRefGoogle Scholar
Pekar, S.. Untersuchungen über die Elektr onentheorie der Kristalle (Berlin: Akademie-Verlag, 1954).CrossRefGoogle Scholar
Szulkin, A. and Weth, T.. Ground state solutions for some indefinite variational problems. J. Funct. Anal. 257 (2009), 3802–3822.CrossRefGoogle Scholar
Van Schaftingen, J. and Xia, J.. Groundstates for a local nonlinear perturbation of the Choquard equations with lower critical exponent. J. Math. Anal. Appl. 464 (2018), 1184–1202.CrossRefGoogle Scholar
Willem, M., Minimax Theorems, Progress in Nonlinear Differential Equations and Their Applications (Birkhäuser: Birkhäuser Basel, 1996).Google Scholar