Fixing a positive integer r and 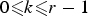 $0 \les k \les r-1$, define
$0 \les k \les r-1$, define 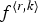 $f^{\langle r,k \rangle }$ for every formal power series f as
$f^{\langle r,k \rangle }$ for every formal power series f as 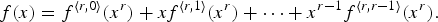 $ f(x) = f^{\langle r,0 \rangle }(x^r)+xf^{\langle r,1 \rangle }(x^r)+ \cdots +x^{r-1}f^{\langle r,r-1 \rangle }(x^r).$ Jochemko recently showed that the polynomial
$ f(x) = f^{\langle r,0 \rangle }(x^r)+xf^{\langle r,1 \rangle }(x^r)+ \cdots +x^{r-1}f^{\langle r,r-1 \rangle }(x^r).$ Jochemko recently showed that the polynomial 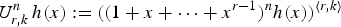 $U^{n}_{r,k}\, h(x) := ( (1+x+\cdots +x^{r-1})^{n} h(x) )^{\langle r,k \rangle }$ has only non-positive zeros for any
$U^{n}_{r,k}\, h(x) := ( (1+x+\cdots +x^{r-1})^{n} h(x) )^{\langle r,k \rangle }$ has only non-positive zeros for any 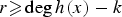 $r \ges \deg h(x) -k$ and any positive integer n. As a consequence, Jochemko confirmed a conjecture of Beck and Stapledon on the Ehrhart polynomial
$r \ges \deg h(x) -k$ and any positive integer n. As a consequence, Jochemko confirmed a conjecture of Beck and Stapledon on the Ehrhart polynomial 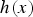 $h(x)$ of a lattice polytope of dimension n, which states that
$h(x)$ of a lattice polytope of dimension n, which states that 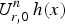 $U^{n}_{r,0}\,h(x)$ has only negative, real zeros whenever
$U^{n}_{r,0}\,h(x)$ has only negative, real zeros whenever 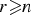 $r\ges n$. In this paper, we provide an alternative approach to Beck and Stapledon's conjecture by proving the following general result: if the polynomial sequence
$r\ges n$. In this paper, we provide an alternative approach to Beck and Stapledon's conjecture by proving the following general result: if the polynomial sequence 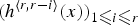 $( h^{\langle r,r-i \rangle }(x))_{1\les i \les r}$ is interlacing, so is
$( h^{\langle r,r-i \rangle }(x))_{1\les i \les r}$ is interlacing, so is 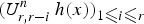 $( U^{n}_{r,r-i}\, h(x) )_{1\les i \les r}$. Our result has many other interesting applications. In particular, this enables us to give a new proof of Savage and Visontai's result on the interlacing property of some refinements of the descent generating functions for coloured permutations. Besides, we derive a Carlitz identity for refined coloured permutations.
$( U^{n}_{r,r-i}\, h(x) )_{1\les i \les r}$. Our result has many other interesting applications. In particular, this enables us to give a new proof of Savage and Visontai's result on the interlacing property of some refinements of the descent generating functions for coloured permutations. Besides, we derive a Carlitz identity for refined coloured permutations.