Hostname: page-component-848d4c4894-wzw2p Total loading time: 0 Render date: 2024-05-07T00:52:51.651Z Has data issue: false hasContentIssue false
  • English
  • Français

A priori bounds and multiplicity of positive solutions for p-Laplacian Neumann problems with sub-critical growth

Part of: Elliptic equations and systems Partial differential equations

Published online by Cambridge University Press:  23 January 2019

Alberto Boscaggin ,
Francesca Colasuonno  and
Benedetta Noris
Alberto Boscaggin
Affiliation:
Dipartimento di Matematica, Università di Torino, via Carlo Alberto 10, 10123Torino, Italia (alberto.boscaggin@unito.it)
Francesca Colasuonno
Affiliation:
Dipartimento di Matematica, Alma Mater Studiorum Università di Bologna, piazza di Porta S. Donato 5, 40126Bologna, Italia (francesca.colasuonno@unibo.it)
Benedetta Noris
Affiliation:
Laboratoire Amiénois de Mathématique Fondamentale et Appliquée, Université de Picardie Jules Verne, 33 rue Saint- Leu, 80039 AMIENS, France (benedetta.noris@u-picardie.fr)
Get access Rights & Permissions [Opens in a new window]

Abstract

Let 1 < p < +∞ and let Ω ⊂ ℝN be either a ball or an annulus. We continue the analysis started in [Boscaggin, Colasuonno, Noris, ESAIM Control Optim. Calc. Var. (2017)], concerning quasilinear Neumann problems of the type

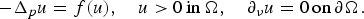$-\Delta _pu = f(u),\quad u > 0\,{\rm in }\,\Omega ,\quad \partial _\nu u = 0\,{\rm on }\,\partial \Omega .$
We suppose that f(0) = f(1) = 0 and that f is negative between the two zeros and positive after. In case Ω is a ball, we also require that f grows less than the Sobolev-critical power at infinity. We prove a priori bounds of radial solutions, focussing in particular on solutions which start above 1. As an application, we use the shooting technique to get existence, multiplicity and oscillatory behaviour (around 1) of non-constant radial solutions.

Keywords

quasilinear elliptic equationsshooting methoda priori estimatesexistence and multiplicityNeumann boundary conditions

MSC classification

Primary: 35J92: Quasilinear elliptic equations with $p$-Laplacian
Secondary: 35A24: Methods of ordinary differential equations 35B05: Oscillation, zeros of solutions, mean value theorems, etc. 35B09: Positive solutions 35B45: A priori estimates
Type
Research Article
Information
Proceedings of the Royal Society of Edinburgh Section A: Mathematics , Volume 150 , Issue 1 , February 2020 , pp. 73 - 102
Copyright
Copyright © Royal Society of Edinburgh 2019

Access options

Get access to the full version of this content by using one of the access options below. (Log in options will check for institutional or personal access. Content may require purchase if you do not have access.)

References

1Adimurthi, and Yadava, S. L.. Existence and nonexistence of positive radial solutions of Neumann problems with critical Sobolev exponents. Arch. Rational Mech. Anal. 115 (1991), 275–296.CrossRefGoogle Scholar
2Adimurthi, and Yadava, S. L.. Nonexistence of positive radial solutions of a quasilinear Neumann problem with a critical Sobolev exponent. Arch. Rational Mech. Anal. 139 (1997), 239–253.Google Scholar
3Adimurthi, , Yadava, S. L. and Knaap, M. C.. A note on a critical exponent problem with Neumann boundary conditions. Nonlinear Anal. 18 (1992), 287–294.CrossRefGoogle Scholar
4Azizieh, C. and Clément, P.. A priori estimates and continuation methods for positive solutions of p-Laplace equations. J. Differ. Equ. 179 (2002), 213–245.CrossRefGoogle Scholar
5Barutello, V., Secchi, S. and Serra, E.. A note on the radial solutions for the supercritical Hénon equation. J. Math. Anal. Appl. 341 (2008), 720–728.CrossRefGoogle Scholar
6Bonheure, D., Noris, B. and Weth, T.. Increasing radial solutions for Neumann problems without growth restrictions. Ann. Inst. H. Poincaré Anal. Non Linéaire 29 (2012), 573–588.CrossRefGoogle Scholar
7Bonheure, D., Grossi, M., Noris, B. and Terracini, S.. Multi-layer radial solutions for a supercritical Neumann problem. J. Differ. Equ. 261 (2016), 455–504.CrossRefGoogle Scholar
8Bonheure, D., Grumiau, C. and Troestler, C.. Multiple radial positive solutions of semilinear elliptic problems with Neumann boundary conditions. Nonlinear Anal. 147 (2016), 236–273.CrossRefGoogle Scholar
9Bonheure, D., Casteras, J.-B. and Noris, B.. Multiple positive solutions of the stationary Keller-Segel system. Calc. Var. Partial Differ. Equ., 56 (2017) Art. 74, 35.CrossRefGoogle Scholar
10Boscaggin, A. and Garrione, M.. Pairs of nodal solutions for a Minkowski-curvature boundary value problem in a ball. Commun. Contemp. Math., doi: 10.1142/S0219199718500062, 2017 (arXiv preprint arXiv:1703.02315).CrossRefGoogle Scholar
11Boscaggin, A. and Zanolin, F.. Pairs of nodal solutions for a class of nonlinear problems with one-sided growth conditions. Adv. Nonlinear Stud. 13 (2013), 13–53.CrossRefGoogle Scholar
12Boscaggin, A., Colasuonno, F. and Noris, B.. Multiple positive solutions for a class of p-Laplacian Neumann problems without growth conditions. ESAIM Control Optim. Calc. Var., doi: 10.1051/cocv/2017074, 2017.CrossRefGoogle Scholar
13Budd, C., Knaap, M. C. and Peletier, L. A.. Asymptotic behaviour of solutions of elliptic equations with critical exponents and Neumann boundary conditions. Proc. Roy. Soc. Edinburgh Sect. A 117 (1991), 225–250.CrossRefGoogle Scholar
14Castro, A. and Kurepa, A.. Infinitely many radially symmetric solutions to a superlinear Dirichlet problem in a ball. Proc. Amer. Math. Soc. 101 (1987), 57–64.CrossRefGoogle Scholar
15Castro, A. and Kurepa, A.. Radially symmetric solutions to a Dirichlet problem involving critical exponents. Trans. Amer. Math. Soc. 343 (1994), 907–926.CrossRefGoogle Scholar
16Castro, A. and Pardo, R.. A priori bounds for positive solutions of subcritical elliptic equations. Rev. Mat. Complut. 28 (2015), 715–731.CrossRefGoogle Scholar
17Colasuonno, F.. A p-Laplacian Neumann problem with a possibly supercritical nonlinearity. Rend. Sem. Mat. Univ. Pol. Torino 74 (2016), 113–122.Google Scholar
18Colasuonno, F. and Noris, B.. A p-Laplacian supercritical Neumann problem. Discrete Contin. Dyn. Syst. 37 (2017), 3025–3057.CrossRefGoogle Scholar
19Colasuonno, F. and Noris, B.. Radial positive solutions for p-Laplacian supercritical Neumann problems. Bruno Pini Mathematical Analysis Seminar 8 (2017), 55–72.Google Scholar
20Cowan, C. and Moameni, A.. A new variational principle, convexity and supercritical Neumann problems. Trans. Amer. Math. Soc., doi: 10.1090/tran/7250, 2017.Google Scholar
21del Pino, M. and Wei, J.. Collapsing steady states of the Keller-Segel system. Nonlinearity 19 (2006), 661–684.CrossRefGoogle Scholar
22del Pino, M., Elgueta, M. and Manásevich, R.. A homotopic deformation along p of a Leray-Schauder degree result and existence for (|u′|p − 2u′)′ + f(t, u) = 0, u(0) = u(T) = 0, p > 1. J. Differ. Equ. 80 (1989), 1–13.CrossRefGoogle Scholar
23del Pino, M. A., Manásevich, R. F. and Murúa, A. E.. Existence and multiplicity of solutions with prescribed period for a second order quasilinear ODE. Nonlinear Anal. 18 (1992), 79–92.CrossRefGoogle Scholar
24Dong, W.. A priori estimates and existence of positive solutions for a quasilinear elliptic equation. J. London Math. Soc. (2) 72 (2005), 645–662.CrossRefGoogle Scholar
25El Hachimi, A. and de Thelin, F.. Infinitely many radially symmetric solutions for a quasilinear elliptic problem in a ball. J. Differ. Equ. 128 (1996), 78–102.CrossRefGoogle Scholar
26Fabry, C. and Fayyad, D.. Periodic solutions of second order differential equations with a p-Laplacian and asymmetric nonlinearities. Rend. Istit. Mat. Univ. Trieste 24 (1994), 1992, 207–227.Google Scholar
27García Huidobro, M., Manásevich, R. and Zanolin, F.. Infinitely many solutions for a Dirichlet problem with a nonhomogeneous p-Laplacian-like operator in a ball. Adv. Differ. Equ. 2 (1997), 203–230.Google Scholar
28Gidas, B. and Spruck, J.. A priori bounds for positive solutions of nonlinear elliptic equations. Comm. Partial Differ. Equ. 6 (1981), 883–901.CrossRefGoogle Scholar
29Grossi, M. and Noris, B.. Positive constrained minimizers for supercritical problems in the ball. Proc. Amer. Math. Soc. 140 (2012), 2141–2154.CrossRefGoogle Scholar
30Lieberman, G. M.. Boundary regularity for solutions of degenerate elliptic equations. Nonlinear Anal. 12 (1988), 1203–1219.CrossRefGoogle Scholar
31Lin, C. S. and Ni, W.-M.. On the diffusion coefficient of a semilinear Neumann problem. In Calculus of variations and partial differential equations (Trento, 1986), volume 1340 of Lecture Notes in Math., pp. 160–174 (Berlin: Springer, 1988).CrossRefGoogle Scholar
32Lin, C.-S., Ni, W.-M. and Takagi, I.. Large amplitude stationary solutions to a chemotaxis system. J. Differ. Equ. 72 (1988), 1–27.CrossRefGoogle Scholar
33Lu, Y., Chen, T. and Ma, R.. On the Bonheure-Noris-Weth conjecture in the case of linearly bounded nonlinearities. Discrete Contin. Dyn. Syst. Ser. B 21 (2016), 2649–2662.CrossRefGoogle Scholar
34McKenna, P. J. and Reichel, W.. A priori bounds for semilinear equations and a new class of critical exponents for Lipschitz domains. J. Funct. Anal. 244 (2007), 220–246.CrossRefGoogle Scholar
35Montefusco, E. and Pucci, P.. Existence of radial ground states for quasilinear elliptic equations. Adv. Differ. Equ. 6 (2001), 959–986.Google Scholar
36Reichel, W. and Walter, W.. Radial solutions of equations and inequalities involving the p-Laplacian. J. Inequal. Appl. 1 (1997), 47–71.Google Scholar
37Reichel, W. and Walter, W.. Sturm-Liouville type problems for the p-Laplacian under asymptotic non-resonance conditions. J. Differ. Equ. 156 (1999), 50–70.CrossRefGoogle Scholar
38Ruiz, D.. A priori estimates and existence of positive solutions for strongly nonlinear problems. J. Differ. Equ. 199 (2004), 96–114.CrossRefGoogle Scholar
39Secchi, S.. Increasing variational solutions for a nonlinear p-Laplace equation without growth conditions. Ann. Mat. Pura Appl. (4) 191 (2012), 469–485.CrossRefGoogle Scholar
40Serra, E. and Tilli, P.. Monotonicity constraints and supercritical Neumann problems. Ann. Inst. H. Poincaré Anal. Non Linéaire 28 (2011), 63–74.CrossRefGoogle Scholar
41Wang, L., Wei, J. and Yan, S.. A Neumann problem with critical exponent in nonconvex domains and Lin-Ni's conjecture. Trans. Amer. Math. Soc. 362 (2010), 4581–4615.CrossRefGoogle Scholar
42Zou, H. H.. A priori estimates and existence for quasi-linear elliptic equations. Calc. Var. Partial Differ. Equ. 33 (2008), 417–437.CrossRefGoogle Scholar