Hostname: page-component-76fb5796d-2lccl Total loading time: 0 Render date: 2024-04-26T04:28:53.932Z Has data issue: false hasContentIssue false
  • English
  • Français

Index estimates for closed minimal submanifolds of the sphere

Part of: Classical differential geometry Global differential geometry Spectral theory and eigenvalue problems

Published online by Cambridge University Press:  17 December 2021

Diego Adauto  and
Márcio Batista Open the ORCID record for Márcio Batista [Opens in a new window]
Diego Adauto
Affiliation:
DME, Universidade do Estado do Rio Grande do Norte, Mossoró, RN, 59610-210, Brazil (diegoalves@uern.br)
Márcio Batista
Affiliation:
CPMAT-IM, Universidade Federal de Alagoas, Maceió, AL, 57072-970, Brazil (mhbs@mat.ufal.br)
Get access Rights & Permissions [Opens in a new window]

Abstract

In this paper we are interested in comparing the spectra of two elliptic operators acting on a closed minimal submanifold of the Euclidean unit sphere. Using an approach introduced by Savo in [A Savo. Index Bounds for Minimal Hypersurfaces of the Sphere. Indiana Univ. Math. J. 59 (2010), 823-837.], we are able to compare the eigenvalues of the stability operator acting on sections of the normal bundle and the Hodge Laplacian operator acting on $1$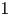-forms. As a byproduct of the technique and under a suitable hypothesis on the Ricci curvature of the submanifold we obtain that its first Betti's number is bounded from above by a multiple of the Morse index, which provide evidence for a well-known conjecture of Schoen and Marques & Neves in the setting of higher codimension.

Keywords

Closed submanifoldsEigenvaluesMorse indexEuclidean sphere

MSC classification

Primary: 35P15: Estimation of eigenvalues, upper and lower bounds
Secondary: 53C42: Immersions (minimal, prescribed curvature, tight, etc.) 53A10: Minimal surfaces, surfaces with prescribed mean curvature
Type
Research Article
Information
Proceedings of the Royal Society of Edinburgh Section A: Mathematics , Volume 152 , Issue 3 , June 2022 , pp. 802 - 816
Check for updates
Copyright
Copyright © The Author(s), 2021. Published by Cambridge University Press on behalf of The Royal Society of Edinburgh

Access options

Get access to the full version of this content by using one of the access options below. (Log in options will check for institutional or personal access. Content may require purchase if you do not have access.)

References

Aiex, N. and Hong, H. Index estimates for surfaces with constant mean curvature in 3-dimensional manifolds. Calc. Var. 60 (2021), 3. doi:10.1007/s00526-020-01855-w.CrossRefGoogle Scholar
Ambrozio, L., Carlotto, A. and Sharp, B. Comparing the Morse index and the first Betti number of minimal hypersurfaces. J. Differ. Geom. 108 (2018), 379–410.CrossRefGoogle Scholar
Cavalcante, M. P. and de Oliveira, D. F. Index estimates for free boundary constant mean curvature surfaces. Pacific J. Math. 305 (2020), 153–163.CrossRefGoogle Scholar
Cavalcante, M. P. and Oliveira, D. Lower bounds for the index of compact constant mean curvature surfaces in $\mathbb {R}^{3}$ and $\mathbb {S}^{3}$. Rev. Mat. Iberoam. 36 (2020), 195–206.CrossRefGoogle Scholar
Chern, S. S., do Carmo, M. and Kobayashi, S, Minimal submanifolds of a sphere with second fundamental form of constant length. 1970 Functional Analysis and Related Fields (Proc. Conf. for M. Stone, Univ. Chicago, Chicago, Ill., 1968) pp. 59–75 (Springer, New York).CrossRefGoogle Scholar
Davies, E. B. Spectral Theory and Differential Operators (Cambridge, Cambridge University Press, 1995).CrossRefGoogle Scholar
do Carmo, M., Ritoré, M. and Ros, A. Compact minimal hypersurfaces with index one in the real projective space. Comment. Math. Helv. 75 (2000), 247–254.CrossRefGoogle Scholar
Gromov, M. Metric structures for Riemannian and non-Riemannian spaces (Boston, MA, Birkhäuser Boston Inc, 2007). xx+585 pp.Google Scholar
Impera, D. and Rimoldi, M. Quantitative index bounds for translators via topology. Math. Z. 292 (2019), 513–527.CrossRefGoogle Scholar
Impera, D., Rimoldi, M. and Savo, A. Index and first Betti number of f-minimal hypersurfaces and self-shrinkers. Rev. Mat. Iberoam. 36 (2020), 817–840.CrossRefGoogle Scholar
Gorodski, C., Mendes, R. A. E. and Radeschi, M. Robust index bounds for minimal hypersurfaces of isoparametric submanifolds and symmetric spaces. Calc. Var. Partial Differ. Equ. 58 (2019), 118. 25 pp.CrossRefGoogle Scholar
Lawson, H. B. Jr. Complete minimal surfaces in $\mathbb {S}^{3}$. Ann. Math. (2) 92 (1970), 335–374.CrossRefGoogle Scholar
Lawson, H. B. and Simons, J.. On stable currents and their application to problems in real and complex geometry. Ann. Math. 98 (1973), 427–450.CrossRefGoogle Scholar
Leung, P. F.. Minimal submanifolds in a sphere. Math. Z. 183 (1983), 75–86.CrossRefGoogle Scholar
Ohnita, Y. Stable minimal submanifolds in compact rank one symmetric spaces. Tôhoku Math. J. 38 (1986), 199–217.CrossRefGoogle Scholar
Perdomo, O. Low index minimal hypersurfaces of spheres. Asian J. Math. 5 (2001), 741–750.CrossRefGoogle Scholar
Ros, A.. One-sided complete stable minimal surfaces. J. Differ. Geom. 74 (2006), 69–92.CrossRefGoogle Scholar
Savo, A. Index bounds for minimal hypersurfaces of the sphere. Indiana Univ. Math. J. 59 (2010), 823–837.CrossRefGoogle Scholar
Simons, J. Minimal varieties in Riemaniann manifolds. Ann. Math. (2) 88 (1968), 62–105.CrossRefGoogle Scholar
Torralbo, F. and Urbano, F. On stable compact minimal submanifolds. Proc. Am. Math. J. 142 (2014), 651–658.CrossRefGoogle Scholar