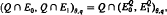Research Article
Period polynomials and congruences for Hecke algebras
-
- Published online by Cambridge University Press:
- 20 January 2009, pp. 217-224
-
- Article
-
- You have access
- Export citation
Optimal functions for a periodic uncertainty principle and multiresolution analysis*
-
- Published online by Cambridge University Press:
- 20 January 2009, pp. 225-242
-
- Article
-
- You have access
- Export citation
Interpolation restricted to decreasing functions and Lorentz spaces*
-
- Published online by Cambridge University Press:
- 20 January 2009, pp. 243-256
-
- Article
-
- You have access
- Export citation
Computing eigenvalues of Sturm-Liouville systems of Bessel type
-
- Published online by Cambridge University Press:
- 20 January 2009, pp. 257-265
-
- Article
-
- You have access
- Export citation
The “maximal” tensor product of operator spaces
-
- Published online by Cambridge University Press:
- 20 January 2009, pp. 267-284
-
- Article
-
- You have access
- Export citation
Real interpolation for divisible cones
-
- Published online by Cambridge University Press:
- 20 January 2009, pp. 285-304
-
- Article
-
- You have access
- Export citation
C*-ideals generated by polynomials
-
- Published online by Cambridge University Press:
- 20 January 2009, pp. 305-309
-
- Article
-
- You have access
- Export citation
A Bernstein-Gabber-Joseph theorem for affine algebras*
-
- Published online by Cambridge University Press:
- 20 January 2009, pp. 311-332
-
- Article
-
- You have access
- Export citation
Some natural subgroups of the Nottingham group
-
- Published online by Cambridge University Press:
- 20 January 2009, pp. 333-339
-
- Article
-
- You have access
- Export citation
Interaction of some meromorphic solutions of the KdV equation
-
- Published online by Cambridge University Press:
- 20 January 2009, pp. 341-348
-
- Article
-
- You have access
- Export citation
Positive solutions and eigenvalues of conjugate boundary value problems
-
- Published online by Cambridge University Press:
- 20 January 2009, pp. 349-374
-
- Article
-
- You have access
- Export citation
The cover associated to a (1,3)-polarized bielliptic abelian surface and its branch locus
-
- Published online by Cambridge University Press:
- 20 January 2009, pp. 375-392
-
- Article
-
- You have access
- Export citation
Action of finite groups on Rees algebras and Gorensteinness in invariant subrings
-
- Published online by Cambridge University Press:
- 20 January 2009, pp. 393-401
-
- Article
-
- You have access
- Export citation
A generalization of the Bernstein polynomials
-
- Published online by Cambridge University Press:
- 20 January 2009, pp. 403-413
-
- Article
-
- You have access
- Export citation
Asymptotic behaviour of solutions to the Becker-Döring equations
-
- Published online by Cambridge University Press:
- 20 January 2009, pp. 415-424
-
- Article
-
- You have access
- Export citation
Book Reviews
M. B. Nathanson Additive number theory: the classical bases (Graduate Texts in Mathematics Vol. 164, Springer-Verlag, Berlin-Heidelberg-New York-London-Paris-Tokyo-Hong Kong, 1996), xiv + 342 pp., 0 387 94656 X (hardback), DM78.
-
- Published online by Cambridge University Press:
- 20 January 2009, p. 425
-
- Article
-
- You have access
- Export citation
E. Spiegel and C. J. O'Donnell Incidence Algebras (Pure and Applied Mathematics Vol. 206, Marcel Dekker, 1997), ix + 335 pp., 0 8247 0036 8, US$125.
-
- Published online by Cambridge University Press:
- 20 January 2009, p. 426
-
- Article
-
- You have access
- Export citation
E. Kissin and V. Shulman Representations on Krein spaces and derivations of C*-algebras (Pitman Monographs and Surveys in Pure and Applied Mathematics Vol. 89, Longman, 1997), iii + 602 pp., 0 582 23157 4, £85.
-
- Published online by Cambridge University Press:
- 20 January 2009, pp. 426-427
-
- Article
-
- You have access
- Export citation
K. Ollerenshaw and D. Brée Most-perfect pandiagonal magic squares: their construction and enumeration (Institute of Mathematics and its Applications, Southend-on-Sea, 1998), xiii + 152 pp., 0 905091 06 X, £19.50.
-
- Published online by Cambridge University Press:
- 20 January 2009, pp. 427-428
-
- Article
-
- You have access
- Export citation
K. Ciesielski Set theory for the working mathematician (London Mathematical Society Student Texts Vol. 39, Cambridge University Press, 1997), xi + 236 pp.; 0 521 59465 0 (paperback), £13.95 (US$19.95); 0521 59441 3 (hardback), £37.50 (US$59.95).
-
- Published online by Cambridge University Press:
- 20 January 2009, p. 429
-
- Article
-
- You have access
- Export citation