Hostname: page-component-84b7d79bbc-5lx2p Total loading time: 0 Render date: 2024-07-27T14:17:38.987Z Has data issue: false hasContentIssue false
  • English
  • Français

A Matrix Form of Taylor's Theorem

Published online by Cambridge University Press:  20 January 2009

H. W. Turnbull
Rights & Permissions [Opens in a new window]

Extract

Core share and HTML view are not available for this content. However, as you have access to this content, a full PDF is available via the ‘Save PDF’ action button.

The following pages continue a line of enquiry begun in a work On Differentiating a Matrix, (Proceedings of the Edinburgh Mathematical Society (2) 1 (1927), 111-128), which arose out of the Cayley operator 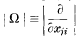, where xij is the ijth element of a square matrix [xij] of order n, and all n2 elements are taken as independent variables. The present work follows up the implications of Theorem III in the original, which stated that

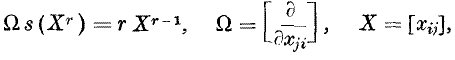
where s (Xr) is the sum of the principal diagonal elements in the matrix Xr. This is now written ΩsXr = rXr – 1 and Ωs is taken as a fundamental operator analogous to ordinary differentiation, but applicable to matrices of any finite order n.

Type
Research Article
Information
Proceedings of the Edinburgh Mathematical Society , Volume 2 , Issue 1 , January 1930 , pp. 33 - 54
Copyright
Copyright © Edinburgh Mathematical Society 1930

References

page 36 note 1 Of. Proc. Edinburgh Math. Soc. (2) 1 (1928), 111–128 (128).CrossRefGoogle Scholar

page 41 note 1 Cullis, . Matrices and Determinoids, Vol. 3 (Cambridge, 1925) 483.Google Scholar

page 41 note 2 Proe. Edin. Math. Soc., loc. cit. 125.Google Scholar

page 42 note 1 CfWeierstrass, , Monatsh. d. Berliner Acad. (1858), p. 214.Google ScholarFrobenius, , Orelle 84 (1878), 17, where a similar formula occurs, reached from another angle.Google Scholar

page 52 note 1 Proc. Edinburgh Math. Soc., loc. cit. p. 128.Google Scholar