Hostname: page-component-76fb5796d-9pm4c Total loading time: 0 Render date: 2024-04-28T14:46:10.423Z Has data issue: false hasContentIssue false
  • English
  • Français

Differential properties of some dense subalgebras of C*-algebras

Published online by Cambridge University Press:  20 January 2009

E. Kissin  and
V. S. Shulman
E. Kissin
Affiliation:
School of Mathematical Sciences, University of North London, Holloway, London N7 8DB, England
V. S. Shulman
Affiliation:
Department of Mathematics, Polytechnic University of Vologda, Vologda, Russia
Rights & Permissions [Opens in a new window]

Abstract

Core share and HTML view are not available for this content. However, as you have access to this content, a full PDF is available via the ‘Save PDF’ action button.

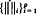The paper studies some classes of dense *-subalgebras B of C*-algebras A whose properties are close to the properties of the algebras of differentiable functions. In terms of a set of norms on B it defines 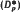-subalgebras of A and establishes that they are locally normal Q*-subalgebras. If x = x* ∈ B and f(t) is a function on Sp(x), some sufficient conditions are given for f(x) to belong to B. For p = 1, in particular, it is shown that 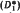-subalgebras are closed under C∞-calculus. If δ is a closed derivation of A, the algebras D(δp) are 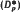-subalgebras of A. In the case when δ is a generator of a one-parameter semigroup of automorphisms of A, it is proved that, in fact, D(δp) are 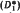-subalgebras. The paper also characterizes those Banach *-algebras which are isomorphic to 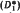subalgebras of C*-algebras.

Type
Research Article
Information
Proceedings of the Edinburgh Mathematical Society , Volume 37 , Issue 3 , October 1994 , pp. 399 - 422
Copyright
Copyright © Edinburgh Mathematical Society 1994

References

REFERENCES

1.Blackadar, B. and Cuntz, J., Differential Banach algebra norms and smooth subalgebras of C*-algebras, J. Operator Theory 26 (1991), 255–282.Google Scholar
2.Bonsal, F. F. and Duncan, J., Complete normed algebras (Springer-Verlag, 1973).CrossRefGoogle Scholar
3.Bratteli, O., Elliott, G. A. and Jorgensen, P. E. T., Decomposition of unbounded derivations into invariant and approximately inner parts, J. Reine Angew. Math. 346 (1984), 166–193.Google Scholar
4.Bratteli, O. and Robinson, D. W., Unbounded derivations of C*-algebras, I&II Comm. Math. Phys. 42 (1975), 255–268 and 46 (1976), 11–30.Google Scholar
5.Bratteli, O. and Robinson, D. W., Operator algebras and Quantum Statistical Mechanics (Springer-Verlag, 1979).CrossRefGoogle Scholar
6.Dunford, N. and Schwartz, J. T., Linear Operators, I&II (Interscience Publ., New York, London, 1963).Google Scholar
7.Hardy, G. H., Littlewood, J. E. and Polya, G., Inequalities (Cambridge Unviersity Press, 1934).Google Scholar
8.Kissin, E. and Shulman, V. S., Dense Q-subalgebras of Banach and C*-algebras and unbounded derivations of Banach and C*-algebras, Proc. Edinburgh Math. Soc., 36 (1993), 261–276.CrossRefGoogle Scholar
9.Longo, R., Automatic relative boundedness of derivations in C*-algebras, J. Funct. Anal. 34 (1979), 21–28.Google Scholar
10.Mciintosh, A., Functions and derivations of C*-algebras, J. Funct. Anal. 30 (1978), 264–275.CrossRefGoogle Scholar
11.Naimark, M. A., Normed algebras (Wolters-Noordhoff Publishing, Groningen, Netherlands, 1972).Google Scholar
12.Powers, R. T., A remark on the domain of an unbounded derivation of a C*-algebra, J. Funct. Anal. 18 (1975), 85–95.CrossRefGoogle Scholar
13.Reiter, H., L1-algebras and Segal algebras (Lecture Notes in Mathematics 231, Springer-Verlag, 1971).CrossRefGoogle Scholar
14.Sakai, S., Operator algebras in dynamical systems (Cambridge University Press, Cambridge, 1991).Google Scholar