Hostname: page-component-848d4c4894-xfwgj Total loading time: 0 Render date: 2024-07-01T21:07:20.904Z Has data issue: false hasContentIssue false
  • English
  • Français

Almost diagonal systems in asymptotic integration

Published online by Cambridge University Press:  20 January 2009

H. Gingold
H. Gingold
Affiliation:
Department of MathematicsWest Virginia UniversityMorgantown WV 26506
Rights & Permissions [Opens in a new window]

Extract

Core share and HTML view are not available for this content. However, as you have access to this content, a full PDF is available via the ‘Save PDF’ action button.

Consider the ordinary linear matrix differential system

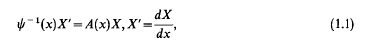
ψ(x) is a scalar mapping, X and A(x) are n by n matrices. Both belong to C1([a,∞)) for some integer l. The stability and asymptotic behaviour of its solutions have been subject to much investigation. See Bellman [2], Levinson [24], Hartman and Wintner [20], Devinatz [9], Fedoryuk [11], Harris and Lutz [16,17,18] and Cassell [30]. The special interest in eigenvalue problems and in the deficiency index problem stimulated a continued interest in asymptotic integration. See e.g. Naimark [36], Eastham and Grundniewicz [10] and [8,9]. Harris and Lutz [16,17,18] succeeded in explaining how to derive many known theorems in asymptotic integration by repeatedly using certain “(1 + Q)” linear transformations.

Type
Research Article
Information
Proceedings of the Edinburgh Mathematical Society , Volume 28 , Issue 2 , June 1985 , pp. 143 - 158
Copyright
Copyright © Edinburgh Mathematical Society 1985

References

REFERENCES

1.Atkinson, F. V., The asymptotic solution of second order differential equations, Ann. Mat. Pura Appl. 37 1954., 347–378.CrossRefGoogle Scholar
2.Bellman, R., The boundedness of solutions of linear differential equations, Duke Math. Journal 14 1948., 111–126.Google Scholar
3.Bellman, R., Stability Theory of Differential Equations McGraw-Hill, New York, 1953.Google Scholar
4.Coddington, E. A. and Levinson, N., Theory of Ordinary Differential Equations (McGraw-Hill, New York, 1955).Google Scholar
5.Coppel, W., Stability and Asymptotic Behavior of Differential Equations (Heath, Boston, 1965).Google Scholar
6.Coppel, W. A., Dichotomies and reducibility, J. Differential Equations 3 1967., 500–521.CrossRefGoogle Scholar
7.Devinatz, A., An asymptotic theory for systems of linear differential equations, Trans. Amer. Math. Soc. 160 1971., 353–363.Google Scholar
8.Devinatz, A., The deficiency index of a certain class of ordinary self-adjoint differential operators, Advances in Math. 8 1972., 434–473.CrossRefGoogle Scholar
9.Devinatz, A., The deficiency index of ordinary self-adjoint differential operators, Pacific J. Math. 16 1966., 243–257.CrossRefGoogle Scholar
10.Eastham, M. S. P. and Grundniewicz, C. G. M., Asymptotic theory and deficiency indices for high-order self-adjoint differential equations, J. London Math. Soc. 24, 1981., 255–271.CrossRefGoogle Scholar
11.Fedoryuk, M., Asymptotic methods in the theory of one-dimensional singular differential operators, Trans. Moskow Math. Soc. 1966., 33–386.Google Scholar
12.Gingold, H., A method of global blockdiagonalization for matrix-valued functions, SIAM, J. Math. Anal. 9 1978., 1076–1082.CrossRefGoogle Scholar
13.Gingold, H. and Hsieh, P. F., Global simplification of a singularly perturbed almost diagonal system, SIAM. J. Math. Anal, (to appear).Google Scholar
14.Gingold, H. and Hsieh, P. F., On global simplification of a singularly perturbed system of linear ordinary differential equations, Funkcial. Ekvac. 25 1982., 269–281.Google Scholar
15.Gingold, H., Asymptotic decompositions on an entire interval for two by two first order linear ordinary differential systems with multi-coalescing turning points. (Preprint WVU).Google Scholar
16.Harris, W. A. JR., and Lutz, D. A., On the asymptotic integration of linear differential systems, J. Math. Anal. Appl. 48 1974., 1–16.Google Scholar
17.Harris, W. A. JR., and Lutz, D. A., Asymptotic integration of adiabatic oscillators, J. Math. Anal. Appl. 51 1975., 76–93.Google Scholar
18.Harris, W. A. and Lutz, D. A., A unified theory of asymptotic integration, J. Math. Anal. Appl. 57 1977., 577–586.CrossRefGoogle Scholar
19.Hartman, P., On a class of perturbations of the harmonic oscillator, Proc. Amer. Math. Soc. 19 1968., 533–540.Google Scholar
20.Hartman, P. and Wintner, A., Asymptotic integration of linear differential equations, Amer. J. Math. 77 1955., 45–86, 932.Google Scholar
21.Hille, E., Lectures on Ordinary Differential Equations (Addison-Wesley, Reading, MA, 1969).Google Scholar
22.Kato, T., Notes on perturbation theory, Bull. Amer. Math. Soc. 61 1955., 164.Google Scholar
23.Kelman, R. B. and Madsen, N. K., Stable motions of the linear adiabatic oscillator, J. Math. Anal. Appl. 21 1968., 458–465.Google Scholar
24.Levinson, N., The asymptotic nature of solutions of linear differential equations, Duke Math. J. 15 1948., 111–126.CrossRefGoogle Scholar
25.Riesz, F. and Sz-Nagy, B., Functional Analysis (Frederick Ungar, New York, 1955).Google Scholar
26.Rudin, W., Real and Complex Analysis (McGraw-Hill, New York, 1966)Google Scholar
27.Rudin, W., Function Theory in Polydiscs (W. A. Benjamin, Inc., New York, 1969).Google Scholar
28.Wasow, , On turning point problems for systems with almost diagonal coefficient matrix, Funkcial. Ekvak. 8 1966., 143–171.Google Scholar
29.Wasow, W., Asymptotic expansions for ordinary differential equations (Interscience, New York, N.Y. 1965).Google Scholar
30.Cassell, J. S., The asymptotic integration of some oscillatory differential equations, Quart. J. Math. Oxford (2) 33 1982., 281–296.CrossRefGoogle Scholar
31.Gingold, H., Simplification of linear homogeneous differential equations with moving singularities. Funkcial. Ekvac. 19, 1976., 203–225.Google Scholar
32.Gingold, H., Dichotomies and moving singularities, simplifications of linear systems, Rend. Circ. Matem-di-Palermo 29 1980., 61–78.Google Scholar
33.Gingold, H., Introduction to differential equations with moving singularities, Rocky Mount. J. Math. 6 1976., 571–574.CrossRefGoogle Scholar
34.Gingold, H. and Rosenblat, S., Differential equations with moving singularities, SIAM. J. Math. Anal. 7 1976., 942–957.CrossRefGoogle Scholar
35.Gingold, H., On the location of zeros of oscillatory solutions of y(n) = c(x)y, Pacific J. Math. 119 (1985).CrossRefGoogle Scholar
36.Naimark, M. A., Linear Differential Operators, Part 1 (Translated by Dawson, E. R., Queen's College, Dundee, Frederich Ungar Publishing Co., Inc. 1967).Google Scholar
37.Pugachev, V. S., On asymptotic representations of the integrals of systems of ordinary differential equations containing a parameter, Mat. Sb. 15 (57) 1954., 13–54 (Russ.).Google Scholar