I. INTRODUCTION
The maximum-entropy method (MEM) enables us to extract the maximum amount of information from observed diffraction data, without any assumptions based on models (Collins, Reference Collins1982). In the so-called MEM/Rietveld analysis (Takata et al., Reference Takata, Nishibori and Sakata2001; Takata, Reference Takata2008) of powder diffraction data, “observed” structure factors F obs(hj) = F obs(Rietveld), where hj denotes indices, hkl, of reflection j, are estimated on the basis of the result of Rietveld analysis (Rietveld, Reference Rietveld1969) and analysed by MEM. However, F obs(Rietveld)'s are doubly biased toward structure factors, F(hj), calculated from structural parameters refined in the Rietveld analysis because both phases and calculated profiles used for the intensity partitioning of overlapped reflections are derived from the structural model (McCusker et al., Reference McCusker, Von Dreele, Cox, Louër and Scardi1999). Though overlapped reflections may be grouped together (Kumazawa et al., Reference Kumazawa, Kubota, Takata and Sakata1993), MEM analysis from powder diffraction data still suffers from the partial loss of structural information because of the overlap of reflections, which is marked in compounds with lower symmetry and in powder diffraction data of relatively low resolution.
MEM-based pattern fitting (MPF) was proposed to address such a problem and determine more reliable electron- or nuclear-density distributions (Izumi et al., Reference Izumi, Kumazawa, Ikeda, Hu, Yamamoto and Oikawa2001; Izumi and Dilanian, Reference Izumi, Dilanian and Pandalai2002; Izumi Reference Izumi2004). In MPF, MEM analyses and whole-pattern fitting (w.p.f.) are alternately repeated (REMEDY cycles) to minimize the bias in favor of the structural model. MPF is particularly effective in representing highly disordered atomic arrangements and anharmonic atomic displacement. For example, Yashima (Reference Yashima2009) has successfully applied MPF to a variety of ionic conductors and clarified conduction paths of mobile ions at high temperatures.
While MEM itself is model free, it is still not free from errors and artifacts. One of the errors is caused by a series-termination effect arising from the availability of only a limited number of reflections (Jauch, Reference Jauch1994; de Vries et al., Reference de Vries, Briels and Feil1996; Palatinus and van Smaalen, Reference Palatinus and van Smaalen2002), although this effect is much less significant in MEM than in Fourier synthesis. On the analysis of X-ray diffraction data, MEM also tends to give large residual errors for some low-Q reflections that contribute most significantly to information entropy, S. Such a tendency of MEM often generates artifacts in calculated electron densities even if accurate standard uncertainties, σ(hj), of F obs(hj)'s are obtainable (de Vries et al., Reference de Vries, Briels and Feil1994; Palatinus and van Smaalen, Reference Palatinus and van Smaalen2002). This problem can be partly solved either by changing a weighting scheme for the F constraint (de Vries et al., Reference de Vries, Briels and Feil1994; Palatinus and van Smaalen, Reference Palatinus and van Smaalen2002) or by imposing a constraint based on higher-order moments of normalized residuals of structure factors, ΔF j = |F obs(hj) − F(hj)|/σ(hj), rather than their second-order moment (Palatinus and van Smaalen, Reference Palatinus and van Smaalen2002).
For MPF analysis, we have been carrying out w.p.f. and MEM analysis with RIETAN-FP (Izumi and Momma, Reference Izumi and Momma2007) and PRIMA (Izumi and Dilanian, Reference Izumi, Dilanian and Pandalai2002), respectively. However, PRIMA lacks in the features of changing weights in the F constraint and the constraint allowing higher-order moments. Though PRIMA is quite efficient in relatively small-scale problems thanks to full utilization of symmetry operations and exhaustive optimization of its code, the use of the discrete Fourier transform (DFT) in PRIMA limits its scalability when processing large-scale problems. In such cases, the use of the fast Fourier transform (FFT) (Tanaka et al., Reference Tanaka, Takata, Nishibori, Kato, Iishi and Sakata2002; van Smaalen et al., Reference van Smaalen, Palatinus and Schneider2003) accelerates MEM analysis considerably. Recent advances in multi-core CPUs have also prompted us to introduce multi-threaded parallel processing in MEM calculations.
The so-called Cambridge algorithm (Skilling and Bryan, Reference Skilling and Bryan1984; Gull and Skilling, Reference Gull and Skilling1999) for MEM analysis is another longed-for-feature, which may be useful in structure refinement from powder diffraction data.
To achieve the above improvements, we have recently developed a new generation of MEM-analysis program Dysnomia (Izumi and Momma, Reference Izumi and Momma2011; Momma and Izumi, Reference Momma and Izumi2011a), which is a successor to PRIMA. The combination of RIETAN-FP and Dysnomia enables us to integrate the new features with the MPF technique. The present study aims at testing the performance and effectiveness of the new features of Dysnomia in MPF analyses of three different types of compounds from their X-ray powder diffraction data.
II. EXPERIMENTAL
Crystal structures of three compounds, taurine, Cu2CO3(OH)2, and Sr9In(PO4)7, were analyzed as test cases for MPF analyses of organic, inorganic, and disordered structures, respectively.
Taurine (2-aminoethanesulfonic acid, C2H7NO3S) is one of a few naturally occurring sulfonic acids, containing a zwitterion (H3N+–(CH2)2–SO3−). A taurine reagent (Sigma-Aldrich, Japan) was dissolved in purified water and recrystallized rapidly by evaporation to dryness, which yielded a fine powder sample with crystallite sizes of less than 10 µm.
Cu2CO3(OH)2 is a natural carbonate mineral, malachite. A sample of malachite, which occurred in the Democratic Republic of the Congo as nearly pure aggregates of fine crystals, was ground in ethanol with an agate mortar for a few minutes to produce a powder.
X-ray powder diffraction data of taurine and Cu2CO3(OH)2 were measured at room temperature on a D8 ADVANCE Vario1 powder diffractometer (Bruker AXS) in modified Debye–Scherrer geometry with Cu Kα 1 radiation from a Ge (111) incident-beam monochromator. A continuous scan mode was adopted with a one-dimensional position sensitive detector, VANTEC-1 (Bruker AXS), with a solid angle of 6°. Each sample was sealed in a borosilicate capillary tube with an inside diameter of 0.7 mm. Intensity data up to 2θ = 100° (sinθ/λ = 0.4972) for taurine and 2θ = 115.489° (sinθ/λ = 0.5489) for Cu2CO3(OH)2 were measured at a step interval of 0.017 438°. Scanning times were 13 796 s per step for taurine and 11 206 s per step for Cu2CO3(OH)2.
Sr9In(PO4)7 is a whitlockite-like phosphate reported by Belik et al. (Reference Belik, Izumi, Ikeda, Okui, Malakho, Morozov and Lazoryak2002). In the present work, synchrotron X-ray powder diffraction data of Sr9In(PO4)7 measured on a powder diffractometer at BL15XU in SPring-8 (Belik et al., Reference Belik, Izumi, Ikeda, Okui, Malakho, Morozov and Lazoryak2002) were reanalyzed by Rietveld and MPF methods from diffraction data up to sinθ/λ = 0.6245.
III. PROCEDURES OF STRUCTURE REFINEMENTS
RIETAN-FP (Izumi and Momma, Reference Izumi and Momma2007) was used for both Rietveld analyses and w.p.f. of the three samples. Crystal data of taurine (Sutherland and Young, Reference Sutherland and Young1963) were used as initial unit-cell and structural parameters whereas those of Cu2CO3(OH)2 (Zigan et al., Reference Zigan, Joswig, Schuster and Mason1977) and Sr9In(PO4)7 (Belik et al., Reference Belik, Izumi, Ikeda, Okui, Malakho, Morozov and Lazoryak2002) reported in the literature were converted by STRUCTURE TIDY (Gelato and Parthé, Reference Gelato and Parthé1987) into those in conformity with standard settings of monoclinic space groups, i.e. from P21/a to P21/c for Cu2CO3(OH)2 and from I2/a to C2/c for Sr9In(PO4)7.
A modified split pseudo-Voigt profile function was used for pattern fitting of taurine and Sr9In(PO4)7 with partial profile relaxation (Izumi, Reference Izumi2003) applied to some reflections in low-angle regions. In the case of Cu2CO3(OH)2, profile broadening of reflections proved to be very anisotropic and could not be adequately modelled by profile functions with a single axis of anisotropic microstrain broadening. Hence, the pseudo-Voigt function of Thompson et al. (Reference Thompson, Cox and Hastings1987) was used in combination with an anisotropic microstrain broadening model proposed by Stephens (Reference Stephens1999), which considerably decreased a reliability (R) index, R wp.
Two types of MEM algorithms are implemented in Dysnomia (Izumi and Momma, Reference Izumi and Momma2011; Momma and Izumi, Reference Momma and Izumi2011a): 0th-order single pixel approximation (ZSPA) (Kumazawa et al., Reference Kumazawa, Takata and Sakata1995; Izumi and Dilanian, Reference Izumi, Dilanian and Pandalai2002) and a variant of the Cambridge algorithm (Skilling and Bryan, Reference Skilling and Bryan1984; Gull and Skilling, Reference Gull and Skilling1999). Dysnomia has an advantage that the latter methodology was achieved without any commercial program library such as MemSys (Gull and Skilling, Reference Gull and Skilling1999).
Dysnomia further adopts a linear combination of generalized F constraints (Palatinus and van Smaalen, Reference Palatinus and van Smaalen2002):
and
 $$C_{Fn}=\displaystyle{1 \over {N_F m_n }}\sum\limits_{\,j=1}^{N_F } {w_j \left({\Delta F_j } \right)^n } - C_{{\rm w}n}=0$$
$$C_{Fn}=\displaystyle{1 \over {N_F m_n }}\sum\limits_{\,j=1}^{N_F } {w_j \left({\Delta F_j } \right)^n } - C_{{\rm w}n}=0$$where n = 2, 4, 6,…, with n = 2 corresponding to the conventional F constraint, λ n is the relative weight for each of C Fn, N F is the number of reflections, m n is the even nth-order central moment of normal (Gaussian) distribution, w j is the weighting factor, and C wn is the criterion for convergence (Izumi and Momma, Reference Izumi and Momma2011).
In addition, Dysnomia allows us to impose static weighting factors, w j, on σ(hj)'s on the basis of the lattice-plane spacing, d j (de Vries et al., Reference de Vries, Briels and Feil1994), or arbitrary weighting factors (Momma and Izumi, Reference Momma and Izumi2011a). Separation of w j from σ(hj) makes it easier to separate the effect of weighting from differences in the overall scale of σ(hj).
Because uniform prior densities are widely used in MEM analyses from powder diffraction data, the present study mainly focuses on MEM analyses using uniform ones. Results of MEM analyses using uniform and non-uniform prior densities are also compared. Electron densities of independent spherical-atom models (procrystal electron densities) were used as non-uniform prior densities, which were computed from atomic scattering factors and final structural parameters obtained in Rietveld analysis. In the case of taurine, PRIMA was also used for MEM analyses for comparison. A utility called MPF_multi was run for automatic MPF analyses, where σ(hj)'s are adjusted by changing a regulatory parameter E as specified in an input file, *.prf, of Dysnomia or PRIMA (Izumi and Momma, Reference Izumi and Momma2011). VESTA (Momma and Izumi, Reference Momma and Izumi2011b) was used to calculate the prior densities and to visualize the resulting electron-density distributions.
All the Rietveld and MPF analyses were carried out on Windows 7 using a PC equipped with an Intel® Core i7 975 processor (3.33 GHz, 4 processing cores and 8 threads) and 12 GB of RAM.
IV. RESULTS AND DISCUSSION
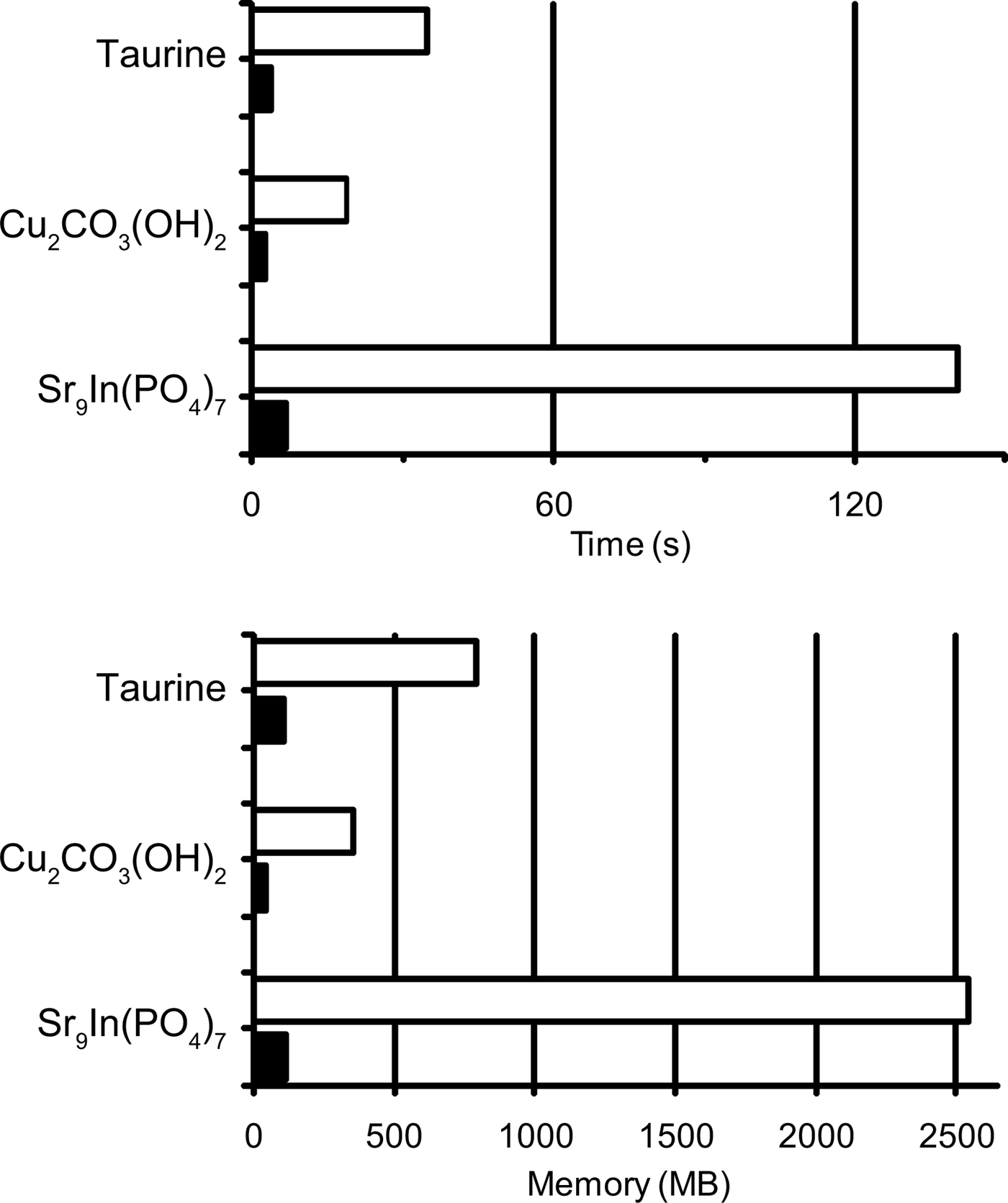
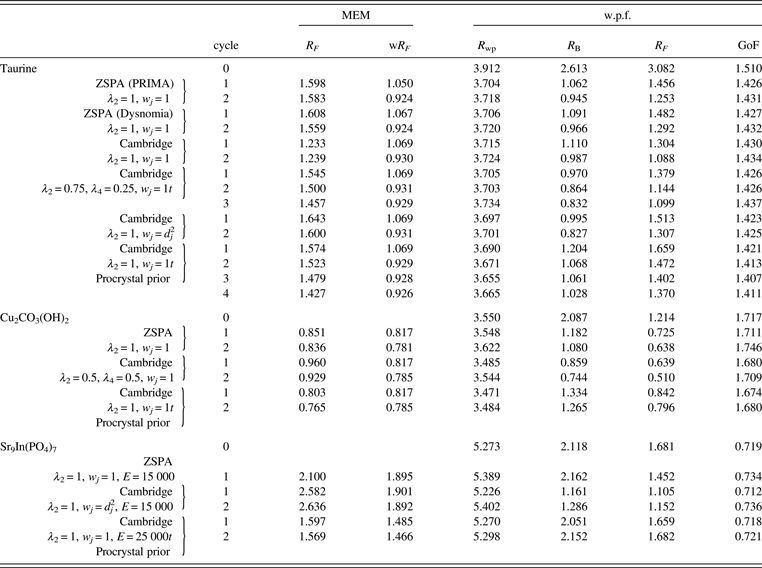
Table I lists the results of Rietveld and MPF analyses of taurine, Cu2CO3(OH)2, and Sr9In(PO4)7. Data for cycle 0 in Table I correspond to those in the final Rietveld analyses. MPF analyses were carried out with several different conditions of MEM analyses. Because Dysnomia automatically determines the convergence criterion to satisfy the conventional F constraint (Momma and Izumi, Reference Momma and Izumi2011a), MEM analyses with the same E value give the same weighted R index, wR F, regardless of the type of constraints and weighting. On the other hand, R indices in w.p.f. are appropriate measures of the capability of MEM in obtaining improved F(hj)'s from model-biased F obs(hj)'s. With Dysnomia, memory usage when dealing with large-scaled data was much lesser owing to the use of FFT than with PRIMA, and parallel processing by the multi-core CPU in Dysnomia shortened computation time dramatically (Figure 1).

Figure 1. Memory usage and elapsed times in MEM analyses of taurine, Cu2CO3(OH)2, and Sr9In(PO4)7 with PRIMA (white bars) and Dysnomia (black bars).
Table I. R indices (%) obtained in the MPF analyses of taurine, Cu2CO3(OH)2, and Sr9In(PO4)7.

A. Taurine
The asymmetric unit of taurine, which is monoclinic with space group P21/c, contains 14 atoms including 7 H atoms (Sutherland and Young, Reference Sutherland and Young1963). In Rietveld analysis of taurine, all the isotropic atomic displacement parameters, U iso, for O sites were constrained to be equal to each other. Simple approximations of U iso(C1) = U iso(C2) and U iso(H1) = U iso(Hn) with n = 2–7 were applied to the U iso parameters of the C and H sites, respectively. In addition, restraints were imposed on bond lengths and angles on the basis of the molecular geometry of taurine reported by Sutherland and Young (Reference Sutherland and Young1963). Degrees of the restraints gradually decreased with progress in structure refinement.
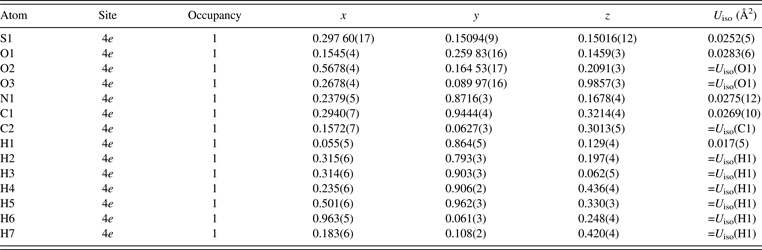
Table II lists refined structural parameters, and Figure 2 shows observed, calculated, and difference plots obtained by the Rietveld analysis of taurine. Final R indices in the Rietveld analysis were sufficiently low: R wp = 3.91% (GoF = R wp/R e = 1.510), R B = 2.61%, and R F = 3.08%. Refined unit-cell parameters were a = 5.282 07(5) Å, b = 11.642 50(11) Å, c = 7.924 13(8) Å, and β = 94.0968(5)°. The length of hydrogen bonding between an H atom in the H3N+ group and an O atom in an adjacent molecule was estimated at 1.76(4) Å. Subsequent REMEDY cycles with PRIMA lowered R wp, R B, and R F to 3.70 (GoF = 1.426), 1.06, and 1.46%, respectively (Table I). Decreases in R indices in the first REMEDY cycle were particularly remarkable. Substantial improvements in the R indices during the MPF analyses are ascribable to the ability of MEM to represent anisotropic atomic displacement and covalent bonding, which were both neglected in the Rietveld analysis, by electron densities in the unit cell.

Figure 2. Observed (cross marks), calculated (upper solid line), and difference (lower solid line) patterns obtained by the Rietveld refinement of taurine. Vertical tick marks denote the peak positions of possible Bragg reflections. The inset shows magnified patterns from 40 to 100° 2θ.
Table II. Structural parameters obtained in the Rietveld analysis of taurine.

Because the distribution of ΔF j's was nearly Gaussian, neither high-order F constraints nor weighting was necessary. As expected, the ZSPA algorithm implemented in Dysnomia gave nearly the same results as with PRIMA. On the other hand, higher order moments of the resulting ΔF j's were found to be significantly larger than those of Gaussian distribution when the Cambridge algorithm was used. R indices during REMEDY cycles were also worse than those obtained with the ZSPA algorithm because ΔF j's of a few strong low-Q reflections were extremely large whereas those of high-Q reflections were very small. The Cambridge algorithm gives solutions close to the true maximum-entropy (MaxEnt) conditions, while the ZSPA algorithm affords solutions far from the MaxEnt conditions (van Smaalen et al., Reference van Smaalen, Palatinus and Schneider2003). Therefore, overestimation of ΔF j's for a few strong low-Q reflections with the Cambridge algorithm is an intrinsic tendency of MEM analysis from X-ray diffraction data (Jauch, Reference Jauch1994). The use of multiple F constraints or static weighting on the basis of d j2 in combination with the Cambridge algorithm corrected such a tendency, giving higher entropy electron densities with R indices comparable to those obtained with the ZSPA algorithm (Table I).
Figure 3(a) shows electron-density distributions determined by the Cambridge algorithm with w j = d j2. Highly covalent C–C, C–N, and S–O bonds are clearly visible in this figure. In addition, when compared with procrystal electron densities calculated from atomic scattering factors and the structural parameters refined in the Rietveld analysis, anisotropic atomic displacements were revealed by doughnut-shaped difference electron densities [Figure 3(b)]. Orientations of the doughnut-shaped difference electron densities are consistent with anisotropic atomic displacements reported in a single-crystal X-ray diffraction study (Görbitz et al., Reference Görbitz, Prydz and Ugland2000). When the results with the Cambridge and unweighted ZSPA algorithms are compared, the ZSPA algorithm gave higher peaks of electron densities at the centers of atoms whereas the Cambridge algorithm assigned more electrons to covalent bonds [Figure 3(c)].

Figure 3. (a) Electron densities determined from the diffraction data of taurine by MPF using the Cambridge algorithm with w j = d j2: ρ(Cambridge). (b) Difference electron densities, ρ(Cambridge)'s minus model electron densities, ρ(procrystal), calculated from atomic scattering factors. (c) Difference electron densities, ρ(Cambridge) − ρ(ZSPA). Equi-density levels are: (a) 1 Å−3, (b) ±0.5 Å−3, and (c) ±0.125 Å−3. (d) and (e) 2D slices of difference electron densities at a position of three oxygen atoms of sulfo group: (d) ρ(Cambridge) − ρ(procrystal), and (e) electron densities calculated by MPF using the Cambridge algorithm with procrystal prior densities, ρ(Cambridge, procrystal) − ρ(procrystal). Anisotropic atomic displacements of oxygen atoms are visualized in (d) by positive difference densities distributed nearly perpendicular to S − O bonds.
On the use of procrystal prior densities in MEM analyses with the Cambridge algorithm, R indices obtained in MPF analyses were slightly better than those in MPF analyses using uniform prior densities. However, the resultant electron densities were very close to the procrystal prior densities, and no anisotropic atomic displacements could be recognized in difference electron densities when compared with procrystal prior ones [Figures 3(d) and 3(e)].
B. Cu2CO3(OH)2
Cu2CO3(OH)2 contains two kinds of edge-sharing CuO6 octahedra, which are elongated perpendicular to a ![]() $\lpar 10\bar 2\rpar $ plane because of the Jahn–Teller effect, connected with carbonate ions as well as hydrogen bonds.
$\lpar 10\bar 2\rpar $ plane because of the Jahn–Teller effect, connected with carbonate ions as well as hydrogen bonds.
For OH sites, two types of structural models were tested; that is, one with hydrogen atoms fixed at positions reported by Zigan et al. (Reference Zigan, Joswig, Schuster and Mason1977), and the other with O and H sites grouped as a virtual chemical species OH. The resulting structural parameters other than hydrogen atoms were mostly consistent with each other, but the latter model gave slightly lower R indices. Therefore, the virtual OH atom model was finally adopted in the Rietveld analysis. In the final Rietveld analysis, U iso's were constrained as follows: U iso(O1) = U iso(O2) = U iso(O3) and U iso(OH4) = U iso(OH5).
In general, refinement of anisotropic atomic displacement parameters, U ij, from X-ray powder diffraction data is rather difficult. Nevertheless, refinement of U ij's of two Cu sites appreciably lowered R wp from 3.686 to 3.550%, which is mainly ascribable to marked thermal vibrations of Cu atoms nearly in parallel with the scattering vector of the strongest ![]() $10\bar 2$ reflection. Angles between the longest principal axes of the Cu sites and
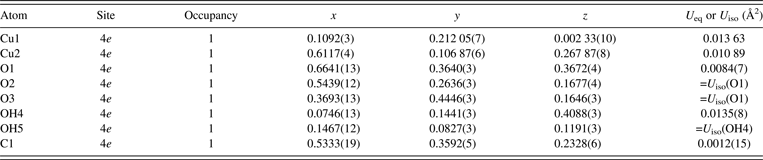
$10\bar 2$ reflection. Angles between the longest principal axes of the Cu sites and ![]() $\lsqb 10\bar 2\rsqb ^{\ast} $ are 174° for Cu1 and 173° for Cu2. Owing to correlations between atomic displacement parameters, the refinement of U ij's of the Cu sites improved the U iso value of the C1 site from −0.0008(15) Å2, which is physically unacceptable, to a more reasonable value of 0.0012(15) Å2.
$\lsqb 10\bar 2\rsqb ^{\ast} $ are 174° for Cu1 and 173° for Cu2. Owing to correlations between atomic displacement parameters, the refinement of U ij's of the Cu sites improved the U iso value of the C1 site from −0.0008(15) Å2, which is physically unacceptable, to a more reasonable value of 0.0012(15) Å2.
Tables III and IV list crystal data resulting from the final Rietveld analysis, which gave observed, calculated, and difference patterns plotted in Figure 4 and fairly low R indices: R wp = 3.550% (GoF = 1.717), R B = 2.09%, and R F = 1.21%. Refined unit-cell parameters were a = 3.244 07(3) Å, b = 11.953 22(9) Å, c = 9.492 87(8) Å, and β = 98.6697(6)°. The longest principal axes of displacement ellipsoids for the Cu sites were roughly parallel to the two axial Cu − O bonds in each CuO6 octahedron, which is physically reasonable and consistent with crystal data obtained in the previous neutron diffraction study (Zigan et al., Reference Zigan, Joswig, Schuster and Mason1977).

Figure 4. Observed, calculated, and difference patterns obtained by the Rietveld refinement for Cu2CO3(OH)2. The inset shows magnified patterns from 40 to 115.5° 2θ.
Table III. Structural parameters obtained in the Rietveld analysis of Cu2CO3(OH)2.

Table IV. Anisotropic atomic displacement parameters, U ij, of the Cu sites obtained in the Rietveld analysis of Cu2CO3(OH)2.

Subsequent MPF analysis with the ZSPA algorithm slightly lowered R wp to 3.548% (GoF = 1.711). However, the central moments of ∆F j with the order of four or higher were found to be significantly larger than those expected for the Gaussian distribution of errors because ∆F j's of a few reflections were significantly overestimated. Imposition of multiple F constraints with λ 2 = 0.9 and λ 4 = 0.1 in combination with the ZSPA algorithm solved such a problem (Figure 5) to decrease R indices appreciably: R wp = 3.500% (GoF = 1.687), R B = 1.05%, and R F = 0.74%. The multiple F constraints in combination with the Cambridge algorithm gave even better R indices (Table I).

Figure 5. Distributions and central moments of ΔF j in the MEM analysis of Cu2CO3(OH)2: (a) the conventional F constraint (λ 2 = 1); (b) the multiple F constraints with the ZSPA algorithm (λ 2 = 0.9 and λ 4 = 0.1); (c) even-order central moments, M n, of ΔF j (n = 2 − 16). Shaded areas in (a) and (b) show the ideal Gaussian distribution.
Figure 6(a) shows the displacement ellipsoid model reported by Zigan et al. (Reference Zigan, Joswig, Schuster and Mason1977), and Figures 6(b) and 6(c) illustrate electron-density distributions determined with the multiple F constraints and Cambridge algorithm, superimposed on a displacement ellipsoid model refined by the Rietveld analysis. A layered structure parallel to the ![]() $\lpar 10\bar 2\rpar $ plane and anisotropic atomic displacements of the Cu sites nearly perpendicular to the layer are clearly seen in Figure 6(b). On the other hand, highly covalent C − O bonds and the more ionic nature of Cu − O bonds are distinctly visible in Figure 6(c). In the present case, differences in electron densities between the conventional F constraint and the multiple F constraints were relatively small because of sufficiently small σ(hj)'s. However, the tendency for MEM to significantly overestimate ∆F j's of some low-Q reflections necessarily generates noises in the resulting electron densities (Palatinus and van Smaalen, Reference Palatinus and van Smaalen2002). Lower R indices obtained with the multiple F constraints (Table I) provide evidence for improvement of MPF analysis.
$\lpar 10\bar 2\rpar $ plane and anisotropic atomic displacements of the Cu sites nearly perpendicular to the layer are clearly seen in Figure 6(b). On the other hand, highly covalent C − O bonds and the more ionic nature of Cu − O bonds are distinctly visible in Figure 6(c). In the present case, differences in electron densities between the conventional F constraint and the multiple F constraints were relatively small because of sufficiently small σ(hj)'s. However, the tendency for MEM to significantly overestimate ∆F j's of some low-Q reflections necessarily generates noises in the resulting electron densities (Palatinus and van Smaalen, Reference Palatinus and van Smaalen2002). Lower R indices obtained with the multiple F constraints (Table I) provide evidence for improvement of MPF analysis.

Figure 6. (a) Crystal structure of Cu2CO3(OH)2 reported by Zigan et al. (Reference Zigan, Joswig, Schuster and Mason1977) without any H atoms. (b) and (c) Electron-density distributions (equi-density level: 1.5 Å−3), which resulted from MPF for Cu2CO3(OH)2, superimposed on a displacement ellipsoid model obtained by the Rietveld analysis.
Peak values of electron densities at the centers of the two Cu atoms were 216 Å−3 (Cu1) and 251 Å−3 (Cu2) while those resulting from the procrystal prior densities were 324 Å−3 (Cu1) and 530 Å−3 (Cu2). Such large differences between the electron densities obtained in the MPF analysis and the procrystal prior ones were observed only at narrow regions near the center of the Cu atoms. These differences arise most probably because of the series-termination effect of MEM analysis from diffraction data with insufficient resolutions and also because of too small atomic displacement parameters refined by the Rietveld analysis. On the use of procrystal prior densities in MEM analyses, peak densities at the centers of the atoms became close to those in the procrystal prior densities. However, even if the use of procrystal prior densities reduces the tendency of MEM to overestimate ∆F j's of low-Q reflections, higher order central moments of ∆F j's were still much larger than those expected for Gaussian distribution, and multiple F constraints were required.
C. Sr9In(PO4)7
The previous Rietveld refinement of Sr9In(PO4)7 revealed that positional disorder of Sr4 atoms causes orientational disorder of phosphate ions with a central P atom at a P1 site (Belik et al., Reference Belik, Izumi, Ikeda, Okui, Malakho, Morozov and Lazoryak2002). The Sr4 site was displaced from the ideal 4b site, (0, 1/2, 0), to a general equivalent position with an occupancy of g = 1/2 whereas the pronounced disorder of oxygen atoms bonded to P1 was absorbed into their U iso's. Consequently, an extraordinarily large U iso value of 0.096(4) Å2 was obtained for an O12 site in the [(P1)O4]3− ion (Belik et al., Reference Belik, Izumi, Ikeda, Okui, Malakho, Morozov and Lazoryak2002). In the present study, the O12 site was split into O12a and O12b sites with g = 1/2 by reference to U ij's of O12 obtained in a preliminary Rietveld analysis. Furthermore, bond lengths, l(P1–O12a) and l(P1–O12b), were restrained in a range of 1.496 ± 0.05 Å (Bergerhoff and Brandenburg, Reference Bergerhoff, Brandenburg and Prince2004).
Table V lists final structural parameters obtained in the Rietveld refinement based on the above revised structural model. Final R indices were R wp = 5.27% (GoF = 0.719), R B = 2.12%, and R F = 1.68%. Refined unit-cell parameters were a = 14.544 90(6) Å, b = 10.663 28(4) Å, c = 18.042 87(8) Å, and β = 112.3485(2)°. U iso(O12a) and U iso(O12b) converged at 0.028(3) Å2, which is much smaller than 0.096(4) Å2 for O12 in the previous Rietveld analysis (Belik et al., Reference Belik, Izumi, Ikeda, Okui, Malakho, Morozov and Lazoryak2002). The Sr4–O12a bond length was 2.739(9) Å, which is comparable with Sr–O bond lengths, 2.59−2.70 Å, of the other Sr sites. In contrast, the Sr4–O12b bond was as long as 3.608(12) Å, which supports the idea that the O12b atom is virtually not bonded to the Sr4 atom.
Table V. Structural parameters obtained in the Rietveld analysis of Sr9In(PO4)7.

In the subsequent MPF analyses, E had to be set at large values of about 250 00 rad−1 on the use of the conventional F constraint; otherwise, R indices in MPF increased in comparison with those in the final Rietveld analysis. However, decreases in σ(hj)'s arising from a large E value tend to generate more noise in the resulting electron densities. On the other hand, the empirical weighting of d j2 with E = 150 00 rad−1 enabled us to obtain smoother electron densities and lower R indices (Table I). As Figure 7 illustrates, both the positional disorder of Sr4 and the orientational disorder of the [(P1)O4]3− ion could be clearly visualized in isosurfaces of electron densities determined by the MPF analysis.

Figure 7. Electron-density distribution in Sr9In(PO4)7 with an equi-density level of 1 Å−3: (a) a unit cell (solid line) viewed along the c axis and (b) electron densities around the disordered atoms viewed along the a* axis with a unit cell represented by dotted lines. Drawing boundaries were 0.35 ≤ x ≤ 0.65, 0.5 ≤ y ≤ 1.5, and −0.05 ≤ z ≤ 1.05.
Weighting of d j4 led to slow convergence, and the solution could not be reached within a practical computation time because of being overweight on low-Q reflections and less emphasis on high-Q ones. To satisfy the conventional F constraint [Izumi and Momma, 2011a; Eq. (3)], the criterion for convergence, C wn, [Izumi and Momma, 2011a; Eq. (5)], had to be significantly smaller than 1. When C wn = 1 was specified as a convergence criterion with weighting of d j4, R indices in the subsequent w.p.f. became much worse than those in the Rietveld analysis.
As in the case with Cu2CO3(OH)2, the use of procrystal prior densities gave electron densities closer to the procrystal ones and higher peak densities at the centers of the atoms. Even for the disordered Sr4, O12a, and O12b sites, spherical distributions of electron densities and very high peak densities were obtained [Figures 8(a) and 8(b)]. Since representation of disordered crystal structures by split-atom models in Rietveld analysis is far from perfect, such spherical distributions of electrons for the disordered sites are ascribable to a bias toward procrystal prior densities. Even though MEM can reconstruct peaks that do not exist in prior densities (de Vries et al., 1996), false characteristics of procrystal prior ones can hardly be erased in powder diffraction because F obs(hj)'s for overlapped reflections are estimated on the basis of the same structural model in the preceding Rietveld analysis (Rietveld, Reference Rietveld1969).

Figure 8. Projection of electron densities in Sr9In(PO4)7 along the [100] direction from x = 0.4 to 0.6. They are calculated by the Cambridge algorithm with (a) uniform prior densities, λ 2 = 1, and w j = d j2, and (b) procrystal prior densities, λ 2 = 1, and w j = 1. Contour lines are plotted up to 5 Å−2 with an interval of 0.5 Å−2.
V. MPF ANALYSIS GUIDELINES
Guidelines derived for MPF analyses from the results of the above three MPF analyses are summarized as follows.
For practical use of multiple F constraints and weighting on the basis of d jx, MEM analysis with the classical F constraint is usually carried out, and then higher order central moments of ∆F j should be checked. If they are larger than those expected for Gaussian distribution, an appropriate constraint should be selected by paying close attention to the d j value of a reflection with the largest ∆F j. If a reflection with a very large d j value has the largest ∆F j, weighting on the basis of d jx is worth a try.
At the solution of MEM with the classical F constraint, the following condition must be satisfied (Jauch, Reference Jauch1994):
 $$\displaystyle{1 \over V}\sum\limits_k {\left({\ln \displaystyle{{\rho _k } \over {\tau _k }}} \right)\exp \left({2\pi {\rm i}{\bi h}_j \cdot {\bi r}_k } \right)}=\lambda \displaystyle{{F_{\rm obs} \lpar {\bi h}_j \rpar - F\lpar {\bi h}_j \rpar } \over {M_j \lsqb \sigma \lpar {\bi h}_j \rpar \rsqb ^2 }}$$
$$\displaystyle{1 \over V}\sum\limits_k {\left({\ln \displaystyle{{\rho _k } \over {\tau _k }}} \right)\exp \left({2\pi {\rm i}{\bi h}_j \cdot {\bi r}_k } \right)}=\lambda \displaystyle{{F_{\rm obs} \lpar {\bi h}_j \rpar - F\lpar {\bi h}_j \rpar } \over {M_j \lsqb \sigma \lpar {\bi h}_j \rpar \rsqb ^2 }}$$where V is the unit-cell volume, ρ k is the normalized density at position rk, τ k is the normalized density derived from prior information, λ is the Lagrangian multiplier, and M j is the multiplicity. On the use of weighting of d jx, Eq. (3) is modified as
 $$\displaystyle{1 \over V}\sum\limits_k {\left({\ln \displaystyle{{\rho _k } \over {\tau _k }}} \right)\exp \left({2\pi {\rm i}{\bi h}_j \cdot {\bi r}_k } \right)}=\lambda d_j^x \displaystyle{{F_{\rm obs} \lpar {\bi h}_j \rpar - F\lpar {\bi h}_j \rpar } \over {M_j \left[{\sigma \lpar {\bi h}_j \rpar } \right]^2 }}$$
$$\displaystyle{1 \over V}\sum\limits_k {\left({\ln \displaystyle{{\rho _k } \over {\tau _k }}} \right)\exp \left({2\pi {\rm i}{\bi h}_j \cdot {\bi r}_k } \right)}=\lambda d_j^x \displaystyle{{F_{\rm obs} \lpar {\bi h}_j \rpar - F\lpar {\bi h}_j \rpar } \over {M_j \left[{\sigma \lpar {\bi h}_j \rpar } \right]^2 }}$$When τ k is uniform, Eq. (4) can be rewritten as
 $$\displaystyle{1 \over {{\rm i}^x V}}\sum\limits_k {\nabla ^x \left({\ln \rho _k } \right)\exp \left({2\pi {\rm i}{\bi h}_j \cdot {\bi r}_k } \right)}=\lambda \displaystyle{{F_{\rm obs} \lpar {\bi h}_j \rpar - F\lpar {\bi h}_j \rpar } \over {M_j \left[{\sigma \lpar {\bi h}_j \rpar } \right]^2 }}$$
$$\displaystyle{1 \over {{\rm i}^x V}}\sum\limits_k {\nabla ^x \left({\ln \rho _k } \right)\exp \left({2\pi {\rm i}{\bi h}_j \cdot {\bi r}_k } \right)}=\lambda \displaystyle{{F_{\rm obs} \lpar {\bi h}_j \rpar - F\lpar {\bi h}_j \rpar } \over {M_j \left[{\sigma \lpar {\bi h}_j \rpar } \right]^2 }}$$which means that the weighting scheme based on d jx corresponds to regarding a weighted average of ρ's adjacent to position k as τ k. Therefore, electron- or nuclear-density distributions in real space smooth down with increasing order, x (de Vries et al., Reference de Vries, Briels and Feil1994; Palatinus and van Smaalen, Reference Palatinus and van Smaalen2002). Weighting of d j4 is reported to be the best in the case of single-crystal X-ray diffraction (de Vries et al., Reference de Vries, Briels and Feil1994). However, weighting with a higher order suffers from slow convergence (Hofmann et al., Reference Hofmann, Netzel and van Smaalen2007). Values of σ(hj) in powder diffraction data generally increase with decreasing d j, which must be the reason why the weighting of d j2 was more appropriate than d j4 in the present case.
If some reflections in the high-Q region have large ∆F j's or weighting on the basis of d jx causes too slow a convergence, x have to be reduced, and the use of multiple F constraints should be considered.
The use of procrystal prior densities reduces the tendency of MEM to overestimate ∆F j's of low-Q reflections in exchange for a more strong bias toward the structural model. However, multiple F constraints or weightings of d jx may be still required to obtain better results of MPF analysis. In general, procrystal prior densities computed on the basis of a structural model in the Rietveld analysis are far less reliable than those calculated from a structural model in single-crystal analysis. Anisotropic atomic displacement parameters can hardly be refined in adequate accuracy from X-ray powder diffraction data. Then, in the case of powder diffraction, not only amplitudes and phases of structure factors but procrystal prior densities are biased toward an insufficient structural model, which explains why the use of procrystal prior densities failed in reconstructing anisotropic atomic displacements in taurine. On the other hand, the use of procrystal prior densities can overcome the limitation of low-resolution data to some extent. At any rate, further investigations on effects of prior densities on results of MPF analyses are highly desired.
VI. CONCLUSION
We have successfully applied the generalized F constraints and weighting scheme based on d j in MPF analyses. These methodologies have already been proven to give improved electron-density distributions from F obs(hj)'s of isolated (non-overlapped) reflections in single-crystal X-ray diffraction. Furthermore, the present work has demonstrated that these enhancements are also effective in more accurate estimation of F(hj)'s from model-biased F obs(hj)'s of overlapped reflections in X-ray powder diffraction.
Because the scale of σ(hj)'s is the only decisive factor to determine wR F at the convergence point in MEM, wR F in MEM is not a good measure of the reliability of electron density distributions reconstructed by imposing different constraints. On the other hand, R wp, R B, and R F in w.p.f. provide more direct information on the reliability of MEM analysis from powder diffraction data.
The tendency of MEM to overestimate ΔF j's of a few strong low-Q reflections was more pronounced on use of the Cambridge algorithm than with the ZSPA algorithm. However, if this tendency was corrected by employing multiple F constraints or weighting based on d j, the Cambridge algorithm gave slightly better results than the ZSPA algorithm.
In conclusion, the improvements described above, high computation speed, memory efficiency, and scalability make MPF analysis with Dysnomia much more practical than that with its predecessor, PRIMA.