Article contents
A Bottom-Up Volume Reconstruction Method for Atom Probe Tomography
Published online by Cambridge University Press: 28 January 2022
Abstract
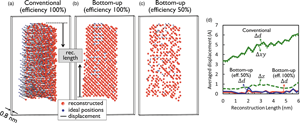
This paper describes a reconstruction method for atom probe tomography based on a bottom-up approach accounting for (i) the final tip morphology (which is frequently induced by inhomogeneous evaporation probabilities across the tip surface due to laser absorption, heat diffusion effects, and inhomogeneous material properties), (ii) the limited (and changing) field of view, and (iii) the detector efficiency. The reconstruction starts from the final tip morphology and reverses the evaporation sequence through the pseudo-deposition of defined small reconstruction volumes, which are then stacked together to create the full three-dimensional (3D) tip. The subdivision in small reconstruction volumes allows the scheme to account for the changing tip shape and field of view as evaporation proceeds. Atoms within the same small reconstruction volume are reconstructed at once by placing atoms back onto their possible lattice sites through a trajectory-matching process involving simulated and experimental hit maps. As the ejected ion trajectories are simulated using detailed electrostatic modeling inside the chamber, no simplifications have been imposed on the shape of the trajectories, projection laws, or tip surface. We demonstrate the superior performance of our approach over the conventional reconstruction method (Bas) for an asymmetrical tip shape.
- Type
- Development and Computation
- Information
- Copyright
- Copyright © The Author(s), 2022. Published by Cambridge University Press on behalf of the Microscopy Society of America
References
- 3
- Cited by





