Article contents
On irredundant components of the kernel of an ideal
Published online by Cambridge University Press: 26 February 2010
Extract
Throughout this paper a ring will mean a commutative ring with identity element. If A is an ideal of the ring R and P is a minimal prime ideal of A, then the intersection Q of all P-primary ideals which contain A is called the isolated primary component of A belonging to P. The ideal Q can also be described as the set of all elements x∈R such that xr∈A for some r∈R\P. If {Pα} is the collection of all minimal prime ideals of A and Qα is the isolated primary component of A belonging to Pα, then 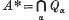 is called the kernel of A.
is called the kernel of A.
- Type
- Research Article
- Information
- Copyright
- Copyright © University College London 1965
References
- 1
- Cited by




