Research Article
On the large sieves of Linnik and Rényi
-
- Published online by Cambridge University Press:
- 26 February 2010, pp. 1-9
-
- Article
- Export citation
On linear relations between roots of unity
-
- Published online by Cambridge University Press:
- 26 February 2010, pp. 107-117
-
- Article
- Export citation
On the dimension of a graph
-
- Published online by Cambridge University Press:
- 26 February 2010, pp. 118-122
-
- Article
- Export citation
On badly approximable numbers
-
- Published online by Cambridge University Press:
- 26 February 2010, pp. 10-20
-
- Article
- Export citation
Plasticity theory and multipolar continuum mechanics
-
- Published online by Cambridge University Press:
- 26 February 2010, pp. 21-26
-
- Article
- Export citation
Metric simultaneous diophantine approximation (II)
-
- Published online by Cambridge University Press:
- 26 February 2010, pp. 123-127
-
- Article
- Export citation
A note on linear transversely isotropic fluids
-
- Published online by Cambridge University Press:
- 26 February 2010, pp. 27-29
-
- Article
- Export citation
Convection in a self-gravitating fluid sphere
-
- Published online by Cambridge University Press:
- 26 February 2010, pp. 128-137
-
- Article
- Export citation
Cubic Diophantine equations: the necessary congruence condition
-
- Published online by Cambridge University Press:
- 26 February 2010, pp. 30-38
-
- Article
- Export citation
The densest double lattice packing of four-spheres
-
- Published online by Cambridge University Press:
- 26 February 2010, pp. 138-142
-
- Article
- Export citation
Cubic Diophantine equations: a supplementary congruence condition
-
- Published online by Cambridge University Press:
- 26 February 2010, pp. 39-48
-
- Article
- Export citation
Lattice coverings of five space by spheres
-
- Published online by Cambridge University Press:
- 26 February 2010, pp. 143-150
-
- Article
- Export citation
Diffusion from an elevated point source into a turbulent atmosphere
-
- Published online by Cambridge University Press:
- 26 February 2010, pp. 49-57
-
- Article
- Export citation
Biquadratic congruences
-
- Published online by Cambridge University Press:
- 26 February 2010, pp. 151-160
-
- Article
- Export citation
Oscillating viscous flows
-
- Published online by Cambridge University Press:
- 26 February 2010, pp. 161-175
-
- Article
- Export citation
Eigen-functions for the strip problem
-
- Published online by Cambridge University Press:
- 26 February 2010, pp. 58-64
-
- Article
- Export citation
The distribution of solutions of congruences
-
- Published online by Cambridge University Press:
- 26 February 2010, pp. 176-192
-
- Article
- Export citation
On irredundant components of the kernel of an ideal
-
- Published online by Cambridge University Press:
- 26 February 2010, pp. 65-72
-
- Article
- Export citation
An investigation of the elastic strip and the annulus
-
- Published online by Cambridge University Press:
- 26 February 2010, pp. 193-200
-
- Article
- Export citation
Metrics for sets of convex bodies
-
- Published online by Cambridge University Press:
- 26 February 2010, pp. 73-88
-
- Article
- Export citation



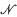 be a non-empty subset of the set of integers
be a non-empty subset of the set of integers
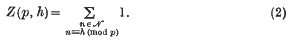

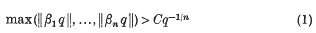
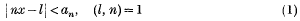
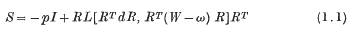
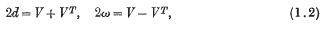
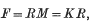
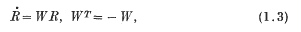
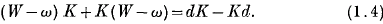
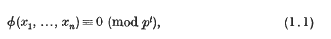

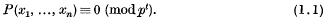
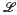
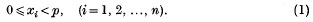
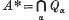 is called the
is called the