Hostname: page-component-848d4c4894-r5zm4 Total loading time: 0 Render date: 2024-06-17T10:33:17.079Z Has data issue: false hasContentIssue false
  • English
  • Français

On Kepler's equation

Published online by Cambridge University Press:  24 October 2008

T. M. Cherry
T. M. Cherry
Affiliation:
University of Melbourne, Australia
Get access Rights & Permissions [Opens in a new window]

Extract

1. Kepler's equation

has, when θ, x are real with 0 < x < 1, just one real root ξ = ξ*(θ, x). For this root there are the well-known formulae, dating from Lagrange and Bessel,

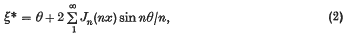
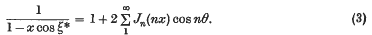
The objects of this paper are (i) to obtain analogous formulae for the unreal roots ξ of the equation, and (ii) to sum the conjugates (as Fourier series in θ) of the series on the right of (2) and (3).

Type
Research Article
Information
Mathematical Proceedings of the Cambridge Philosophical Society , Volume 51 , Issue 1 , January 1955 , pp. 81 - 91
Copyright
Copyright © Cambridge Philosophical Society 1955

Access options

Get access to the full version of this content by using one of the access options below. (Log in options will check for institutional or personal access. Content may require purchase if you do not have access.)

References

† It may be emphasized that (38) is not an analytic continuation of (31); it is got by combining a continuation of (8) with a continuation, along a different path, of the conjugate of (8).