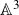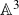0. Introduction
This paper has a two-fold goal: to compute, and to study the asymptotic behaviour of the generating function of rank r motivic Donaldson–Thomas (DT in short) invariants of
![]() ${\mathbb{A}}^3$
, namely the generating series
${\mathbb{A}}^3$
, namely the generating series
Here
![]() $\mathcal M_{{\mathbb{C}}}$
is a suitable motivic ring and
$\mathcal M_{{\mathbb{C}}}$
is a suitable motivic ring and
![]() $[ \!\cdot\! ]_{\text{vir}} \in \mathcal M_{{\mathbb{C}}}$
is the virtual motive (cf. Section 1·1), induced by the critical locus structure on the Quot scheme
$[ \!\cdot\! ]_{\text{vir}} \in \mathcal M_{{\mathbb{C}}}$
is the virtual motive (cf. Section 1·1), induced by the critical locus structure on the Quot scheme
![]() ${\textrm{Quot}}_{{\mathbb{A}}^3}(\mathscr O^{\oplus r},n)$
parametrising 0-dimensional quotients of length n of the free sheaf
${\textrm{Quot}}_{{\mathbb{A}}^3}(\mathscr O^{\oplus r},n)$
parametrising 0-dimensional quotients of length n of the free sheaf
![]() $\mathscr O^{\oplus r}$
.
$\mathscr O^{\oplus r}$
.
The following is our first main result.
Theorem 0·1. There is an identity
 \begin{equation} \mathsf{DT}_r^{\textrm{points}}({\mathbb{A}}^3,q) =\prod_{m\geq 1}\prod_{k=0}^{rm-1}\left(1-{\mathbb{L}}^{2+k-\frac{rm}{2}}q^{m}\right)^{-1}.\end{equation}
\begin{equation} \mathsf{DT}_r^{\textrm{points}}({\mathbb{A}}^3,q) =\prod_{m\geq 1}\prod_{k=0}^{rm-1}\left(1-{\mathbb{L}}^{2+k-\frac{rm}{2}}q^{m}\right)^{-1}.\end{equation}
Moreover, this series factors as r copies of shifted rank 1 contributions: there is an identity
The result was first obtained in the case
![]() $r=1$
by Behrend, Bryan and Szendrői [Reference Behrend, Bryan and Szendrői3] via an explicit motivic vanishing cycle calculation. Formula (0·2) follows by combining Formula (0·1) and Lemma 2.5 with one another. The approach of Section 2·3, where we prove Formula (0·1), is based on the techniques of motivic wall-crossing for framed objects developed by Mozgovoy [Reference Mozgovoy27, Reference Mozgovoy28] building on the Kontsevich–Soibelman wall-crossing [Reference Kontsevich and Soibelman20]. This approach allows us us to express the invariants for
$r=1$
by Behrend, Bryan and Szendrői [Reference Behrend, Bryan and Szendrői3] via an explicit motivic vanishing cycle calculation. Formula (0·2) follows by combining Formula (0·1) and Lemma 2.5 with one another. The approach of Section 2·3, where we prove Formula (0·1), is based on the techniques of motivic wall-crossing for framed objects developed by Mozgovoy [Reference Mozgovoy27, Reference Mozgovoy28] building on the Kontsevich–Soibelman wall-crossing [Reference Kontsevich and Soibelman20]. This approach allows us us to express the invariants for
![]() ${\textrm{Quot}}_{{\mathbb{A}}^3}(\mathscr O^{\oplus r},n)$
, which we view as ‘r-framed’ DT invariants, in terms of the universal series of the invariants of unframed representations of the 3-loop quiver in a critical chamber. These ideas can be employed to compute framed motivic DT invariants of small crepant resolutions of affine toric Calabi–Yau 3-folds [Reference Cazzaniga and Ricolfi8], which also exhibit similar factorisation properties.
${\textrm{Quot}}_{{\mathbb{A}}^3}(\mathscr O^{\oplus r},n)$
, which we view as ‘r-framed’ DT invariants, in terms of the universal series of the invariants of unframed representations of the 3-loop quiver in a critical chamber. These ideas can be employed to compute framed motivic DT invariants of small crepant resolutions of affine toric Calabi–Yau 3-folds [Reference Cazzaniga and Ricolfi8], which also exhibit similar factorisation properties.
The fact that partition functions of rank r invariants factor as r copies of partition functions of rank 1 invariants, shifted just as in Formula (0·2), has also been observed in the context of K-theoretic DT theory of
![]() ${\mathbb{A}}^3$
[Reference Fasola, Monavari and Ricolfi14], as well as in string theory [Reference Nekrasov and Piazzalunga29] and other motivic settings, such as [Reference Cazzaniga and Ricolfi8, Reference Monavari and Ricolfi23]. Recent work of Feyzbakhsh–Thomas [Reference Feyzbakhsh and Thomas16] shows that general higher rank DT invariants can be linked back to genuine rank 1 DT invariants: we believe our Formula (0·2) is an explicit (motivic) shadow of this general principle. The exponential form of Formula (0·1) has been exploited in [Reference Ricolfi35] to define higher rank motivic DT invariants for an arbitrary smooth quasiprojective 3-fold.
${\mathbb{A}}^3$
[Reference Fasola, Monavari and Ricolfi14], as well as in string theory [Reference Nekrasov and Piazzalunga29] and other motivic settings, such as [Reference Cazzaniga and Ricolfi8, Reference Monavari and Ricolfi23]. Recent work of Feyzbakhsh–Thomas [Reference Feyzbakhsh and Thomas16] shows that general higher rank DT invariants can be linked back to genuine rank 1 DT invariants: we believe our Formula (0·2) is an explicit (motivic) shadow of this general principle. The exponential form of Formula (0·1) has been exploited in [Reference Ricolfi35] to define higher rank motivic DT invariants for an arbitrary smooth quasiprojective 3-fold.
Formula (0·1) allows us to interpret the refined DT invariants of
![]() ${\textrm{Quot}}_{{\mathbb{A}}^3}(\mathscr O^{\oplus r},n)$
in terms of a weighted count of r-tuples of plane partitions
${\textrm{Quot}}_{{\mathbb{A}}^3}(\mathscr O^{\oplus r},n)$
in terms of a weighted count of r-tuples of plane partitions
![]() $\overline{\pi}=(\pi_{1}, \ldots, \pi_{r})$
of total size n (also known in the physics literature as r-coloured plane partitions). Setting
$\overline{\pi}=(\pi_{1}, \ldots, \pi_{r})$
of total size n (also known in the physics literature as r-coloured plane partitions). Setting
![]() $T={\mathbb{L}}^{1/2}$
, the coefficient of
$T={\mathbb{L}}^{1/2}$
, the coefficient of
![]() $q^{n}$
in
$q^{n}$
in
![]() $\mathsf{DT}_r^{\textrm{points}}({\mathbb{A}}^3,q)$
can be written as
$\mathsf{DT}_r^{\textrm{points}}({\mathbb{A}}^3,q)$
can be written as
where
![]() $S_{n,r}$
is a certain explicit random variable on the space of r-tuples of plane partitions. In Section 3, we describe the asymptotic behaviour of (a renormalisation of) the refined DT generating series, generalising A. Morrison’s result for
$S_{n,r}$
is a certain explicit random variable on the space of r-tuples of plane partitions. In Section 3, we describe the asymptotic behaviour of (a renormalisation of) the refined DT generating series, generalising A. Morrison’s result for
![]() $r=1$
[Reference Morrison24]. We discuss the relationship with Morrison’s work in Section 3·1.
$r=1$
[Reference Morrison24]. We discuss the relationship with Morrison’s work in Section 3·1.
The following is our second main result. It will be proved in Theorem 3.2 in the main body.
Theorem 0·2. As
![]() $n\to \infty$
, the normalised random variable
$n\to \infty$
, the normalised random variable
![]() $n^{-2/3}S_{n,r}$
converges in distribution to
$n^{-2/3}S_{n,r}$
converges in distribution to
![]() $\mathcal{N}(\mu, \sigma^2)$
with
$\mathcal{N}(\mu, \sigma^2)$
with
where
![]() $\zeta(s)$
is Riemann’s zeta function.
$\zeta(s)$
is Riemann’s zeta function.
In the final part of the introduction, we discuss some relation with existing work on asymptotics of plane partitions and counting invariants, from a mathematical and physics perspective.
The asymptotics of (various refinements of) the generating function of plane partitions has attracted quite a lot of attention in the mathematical community, since the objects involved sit in the intersection between several areas of mathematics: random variables and distributions, combinatorics, algebraic geometry, string theory. See [Reference Wright36] for E. M. Wright’s seminal work on the asymptotics of actual partitions, without refinements. Morrison based his work [Reference Morrison24] on Wright’s analysis, and our analysis in turn builds on Morrison’s. As far as the ubiquity of Gaussian distributions is concerned, besides Morrison’s paper we would like to mention the work by Panario–Richmond–Young [Reference Panario, Richmond and Young30] who, on the other hand, refine the plane partition counts by considering a colouring of the parts
![]() $\pi_{i,j}$
of a plane partition
$\pi_{i,j}$
of a plane partition
![]() $\pi$
according to the parity of
$\pi$
according to the parity of
![]() $i-j$
, in order to study the asymptotic behaviour of the difference between the 0-coloured and 1-coloured partition functions: the result is (asymptotycally) Gaussian, and geometrically corresponds to the 3-dimensional orbifold
$i-j$
, in order to study the asymptotic behaviour of the difference between the 0-coloured and 1-coloured partition functions: the result is (asymptotycally) Gaussian, and geometrically corresponds to the 3-dimensional orbifold
![]() ${\mathbb{A}}^1 \times [{\mathbb{A}}^2/{\mathbb{Z}}_2]$
. From the physics literature, we refer the reader to [Reference Zahabi37] and the references therein for a related analysis of the asymptotics of BPS states starting from a quiver perspective.
${\mathbb{A}}^1 \times [{\mathbb{A}}^2/{\mathbb{Z}}_2]$
. From the physics literature, we refer the reader to [Reference Zahabi37] and the references therein for a related analysis of the asymptotics of BPS states starting from a quiver perspective.
The higher rank motivic DT partition function of
![]() ${\mathbb{A}}^3$
is rather similar in shape to the K-theoretic partition function [Reference Fasola, Monavari and Ricolfi14, theorem A], although the latter is defined via torus localisation, and no torus-equivariance is present on the motivic side. However, given the similarity, one could still ask: what is the K-theoretic counterpart of our Theorem 0·2? Although we do not have a definite answer, it is worth noting that the K-theoretic DT invariants also satisfy a remarkable ‘regularity’ property: the coefficient of
${\mathbb{A}}^3$
is rather similar in shape to the K-theoretic partition function [Reference Fasola, Monavari and Ricolfi14, theorem A], although the latter is defined via torus localisation, and no torus-equivariance is present on the motivic side. However, given the similarity, one could still ask: what is the K-theoretic counterpart of our Theorem 0·2? Although we do not have a definite answer, it is worth noting that the K-theoretic DT invariants also satisfy a remarkable ‘regularity’ property: the coefficient of
![]() $q^n$
in the K-theoretic DT series can be written as
$q^n$
in the K-theoretic DT series can be written as
where
![]() $t_i$
and
$t_i$
and
![]() $w_j$
are equivariant parameters of a torus
$w_j$
are equivariant parameters of a torus
![]() $\textbf{T} = {\mathbb{G}}_m^{3} \times {\mathbb{G}}_m^{r}$
acting on
$\textbf{T} = {\mathbb{G}}_m^{3} \times {\mathbb{G}}_m^{r}$
acting on
![]() ${\textrm{Quot}}_{{\mathbb{A}}^3}(\mathscr O^{\oplus r},n)$
, and
${\textrm{Quot}}_{{\mathbb{A}}^3}(\mathscr O^{\oplus r},n)$
, and
![]() $\mathsf Y_{\overline \pi}$
is a (rather complicated) function of these parameters. The remarkable property (see [Reference Fasola, Monavari and Ricolfi14, theorem 6.5]) is that – as suggested by the notation – the right – hand side does not depend on
$\mathsf Y_{\overline \pi}$
is a (rather complicated) function of these parameters. The remarkable property (see [Reference Fasola, Monavari and Ricolfi14, theorem 6.5]) is that – as suggested by the notation – the right – hand side does not depend on
![]() $w_1,\ldots,w_r$
, even though the individual summands do. This phenomenon is known in string theory as ‘independence on Coulomb moduli’ [Reference Del Zotto, Nekrasov, Piazzalunga and Zabzine12].
$w_1,\ldots,w_r$
, even though the individual summands do. This phenomenon is known in string theory as ‘independence on Coulomb moduli’ [Reference Del Zotto, Nekrasov, Piazzalunga and Zabzine12].
Whether this symmetry property, used crucially for the computation of K-theoretic DT invariants, is an actual shadow of a Gaussian distribution, is a mistery that we leave for the future to explore.
1. Background material
1·1. Rings of motives
Let
![]() $K_0(St_{{\mathbb{C}}})$
be the Grothendieck ring of stacks. It can be defined as the localisation of the ordinary Grothendieck ring of varieties
$K_0(St_{{\mathbb{C}}})$
be the Grothendieck ring of stacks. It can be defined as the localisation of the ordinary Grothendieck ring of varieties
![]() $K_0(\text{Var}_{{\mathbb{C}}})$
at the classes
$K_0(\text{Var}_{{\mathbb{C}}})$
at the classes
![]() $[\textrm{GL}_k]$
of general linear groups [Reference Bridgeland4]. The invariants we want to study will live in the extended ring
$[\textrm{GL}_k]$
of general linear groups [Reference Bridgeland4]. The invariants we want to study will live in the extended ring
where
![]() ${\mathbb{L}} = [{\mathbb{A}}^1] \in K_0(\text{Var}_{{\mathbb{C}}}) \to K_0({\textrm{St}}_{{\mathbb{C}}})$
is the Lefschetz motive.
${\mathbb{L}} = [{\mathbb{A}}^1] \in K_0(\text{Var}_{{\mathbb{C}}}) \to K_0({\textrm{St}}_{{\mathbb{C}}})$
is the Lefschetz motive.
1·1·1. The virtual motive of a critical locus
Let U be a smooth d-dimensional
![]() ${\mathbb{C}}$
-scheme,
${\mathbb{C}}$
-scheme,
![]() $f\colon U \to {\mathbb{A}}^1$
a regular function. The virtual motive of the critical locus
$f\colon U \to {\mathbb{A}}^1$
a regular function. The virtual motive of the critical locus
![]() $\text{crit}\; f = Z( \text{d} f) \subset U$
, depending on the pair (U, f), is defined in [Reference Behrend, Bryan and Szendrői3] as the motivic class
$\text{crit}\; f = Z( \text{d} f) \subset U$
, depending on the pair (U, f), is defined in [Reference Behrend, Bryan and Szendrői3] as the motivic class
where
![]() $[\phi_f] \in K_0^{\hat\mu}(\text{Var}_{{\mathbb{C}}})$
is the (absolute) motivic vanishing cycle class defined by Denef and Loeser [Reference Denef and Loeser13]. The ‘
$[\phi_f] \in K_0^{\hat\mu}(\text{Var}_{{\mathbb{C}}})$
is the (absolute) motivic vanishing cycle class defined by Denef and Loeser [Reference Denef and Loeser13]. The ‘
![]() $\hat\mu$
’ decoration means that we are considering
$\hat\mu$
’ decoration means that we are considering
![]() $\hat\mu$
-equivariant motives, where
$\hat\mu$
-equivariant motives, where
![]() $\hat\mu$
is the group of all roots of unity. However, the motivic invariants studied here will live in the subring
$\hat\mu$
is the group of all roots of unity. However, the motivic invariants studied here will live in the subring
![]() ${\mathcal M}_{{\mathbb{C}}}\subset {\mathcal M}_{{\mathbb{C}}}^{\hat\mu}$
of classes carrying the trivial
${\mathcal M}_{{\mathbb{C}}}\subset {\mathcal M}_{{\mathbb{C}}}^{\hat\mu}$
of classes carrying the trivial
![]() $\hat\mu$
-action.
$\hat\mu$
-action.
Example 1·1. Set
![]() $f = 0$
. Then
$f = 0$
. Then
![]() $\text{crit}\; f = U$
and
$\text{crit}\; f = U$
and
![]() $[U]_{\text{vir}} = {\mathbb{L}}^{-(\dim U)/2}\cdot [U]$
. For instance,
$[U]_{\text{vir}} = {\mathbb{L}}^{-(\dim U)/2}\cdot [U]$
. For instance,
![]() $[{\textrm{GL}}_k]_{\text{vir}} = {\mathbb{L}}^{-k^2/2}\cdot [{\textrm{GL}}_k]$
.
$[{\textrm{GL}}_k]_{\text{vir}} = {\mathbb{L}}^{-k^2/2}\cdot [{\textrm{GL}}_k]$
.
Remark 1·2. We use lambda-ring conventions on
![]() $\mathcal M_{{\mathbb{C}}}$
from [Reference Behrend, Bryan and Szendrői3, Reference Davison and Ricolfi11]. In particular we use the definition of
$\mathcal M_{{\mathbb{C}}}$
from [Reference Behrend, Bryan and Szendrői3, Reference Davison and Ricolfi11]. In particular we use the definition of
![]() $[\text{crit}\; f]_{\text{vir}}$
from [Reference Behrend, Bryan and Szendrői3, section 2.8], which differs (slightly) from the one in [Reference Morrison, Mozgovoy, Nagao and Szendröi25]. The difference amounts to the substitution
$[\text{crit}\; f]_{\text{vir}}$
from [Reference Behrend, Bryan and Szendrői3, section 2.8], which differs (slightly) from the one in [Reference Morrison, Mozgovoy, Nagao and Szendröi25]. The difference amounts to the substitution
![]() ${\mathbb{L}}^{1/2}\to -{\mathbb{L}}^{1/2}$
. The Euler number specialisation with our conventions is
${\mathbb{L}}^{1/2}\to -{\mathbb{L}}^{1/2}$
. The Euler number specialisation with our conventions is
![]() ${\mathbb{L}}^{1/2}\to -1$
.
${\mathbb{L}}^{1/2}\to -1$
.
1·2. Quivers: framings, and motivic quantum torus
A quiver Q is a finite directed graph, determined by its sets
![]() $Q_0$
and
$Q_0$
and
![]() $Q_1$
of vertices and edges, respectively, along with the maps h,
$Q_1$
of vertices and edges, respectively, along with the maps h,
![]() $t\colon Q_1 \to Q_0$
specifying where an edge starts or ends. We use the notation
$t\colon Q_1 \to Q_0$
specifying where an edge starts or ends. We use the notation
to denote the tail and the head of an edge
![]() $a \in Q_1$
.
$a \in Q_1$
.
All quivers in this paper will be assumed connected. The path algebra
![]() ${\mathbb{C}} Q$
of a quiver Q is defined, as a
${\mathbb{C}} Q$
of a quiver Q is defined, as a
![]() ${\mathbb{C}}$
-vector space, by using as a
${\mathbb{C}}$
-vector space, by using as a
![]() ${\mathbb{C}}$
-basis the set of all paths in the quiver, including a trivial path
${\mathbb{C}}$
-basis the set of all paths in the quiver, including a trivial path
![]() $\epsilon_i$
for each
$\epsilon_i$
for each
![]() $i \in Q_0$
. The product is defined by concatenation of paths whenever the operation is possible, and is set to be 0 otherwise. The identity element is
$i \in Q_0$
. The product is defined by concatenation of paths whenever the operation is possible, and is set to be 0 otherwise. The identity element is
![]() $\sum_{i\in Q_0}\epsilon_i \in {\mathbb{C}} Q$
.
$\sum_{i\in Q_0}\epsilon_i \in {\mathbb{C}} Q$
.
On a quiver Q one can define the Euler–Ringel form
![]() $\chi_Q(-,-)\colon {\mathbb{Z}}^{Q_0}\times {\mathbb{Z}}^{Q_0} \to {\mathbb{Z}}$
by
$\chi_Q(-,-)\colon {\mathbb{Z}}^{Q_0}\times {\mathbb{Z}}^{Q_0} \to {\mathbb{Z}}$
by
as well as the skew-symmetric form
Definition 1·3. (r-framing) Let Q be a quiver with a distinguished vertex
![]() $0\in Q_0$
, and let r be a positive integer. We define the quiver
$0\in Q_0$
, and let r be a positive integer. We define the quiver
![]() $\widetilde Q$
by adding one vertex, labelled
$\widetilde Q$
by adding one vertex, labelled
![]() $\infty$
, to the original vertices in
$\infty$
, to the original vertices in
![]() $Q_0$
, and r edges
$Q_0$
, and r edges
![]() $\infty\to 0$
. We refer to
$\infty\to 0$
. We refer to
![]() $\widetilde Q$
as the r-framed quiver obtained out of (Q, 0).
$\widetilde Q$
as the r-framed quiver obtained out of (Q, 0).
Let Q be a quiver. Define its motivic quantum torus (or twisted motivic algebra) as
with product
If
![]() $\widetilde{Q}$
is the r-framed quiver associated to (Q, 0), one has a decomposition
$\widetilde{Q}$
is the r-framed quiver associated to (Q, 0), one has a decomposition
 \begin{equation*}\mathcal T_{\widetilde{Q}} = \left(\prod_{d\geq 0} {\mathcal M}_{{\mathbb{C}}}\cdot y_\infty^d\right) \oplus \mathcal T_Q ,\end{equation*}
\begin{equation*}\mathcal T_{\widetilde{Q}} = \left(\prod_{d\geq 0} {\mathcal M}_{{\mathbb{C}}}\cdot y_\infty^d\right) \oplus \mathcal T_Q ,\end{equation*}
where we have set
![]() $y_\infty = y^{(1,\textbf{0})}$
. A generator
$y_\infty = y^{(1,\textbf{0})}$
. A generator
![]() $y^\alpha \in \mathcal T_Q$
will be identified with its image
$y^\alpha \in \mathcal T_Q$
will be identified with its image
![]() $y^{(0,\alpha)} \in \mathcal T_{\widetilde{Q}}$
.
$y^{(0,\alpha)} \in \mathcal T_{\widetilde{Q}}$
.
1·3. Quiver representations and their stability
Let Q be a quiver. A representation
![]() $\rho$
of Q is the datum of a finite dimensional
$\rho$
of Q is the datum of a finite dimensional
![]() ${\mathbb{C}}$
-vector space
${\mathbb{C}}$
-vector space
![]() $\rho_i$
for every vertex
$\rho_i$
for every vertex
![]() $i\in Q_0$
, and a linear map
$i\in Q_0$
, and a linear map
![]() $\rho(a)\colon \rho_i\to \rho_j$
for every edge
$\rho(a)\colon \rho_i\to \rho_j$
for every edge
![]() $a\colon i\to j$
in
$a\colon i\to j$
in
![]() $Q_1$
. The dimension vector of
$Q_1$
. The dimension vector of
![]() $\rho$
is
$\rho$
is
![]() $\underline{\dim}\,\rho = (\dim_{{\mathbb{C}}} \rho_i)_i\in \mathbb N^{Q_0}$
, where
$\underline{\dim}\,\rho = (\dim_{{\mathbb{C}}} \rho_i)_i\in \mathbb N^{Q_0}$
, where
![]() ${\mathbb{N}}={\mathbb{Z}}_{\geq 0}$
.
${\mathbb{N}}={\mathbb{Z}}_{\geq 0}$
.
Convention 1·1. Let Q be a quiver,
![]() $\widetilde Q$
its r-framing. The dimension vector of a representation
$\widetilde Q$
its r-framing. The dimension vector of a representation
![]() $\widetilde \rho$
of
$\widetilde \rho$
of
![]() $\widetilde Q$
will be denoted by
$\widetilde Q$
will be denoted by
![]() $(d,\alpha)$
, where
$(d,\alpha)$
, where
![]() $d = \dim_{{\mathbb{C}}}\widetilde{\rho}_\infty \in {\mathbb{N}}$
and
$d = \dim_{{\mathbb{C}}}\widetilde{\rho}_\infty \in {\mathbb{N}}$
and
![]() $\alpha \in {\mathbb{N}}^{Q_0}$
.
$\alpha \in {\mathbb{N}}^{Q_0}$
.
The space of all representations of Q with a fixed dimension vector
![]() $\alpha\in \mathbb N^{Q_0}$
is the affine space
$\alpha\in \mathbb N^{Q_0}$
is the affine space
The gauge group
![]() ${\textrm{GL}}_\alpha = \prod_{i\in Q_0} {\textrm{GL}}_{\alpha_i}$
acts on
${\textrm{GL}}_\alpha = \prod_{i\in Q_0} {\textrm{GL}}_{\alpha_i}$
acts on
![]() $\textrm{R}(Q,\alpha)$
by
$\textrm{R}(Q,\alpha)$
by
![]() $(g_i)_i \cdot (\rho(a))_{a\in Q_1} = (g_{h(a)}\circ\rho(a)\circ g_{t(a)}^{-1})_{a \in Q_1}$
.
$(g_i)_i \cdot (\rho(a))_{a\in Q_1} = (g_{h(a)}\circ\rho(a)\circ g_{t(a)}^{-1})_{a \in Q_1}$
.
Following [Reference Morrison, Mozgovoy, Nagao and Szendröi25], we recall the notion of (semi)stability of a representation.
Definition 1·4. A central charge is a group homomorphism
![]() $\text{Z}\colon \mathbb Z^{Q_0}\to {\mathbb{C}}$
such that the image of
$\text{Z}\colon \mathbb Z^{Q_0}\to {\mathbb{C}}$
such that the image of
![]() $\mathbb N^{Q_0}\setminus 0$
lies inside
$\mathbb N^{Q_0}\setminus 0$
lies inside
![]() $\mathbb H_+ = \{re^{\sqrt{-1}\pi\varphi}|r>0,\,0<\varphi\leq 1\}$
. For every
$\mathbb H_+ = \{re^{\sqrt{-1}\pi\varphi}|r>0,\,0<\varphi\leq 1\}$
. For every
![]() $\alpha\in \mathbb N^{Q_0}\setminus 0$
, we denote by
$\alpha\in \mathbb N^{Q_0}\setminus 0$
, we denote by
![]() $\varphi(\alpha)$
the real number
$\varphi(\alpha)$
the real number
![]() $\varphi$
such that
$\varphi$
such that
![]() $\text{Z}(\alpha) = re^{\sqrt{-1}\pi\varphi}$
. It is called the phase of
$\text{Z}(\alpha) = re^{\sqrt{-1}\pi\varphi}$
. It is called the phase of
![]() $\alpha$
with respect to Z.
$\alpha$
with respect to Z.
Note that every vector
![]() $\zeta\in {\mathbb{R}}^{Q_0}$
induces a central charge
$\zeta\in {\mathbb{R}}^{Q_0}$
induces a central charge
![]() $\text{Z}_{\zeta}$
if we set
$\text{Z}_{\zeta}$
if we set
![]() $\text{Z}_{\zeta}(\alpha) = -\zeta\cdot \alpha + \lvert\alpha\rvert\sqrt{-1}$
, where
$\text{Z}_{\zeta}(\alpha) = -\zeta\cdot \alpha + \lvert\alpha\rvert\sqrt{-1}$
, where
![]() $\lvert\alpha\rvert = \sum_{i \in Q_0}\alpha_i$
. We denote by
$\lvert\alpha\rvert = \sum_{i \in Q_0}\alpha_i$
. We denote by
![]() $\varphi_\zeta$
the induced phase function, and we set
$\varphi_\zeta$
the induced phase function, and we set
![]() $\varphi_\zeta(\rho) = \varphi_\zeta(\underline{\dim}\,\rho)$
for every representation
$\varphi_\zeta(\rho) = \varphi_\zeta(\underline{\dim}\,\rho)$
for every representation
![]() $\rho$
of Q.
$\rho$
of Q.
Definition 1·5. Fix
![]() $\zeta\in {\mathbb{R}}^{Q_0}$
. A representation
$\zeta\in {\mathbb{R}}^{Q_0}$
. A representation
![]() $\rho$
of Q is called
$\rho$
of Q is called
![]() $\zeta$
-semistable if
$\zeta$
-semistable if
for every nonzero proper subrepresentation
![]() $0\neq \rho'\subsetneq \rho$
. If ‘
$0\neq \rho'\subsetneq \rho$
. If ‘
![]() $\leq$
’ can be replaced by ‘
$\leq$
’ can be replaced by ‘
![]() $<$
’, we say that
$<$
’, we say that
![]() $\rho$
is
$\rho$
is
![]() $\zeta$
-stable. Vectors
$\zeta$
-stable. Vectors
![]() $\zeta\in {\mathbb{R}}^{Q_0}$
are referred to as stability parameters.
$\zeta\in {\mathbb{R}}^{Q_0}$
are referred to as stability parameters.
Definition 1·6. Let
![]() $\alpha \in {\mathbb{N}}^{Q_0}$
be a dimension vector. A stability parameter
$\alpha \in {\mathbb{N}}^{Q_0}$
be a dimension vector. A stability parameter
![]() $\zeta$
is called
$\zeta$
is called
![]() $\alpha$
-generic if for any
$\alpha$
-generic if for any
![]() $0<\beta<\alpha$
one has
$0<\beta<\alpha$
one has
![]() $\varphi_\zeta(\beta) \neq \varphi_\zeta(\alpha)$
.
$\varphi_\zeta(\beta) \neq \varphi_\zeta(\alpha)$
.
The sets of
![]() $\zeta$
-stable and
$\zeta$
-stable and
![]() $\zeta$
-semistable representations with given dimension vector
$\zeta$
-semistable representations with given dimension vector
![]() $\alpha$
form a chain of open subsets
$\alpha$
form a chain of open subsets
If
![]() $\zeta$
is
$\zeta$
is
![]() $\alpha$
-generic, one has
$\alpha$
-generic, one has
![]() $\textrm{R}^{\zeta\text{-st}}(Q,\alpha) = \textrm{R}^{\zeta\text{-ss}}(Q,\alpha)$
.
$\textrm{R}^{\zeta\text{-st}}(Q,\alpha) = \textrm{R}^{\zeta\text{-ss}}(Q,\alpha)$
.
1·4. Quivers with potential
Let Q be a quiver, and let
![]() ${\mathbb{C}} Q$
be the path algebra of Q. A finite linear combination of cyclic paths
${\mathbb{C}} Q$
be the path algebra of Q. A finite linear combination of cyclic paths
![]() $W \in {\mathbb{C}} Q$
is called a potential. Given a cyclic path w and an arrow
$W \in {\mathbb{C}} Q$
is called a potential. Given a cyclic path w and an arrow
![]() $a \in Q_1$
, one defines the noncommutative derivative
$a \in Q_1$
, one defines the noncommutative derivative
 \begin{equation*}\frac{\partial w}{\partial a} =\sum_{\substack{w=cac' \\ c,c'\text{ paths in }Q}}c'c\,\in\,{\mathbb{C}} Q.\end{equation*}
\begin{equation*}\frac{\partial w}{\partial a} =\sum_{\substack{w=cac' \\ c,c'\text{ paths in }Q}}c'c\,\in\,{\mathbb{C}} Q.\end{equation*}
This rule extends to an operator
![]() $\partial/\partial a$
acting on every potential. The Jacobi algebra
$\partial/\partial a$
acting on every potential. The Jacobi algebra
![]() $J=J_{Q,W}$
of (Q, W) is the quotient of
$J=J_{Q,W}$
of (Q, W) is the quotient of
![]() ${\mathbb{C}} Q$
by the two-sided ideal generated by
${\mathbb{C}} Q$
by the two-sided ideal generated by
![]() $\partial W/\partial a$
for all edges
$\partial W/\partial a$
for all edges
![]() $a \in Q_1$
. For every
$a \in Q_1$
. For every
![]() $\alpha \in {\mathbb{N}}^{Q_0}$
, the potential
$\alpha \in {\mathbb{N}}^{Q_0}$
, the potential
![]() $W = \sum_ca_cc$
determines a regular function
$W = \sum_ca_cc$
determines a regular function
The points in the critical locus
![]() $\text{crit}\; f_\alpha \subset R(Q,\alpha)$
correspond to
$\text{crit}\; f_\alpha \subset R(Q,\alpha)$
correspond to
![]() $\alpha$
-dimensional J-modules.
$\alpha$
-dimensional J-modules.
Fix an
![]() $\alpha$
-generic stability parameter
$\alpha$
-generic stability parameter
![]() $\zeta \in {\mathbb{R}}^{Q_0}$
. If
$\zeta \in {\mathbb{R}}^{Q_0}$
. If
![]() $f_{\zeta,\alpha} \colon \textrm{R}^{\zeta\text{-st}}(Q,\alpha)\to {\mathbb{A}}^1$
is the restriction of
$f_{\zeta,\alpha} \colon \textrm{R}^{\zeta\text{-st}}(Q,\alpha)\to {\mathbb{A}}^1$
is the restriction of
![]() $f_\alpha$
, then
$f_\alpha$
, then
are, by definition, the stacks of
![]() $\alpha$
-dimensional J-modules and
$\alpha$
-dimensional J-modules and
![]() $\zeta$
-stable J-modules.
$\zeta$
-stable J-modules.
Definition 1·7. A quiver with potential (Q, W) admits a cut if there is a subset
![]() $I \subset Q_1$
such that every cyclic monomial appearing in W contains exactly one edge in I.
$I \subset Q_1$
such that every cyclic monomial appearing in W contains exactly one edge in I.
From now on we assume (Q, W) admits a cut. This condition ensures that the motive
![]() $[\mathfrak M(J,\alpha)]_{\text{vir}}$
introduced in the next definition lives in
$[\mathfrak M(J,\alpha)]_{\text{vir}}$
introduced in the next definition lives in
![]() $\mathcal M_{{\mathbb{C}}}$
. The 3-loop quiver
$\mathcal M_{{\mathbb{C}}}$
. The 3-loop quiver
![]() $L_3$
with the cubic potential
$L_3$
with the cubic potential
![]() $W=A_3[A_1,A_2]$
has
$W=A_3[A_1,A_2]$
has
![]() $I=\{A_3\}$
as a cut. We go back to this in Example 1·13.
$I=\{A_3\}$
as a cut. We go back to this in Example 1·13.
Definition 1·8 ([Reference Morrison, Mozgovoy, Nagao and Szendröi25]). We define motivic Donaldson–Thomas invariants
in
![]() ${\mathcal M}_{{\mathbb{C}}}$
, where
${\mathcal M}_{{\mathbb{C}}}$
, where
![]() $[{\textrm{GL}}_\alpha]_{\text{vir}}$
is taken as in Example 1·1. The generating function
$[{\textrm{GL}}_\alpha]_{\text{vir}}$
is taken as in Example 1·1. The generating function
is called the universal series of (Q, W).
By [Reference Morrison, Mozgovoy, Nagao and Szendröi25, lemma 1.9], since we assumed the existence of a cut, we have an identity
![]() $ \left[\mathfrak M_\zeta(J,\alpha)\right]_{\text{vir}} = [\text{crit}\; f_{\zeta,\alpha}]_{\text{vir}}/[\textrm{G}_\alpha]_{\text{vir}}$
as long as
$ \left[\mathfrak M_\zeta(J,\alpha)\right]_{\text{vir}} = [\text{crit}\; f_{\zeta,\alpha}]_{\text{vir}}/[\textrm{G}_\alpha]_{\text{vir}}$
as long as
![]() $\alpha$
has 1 as one of its components.
$\alpha$
has 1 as one of its components.
Definition 1·9. A stability parameter
![]() $\zeta \in {\mathbb{R}}^{Q_0}$
is called generic if
$\zeta \in {\mathbb{R}}^{Q_0}$
is called generic if
![]() $\zeta\cdot \underline{\dim}\,\rho \neq 0$
for every nontrivial
$\zeta\cdot \underline{\dim}\,\rho \neq 0$
for every nontrivial
![]() $\zeta$
-stable J-module
$\zeta$
-stable J-module
![]() $\rho$
.
$\rho$
.
1·5. Framed motivic DT invariants
Let Q be a quiver,
![]() $r\geq 1$
be an integer, and consider its r-framing
$r\geq 1$
be an integer, and consider its r-framing
![]() $\widetilde Q$
with respect to a vertex
$\widetilde Q$
with respect to a vertex
![]() $0 \in Q_0$
(Definition 1·3). A representation
$0 \in Q_0$
(Definition 1·3). A representation
![]() $\widetilde \rho$
of
$\widetilde \rho$
of
![]() $\widetilde Q$
can be uniquely written as a pair
$\widetilde Q$
can be uniquely written as a pair
![]() $(u,\rho)$
, where
$(u,\rho)$
, where
![]() $\rho$
is a representation of Q and
$\rho$
is a representation of Q and
![]() $u = (u_1,\dots,u_r)$
is an r-tuple of linear maps
$u = (u_1,\dots,u_r)$
is an r-tuple of linear maps
![]() $u_i\colon \widetilde{\rho}_\infty\to \rho_0$
. From now on, we assume our framed representations to satisfy
$u_i\colon \widetilde{\rho}_\infty\to \rho_0$
. From now on, we assume our framed representations to satisfy
![]() $\dim_{{\mathbb{C}}} \widetilde{\rho}_\infty = 1$
, so that according to Convention 1·1 we can write
$\dim_{{\mathbb{C}}} \widetilde{\rho}_\infty = 1$
, so that according to Convention 1·1 we can write
![]() $\underline{\dim}\,\widetilde \rho=(1,\underline{\dim}\,\rho)$
. We also view
$\underline{\dim}\,\widetilde \rho=(1,\underline{\dim}\,\rho)$
. We also view
![]() $\rho$
as a subrepresentation of
$\rho$
as a subrepresentation of
![]() $\widetilde{\rho}$
of dimension
$\widetilde{\rho}$
of dimension
![]() $(0,\underline{\dim}\,\rho)$
, based at the vertex
$(0,\underline{\dim}\,\rho)$
, based at the vertex
![]() $0 \in Q_0$
.
$0 \in Q_0$
.
Definition 1·10. Fix
![]() $\zeta\in \mathbb R^{Q_0}$
. A representation
$\zeta\in \mathbb R^{Q_0}$
. A representation
![]() $(u,\rho)$
of
$(u,\rho)$
of
![]() $\widetilde Q$
(resp. a
$\widetilde Q$
(resp. a
![]() $\widetilde J$
-module) with
$\widetilde J$
-module) with
![]() $\dim_{{\mathbb{C}}} \widetilde{\rho}_\infty = 1$
is said to be
$\dim_{{\mathbb{C}}} \widetilde{\rho}_\infty = 1$
is said to be
![]() $\zeta$
-(semi)stable if it is
$\zeta$
-(semi)stable if it is
![]() $(\zeta_\infty,\zeta)$
-(semi)stable in the sense of Definition 1·5, where
$(\zeta_\infty,\zeta)$
-(semi)stable in the sense of Definition 1·5, where
![]() $\zeta_\infty = -\zeta\cdot \underline{\dim}\,\rho$
.
$\zeta_\infty = -\zeta\cdot \underline{\dim}\,\rho$
.
We now define motivic DT invariants for moduli stacks of r-framed representations of a given quiver Q. Fix a potential W on Q. Let
![]() $\widetilde{Q}$
be the r-framing of Q at a given vertex
$\widetilde{Q}$
be the r-framing of Q at a given vertex
![]() $0 \in Q_0$
, and let
$0 \in Q_0$
, and let
![]() $\widetilde J$
be the Jacobi algebra
$\widetilde J$
be the Jacobi algebra
![]() $J_{\widetilde{Q},W}$
, where W is viewed as a potential on
$J_{\widetilde{Q},W}$
, where W is viewed as a potential on
![]() $\widetilde Q$
in the obvious way. For a generic stability parameter
$\widetilde Q$
in the obvious way. For a generic stability parameter
![]() $\zeta \in {\mathbb{R}}^{Q_0}$
, and an arbitrary dimension vector
$\zeta \in {\mathbb{R}}^{Q_0}$
, and an arbitrary dimension vector
![]() $\alpha \in {\mathbb{N}}^{Q_0}$
, set
$\alpha \in {\mathbb{N}}^{Q_0}$
, set
As in Section 1·4, consider the trace map
![]() $f_{\widetilde{\alpha}}\colon \textrm{R}(\widetilde{Q},\widetilde{\alpha})\to {\mathbb{A}}^1$
, induced by W, and its restriction to the framed-stable locus
$f_{\widetilde{\alpha}}\colon \textrm{R}(\widetilde{Q},\widetilde{\alpha})\to {\mathbb{A}}^1$
, induced by W, and its restriction to the framed-stable locus
![]() $f_{\widetilde{\zeta},\widetilde{\alpha}}\colon \textrm{R}^{\widetilde{\zeta}\text{-st}}(\widetilde{Q},\widetilde{\alpha}) \to {\mathbb{A}}^1$
. Define the moduli stacks
$f_{\widetilde{\zeta},\widetilde{\alpha}}\colon \textrm{R}^{\widetilde{\zeta}\text{-st}}(\widetilde{Q},\widetilde{\alpha}) \to {\mathbb{A}}^1$
. Define the moduli stacks
Note that we are not quotienting by
![]() ${\textrm{GL}}_{\widetilde{\alpha}} = {\textrm{GL}}_\alpha \times {\mathbb{C}}^\times$
, but only by
${\textrm{GL}}_{\widetilde{\alpha}} = {\textrm{GL}}_\alpha \times {\mathbb{C}}^\times$
, but only by
![]() ${\textrm{GL}}_\alpha$
.
${\textrm{GL}}_\alpha$
.
Definition 1·11. (See [Reference Morrison, Mozgovoy, Nagao and Szendröi25] for
![]() $r=1$
) We define r-framed motivic Donaldson–Thomas invariants
$r=1$
) We define r-framed motivic Donaldson–Thomas invariants
in
![]() $\mathcal M_{{\mathbb{C}}}$
, and the associated motivic generating functions
$\mathcal M_{{\mathbb{C}}}$
, and the associated motivic generating functions
 \begin{align*}\widetilde A_U&= \sum_{\alpha \in {\mathbb{N}}^{Q_0}} \,\left[\mathfrak M(\widetilde J,\alpha) \right]_{\text{vir}}\cdot y^{\widetilde\alpha} \in \mathcal T_{\widetilde Q} \\\mathsf Z_\zeta&= \sum_{\alpha \in {\mathbb{N}}^{Q_0}} \,\left[\mathfrak M_\zeta(\widetilde J,\alpha) \right]_{\text{vir}}\cdot y^{\widetilde\alpha} \in \mathcal T_{\widetilde Q}.\end{align*}
\begin{align*}\widetilde A_U&= \sum_{\alpha \in {\mathbb{N}}^{Q_0}} \,\left[\mathfrak M(\widetilde J,\alpha) \right]_{\text{vir}}\cdot y^{\widetilde\alpha} \in \mathcal T_{\widetilde Q} \\\mathsf Z_\zeta&= \sum_{\alpha \in {\mathbb{N}}^{Q_0}} \,\left[\mathfrak M_\zeta(\widetilde J,\alpha) \right]_{\text{vir}}\cdot y^{\widetilde\alpha} \in \mathcal T_{\widetilde Q}.\end{align*}
The fact that the r-framed invariants (1·3) live in
![]() $\mathcal M_{{\mathbb{C}}}$
(i.e. have no monodromy) follows from [Reference Morrison, Mozgovoy, Nagao and Szendröi25, Lemma 1·10]. The reason is that the dimension vector
$\mathcal M_{{\mathbb{C}}}$
(i.e. have no monodromy) follows from [Reference Morrison, Mozgovoy, Nagao and Szendröi25, Lemma 1·10]. The reason is that the dimension vector
![]() $\widetilde{\alpha} = (1,\alpha)$
contains ‘1’ as a component.
$\widetilde{\alpha} = (1,\alpha)$
contains ‘1’ as a component.
1·6. Dimensional reduction
If I is a cut for (Q, W), one can define a new quiver
![]() $Q_I = (Q_0,Q_1\setminus I)$
. Let
$Q_I = (Q_0,Q_1\setminus I)$
. Let
![]() $J_{W,I}$
be the quotient of
$J_{W,I}$
be the quotient of
![]() ${\mathbb{C}} Q_I$
by the two-sided ideal generated by the noncommutative derivatives
${\mathbb{C}} Q_I$
by the two-sided ideal generated by the noncommutative derivatives
![]() $\partial W/\partial a$
for
$\partial W/\partial a$
for
![]() $a \in I$
. Let
$a \in I$
. Let
![]() $\textrm{R}(J_{W,I},\alpha) \subset \textrm{R}(Q_I,\alpha)$
be the space of
$\textrm{R}(J_{W,I},\alpha) \subset \textrm{R}(Q_I,\alpha)$
be the space of
![]() $J_{W,I}$
-modules of dimension vector
$J_{W,I}$
-modules of dimension vector
![]() $\alpha$
. Then one has the following dimensional reduction principle.
$\alpha$
. Then one has the following dimensional reduction principle.
Proposition 1·12. ([Reference Morrison, Mozgovoy, Nagao and Szendröi25, proposition 1·15]) Suppose I is a cut for (Q, W). Set
![]() $\textrm{d}_I(\alpha) = \sum_{a \in I}\alpha_{t(a)}\alpha_{h(a)}$
. Then
$\textrm{d}_I(\alpha) = \sum_{a \in I}\alpha_{t(a)}\alpha_{h(a)}$
. Then
 \begin{equation*}A_U = \sum_{\alpha \in {\mathbb{N}}^{Q_0}}{\mathbb{L}}^{\frac{1}{2}\chi_Q(\alpha,\alpha) + \textrm{d}_I(\alpha)}\frac{[{\textrm{R}}(J_{W,I},\alpha)]}{[{\textrm{GL}}_\alpha]} \cdot y^\alpha.\end{equation*}
\begin{equation*}A_U = \sum_{\alpha \in {\mathbb{N}}^{Q_0}}{\mathbb{L}}^{\frac{1}{2}\chi_Q(\alpha,\alpha) + \textrm{d}_I(\alpha)}\frac{[{\textrm{R}}(J_{W,I},\alpha)]}{[{\textrm{GL}}_\alpha]} \cdot y^\alpha.\end{equation*}
Example 1·13. Let
![]() $Q=L_3$
be the 3-loop quiver (see Figure 1, and remove the framing vertex to obtain a picture of this quiver) with the potential
$Q=L_3$
be the 3-loop quiver (see Figure 1, and remove the framing vertex to obtain a picture of this quiver) with the potential
![]() $W=A_3[A_1,A_2]$
. Notice that
$W=A_3[A_1,A_2]$
. Notice that
![]() $J=J_{L_3,W}={\mathbb{C}}[x,y,z]$
, and
$J=J_{L_3,W}={\mathbb{C}}[x,y,z]$
, and
![]() $I = \{A_3\}$
is a cut for
$I = \{A_3\}$
is a cut for
![]() $(L_3,W)$
. The quiver
$(L_3,W)$
. The quiver
![]() $Q_I$
is the 2-loop quiver and
$Q_I$
is the 2-loop quiver and
![]() $J_{W,I} = {\mathbb{C}}[x,y]$
. We have
$J_{W,I} = {\mathbb{C}}[x,y]$
. We have
![]() $\text{d}_I(n)=n^2$
and
$\text{d}_I(n)=n^2$
and
![]() $\chi_Q(n,n)=-2n^2$
. Therefore Proposition 1·12 yields an identity
$\chi_Q(n,n)=-2n^2$
. Therefore Proposition 1·12 yields an identity
where
![]() $R(J_{W,I},n)$
is identified with the commuting variety
$R(J_{W,I},n)$
is identified with the commuting variety
and the second identity in (1·4) is the Feit–Fine formula [Reference Behrend, Bryan and Szendrői3, Reference Bryan and Morrison5, Reference Feit and Fine15].

Fig. 1. The r-framed 3-loop quiver
![]() $\widetilde{L}_3$
.
$\widetilde{L}_3$
.

Fig. 2. An illustration of Proposition 2·6.
Remark 1·14. The universal series
![]() $A_{U}$
has been computed for several homogeneous deformations of the potential W of example 1·13 in [Reference Andrew Morrison, Pym and Szendrői7].
$A_{U}$
has been computed for several homogeneous deformations of the potential W of example 1·13 in [Reference Andrew Morrison, Pym and Szendrői7].
2. Motivic DT invariants of the Quot scheme of points
2·1. Stability on the framed 3-loop quiver
The main character in this section is the framed quiver
![]() $\widetilde{L}_3$
of Figure 1, which we equip with the potential
$\widetilde{L}_3$
of Figure 1, which we equip with the potential
![]() $W=A_3[A_1,A_2]$
.
$W=A_3[A_1,A_2]$
.
Definition 2·1. Let
![]() $\widetilde{\rho}=(u,\rho)$
be a representation of
$\widetilde{\rho}=(u,\rho)$
be a representation of
![]() $\widetilde{L}_3$
of dimension (1, n). We denote by
$\widetilde{L}_3$
of dimension (1, n). We denote by
![]() $\langle{u,\rho}\rangle \subset \widetilde{\rho}$
the smallest subrepresentation of
$\langle{u,\rho}\rangle \subset \widetilde{\rho}$
the smallest subrepresentation of
![]() $\widetilde{\rho}$
containing
$\widetilde{\rho}$
containing
![]() $u(\rho_{\infty})$
. More precisely, if
$u(\rho_{\infty})$
. More precisely, if
![]() $\rho = (A_1,A_2,A_3) \in R(L_3,n)$
, then
$\rho = (A_1,A_2,A_3) \in R(L_3,n)$
, then
![]() $\langle{u,\rho}\rangle$
is the subrepresentation of
$\langle{u,\rho}\rangle$
is the subrepresentation of
![]() $\widetilde\rho$
with
$\widetilde\rho$
with
![]() ${\langle{u,\rho}\rangle}_\infty = \widetilde{\rho}_\infty = {\mathbb{C}}$
and
${\langle{u,\rho}\rangle}_\infty = \widetilde{\rho}_\infty = {\mathbb{C}}$
and
and with linear maps induced naturally by those defined by
![]() $\widetilde{\rho}$
.
$\widetilde{\rho}$
.
From now on we identify the space of stability parameters for
![]() $L_3$
with
$L_3$
with
![]() ${\mathbb{R}}$
.
${\mathbb{R}}$
.
Lemma 2·2. Let
![]() $\zeta\in {\mathbb{R}}$
be a stability parameter, and let
$\zeta\in {\mathbb{R}}$
be a stability parameter, and let
![]() $\widetilde{\rho} = (u,\rho)$
be a representation of
$\widetilde{\rho} = (u,\rho)$
be a representation of
![]() $ \ \widetilde{L}_3$
of dimension (1, n). Set
$ \ \widetilde{L}_3$
of dimension (1, n). Set
![]() $\widetilde \zeta = (-n\zeta,\zeta)$
. Then:
$\widetilde \zeta = (-n\zeta,\zeta)$
. Then:
-
(i) if
 $\zeta<0$
,
$\zeta<0$
,
 $\widetilde{\rho}$
is
$\widetilde{\rho}$
is
 $\zeta$
-semistable if and only if it is
$\zeta$
-semistable if and only if it is
 $\zeta$
-stable if and only if
$\zeta$
-stable if and only if
 $\widetilde{\rho}=\langle{u,\rho}\rangle$
;
$\widetilde{\rho}=\langle{u,\rho}\rangle$
; -
(ii) if
 $\zeta=0$
,
$\zeta=0$
,
 $\widetilde{\rho}$
is
$\widetilde{\rho}$
is
 $\zeta$
-semistable;
$\zeta$
-semistable; -
(iii) if
 $\zeta>0$
,
$\zeta>0$
,
 $\widetilde{\rho}$
is
$\widetilde{\rho}$
is
 $\zeta$
-semistable if and only if it is
$\zeta$
-semistable if and only if it is
 $\zeta$
-stable if and only if
$\zeta$
-stable if and only if
 $n=0$
.
$n=0$
.
Proof. For the case
![]() $\zeta<0$
we refer to [Reference Beentjes and Ricolfi1, proposition 2·4]. Consider the case
$\zeta<0$
we refer to [Reference Beentjes and Ricolfi1, proposition 2·4]. Consider the case
![]() $\zeta>0$
. If we had
$\zeta>0$
. If we had
![]() $n = \dim_{{\mathbb{C}}}\widetilde{\rho}_0 > 0$
, then
$n = \dim_{{\mathbb{C}}}\widetilde{\rho}_0 > 0$
, then
![]() $\rho \subset \widetilde{\rho}$
would be destabilising, for
$\rho \subset \widetilde{\rho}$
would be destabilising, for
![]() $\text{Z}_{\widetilde{\zeta}}(0,n) = -n\zeta + n\sqrt{-1}$
implies
$\text{Z}_{\widetilde{\zeta}}(0,n) = -n\zeta + n\sqrt{-1}$
implies
![]() $\varphi_{\widetilde{\zeta}}(\rho) > 1/2 = \varphi_{\widetilde{\zeta}}(\widetilde{\rho})$
, since
$\varphi_{\widetilde{\zeta}}(\rho) > 1/2 = \varphi_{\widetilde{\zeta}}(\widetilde{\rho})$
, since
![]() $\text{Z}_{\widetilde{\zeta}}(1,n)=(n+1)\sqrt{-1}$
has vanishing real part. On the other hand, if
$\text{Z}_{\widetilde{\zeta}}(1,n)=(n+1)\sqrt{-1}$
has vanishing real part. On the other hand, if
![]() $n = 0$
then
$n = 0$
then
![]() $\widetilde{\rho}$
is simple and hence
$\widetilde{\rho}$
is simple and hence
![]() $\zeta$
-stable. In the case
$\zeta$
-stable. In the case
![]() $\zeta=0$
there is nothing to prove, as all representations have phase
$\zeta=0$
there is nothing to prove, as all representations have phase
![]() $1/2$
.
$1/2$
.
Consider the following regions of the space of stability parameters
![]() ${\mathbb{R}}$
:
${\mathbb{R}}$
:
-
o
 $\Omega_{+} = \{\zeta\in {\mathbb{R}} | \zeta < 0 \}$
,
$\Omega_{+} = \{\zeta\in {\mathbb{R}} | \zeta < 0 \}$
, -
o
 $\Omega_{0} = \{\zeta\in {\mathbb{R}} | \zeta=0 \}$
,
$\Omega_{0} = \{\zeta\in {\mathbb{R}} | \zeta=0 \}$
, -
o
 $\Omega_{-} = \{\zeta\in {\mathbb{R}} | \zeta > 0\}$
.
$\Omega_{-} = \{\zeta\in {\mathbb{R}} | \zeta > 0\}$
.
By Lemma 2·2 the space of stability parameters on
![]() $\widetilde{{L}}_3$
admits a particularly simple wall-and-chamber decomposition
$\widetilde{{L}}_3$
admits a particularly simple wall-and-chamber decomposition
![]() ${\mathbb{R}} = \Omega_{+} \amalg \Omega_{0} \amalg \Omega_{-}$
with one wall (the origin) and two chambers.
${\mathbb{R}} = \Omega_{+} \amalg \Omega_{0} \amalg \Omega_{-}$
with one wall (the origin) and two chambers.
2·2. The virtual motive of the Quot scheme of points
Let
![]() $\widetilde{L}_3$
be the r-framed 3-loop quiver (Figure 1), and fix the potential
$\widetilde{L}_3$
be the r-framed 3-loop quiver (Figure 1), and fix the potential
![]() $W=A_3[A_1,A_2]$
. Fix a stability parameter
$W=A_3[A_1,A_2]$
. Fix a stability parameter
![]() $\zeta^+ \in \Omega_+ = {\mathbb{R}}_{<0}$
. Fixing
$\zeta^+ \in \Omega_+ = {\mathbb{R}}_{<0}$
. Fixing
![]() $n\geq 0$
and setting
$n\geq 0$
and setting
![]() $\widetilde{\zeta}^+ = (-n\zeta,\zeta)$
,
$\widetilde{\zeta}^+ = (-n\zeta,\zeta)$
,
![]() $\widetilde n = (1,n)$
, the quotient stack
$\widetilde n = (1,n)$
, the quotient stack
is a smooth quasiprojective variety of dimension
![]() $2n^2+rn$
, called the noncommutative Quot scheme in [Reference Beentjes and Ricolfi1]. The regular function
$2n^2+rn$
, called the noncommutative Quot scheme in [Reference Beentjes and Ricolfi1]. The regular function
![]() $f_n\colon \textrm{R}(\widetilde{L}_3,\widetilde n) \to {\mathbb{A}}^1$
given by taking the trace of W descends to a regular function on
$f_n\colon \textrm{R}(\widetilde{L}_3,\widetilde n) \to {\mathbb{A}}^1$
given by taking the trace of W descends to a regular function on
![]() $\mathfrak M_{\zeta^+}(\widetilde{L}_3,n)$
, still denoted
$\mathfrak M_{\zeta^+}(\widetilde{L}_3,n)$
, still denoted
![]() $f_n$
. We have the following description of the Quot scheme of length n quotients of
$f_n$
. We have the following description of the Quot scheme of length n quotients of
![]() $\mathscr O_{{\mathbb{A}}^3}^{\oplus r}$
.
$\mathscr O_{{\mathbb{A}}^3}^{\oplus r}$
.
Proposition 2·3. ([Reference Beentjes and Ricolfi1, theorem 2·6]) There is an identity of closed subschemes
Thanks to Proposition 2·3, we can form the virtual motives of the Quot scheme, as in Section 1·1·1, and define their generating function
Remark 2·4. The main result of [Reference Behrend, Bryan and Szendrői3] is the formula
 \begin{equation*}\mathsf{DT}_1^{\textrm{points}}({\mathbb{A}}^3,q) = \prod_{m\geq 1}\prod_{k=0}^{m-1}\left(1-{\mathbb{L}}^{2+k-\frac{m}{2}}q^m\right)^{-1}.\end{equation*}
\begin{equation*}\mathsf{DT}_1^{\textrm{points}}({\mathbb{A}}^3,q) = \prod_{m\geq 1}\prod_{k=0}^{m-1}\left(1-{\mathbb{L}}^{2+k-\frac{m}{2}}q^m\right)^{-1}.\end{equation*}
The series
![]() $\mathsf{DT}_1^{\textrm{points}}(Y,q)$
studied in [Reference Behrend, Bryan and Szendrői3] for an arbitrary smooth 3-fold Y also appeared in [Reference Davison and Ricolfi11] as the wall-crossing factor in the motivic DT/PT correspondence based at a fixed smooth curve
$\mathsf{DT}_1^{\textrm{points}}(Y,q)$
studied in [Reference Behrend, Bryan and Szendrői3] for an arbitrary smooth 3-fold Y also appeared in [Reference Davison and Ricolfi11] as the wall-crossing factor in the motivic DT/PT correspondence based at a fixed smooth curve
![]() $C \subset Y$
in Y. This correspondence refined its enumerative counterpart [Reference Ricolfi32, Reference Ricolfi33]. The same phenomenon occurred in [Reference Morrison, Mozgovoy, Nagao and Szendröi25, Reference Morrison and Nagao26] in the context of framed motivic DT invariants. See [Reference Bridgeland4, Reference Ricolfi35] for a generalisation
$C \subset Y$
in Y. This correspondence refined its enumerative counterpart [Reference Ricolfi32, Reference Ricolfi33]. The same phenomenon occurred in [Reference Morrison, Mozgovoy, Nagao and Szendröi25, Reference Morrison and Nagao26] in the context of framed motivic DT invariants. See [Reference Bridgeland4, Reference Ricolfi35] for a generalisation
![]() $\mathsf{DT}_r^{\textrm{points}}(Y,q)$
of (2·1) to an arbitrary smooth 3-fold Y. See [Reference Ricolfi34] for a plethystic formula expressing the naive motives
$\mathsf{DT}_r^{\textrm{points}}(Y,q)$
of (2·1) to an arbitrary smooth 3-fold Y. See [Reference Ricolfi34] for a plethystic formula expressing the naive motives
![]() $[{\textrm{Quot}}_Y(F,n)] \in K_0(\text{Var}_{{\mathbb{C}}})$
in terms of the motives of the punctual Quot schemes.
$[{\textrm{Quot}}_Y(F,n)] \in K_0(\text{Var}_{{\mathbb{C}}})$
in terms of the motives of the punctual Quot schemes.
The main identity of Theorem 0·1
 \begin{equation}\mathsf{DT}_r^{\textrm{points}}({\mathbb{A}}^3,q) = \prod_{m\geq 1}\prod_{k=0}^{rm-1}\left(1-{\mathbb{L}}^{2+k-\frac{rm}{2}}q^m\right)^{-1}\end{equation}
\begin{equation}\mathsf{DT}_r^{\textrm{points}}({\mathbb{A}}^3,q) = \prod_{m\geq 1}\prod_{k=0}^{rm-1}\left(1-{\mathbb{L}}^{2+k-\frac{rm}{2}}q^m\right)^{-1}\end{equation}
will be proved in the next subsection. An argument following closely the technique used in the
![]() $r=1$
case by Behrend–Bryan–Szendrői [Reference Behrend, Bryan and Szendrői3], was given in the PhD theses of the first and third authors [Reference Cazzaniga6, Reference Ricolfi31]. In the following subsection, we will instead exploit an r-framed version of motivic wall-crossing. This technique, inspired by [Reference Morrison, Mozgovoy, Nagao and Szendröi25, Reference Morrison and Nagao26, Reference Mozgovoy28], will be also applied to small crepant resolutions of affine toric Calabi–Yau 3-folds in [Reference Cazzaniga and Ricolfi8].
$r=1$
case by Behrend–Bryan–Szendrői [Reference Behrend, Bryan and Szendrői3], was given in the PhD theses of the first and third authors [Reference Cazzaniga6, Reference Ricolfi31]. In the following subsection, we will instead exploit an r-framed version of motivic wall-crossing. This technique, inspired by [Reference Morrison, Mozgovoy, Nagao and Szendröi25, Reference Morrison and Nagao26, Reference Mozgovoy28], will be also applied to small crepant resolutions of affine toric Calabi–Yau 3-folds in [Reference Cazzaniga and Ricolfi8].
Granting (2·2) for the moment, we prove in the next lemma the second assertion in Theorem 0·1, i.e. Formula (0·2).
Lemma 2·5. There is an identity
 \begin{equation}\prod_{m\geq 1}\prod_{k=0}^{rm-1}\left(1-{\mathbb{L}}^{2+k-\frac{rm}{2}}q^m\right)^{-1} \,=\, \prod_{i=1}^r \mathsf{DT}_1^{\textrm{points}}\left({\mathbb{A}}^3,q{\mathbb{L}}^{\frac{-r-1}{2}+i}\right).\end{equation}
\begin{equation}\prod_{m\geq 1}\prod_{k=0}^{rm-1}\left(1-{\mathbb{L}}^{2+k-\frac{rm}{2}}q^m\right)^{-1} \,=\, \prod_{i=1}^r \mathsf{DT}_1^{\textrm{points}}\left({\mathbb{A}}^3,q{\mathbb{L}}^{\frac{-r-1}{2}+i}\right).\end{equation}
Proof. The sought after identity follows from a simple manipulation:
 \begin{align*} \prod_{i=1}^r\mathsf{DT}_1^{\textrm{points}}({\mathbb{A}}^3,q{\mathbb{L}}^{\frac{-r-1}{2}+i}) &\,=\,\prod_{i=1}^r \prod_{m\geq 1}\prod_{k=0}^{m-1}\left(1-{\mathbb{L}}^{2+k-\frac{m}{2}}{\mathbb{L}}^{\frac{-r-1}{2}m+im}q^m\right)^{-1} \\ &\,=\,\prod_{m\geq 1}\prod_{k=0}^{m-1}\prod_{i=1}^r \left(1-{\mathbb{L}}^{2+k+(i-1)m-\frac{rm}{2}}q^m\right)^{-1} \\ &\,=\,\prod_{m\geq 1}\prod_{k=0}^{rm-1}\left(1-{\mathbb{L}}^{2+k-\frac{rm}{2}}q^m\right)^{-1},\end{align*}
\begin{align*} \prod_{i=1}^r\mathsf{DT}_1^{\textrm{points}}({\mathbb{A}}^3,q{\mathbb{L}}^{\frac{-r-1}{2}+i}) &\,=\,\prod_{i=1}^r \prod_{m\geq 1}\prod_{k=0}^{m-1}\left(1-{\mathbb{L}}^{2+k-\frac{m}{2}}{\mathbb{L}}^{\frac{-r-1}{2}m+im}q^m\right)^{-1} \\ &\,=\,\prod_{m\geq 1}\prod_{k=0}^{m-1}\prod_{i=1}^r \left(1-{\mathbb{L}}^{2+k+(i-1)m-\frac{rm}{2}}q^m\right)^{-1} \\ &\,=\,\prod_{m\geq 1}\prod_{k=0}^{rm-1}\left(1-{\mathbb{L}}^{2+k-\frac{rm}{2}}q^m\right)^{-1},\end{align*}
as claimed.
2·3. Calculation via wall-crossing
In this subsection we prove Theorem 0·1. Consider the universal generating function
as an element of the motivic quantum torus. To (generic) stability parameters
![]() $\zeta^{\pm} \in \Omega_{\pm}$
we associate elements (cf. Definition 1·11)
$\zeta^{\pm} \in \Omega_{\pm}$
we associate elements (cf. Definition 1·11)
By Lemma 2·2 (iii), we have an identity
whereas the series
![]() $\mathsf Z_{\zeta^+}$
is, essentially, a “shift” of the generating function
$\mathsf Z_{\zeta^+}$
is, essentially, a “shift” of the generating function
![]() $\mathsf{DT}_r^{\textrm{points}}({\mathbb{A}}^3,y^{(0,1)})$
. More precisely, by Proposition 2·3 we have an identification
$\mathsf{DT}_r^{\textrm{points}}({\mathbb{A}}^3,y^{(0,1)})$
. More precisely, by Proposition 2·3 we have an identification
of critical loci sitting inside the noncommutative Quot scheme; in particular, the associated virtual motives are the same. The shift is intended in the following sense: since
![]() ${\langle{(0,n),(1,0)}\rangle}_{\widetilde{L}_3} = rn$
, the product rule (1·1) yields the identity
${\langle{(0,n),(1,0)}\rangle}_{\widetilde{L}_3} = rn$
, the product rule (1·1) yields the identity
Since we can express
![]() $y^{(0,n)}$
as the n-fold product of
$y^{(0,n)}$
as the n-fold product of
![]() $y^{(0,1)}$
with itself, we obtain
$y^{(0,1)}$
with itself, we obtain
The last generating function we need to analyse is
whose n-th coefficient is the virtual motive of the stack of 0-dimensional
![]() ${\mathbb{C}}[x,y,z]$
-modules of length n. This was already computed in Example 1·13:
${\mathbb{C}}[x,y,z]$
-modules of length n. This was already computed in Example 1·13:
Proposition 2·6. In
![]() $\mathcal T_{\widetilde{L}_3}$
, there are identities
$\mathcal T_{\widetilde{L}_3}$
, there are identities
Proof. Let
![]() $\widetilde{\rho} = (u,\rho)$
be a
$\widetilde{\rho} = (u,\rho)$
be a
![]() $\widetilde{J}$
-module. Consider
$\widetilde{J}$
-module. Consider
![]() $\zeta^+\in \Omega_{+}$
, and let
$\zeta^+\in \Omega_{+}$
, and let
![]() $\langle{u,\rho}\rangle\subset \widetilde{\rho}$
be the submodule introduced in Definition 2·1. We have that
$\langle{u,\rho}\rangle\subset \widetilde{\rho}$
be the submodule introduced in Definition 2·1. We have that
![]() $\langle{u,\rho}\rangle$
is
$\langle{u,\rho}\rangle$
is
![]() $\zeta^+$
-stable by Lemma 2·2(i) and the quotient
$\zeta^+$
-stable by Lemma 2·2(i) and the quotient
![]() $\widetilde{\rho}/\langle{u,\rho}\rangle$
is supported at the vertex 0. From this we deduce the decomposition
$\widetilde{\rho}/\langle{u,\rho}\rangle$
is supported at the vertex 0. From this we deduce the decomposition
![]() $\widetilde{A}_U=\mathsf Z_{\zeta^+}\cdot A_{U}$
.
$\widetilde{A}_U=\mathsf Z_{\zeta^+}\cdot A_{U}$
.
Consider now
![]() $\zeta^- \in \Omega_{-}$
. The quotient of
$\zeta^- \in \Omega_{-}$
. The quotient of
![]() $\widetilde{\rho}$
by the submodule
$\widetilde{\rho}$
by the submodule
![]() $\rho$
based at the vertex 0 is the simple module supported at the framing vertex
$\rho$
based at the vertex 0 is the simple module supported at the framing vertex
![]() $\infty$
. By Lemma 2·2 (iii) this is the unique
$\infty$
. By Lemma 2·2 (iii) this is the unique
![]() $\zeta^-$
-stable module for the current choice of
$\zeta^-$
-stable module for the current choice of
![]() $\zeta^-$
, so we obtain the decomposition
$\zeta^-$
, so we obtain the decomposition
![]() $\widetilde{A}_U=A_{U}\cdot \mathsf Z_{\zeta^-}$
.
$\widetilde{A}_U=A_{U}\cdot \mathsf Z_{\zeta^-}$
.
Remark 2·7. In the previous proof, the decompositions in the motivic quantum torus follow directly from the functoriality of the Harder–Narasimhan filtration, combined with the existence of a well-defined motivic integration map, for which we refer to Mozgovoy’s work [Reference Mozgovoy27, Reference Mozgovoy28], formalising an original construction by Kontsevich–Soibelman [Reference Kontsevich and Soibelman20].
Note that we have an identity
where we have used (2·5) for the second equality. By Formula (2·6), the left-hand term of Formula (2·8) can then be rewritten as
 \begin{equation*}\mathsf{DT}_r^{\textrm{points}}\left({\mathbb{A}}^3,{\mathbb{L}}^{-\frac{r}{2}} y^{(0,1)}\right)\cdot \sum_{n\geq 0}\,\bigl[\mathfrak{M}(J,n)\bigr]_{\text{vir}}\cdot y_{\infty} \cdot y^{(0,n)} \\ \quad \quad \quad \quad \quad \quad \quad \quad \quad \quad \quad \quad \quad \quad \quad \quad \quad \quad \quad \quad \quad \quad \quad \quad =\mathsf{DT}_r^{\textrm{points}}\left({\mathbb{A}}^3,{\mathbb{L}}^{-\frac{r}{2}} y^{(0,1)}\right)\cdot \sum_{n\geq 0}\,\bigl[\mathfrak{M}(J,n)\bigr]_{\text{vir}} {\mathbb{L}}^{-rn}\cdot y^{(0,n)}\cdot y_{\infty}.\end{equation*}
\begin{equation*}\mathsf{DT}_r^{\textrm{points}}\left({\mathbb{A}}^3,{\mathbb{L}}^{-\frac{r}{2}} y^{(0,1)}\right)\cdot \sum_{n\geq 0}\,\bigl[\mathfrak{M}(J,n)\bigr]_{\text{vir}}\cdot y_{\infty} \cdot y^{(0,n)} \\ \quad \quad \quad \quad \quad \quad \quad \quad \quad \quad \quad \quad \quad \quad \quad \quad \quad \quad \quad \quad \quad \quad \quad \quad =\mathsf{DT}_r^{\textrm{points}}\left({\mathbb{A}}^3,{\mathbb{L}}^{-\frac{r}{2}} y^{(0,1)}\right)\cdot \sum_{n\geq 0}\,\bigl[\mathfrak{M}(J,n)\bigr]_{\text{vir}} {\mathbb{L}}^{-rn}\cdot y^{(0,n)}\cdot y_{\infty}.\end{equation*}
Therefore, by Equation (2·4), identifying the two expressions for
![]() $\widetilde{A}_U$
in Equation (2·8) yields
$\widetilde{A}_U$
in Equation (2·8) yields
which is equivalent to
 \begin{equation*}\mathsf{DT}_r^{\textrm{points}}\left({\mathbb{A}}^3,{\mathbb{L}}^{-\frac{r}{2}} y^{(0,1)}\right) = \frac{A_U\left(y^{(0,1)}\right)}{A_U\left({\mathbb{L}}^{-r}y^{(0,1)}\right)}.\end{equation*}
\begin{equation*}\mathsf{DT}_r^{\textrm{points}}\left({\mathbb{A}}^3,{\mathbb{L}}^{-\frac{r}{2}} y^{(0,1)}\right) = \frac{A_U\left(y^{(0,1)}\right)}{A_U\left({\mathbb{L}}^{-r}y^{(0,1)}\right)}.\end{equation*}
Setting
![]() $q = {\mathbb{L}}^{-\frac{r}{2}}y^{(0,1)}$
, and using Equation (2·7), a simple substitution yields
$q = {\mathbb{L}}^{-\frac{r}{2}}y^{(0,1)}$
, and using Equation (2·7), a simple substitution yields
 \begin{align*} \mathsf{DT}_r^{\textrm{points}}({\mathbb{A}}^3,q) &= \frac{A_U\left({\mathbb{L}}^{\frac{r}{2}}q\right)}{A_U\left({\mathbb{L}}^{-\frac{r}{2}}q\right)} \\ &=\prod_{m\geq 1}\prod_{j\geq 0}\frac{\left(1-\mathbb L^{1-j+\frac{rm}{2}}q^m\right)^{-1}}{\left(1-\mathbb L^{1-j-\frac{rm}{2}}q^m\right)^{-1}}\\&=\prod_{m\geq 1}\prod_{j=0}^{rm-1}\left(1-\mathbb L^{1-j+\frac{rm}{2}}q^m\right)^{-1}\\&=\prod_{m\geq 1}\prod_{k=0}^{rm-1}\left(1-\mathbb L^{2+k-\frac{rm}{2}}q^m\right)^{-1}.\end{align*}
\begin{align*} \mathsf{DT}_r^{\textrm{points}}({\mathbb{A}}^3,q) &= \frac{A_U\left({\mathbb{L}}^{\frac{r}{2}}q\right)}{A_U\left({\mathbb{L}}^{-\frac{r}{2}}q\right)} \\ &=\prod_{m\geq 1}\prod_{j\geq 0}\frac{\left(1-\mathbb L^{1-j+\frac{rm}{2}}q^m\right)^{-1}}{\left(1-\mathbb L^{1-j-\frac{rm}{2}}q^m\right)^{-1}}\\&=\prod_{m\geq 1}\prod_{j=0}^{rm-1}\left(1-\mathbb L^{1-j+\frac{rm}{2}}q^m\right)^{-1}\\&=\prod_{m\geq 1}\prod_{k=0}^{rm-1}\left(1-\mathbb L^{2+k-\frac{rm}{2}}q^m\right)^{-1}.\end{align*}
Formula (0·1) is proved. By Lemma 2·5, Theorem 0·1 is proved.
Remark 2·8. The generating function
![]() $\mathsf{DT}_r^{\textrm{points}}({\mathbb{A}}^3,(-1)^rq)$
admits the plethystic expression
$\mathsf{DT}_r^{\textrm{points}}({\mathbb{A}}^3,(-1)^rq)$
admits the plethystic expression
 \begin{equation*}\mathsf{DT}_r^{\textrm{points}}({\mathbb{A}}^3,(-1)^rq) =Exp\left(\frac{(-1)^rq\mathbb L^{\frac{3}{2}}}{\bigl(1-(-\mathbb L^{-\frac{1}{2}})^rq\bigr)\bigl(1-(-\mathbb L^{\frac{1}{2}})^rq\bigr)}\frac{\mathbb L^{-\frac{r}{2}}-\mathbb L^{\frac{r}{2}}}{\mathbb L^{-\frac{1}{2}}-\mathbb L^{\frac{1}{2}}}\right).\end{equation*}
\begin{equation*}\mathsf{DT}_r^{\textrm{points}}({\mathbb{A}}^3,(-1)^rq) =Exp\left(\frac{(-1)^rq\mathbb L^{\frac{3}{2}}}{\bigl(1-(-\mathbb L^{-\frac{1}{2}})^rq\bigr)\bigl(1-(-\mathbb L^{\frac{1}{2}})^rq\bigr)}\frac{\mathbb L^{-\frac{r}{2}}-\mathbb L^{\frac{r}{2}}}{\mathbb L^{-\frac{1}{2}}-\mathbb L^{\frac{1}{2}}}\right).\end{equation*}
This is exploited in [Reference Ricolfi35, section Reference Bridgeland4] to define
![]() $[{\textrm{Quot}}_Y(F,n)]_{\text{vir}}$
for all 3-folds Y and locally free sheaves F over Y. The shift by the sign
$[{\textrm{Quot}}_Y(F,n)]_{\text{vir}}$
for all 3-folds Y and locally free sheaves F over Y. The shift by the sign
![]() $(\!-1)^r$
is needed in order to write the series as a plethystic exponential (and cannot be naively removed from both sides). This is the case for K-theoretic DT invariants as well [Reference Fasola, Monavari and Ricolfi14, theorem A].
$(\!-1)^r$
is needed in order to write the series as a plethystic exponential (and cannot be naively removed from both sides). This is the case for K-theoretic DT invariants as well [Reference Fasola, Monavari and Ricolfi14, theorem A].
Remark 2·9. The Euler number specialisation
![]() ${\mathbb{L}}^{1/2} \to -1$
applied to Formula (0·1) yields a formula for the generating function of virtual Euler characteristics of Quot schemes,
${\mathbb{L}}^{1/2} \to -1$
applied to Formula (0·1) yields a formula for the generating function of virtual Euler characteristics of Quot schemes,
where
![]() $\mathsf M(q) = \prod_{m\geq 1}(1-q^m)^{-m}$
is the MacMahon function, the generating function of plane partitions, and where
$\mathsf M(q) = \prod_{m\geq 1}(1-q^m)^{-m}$
is the MacMahon function, the generating function of plane partitions, and where
![]() $\chi_{\text{vir}}(-) = \chi(-,\nu)$
is the Euler characteristic weighted by Behrend’s microlocal function [Reference Behrend2]. The above identity can be seen as the Calabi–Yau specialisation (i.e. the specialisation
$\chi_{\text{vir}}(-) = \chi(-,\nu)$
is the Euler characteristic weighted by Behrend’s microlocal function [Reference Behrend2]. The above identity can be seen as the Calabi–Yau specialisation (i.e. the specialisation
![]() $s_1+s_2+s_3 = 0$
) of the generating function of cohomological Donaldson–Thomas invariants of
$s_1+s_2+s_3 = 0$
) of the generating function of cohomological Donaldson–Thomas invariants of
![]() ${\mathbb{A}}^3$
,
${\mathbb{A}}^3$
,
obtained in [Reference Fasola, Monavari and Ricolfi14, theorem B] as a higher rank version of [Reference Maulik, Nekrasov, Okounkov and Pandharipande22, theorem 1], where
![]() $s_1$
,
$s_1$
,
![]() $s_2$
and
$s_2$
and
![]() $s_3$
are the equivariant parameters of the torus
$s_3$
are the equivariant parameters of the torus
![]() ${\mathbb{T}} = {\mathbb{G}}_m^3$
acting on the Quot scheme.
${\mathbb{T}} = {\mathbb{G}}_m^3$
acting on the Quot scheme.
3. The normal limit law and asymptotics
In Section 3·1, we introduce a family of random variables on the space of r-coloured plane partitions, and we describe the asymptotics of the members of the family after suitable normalisation in Proposition 3·1. Theorem 0·2, the main theorem of the section, is deduced from Proposition 3·1 in Section 3·2. Finally, Section 3·3 is entirely devoted to the proof of Proposition 3·1.
3·1. Random variables on r-coloured plane partitions
We introduce a multivariate function
 \begin{equation} F(u,v,w,z)=\prod_{l=1}^{r}\prod_{m\geq 1}\prod_{k=1}^{m}\left(1-wu^{k}v^{ml}z^m\right)^{-1}.\end{equation}
\begin{equation} F(u,v,w,z)=\prod_{l=1}^{r}\prod_{m\geq 1}\prod_{k=1}^{m}\left(1-wu^{k}v^{ml}z^m\right)^{-1}.\end{equation}
The coefficient of
![]() $z^n$
is a polynomial on the three variables u, v and w, which we denote by
$z^n$
is a polynomial on the three variables u, v and w, which we denote by
![]() $Q_{n}(u,v,w)$
, whose coefficients are nonnegative integers. When
$Q_{n}(u,v,w)$
, whose coefficients are nonnegative integers. When
![]() $u=v=w=1$
, we obtain the well known MacMahon function raised to the power r, which is the generating function for the r-tuples of plane partitions. Hence,
$u=v=w=1$
, we obtain the well known MacMahon function raised to the power r, which is the generating function for the r-tuples of plane partitions. Hence,
![]() $Q_{n}(1,1,1)$
is the number of r-tuples of plane partitions of total size n, i.e. the number of r-coloured plane partitions
$Q_{n}(1,1,1)$
is the number of r-tuples of plane partitions of total size n, i.e. the number of r-coloured plane partitions
![]() $(\pi_1,\, \pi_2, \, \dots, \, \pi_r)$
such that
$(\pi_1,\, \pi_2, \, \dots, \, \pi_r)$
such that
![]() $\sum_{j=1}^{r}\lvert\pi_j\rvert=n$
, where
$\sum_{j=1}^{r}\lvert\pi_j\rvert=n$
, where
![]() $\lvert\pi_j\rvert$
denotes the sum of the entries of the plane partition
$\lvert\pi_j\rvert$
denotes the sum of the entries of the plane partition
![]() $\pi_j$
(or the number of boxes, cf. Figure 3). The polynomial
$\pi_j$
(or the number of boxes, cf. Figure 3). The polynomial
![]() $Q_{n}(u,v,w)$
, when divided by
$Q_{n}(u,v,w)$
, when divided by
![]() $Q_{n}(1,1,1)$
, represents the joint probability generating function of some random variables
$Q_{n}(1,1,1)$
, represents the joint probability generating function of some random variables
![]() $X_n$
,
$X_n$
,
![]() $Y_n$
, and
$Y_n$
, and
![]() $Z_n$
on the space of r-coloured plane partitions of size n, where each r-tuple is equally likely. More precisely, we have
$Z_n$
on the space of r-coloured plane partitions of size n, where each r-tuple is equally likely. More precisely, we have
To describe these random variables, we need to define certain parameters of plane partitions. For a plane partition
![]() $\pi$
, let
$\pi$
, let
![]() $\Delta(\pi)$
denote the sum of the diagonal parts of
$\Delta(\pi)$
denote the sum of the diagonal parts of
![]() $\pi$
,
$\pi$
,
![]() $\Delta_{+}(\pi)$
denote the sum of the upper diagonal parts, and
$\Delta_{+}(\pi)$
denote the sum of the upper diagonal parts, and
![]() $\Delta_{-}(\pi)$
denote the sum of the lower diagonal parts. See Figure 3 for an example of a plane partition showing the values of these parameters.
$\Delta_{-}(\pi)$
denote the sum of the lower diagonal parts. See Figure 3 for an example of a plane partition showing the values of these parameters.

Fig. 3. A plane partition
![]() $\pi$
of size
$\pi$
of size
![]() $\lvert\pi\rvert=31$
,
$\lvert\pi\rvert=31$
,
![]() $\Delta(\pi)=9$
,
$\Delta(\pi)=9$
,
![]() $\Delta_{+}(\pi)=12$
, and
$\Delta_{+}(\pi)=12$
, and
![]() $\Delta_{-}(\pi)=10$
.
$\Delta_{-}(\pi)=10$
.
The parameter
![]() $\Delta(\pi)$
is also known as the trace of
$\Delta(\pi)$
is also known as the trace of
![]() $\pi$
and it has been studied in the literature, see for instance [Reference Kamenov and Mutafchiev19] and the references therein. In particular, one has
$\pi$
and it has been studied in the literature, see for instance [Reference Kamenov and Mutafchiev19] and the references therein. In particular, one has
Similarly, we can find in [Reference Morrison24] that
 \begin{equation*}\prod_{m\geq 1}\prod_{k=1}^{m}(1-q^{2k-m}z^{m})^{-1}=\sum_{\pi}q^{\Delta(\pi)+\Delta_{+}(\pi)-\Delta_{-}(\pi)}z^{\lvert\pi\rvert}.\end{equation*}
\begin{equation*}\prod_{m\geq 1}\prod_{k=1}^{m}(1-q^{2k-m}z^{m})^{-1}=\sum_{\pi}q^{\Delta(\pi)+\Delta_{+}(\pi)-\Delta_{-}(\pi)}z^{\lvert\pi\rvert}.\end{equation*}
We can easily deduce from these two identities that for an r-coloured plane partition
![]() $\overline{\pi} = (\pi_1, \pi_2, \ldots, \pi_r)$
of total size n, we have
$\overline{\pi} = (\pi_1, \pi_2, \ldots, \pi_r)$
of total size n, we have
 \begin{align*} X_n\left(\overline{\pi}\right)& =\frac{n}{2}+\frac{1}{2}\left( \sum_{l=1}^{r}\left(\Delta(\pi_l)+\Delta_{+}(\pi_l)-\Delta_{-}(\pi_l)\right)\right)\\ &=\sum_{l=1}^{r}\left(\Delta(\pi_l)+\Delta_{+}(\pi_l)\right),\\ Y_n\left(\overline{\pi}\right)& = \sum_{l=1}^{r}l|\pi_l|, \ \ \text{and}\\ Z_n\left(\overline{\pi}\right)& = \sum_{l=1}^{r}\Delta(\pi_l).\end{align*}
\begin{align*} X_n\left(\overline{\pi}\right)& =\frac{n}{2}+\frac{1}{2}\left( \sum_{l=1}^{r}\left(\Delta(\pi_l)+\Delta_{+}(\pi_l)-\Delta_{-}(\pi_l)\right)\right)\\ &=\sum_{l=1}^{r}\left(\Delta(\pi_l)+\Delta_{+}(\pi_l)\right),\\ Y_n\left(\overline{\pi}\right)& = \sum_{l=1}^{r}l|\pi_l|, \ \ \text{and}\\ Z_n\left(\overline{\pi}\right)& = \sum_{l=1}^{r}\Delta(\pi_l).\end{align*}
When
![]() $r=1$
, Kamenov and Mutafchiev [Reference Kamenov and Mutafchiev19] proved that the distribution of the trace of a random plane partition of size n, when suitably normalised, is asymptotically normal. Morrison [Reference Morrison24] also established asymptotic normality for any random variable of the form
$r=1$
, Kamenov and Mutafchiev [Reference Kamenov and Mutafchiev19] proved that the distribution of the trace of a random plane partition of size n, when suitably normalised, is asymptotically normal. Morrison [Reference Morrison24] also established asymptotic normality for any random variable of the form
![]() $\delta\Delta(\pi)+\Delta_{+}(\pi)-\Delta_{-}(\pi)$
, where
$\delta\Delta(\pi)+\Delta_{+}(\pi)-\Delta_{-}(\pi)$
, where
![]() $\pi$
is a random plane partition of size n and
$\pi$
is a random plane partition of size n and
![]() $\delta$
is a fixed real number. We show that for any fixed integer
$\delta$
is a fixed real number. We show that for any fixed integer
![]() $r\geq 1$
, any nontrivial linear combination of the variables
$r\geq 1$
, any nontrivial linear combination of the variables
![]() $X_n$
,
$X_n$
,
![]() $Y_n$
and
$Y_n$
and
![]() $Z_n$
, when suitably normalised, converges weakly to a normal distribution. It is worth noting that the random variable
$Z_n$
, when suitably normalised, converges weakly to a normal distribution. It is worth noting that the random variable
![]() $Y_n$
is non-constant only when
$Y_n$
is non-constant only when
![]() $r>1$
.
$r>1$
.
Proposition 3·1. For any fixed real vector
![]() $(\alpha,\beta,\gamma)\neq (0,0,0)$
, there exist sequences of real numbers
$(\alpha,\beta,\gamma)\neq (0,0,0)$
, there exist sequences of real numbers
![]() $\mu_n$
and
$\mu_n$
and
![]() $\sigma_n\geq 0$
such that the normalised random variable
$\sigma_n\geq 0$
such that the normalised random variable
converges weakly to the standard normal distribution. Moreover,
![]() $\mu_n$
and
$\mu_n$
and
![]() $\sigma_n$
satisfy the following asymptotic formulas as
$\sigma_n$
satisfy the following asymptotic formulas as
![]() $n\to \infty$
:
$n\to \infty$
:
 \begin{align*}\mu_n&\,\,=\,\,\left(\frac{1}{2}\alpha+\frac{r+1}{2} \beta\right)n+\frac{r^{1/3}\zeta(2)(\alpha+2\gamma)}{2^{5/3}(\zeta(3))^{2/3}}\, n^{2/3}+\mathcal{O}(n^{1/3}), \, \text{ and }\,\\\sigma_n^2 &\,\,\sim\,\,\begin{cases}\displaystyle \frac{\alpha^2+(r^2-1)\beta^2}{2^{7/3}(r\zeta(3))^{1/3}}\, n^{4/3}\, & \text{ if } (\alpha,\beta)\neq (0,0),\\[2em]\displaystyle \frac{r^{1/3}\gamma^2}{3(2\zeta(3))^{2/3}} n^{2/3}\log n \, & \text{otherwise.}\end{cases}\end{align*}
\begin{align*}\mu_n&\,\,=\,\,\left(\frac{1}{2}\alpha+\frac{r+1}{2} \beta\right)n+\frac{r^{1/3}\zeta(2)(\alpha+2\gamma)}{2^{5/3}(\zeta(3))^{2/3}}\, n^{2/3}+\mathcal{O}(n^{1/3}), \, \text{ and }\,\\\sigma_n^2 &\,\,\sim\,\,\begin{cases}\displaystyle \frac{\alpha^2+(r^2-1)\beta^2}{2^{7/3}(r\zeta(3))^{1/3}}\, n^{4/3}\, & \text{ if } (\alpha,\beta)\neq (0,0),\\[2em]\displaystyle \frac{r^{1/3}\gamma^2}{3(2\zeta(3))^{2/3}} n^{2/3}\log n \, & \text{otherwise.}\end{cases}\end{align*}
Looking at the asymptotic behaviour of the random variables
![]() $X_n$
,
$X_n$
,
![]() $Y_n$
and
$Y_n$
and
![]() $Z_n$
, when divided by
$Z_n$
, when divided by
![]() $n^{2/3}$
, we observe from the above result that the random variable
$n^{2/3}$
, we observe from the above result that the random variable
![]() $n^{-2/3}Z_n$
degenerates as
$n^{-2/3}Z_n$
degenerates as
![]() $n\to \infty$
. Furthermore, by the Camér–Wold device [Reference Cramér and Wold9], the random variables
$n\to \infty$
. Furthermore, by the Camér–Wold device [Reference Cramér and Wold9], the random variables
![]() $n^{-2/3}X_n$
,
$n^{-2/3}X_n$
,
![]() $n^{-2/3}Y_n$
converge jointly to a bivariate normal distribution with a diagonal covariance matrix. The appropriate normalisation of
$n^{-2/3}Y_n$
converge jointly to a bivariate normal distribution with a diagonal covariance matrix. The appropriate normalisation of
![]() $Z_n$
is
$Z_n$
is
![]() $n^{-1/3}(\log n)^{-1/2}Z_n$
which is, when centred, asymptotically normal. This asymptotic normality and the asymptotic formulas for
$n^{-1/3}(\log n)^{-1/2}Z_n$
which is, when centred, asymptotically normal. This asymptotic normality and the asymptotic formulas for
![]() $\mu_n$
and
$\mu_n$
and
![]() $\sigma_n^2$
agree with the main result in [Reference Kamenov and Mutafchiev19] when
$\sigma_n^2$
agree with the main result in [Reference Kamenov and Mutafchiev19] when
![]() $r=1$
and
$r=1$
and
![]() $(\alpha,\beta,\gamma)=(0,0,1).$
$(\alpha,\beta,\gamma)=(0,0,1).$
Convention 3·1. We shall use the Vinogradov notation
![]() $\ll$
interchangeably with the
$\ll$
interchangeably with the
![]() $\mathcal O$
-notation. For instance, by
$\mathcal O$
-notation. For instance, by
![]() $f(n)\ll g(n)$
(or
$f(n)\ll g(n)$
(or
![]() $g(n)\gg f(n)$
) as
$g(n)\gg f(n)$
) as
![]() $n\to\infty$
, we mean that there exists a positive constant C such that
$n\to\infty$
, we mean that there exists a positive constant C such that
![]() $|f(n)|\leq Cg(n)$
for sufficiently large n.
$|f(n)|\leq Cg(n)$
for sufficiently large n.
Theorem 0·2 now follows immediately from Proposition 3·1 as we will see next.
3·2. Deducing Theorem 0·2
Granting Proposition 3·1, we can now finish the proof of Theorem 0·2, our second main result.
Theorem 3·2. As
![]() $n\to \infty$
, the normalised random variable
$n\to \infty$
, the normalised random variable
![]() $n^{-2/3}S_{n,r}$
converges in distribution to
$n^{-2/3}S_{n,r}$
converges in distribution to
![]() $\mathcal{N}(\mu, \sigma^2)$
with
$\mathcal{N}(\mu, \sigma^2)$
with
where
![]() $\zeta(s)$
is Riemann’s zeta function.
$\zeta(s)$
is Riemann’s zeta function.
Proof. With the change of variable
![]() $T={\mathbb{L}}^{1/2}$
, the combination of the equations (0·1) and (0·2) in Theorem 0·1 yields
$T={\mathbb{L}}^{1/2}$
, the combination of the equations (0·1) and (0·2) in Theorem 0·1 yields
 \begin{equation*}\mathsf{DT}_r^{\textrm{points}}({\mathbb{A}}^3,q) =\prod_{l=1}^{r}\prod_{m\geq 1}\prod_{k=0}^{m-1}\left(1-T^{4+2k-m}\Big(qT^{-r-1+2l}\Big)^m\right)^{-1}.\end{equation*}
\begin{equation*}\mathsf{DT}_r^{\textrm{points}}({\mathbb{A}}^3,q) =\prod_{l=1}^{r}\prod_{m\geq 1}\prod_{k=0}^{m-1}\left(1-T^{4+2k-m}\Big(qT^{-r-1+2l}\Big)^m\right)^{-1}.\end{equation*}
The product on the right-hand side can be expressed in terms of our auxiliary function F(u, v, w, z) defined at the beginning of this section. First we write it as follows
 \begin{equation*} \prod_{l=1}^{r}\prod_{m\geq 1}\prod_{k=0}^{m-1}\left(1-T^{4+m-2(m-k)}\Big(qT^{r+1-2(r-l+1)}\Big)^m\right)^{-1}.\end{equation*}
\begin{equation*} \prod_{l=1}^{r}\prod_{m\geq 1}\prod_{k=0}^{m-1}\left(1-T^{4+m-2(m-k)}\Big(qT^{r+1-2(r-l+1)}\Big)^m\right)^{-1}.\end{equation*}
If k goes from 0 to
![]() $m-1$
, then
$m-1$
, then
![]() $m-k$
goes from m to 1. Similarly, if l goes from 1 to r, then
$m-k$
goes from m to 1. Similarly, if l goes from 1 to r, then
![]() $r-l+1$
goes from r to 1. Therefore, we have
$r-l+1$
goes from r to 1. Therefore, we have
 \begin{align*}\mathsf{DT}_r^{\textrm{points}}({\mathbb{A}}^3,q)& =\prod_{l=1}^{r}\prod_{m\geq 1}\prod_{k=1}^{m}\left(1-T^{4+m-2k}(T^{r+1-2l}q)^m\right)^{-1}\\& = \prod_{l=1}^{r}\prod_{m\geq 1}\prod_{k=1}^{m}\left(1-T^{4-2k-2ml}(T^{r+2}q)^m\right)^{-1}\\& =F(T^{-2},T^{-2},T^4,T^{r+2}q).\end{align*}
\begin{align*}\mathsf{DT}_r^{\textrm{points}}({\mathbb{A}}^3,q)& =\prod_{l=1}^{r}\prod_{m\geq 1}\prod_{k=1}^{m}\left(1-T^{4+m-2k}(T^{r+1-2l}q)^m\right)^{-1}\\& = \prod_{l=1}^{r}\prod_{m\geq 1}\prod_{k=1}^{m}\left(1-T^{4-2k-2ml}(T^{r+2}q)^m\right)^{-1}\\& =F(T^{-2},T^{-2},T^4,T^{r+2}q).\end{align*}
This implies that
where
![]() $M_{n,r}(T)$
is, as defined in (0·3), the coefficient of
$M_{n,r}(T)$
is, as defined in (0·3), the coefficient of
![]() $q^n$
in
$q^n$
in
![]() $\mathsf{DT}_r^{\textrm{points}}({\mathbb{A}}^3,q)$
. The second equality in (3·3) makes use of Equation (3·2). Thus,
$\mathsf{DT}_r^{\textrm{points}}({\mathbb{A}}^3,q)$
. The second equality in (3·3) makes use of Equation (3·2). Thus,
![]() $S_{n,r}$
has the same distribution as
$S_{n,r}$
has the same distribution as
![]() $4Z_n-2X_n-2Y_n+(r+2)n$
— a shifted linear combination of the variables
$4Z_n-2X_n-2Y_n+(r+2)n$
— a shifted linear combination of the variables
![]() $X_n$
,
$X_n$
,
![]() $Y_n$
, and
$Y_n$
, and
![]() $Z_n$
. Now, applying Proposition 3·1 with
$Z_n$
. Now, applying Proposition 3·1 with
![]() $(\alpha, \beta, \gamma) = (-2, -2, 4)$
, we deduce that the normalised random variable
$(\alpha, \beta, \gamma) = (-2, -2, 4)$
, we deduce that the normalised random variable
![]() $n^{-2/3}(4Z_n-2X_n-2Y_n+(r+2)n)$
converges weakly to the normal distribution
$n^{-2/3}(4Z_n-2X_n-2Y_n+(r+2)n)$
converges weakly to the normal distribution
![]() $\mathcal{N}(\mu,\sigma^2)$
with
$\mathcal{N}(\mu,\sigma^2)$
with
which proves Theorem 0·2.
3·3. Proof of Proposition 3·1
Morrison used the method of moments to prove his result in [Reference Morrison24]. However, due to the appearance of the second variable
![]() $Y_n$
and the complication that comes with it, we decided to use a different approach. We follow the method that Hwang used in [Reference Hwang18] to prove limit theorems for the number of parts in the so-called restricted partitions (these are one dimensional partitions with some restrictions on the parts). The first part of the proof is based on the saddle-point method to get an asymptotic formula for
$Y_n$
and the complication that comes with it, we decided to use a different approach. We follow the method that Hwang used in [Reference Hwang18] to prove limit theorems for the number of parts in the so-called restricted partitions (these are one dimensional partitions with some restrictions on the parts). The first part of the proof is based on the saddle-point method to get an asymptotic formula for
![]() $Q_{n}(u,v,w)$
as
$Q_{n}(u,v,w)$
as
![]() $n\to\infty$
, and the second is a perturbation technique to deduce the central limit theorem.
$n\to\infty$
, and the second is a perturbation technique to deduce the central limit theorem.
3·3·1. Saddle-point method
The goal here is to obtain an asymptotic formula for
![]() $Q_{n}(u,v,w)$
as
$Q_{n}(u,v,w)$
as
![]() $n\to\infty$
, where (u, v, w) is allowed to vary in a fixed real neighbourhood of (1, 1, 1). To simplify our notation, define
$n\to\infty$
, where (u, v, w) is allowed to vary in a fixed real neighbourhood of (1, 1, 1). To simplify our notation, define
![]() $\Phi(t)=-\log\!(1-e^{-t})$
, and for real numbers a, b and c, we let
$\Phi(t)=-\log\!(1-e^{-t})$
, and for real numbers a, b and c, we let
 \begin{equation*}f(x,y)=\sum_{l=1}^{r}\sum_{m=1}^{\infty}\sum_{k=1}^{m}\Phi(xm+y(c+ak+mbl)).\end{equation*}
\begin{equation*}f(x,y)=\sum_{l=1}^{r}\sum_{m=1}^{\infty}\sum_{k=1}^{m}\Phi(xm+y(c+ak+mbl)).\end{equation*}
The function f depends on (a, b, c) but we drop this dependence for now to ease notation. Also, for a positive number
![]() $\rho$
, we make the substitution
$\rho$
, we make the substitution
![]() $z=e^{-\tau}$
, where
$z=e^{-\tau}$
, where
![]() $\tau=\rho+it$
. Hence,
$\tau=\rho+it$
. Hence,
 \begin{equation*}f(\tau,\rho)=-\sum_{l=1}^{r}\sum_{m=1}^{\infty}\sum_{k=1}^{m}\log\left(1-e^{-\rho(c+ak+mbl)-\tau m}\right)=\log F(e^{-a\rho},e^{-b\rho},e^{-c\rho},e^{-\tau}).\end{equation*}
\begin{equation*}f(\tau,\rho)=-\sum_{l=1}^{r}\sum_{m=1}^{\infty}\sum_{k=1}^{m}\log\left(1-e^{-\rho(c+ak+mbl)-\tau m}\right)=\log F(e^{-a\rho},e^{-b\rho},e^{-c\rho},e^{-\tau}).\end{equation*}
One can easily verify that if (u, v, w) is bounded (which is the case throughout this section), then there exists a fixed positive real number R such that the product in (3·1) converges absolutely whenever
![]() $|z|<R$
. Hence, F(u, v, w, z), as function of z, is analytic in a complex neighbourhood of 0. By Cauchy’s integral formula, we have
$|z|<R$
. Hence, F(u, v, w, z), as function of z, is analytic in a complex neighbourhood of 0. By Cauchy’s integral formula, we have
We now use the saddle-point method to estimate the above integral. We choose
![]() $\rho$
to be the positive solution of the equation
$\rho$
to be the positive solution of the equation
 \begin{equation}n=-f_{x}(\rho,\rho)=\sum_{l=1}^{r}\sum_{m=1}^{\infty}\sum_{k=1}^{m}\frac{me^{-\rho(m+(c+ak+mbl))}}{1-e^{-\rho(m+(c+ak+mbl))}},\end{equation}
\begin{equation}n=-f_{x}(\rho,\rho)=\sum_{l=1}^{r}\sum_{m=1}^{\infty}\sum_{k=1}^{m}\frac{me^{-\rho(m+(c+ak+mbl))}}{1-e^{-\rho(m+(c+ak+mbl))}},\end{equation}
where
![]() $f_x$
denotes the partial derivative of f with respect to x. Similar notations will be used for other partial derivatives. Note that there is a unique positive solution
$f_x$
denotes the partial derivative of f with respect to x. Similar notations will be used for other partial derivatives. Note that there is a unique positive solution
![]() $\rho=\rho(n,a,b,c)$
of Equation (3·5) since the function defined by the series is strictly decreasing as a function of
$\rho=\rho(n,a,b,c)$
of Equation (3·5) since the function defined by the series is strictly decreasing as a function of
![]() $\rho$
, provided that a, b and c are small enough (it suffices for instance to assume that
$\rho$
, provided that a, b and c are small enough (it suffices for instance to assume that
![]() $|c|+|a|+r|b|<1$
). Furthermore, we observe that
$|c|+|a|+r|b|<1$
). Furthermore, we observe that
![]() $\rho\to0$
as
$\rho\to0$
as
![]() $n\to \infty$
. The following lemma reveals the asymptotic dependence between n and
$n\to \infty$
. The following lemma reveals the asymptotic dependence between n and
![]() $\rho$
.
$\rho$
.
Lemma 3·3. Let
![]() $\epsilon$
be a number in the interval
$\epsilon$
be a number in the interval
![]() $[0,1/2]$
and
$[0,1/2]$
and
![]() $\rho$
be the solution of Equation (3·5). Then we have
$\rho$
be the solution of Equation (3·5). Then we have
as
![]() $n\to\infty$
, uniformly for
$n\to\infty$
, uniformly for
![]() $|c|+|a|+r|b|\leq \epsilon$
, where the implied constants in the
$|c|+|a|+r|b|\leq \epsilon$
, where the implied constants in the
![]() $\mathcal{O}$
-terms are independent of
$\mathcal{O}$
-terms are independent of
![]() $\epsilon.$
$\epsilon.$
Proof. Recall from (3·5) that
 \begin{equation*}n =-f_x(\rho,\rho)=-\sum_{l=1}^{r}\sum_{m=1}^{\infty}\sum_{k=1}^{m}m\Phi'\!\left(\rho m\left(1+\frac{c+ak+mbl}{m}\right)\right).\end{equation*}
\begin{equation*}n =-f_x(\rho,\rho)=-\sum_{l=1}^{r}\sum_{m=1}^{\infty}\sum_{k=1}^{m}m\Phi'\!\left(\rho m\left(1+\frac{c+ak+mbl}{m}\right)\right).\end{equation*}
Under the assumption that
![]() $|c|+|a|+r|b|\leq \epsilon$
, for any
$|c|+|a|+r|b|\leq \epsilon$
, for any
![]() $m\geq 1$
,
$m\geq 1$
,
![]() $1\leq k\leq m$
and
$1\leq k\leq m$
and
![]() $1\leq l\leq r$
, we have
$1\leq l\leq r$
, we have
Moreover, the function
![]() $\Phi'(x)$
is an increasing function. Therefore,
$\Phi'(x)$
is an increasing function. Therefore,
Multiplying by m and summing over
![]() $m\geq 1$
,
$m\geq 1$
,
![]() $1\leq k\leq m$
and
$1\leq k\leq m$
and
![]() $1\leq l\leq r$
, we obtain
$1\leq l\leq r$
, we obtain
We can obtain asymptotic estimates of the lower and upper bounds as
![]() $\rho\to0^+$
. This can be done via Mellin transform. The reader can consult [Reference Flajolet, Gourdon and Dumas17] for a comprehensive survey on the Mellin transform method. The Mellin transform of
$\rho\to0^+$
. This can be done via Mellin transform. The reader can consult [Reference Flajolet, Gourdon and Dumas17] for a comprehensive survey on the Mellin transform method. The Mellin transform of
![]() $f_x((1-\epsilon)t,0)$
is
$f_x((1-\epsilon)t,0)$
is
which has simple poles at
![]() $s=3$
and
$s=3$
and
![]() $s=1$
. The other singularities are precisely at the negative odd integers. Thus, we have
$s=1$
. The other singularities are precisely at the negative odd integers. Thus, we have
 \begin{align} f_x((1-\epsilon)\rho,0) & =-\frac{2r\zeta(3)}{(1-\epsilon)^{3}}\, \rho^{-3}\nonumber\\ & \quad +\frac{r}{12(1-\epsilon)}\, \rho^{-1}-\frac{r}{2\pi i }\int_{-i\infty}^{i\infty}\zeta(s-2)\zeta(s)\Gamma(s)((1-\epsilon)\rho)^{-s}ds.\end{align}
\begin{align} f_x((1-\epsilon)\rho,0) & =-\frac{2r\zeta(3)}{(1-\epsilon)^{3}}\, \rho^{-3}\nonumber\\ & \quad +\frac{r}{12(1-\epsilon)}\, \rho^{-1}-\frac{r}{2\pi i }\int_{-i\infty}^{i\infty}\zeta(s-2)\zeta(s)\Gamma(s)((1-\epsilon)\rho)^{-s}ds.\end{align}
Since
![]() $|\zeta(it-2)\zeta(it)\Gamma(it)|$
decays exponentially fast as
$|\zeta(it-2)\zeta(it)\Gamma(it)|$
decays exponentially fast as
![]() $t\to \pm\infty$
, the absolute value of the integral on the right-hand side is bounded by an absolute constant. The same argument works for the estimate of the upper bound
$t\to \pm\infty$
, the absolute value of the integral on the right-hand side is bounded by an absolute constant. The same argument works for the estimate of the upper bound
![]() $f_x((1+\epsilon)\rho,0)$
. This completes the proof of the lemma.
$f_x((1+\epsilon)\rho,0)$
. This completes the proof of the lemma.
Next, we split the integral on the right-hand side of (3·4) into two parts as follows: let
where C is an absolute constant in the interval
![]() $(5/3, 2)$
, and let
$(5/3, 2)$
, and let
![]() $\mathcal{I}_2=Q_{n}(e^{-a\rho},e^{-b\rho},e^{-c\rho})-\mathcal{I}_1$
.
$\mathcal{I}_2=Q_{n}(e^{-a\rho},e^{-b\rho},e^{-c\rho})-\mathcal{I}_1$
.
Estimate of
![]() $\mathcal{I}_1$
$\mathcal{I}_1$
For the rest of this section, we work under the condition of Lemma 3·3, that is
![]() $|c|+|a|+r|b|\leq \epsilon$
and
$|c|+|a|+r|b|\leq \epsilon$
and
![]() $\epsilon\in [0,1/2]$
. For
$\epsilon\in [0,1/2]$
. For
![]() $-\rho^{C}\leq t\leq \rho^{C}$
, Equation (3·5) and a Taylor approximation of
$-\rho^{C}\leq t\leq \rho^{C}$
, Equation (3·5) and a Taylor approximation of
![]() $f(\rho+it,\rho)$
give
$f(\rho+it,\rho)$
give
where the implied constant in the error term is absolute. To estimate the error term, observe that
 \begin{equation*}f_{xxx}(\tau,\rho)=-\sum_{l=1}^{r}\sum_{m=1}^{\infty}\sum_{k=1}^{m}\frac{m^3e^{-\tau m-\rho(c+ak+mbl)}(1+e^{-\tau m-\rho(c+ak+mbl)})}{(1-e^{-\tau m-\rho(c+ak+mbl)})^3}.\end{equation*}
\begin{equation*}f_{xxx}(\tau,\rho)=-\sum_{l=1}^{r}\sum_{m=1}^{\infty}\sum_{k=1}^{m}\frac{m^3e^{-\tau m-\rho(c+ak+mbl)}(1+e^{-\tau m-\rho(c+ak+mbl)})}{(1-e^{-\tau m-\rho(c+ak+mbl)})^3}.\end{equation*}
For any real number
![]() $\theta$
and
$\theta$
and
![]() $\tau=\rho+i\theta$
we have
$\tau=\rho+i\theta$
we have
Hence
![]() $|f_{xxx}(\rho+i\theta,\rho)|$
is bounded above by
$|f_{xxx}(\rho+i\theta,\rho)|$
is bounded above by
![]() $|f_{xxx}(\rho,\rho)|$
. We can estimate
$|f_{xxx}(\rho,\rho)|$
. We can estimate
![]() $|f_{xxx}(\rho,\rho)|$
as we did for
$|f_{xxx}(\rho,\rho)|$
as we did for
![]() $f_{x}(\rho,\rho)$
in the proof of Lemma 3·3. We obtain
$f_{x}(\rho,\rho)$
in the proof of Lemma 3·3. We obtain
where the implied constant depends only on r. Therefore, for
![]() $\lvert t \rvert\leq \rho^{C}$
we have
$\lvert t \rvert\leq \rho^{C}$
we have
Since we chose
![]() $C>5/3$
, we have
$C>5/3$
, we have
![]() $\rho^{3C-5}=o(1)$
. Thus
$\rho^{3C-5}=o(1)$
. Thus
It remains to estimate the integral on the right-hand side as
![]() $\rho\to 0^+$
. Note that
$\rho\to 0^+$
. Note that
![]() $f_{xx}(\rho,\rho)>0$
and
$f_{xx}(\rho,\rho)>0$
and
![]() $f_{xx}(\rho,\rho) \gg \rho^{-4} $
(again via Mellin transform as in Lemma 3·3), so we have
$f_{xx}(\rho,\rho) \gg \rho^{-4} $
(again via Mellin transform as in Lemma 3·3), so we have
 \begin{align*}\int_{-\rho^{C}}^{\rho^{C}}e^{-f_{xx}(\rho,\rho)t^2/2}\, dt& = \int_{-\infty}^{\infty}e^{-f_{xx}(\rho,\rho)t^2/2}\, dt-2\int_{\rho^{C}}^{\infty}e^{-f_{xx}(\rho,\rho)t^2/2}\, dt\\& =\sqrt{\frac{2\pi}{f_{xx}(\rho,\rho)}}+\mathcal{O}\left(\int_{\rho^{C}}^{\infty}e^{-\rho^{C}f_{xx}(\rho,\rho)t/2}\, dt\right)\\& =\sqrt{\frac{2\pi}{f_{xx}(\rho,\rho)}}+\mathcal{O}\left(\rho^{4-c}e^{-A\rho^{2C-4}}\right),\end{align*}
\begin{align*}\int_{-\rho^{C}}^{\rho^{C}}e^{-f_{xx}(\rho,\rho)t^2/2}\, dt& = \int_{-\infty}^{\infty}e^{-f_{xx}(\rho,\rho)t^2/2}\, dt-2\int_{\rho^{C}}^{\infty}e^{-f_{xx}(\rho,\rho)t^2/2}\, dt\\& =\sqrt{\frac{2\pi}{f_{xx}(\rho,\rho)}}+\mathcal{O}\left(\int_{\rho^{C}}^{\infty}e^{-\rho^{C}f_{xx}(\rho,\rho)t/2}\, dt\right)\\& =\sqrt{\frac{2\pi}{f_{xx}(\rho,\rho)}}+\mathcal{O}\left(\rho^{4-c}e^{-A\rho^{2C-4}}\right),\end{align*}
where
![]() $A>0$
and the hidden constants in the error terms above depend only on r. Thus, since we chose
$A>0$
and the hidden constants in the error terms above depend only on r. Thus, since we chose
![]() $C<2$
, the term
$C<2$
, the term
![]() $\rho^{4-c}e^{-A\rho^{2C-4}}$
tends to zero faster than any power of
$\rho^{4-c}e^{-A\rho^{2C-4}}$
tends to zero faster than any power of
![]() $\rho$
as
$\rho$
as
![]() $\rho\to0^{+}$
. Hence, we obtain an estimate for
$\rho\to0^{+}$
. Hence, we obtain an estimate for
![]() $\mathcal{I}_1$
$\mathcal{I}_1$
This estimate holds uniformly for
![]() $|c|+|a|+r|b|\leq \epsilon$
and
$|c|+|a|+r|b|\leq \epsilon$
and
![]() $\epsilon\in [0,1/2]$
.
$\epsilon\in [0,1/2]$
.
Estimate of
![]() $\mathcal{I}_2$
$\mathcal{I}_2$
We will prove that
![]() $|\mathcal I_2|$
is much smaller than
$|\mathcal I_2|$
is much smaller than
![]() $|\mathcal I_1|$
. To this end, we assume that
$|\mathcal I_1|$
. To this end, we assume that
![]() $\rho^{C}< t \leq \pi$
, where C is as before. We have
$\rho^{C}< t \leq \pi$
, where C is as before. We have
 \begin{align*} \text{Re} (f(\rho+it,\rho))-f(\rho,\rho)& \,\,=\,\,-\sum_{l=1}^r\sum_{m=1}^{\infty}\sum_{k=1}^{m}\sum_{j=1}^{\infty}j^{-1}e^{-j\rho(m+(c+ak+mbl))}(1-\cos\!(mt))\\& \,\,\leq\,\, -\sum_{l=1}^r\sum_{m=1}^{\infty}\sum_{k=1}^{m}e^{-\rho(m+(c+ak+mbl))}\left(1-\cos\!(mt)\right)\\& \,\,\leq\,\, -r\sum_{m=1}^{\infty}me^{-\rho(1+\epsilon)m}(1-\cos\!(mt)).\end{align*}
\begin{align*} \text{Re} (f(\rho+it,\rho))-f(\rho,\rho)& \,\,=\,\,-\sum_{l=1}^r\sum_{m=1}^{\infty}\sum_{k=1}^{m}\sum_{j=1}^{\infty}j^{-1}e^{-j\rho(m+(c+ak+mbl))}(1-\cos\!(mt))\\& \,\,\leq\,\, -\sum_{l=1}^r\sum_{m=1}^{\infty}\sum_{k=1}^{m}e^{-\rho(m+(c+ak+mbl))}\left(1-\cos\!(mt)\right)\\& \,\,\leq\,\, -r\sum_{m=1}^{\infty}me^{-\rho(1+\epsilon)m}(1-\cos\!(mt)).\end{align*}
Moreover,
 \begin{equation*}\sum_{m=1}^{\infty}me^{-\rho(1+\epsilon)m}(1-\cos\!(mt)) =\frac{e^{\rho(1+\epsilon)}}{(e^{\rho(1+\epsilon)}-1)^2}-\text{Re}\left( \frac{e^{\rho(1+\epsilon)+it}}{(e^{\rho(1+\epsilon)+it}-1)^2}\right).\end{equation*}
\begin{equation*}\sum_{m=1}^{\infty}me^{-\rho(1+\epsilon)m}(1-\cos\!(mt)) =\frac{e^{\rho(1+\epsilon)}}{(e^{\rho(1+\epsilon)}-1)^2}-\text{Re}\left( \frac{e^{\rho(1+\epsilon)+it}}{(e^{\rho(1+\epsilon)+it}-1)^2}\right).\end{equation*}
A lower estimate of the same term can be found in the proof of [Reference Luca and Ralaivaosaona21, lemma 5]. By the same argument as the one given in loc. cit., but with
![]() $\lvert t \rvert\geq \rho^{C}$
, we get
$\lvert t \rvert\geq \rho^{C}$
, we get
 \begin{equation*}\sum_{m=1}^{\infty}me^{-\rho(1+\epsilon)m}(1-\cos\!(mt)) \gg \left(\rho(1+\epsilon)\right)^{2C-4} \ \ \text{as}\ \ \rho\to0^+,\end{equation*}
\begin{equation*}\sum_{m=1}^{\infty}me^{-\rho(1+\epsilon)m}(1-\cos\!(mt)) \gg \left(\rho(1+\epsilon)\right)^{2C-4} \ \ \text{as}\ \ \rho\to0^+,\end{equation*}
where the implied constant is independent of
![]() $\epsilon.$
$\epsilon.$
Noting that
![]() $2C-4<0$
, we deduce that
$2C-4<0$
, we deduce that
![]() $\exp\!\left( \text{Re} (f(\rho+it,\rho))-f(\rho,\rho)\right)$
tends to zero faster than any power of
$\exp\!\left( \text{Re} (f(\rho+it,\rho))-f(\rho,\rho)\right)$
tends to zero faster than any power of
![]() $\rho$
as
$\rho$
as
![]() $\rho\to0^+$
. Thus, by (3·8), we find
$\rho\to0^+$
. Thus, by (3·8), we find
which tends to zero faster than any power of
![]() $\rho$
as
$\rho$
as
![]() $\rho\to0^+$
. Recalling that
$\rho\to0^+$
. Recalling that
![]() $Q_{n}(e^{-a\rho},e^{-b\rho},e^{-c\rho})=\mathcal{I}_1+\mathcal{I}_2$
, we finally obtain
$Q_{n}(e^{-a\rho},e^{-b\rho},e^{-c\rho})=\mathcal{I}_1+\mathcal{I}_2$
, we finally obtain
uniformly for
![]() $|c|+|a|+r|b|\leq \epsilon$
and
$|c|+|a|+r|b|\leq \epsilon$
and
![]() $\epsilon\in [0,1/2]$
, where
$\epsilon\in [0,1/2]$
, where
![]() $\rho$
is the solution of Equation (3·5).
$\rho$
is the solution of Equation (3·5).
3·3·2. Perturbation
Here we set
![]() $u=e^{\eta\alpha}$
,
$u=e^{\eta\alpha}$
,
![]() $v=e^{\eta\beta}$
, and
$v=e^{\eta\beta}$
, and
![]() $w=e^{\eta\gamma}$
where
$w=e^{\eta\gamma}$
where
![]() $(\alpha,\beta,\gamma)$
is fixed and
$(\alpha,\beta,\gamma)$
is fixed and
![]() $\eta$
can vary in a small open interval containing zero. Hence, Equation (3·2) becomes
$\eta$
can vary in a small open interval containing zero. Hence, Equation (3·2) becomes
The right-hand side is the moment generating function of the random variable
![]() $\alpha X_n+\beta Y_n+\gamma Z_n$
. From now on, let
$\alpha X_n+\beta Y_n+\gamma Z_n$
. From now on, let
![]() $\rho_0$
be the unique positive number such that
$\rho_0$
be the unique positive number such that
![]() $n=-f_x(\rho_0,0).$
Then, by Lemma 3·3 (with
$n=-f_x(\rho_0,0).$
Then, by Lemma 3·3 (with
![]() $\epsilon= 0$
) we have
$\epsilon= 0$
) we have
![]() $n\sim 2r\zeta(3)\rho_0^{-3}.$
Moreover, if we write
$n\sim 2r\zeta(3)\rho_0^{-3}.$
Moreover, if we write
![]() $u=e^{-a \rho}$
,
$u=e^{-a \rho}$
,
![]() $v=e^{-b \rho}$
, and
$v=e^{-b \rho}$
, and
![]() $w=e^{-\gamma\rho}$
for
$w=e^{-\gamma\rho}$
for
![]() $\rho>0$
as before, then we have
$\rho>0$
as before, then we have
![]() $a=-\alpha\eta \rho^{-1}$
,
$a=-\alpha\eta \rho^{-1}$
,
![]() $b=-\beta\eta \rho^{-1}$
, and
$b=-\beta\eta \rho^{-1}$
, and
![]() $c=-\gamma\eta \rho^{-1}$
. This implies that
$c=-\gamma\eta \rho^{-1}$
. This implies that
Now, if we choose
![]() $\eta$
and
$\eta$
and
![]() $\rho$
in such a way that
$\rho$
in such a way that
![]() $\eta\rho^{-1}=o(1)$
and
$\eta\rho^{-1}=o(1)$
and
![]() $\rho\to 0$
as
$\rho\to 0$
as
![]() $n\to \infty$
, then by Lemma 3·3 (with
$n\to \infty$
, then by Lemma 3·3 (with
![]() $\epsilon\to 0$
), we get
$\epsilon\to 0$
), we get
Observe that it is possible to choose such
![]() $\eta$
and
$\eta$
and
![]() $\rho>0$
that satisfy
$\rho>0$
that satisfy
![]() $\eta=o(\rho_0)$
and
$\eta=o(\rho_0)$
and
![]() $\rho=o(\rho_0)$
. In this case, the above asymptotic formula implies that
$\rho=o(\rho_0)$
. In this case, the above asymptotic formula implies that
![]() $-f_x(\rho,\rho)>-f_x(\rho_0,0)=n$
for large enough n. Similarly, we can also choose
$-f_x(\rho,\rho)>-f_x(\rho_0,0)=n$
for large enough n. Similarly, we can also choose
![]() $\eta$
and
$\eta$
and
![]() $\rho>0$
such that
$\rho>0$
such that
![]() $\eta=o(\rho_0)$
,
$\eta=o(\rho_0)$
,
![]() $\rho\to 0$
,
$\rho\to 0$
,
![]() $\eta\rho^{-1}=o(1)$
, and
$\eta\rho^{-1}=o(1)$
, and
![]() ${\rho}/{\rho_0}\to \infty$
. This time, the asymptotic formula gives
${\rho}/{\rho_0}\to \infty$
. This time, the asymptotic formula gives
![]() $-f_x(\rho,\rho)<n$
. Hence, for
$-f_x(\rho,\rho)<n$
. Hence, for
![]() $\eta=o(\rho_0)$
and n large enough, the equation
$\eta=o(\rho_0)$
and n large enough, the equation
![]() $n=-f_x(\rho,\rho)$
has a unique solution, which we denote by
$n=-f_x(\rho,\rho)$
has a unique solution, which we denote by
![]() $\rho(\eta)$
. Furthermore, it satisfies
$\rho(\eta)$
. Furthermore, it satisfies
![]() $\rho(\eta)\to 0$
and
$\rho(\eta)\to 0$
and
![]() $\eta\rho(\eta)^{-1}=o(1)$
as
$\eta\rho(\eta)^{-1}=o(1)$
as
![]() $n\to \infty$
. Therefore, we also have
$n\to \infty$
. Therefore, we also have
The latter and the asymptotic estimate
![]() $n\sim 2r\zeta(3)\rho_0^{-3}$
yield
$n\sim 2r\zeta(3)\rho_0^{-3}$
yield
![]() $\rho(\eta)\sim \rho_0$
as
$\rho(\eta)\sim \rho_0$
as
![]() $n\to \infty$
whenever
$n\to \infty$
whenever
![]() $\eta=o(\rho_0)$
.
$\eta=o(\rho_0)$
.
From this point onward, we assume that
![]() $\eta=o(\rho_0).$
Since
$\eta=o(\rho_0).$
Since
![]() $\rho(\eta)$
and
$\rho(\eta)$
and
![]() $\rho_0$
are asymptotically equivalent as
$\rho_0$
are asymptotically equivalent as
![]() $n\to \infty$
, so are
$n\to \infty$
, so are
![]() $f_{xx}(\rho(\eta), \rho(\eta))$
and
$f_{xx}(\rho(\eta), \rho(\eta))$
and
![]() $f_{xx}(\rho_0, 0).$
Thus, by (3·9), we have
$f_{xx}(\rho_0, 0).$
Thus, by (3·9), we have
We want to obtain a precise asymptotic estimate of the exponent of the right-hand side that holds uniformly for
![]() $\eta=o(\rho_0)$
. We will use a Taylor approximation of the function
$\eta=o(\rho_0)$
. We will use a Taylor approximation of the function
![]() $f(\rho(\eta),\rho(\eta))$
when
$f(\rho(\eta),\rho(\eta))$
when
![]() $\eta$
is near 0 (noting that the parameters a, b, and c are themselves functions of
$\eta$
is near 0 (noting that the parameters a, b, and c are themselves functions of
![]() $\eta$
). So to highlight the variable
$\eta$
). So to highlight the variable
![]() $\eta$
, we define
$\eta$
, we define
 \begin{align*} g(x,y) & =\log F(e^{y\alpha},e^{y\beta},e^{y\gamma},e^{-x})\\ &=-\sum_{l=1}^{r}\sum_{m=1}^{\infty}\sum_{k=1}^{m}\log\left(1-e^{y(\gamma+\alpha k+m\beta l)-x m}\right)\\ &=\sum_{l=1}^{r}\sum_{m=1}^{\infty}\sum_{k=1}^{m}\Phi(xm-y(\gamma+\alpha k+m\beta l)).\end{align*}
\begin{align*} g(x,y) & =\log F(e^{y\alpha},e^{y\beta},e^{y\gamma},e^{-x})\\ &=-\sum_{l=1}^{r}\sum_{m=1}^{\infty}\sum_{k=1}^{m}\log\left(1-e^{y(\gamma+\alpha k+m\beta l)-x m}\right)\\ &=\sum_{l=1}^{r}\sum_{m=1}^{\infty}\sum_{k=1}^{m}\Phi(xm-y(\gamma+\alpha k+m\beta l)).\end{align*}
This is essentially the same as the function f(x, y) (if (a, b, c) is replaced by
![]() $(\!-\alpha, -\beta, -\gamma)$
). However, in our case we have
$(\!-\alpha, -\beta, -\gamma)$
). However, in our case we have
![]() $a=-\alpha\eta \rho(\eta)^{-1}$
,
$a=-\alpha\eta \rho(\eta)^{-1}$
,
![]() $b=-\beta\eta \rho(\eta)^{-1}$
, and
$b=-\beta\eta \rho(\eta)^{-1}$
, and
![]() $c=-\gamma\eta \rho(\eta)^{-1}$
. Hence, the meanings of the first and second variables will be different. For instance, we have the equation
$c=-\gamma\eta \rho(\eta)^{-1}$
. Hence, the meanings of the first and second variables will be different. For instance, we have the equation
Similarly, the saddle-point equation
![]() $n=-f_x(\rho(\eta),\rho(\eta))$
becomes
$n=-f_x(\rho(\eta),\rho(\eta))$
becomes
![]() $n=-g_x(\rho(\eta),\eta).$
First, we apply implicit differentiation (with respect to
$n=-g_x(\rho(\eta),\eta).$
First, we apply implicit differentiation (with respect to
![]() $\eta$
) to the latter equation, then by the mean value theorem, we get
$\eta$
) to the latter equation, then by the mean value theorem, we get
for some real number
![]() $\theta$
between 0 and
$\theta$
between 0 and
![]() $\eta.$
We can estimate
$\eta.$
We can estimate
![]() $g_{xy}(\rho(\theta),\theta)$
and
$g_{xy}(\rho(\theta),\theta)$
and
![]() $g_{xx}(\rho(\theta),\theta)$
via Mellin transform in the same way as in the proof of Lemma 3·3, but we need the Mellin transforms of the functions
$g_{xx}(\rho(\theta),\theta)$
via Mellin transform in the same way as in the proof of Lemma 3·3, but we need the Mellin transforms of the functions
![]() $g_{xx}(t,0)$
and
$g_{xx}(t,0)$
and
![]() $g_{xy}(t,0)$
. The Mellin transform of
$g_{xy}(t,0)$
. The Mellin transform of
![]() $g_{xx}(t,0)$
is
$g_{xx}(t,0)$
is
![]() $r\zeta(s-3)\zeta(s-1)\Gamma(s)$
. To determine the Mellin transform of
$r\zeta(s-3)\zeta(s-1)\Gamma(s)$
. To determine the Mellin transform of
![]() $g_{x,y}(t,0)$
, first we write
$g_{x,y}(t,0)$
, first we write
 \begin{align*} g_{x,y}(t,0) & \,\,=\,\,-\sum_{l=1}^{r}\sum_{m=1}^{\infty}\sum_{k=1}^{m}m(\gamma+\alpha k+m\beta l)\Phi''(tm)\\ & \,\,=\,\, -\sum_{m=1}^{\infty}m\!\left(rm\gamma+r\alpha\frac{m^2+m}{2}+m^2\beta\frac{r^2+r}{2}\right)\Phi''(tm)\\ & \,\,=\,\, -\frac{r}{2}\sum_{m=1}^{\infty}\left((\alpha+(r+1)\beta) m^3+(\alpha+2\gamma)m^2\right)\Phi''(tm).\end{align*}
\begin{align*} g_{x,y}(t,0) & \,\,=\,\,-\sum_{l=1}^{r}\sum_{m=1}^{\infty}\sum_{k=1}^{m}m(\gamma+\alpha k+m\beta l)\Phi''(tm)\\ & \,\,=\,\, -\sum_{m=1}^{\infty}m\!\left(rm\gamma+r\alpha\frac{m^2+m}{2}+m^2\beta\frac{r^2+r}{2}\right)\Phi''(tm)\\ & \,\,=\,\, -\frac{r}{2}\sum_{m=1}^{\infty}\left((\alpha+(r+1)\beta) m^3+(\alpha+2\gamma)m^2\right)\Phi''(tm).\end{align*}
Since the Mellin transform of
![]() $\Phi''(t)$
is
$\Phi''(t)$
is
![]() $\zeta(s-1)\Gamma(s)$
, the Mellin transform of
$\zeta(s-1)\Gamma(s)$
, the Mellin transform of
![]() $g_{x,y}(t,0)$
is
$g_{x,y}(t,0)$
is
We deduce the following asymptotic formulas as
![]() $\rho\to0^{+}$
:
$\rho\to0^{+}$
:
The fact that
![]() $\rho(\theta)\sim \rho_0$
(since
$\rho(\theta)\sim \rho_0$
(since
![]() $|\theta|\leq |\eta|=o(\rho_0)$
) and the argument in the proof of Lemma 3·3 (with
$|\theta|\leq |\eta|=o(\rho_0)$
) and the argument in the proof of Lemma 3·3 (with
![]() $\epsilon\to 0$
) imply
$\epsilon\to 0$
) imply
Similarly, we have the following estimate for the third partial derivatives
uniformly for
![]() $\theta=o(\rho_0)$
, and for any nonnegative integers k and l such that
$\theta=o(\rho_0)$
, and for any nonnegative integers k and l such that
![]() $k+l=3$
. This shows that if
$k+l=3$
. This shows that if
![]() $\eta=o(\rho_0)$
, then we have the Taylor approximation
$\eta=o(\rho_0)$
, then we have the Taylor approximation
 $$\matrix{
{g(\rho (\eta ),\eta ) = g({\rho _0},0) + {g_y}({\rho _0},0)\eta + {g_x}({\rho _0},0)(\rho (\eta ) - {\rho _0})} \hfill \cr
{ + {1 \over 2}({g_{yy}}({\rho _0},0){\mkern 1mu} {\eta ^2} + 2{g_{xy}}({\rho _0},0){\mkern 1mu} \eta (\rho (\eta ) - {\rho _0}) + {g_{xx}}({\rho _0},0){\mkern 1mu} {{(\rho (\eta ) - {\rho _0})}^2}) + {\cal O}(|\eta {|^3}\rho _0^{ - 5}),} \hfill \cr
} $$
$$\matrix{
{g(\rho (\eta ),\eta ) = g({\rho _0},0) + {g_y}({\rho _0},0)\eta + {g_x}({\rho _0},0)(\rho (\eta ) - {\rho _0})} \hfill \cr
{ + {1 \over 2}({g_{yy}}({\rho _0},0){\mkern 1mu} {\eta ^2} + 2{g_{xy}}({\rho _0},0){\mkern 1mu} \eta (\rho (\eta ) - {\rho _0}) + {g_{xx}}({\rho _0},0){\mkern 1mu} {{(\rho (\eta ) - {\rho _0})}^2}) + {\cal O}(|\eta {|^3}\rho _0^{ - 5}),} \hfill \cr
} $$
where the implied constant in the error term is independent of n. Using (3·15) and saddle-point equation
![]() $n=-g_x(\rho_0,0)$
, we deduce that
$n=-g_x(\rho_0,0)$
, we deduce that
 $$\matrix{
{g(\rho (\eta ),\eta ) - g({\rho _0},0) + n(\rho (\eta ) - {\rho _0}) = } \hfill \cr
{\quad \quad \quad \quad \quad \quad \quad {g_y}({\rho _0},0)\eta + \left( {{{{g_{yy}}({\rho _0},0){g_{xx}}({\rho _0},0) - {{({g_{xy}}({\rho _0},0))}^2}} \over {{g_{xx}}({\rho _0},0)}}} \right){{{\eta ^2}} \over 2} + {\cal O}(|\eta {|^3}\rho _0^{ - 5}).} \hfill \cr
} $$
$$\matrix{
{g(\rho (\eta ),\eta ) - g({\rho _0},0) + n(\rho (\eta ) - {\rho _0}) = } \hfill \cr
{\quad \quad \quad \quad \quad \quad \quad {g_y}({\rho _0},0)\eta + \left( {{{{g_{yy}}({\rho _0},0){g_{xx}}({\rho _0},0) - {{({g_{xy}}({\rho _0},0))}^2}} \over {{g_{xx}}({\rho _0},0)}}} \right){{{\eta ^2}} \over 2} + {\cal O}(|\eta {|^3}\rho _0^{ - 5}).} \hfill \cr
} $$
Let us define
and we choose
![]() $\eta={t}/{\sigma_n}$
where t is a fixed real number. Then our estimate (3·11) becomes
$\eta={t}/{\sigma_n}$
where t is a fixed real number. Then our estimate (3·11) becomes
as
![]() $n\to\infty$
(this is valid as long as
$n\to\infty$
(this is valid as long as
![]() $\eta={t}/{\sigma_n}=o(\rho_0)$
, but we do not even know at this stage whether
$\eta={t}/{\sigma_n}=o(\rho_0)$
, but we do not even know at this stage whether
![]() $\sigma_n^2$
is positive). Hence, let us estimate
$\sigma_n^2$
is positive). Hence, let us estimate
![]() $\sigma_n^2$
.
$\sigma_n^2$
.
Assume first that
![]() $(\alpha,\beta)\neq (0,0)$
. Once again, by the Mellin transform technique, we have
$(\alpha,\beta)\neq (0,0)$
. Once again, by the Mellin transform technique, we have
Putting the estimates (3·13), (3·14) and (3·18) into the formula for
![]() $\sigma_n^2$
in (3·16), we have
$\sigma_n^2$
in (3·16), we have
Hence,
![]() $\eta=\mathcal{O}(\rho_0^2)$
and the estimate (3·17) becomes
$\eta=\mathcal{O}(\rho_0^2)$
and the estimate (3·17) becomes
Therefore, if
![]() $(\alpha,\beta)\neq (0,0)$
and t is any fixed real number, then the latter identity together with (3·10) yield
$(\alpha,\beta)\neq (0,0)$
and t is any fixed real number, then the latter identity together with (3·10) yield
as
![]() $n\to \infty$
. This means, by Curtiss’ theorem [Reference Curtiss10], that
$n\to \infty$
. This means, by Curtiss’ theorem [Reference Curtiss10], that
To obtain the asymptotic formulas for
![]() $\sigma_n^2$
and
$\sigma_n^2$
and
![]() $\mu_n$
, recall from the saddle-point equation and (3·7) (with
$\mu_n$
, recall from the saddle-point equation and (3·7) (with
![]() $\epsilon=0$
) that
$\epsilon=0$
) that
![]() $n= 2r\zeta(3)\rho_0^{-3}-{1}/{12}r\rho_0^{-1}+\mathcal{O}(1)$
. Inverting this yields
$n= 2r\zeta(3)\rho_0^{-3}-{1}/{12}r\rho_0^{-1}+\mathcal{O}(1)$
. Inverting this yields
So we first estimate
![]() $\sigma_n^2$
and
$\sigma_n^2$
and
![]() $\mu_n$
in terms of
$\mu_n$
in terms of
![]() $\rho_0$
, then use the above to get the asymptotic formulas in terms of n. Such an estimate for
$\rho_0$
, then use the above to get the asymptotic formulas in terms of n. Such an estimate for
![]() $\sigma_n^2$
is already given in (3·19). The estimate of
$\sigma_n^2$
is already given in (3·19). The estimate of
![]() $\mu_n$
can be obtained easily from the Mellin transform of
$\mu_n$
can be obtained easily from the Mellin transform of
![]() $g_y(t,0)$
, which is
$g_y(t,0)$
, which is
By a straightforward calculation, we have
If we now assume that
![]() $(\alpha,\beta)=(0,0)$
but
$(\alpha,\beta)=(0,0)$
but
![]() $\gamma\neq 0$
, then the Mellin transform of
$\gamma\neq 0$
, then the Mellin transform of
![]() $g_{yy}(t,0)$
is
$g_{yy}(t,0)$
is
![]() $r\gamma^2\zeta(s-1)^2\Gamma(s)$
whose dominant singularity is a double pole at
$r\gamma^2\zeta(s-1)^2\Gamma(s)$
whose dominant singularity is a double pole at
![]() $s=2$
. This leads to the asymptotic formula
$s=2$
. This leads to the asymptotic formula
![]() $g_{yy}(\rho_0,0)= r\gamma^2\rho_0^{-2}\log\left(\rho_0^{-1}\right)+\mathcal{O}(\rho_0^{-2}).$
Hence, the formula in (3·16) gives
$g_{yy}(\rho_0,0)= r\gamma^2\rho_0^{-2}\log\left(\rho_0^{-1}\right)+\mathcal{O}(\rho_0^{-2}).$
Hence, the formula in (3·16) gives
Thus, for a fixed real number t, we have
So we still have our desired condition that
![]() $\eta=o(\rho_0)$
. Moreover, applying (3·13) and (3·14) with
$\eta=o(\rho_0)$
. Moreover, applying (3·13) and (3·14) with
![]() $(\alpha,\beta)=(0,0)$
, the estimate (3·15) becomes
$(\alpha,\beta)=(0,0)$
, the estimate (3·15) becomes
On the other hand, for any
![]() $\theta=o(\rho_0)$
, we have the following:
$\theta=o(\rho_0)$
, we have the following:
 \begin{align*} g_{xxx}(\rho(\theta),\theta)&\,\,=\,\,\mathcal{O}(\rho_0^{-5}), & g_{xxy}(\rho(\theta),\theta)\,\,=\,\,\mathcal{O}(\rho_0^{-4}),\\ g_{xyy}(\rho(\theta),\theta)&\,\,=\,\,\mathcal{O}(\rho_0^{-3}|\log \rho_0|), & g_{yyy}(\rho(\theta),\theta)\,\,=\,\,\mathcal{O}(\rho_0^{-3}).\end{align*}
\begin{align*} g_{xxx}(\rho(\theta),\theta)&\,\,=\,\,\mathcal{O}(\rho_0^{-5}), & g_{xxy}(\rho(\theta),\theta)\,\,=\,\,\mathcal{O}(\rho_0^{-4}),\\ g_{xyy}(\rho(\theta),\theta)&\,\,=\,\,\mathcal{O}(\rho_0^{-3}|\log \rho_0|), & g_{yyy}(\rho(\theta),\theta)\,\,=\,\,\mathcal{O}(\rho_0^{-3}).\end{align*}
Therefore, (3·17) becomes
Just as in the previous case, this is enough to prove the central limit theorem. The asymptotic formula for the variance in terms of n can be obtained from (3·21) using (3·20). The proof of Proposition 3·1 is complete.
Acknowledgments
The very existence of this work owes a debt to Balázs Szendrői, who brought the authors together. We thank him for his support and for generously sharing his ideas throughout the years. We also thank the referees for their useful comments and suggested improvements on the text. A.C. thanks the African Institute for Mathematical Sciences (AIMS), South Africa, for support during the first part of this collaboration. D.R. is supported by the Division for Research Development (DRD) of Stellenbosch University and the National Research Foundation (NRF) of South Africa, Grant number: 129413. A.R. is supported by Dipartimenti di Eccellenza and thanks SISSA for the excellent working conditions.