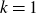1. Introduction
A k-multiset permutation of size n is a word with letters in
![]() $\{1,2,\dots, n\}$
such that each letter appears exactly k times. When this is convenient we identify a multiset permutation
$\{1,2,\dots, n\}$
such that each letter appears exactly k times. When this is convenient we identify a multiset permutation
![]() $s=\!\left(s(1),\dots,s(kn)\right)$
and the set of points
$s=\!\left(s(1),\dots,s(kn)\right)$
and the set of points
![]() $\{(i,s(i)),\ 1\leq i\leq kn\}$
. We introduce two partial orders over the quarter-plane
$\{(i,s(i)),\ 1\leq i\leq kn\}$
. We introduce two partial orders over the quarter-plane
![]() $[0,\infty)^2$
:
$[0,\infty)^2$
:
 \begin{align*}(x,y)\prec (x',y') &\text{ if } x\lt x'\text{ and }y\lt y',\\[5pt] (x,y)\preccurlyeq (x',y') &\text{ if } x\lt x'\text{ and }y\leq y'.\end{align*}
\begin{align*}(x,y)\prec (x',y') &\text{ if } x\lt x'\text{ and }y\lt y',\\[5pt] (x,y)\preccurlyeq (x',y') &\text{ if } x\lt x'\text{ and }y\leq y'.\end{align*}
For a finite set
![]() $\mathcal{P}$
of points in the quarter-plane we put
$\mathcal{P}$
of points in the quarter-plane we put
 \begin{align*}\mathcal{L}_{\lt }(\mathcal{P})&=\max\left\{L; \hbox{ there exists }P_1 \prec P_2 \prec \dots \prec P_L, \text{ where each }P_i \in \mathcal{P} \right\},\\[5pt] \mathcal{L}_{\leq }(\mathcal{P})&=\max\left\{L; \hbox{ there exists }P_1\preccurlyeq P_2 \preccurlyeq\dots \preccurlyeq P_L, \text{ where each }P_i \in \mathcal{P} \right\}.\end{align*}
\begin{align*}\mathcal{L}_{\lt }(\mathcal{P})&=\max\left\{L; \hbox{ there exists }P_1 \prec P_2 \prec \dots \prec P_L, \text{ where each }P_i \in \mathcal{P} \right\},\\[5pt] \mathcal{L}_{\leq }(\mathcal{P})&=\max\left\{L; \hbox{ there exists }P_1\preccurlyeq P_2 \preccurlyeq\dots \preccurlyeq P_L, \text{ where each }P_i \in \mathcal{P} \right\}.\end{align*}
In words the integer
![]() $\mathcal{L}_{\lt }(\mathcal{P})$
(resp.
$\mathcal{L}_{\lt }(\mathcal{P})$
(resp.
![]() $\mathcal{L}_{\leq }(\mathcal{P})$
) is the length of the longest increasing (resp. non-decreasing) subsequence of
$\mathcal{L}_{\leq }(\mathcal{P})$
) is the length of the longest increasing (resp. non-decreasing) subsequence of
![]() $\mathcal{P}$
.
$\mathcal{P}$
.

Fig. 1. A uniform 5-multiset permutation
![]() $S_{5;30}$
of size
$S_{5;30}$
of size
![]() $n=30$
and one of its longest non-decreasing subsequences.
$n=30$
and one of its longest non-decreasing subsequences.
Let
![]() $S_{k;n}$
be a k-multiset permutation of size n drawn uniformly among the
$S_{k;n}$
be a k-multiset permutation of size n drawn uniformly among the
![]() ${(kn)!}/{k!^n}$
possibilities. In the case
${(kn)!}/{k!^n}$
possibilities. In the case
![]() $k=1$
the word
$k=1$
the word
![]() $S_{1;n}$
is simply a uniform permutation and estimating
$S_{1;n}$
is simply a uniform permutation and estimating
![]() $\mathcal{L}_{\lt }(S_{1;n})=\mathcal{L}_{\leq }(S_{1;n})$
is known as the Hammersley or Ulam–Hammersley problem. The first order was solved by Veršik and Kerov [
Reference Veršik and KerovVK77
] and simultaneously by Logan and Shepp:
$\mathcal{L}_{\lt }(S_{1;n})=\mathcal{L}_{\leq }(S_{1;n})$
is known as the Hammersley or Ulam–Hammersley problem. The first order was solved by Veršik and Kerov [
Reference Veršik and KerovVK77
] and simultaneously by Logan and Shepp:
Note that the above limit also holds in probability:
![]() $\mathcal{L}_{\lt }(S_{1;n})= 2\sqrt{n}+\mathrm{o}_{\mathbb{P}}(\sqrt{n})$
. This problem has a long history and has revealed deep and unexpected connections between combinatorics, interacting particle systems, calculus of variations, random matrix theory, representation theory. We refer to Romik [
Reference RomikRom15
] for a very nice description of this problem and some of its ramifications.
$\mathcal{L}_{\lt }(S_{1;n})= 2\sqrt{n}+\mathrm{o}_{\mathbb{P}}(\sqrt{n})$
. This problem has a long history and has revealed deep and unexpected connections between combinatorics, interacting particle systems, calculus of variations, random matrix theory, representation theory. We refer to Romik [
Reference RomikRom15
] for a very nice description of this problem and some of its ramifications.
In the context of card guessing games it is asked in [
Reference Clifton, Deb, Huang, Spiro and YooCDH+22
, question 4·3] the behaviour of
![]() $\mathcal{L}_{\lt }(S_{k;n})$
for a fixed k (see Fig. 1 for an example). Using the Veršik–Kerov Theorem we can make an educated guess. The intuition is that, for fixed k, it is quite unlikely that many points at the same height contribute to the same longest increasing/non-decreasing subsequence. Thus at the first order everything should happen as if the kn points had distinct heights and we expect that
$\mathcal{L}_{\lt }(S_{k;n})$
for a fixed k (see Fig. 1 for an example). Using the Veršik–Kerov Theorem we can make an educated guess. The intuition is that, for fixed k, it is quite unlikely that many points at the same height contribute to the same longest increasing/non-decreasing subsequence. Thus at the first order everything should happen as if the kn points had distinct heights and we expect that
The original motivation of this paper was to make this approximation rigorous. We actually adress this question in the case where k depends on n.
Theorem 1 (Longest increasing subsequences). Let
![]() $(k_n)$
be a sequence of integers such that
$(k_n)$
be a sequence of integers such that
![]() $k_n\leq n$
for all n. Then
$k_n\leq n$
for all n. Then
(Of course if
![]() $k_n=o(n)$
then the RHS of (1) reduces to
$k_n=o(n)$
then the RHS of (1) reduces to
![]() $2\sqrt{nk_n}+\mathrm{o}(\sqrt{nk_n})$
.)
$2\sqrt{nk_n}+\mathrm{o}(\sqrt{nk_n})$
.)
Remark 1. If
![]() $k_n\geq n$
for some n then the following greedy strategy shows that
$k_n\geq n$
for some n then the following greedy strategy shows that
![]() $\mathbb{E}[\mathcal{L}_{\lt }(S_{k_n;n})]= n-\mathrm{o}(n)$
so the picture is complete.
$\mathbb{E}[\mathcal{L}_{\lt }(S_{k_n;n})]= n-\mathrm{o}(n)$
so the picture is complete.
Indeed, first choose the leftmost point
![]() $(x_1,1)$
in
$(x_1,1)$
in
![]() $S_{k_n;n}$
which has height 1. Then recursively define
$S_{k_n;n}$
which has height 1. Then recursively define
![]() $(x_\ell,\ell)$
at the leftmost point (if any) in
$(x_\ell,\ell)$
at the leftmost point (if any) in
![]() $S_{k_n;n}$
with height
$S_{k_n;n}$
with height
![]() $\ell$
such that
$\ell$
such that
![]() $x_\ell \gt x_{\ell-1}$
, and so on until you are stuck (either because
$x_\ell \gt x_{\ell-1}$
, and so on until you are stuck (either because
![]() $\ell=n$
or because there is no point in
$\ell=n$
or because there is no point in
![]() $S_{k_n;n}\cap (x_{\ell-1},kn]\times\left\{\ell\right\}$
). A few elementary computations show that this strategy defines an increasing path of length
$S_{k_n;n}\cap (x_{\ell-1},kn]\times\left\{\ell\right\}$
). A few elementary computations show that this strategy defines an increasing path of length
![]() $n-\mathrm{o}(n)$
with probability tending to one. As
$n-\mathrm{o}(n)$
with probability tending to one. As
![]() $\mathcal{L}_{\lt }(S_{k_n;n}) \leq n$
a.s. this yields
$\mathcal{L}_{\lt }(S_{k_n;n}) \leq n$
a.s. this yields
![]() $\mathbb{E}[\mathcal{L}_{\lt }(S_{k_n;n})]= n-\mathrm{o}(n)$
.
$\mathbb{E}[\mathcal{L}_{\lt }(S_{k_n;n})]= n-\mathrm{o}(n)$
.
Theorem 2 (Longest non-decreasing subsequences). Let
![]() $(k_n)$
be an arbitrary sequence of integers. Then
$(k_n)$
be an arbitrary sequence of integers. Then
Strategy of proof and organisation of the paper. In Section 2 we first provide the proof of Theorems 1 and 2 in the case of a constant or slowly growing sequence
![]() $(k_n)$
. The proof is elementary (assuming the Veršik–Kerov Theorem is known).
$(k_n)$
. The proof is elementary (assuming the Veršik–Kerov Theorem is known).
For the general case we first borrow a few tools in the literature. In particular we introduce and analyse poissonised versions of
![]() $\mathcal{L}_{\lt }(S_{k_n;n}),\mathcal{L}_{\leq }(S_{k_n;n})$
. As already suggested by Hammersley ([
Reference HammersleyHam72
, section 9]) and achieved by Aldous–Diaconis [
Reference Aldous and DiaconisAD95
] the case
$\mathcal{L}_{\lt }(S_{k_n;n}),\mathcal{L}_{\leq }(S_{k_n;n})$
. As already suggested by Hammersley ([
Reference HammersleyHam72
, section 9]) and achieved by Aldous–Diaconis [
Reference Aldous and DiaconisAD95
] the case
![]() $k=1$
can be tackled by considering an interacting particle system which is now known as the Hammersley or Hammersley–Aldous–Diaconis (HAD) process.
$k=1$
can be tackled by considering an interacting particle system which is now known as the Hammersley or Hammersley–Aldous–Diaconis (HAD) process.
In Section 3 we introduce and analyse the two variants of the Hammersley process adapted to multiset permutations. The first one is the discrete-time HAD process [
Reference FerrariFer96, Reference Ferrari and MartinFM06
], the second one appeared in [
Reference BoyerBoy22
] with a connection to the O’Connell–Yor Brownian polymer. The standard path to analyse Hammersley-like processes consists in using subadditivity to prove the existence of a limiting shape and then proving that this limiting shape satisfies a variational problem. Typically this variational problem is solved either using convex duality [
Reference SeppäläinenSep97, Reference Ciech and GeorgiouCG19
] or through the analysis of second class particles [
Reference Cator and GroeneboomCG06, Reference Ciech and GeorgiouCG19
]. The issue here is that since we allow
![]() $k_n$
to have different scales we cannot use this approach and we need to derive non-asymptotic bounds for both processes. This is the purpose of Theorem 9 whose proof is the most technical part of the paper. In Section 4 we detail the multivariate de-poissonisation procedure in order to conclude the proof of Theorem 1. De-poissonisation is more convoluted for non-decreasing subsequences: see Section 5.
$k_n$
to have different scales we cannot use this approach and we need to derive non-asymptotic bounds for both processes. This is the purpose of Theorem 9 whose proof is the most technical part of the paper. In Section 4 we detail the multivariate de-poissonisation procedure in order to conclude the proof of Theorem 1. De-poissonisation is more convoluted for non-decreasing subsequences: see Section 5.
Beyond expectation. In the course of the proof we actually obtain results beyond the estimation of the expectation. We obtain concentration inequalities for the poissonised version of
![]() $\mathcal{L}_{\lt }(S_{k_n;n}),\mathcal{L}_{\leq }(S_{k_n;n})$
: see Theorem 9 and also the discussion in Section 6. We also obtain the convergence in probability, unfortunately for some technical reasons we miss a small range of scales of
$\mathcal{L}_{\lt }(S_{k_n;n}),\mathcal{L}_{\leq }(S_{k_n;n})$
: see Theorem 9 and also the discussion in Section 6. We also obtain the convergence in probability, unfortunately for some technical reasons we miss a small range of scales of
![]() $(k_n)$
’s.
$(k_n)$
’s.
Proposition 3. Let
![]() $(k_n)$
be either a small or a large sequence. Then
$(k_n)$
be either a small or a large sequence. Then
We refer to (3),(31) below for the formal definitions of small/large sequences. Let us just say that sequences such that
![]() $k_n=\mathcal{O}((\!\log n)^{1-{\varepsilon}})$
for some
$k_n=\mathcal{O}((\!\log n)^{1-{\varepsilon}})$
for some
![]() ${\varepsilon}\gt 0$
are small while sequences such that
${\varepsilon}\gt 0$
are small while sequences such that
![]() $(\!\log n)^{1+{\varepsilon}}=\mathcal{O}(k_n)$
are large. Sequences in-between are neither small nor large so in Proposition 3 we miss scales like
$(\!\log n)^{1+{\varepsilon}}=\mathcal{O}(k_n)$
are large. Sequences in-between are neither small nor large so in Proposition 3 we miss scales like
![]() $k_n\approx \log(n)$
.
$k_n\approx \log(n)$
.
Regarding fluctuations a famous result by Baik, Deift and Johansson [ Reference Baik, Deift and JohanssonBDJ99 , theorem 1·1] states that
where TW is the Tracy–Widom distribution. The intuition given by the comparison with the Hammersley process would suggest that the fluctuations of
![]() $\mathcal{L}_{\lt }(S_{k_n;n})$
,
$\mathcal{L}_{\lt }(S_{k_n;n})$
,
![]() $\mathcal{L}_{\leq }(S_{k_n;n})$
might be of order
$\mathcal{L}_{\leq }(S_{k_n;n})$
might be of order
![]() $(k_n n)^{1/6}$
as long as
$(k_n n)^{1/6}$
as long as
![]() $(k_n)$
does not grow too fast. A natural question to explore for furthering this work would involve understanding for which
$(k_n)$
does not grow too fast. A natural question to explore for furthering this work would involve understanding for which
![]() $(k_n)$
the model preserves KPZ scaling exponents. The non-asymptotic estimates of Section 3 could serve as a first step in this direction.
$(k_n)$
the model preserves KPZ scaling exponents. The non-asymptotic estimates of Section 3 could serve as a first step in this direction.
Comparison with previous works. There are only few random sets
![]() $\mathcal{P}$
for which the asymptotics of
$\mathcal{P}$
for which the asymptotics of
![]() $\mathcal{L}_{\lt }(\mathcal{P}),\mathcal{L}_{\leq }(\mathcal{P})$
are known:
$\mathcal{L}_{\lt }(\mathcal{P}),\mathcal{L}_{\leq }(\mathcal{P})$
are known:
-
(i) as already mentioned, the case of a uniform permutation (and its poissonised version) is very well understood, via different approaches. For proofs close to the spirit of the present paper, we refer to [ Reference Aldous and DiaconisAD95 ] and [ Reference Cator and GroeneboomCG05 ];
-
(ii) the case where
 $\mathcal{P}$
is given by a field of i.i.d. Bernoulli random variables on the square grid has been solved by Seppäläinen in [
Reference SeppäläinenSep97
] for
$\mathcal{P}$
is given by a field of i.i.d. Bernoulli random variables on the square grid has been solved by Seppäläinen in [
Reference SeppäläinenSep97
] for
 $\mathcal{L}_{\lt }$
and in [
Reference SeppäläinenSep98
] for
$\mathcal{L}_{\lt }$
and in [
Reference SeppäläinenSep98
] for
 $\mathcal{L}_{\leq }$
. (See [
Reference Basdevant, Enriquez, Gerin and GouéréBEGG16
] for an elementary proof of both results.)
$\mathcal{L}_{\leq }$
. (See [
Reference Basdevant, Enriquez, Gerin and GouéréBEGG16
] for an elementary proof of both results.)
We are not aware of previous results for multiset permutations. However Theorems 1 and 2 in the linear regime
![]() $k_n\sim \mathrm{constant}\times n$
should be compared to a result by Biane ([
Reference BianeBia01
, theorem 3]).
$k_n\sim \mathrm{constant}\times n$
should be compared to a result by Biane ([
Reference BianeBia01
, theorem 3]).
We need a few notations to describe his result. Let
![]() $\mathcal{W}_{q_N;N}$
be the random word given by of
$\mathcal{W}_{q_N;N}$
be the random word given by of
![]() $q_N$
i.i.d. uniform letters in
$q_N$
i.i.d. uniform letters in
![]() $\{1,2,\dots, N\}$
. The word
$\{1,2,\dots, N\}$
. The word
![]() $\mathcal{W}_{q_N;N}$
is not a multiset permutation but since for large N there are in average
$\mathcal{W}_{q_N;N}$
is not a multiset permutation but since for large N there are in average
![]() $q_N/N$
points on each horizontal line of
$q_N/N$
points on each horizontal line of
![]() $\mathcal{W}_{q_N;N}$
we expect that
$\mathcal{W}_{q_N;N}$
we expect that
![]() $\mathcal{L}_\lt (\mathcal{W}_{q_N;N}) \approx \mathcal{L}_\lt (S_{q_N/N;N})$
and
$\mathcal{L}_\lt (\mathcal{W}_{q_N;N}) \approx \mathcal{L}_\lt (S_{q_N/N;N})$
and
![]() $\mathcal{L}_\leq (\mathcal{W}_{q_N;N})\approx \mathcal{L}_\leq (S_{q_N/N;N}) $
.
$\mathcal{L}_\leq (\mathcal{W}_{q_N;N})\approx \mathcal{L}_\leq (S_{q_N/N;N}) $
.
Biane obtains the exact limiting shape of the random Young Tableau induced through the RSK correspondence by
![]() $\mathcal{W}_{q_N;N}$
in the regime where
$\mathcal{W}_{q_N;N}$
in the regime where
![]() $\sqrt{q_N}/N \to c$
for some constant
$\sqrt{q_N}/N \to c$
for some constant
![]() $c\gt 0$
. As the length of the first row (resp. the number of rows) in the Young Tableau corresponds to the length of the longest non-decreasing subsequence in
$c\gt 0$
. As the length of the first row (resp. the number of rows) in the Young Tableau corresponds to the length of the longest non-decreasing subsequence in
![]() $\mathcal{W}_{k;n}$
(resp. the length of the longest decreasing sequence) a consequence of ([
Reference BianeBia01
, theorem 3]) is that, in probability,
$\mathcal{W}_{k;n}$
(resp. the length of the longest decreasing sequence) a consequence of ([
Reference BianeBia01
, theorem 3]) is that, in probability,
For that regime our Theorems 1 and 2 respectively suggest:
 \begin{align*}\mathcal{L}_\lt (\mathcal{W}_{q_N;N}) \approx \mathcal{L}_\lt (S_{q_N/N;N}) \approx \mathcal{L}_\lt (S_{c^2 N;N}) \sim 2Nc-c^2N\sim (2-c)\sqrt{q_N},\\[5pt] \mathcal{L}_\leq (\mathcal{W}_{q_N;N})\approx \mathcal{L}_\leq (S_{q_N/N;N}) \approx \mathcal{L}_\leq (S_{c^2 N;N}) \sim 2Nc+c^2N\sim (2+c)\sqrt{q_N},\end{align*}
\begin{align*}\mathcal{L}_\lt (\mathcal{W}_{q_N;N}) \approx \mathcal{L}_\lt (S_{q_N/N;N}) \approx \mathcal{L}_\lt (S_{c^2 N;N}) \sim 2Nc-c^2N\sim (2-c)\sqrt{q_N},\\[5pt] \mathcal{L}_\leq (\mathcal{W}_{q_N;N})\approx \mathcal{L}_\leq (S_{q_N/N;N}) \approx \mathcal{L}_\leq (S_{c^2 N;N}) \sim 2Nc+c^2N\sim (2+c)\sqrt{q_N},\end{align*}
which is indeed consistent with Biane’s result.
2. Preliminaries: the case of small
 $k_n$
$k_n$
We first prove Theorems 1 and 2 in the case of a small sequence
![]() $(k_n)$
. We say that a sequence
$(k_n)$
. We say that a sequence
![]() $(k_n)$
of integers is small if
$(k_n)$
of integers is small if
Note that a sequence of the form
![]() $k_n=(\!\log n)^{1-{\varepsilon}}$
is small while
$k_n=(\!\log n)^{1-{\varepsilon}}$
is small while
![]() $k_n=\log n$
is not small.
$k_n=\log n$
is not small.
Proof of Theorems
1 and 2 in the case of a small sequence
![]() $(k_n)$
. (In order to lighten notation we skip the dependence in n and write
$(k_n)$
. (In order to lighten notation we skip the dependence in n and write
![]() $k=k_n$
.)
$k=k_n$
.)
Let
![]() $\sigma_{kn}$
be a random uniform permutation of size kn. We can associate to
$\sigma_{kn}$
be a random uniform permutation of size kn. We can associate to
![]() $\sigma_{kn}$
a k-multiset permutation
$\sigma_{kn}$
a k-multiset permutation
![]() $S_{k;n}$
in the following way. For every
$S_{k;n}$
in the following way. For every
![]() $1\leq i\leq kn$
we put
$1\leq i\leq kn$
we put
It is clear that
![]() $S_{k;n}$
is uniform and we have
$S_{k;n}$
is uniform and we have
The Veršik–Kerov Theorem says that the middle term in the above inequality grows like
![]() $2\sqrt{kn}$
. Hence we need to show that if
$2\sqrt{kn}$
. Hence we need to show that if
![]() $(k_n)$
is small then
$(k_n)$
is small then
which proves the small case of Proposition 3 and Theorems 1 and 2. For this purpose we introduce for every
![]() $\delta \gt 0$
the event
$\delta \gt 0$
the event
If
![]() $\mathcal{E}_\delta$
occurs then in particular there exists a non-decreasing subsequence with
$\mathcal{E}_\delta$
occurs then in particular there exists a non-decreasing subsequence with
![]() $\delta \sqrt{n}$
ties, i.e. points of
$\delta \sqrt{n}$
ties, i.e. points of
![]() $S_{k;n}$
which are at the same height as their predecessor in the subsequence. These ties have distinct heights
$S_{k;n}$
which are at the same height as their predecessor in the subsequence. These ties have distinct heights
![]() $1\leq i_1\lt \dots \lt i_\ell \leq n$
for some
$1\leq i_1\lt \dots \lt i_\ell \leq n$
for some
![]() $\delta \sqrt{n}/k \leq \ell \leq \delta \sqrt{n}$
. Fix
$\delta \sqrt{n}/k \leq \ell \leq \delta \sqrt{n}$
. Fix
Integers
![]() $m_1,\dots, m_\ell \geq 2$
such that
$m_1,\dots, m_\ell \geq 2$
such that
![]() $(m_1-1)+\dots +(m_\ell -1) = \delta \sqrt{n}$
;
$(m_1-1)+\dots +(m_\ell -1) = \delta \sqrt{n}$
;
Column indices
![]() $r_{1,1}\lt \dots \lt r_{1,m_1}\lt r_{2,1}\lt r_{2,m_1}\lt \dots\lt r_{\ell,1} \lt \dots \lt r_{1,m_\ell}$
.
$r_{1,1}\lt \dots \lt r_{1,m_1}\lt r_{2,1}\lt r_{2,m_1}\lt \dots\lt r_{\ell,1} \lt \dots \lt r_{1,m_\ell}$
.
We then introduce the event (Fig. 2)
 \begin{multline*}F=F\!\left((i_\ell)_\ell, (r_{i,j})_{i\leq \ell,j\leq m_i}\right) \\[5pt] = \left\{ S(r_{1,1})=\dots = S(r_{1,m_1})=i_1,\dots,S(r_{\ell,1})=\dots = S(r_{1,m_\ell})=i_\ell\right\}.\end{multline*}
\begin{multline*}F=F\!\left((i_\ell)_\ell, (r_{i,j})_{i\leq \ell,j\leq m_i}\right) \\[5pt] = \left\{ S(r_{1,1})=\dots = S(r_{1,m_1})=i_1,\dots,S(r_{\ell,1})=\dots = S(r_{1,m_\ell})=i_\ell\right\}.\end{multline*}
By the union bound (we skip the integer parts)
Using that
we obtain
 \begin{align*}\sum_{(r_{i,j})_{i\leq \ell,j\leq m_i}}\mathbb{P}(F)&=\frac{1}{\binom{kn}{k\ k\ \dots\ k}}\underbrace{\binom{nk}{\sum m_i}}_{\text{choices of \textit{r}'s}} \underbrace{\binom{\delta\sqrt{n}-1}{\ell-1}}_{\text{choices of }m'_{\!\!i}s}\\[5pt] &\quad \times \underbrace{\binom{kn-\sum m_i}{(k-m_1)\ (k-m_2)\ \dots (k-m_\ell) k \dots k}}_{\text{choices of $kn-\sum m_i$ remaining points}}\\[5pt] &= \frac{(k!)^\ell(\delta\sqrt{n}-1)!}{(\delta\sqrt{n}+\ell)!(\delta\sqrt{n}-\ell)!(\ell-1)!(k-m_1)!(k-m_2)!\times \dots \times (k-m_\ell)!}.\end{align*}
\begin{align*}\sum_{(r_{i,j})_{i\leq \ell,j\leq m_i}}\mathbb{P}(F)&=\frac{1}{\binom{kn}{k\ k\ \dots\ k}}\underbrace{\binom{nk}{\sum m_i}}_{\text{choices of \textit{r}'s}} \underbrace{\binom{\delta\sqrt{n}-1}{\ell-1}}_{\text{choices of }m'_{\!\!i}s}\\[5pt] &\quad \times \underbrace{\binom{kn-\sum m_i}{(k-m_1)\ (k-m_2)\ \dots (k-m_\ell) k \dots k}}_{\text{choices of $kn-\sum m_i$ remaining points}}\\[5pt] &= \frac{(k!)^\ell(\delta\sqrt{n}-1)!}{(\delta\sqrt{n}+\ell)!(\delta\sqrt{n}-\ell)!(\ell-1)!(k-m_1)!(k-m_2)!\times \dots \times (k-m_\ell)!}.\end{align*}
Bounding each factor
![]() $(k-m_i)!$
by 1 we get
$(k-m_i)!$
by 1 we get
 \begin{align*}\sum_{(r_{i,j})_{i\leq \ell,j\leq m_i}}\mathbb{P}(F)\leq \frac{(k!)^\ell}{(\delta\sqrt{n})^{\ell +1}(\delta\sqrt{n}-\ell)!(\ell-1)!}.\end{align*}
\begin{align*}\sum_{(r_{i,j})_{i\leq \ell,j\leq m_i}}\mathbb{P}(F)\leq \frac{(k!)^\ell}{(\delta\sqrt{n})^{\ell +1}(\delta\sqrt{n}-\ell)!(\ell-1)!}.\end{align*}

Fig. 2. The event F: a subsequence with
![]() $\delta\sqrt{n}$
(ties are surrounded) is depicted with
$\delta\sqrt{n}$
(ties are surrounded) is depicted with
![]() $\times$
’s.
$\times$
’s.
We now sum over
![]() $1\leq i_1\lt \dots \leq i_\ell \leq n$
and then sum over
$1\leq i_1\lt \dots \leq i_\ell \leq n$
and then sum over
![]() $\ell$
:
$\ell$
:
 \begin{align}\mathbb{P}(\mathcal{E}_\delta)&\leq \sum_{\ell= \delta\sqrt{n}/k}^{\delta\sqrt{n}} \binom{n}{\ell} \frac{(k!)^\ell}{(\delta\sqrt{n})^{\ell+1} (\delta\sqrt{n}-\ell)!(\ell-1)!} \notag\\[5pt] &\leq \sum_{\ell= \delta\sqrt{n}/k}^{\delta\sqrt{n}-3} \binom{n}{\ell} \frac{(k!)^\ell}{(\delta\sqrt{n})^{\ell+1} (\delta\sqrt{n}-\ell)!(\ell-1)!}+ 3 \binom{n}{\delta\sqrt{n}} \frac{(k!)^{\delta\sqrt{n}}}{(\delta\sqrt{n})^{\delta\sqrt{n}-2} (\delta\sqrt{n}-3)!} \end{align}
\begin{align}\mathbb{P}(\mathcal{E}_\delta)&\leq \sum_{\ell= \delta\sqrt{n}/k}^{\delta\sqrt{n}} \binom{n}{\ell} \frac{(k!)^\ell}{(\delta\sqrt{n})^{\ell+1} (\delta\sqrt{n}-\ell)!(\ell-1)!} \notag\\[5pt] &\leq \sum_{\ell= \delta\sqrt{n}/k}^{\delta\sqrt{n}-3} \binom{n}{\ell} \frac{(k!)^\ell}{(\delta\sqrt{n})^{\ell+1} (\delta\sqrt{n}-\ell)!(\ell-1)!}+ 3 \binom{n}{\delta\sqrt{n}} \frac{(k!)^{\delta\sqrt{n}}}{(\delta\sqrt{n})^{\delta\sqrt{n}-2} (\delta\sqrt{n}-3)!} \end{align}
Using the two following inequalities valid for every
![]() $j\leq m$
(see e.g. [
Reference Cormen, Leiserson, Rivest and SteinCLRS09
, equation (C.5)])
$j\leq m$
(see e.g. [
Reference Cormen, Leiserson, Rivest and SteinCLRS09
, equation (C.5)])
we first obtain that if
![]() $k_n!=\mathrm{o}(\sqrt{n})$
(which is the case if
$k_n!=\mathrm{o}(\sqrt{n})$
(which is the case if
![]() $(k_n)$
is small) then the last term of (5) tends to zero. Regarding the sum we write
$(k_n)$
is small) then the last term of (5) tends to zero. Regarding the sum we write
 \begin{align}\mathbb{P}(\mathcal{E}_\delta)&\leq \sum_{\ell= \delta\sqrt{n}/k}^{\delta\sqrt{n}-3}\!\left(\frac{ne}{\ell}\right)^\ell \frac{(k!)^\ell}{(\delta\sqrt{n})^{\ell+1}(\delta\sqrt{n}-\ell)^{\delta\sqrt{n}-\ell}e^{-\delta\sqrt{n}+\ell} (\ell-1)^{\ell-1}e^{-\ell+1}} + \mathrm{o}(1)\notag\\[5pt] &\leq \sum_{\ell= \delta\sqrt{n}/k}^{\delta\sqrt{n}-3}\!\left(\frac{nek!(\delta\sqrt{n}-\ell)}{\delta\sqrt{n}\ell(\ell-1)}\right)^\ell \underbrace{\frac{(\ell-1)e^{-1}}{\delta\sqrt{n}}}_{\leq 1} \bigg(\underbrace{\frac{e}{\delta\sqrt{n}-\ell}}_{\leq e/3\lt 1}\bigg)^{\delta\sqrt{n}}+ \mathrm{o}(1)\notag\\[5pt] &\leq \sum_{\ell= \delta\sqrt{n}/k}^{\delta\sqrt{n}-3}\!\left(\frac{\sqrt{n}ek!(\delta\sqrt{n}-\ell)}{\delta\ell(\ell-1)}\right)^\ell \!\left(\frac{e}{\delta\sqrt{n}-\ell}\right)^{\ell}+ \mathrm{o}(1)\notag\\[5pt] &\leq \sum_{\ell= \delta\sqrt{n}/k}^{\delta\sqrt{n}-3}\!\left(\frac{\sqrt{n}e^2k!}{\delta\ell(\ell-1)}\right)^\ell + \mathrm{o}(1) \leq \sum_{\ell= \delta\sqrt{n}/k}^{\delta\sqrt{n}-3}\!\left(\frac{e^2k^2 k!}{\delta^3 \sqrt{n}}\right)^\ell + \mathrm{o}(1)\end{align}
\begin{align}\mathbb{P}(\mathcal{E}_\delta)&\leq \sum_{\ell= \delta\sqrt{n}/k}^{\delta\sqrt{n}-3}\!\left(\frac{ne}{\ell}\right)^\ell \frac{(k!)^\ell}{(\delta\sqrt{n})^{\ell+1}(\delta\sqrt{n}-\ell)^{\delta\sqrt{n}-\ell}e^{-\delta\sqrt{n}+\ell} (\ell-1)^{\ell-1}e^{-\ell+1}} + \mathrm{o}(1)\notag\\[5pt] &\leq \sum_{\ell= \delta\sqrt{n}/k}^{\delta\sqrt{n}-3}\!\left(\frac{nek!(\delta\sqrt{n}-\ell)}{\delta\sqrt{n}\ell(\ell-1)}\right)^\ell \underbrace{\frac{(\ell-1)e^{-1}}{\delta\sqrt{n}}}_{\leq 1} \bigg(\underbrace{\frac{e}{\delta\sqrt{n}-\ell}}_{\leq e/3\lt 1}\bigg)^{\delta\sqrt{n}}+ \mathrm{o}(1)\notag\\[5pt] &\leq \sum_{\ell= \delta\sqrt{n}/k}^{\delta\sqrt{n}-3}\!\left(\frac{\sqrt{n}ek!(\delta\sqrt{n}-\ell)}{\delta\ell(\ell-1)}\right)^\ell \!\left(\frac{e}{\delta\sqrt{n}-\ell}\right)^{\ell}+ \mathrm{o}(1)\notag\\[5pt] &\leq \sum_{\ell= \delta\sqrt{n}/k}^{\delta\sqrt{n}-3}\!\left(\frac{\sqrt{n}e^2k!}{\delta\ell(\ell-1)}\right)^\ell + \mathrm{o}(1) \leq \sum_{\ell= \delta\sqrt{n}/k}^{\delta\sqrt{n}-3}\!\left(\frac{e^2k^2 k!}{\delta^3 \sqrt{n}}\right)^\ell + \mathrm{o}(1)\end{align}
which tends to zero for every
![]() $\delta \gt 0$
, as long as
$\delta \gt 0$
, as long as
![]() $(k_n)$
satisfies (3). This proves that
$(k_n)$
satisfies (3). This proves that
![]() $ \mathcal{L}_{\leq }(S_{k;n})= \mathcal{L}_{\lt }(S_{k;n}) +o_\mathbb{P}(\sqrt{kn})$
. Combining this with (4), this proves that
$ \mathcal{L}_{\leq }(S_{k;n})= \mathcal{L}_{\lt }(S_{k;n}) +o_\mathbb{P}(\sqrt{kn})$
. Combining this with (4), this proves that
which is the “small” case of Proposition 3 since
![]() $k_n= \mathrm{o}(\sqrt{nk_n})$
.
$k_n= \mathrm{o}(\sqrt{nk_n})$
.
To conclude the proof of small cases of Theorems 1 and 2 we observe that we have the crude bounds
![]() $ \mathcal{L}_{\lt }(S_{k;n})\leq n$
and
$ \mathcal{L}_{\lt }(S_{k;n})\leq n$
and
![]() $ \mathcal{L}_{\leq }(S_{k;n})\leq nk_n$
. This allows us to write
$ \mathcal{L}_{\leq }(S_{k;n})\leq nk_n$
. This allows us to write
Together with equation (6) this implies that
We use again Veršik–Kerov and (4) to deduce that both sides are
![]() $2\sqrt{nk_n}+\mathrm{o}(\sqrt{nk_n})$
.
$2\sqrt{nk_n}+\mathrm{o}(\sqrt{nk_n})$
.
3. Poissonisation: variants of the Hammersley process
In this section we define formally and analyse two semi-discrete variants of the Hammersley process.
Remark 2. In the sequel,
![]() ${\textit{Poisson}}(\mu)$
(resp.
${\textit{Poisson}}(\mu)$
(resp.
![]() ${\textit{Binomial}} (n,q)$
) stand for generic random variables with Poisson distribution with mean
${\textit{Binomial}} (n,q)$
) stand for generic random variables with Poisson distribution with mean
![]() $\mu$
(resp. Binomial distribution with parameters n, q).
$\mu$
(resp. Binomial distribution with parameters n, q).
Notation
![]() $\mathrm{Geometric}_{\geq 0}(1-\beta)$
stands for a geometric random variable with the convention
$\mathrm{Geometric}_{\geq 0}(1-\beta)$
stands for a geometric random variable with the convention
![]() $\mathbb{P}(\textit{Geometric}_{\geq 0}(1-\beta)=k)=(1-\beta)\beta^k$
for
$\mathbb{P}(\textit{Geometric}_{\geq 0}(1-\beta)=k)=(1-\beta)\beta^k$
for
![]() $k\geq 0$
. In particular
$k\geq 0$
. In particular
![]() $\mathbb{E}[\textit{Geometric}_{\geq 0}(1-\beta)]={\beta}/({1-\beta})$
.
$\mathbb{E}[\textit{Geometric}_{\geq 0}(1-\beta)]={\beta}/({1-\beta})$
.
3·1. Definitions of the processes
 $L_\lt (t)$
and
$L_\lt (t)$
and
 $L_\leq (t)$
$L_\leq (t)$
For a parameter
![]() $\lambda\gt 0$
let
$\lambda\gt 0$
let
![]() $\Pi^{(\lambda)}$
be the random set
$\Pi^{(\lambda)}$
be the random set
![]() $\Pi^{(\lambda)}=\cup_i \Pi_i^{(\lambda)}$
where
$\Pi^{(\lambda)}=\cup_i \Pi_i^{(\lambda)}$
where
![]() $\Pi^{(\lambda)}_i$
’s are independent and each
$\Pi^{(\lambda)}_i$
’s are independent and each
![]() $\Pi^{(\lambda)}_i$
is a homogeneous Poisson Point Process (PPP) with intensity
$\Pi^{(\lambda)}_i$
is a homogeneous Poisson Point Process (PPP) with intensity
![]() $\lambda$
on
$\lambda$
on
![]() $(0,\infty)\times\{i\}$
. For simplicity set
$(0,\infty)\times\{i\}$
. For simplicity set
The goal of this section is to obtain non-asymptotic bounds for
![]() $\mathcal{L}_\lt \!\left(\Pi^{(\lambda)}_{x,t}\right)$
and
$\mathcal{L}_\lt \!\left(\Pi^{(\lambda)}_{x,t}\right)$
and
![]() $\mathcal{L}_\leq \!\left( \Pi^{(\lambda)}_{x,t}\right)$
. Indeed if we then choose
$\mathcal{L}_\leq \!\left( \Pi^{(\lambda)}_{x,t}\right)$
. Indeed if we then choose
then there are
![]() $kn+\mathcal{O}(\sqrt{kn})$
points on each line of a
$kn+\mathcal{O}(\sqrt{kn})$
points on each line of a
![]() $\Pi^{(\lambda)}_{x,t}$
and we expect that
$\Pi^{(\lambda)}_{x,t}$
and we expect that
Fix
![]() $x\gt 1$
throughout the section. For every
$x\gt 1$
throughout the section. For every
![]() $t\in \{0,1,2,\dots \}$
the function
$t\in \{0,1,2,\dots \}$
the function
![]() $y\in[0,x] \mapsto \mathcal{L}_\lt (y,t)$
(resp.
$y\in[0,x] \mapsto \mathcal{L}_\lt (y,t)$
(resp.
![]() $\mathcal{L}_\leq (y,t)$
) is a non-decreasing integer-valued function whose all steps are equal to
$\mathcal{L}_\leq (y,t)$
) is a non-decreasing integer-valued function whose all steps are equal to
![]() $+1$
. Therefore this function is completely determined by the finite set
$+1$
. Therefore this function is completely determined by the finite set
(Respectively:
Sets
![]() $L_\lt (t)$
and
$L_\lt (t)$
and
![]() $L_\leq (t)$
are finite subsets of [0, x] whose elements are considered as particles. It is easy to see that for fixed
$L_\leq (t)$
are finite subsets of [0, x] whose elements are considered as particles. It is easy to see that for fixed
![]() $x\gt 0$
both processes
$x\gt 0$
both processes
![]() $(L_\lt (t))_t$
and
$(L_\lt (t))_t$
and
![]() $(L_\leq (t))_t$
are Markov processes taking their values in the family of point processes of [0, x].
$(L_\leq (t))_t$
are Markov processes taking their values in the family of point processes of [0, x].
Exactly the same way as for the classical Hammersley process ([ Reference HammersleyHam72 , section 9], [ Reference Aldous and DiaconisAD95 ]) the individual dynamic of particles is very easy to describe:
The process
![]() $L_\lt $
. We put
$L_\lt $
. We put
![]() $L_\lt (0)=\emptyset$
. In order to define
$L_\lt (0)=\emptyset$
. In order to define
![]() $L_\lt (t+1)$
from
$L_\lt (t+1)$
from
![]() $L_\lt (t)$
we consider particles from left to right. A particle at y in
$L_\lt (t)$
we consider particles from left to right. A particle at y in
![]() $L_\lt (t)$
moves at time
$L_\lt (t)$
moves at time
![]() $t+1$
at the location of the leftmost available point z in
$t+1$
at the location of the leftmost available point z in
![]() $\Pi_{t+1}^{(\lambda)}\cap(0,y)$
(if any, otherwise it stays at y). This point z is not available anymore for subsequent particles, as well as every other point of
$\Pi_{t+1}^{(\lambda)}\cap(0,y)$
(if any, otherwise it stays at y). This point z is not available anymore for subsequent particles, as well as every other point of
![]() $\Pi_{t+1}^{(\lambda)}\cap (0,y)$
.
$\Pi_{t+1}^{(\lambda)}\cap (0,y)$
.

If there is a point in
![]() $\Pi_{t+1}^{(\lambda)}$
which is on the right of
$\Pi_{t+1}^{(\lambda)}$
which is on the right of
![]() $y'\;:\!=\; \max \{ L_\lt (t)\}$
then a new particle is created in
$y'\;:\!=\; \max \{ L_\lt (t)\}$
then a new particle is created in
![]() $L_\lt (t+1)$
, located at the leftmost point in
$L_\lt (t+1)$
, located at the leftmost point in
![]() $\Pi_{t+1}^{(\lambda)}\cap (y',x)$
. (In pictures this new particle comes from the right.)
$\Pi_{t+1}^{(\lambda)}\cap (y',x)$
. (In pictures this new particle comes from the right.)

Fig. 3. Our four variants of the Hammersley process (time goes from bottom to top). Top left: the process
![]() $L_\lt (t)$
. Top right: the process
$L_\lt (t)$
. Top right: the process
![]() $L_\leq (t)$
. Bottom left: the process
$L_\leq (t)$
. Bottom left: the process
![]() $L^{(\alpha,p)}_{\lt }(t)$
. Bottom right: the process
$L^{(\alpha,p)}_{\lt }(t)$
. Bottom right: the process
![]() $L^{(\beta,\beta^\star)}_{\leq }(t)$
.
$L^{(\beta,\beta^\star)}_{\leq }(t)$
.
A realization of
![]() $L_\lt $
is shown on top-left of Fig. 3.
$L_\lt $
is shown on top-left of Fig. 3.
The process
![]() $L_\leq $
. We put
$L_\leq $
. We put
![]() $L_\leq (0)=\emptyset$
. In order to define
$L_\leq (0)=\emptyset$
. In order to define
![]() $L_\leq (t+1)$
from
$L_\leq (t+1)$
from
![]() $L_\leq (t)$
we also consider particles from left to right. A particle at y in
$L_\leq (t)$
we also consider particles from left to right. A particle at y in
![]() $L_\leq (t)$
moves at time
$L_\leq (t)$
moves at time
![]() $t+1$
at the location of the leftmost available point z in
$t+1$
at the location of the leftmost available point z in
![]() $\Pi_{t+1}^{(\lambda)}\cap(0,y)$
. This point z is not available anymore for subsequent particles, other points in (z, y) remain available.
$\Pi_{t+1}^{(\lambda)}\cap(0,y)$
. This point z is not available anymore for subsequent particles, other points in (z, y) remain available.

-
If there is a point in
 $\Pi_{t+1}^{(\lambda)}$
which is on the right of
$\Pi_{t+1}^{(\lambda)}$
which is on the right of
 $y'\;:\!=\; \max\{ L_\lt (t)\}$
then new particles are created in
$y'\;:\!=\; \max\{ L_\lt (t)\}$
then new particles are created in
 $L_\lt (t+1)$
, one for each point in
$L_\lt (t+1)$
, one for each point in
 $\Pi_{t+1}^{(\lambda)}\cap (y',x)$
.
$\Pi_{t+1}^{(\lambda)}\cap (y',x)$
. -
A realization of
 $L_\leq $
is shown in top-right of Figure 3.
$L_\leq $
is shown in top-right of Figure 3.
Processes
![]() $L_{\lt }(t)$
and
$L_{\lt }(t)$
and
![]() $L_{\leq }(t)$
are designed in such a way that they record the length of longest increasing/non-decreasing paths in
$L_{\leq }(t)$
are designed in such a way that they record the length of longest increasing/non-decreasing paths in
![]() $\Pi$
. In fact particles trajectories correspond to the level sets of the functions
$\Pi$
. In fact particles trajectories correspond to the level sets of the functions
![]() $(x,t)\mapsto \mathcal{L}_\lt \!\left( \Pi^{(\lambda)}_{x,t}\right)$
,
$(x,t)\mapsto \mathcal{L}_\lt \!\left( \Pi^{(\lambda)}_{x,t}\right)$
,
![]() $(x,t)\mapsto \mathcal{L}_\leq \!\left( \Pi^{(\lambda)}_{x,t}\right)$
.
$(x,t)\mapsto \mathcal{L}_\leq \!\left( \Pi^{(\lambda)}_{x,t}\right)$
.
Proposition 4. For every x,
where on each right-hand side we consider the particle system on [0, x].
Proof. We are merely restating the original construction from Hammersley ([
Reference HammersleyHam72
, section 9]). We only do the case of
![]() $L_\lt (t)$
.
$L_\lt (t)$
.
Let us call each particle trajectory a Hammersley line. By construction each Hammersley line is a broken line starting from the right of the box
![]() $[0,x]\times [0,t]$
and is formed by a succession of north/west line segments. Because of this, two distinct points in a given longest increasing subsequence of
$[0,x]\times [0,t]$
and is formed by a succession of north/west line segments. Because of this, two distinct points in a given longest increasing subsequence of
![]() $\Pi^{(\lambda)}_{x,t}$
cannot belong to the same Hammersley line. Since there are
$\Pi^{(\lambda)}_{x,t}$
cannot belong to the same Hammersley line. Since there are
![]() $L_\lt (t)$
Hammersley’s lines this gives
$L_\lt (t)$
Hammersley’s lines this gives
![]() $\mathcal{L}_\lt \!\left( \Pi^{(\lambda)}_{x,t}\right) \leq \mathrm{card}(L_\lt (t))$
.
$\mathcal{L}_\lt \!\left( \Pi^{(\lambda)}_{x,t}\right) \leq \mathrm{card}(L_\lt (t))$
.
In order to prove the converse inequality we build from this graphical construction a longest increcreasing subsequence of
![]() $ \Pi^{(\lambda)}_{x,t}$
with exactly one point on each Hammersley line. To do so, we order Hammersley’s lines from bottom-left to top-right, and we build our path starting from the top-right corner. We first choose any point of
$ \Pi^{(\lambda)}_{x,t}$
with exactly one point on each Hammersley line. To do so, we order Hammersley’s lines from bottom-left to top-right, and we build our path starting from the top-right corner. We first choose any point of
![]() $\Pi^{(\lambda)}_{x,t}$
belonging to the last Hammersley line. We then proceed by induction: we choose the next point among the points of of
$\Pi^{(\lambda)}_{x,t}$
belonging to the last Hammersley line. We then proceed by induction: we choose the next point among the points of of
![]() $\Pi^{(\lambda)}_{x,t}$
lying on the previous Hammersley line such that the subsequence remains increasing. (This is possible since Hammersley’s lines only have North/West line segments.) This proves
$\Pi^{(\lambda)}_{x,t}$
lying on the previous Hammersley line such that the subsequence remains increasing. (This is possible since Hammersley’s lines only have North/West line segments.) This proves
![]() $\mathcal{L}_\lt \!\left( \Pi^{(\lambda)}_{x,t}\right) \geq \mathrm{card}(L_\lt (t))$
.
$\mathcal{L}_\lt \!\left( \Pi^{(\lambda)}_{x,t}\right) \geq \mathrm{card}(L_\lt (t))$
.
3·2. Sources and sinks: stationarity
Proposition 4 tells us that in on our way to prove Theorem 1 and Theorem 2 we need to understand the asymptotic behaviour of processes
![]() $L_{\lt },L_{\leq }$
.
$L_{\lt },L_{\leq }$
.
It is proved in [
Reference Ferrari and MartinFM06
] that the homogeneous PPP with intensity
![]() $\alpha$
on
$\alpha$
on
![]() $\mathbb{R}$
is stationary for
$\mathbb{R}$
is stationary for
![]() $(L_\lt (t))_t$
. However we need non-asymptotic estimates for
$(L_\lt (t))_t$
. However we need non-asymptotic estimates for
![]() $(L_\lt (t))_t$
(and
$(L_\lt (t))_t$
(and
![]() $(L_\leq (t))_t$
) on a given interval (0, x). To solve this issue we use the trick of sources/sinks introduced formally and exploited by Cator and Groeneboom [
Reference Cator and GroeneboomCG05
] for the continuous HAD process:
$(L_\leq (t))_t$
) on a given interval (0, x). To solve this issue we use the trick of sources/sinks introduced formally and exploited by Cator and Groeneboom [
Reference Cator and GroeneboomCG05
] for the continuous HAD process:
-
Sources form a finite subset of
 $[0,x]\times \{0\}$
which plays the role of the initial configuration
$[0,x]\times \{0\}$
which plays the role of the initial configuration
 $L_\lt (0),L_\leq (0)$
.
$L_\lt (0),L_\leq (0)$
. -
Sinks are points of
 $\{0\}\times [1,t] $
which add up to
$\{0\}\times [1,t] $
which add up to
 $\Pi^{(\lambda)}$
when one defines the dynamics of
$\Pi^{(\lambda)}$
when one defines the dynamics of
 $L_\lt (t),L_\leq (t)$
. For
$L_\lt (t),L_\leq (t)$
. For
 $L_\leq (t)$
it makes sense to add several sinks at the same location (0, i) so sinks may have a multiplicity.
$L_\leq (t)$
it makes sense to add several sinks at the same location (0, i) so sinks may have a multiplicity.
Examples of dynamics of
![]() $L_\lt, L_\leq $
under the influence of sources/sinks is illustrated at the bottom of Figure 3.
$L_\lt, L_\leq $
under the influence of sources/sinks is illustrated at the bottom of Figure 3.
Here is the discrete-time analogous of [ Reference Cator and GroeneboomCG05 , theorem 3·1]:
Lemma 5. For every
![]() $\lambda,\alpha\gt 0$
let
$\lambda,\alpha\gt 0$
let
![]() $L^{(\alpha,p)}_{\lt }(t)$
be the Hammersley process defined
$L^{(\alpha,p)}_{\lt }(t)$
be the Hammersley process defined
![]() $L_{\lt }(t)$
with:
$L_{\lt }(t)$
with:
-
(i) sources distributed according to a homogeneous PPP with intensity
 $\alpha$
on
$\alpha$
on
 $[0,x]\times \{0\}$
;
$[0,x]\times \{0\}$
; -
(ii) sinks distributed according to i.i.d.
 $\mathrm{Bernoulli}(p)$
with (7)If sources, sinks, and
$\mathrm{Bernoulli}(p)$
with (7)If sources, sinks, and \begin{equation}\frac{\lambda}{\lambda +\alpha}=p.\end{equation}
\begin{equation}\frac{\lambda}{\lambda +\alpha}=p.\end{equation}
 $\Pi^{(\lambda)}$
are independent then the process
$\Pi^{(\lambda)}$
are independent then the process
 $\!\left(L^{(\alpha,p)}_{\lt }(t)\right)_{t\geq 0}$
is stationary.
$\!\left(L^{(\alpha,p)}_{\lt }(t)\right)_{t\geq 0}$
is stationary.
Lemma 6. For every
![]() $\beta\gt \lambda\gt 0$
, let
$\beta\gt \lambda\gt 0$
, let
![]() $L^{(\beta,\beta^\star)}_{\leq }(t)$
be the Hammersley process defined like
$L^{(\beta,\beta^\star)}_{\leq }(t)$
be the Hammersley process defined like
![]() $L_{\leq }(t)$
with additional sources and sinks:
$L_{\leq }(t)$
with additional sources and sinks:
-
(i) sources distributed according to a homogeneous PPP with intensity
 $\beta$
on
$\beta$
on
 $[0,x]\times \{0\}$
;
$[0,x]\times \{0\}$
; -
(ii) sinks distributed according to i.i.d.
 $\mathrm{Geometric}_{\geq 0}(1-\beta^\star)$
with (8)
$\mathrm{Geometric}_{\geq 0}(1-\beta^\star)$
with (8) \begin{equation}\beta^\star\beta =\lambda.\end{equation}
\begin{equation}\beta^\star\beta =\lambda.\end{equation}
If sources, sinks and
![]() $\Pi^{(\lambda)}$
are independent then the process
$\Pi^{(\lambda)}$
are independent then the process
![]() $\!\left(L^{(\beta,\beta^\star)}_{\leq }(t)\right)_{t\geq 0}$
is stationary.
$\!\left(L^{(\beta,\beta^\star)}_{\leq }(t)\right)_{t\geq 0}$
is stationary.
Proof of Lemmas
5 and 6. Lemma 6 could be obtained from minor adjustments of [
Reference BoyerBoy22
, chapter 3, lemma 3·2]. (Be aware that we have to switch
![]() $x\leftrightarrow t$
and sources
$x\leftrightarrow t$
and sources
![]() $\leftrightarrow$
sinks in [
Reference BoyerBoy22
] in order to fit our setup.) For the sake of the reader we however propose the following alternative proof which explains where (8) come from.
$\leftrightarrow$
sinks in [
Reference BoyerBoy22
] in order to fit our setup.) For the sake of the reader we however propose the following alternative proof which explains where (8) come from.
Consider for some fixed
![]() $t\geq 1$
the process
$t\geq 1$
the process
![]() $(H_y)_{0\leq y\leq x} $
given by the number of Hammersley lines passing through the point (y, t) (Fig. 4).
$(H_y)_{0\leq y\leq x} $
given by the number of Hammersley lines passing through the point (y, t) (Fig. 4).

Fig. 4. A sample of the process H.
The initial value
![]() $H_0$
is the number of sinks at (0, t), which is distributed as a
$H_0$
is the number of sinks at (0, t), which is distributed as a
![]() $\mathrm{Geometric}_{\geq 0}(1-\beta^\star)$
. The process
$\mathrm{Geometric}_{\geq 0}(1-\beta^\star)$
. The process
![]() $(H_y)$
is a random walk (reflected at zero) with ’
$(H_y)$
is a random walk (reflected at zero) with ’
![]() $+1$
rate’ equal to
$+1$
rate’ equal to
![]() $\lambda$
and ’
$\lambda$
and ’
![]() $-1$
rate’ equal to
$-1$
rate’ equal to
![]() $\beta$
. (Jumps of
$\beta$
. (Jumps of
![]() $(H_y)$
are independent from sinks as sinks are independent from
$(H_y)$
are independent from sinks as sinks are independent from
![]() $\Pi^{(\lambda)}$
.) The
$\Pi^{(\lambda)}$
.) The
![]() $\mathrm{Geometric}_{\geq 0}(1-\beta^\star)$
distribution is stationary for this random walk exactly when (8) holds. The set of points of
$\mathrm{Geometric}_{\geq 0}(1-\beta^\star)$
distribution is stationary for this random walk exactly when (8) holds. The set of points of
![]() $L^{(\beta,\beta^\star)}_{\leq }(t)$
is given by the union of
$L^{(\beta,\beta^\star)}_{\leq }(t)$
is given by the union of
![]() $\Pi_t^{(\lambda)}$
and the points of
$\Pi_t^{(\lambda)}$
and the points of
![]() $L^{(\beta,\beta^\star)}_{\leq }(t)$
that do not correspond to a ’
$L^{(\beta,\beta^\star)}_{\leq }(t)$
that do not correspond to a ’
![]() $-1$
’ jump. Computations given in Appendix B show that this is distributed as a homogeneous PPP with intensity
$-1$
’ jump. Computations given in Appendix B show that this is distributed as a homogeneous PPP with intensity
![]() $\beta$
.
$\beta$
.
Lemma 5 is proved exactly in the same way, calculations are even easier. In this case the corresponding process
![]() $(H_y)_{0\leq y\leq x} $
takes its values in
$(H_y)_{0\leq y\leq x} $
takes its values in
![]() $\{0,1\}$
and its stationary distribution is the Bernoulli distribution with mean
$\{0,1\}$
and its stationary distribution is the Bernoulli distribution with mean
![]() $\lambda/(\alpha+\lambda)$
, hence (7).
$\lambda/(\alpha+\lambda)$
, hence (7).
3·3. Processes
 $L_\lt (t)$
and
$L_\lt (t)$
and
 $L_\leq (t)$
: non-asymptotic bounds
$L_\leq (t)$
: non-asymptotic bounds
From Lemmas 5 and 6 it is straightforward to derive non-asymptotic upper bounds for
![]() $L_\lt (t),L_\leq (t)$
.
$L_\lt (t),L_\leq (t)$
.
For
![]() $y\leq x$
let
$y\leq x$
let
![]() $\textsf{So}^{(\alpha)}_x$
be the random set of sources with intensity
$\textsf{So}^{(\alpha)}_x$
be the random set of sources with intensity
![]() $\alpha$
and for
$\alpha$
and for
![]() $s\leq t$
let
$s\leq t$
let
![]() $\textsf{Si}^{(p)}_t$
the random set of sinks with intensity p. In particular,
$\textsf{Si}^{(p)}_t$
the random set of sinks with intensity p. In particular,
It is convenient to use the notation
![]() $\mathcal{L}_{=\lt }(\mathcal{P})$
which is, as before, the length of the longest increasing path taking points in
$\mathcal{L}_{=\lt }(\mathcal{P})$
which is, as before, the length of the longest increasing path taking points in
![]() $\mathcal{P}$
but when the path is also allowed to go through several sources (which have however the same y-coordinate) or several sinks (which have the same x-coordinate). Formally,
$\mathcal{P}$
but when the path is also allowed to go through several sources (which have however the same y-coordinate) or several sinks (which have the same x-coordinate). Formally,
where
 \begin{align*}(x,y)=\prec (x',y') \text{ if }\begin{cases} &x\lt x'\text{ and }y\lt y', \\[5pt] \text{ or } &x=x'=0 \text{ and }y\lt y', \\[5pt] \text{ or } &x\lt x' \text{ and }y=y'=0.\end{cases}\end{align*}
\begin{align*}(x,y)=\prec (x',y') \text{ if }\begin{cases} &x\lt x'\text{ and }y\lt y', \\[5pt] \text{ or } &x=x'=0 \text{ and }y\lt y', \\[5pt] \text{ or } &x\lt x' \text{ and }y=y'=0.\end{cases}\end{align*}
Proposition 4 generalises easily to the settings of sinks and sources.
Claim 1.
Proof of the Claim. By the same reasoning as in the proof of Proposition 4 the LHS is exactly the number of broken lines in the box
![]() $[0,x]\times [0,t]$
. Each such line escapes the box either through the left (it thus corresponds to a sink) or through the top (and is thus counted by
$[0,x]\times [0,t]$
. Each such line escapes the box either through the left (it thus corresponds to a sink) or through the top (and is thus counted by
![]() $L^{(\alpha,p)}_{\lt }(t)$
).
$L^{(\alpha,p)}_{\lt }(t)$
).
Lemma 7 (Domination for
![]() $\mathcal{L}_\lt $
). For every
$\mathcal{L}_\lt $
). For every
![]() $\alpha,p \in(0,1)$
such that (7) holds, there is a stochastic domination of the form:
$\alpha,p \in(0,1)$
such that (7) holds, there is a stochastic domination of the form:
(The
![]() $ {\mathrm{Poisson}}$
and
$ {\mathrm{Poisson}}$
and
![]() ${\mathrm{Binomial}} $
random variables involved in (10) are not independent.)
${\mathrm{Binomial}} $
random variables involved in (10) are not independent.)
Proof. Adding sources and sinks may not decrease longest increasing paths. Thus,
 \begin{align*}\mathcal{L}_\lt \!\left( \Pi^{(\lambda)}_{x,t}\right) &\preccurlyeq \mathcal{L}_{=\lt }\!\left( \Pi^{(\lambda)}_{x,t}\cup \textsf{So}^{(\alpha)}_x\cup \textsf{Si}^{(p)}_t\right) \\[5pt] &= L^{(\alpha,p)}_{\lt }(t)+\mathrm{card}(\textsf{Si}^{(p)})\text{ (using (9))}\\[5pt] &\stackrel{\text{(d)}}{=} L^{(\alpha,p)}_{\lt }(0)+\mathrm{card}(\textsf{Si}^{(p)}) \text{ (using stationarity: Lemma 5)}\\[5pt] &\stackrel{\text{(d)}}{=} {\mathrm{Poisson}}(x\alpha)+ {\mathrm{Binomial}} (t,p).\end{align*}
\begin{align*}\mathcal{L}_\lt \!\left( \Pi^{(\lambda)}_{x,t}\right) &\preccurlyeq \mathcal{L}_{=\lt }\!\left( \Pi^{(\lambda)}_{x,t}\cup \textsf{So}^{(\alpha)}_x\cup \textsf{Si}^{(p)}_t\right) \\[5pt] &= L^{(\alpha,p)}_{\lt }(t)+\mathrm{card}(\textsf{Si}^{(p)})\text{ (using (9))}\\[5pt] &\stackrel{\text{(d)}}{=} L^{(\alpha,p)}_{\lt }(0)+\mathrm{card}(\textsf{Si}^{(p)}) \text{ (using stationarity: Lemma 5)}\\[5pt] &\stackrel{\text{(d)}}{=} {\mathrm{Poisson}}(x\alpha)+ {\mathrm{Binomial}} (t,p).\end{align*}
Taking expectations in (10) we obtain
The LHS in the above equation does not depend on
![]() $\alpha,p$
so the idea is to apply (10) with the minimising choice
$\alpha,p$
so the idea is to apply (10) with the minimising choice
i.e.
We have proved
(Compare with (1).) We have a similar statement for non-decreasing subsequences:
Lemma 8 (Domination for
![]() $\mathcal{L}_\leq $
). For every
$\mathcal{L}_\leq $
). For every
![]() $\beta,\beta^\star \in(0,1)$
such that (8) holds, there is a stochastic domination of the form:
$\beta,\beta^\star \in(0,1)$
such that (8) holds, there is a stochastic domination of the form:
where
![]() $\mathcal{G}_i^{(\beta^\star)}$
’s are i.i.d.
$\mathcal{G}_i^{(\beta^\star)}$
’s are i.i.d.
![]() $\mathrm{Geometric}_{\geq 0}(1-\beta^\star)$
.
$\mathrm{Geometric}_{\geq 0}(1-\beta^\star)$
.
We put
i.e.
(In particular
![]() $\bar{\beta}\gt \lambda$
, as required in Lemma 6.) Equation (12) yields
$\bar{\beta}\gt \lambda$
, as required in Lemma 6.) Equation (12) yields
(Compare with (2).)
Theorem 9 (Concentration for
![]() $\mathcal{L}_\lt $
,
$\mathcal{L}_\lt $
,
![]() $\mathcal{L}_\leq $
). There exist strictly positive functions g, h such that for all
$\mathcal{L}_\leq $
). There exist strictly positive functions g, h such that for all
![]() $\varepsilon\gt 0$
and for every
$\varepsilon\gt 0$
and for every
![]() $x,t\geq 1$
,
$x,t\geq 1$
,
![]() $\lambda \gt 0$
such that
$\lambda \gt 0$
such that
![]() $t\geq x\lambda$
:
$t\geq x\lambda$
:
Similarly:
For the proof of Theorem 9 we will focus on the case of
![]() $\mathcal{L}_\lt $
, i.e. Equations (16), (17). When necessary we will give the slight modification needed to prove Equations (18) and (19). The beginning of the proof mimics lemmas 4·1 and 4·2 in [
Reference Basdevant, Enriquez, Gerin and GouéréBEGG16
].
$\mathcal{L}_\lt $
, i.e. Equations (16), (17). When necessary we will give the slight modification needed to prove Equations (18) and (19). The beginning of the proof mimics lemmas 4·1 and 4·2 in [
Reference Basdevant, Enriquez, Gerin and GouéréBEGG16
].
We first prove similar bounds for the stationary processes with minimising sources and sinks.
Lemma 10 (Concentration for
![]() $\mathcal{L}_\lt $
with sources and sinks). Let
$\mathcal{L}_\lt $
with sources and sinks). Let
![]() $\bar{\alpha},\bar{p}$
be defined by (11). There exists a strictly positive function
$\bar{\alpha},\bar{p}$
be defined by (11). There exists a strictly positive function
![]() $g_1$
such that for all
$g_1$
such that for all
![]() $\varepsilon\gt 0$
and for every
$\varepsilon\gt 0$
and for every
![]() $x,t\geq 1$
,
$x,t\geq 1$
,
![]() $\lambda \gt 0$
such that
$\lambda \gt 0$
such that
![]() $t\geq x\lambda$
:
$t\geq x\lambda$
:
Proof of Lemma 10. By stationarity (Lemma 5) we have
Then
 \begin{align*} {\mathbb{P}}(\mathcal{L}_{=\lt }(\Pi^{(\lambda)}_{x,t}\cup \textsf{So}^{(\bar{\alpha})}_x\cup \textsf{Si}^{(\bar{p})}_t&\gt (1+{\varepsilon})(2\sqrt{xt\lambda}-x\lambda))\\[5pt] &\le {\mathbb{P}}\!\left({\mathrm{Poisson}}(x\bar{\alpha})\gt \left(1+\frac{\varepsilon}{2}\right)\left(\sqrt{xt\lambda}-x\lambda\right)\right)\\[5pt] &+ {\mathbb{P}}\!\left({\mathrm{Binomial}} (t,\bar{p})\gt (1+\frac{\varepsilon}{2})\sqrt{xt\lambda}\right).\end{align*}
\begin{align*} {\mathbb{P}}(\mathcal{L}_{=\lt }(\Pi^{(\lambda)}_{x,t}\cup \textsf{So}^{(\bar{\alpha})}_x\cup \textsf{Si}^{(\bar{p})}_t&\gt (1+{\varepsilon})(2\sqrt{xt\lambda}-x\lambda))\\[5pt] &\le {\mathbb{P}}\!\left({\mathrm{Poisson}}(x\bar{\alpha})\gt \left(1+\frac{\varepsilon}{2}\right)\left(\sqrt{xt\lambda}-x\lambda\right)\right)\\[5pt] &+ {\mathbb{P}}\!\left({\mathrm{Binomial}} (t,\bar{p})\gt (1+\frac{\varepsilon}{2})\sqrt{xt\lambda}\right).\end{align*}
Recall that
![]() $x\bar{\alpha}=\sqrt{xt\lambda}-x\lambda$
,
$x\bar{\alpha}=\sqrt{xt\lambda}-x\lambda$
,
![]() $t\bar{p}=\sqrt{xt\lambda}$
. Using the tail inequality for the Poisson distribution (Lemma 15):
$t\bar{p}=\sqrt{xt\lambda}$
. Using the tail inequality for the Poisson distribution (Lemma 15):
Using the tail inequality for the binomial (Lemma 16) we get
The proof of (21) is identical. This shows Lemma 10 with
![]() $g_1({\varepsilon})={\varepsilon}^2/12$
.
$g_1({\varepsilon})={\varepsilon}^2/12$
.
For longest non-decreasing subsequences we have a statement similar to Lemma 10. The only modification in the proof is that in order to estimate the number of sinks one has to replace Lemma 16 (tail inequality for the Binomial) by Lemma 17 (tail inequality for a sum of geometric random variablesFootnote 1). During the proof we need to bound
![]() $\sqrt{xt\lambda}+x\lambda$
by
$\sqrt{xt\lambda}+x\lambda$
by
![]() $\sqrt{xt\lambda}$
, this explains the form of the right-hand side in Equations (18) and (19).
$\sqrt{xt\lambda}$
, this explains the form of the right-hand side in Equations (18) and (19).
Proof of Theorem
9. Adding sources/sinks may not decrease
![]() $\mathcal{L}_{\lt }$
so
$\mathcal{L}_{\lt }$
so
thus the upper bound (16) is a direct consequence of Lemma 10.

Fig. 5. A sample of
![]() $\Pi^{(\lambda)}_{x,t}$
, sources, sinks, and the corresponding trajectories of particles. Here
$\Pi^{(\lambda)}_{x,t}$
, sources, sinks, and the corresponding trajectories of particles. Here
![]() $\mathcal{L}_{=\lt }(\Pi^{(\lambda)}_{x,t}\cup \textsf{So}^{(\alpha)}_x\cup \textsf{Si}^{(p)}_t)=5$
and
$\mathcal{L}_{=\lt }(\Pi^{(\lambda)}_{x,t}\cup \textsf{So}^{(\alpha)}_x\cup \textsf{Si}^{(p)}_t)=5$
and
![]() $L^{(\alpha,p)}_{\lt }(t)=2$
(two remaining particles at the top of the box).
$L^{(\alpha,p)}_{\lt }(t)=2$
(two remaining particles at the top of the box).
Let us now prove the lower bound. We consider the length of a maximising path among those using sources from 0 to
![]() ${\varepsilon} x$
and then only increasing points of
${\varepsilon} x$
and then only increasing points of
![]() $\Pi^{(\lambda)}_{x,t}\cap \!\left([{\varepsilon} x,x]\times [0,t]\right)$
(see Figure 5). Formally we set
$\Pi^{(\lambda)}_{x,t}\cap \!\left([{\varepsilon} x,x]\times [0,t]\right)$
(see Figure 5). Formally we set
 \begin{align}L_{=\lt, {\varepsilon}}^\star&\;:\!=\;\mathrm{card}\!\left(\textsf{So}^{(\bar{\alpha})}_{{\varepsilon} x}\right)+\mathcal{L}_{\lt }\!\left( (\Pi^{(\lambda)}_{x,t}\cap \left([{\varepsilon} x,x]\times [0,t]\right)\right)\notag\\ &\stackrel{\text{(d)}}{=}{\mathrm{Poisson}}({\varepsilon} x\bar{\alpha}) + \mathcal{L}_{\lt }\!\left( (\Pi^{(\lambda)}_{x,t}\cap \left([{\varepsilon} x,x]\times [0,t]\right)\right).\end{align}
\begin{align}L_{=\lt, {\varepsilon}}^\star&\;:\!=\;\mathrm{card}\!\left(\textsf{So}^{(\bar{\alpha})}_{{\varepsilon} x}\right)+\mathcal{L}_{\lt }\!\left( (\Pi^{(\lambda)}_{x,t}\cap \left([{\varepsilon} x,x]\times [0,t]\right)\right)\notag\\ &\stackrel{\text{(d)}}{=}{\mathrm{Poisson}}({\varepsilon} x\bar{\alpha}) + \mathcal{L}_{\lt }\!\left( (\Pi^{(\lambda)}_{x,t}\cap \left([{\varepsilon} x,x]\times [0,t]\right)\right).\end{align}
The idea is that for any fixed
![]() ${\varepsilon}$
the paths contributing to
${\varepsilon}$
the paths contributing to
![]() $L_{=\lt, {\varepsilon}}^\star$
will typically not contribute to
$L_{=\lt, {\varepsilon}}^\star$
will typically not contribute to
![]() $\mathcal{L}_{=\lt }\!\left( \Pi^{(\lambda)}_{x,t}\cup \textsf{So}^{(\bar{\alpha})}_x\cup \textsf{Si}^{(\bar{p})}_t\right) =L^{(\bar{\alpha},p)}_{\lt }(t)+\mathrm{card}(\textsf{Si}^{(\bar{p})}_t)$
. Indeed Equation (23) suggests that for large x, t
$\mathcal{L}_{=\lt }\!\left( \Pi^{(\lambda)}_{x,t}\cup \textsf{So}^{(\bar{\alpha})}_x\cup \textsf{Si}^{(\bar{p})}_t\right) =L^{(\bar{\alpha},p)}_{\lt }(t)+\mathrm{card}(\textsf{Si}^{(\bar{p})}_t)$
. Indeed Equation (23) suggests that for large x, t
 \begin{align*}L_{=\lt, {\varepsilon}}^\star&\approx \mathbb{E}[{\mathrm{Poisson}}({\varepsilon} x\bar{\alpha})] + \mathbb{E}\left[\mathcal{L}_{\lt }\!\left( \Pi^{(\lambda)}_{x,t}\cap \!\left([{\varepsilon} x,x]\times [0,t]\right)\right)\right]\\[5pt] &\approx x{\varepsilon}\bar{\alpha} + 2\sqrt{x(1-{\varepsilon})\lambda t}-x(1-{\varepsilon})\lambda\\[5pt] & = 2\sqrt{x\lambda t} -x\lambda -\sqrt{xt\lambda}\delta({\varepsilon}),\end{align*}
\begin{align*}L_{=\lt, {\varepsilon}}^\star&\approx \mathbb{E}[{\mathrm{Poisson}}({\varepsilon} x\bar{\alpha})] + \mathbb{E}\left[\mathcal{L}_{\lt }\!\left( \Pi^{(\lambda)}_{x,t}\cap \!\left([{\varepsilon} x,x]\times [0,t]\right)\right)\right]\\[5pt] &\approx x{\varepsilon}\bar{\alpha} + 2\sqrt{x(1-{\varepsilon})\lambda t}-x(1-{\varepsilon})\lambda\\[5pt] & = 2\sqrt{x\lambda t} -x\lambda -\sqrt{xt\lambda}\delta({\varepsilon}),\end{align*}
where
![]() $\delta({\varepsilon})=2-{\varepsilon}-2\sqrt{1-{\varepsilon}}$
is positive and increasing. In order to make the above approximation rigorous we first write
$\delta({\varepsilon})=2-{\varepsilon}-2\sqrt{1-{\varepsilon}}$
is positive and increasing. In order to make the above approximation rigorous we first write
where
 \begin{align*}{\mathbb{P}}_1&= {\mathbb{P}}\!\left({\mathrm{Poisson}}(x{\varepsilon}\bar{\alpha})\ge x{\varepsilon}\bar{\alpha} + \tfrac{1}{4}\sqrt{xt\lambda}\delta({\varepsilon})\right),\\[5pt] {\mathbb{P}}_2&={\mathbb{P}}\!\left( \mathcal{L}_{\lt } (\Pi^{(\lambda)}_{x,t}\cap \!\left([{\varepsilon} x,x]\times [0,t]\right) \geq 2\sqrt{x(1-{\varepsilon})\lambda t} -x(1-{\varepsilon})\lambda +\tfrac{1}{4}\sqrt{xt\lambda}\delta({\varepsilon})\right).\end{align*}
\begin{align*}{\mathbb{P}}_1&= {\mathbb{P}}\!\left({\mathrm{Poisson}}(x{\varepsilon}\bar{\alpha})\ge x{\varepsilon}\bar{\alpha} + \tfrac{1}{4}\sqrt{xt\lambda}\delta({\varepsilon})\right),\\[5pt] {\mathbb{P}}_2&={\mathbb{P}}\!\left( \mathcal{L}_{\lt } (\Pi^{(\lambda)}_{x,t}\cap \!\left([{\varepsilon} x,x]\times [0,t]\right) \geq 2\sqrt{x(1-{\varepsilon})\lambda t} -x(1-{\varepsilon})\lambda +\tfrac{1}{4}\sqrt{xt\lambda}\delta({\varepsilon})\right).\end{align*}
Using the tail inequality for the Poisson distribution (see Lemma 15) we have that
Besides
 \begin{align}{\mathbb{P}}_2 &\leq {\mathbb{P}}\!\left( \mathcal{L}_{\lt } (\Pi^{(\lambda)}_{x,t}\cap \!\left([{\varepsilon} x,x]\times [0,t]\right) \geq \!\left(2\sqrt{x(1-{\varepsilon})\lambda t} -x(1-{\varepsilon})\lambda\right)\times (1+\tfrac{1}{8}\delta({\varepsilon})) \right)\notag\\[5pt] &\leq \exp\!\left(\!-g(\delta({\varepsilon})/8) (\sqrt{x(1-{\varepsilon})t\lambda}-x(1-{\varepsilon})\lambda) \right) \text{(using the upper bound (16))}.\notag\end{align}
\begin{align}{\mathbb{P}}_2 &\leq {\mathbb{P}}\!\left( \mathcal{L}_{\lt } (\Pi^{(\lambda)}_{x,t}\cap \!\left([{\varepsilon} x,x]\times [0,t]\right) \geq \!\left(2\sqrt{x(1-{\varepsilon})\lambda t} -x(1-{\varepsilon})\lambda\right)\times (1+\tfrac{1}{8}\delta({\varepsilon})) \right)\notag\\[5pt] &\leq \exp\!\left(\!-g(\delta({\varepsilon})/8) (\sqrt{x(1-{\varepsilon})t\lambda}-x(1-{\varepsilon})\lambda) \right) \text{(using the upper bound (16))}.\notag\end{align}
Finally we can find some positive h such that
One proves exactly in the same way a similar bound for the length of a maximizing path among those using sinks in
![]() $\{0\}\times [0,{\varepsilon} t]$
and then only increasing points of
$\{0\}\times [0,{\varepsilon} t]$
and then only increasing points of
![]() $\Pi^{(\lambda)}_{x,t}\cap \!\left([0,x]\times [{\varepsilon} t,t]\right)$
.
$\Pi^{(\lambda)}_{x,t}\cap \!\left([0,x]\times [{\varepsilon} t,t]\right)$
.
Choose now one of the maximizing paths
![]() $\mathcal{P}$
for
$\mathcal{P}$
for
![]() $\mathcal{L}_{=\lt }\!\left( \Pi^{(\lambda)}_{x,t}\cup \textsf{So}^{(\bar{\alpha})}_x\cup \textsf{Si}^{(\bar{p})}_t\right)$
(if there are many of them, choose one arbitrarily in a deterministic way: the lowest, say). Denote by
$\mathcal{L}_{=\lt }\!\left( \Pi^{(\lambda)}_{x,t}\cup \textsf{So}^{(\bar{\alpha})}_x\cup \textsf{Si}^{(\bar{p})}_t\right)$
(if there are many of them, choose one arbitrarily in a deterministic way: the lowest, say). Denote by
![]() $\textsf{sources}(\mathcal{P})$
and
$\textsf{sources}(\mathcal{P})$
and
![]() $\textsf{sinks}(\mathcal{P})$
the number of sources and sinks in the path
$\textsf{sinks}(\mathcal{P})$
the number of sources and sinks in the path
![]() $\mathcal{P}$
:
$\mathcal{P}$
:
In Figure 5 the path
![]() $\mathcal{P}$
is sketched, in that example
$\mathcal{P}$
is sketched, in that example
![]() $\textsf{sources}(\mathcal{P})=2$
,
$\textsf{sources}(\mathcal{P})=2$
,
![]() $\textsf{sinks}(\mathcal{P})=0$
.
$\textsf{sinks}(\mathcal{P})=0$
.
Lemma 11. There exists a positive function
![]() $\psi$
such that for all real
$\psi$
such that for all real
![]() $\eta \gt 0$
$\eta \gt 0$
Proof of Lemma
11. (As the left-hand side is non-increasing in
![]() $\eta$
it is enough to prove the lemma for
$\eta$
it is enough to prove the lemma for
![]() $\eta\lt 1$
.)
$\eta\lt 1$
.)
If the event
![]() $\left\{\textsf{sources}(\mathcal{P})\geq \eta \sqrt{x\lambda t}\right\}$
holds then there exists a (random)
$\left\{\textsf{sources}(\mathcal{P})\geq \eta \sqrt{x\lambda t}\right\}$
holds then there exists a (random)
![]() ${\varepsilon}$
such that the two following events occur:
${\varepsilon}$
such that the two following events occur:
 \begin{align*}\textsf{So}_{{\varepsilon} x}&\geq \eta \sqrt{x\lambda t};\\[5pt]L_{=\lt, {\varepsilon}}^\star =\mathcal{L}_{=\lt }&\!\left( \Pi^{(\lambda)}_{x,t}\cup \textsf{So}^{(\bar{\alpha})}_x\cup \textsf{Si}^{(\bar{p})}_t\right) =L^{(\bar{\alpha},\bar{p})}_{\lt }(t)+\mathrm{card}(\textsf{Si}^{(\bar{p})}_t).\end{align*}
\begin{align*}\textsf{So}_{{\varepsilon} x}&\geq \eta \sqrt{x\lambda t};\\[5pt]L_{=\lt, {\varepsilon}}^\star =\mathcal{L}_{=\lt }&\!\left( \Pi^{(\lambda)}_{x,t}\cup \textsf{So}^{(\bar{\alpha})}_x\cup \textsf{Si}^{(\bar{p})}_t\right) =L^{(\bar{\alpha},\bar{p})}_{\lt }(t)+\mathrm{card}(\textsf{Si}^{(\bar{p})}_t).\end{align*}
This implies that this random
![]() ${\varepsilon}$
is larger than
${\varepsilon}$
is larger than
![]() $\eta/2\gt 0$
unless the number of sources in
$\eta/2\gt 0$
unless the number of sources in
![]() $[0,x\eta/2]$
is improbably high:
$[0,x\eta/2]$
is improbably high:
Therefore
 \begin{align*}\begin{array}{r c l }\mathbb{P}(\textsf{sources}(\mathcal{P})\geq \eta \sqrt{x\lambda t}) &\leq &\ \mathbb{P}(\textsf{So}_{\eta x/2}\geq \eta \sqrt{x\lambda t}) \\ &+ &\ \mathbb{P}(L^{(\bar{\alpha},\bar{p})}_{\lt }(t) \leq \sqrt{x\lambda t} -x\lambda - \tfrac{1}{4}\delta(\eta/3)\sqrt{x\lambda t}) \\ &+ &\ \mathbb{P}(\mathrm{card}(\textsf{Si}^{(\bar{p})}_t)\leq \sqrt{x\lambda t} - \tfrac{1}{4}\delta(\eta/3)\sqrt{x\lambda t})\\ &+ &\ \mathbb{P}(L_{=\lt, \varepsilon}^\star \geq 2\sqrt{x\lambda t} -x\lambda -\tfrac{1}{2}\delta(\eta/3)\sqrt{x\lambda t}\text{ for some }\eta/2\leq \varepsilon \leq 1 ).\end{array}\end{align*}
\begin{align*}\begin{array}{r c l }\mathbb{P}(\textsf{sources}(\mathcal{P})\geq \eta \sqrt{x\lambda t}) &\leq &\ \mathbb{P}(\textsf{So}_{\eta x/2}\geq \eta \sqrt{x\lambda t}) \\ &+ &\ \mathbb{P}(L^{(\bar{\alpha},\bar{p})}_{\lt }(t) \leq \sqrt{x\lambda t} -x\lambda - \tfrac{1}{4}\delta(\eta/3)\sqrt{x\lambda t}) \\ &+ &\ \mathbb{P}(\mathrm{card}(\textsf{Si}^{(\bar{p})}_t)\leq \sqrt{x\lambda t} - \tfrac{1}{4}\delta(\eta/3)\sqrt{x\lambda t})\\ &+ &\ \mathbb{P}(L_{=\lt, \varepsilon}^\star \geq 2\sqrt{x\lambda t} -x\lambda -\tfrac{1}{2}\delta(\eta/3)\sqrt{x\lambda t}\text{ for some }\eta/2\leq \varepsilon \leq 1 ).\end{array}\end{align*}
Let us call the four terms in the right-hand of the above display
![]() $\mathbb{P}_3,\mathbb{P}_4,\mathbb{P}_5,\mathbb{P}_6$
respectively.
$\mathbb{P}_3,\mathbb{P}_4,\mathbb{P}_5,\mathbb{P}_6$
respectively.
From previous calculations, the three first terms in the above display are less than
![]() $\exp\!(\!-\!\phi(\eta)(\sqrt{x\lambda t}-x\lambda))$
for some positive function
$\exp\!(\!-\!\phi(\eta)(\sqrt{x\lambda t}-x\lambda))$
for some positive function
![]() $\phi$
. To see why:
$\phi$
. To see why:
-
(i) we bound
 ${\mathbb{P}}_3$
with Lemma 15 again (recall
${\mathbb{P}}_3$
with Lemma 15 again (recall
 $\textsf{So}_{\eta x/2}$
is a Poisson random variable);
$\textsf{So}_{\eta x/2}$
is a Poisson random variable); -
(ii) the term
 ${\mathbb{P}}_4$
is bounded thanks to Lemma 10 (recall also (9));
${\mathbb{P}}_4$
is bounded thanks to Lemma 10 (recall also (9)); -
(iii) we bound
 ${\mathbb{P}}_5$
with Lemma 16 (recall that
${\mathbb{P}}_5$
with Lemma 16 (recall that
 $\textsf{Si}^{(\bar{p})}_t$
is a Binomial).
$\textsf{Si}^{(\bar{p})}_t$
is a Binomial).
To conclude the proof it remains to bound
![]() ${\mathbb{P}}_6$
. Let K be an integer larger than
${\mathbb{P}}_6$
. Let K be an integer larger than
![]() $144/\eta^3$
, by definition of
$144/\eta^3$
, by definition of
![]() $L_{=\lt, {\varepsilon}}^\star$
we have for every
$L_{=\lt, {\varepsilon}}^\star$
we have for every
![]() $1\leq k\leq \lceil xK \rceil$
and every
$1\leq k\leq \lceil xK \rceil$
and every
![]() ${\varepsilon} \in[{k}/{K},({k+1})/{K})$
${\varepsilon} \in[{k}/{K},({k+1})/{K})$
Thus
 \begin{align}\mathbb{P}\bigg(\bigcup_{\eta/2\leq {\varepsilon} \leq 1} & \left\{L_{=\lt, {\varepsilon}}^\star \gt 2\sqrt{x\lambda t} -x\lambda -\tfrac{1}{2}\delta(\eta/3)\sqrt{x\lambda t}\right\} \bigg)\notag\\[5pt] & \leq \sum_{k\geq \lfloor \eta K/2\rfloor } \mathbb{P}\!\left(L_{=\lt, k/K}^\star \gt 2\sqrt{x\lambda t} -x\lambda -\delta(\eta/3)\sqrt{x\lambda t} \right)\notag\\[5pt] & \quad + \sum_{k\geq \lfloor \eta K/2\rfloor } \mathbb{P}\!\left(\mathrm{card}(\textsf{So}^{(\bar{\alpha})}_x \cap [\tfrac{k}{K},\tfrac{k+1}{K}]) \gt \tfrac{1}{2}\delta(\eta/3)\sqrt{x\lambda t}\right)\notag\\[5pt] &\leq \sum_{k\geq \lfloor \eta K/2\rfloor } \mathbb{P}\!\left(L_{=\lt, k/K}^\star \gt 2\sqrt{x\lambda t} -x\lambda -\delta(k/K)\sqrt{x\lambda t} \right) \quad\notag\\[5pt] &\quad + \sum_{k\geq \lfloor \eta K/2\rfloor } \mathbb{P}\!\left(\mathrm{card}(\textsf{So}^{(\bar{\alpha})}_x \cap [\tfrac{k}{K},\tfrac{k+1}{K}]) \gt \tfrac{1}{2}\delta(\eta/3)\sqrt{x\lambda t}\right)\notag.\end{align}
\begin{align}\mathbb{P}\bigg(\bigcup_{\eta/2\leq {\varepsilon} \leq 1} & \left\{L_{=\lt, {\varepsilon}}^\star \gt 2\sqrt{x\lambda t} -x\lambda -\tfrac{1}{2}\delta(\eta/3)\sqrt{x\lambda t}\right\} \bigg)\notag\\[5pt] & \leq \sum_{k\geq \lfloor \eta K/2\rfloor } \mathbb{P}\!\left(L_{=\lt, k/K}^\star \gt 2\sqrt{x\lambda t} -x\lambda -\delta(\eta/3)\sqrt{x\lambda t} \right)\notag\\[5pt] & \quad + \sum_{k\geq \lfloor \eta K/2\rfloor } \mathbb{P}\!\left(\mathrm{card}(\textsf{So}^{(\bar{\alpha})}_x \cap [\tfrac{k}{K},\tfrac{k+1}{K}]) \gt \tfrac{1}{2}\delta(\eta/3)\sqrt{x\lambda t}\right)\notag\\[5pt] &\leq \sum_{k\geq \lfloor \eta K/2\rfloor } \mathbb{P}\!\left(L_{=\lt, k/K}^\star \gt 2\sqrt{x\lambda t} -x\lambda -\delta(k/K)\sqrt{x\lambda t} \right) \quad\notag\\[5pt] &\quad + \sum_{k\geq \lfloor \eta K/2\rfloor } \mathbb{P}\!\left(\mathrm{card}(\textsf{So}^{(\bar{\alpha})}_x \cap [\tfrac{k}{K},\tfrac{k+1}{K}]) \gt \tfrac{1}{2}\delta(\eta/3)\sqrt{x\lambda t}\right)\notag.\end{align}
In the last inequality we use the facts that
![]() $K\gt {144}/{\eta^3}\gt {6}/{\eta}$
and that
$K\gt {144}/{\eta^3}\gt {6}/{\eta}$
and that
![]() $\delta$
is increasing. Using now (25) it holds that
$\delta$
is increasing. Using now (25) it holds that
 \begin{align}\mathbb{P}\bigg(\bigcup_{\eta/2\leq {\varepsilon} \leq 1} & \left\{L_{=\lt, {\varepsilon}}^\star \gt 2\sqrt{x\lambda t} -x\lambda -\tfrac{1}{2}\delta(\eta/3)\sqrt{x\lambda t}\right\} \bigg)\notag\\[5pt] \leq &\sum_{k\geq \lfloor \eta K/2\rfloor } \exp\!(\!-\!h(k/K) (\sqrt{xt\lambda}-x\lambda))\qquad\notag\\[5pt] + &K \times \mathbb{P}\!\left(\mathrm{Poisson}(\bar{\alpha}/K)\gt \tfrac{1}{2}\delta(\eta/3)\sqrt{x\lambda t}\right)\notag\\[5pt] \leq &\ K \exp\!(\!-\!h(\eta/3) (\sqrt{xt\lambda}-x\lambda)) \\[5pt] + & K \times \mathbb{P}\!\left(\mathrm{Poisson}(\bar{\alpha}/K)\gt \tfrac{1}{2}\delta(\eta/3)\sqrt{x\lambda t}\right).\notag\end{align}
\begin{align}\mathbb{P}\bigg(\bigcup_{\eta/2\leq {\varepsilon} \leq 1} & \left\{L_{=\lt, {\varepsilon}}^\star \gt 2\sqrt{x\lambda t} -x\lambda -\tfrac{1}{2}\delta(\eta/3)\sqrt{x\lambda t}\right\} \bigg)\notag\\[5pt] \leq &\sum_{k\geq \lfloor \eta K/2\rfloor } \exp\!(\!-\!h(k/K) (\sqrt{xt\lambda}-x\lambda))\qquad\notag\\[5pt] + &K \times \mathbb{P}\!\left(\mathrm{Poisson}(\bar{\alpha}/K)\gt \tfrac{1}{2}\delta(\eta/3)\sqrt{x\lambda t}\right)\notag\\[5pt] \leq &\ K \exp\!(\!-\!h(\eta/3) (\sqrt{xt\lambda}-x\lambda)) \\[5pt] + & K \times \mathbb{P}\!\left(\mathrm{Poisson}(\bar{\alpha}/K)\gt \tfrac{1}{2}\delta(\eta/3)\sqrt{x\lambda t}\right).\notag\end{align}
We finally bound the last display. First recall from our notation that
Then:
 \begin{align} \mathbb{P}\!\left(\mathrm{Poisson}(\bar{\alpha}/K)\gt \tfrac{1}{2}\delta(\eta/3)\sqrt{x\lambda t}\right) &=\mathbb{P}\!\left(\mathrm{Poisson}(\bar{\alpha}/K)\gt \bar{\alpha}/K-\bar{\alpha}/K+\tfrac{1}{2}\delta(\eta/3)\sqrt{x\lambda t}\right)\notag\\[5pt] &\leq \mathbb{P}\!\left(\mathrm{Poisson}(\bar{\alpha}/K)\gt \bar{\alpha}/K+\sqrt{x\lambda t}\!\left( -\frac{1}{xK}+\frac{1}{2}\delta(\eta/3)\right)\! \right)\notag\\[5pt] &\leq \mathbb{P}\!\left(\mathrm{Poisson}(\bar{\alpha}/K)\gt \bar{\alpha}/K+\sqrt{x\lambda t}\!\left( -\frac{\eta^3}{144}+\frac{\eta^2}{72}\right) \!\right).\end{align}
\begin{align} \mathbb{P}\!\left(\mathrm{Poisson}(\bar{\alpha}/K)\gt \tfrac{1}{2}\delta(\eta/3)\sqrt{x\lambda t}\right) &=\mathbb{P}\!\left(\mathrm{Poisson}(\bar{\alpha}/K)\gt \bar{\alpha}/K-\bar{\alpha}/K+\tfrac{1}{2}\delta(\eta/3)\sqrt{x\lambda t}\right)\notag\\[5pt] &\leq \mathbb{P}\!\left(\mathrm{Poisson}(\bar{\alpha}/K)\gt \bar{\alpha}/K+\sqrt{x\lambda t}\!\left( -\frac{1}{xK}+\frac{1}{2}\delta(\eta/3)\right)\! \right)\notag\\[5pt] &\leq \mathbb{P}\!\left(\mathrm{Poisson}(\bar{\alpha}/K)\gt \bar{\alpha}/K+\sqrt{x\lambda t}\!\left( -\frac{\eta^3}{144}+\frac{\eta^2}{72}\right) \!\right).\end{align}
We can find a positive function
![]() $\varphi$
such that (26) and (27) are both less than
$\varphi$
such that (26) and (27) are both less than
![]() $({144}/{\eta}) e^{-\varphi(\eta) (\sqrt{xt\lambda}-x\lambda)}$
. We then choose a positive function
$({144}/{\eta}) e^{-\varphi(\eta) (\sqrt{xt\lambda}-x\lambda)}$
. We then choose a positive function
![]() $\psi$
such that
$\psi$
such that
and thus
![]() $\mathbb{P}(\textsf{sources}(\mathcal{P})\geq \eta \sqrt{x\lambda t})\leq \exp\!(\!-\!\psi(\eta) (\sqrt{xt\lambda}-x\lambda))$
. With minor modifications one proves the same bound for sinks (possibly by changing
$\mathbb{P}(\textsf{sources}(\mathcal{P})\geq \eta \sqrt{x\lambda t})\leq \exp\!(\!-\!\psi(\eta) (\sqrt{xt\lambda}-x\lambda))$
. With minor modifications one proves the same bound for sinks (possibly by changing
![]() $\psi$
):
$\psi$
):
![]() $ \mathbb{P}(\textsf{sinks}(\mathcal{P})\geq \eta \sqrt{x\lambda t})\leq \exp\!(\!-\!\psi(\eta) (\sqrt{xt\lambda}-x\lambda))$
and Lemma 11 is proved.
$ \mathbb{P}(\textsf{sinks}(\mathcal{P})\geq \eta \sqrt{x\lambda t})\leq \exp\!(\!-\!\psi(\eta) (\sqrt{xt\lambda}-x\lambda))$
and Lemma 11 is proved.
We can conclude the proof of the lower bound in Theorem 9. Let us write
4. Proof of Theorem 1 when
 $k_n\to +\infty$
: de-Poissonisation
$k_n\to +\infty$
: de-Poissonisation
In order to conclude the proof of Theorem 1 it remains to de-Poissonise Theorem 9. We need a few notation. For any integers
![]() $i_1,\dots,i_n$
let
$i_1,\dots,i_n$
let
![]() $\mathcal{S}_{i_1,\dots,i_n}$
be the random set of points given by
$\mathcal{S}_{i_1,\dots,i_n}$
be the random set of points given by
![]() $i_\ell$
uniform points on each horizontal line:
$i_\ell$
uniform points on each horizontal line:
where
![]() $(U_{\ell,r})_{\ell,r}$
is an array of i.i.d. uniform random variables in [0,1]. Set also
$(U_{\ell,r})_{\ell,r}$
is an array of i.i.d. uniform random variables in [0,1]. Set also
![]() $e_{i_1,\dots,i_n} =\mathbb{E}[\mathcal{L}_{\lt }(\mathcal{S}_{i_1,\dots,i_n})].$
By uniformity of U’s we have the identity
$e_{i_1,\dots,i_n} =\mathbb{E}[\mathcal{L}_{\lt }(\mathcal{S}_{i_1,\dots,i_n})].$
By uniformity of U’s we have the identity
![]() $\mathbb{E}[\mathcal{L}_{\lt }(S_{k;n})]=e_{k,\dots,k}$
and therefore our problem reduces to estimating
$\mathbb{E}[\mathcal{L}_{\lt }(S_{k;n})]=e_{k,\dots,k}$
and therefore our problem reduces to estimating
![]() $e_{k,\dots,k}$
. On the other hand if
$e_{k,\dots,k}$
. On the other hand if
![]() $X_1,\dots,X_n$
are i.i.d. Poisson random variables with mean k then
$X_1,\dots,X_n$
are i.i.d. Poisson random variables with mean k then
The last equality is obtained by combining Theorem 9 for
with the trivial bound
![]() $\mathcal{L}_{\lt }(\Pi_{nk_n,n}^{(1/n)})\leq n$
. In order to exploit (28) we need the following smoothness estimate.
$\mathcal{L}_{\lt }(\Pi_{nk_n,n}^{(1/n)})\leq n$
. In order to exploit (28) we need the following smoothness estimate.
Lemma 12. For every
![]() $i_1,\dots,i_n$
and
$i_1,\dots,i_n$
and
![]() $j_1,\dots,j_n$
$j_1,\dots,j_n$
 \begin{align*}\left| e_{i_1,\dots,i_n} - e_{j_1,\dots,j_n} \right| \leq 6\sqrt{\sum_{\ell=1}^n |i_\ell-j_\ell |}.\end{align*}
\begin{align*}\left| e_{i_1,\dots,i_n} - e_{j_1,\dots,j_n} \right| \leq 6\sqrt{\sum_{\ell=1}^n |i_\ell-j_\ell |}.\end{align*}
Proof. Let
![]() $\mathcal{S}=\mathcal{S}_{i_1,\dots,i_n}$
be as above. If we replace in
$\mathcal{S}=\mathcal{S}_{i_1,\dots,i_n}$
be as above. If we replace in
![]() $\mathcal{S}$
the y-coordinate of each point of the form
$\mathcal{S}$
the y-coordinate of each point of the form
![]() $(x,\ell)$
by a new y-coordinate uniform in the interval
$(x,\ell)$
by a new y-coordinate uniform in the interval
![]() $(\ell,\ell+1)$
(independent from anything else) then this defines a uniform permutation
$(\ell,\ell+1)$
(independent from anything else) then this defines a uniform permutation
![]() $\sigma_{i_1+\dots +i_n}$
of size
$\sigma_{i_1+\dots +i_n}$
of size
![]() $i_1+\dots +i_n$
. The longest increasing subsequence in
$i_1+\dots +i_n$
. The longest increasing subsequence in
![]() $\mathcal{S}$
is mapped onto an increasing subsequence in
$\mathcal{S}$
is mapped onto an increasing subsequence in
![]() $\sigma_{i_1+\dots +i_n}$
and thus this construction shows the stochastic domination
$\sigma_{i_1+\dots +i_n}$
and thus this construction shows the stochastic domination
![]() $\mathcal{L}_{\lt }(\mathcal{S}_{i_1,\dots,i_n}) \preccurlyeq \mathcal{L}_{\lt }(\sigma_{i_1+\dots +i_n}).$
Thus for every
$\mathcal{L}_{\lt }(\mathcal{S}_{i_1,\dots,i_n}) \preccurlyeq \mathcal{L}_{\lt }(\sigma_{i_1+\dots +i_n}).$
Thus for every
![]() $i_1,\dots,i_n$
,
$i_1,\dots,i_n$
,
(The second inequality follows for example from [
Reference SteeleSte97
, lemma 1·4·1].) Besides, consider for two n-tuples
![]() $i_1,\dots,i_n$
and
$i_1,\dots,i_n$
and
![]() $j_1,\dots,j_n$
two independent sets of points
$j_1,\dots,j_n$
two independent sets of points
![]() $\mathcal{S}_{i_1,\dots,i_n}$
,
$\mathcal{S}_{i_1,\dots,i_n}$
,
![]() $ \widetilde{\mathcal{S}}_{j_1,\dots,j_n}$
then
$ \widetilde{\mathcal{S}}_{j_1,\dots,j_n}$
then
This proves that
(In particular
![]() $(i_1,\dots,i_n)\mapsto e_{i_1,\dots,i_n}$
is non-decreasing with respect to any of its coordinates.) Therefore
$(i_1,\dots,i_n)\mapsto e_{i_1,\dots,i_n}$
is non-decreasing with respect to any of its coordinates.) Therefore
 \begin{align*}e_{i_1,\dots,i_n}&\leq e_{(i_1-j_1)^+,\dots,(i_n-j_n)^+} + e_{j_1-(i_1-j_1)^-,\dots,j_n-(i_n-j_n)^-}\\[5pt] &\leq e_{|i_1-j_1|,\dots,|i_n-j_n|} + e_{j_1,\dots,j_n}.\end{align*}
\begin{align*}e_{i_1,\dots,i_n}&\leq e_{(i_1-j_1)^+,\dots,(i_n-j_n)^+} + e_{j_1-(i_1-j_1)^-,\dots,j_n-(i_n-j_n)^-}\\[5pt] &\leq e_{|i_1-j_1|,\dots,|i_n-j_n|} + e_{j_1,\dots,j_n}.\end{align*}
By switching the role of i’s and j’s:
 \begin{align*}|e_{i_1,\dots,i_n}-e_{j_1,\dots,j_n}| \leq e_{|i_1-j_1|,\dots,|i_n-j_n|}\leq 6\sqrt{\sum_{\ell=1}^n |i_\ell-j_\ell |},\end{align*}
\begin{align*}|e_{i_1,\dots,i_n}-e_{j_1,\dots,j_n}| \leq e_{|i_1-j_1|,\dots,|i_n-j_n|}\leq 6\sqrt{\sum_{\ell=1}^n |i_\ell-j_\ell |},\end{align*}
using (29).
Proof of Theorem
1 for any sequence
![]() $(k_n)\to +\infty$
. Using smoothness we write
$(k_n)\to +\infty$
. Using smoothness we write
 \begin{align}|e_{k,\dots,k} - \mathbb{E}[e_{X_1,\dots,X_n}]|\leq \mathbb{E}\left[|e_{k,\dots,k} - e_{X_1,\dots,X_n}|\right]\leq 6\times \mathbb{E}\left[ \!\left(\sum_{\ell=1}^n | X_\ell-k |\right)^{1/2}\right].\end{align}
\begin{align}|e_{k,\dots,k} - \mathbb{E}[e_{X_1,\dots,X_n}]|\leq \mathbb{E}\left[|e_{k,\dots,k} - e_{X_1,\dots,X_n}|\right]\leq 6\times \mathbb{E}\left[ \!\left(\sum_{\ell=1}^n | X_\ell-k |\right)^{1/2}\right].\end{align}
Using twice the Cauchy–Schwarz inequality:
 \begin{align*}\mathbb{E}\left[ \!\left(\sum_{\ell=1}^n | X_\ell-k |\right)^{1/2}\right]&\leq \sqrt{\mathbb{E}\left[ \sum_{\ell=1}^n | X_\ell-k |\right]}\\[5pt] &\leq \sqrt{n \mathbb{E}\left[ | X_1-k |\right]}\\[5pt] &\leq \sqrt{n \mathbb{E}\left[ | X_1-k |^{2}\right]^{1/2}}= \sqrt{n \sqrt{\mathrm{Var}(X_1)}}= \sqrt{n \sqrt{k}}.\end{align*}
\begin{align*}\mathbb{E}\left[ \!\left(\sum_{\ell=1}^n | X_\ell-k |\right)^{1/2}\right]&\leq \sqrt{\mathbb{E}\left[ \sum_{\ell=1}^n | X_\ell-k |\right]}\\[5pt] &\leq \sqrt{n \mathbb{E}\left[ | X_1-k |\right]}\\[5pt] &\leq \sqrt{n \mathbb{E}\left[ | X_1-k |^{2}\right]^{1/2}}= \sqrt{n \sqrt{\mathrm{Var}(X_1)}}= \sqrt{n \sqrt{k}}.\end{align*}
If
![]() $k=k_n\to \infty$
then the last display is a
$k=k_n\to \infty$
then the last display is a
![]() $o(\sqrt{nk_n})$
and Equations (30) and (28) show that
$o(\sqrt{nk_n})$
and Equations (30) and (28) show that
5. Proof of Theorem 2
5·1. Proof for large
 $(k_n)$
$(k_n)$
We now prove Theorem 2 for a large sequence
![]() $(k_n)$
. We say that
$(k_n)$
. We say that
![]() $(k_n)$
is large if
$(k_n)$
is large if
for some
![]() $\alpha \in(0,1) $
. Recall that
$\alpha \in(0,1) $
. Recall that
![]() $k_n=\log n$
is not large while
$k_n=\log n$
is not large while
![]() $k_n=(\!\log n)^{1+{\varepsilon}}$
is large.
$k_n=(\!\log n)^{1+{\varepsilon}}$
is large.
We first observe that de-Poissonisation cannot be applied as in the previous section. We lack smoothness as, for instance,
![]() $\mathbb{E}[\mathcal{L}_{\leq }(\mathcal{S}_{i_1,0,0,\dots,0})]=i_1\neq \mathcal{O}(\sqrt{\sum i_\ell})$
. The strategy is to apply Theorem 9 with
$\mathbb{E}[\mathcal{L}_{\leq }(\mathcal{S}_{i_1,0,0,\dots,0})]=i_1\neq \mathcal{O}(\sqrt{\sum i_\ell})$
. The strategy is to apply Theorem 9 with
(The exact value of
![]() $\lambda_n$
will be different for the proofs of the lower and upper bounds.)
$\lambda_n$
will be different for the proofs of the lower and upper bounds.)
Proof of the upper bound of (2) for large
![]() $(k_n)$
.
$(k_n)$
.
Choose
![]() $\alpha$
such that
$\alpha$
such that
![]() $n^2k_n\exp\!(\!-\!k_n^{\alpha})= \mathrm{o}(\sqrt{nk_n})$
. Put
$n^2k_n\exp\!(\!-\!k_n^{\alpha})= \mathrm{o}(\sqrt{nk_n})$
. Put
Let
![]() $E_n^{\lambda_n}$
be the event
$E_n^{\lambda_n}$
be the event
The event
![]() $E_n$
occurs with large probability. Indeed,
$E_n$
occurs with large probability. Indeed,
 \begin{align}1-\mathbb{P}(E_n^{\lambda_n})&\leq n \mathbb{P}\!\left( {\mathrm{Poisson}}(nk_n \lambda_n) \leq k_n\right)\notag \\[5pt] &\leq n \mathbb{P}\!\left( {\mathrm{Poisson}}(nk_n \lambda_n) \leq nk_n \lambda_n +k_n- nk_n \lambda_n\right)\notag\\[5pt] &\leq n \mathbb{P}\!\left( {\mathrm{Poisson}}(nk_n \lambda_n) \leq nk_n \lambda_n -k_n\delta_n\right)\notag\\[5pt] &\leq n\exp\!\left(\!-\!\frac{k_n^2\delta_n^2}{4nk_n\lambda_n}\right) \leq n\exp\!\left(\!-\!\tfrac{1}{8}k_n\delta_n^2\right)= n\exp\!\left(\!-\!\tfrac{1}{8}k_n^{\alpha}\right). \end{align}
\begin{align}1-\mathbb{P}(E_n^{\lambda_n})&\leq n \mathbb{P}\!\left( {\mathrm{Poisson}}(nk_n \lambda_n) \leq k_n\right)\notag \\[5pt] &\leq n \mathbb{P}\!\left( {\mathrm{Poisson}}(nk_n \lambda_n) \leq nk_n \lambda_n +k_n- nk_n \lambda_n\right)\notag\\[5pt] &\leq n \mathbb{P}\!\left( {\mathrm{Poisson}}(nk_n \lambda_n) \leq nk_n \lambda_n -k_n\delta_n\right)\notag\\[5pt] &\leq n\exp\!\left(\!-\!\frac{k_n^2\delta_n^2}{4nk_n\lambda_n}\right) \leq n\exp\!\left(\!-\!\tfrac{1}{8}k_n\delta_n^2\right)= n\exp\!\left(\!-\!\tfrac{1}{8}k_n^{\alpha}\right). \end{align}
At the last line we used Lemma 15. The latter probability tends to 0 as
![]() $(k_n)$
is large.
$(k_n)$
is large.
Lemma 13. Random sets
![]() $S_{k_n;n}$
and
$S_{k_n;n}$
and
![]() $\Pi_{nk_n,n}^{(\lambda_n)} $
can be defined on the same probability space in such a way that
$\Pi_{nk_n,n}^{(\lambda_n)} $
can be defined on the same probability space in such a way that
Proof of Lemma
13. Draw a sample of
![]() $\Pi_{nk_n,n}^{(\lambda_n)} $
and let
$\Pi_{nk_n,n}^{(\lambda_n)} $
and let
![]() $\tilde{\Pi}_{nk_n,n}^{(\lambda_n)} $
be the subset of
$\tilde{\Pi}_{nk_n,n}^{(\lambda_n)} $
be the subset of
![]() $\Pi_{nk_n,n}^{(\lambda_n)}$
obtained by keeping only the
$\Pi_{nk_n,n}^{(\lambda_n)}$
obtained by keeping only the
![]() $k_n$
leftmost points in each row. If
$k_n$
leftmost points in each row. If
![]() $E_n^{\lambda_n}$
occurs then the relative orders of points in
$E_n^{\lambda_n}$
occurs then the relative orders of points in
![]() $\tilde{\Pi}_{nk_n,n}^{(\lambda_n)}$
corresponds to a uniform
$\tilde{\Pi}_{nk_n,n}^{(\lambda_n)}$
corresponds to a uniform
![]() $k_n$
-multiset permutation. If
$k_n$
-multiset permutation. If
![]() $E_n^{\lambda_n}$
does not hold we bound
$E_n^{\lambda_n}$
does not hold we bound
![]() $\mathcal{L}_{\leq }(S_{k_n;n})$
by the worst case
$\mathcal{L}_{\leq }(S_{k_n;n})$
by the worst case
![]() $nk_n$
.
$nk_n$
.
Taking expectations in (33) and using the upper bound (15) yields
hence the upper bound in (2).
Proof of the lower bound of (2) for large
![]() $(k_n)$
. Choose now
$(k_n)$
. Choose now
![]() $\lambda_n=({1}/{n})(1-\delta_n)$
with
$\lambda_n=({1}/{n})(1-\delta_n)$
with
![]() $\delta_n=k_n^{-(1-\alpha)/2}$
. Let
$\delta_n=k_n^{-(1-\alpha)/2}$
. Let
![]() $F_n$
be the event
$F_n$
be the event
The event
![]() $F_n^{\lambda_n}$
occurs with large probability. Indeed
$F_n^{\lambda_n}$
occurs with large probability. Indeed
which tends to zero. Random sets
![]() $S_{k_n;n}$
and
$S_{k_n;n}$
and
![]() $\Pi_{nk_n,n}^{(\lambda_n)}$
can be defined on the same probability space in such a way that
$\Pi_{nk_n,n}^{(\lambda_n)}$
can be defined on the same probability space in such a way that
Therefore
 \begin{multline}\mathbb{P}\!\left(\mathcal{L}_{\leq }(S_{k_n;n}) \lt (2\sqrt{nk_n(1-\delta_n)}+ k_n(1-\delta_n))(1-{\varepsilon})\right) \leq \\[5pt] \mathbb{P}\!\left( \mathcal{L}_{\leq }(\Pi_{nk_n,n}^{(\lambda_n)})\lt (2\sqrt{nk_n(1-\delta_n)}+ k_n(1-\delta_n))(1-{\varepsilon})\right)+ \mathbb{P}\!\left(\text{not }F_n^{\lambda_n}\right).\notag\end{multline}
\begin{multline}\mathbb{P}\!\left(\mathcal{L}_{\leq }(S_{k_n;n}) \lt (2\sqrt{nk_n(1-\delta_n)}+ k_n(1-\delta_n))(1-{\varepsilon})\right) \leq \\[5pt] \mathbb{P}\!\left( \mathcal{L}_{\leq }(\Pi_{nk_n,n}^{(\lambda_n)})\lt (2\sqrt{nk_n(1-\delta_n)}+ k_n(1-\delta_n))(1-{\varepsilon})\right)+ \mathbb{P}\!\left(\text{not }F_n^{\lambda_n}\right).\notag\end{multline}
and we conclude with (19).
5·2. The gap between small and large
 $(k_n)$
: conclusion of the proof of Theorem 2
$(k_n)$
: conclusion of the proof of Theorem 2
After I circulated a preliminary version of this paper, Valentin Féray came up with a simple argument for bridging the gap between small and large
![]() $(k_n)$
. This allows to prove Theorem 2 for an arbitrary sequence
$(k_n)$
. This allows to prove Theorem 2 for an arbitrary sequence
![]() $(k_n)$
, I reproduce his argument here with his permission.
$(k_n)$
, I reproduce his argument here with his permission.
Lemma 14. Let n, k, A be positive integers. Two random uniform multiset permutations
![]() $\widetilde{S}_{kA ;\lfloor n/A\rfloor}$
and
$\widetilde{S}_{kA ;\lfloor n/A\rfloor}$
and
![]() $S_{k;n}$
can be built on the same probability space in such a way that
$S_{k;n}$
can be built on the same probability space in such a way that
Proof of Lemma
14. Draw
![]() $S_{k;n}$
uniformly at random, the idea is to group all points of
$S_{k;n}$
uniformly at random, the idea is to group all points of
![]() $S_{k;n}$
whose height is between 1 and A, to group all points whose height is between
$S_{k;n}$
whose height is between 1 and A, to group all points whose height is between
![]() $A+1$
and 2A, and so on.
$A+1$
and 2A, and so on.
Formally, denote by
![]() $1\leq i_1\lt i_2\lt \dots\lt i_{kA\lfloor n/A\rfloor}$
the indices such that
$1\leq i_1\lt i_2\lt \dots\lt i_{kA\lfloor n/A\rfloor}$
the indices such that
![]() $1\leq i_\ell \leq \lfloor n/A\rfloor$
for every
$1\leq i_\ell \leq \lfloor n/A\rfloor$
for every
![]() $\ell$
(see Fig. 6). For
$\ell$
(see Fig. 6). For
![]() $1\leq \ell \leq kA \lfloor n/A\rfloor$
put
$1\leq \ell \leq kA \lfloor n/A\rfloor$
put

Fig. 6. Illustration of the notation of Lemma 14. Top: the multiset permutation
![]() $S_{k;n}$
. Bottom: the corresponding
$S_{k;n}$
. Bottom: the corresponding
![]() $\widetilde{S}$
. The longest non-decreasing subsequence in
$\widetilde{S}$
. The longest non-decreasing subsequence in
![]() $S_{k;n}$
(circled points) is mapped onto a non-decreasing subsequence in
$S_{k;n}$
(circled points) is mapped onto a non-decreasing subsequence in
![]() $\widetilde{S}$
, except one point with height
$\widetilde{S}$
, except one point with height
![]() $\gt A\lfloor n/A\rfloor$
.
$\gt A\lfloor n/A\rfloor$
.
The word
![]() $\widetilde{S}$
is a uniform kA-multiset permutation of size
$\widetilde{S}$
is a uniform kA-multiset permutation of size
![]() $ \lfloor n/A\rfloor$
. A longest non-decreasing subsequence in S is mapped onto a non-decreasing subsequence in
$ \lfloor n/A\rfloor$
. A longest non-decreasing subsequence in S is mapped onto a non-decreasing subsequence in
![]() $\widetilde{S}$
, except maybe some points with height
$\widetilde{S}$
, except maybe some points with height
![]() $\gt A\lfloor n/A\rfloor$
(there are no more than kA such points). This shows the Lemma.
$\gt A\lfloor n/A\rfloor$
(there are no more than kA such points). This shows the Lemma.
We conclude the proof of Theorem 2 by an estimation of
![]() $\mathbb{E}[\mathcal{L}_{\leq }\!\left(S_{k_n ; n}\right) ]$
in the case where there are infinitely many
$\mathbb{E}[\mathcal{L}_{\leq }\!\left(S_{k_n ; n}\right) ]$
in the case where there are infinitely many
![]() $k_n$
’s such that, say,
$k_n$
’s such that, say,
![]() $(\!\log n)^{3/4}\leq k_n \leq (\!\log n)^{5/4}$
. For the lower bound the job is already done by Theorem 1 since
$(\!\log n)^{3/4}\leq k_n \leq (\!\log n)^{5/4}$
. For the lower bound the job is already done by Theorem 1 since
which is of course also
![]() $2\sqrt{nk_n}+\mathrm{o}(nk_n)$
for this range of
$2\sqrt{nk_n}+\mathrm{o}(nk_n)$
for this range of
![]() $(k_n)$
. For the upper bound take
$(k_n)$
. For the upper bound take
![]() $A=\lfloor \log n\rfloor$
in Lemma 14:
$A=\lfloor \log n\rfloor$
in Lemma 14:
and we can apply the large case since
Thus the right-hand side of (34) is also
![]() $2\sqrt{nk_n}+\mathrm{o}(\sqrt{nk_n})$
.
$2\sqrt{nk_n}+\mathrm{o}(\sqrt{nk_n})$
.
6. Conclusion: Proof of Proposition 3
In this short section we give the arguments needed to enhance estimates in expectation into convergences in probability. We have to prove that for every
![]() ${\varepsilon}\gt 0$
:
${\varepsilon}\gt 0$
:
 \begin{align*}\mathbb{P}\!\left(L_{\lt }\!\left(S_{k_n ; n}\right) \gt (2\sqrt{nk_n}-k_n)(1+{\varepsilon})\right)&\to 0,\\[5pt] \mathbb{P}\!\left(L_{\lt }\!\left(S_{k_n ; n}\right) \lt (2\sqrt{nk_n}-k_n)(1-{\varepsilon})\right)&\to 0,\\[5pt] \mathbb{P}\!\left(L_{\leq }\!\left(S_{k_n ; n}\right) \gt (2\sqrt{nk_n}+k_n)(1+{\varepsilon})\right)&\to 0,\\[5pt] \mathbb{P}\!\left(L_{\leq }\!\left(S_{k_n ; n}\right) \lt (2\sqrt{nk_n}+k_n)(1-{\varepsilon})\right)&\to 0\end{align*}
\begin{align*}\mathbb{P}\!\left(L_{\lt }\!\left(S_{k_n ; n}\right) \gt (2\sqrt{nk_n}-k_n)(1+{\varepsilon})\right)&\to 0,\\[5pt] \mathbb{P}\!\left(L_{\lt }\!\left(S_{k_n ; n}\right) \lt (2\sqrt{nk_n}-k_n)(1-{\varepsilon})\right)&\to 0,\\[5pt] \mathbb{P}\!\left(L_{\leq }\!\left(S_{k_n ; n}\right) \gt (2\sqrt{nk_n}+k_n)(1+{\varepsilon})\right)&\to 0,\\[5pt] \mathbb{P}\!\left(L_{\leq }\!\left(S_{k_n ; n}\right) \lt (2\sqrt{nk_n}+k_n)(1-{\varepsilon})\right)&\to 0\end{align*}
We only write the details for the first case, as the three other ones are almost identical.
The case where
![]() $(k_n)$
is small has been proved in Section 2 so it remains to prove the case where
$(k_n)$
is small has been proved in Section 2 so it remains to prove the case where
![]() $(k_n)$
is large. We reuse the event
$(k_n)$
is large. We reuse the event
![]() $E_n^{\lambda_n}$
introduced in Section 5·1.
$E_n^{\lambda_n}$
introduced in Section 5·1.
 \begin{align*}\mathbb{P}\big(L_{\lt }\!\left(S_{k_n ; n}\right)&\gt (2\sqrt{nk_n}-k_n)(1+{\varepsilon}) \big)\\[5pt] & \leq \mathbb{P}\!\left(E_n^{\lambda_n} \text{ does not occur}\right)\\[5pt] &\quad + \mathbb{P}\!\left(\mathcal{L}_{\lt }\!\left(\Pi^{(\lambda_n)}_{nk_n,n}\right)\gt (1+\delta_n)(2\sqrt{nk_n}-k_n)\frac{1+{\varepsilon}}{1+\delta_n}\right)\\[5pt] &\leq n\exp\!\left(\!-\!\tfrac{1}{8}k_n^{\alpha}\right) \qquad \text{(recall (32))}\\[5pt] &\quad + \mathbb{P}\!\left(\mathcal{L}_{\lt }\!\left(\Pi^{(\lambda_n)}_{nk_n,n}\right)\gt (2\sqrt{nk_n(1+\delta_n)}-k_n(1+\delta_n))\frac{1+{\varepsilon}}{1+\delta_n}\right)\\[5pt] & \leq n\exp\!\left(\!-\!\tfrac{1}{8}k_n^{\alpha}\right) + \exp\!(\!-\!\tilde{g}(\varepsilon/2)(\sqrt{nk_n}-k_n)),\end{align*}
\begin{align*}\mathbb{P}\big(L_{\lt }\!\left(S_{k_n ; n}\right)&\gt (2\sqrt{nk_n}-k_n)(1+{\varepsilon}) \big)\\[5pt] & \leq \mathbb{P}\!\left(E_n^{\lambda_n} \text{ does not occur}\right)\\[5pt] &\quad + \mathbb{P}\!\left(\mathcal{L}_{\lt }\!\left(\Pi^{(\lambda_n)}_{nk_n,n}\right)\gt (1+\delta_n)(2\sqrt{nk_n}-k_n)\frac{1+{\varepsilon}}{1+\delta_n}\right)\\[5pt] &\leq n\exp\!\left(\!-\!\tfrac{1}{8}k_n^{\alpha}\right) \qquad \text{(recall (32))}\\[5pt] &\quad + \mathbb{P}\!\left(\mathcal{L}_{\lt }\!\left(\Pi^{(\lambda_n)}_{nk_n,n}\right)\gt (2\sqrt{nk_n(1+\delta_n)}-k_n(1+\delta_n))\frac{1+{\varepsilon}}{1+\delta_n}\right)\\[5pt] & \leq n\exp\!\left(\!-\!\tfrac{1}{8}k_n^{\alpha}\right) + \exp\!(\!-\!\tilde{g}(\varepsilon/2)(\sqrt{nk_n}-k_n)),\end{align*}
for large enough n and for some positive
![]() $\tilde{g}$
, using (16). This tends to zero as desired.
$\tilde{g}$
, using (16). This tends to zero as desired.
The lower bound for
![]() $L_{\lt }(S_{k_n ; n})$
is proved in the same way. For the convergence of
$L_{\lt }(S_{k_n ; n})$
is proved in the same way. For the convergence of
![]() $L_{\leq }(S_{k_n ; n})$
we reuse the event
$L_{\leq }(S_{k_n ; n})$
we reuse the event
![]() $F_n^{\lambda_n}$
with
$F_n^{\lambda_n}$
with
![]() $\lambda_n=({1}/{n})(1+\log(n))$
.
$\lambda_n=({1}/{n})(1+\log(n))$
.
A. Useful tail inequalities
We collect here for convenience some (non-optimal) tail inequalities.
Lemma 15 (See [
Reference Janson, Łuczak and RucinskiJŁR00
, chapter 2]). Let
![]() ${\mathrm{Poisson}}(\lambda)$
be a Poisson random variable with mean
${\mathrm{Poisson}}(\lambda)$
be a Poisson random variable with mean
![]() $\lambda$
. For every
$\lambda$
. For every
![]() $A\gt 0$
$A\gt 0$
Lemma 16 ([
Reference Janson, Łuczak and RucinskiJŁR00
, theorem 2·1]). Let
![]() ${\mathrm{Binomial}} (n,p)$
be a Binomial random variable with parameters (n,p). For
${\mathrm{Binomial}} (n,p)$
be a Binomial random variable with parameters (n,p). For
![]() $0\lt \varepsilon\lt 1$
,
$0\lt \varepsilon\lt 1$
,
 \begin{align*}\mathbb{P}( {\mathrm{Binomial}} (n,p)\leq np-\varepsilon np) &\leq \exp\!\left(\!-{\varepsilon}^2 np/2\right),\\[5pt] \mathbb{P}( {\mathrm{Binomial}} (n,p) \geq np + \varepsilon np) &\leq \exp\!\left(\!-{\varepsilon}^2 np/3\right).\end{align*}
\begin{align*}\mathbb{P}( {\mathrm{Binomial}} (n,p)\leq np-\varepsilon np) &\leq \exp\!\left(\!-{\varepsilon}^2 np/2\right),\\[5pt] \mathbb{P}( {\mathrm{Binomial}} (n,p) \geq np + \varepsilon np) &\leq \exp\!\left(\!-{\varepsilon}^2 np/3\right).\end{align*}
Lemma 17. Fix
![]() $\alpha\in(0,1)$
and let
$\alpha\in(0,1)$
and let
![]() $\mathcal{G}_1^{(\alpha)}, \dots, \mathcal{G}_k^{(\alpha)}$
be i.i.d. random variables with distribution
$\mathcal{G}_1^{(\alpha)}, \dots, \mathcal{G}_k^{(\alpha)}$
be i.i.d. random variables with distribution
![]() $\mathrm{Geometric}_{\geq 0}(1-\alpha)$
. Then
$\mathrm{Geometric}_{\geq 0}(1-\alpha)$
. Then
![]() $\mathbb{E}[\mathcal{G}_1^{(\alpha)}]={\alpha}/({1-\alpha})$
and for every
$\mathbb{E}[\mathcal{G}_1^{(\alpha)}]={\alpha}/({1-\alpha})$
and for every
![]() $0\lt \varepsilon\lt 1$
,
$0\lt \varepsilon\lt 1$
,
 \begin{align*}\mathbb{P}\!\left( \mathcal{G}_1^{(\alpha)}+\dots + \mathcal{G}_k^{(\alpha)}\geq (1+{\varepsilon})k\frac{\alpha}{1-\alpha}\right) &\leq \exp\!\left(\!-{\varepsilon}^2 k \alpha/20 \right),\\[5pt] \mathbb{P}\!\left( \mathcal{G}_1^{(\alpha)}+\dots + \mathcal{G}_k^{(\alpha)}\leq (1-{\varepsilon})k\frac{\alpha}{1-\alpha}\right) &\leq \exp\!\left(\!-{\varepsilon}^2 k \alpha/20 \right).\end{align*}
\begin{align*}\mathbb{P}\!\left( \mathcal{G}_1^{(\alpha)}+\dots + \mathcal{G}_k^{(\alpha)}\geq (1+{\varepsilon})k\frac{\alpha}{1-\alpha}\right) &\leq \exp\!\left(\!-{\varepsilon}^2 k \alpha/20 \right),\\[5pt] \mathbb{P}\!\left( \mathcal{G}_1^{(\alpha)}+\dots + \mathcal{G}_k^{(\alpha)}\leq (1-{\varepsilon})k\frac{\alpha}{1-\alpha}\right) &\leq \exp\!\left(\!-{\varepsilon}^2 k \alpha/20 \right).\end{align*}
Proof of Lemma 17. We will use the two inequalities:
Fix
![]() $\lambda$
such that
$\lambda$
such that
![]() $|\lambda| \lt \min\left\{1,(1-\alpha)/4\alpha\right\}$
so that
$|\lambda| \lt \min\left\{1,(1-\alpha)/4\alpha\right\}$
so that
![]() $({\alpha}/({1-\alpha})) |\lambda+\lambda^2|\lt 1/2$
:
$({\alpha}/({1-\alpha})) |\lambda+\lambda^2|\lt 1/2$
:
 \begin{align*}\mathbb{E}[e^{\lambda(\mathcal{G}_1^{(\alpha)}-\frac{\alpha}{1-\alpha})} ]&=\frac{(1-\alpha) }{1-\alpha e^{\lambda}}e^{-\lambda \frac{\alpha}{1-\alpha}}=\frac{1 }{1-\frac{\alpha}{1-\alpha} (e^{\lambda}-1)}e^{-\lambda \frac{\alpha}{1-\alpha}}\\[5pt] &\leq \frac{1 }{1-\frac{\alpha}{1-\alpha} (\lambda+\lambda^2)}e^{-\lambda \frac{\alpha}{1-\alpha}}\\[5pt] &\leq \exp\!\left(\frac{\alpha}{1-\alpha} (\lambda+\lambda^2)+\!\left(\frac{\alpha}{1-\alpha}\right)^2 (\lambda+\lambda^2)^2 -\lambda \frac{\alpha}{1-\alpha}\right)\\[5pt] &\leq \exp\!\left(\frac{\alpha}{(1-\alpha)^2}\lambda^2 \!\left(2+\lambda^2+2\lambda\right)\right)\leq \exp\!\left( 5\lambda^2 \frac{\alpha}{(1-\alpha)^2}\right).\end{align*}
\begin{align*}\mathbb{E}[e^{\lambda(\mathcal{G}_1^{(\alpha)}-\frac{\alpha}{1-\alpha})} ]&=\frac{(1-\alpha) }{1-\alpha e^{\lambda}}e^{-\lambda \frac{\alpha}{1-\alpha}}=\frac{1 }{1-\frac{\alpha}{1-\alpha} (e^{\lambda}-1)}e^{-\lambda \frac{\alpha}{1-\alpha}}\\[5pt] &\leq \frac{1 }{1-\frac{\alpha}{1-\alpha} (\lambda+\lambda^2)}e^{-\lambda \frac{\alpha}{1-\alpha}}\\[5pt] &\leq \exp\!\left(\frac{\alpha}{1-\alpha} (\lambda+\lambda^2)+\!\left(\frac{\alpha}{1-\alpha}\right)^2 (\lambda+\lambda^2)^2 -\lambda \frac{\alpha}{1-\alpha}\right)\\[5pt] &\leq \exp\!\left(\frac{\alpha}{(1-\alpha)^2}\lambda^2 \!\left(2+\lambda^2+2\lambda\right)\right)\leq \exp\!\left( 5\lambda^2 \frac{\alpha}{(1-\alpha)^2}\right).\end{align*}
Thus, for every
![]() $|\lambda|\lt {1}/{\beta}\;:\!=\;\min\left\{1,(1-\alpha)/4\alpha\right\}$
it holds that
$|\lambda|\lt {1}/{\beta}\;:\!=\;\min\left\{1,(1-\alpha)/4\alpha\right\}$
it holds that
![]() $\mathbb{E}[e^{\lambda(\sum_{i=1}^k\mathcal{G}_i^{(\alpha)}-k\frac{\alpha}{1-\alpha})} ]\leq \exp\!\left({\nu^2\lambda^2}/{2}\right)$
where
$\mathbb{E}[e^{\lambda(\sum_{i=1}^k\mathcal{G}_i^{(\alpha)}-k\frac{\alpha}{1-\alpha})} ]\leq \exp\!\left({\nu^2\lambda^2}/{2}\right)$
where
![]() $\nu^2\;:\!=\;10k\alpha/(1-\alpha)^2$
.
$\nu^2\;:\!=\;10k\alpha/(1-\alpha)^2$
.
This says that for every
![]() $k\geq 1$
the random variable
$k\geq 1$
the random variable
![]() $\mathcal{G}_1^{(\alpha)}+\dots + \mathcal{G}_k^{(\alpha)}$
is subexponential and the Chernov method applies (use e.g. [
Reference WainwrightWai19
, proposition 2·9] with
$\mathcal{G}_1^{(\alpha)}+\dots + \mathcal{G}_k^{(\alpha)}$
is subexponential and the Chernov method applies (use e.g. [
Reference WainwrightWai19
, proposition 2·9] with
![]() $t={\varepsilon} k\alpha/(1-\alpha)$
):
$t={\varepsilon} k\alpha/(1-\alpha)$
):
 \begin{align*}& \mathbb{P}\!\left( \mathcal{G}_1^{(\alpha)}+\dots + \mathcal{G}_k^{(\alpha)}\geq (1+{\varepsilon})k\frac{\alpha}{1-\alpha}\right)\\[5pt] &\leq \exp\!\left(\!-\!\frac{t^2}{2\nu^2} \right)=\exp\!\left(\!-{\varepsilon}^2 k^2 \frac{\alpha^2}{(1-\alpha)^2}\times \frac{(1-\alpha)^2}{2\times 10 k\alpha} \right)\\[5pt] &=\exp\!\left(\!-{\varepsilon}^2 k \alpha/20 \right),\end{align*}
\begin{align*}& \mathbb{P}\!\left( \mathcal{G}_1^{(\alpha)}+\dots + \mathcal{G}_k^{(\alpha)}\geq (1+{\varepsilon})k\frac{\alpha}{1-\alpha}\right)\\[5pt] &\leq \exp\!\left(\!-\!\frac{t^2}{2\nu^2} \right)=\exp\!\left(\!-{\varepsilon}^2 k^2 \frac{\alpha^2}{(1-\alpha)^2}\times \frac{(1-\alpha)^2}{2\times 10 k\alpha} \right)\\[5pt] &=\exp\!\left(\!-{\varepsilon}^2 k \alpha/20 \right),\end{align*}
as long as
which is always the case if
![]() ${\varepsilon} \lt 1$
. The similar inequality holds for the left-tail bound (see [
Reference WainwrightWai19
, proposition 2·9] again).
${\varepsilon} \lt 1$
. The similar inequality holds for the left-tail bound (see [
Reference WainwrightWai19
, proposition 2·9] again).
B. An invariance property for the M/M/1 queue
To conclude we state and prove the very simple property of the recurrent M/M/1 queue which allows to prove stationarity in Lemma 6. It is very close to Burke’s property of the discrete HAD process [ Reference Ferrari and MartinFM06 ].
Let
![]() $\beta\gt \lambda\gt 0$
be fixed parameters. Consider two independent homogeneous Poisson Point Process (PPP)
$\beta\gt \lambda\gt 0$
be fixed parameters. Consider two independent homogeneous Poisson Point Process (PPP)
![]() $\Pi_\nearrow,\Pi_\searrow$
over
$\Pi_\nearrow,\Pi_\searrow$
over
![]() $(0,+\infty)$
with respective intensities
$(0,+\infty)$
with respective intensities
![]() $\lambda,\beta$
. Let
$\lambda,\beta$
. Let
![]() $(H_y)_{y\geq 0}$
be the queue whose ’+1’ steps (customer arrivals) are given by
$(H_y)_{y\geq 0}$
be the queue whose ’+1’ steps (customer arrivals) are given by
![]() $\Pi_\nearrow$
and ’-1’ steps (service times) are given by
$\Pi_\nearrow$
and ’-1’ steps (service times) are given by
![]() $\Pi_\searrow$
and whose initial distribution
$\Pi_\searrow$
and whose initial distribution
![]() $H_0$
is drawn (independently from
$H_0$
is drawn (independently from
![]() $\Pi_\nearrow,\Pi_\searrow$
) according to a
$\Pi_\nearrow,\Pi_\searrow$
) according to a
![]() $\mathrm{Geometric}_{\geq 0}(1-\beta^\star)$
with
$\mathrm{Geometric}_{\geq 0}(1-\beta^\star)$
with
![]() $\beta^\star=\lambda/\beta$
.
$\beta^\star=\lambda/\beta$
.
Let
![]() $\Pi_0$
be the point process given by unused service times:
$\Pi_0$
be the point process given by unused service times:
Lemma 18. The process
![]() $\overline{\Pi}\;:\!=\;\Pi_\nearrow\cup \Pi_0$
is a homogeneous PPP with intensity
$\overline{\Pi}\;:\!=\;\Pi_\nearrow\cup \Pi_0$
is a homogeneous PPP with intensity
![]() $\beta$
.
$\beta$
.
Proof. (The reader is invited to look at Fig. B1 for notation.)
The point process
![]() $\Pi_\nearrow\cup \Pi_\searrow$
is a homogeneous PPP with intensity
$\Pi_\nearrow\cup \Pi_\searrow$
is a homogeneous PPP with intensity
![]() $\lambda+\beta$
, independent from
$\lambda+\beta$
, independent from
![]() $H_0$
. We claim that
$H_0$
. We claim that
![]() $\overline{\Pi}$
is a subset of
$\overline{\Pi}$
is a subset of
![]() $\Pi_\nearrow\cup \Pi_\searrow$
where each point in
$\Pi_\nearrow\cup \Pi_\searrow$
where each point in
![]() $\Pi_\nearrow\cup \Pi_\searrow$
is taken independently with probability
$\Pi_\nearrow\cup \Pi_\searrow$
is taken independently with probability
![]() $\beta/(\lambda+\beta)$
, it is therefore a homogeneous PPP with intensity
$\beta/(\lambda+\beta)$
, it is therefore a homogeneous PPP with intensity
![]() $\beta$
.
$\beta$
.
We need a few notation in order to prove the claim. Set
![]() $P_0=0$
and for
$P_0=0$
and for
![]() $i\geq 1$
let
$i\geq 1$
let
![]() $P_i$
be the ith point of
$P_i$
be the ith point of
![]() $\Pi_\nearrow\cup \Pi_\searrow$
and let
$\Pi_\nearrow\cup \Pi_\searrow$
and let
![]() $(\tilde{H}_i)_{i\geq 0}$
be the discrete-time embedded chain associated to H, i.e.
$(\tilde{H}_i)_{i\geq 0}$
be the discrete-time embedded chain associated to H, i.e.
![]() $\tilde{H}_i=H_{P_i}$
for every i.
$\tilde{H}_i=H_{P_i}$
for every i.
We will prove by induction that for every
![]() $i\geq 1$
:
$i\geq 1$
:
-
the points
 $P_i$
belongs to
$P_i$
belongs to
 $\overline{\Pi}$
with probability
$\overline{\Pi}$
with probability
 $\beta/(\lambda+\beta)$
independently from the events
$\beta/(\lambda+\beta)$
independently from the events
 $\{P_1\in \overline{\Pi}\},\dots,\{P_{i-1}\in\overline{\Pi}\}$
;
$\{P_1\in \overline{\Pi}\},\dots,\{P_{i-1}\in\overline{\Pi}\}$
; -
 $\tilde{H}_i$
is independent from
$\tilde{H}_i$
is independent from
 $\{P_1\in \overline{\Pi}\},\dots,\{P_{i}\in\overline{\Pi}\}$
and is a
$\{P_1\in \overline{\Pi}\},\dots,\{P_{i}\in\overline{\Pi}\}$
and is a
 $\mathrm{Geometric}_{\geq 0}(1-\beta^\star)$
.
$\mathrm{Geometric}_{\geq 0}(1-\beta^\star)$
.
This implies the claim and proves the Lemma. For the base case:
 \begin{align*}\mathbb{P}(P_1\in \overline{\Pi},\tilde{H}_1=k)&= \mathbb{P}(P_1\in \Pi_\nearrow, \tilde{H}_0=k-1 )\textbf{1}_{k\geq 1}+\mathbb{P}(P_1\in \Pi_\searrow,\tilde{H}_0=0)\textbf{1}_{k=0},\\[5pt] &=\frac{\lambda}{\lambda+\beta}\times (1-\beta^\star)(\beta^\star)^{k-1}\textbf{1}_{k\geq 1}+ \frac{\beta}{\lambda+\beta}\times (1-\beta^\star)\textbf{1}_{k=0},\\[5pt] &=\frac{\beta}{\lambda+\beta}\times (1-\beta^\star)(\beta^\star)^{k}\qquad \text{(recall $\beta\beta^\star=\lambda$).}\end{align*}
\begin{align*}\mathbb{P}(P_1\in \overline{\Pi},\tilde{H}_1=k)&= \mathbb{P}(P_1\in \Pi_\nearrow, \tilde{H}_0=k-1 )\textbf{1}_{k\geq 1}+\mathbb{P}(P_1\in \Pi_\searrow,\tilde{H}_0=0)\textbf{1}_{k=0},\\[5pt] &=\frac{\lambda}{\lambda+\beta}\times (1-\beta^\star)(\beta^\star)^{k-1}\textbf{1}_{k\geq 1}+ \frac{\beta}{\lambda+\beta}\times (1-\beta^\star)\textbf{1}_{k=0},\\[5pt] &=\frac{\beta}{\lambda+\beta}\times (1-\beta^\star)(\beta^\star)^{k}\qquad \text{(recall $\beta\beta^\star=\lambda$).}\end{align*}
More generally let
![]() $E_j$
be one of the two events
$E_j$
be one of the two events
![]() $P_j\in \overline{\Pi}/P_j\notin \overline{\Pi}$
:
$P_j\in \overline{\Pi}/P_j\notin \overline{\Pi}$
:
 \begin{align*}\mathbb{P}(P_i\in \overline{\Pi},\tilde{H}_i=k\ |\ E_1,\dots,E_{i-1})= &\ \mathbb{P}(P_i\in \Pi_\nearrow, \tilde{H}_{i-1}=k-1 \ |\ E_1,\dots,E_{i-1} )\textbf{1}_{k\geq 1}\\[5pt] +&\ \mathbb{P}(P_i\in \Pi_\searrow,\tilde{H}_{i-1}=0\ |\ E_1,\dots,E_{i-1})\textbf{1}_{k=0},\\[5pt] =&\ \mathbb{P}(P_i\in \Pi_\nearrow, \tilde{H}_{i-1}=k-1)\textbf{1}_{k\geq 1}\\[5pt] +&\ \mathbb{P}(P_i\in \Pi_\searrow,\tilde{H}_{i-1}=0)\textbf{1}_{k=0},\quad \text{(by induction hypothesis).}\\[5pt] =&\ \frac{\beta}{\lambda+\beta}\times (1-\beta^\star)(\beta^\star)^{k}.\end{align*}
\begin{align*}\mathbb{P}(P_i\in \overline{\Pi},\tilde{H}_i=k\ |\ E_1,\dots,E_{i-1})= &\ \mathbb{P}(P_i\in \Pi_\nearrow, \tilde{H}_{i-1}=k-1 \ |\ E_1,\dots,E_{i-1} )\textbf{1}_{k\geq 1}\\[5pt] +&\ \mathbb{P}(P_i\in \Pi_\searrow,\tilde{H}_{i-1}=0\ |\ E_1,\dots,E_{i-1})\textbf{1}_{k=0},\\[5pt] =&\ \mathbb{P}(P_i\in \Pi_\nearrow, \tilde{H}_{i-1}=k-1)\textbf{1}_{k\geq 1}\\[5pt] +&\ \mathbb{P}(P_i\in \Pi_\searrow,\tilde{H}_{i-1}=0)\textbf{1}_{k=0},\quad \text{(by induction hypothesis).}\\[5pt] =&\ \frac{\beta}{\lambda+\beta}\times (1-\beta^\star)(\beta^\star)^{k}.\end{align*}

Fig. B1. Notation of Lemma 18. Points of
![]() $\overline{\Pi}$
are depicted with
$\overline{\Pi}$
are depicted with
![]() $\star$
’s.
$\star$
’s.
Acknowledgements
This work started as a collaboration with Anne–Laure Basdevant, I would like to thank her very warmly. I am also extremely indebted to Valentin Féray for Lemma 14 and for having enlightened me on the links with [ Reference BianeBia01 ]. Finally, thanks to the authors of [ Reference Clifton, Deb, Huang, Spiro and YooCDH+22 ] for their stimulating paper and to anonymous referees for their careful readings.